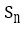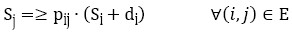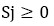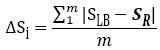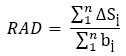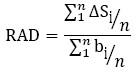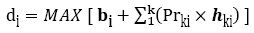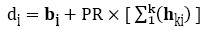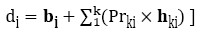I. Introduction
The Stochastic Project Scheduling Problem (SPSP) is a type of mathematical optimization problem that incorporates stochastic parameters within the decision process. The activities duration has been one of the main random parameters considered in optimization models of this type.
The study of the scheduled activities of a project with random duration of activities begins with the Program Evaluation and Review Techniques (PERT) released during the end of the 1950s [1]. From that moment, the methodological proposals to deal with the PSP are diverse. In 2000, Pontrandolfo [2] proposed an algorithm based on a set of equations to compute the total duration of a project, taking as input data the mean and the variance of each activity, and the probability of occurrence of each path or possible route of the project. Then in 2005, Lee [3] developed a software support on Monte Carlo simulation techniques, to estimate the probability of completing a project by a deadline.
The critical chain method was designed in 1997 by Goldratt [4], in order to treat the uncertainty in the scheduling of projects. This method inserts extra time (buffers) in some strategic points within the project network. Based on Goldratt, Van De Vonder, Demeulemeester, Herroelen, and Leus [5] evaluated whether it was better to create feed and project buffers or to insert scattered buffers along the project baseline. In 2009, Rezaie, Manouchehrabadi, and Shirkouhi [6] defined the buffer size of the project from the coefficient of variation associated with the activities duration. Subsequently, Bie, Cui, and Zhang [7] determined the buffer size taking into account the degree of dependence and the dependency factor among the activities of the project.
The PSP with random duration of activities has also been solved through Genetic Algorithms. In 2005, a genetic algorithm within a simulation process was proposed by Hua Ke and Baoding Liu [8]. This procedure was applied to three different models: the expected cost model, which minimizes the expected cost taking into account the time constraints of the project, the α-cost model where the cost is minimized and the contraints are met with at least some given confidence level and finally the probability maximization model, where the probability that the total cost does not exceed the budget is maximized and the probability of finishing the project before the due date should be larger than a predetermined confidence level. In 2012, Ke, Ma, and Chen [9] proposed a method based on a genetic algorithm, which determines the critical path of the project bearing in mind the appearance of random delays.
Exact methods of solution have been applied by other authors: Gutjahr, Strauss, and Wagner [10] developed a variant of the Branch and Bound algorithm focused on the selection of strategies to reduce the activity durations. Jaskowski and Biruk [11] presented a robust methodology based on both simulation process and mixed integer linear programming model, to determine buffer size and the appropiate location of the buffers within the project linebase.
On the other hand, in the scientific literature, some procedures have been specially designed to solve the PSP with random duration of activities: Valadares-Tavares, Antunes-Ferreira, and Silva-Coelho [12] studied the project’s risks from an uncertainty function that depends on both cost and activities duration. Mizuyama [13] formulated the PSP as a probabilistic decision-making process in multiple stages. Mitchell and Klastorin [14] designed an algorithm to decide how much to compress the activities in order to minimize the expected total cost. Creemers, Leus, and Lambrecht [15] used a Markov process supported in a detailed division of the state space. Other solution algorithms were identified in this literature review: the cloud model [16], the Petri networks [17], the cross-entropy method [18], [19], and the dependent structure matrix [20], [21], [22].
Solution procedures to solve PSP were classified by Brčić, Kalpic, and Fertalj [23], according to three specific approaches: first, a predictive strategy that takes the average activities duration as input data and creates a project baseline. Second, a proactive strategy that takes into account the variation of the activities duration, generating a robust baseline for the project. Third, a reactive strategy that re-schedules the original schedule when an unexpected event takes place. However, Rostami, Creemers and Leus [24] presented an alternative reactive strategy, called purely reactive strategy, on-line strategy, and also known as stochastic scheduling, one that does not generates a project baseline, requiring the design of a policy or decision rule to schedule the activities.
In the proactive scheduling case, a robust solution should be provided by the mathematical model, in other words, the baseline generated will require few adjustments every time that the disruptions affect the estimated times. For this reason, several robustness measures have been designed to evaluate the performance of the proposed procedures to solve the PSP with non-deterministic activities duration.
In this article, a new measure to evaluate the robustness is presented. This measure is based in a traditional concept that seeks to minimize the value of the differences between the planned start times in the project baseline and the real executed start times.
In Section 1, a relevant literature review for the robustness measures are addressed. Subsequently, a basic description of both Project Scheduling Problem and solution strategy are presented in Section 2. In Section 3, the Relative Average Deviation (RAD) as a robustsness measure is presented. After, a study case is developed in Section 4 and finally conclusions are given in Section 5.
II. Relevant Literature Review
A robust scheduling is a feasible solution with a minimum deviation from the optimal values of each scenario generated by the random parameters of the model. In project scheduling, quality robustness and solution robustness are the most common measures of robustness. In the first case, the capacity to support the disruptions that affect the project deadline are analized. In the second, the ability to support the disruptions that affect the activities start times are examined [25].
Herroelen and Leus [25] developed a model to solve the PSP with non-deterministic activity durations and obtained a robust solution using a robustness measure based on the previous research of Leon, Wu, and Storer [26]. This measure, called the expected weighted deviation, computes the value of differences between the planned start times and the real executed start times. The expected weighted deviation is one of the most used measures to evaluate the robustness of the baselines generated by the optimization algorithms.
However, with a different approach, Chtourou and Haouari [27] proposed twelve surrogate robustness measures, all based on the activity free slack. According to the authors, the free slacks indicate the time that an activity can be delayed without affecting the start time of their successors, while maintaining the viability of the resources. Subsequently, Hazır, Haouari and Erel [28] designed new robustness measures based on the same concept of free slack. These measures consider the weighted slack, a slack utility function, the dispersion of slacks, the percentage of potentially critical activities and the project buffer size.
In 2013, Khemakhem and Chtourou [29] proposed efficient measures to evaluate the robustness of the baseline obtained for the Resource Constraint Project Scheduling Problem with random duration of activities. The new measures were statistically evaluated and applied to the solutions obtained to the standard set j30 [30]. Additionally, a particular disruption scheme was taken into account. Finally, Xiong, Liu, Chen, and Abbass [31] designed a new surrogate robustness measure that took into account the presence of hybrid effects on the project duration, the cost, and the precedences. This new measure was used to solve a particular type of problem called Stochastic Extended Resource Investment Project Scheduling Problem.
III. The PSP with random duration of activities
A. Description
The Project Scheduling Problem (PSP) is a typical problem of the scientific literature related with scheduling. The PSP refers to a set of n activities that must be executed according to a precedence order specified for the project. Each activity is represented by a subscript (i or j), which takes values between 1 and n. For practical programming reasons, 1 and n are almost always fictitious activities whose durations are zero. The time horizon T where these activities will be scheduled, is divided into partial periods, each one is represented by the subscript t.
The optimal solution is found by comparing the possible combinations to schedule the activities of the project. This comparison requires an iterative process that becomes complex when the number of activities increases. The solution to the problem will provide information related to the planned start time for each activity (Si) and the minimum value of the objective function (Sn), which represents the due date of the project.
The PSP mathematical formulation can be expressed as a linear program:
Minimize
Subject to:
The decision variable Si represents the planned start time of each activity i, di represents its random duration and pij corresponds to a binary parameter, which is equal to 1 if activity i precedes activity j. Finally, E refers to the set of precedences between project activities.
B. Proactive strategy to solve the PSP with random duration of activities
A proactive strategy is supported in procedures that seek to generate baselines capable to face the disruptions that may occur during the execution of projects. Within this approach, three types of solution are grouped [23]: the redundancy based methods, the robust scheduling methods and contingent scheduling.
The redundancy based methods add extra time to the original duration of each project activity, therefore, if any eventuality ocurrs, this extra time can be consumed. As is detailed below, a possibility to compute the extra time, require to identify the potential risks of the project and quantify their impact on each activity.
In 2004, Ökmen, and Özta developed a risk analysis model called Judgmental Risk Analysis Process [32]. The Judgmental Risk Analysis Process was defined as a pessimistic risk analysis methodology because the extra time is obtained from the worst scenarios generated by a simulation process based on Monte Carlo techniques. In 2007, a model to evaluate the project’s risks, to propose mitigation actions, to evaluate their impact in different scenarios and to establish the project duration was presented by Zafra-Cabeza, Ridao, and Camacho [33]. The extra time of each activity was obtained bearing in mind both the risk occurrence probability and its impact.
On the other hand, Mansoorzadeh, Yusof, Mansoorzadeh, and Zeynal [34] proposed a framework based on the integration of risk management and Critical Chain Project Management. The extra time of each activity was estimated from the fuzzy failure mode and effect analysis technique. Finally, Zhang, Shi, and Díaz [35] proposed a procedure based on the gray prediction model to monitor and control the software projects. In this case, the extra time of each activity was based on the risk occurrence probability, the estimated impact and the project manager’s risk aversion.
Similar to the previous proposals, the three methods presented in this article all have the following phases:
Identifying the risks associated with each project activity.
Determining the extra time required to face with disruptions.
Obtaining the project baseline throught the linear program presented in section III, literal A. In this article, the linear program was programmed in GAMS.
Subsequently, in order to select the most robust baseline, a new robustness measure called Relative Medium Deviation (RAD) will be applied.
IV. Robustness Measure Proposed
Based on the definition of Herroelen and Leus [25] and the work of Cervantes [36], the deviation between planned start times and executed start times (obtained by simulation) was determined:
In equation (4), SLB corresponds to the planned start time in the project baseline for each activity i, SR represents the executed start time (obtained through a simulation process with m scenarios) and ∆Si the average deviation of each activity.
Once ∆Si is obtained, the duration of all project activities (∑bi) are determined and the Relative Average Deviation (RAD) is calculated by means of equation (5).
In equation (5), n refers to the number of project activities and bi represents the nominal duration of each activity, which can be associated with its deterministic duration (duration free of risks).
As can be observed, the Relative Average Deviation (RAD) utilizes the duration of project activities (∑bi) as a reference to standardize the expression ∑∆Si. Then, this measure avoids that the robustness has been analized in absolute terms, as would occur if only the expression ∑∆Si is taken into account.
The RAD could also be expressed as:
In the equation (6), the numerator reflects the average deviation of the start times per activity and the denominator the average duration per activity. Therefore, the RAD refers to the fraction of time that the start times of the activities can deviate in relation to their duration.
V. The Relative Average Deviation Applied in a Case Study
Initially, three methods to solve the PSP with random duration of activities will be described and then a case study will be presented. Later, the case study will be solved by each method and finally the robustness of the three baselines generated will be evaluated.
A. Three methods used to solve the PSP with random duration of activities
To begin, it is necessary to identify the following information:
Basic activity duration (bi): Expressed as a probability distribution associated to the duration free of risk, in other words, the appeareance of risk during the execution activity is not assumed. Therefore, the variance of this probability distribution can only be attributed to small changes in the level of productivity of the people who perform the work.
Risk identification: A list with the risks that may affect each activity must be prepared. Changes in weather conditions, delay in delivery of materials or resignation of employees are typical examples of risks.
Risk occurrence probability (Prki): For each risk k that affects the activity i, the risk occurrence probability must be defined. In this article, the risks are assumed as independent of each other and the risk occurrence probability along the project planning horizon is considered constant.
Extra task: The appearance of an extra task is a consequence of the occurrence of unwanted events (risks). An extra task associated with the risk k and that affects the activity i, will have a duration denoted as hki. This duration is also represented by a new probability distribution.
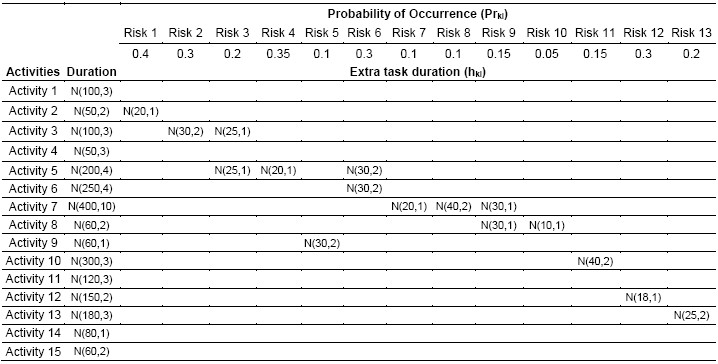
Based on the above information, a matrix to relate both activities and risks must be built. Table 1 presents an example created by the authors, where the basics activity durations and the extra task durations are represented by probability distributions. In this example, the risk 3 affects the project activities numbers 1 and 2, but its probability of occurrence and its duration (impact) are different.
Considering the previous information, the activity durations (di) can be computed following the guidelines of some redundancy based methods. In this article, the methods used to calculate di follow the guidelines of the Judgmental Risk Analysis Process [32] and the model applied by Zafra-Cabeza, Ridao, and Camacho [33] in their work on risk analysis and mitigation.
Method A: In this case, the estimated duration (di) corresponds to the highest value obtained after a simulation process:
In equation (7), bi refers to the expected duration of basic activity i, Prki indicates the probability that the risk k appears in the activity i and hki is a simulated value for the extra task duration (hki). The h ki values are generated according to the probability distribution showed in the Risk Activity Matrix.
Method B: The estimated duration is calculated from the equation (8):
Here, PR represents the average value of the risk occurence probabilities.
Method C: In this case, the estimated duration (di) is obtained from the equation (9):
B. Case study
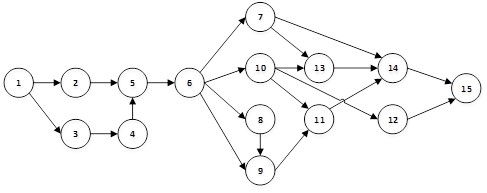
The case study has been designed by the authors and is based on the construction project of a recreational park. The activities required, their duration expressed in hours and the precedence relationships are listed in Table 2.
The network diagram used is presented in Figure 1.
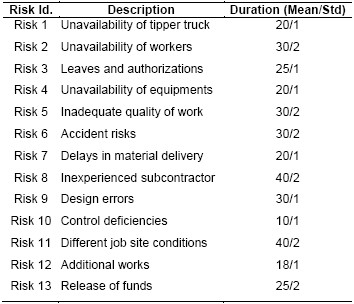
In Table 3, the risks that can affect the project are detailed, and the risk activity matrix appears in Table 4. In this example, the risk occurrence probability is the same when the same risks affect two different activities.
C. Case study solution
Method A: Based on Table 4, 1000 random data were generated in order to apply equation (7), and to obtain the highest value (di) for each activity. The estimated durations (expressed in hours) and the start times after solving the linear problem showed in section III literal A were obtained and collected in Table 5.
In addition, the due date of the project (Sn) was obtained. In this case, Sn = 1487.6.
Method B: Based on Table 4 and applying the equation (8), the total extra task duration per activity and the average risk occurrence probability were computed (PR=0.209). The estimated duration and the start times obtained are to solve the linear program described in section III literal A, and are collected in Table 6.
In this case, the baseline finish is Sn= 1477.5.
Method C:Table 7 presents the estimated duration (di) obtained from equation (9) and the start times are obtained by solving the linear program described in the section III literal A.
This new solution indicates that the baseline finish is Sn = 1479.5.
D. Comparation between baselines generated
The best baseline is selected from the best robustness indicator. In this case, the best solution will be the baseline with the lowest value in the Relative Average Deviation (RAD).
Initially, a simulation process was carried out in order to generate 10000 different scenarios for the activities duration. Then the start times (SR ) for each scenario, were obtained using a simulation model developed in GAMS.
Based on this information, each value ∆Si was computed and subsequenty the value ∑∆Si for each method applied. Table 8 includes the results obtained.
The comparative analysis indicates that the baseline generated by method C is slightly more robust than methods A and B. The result is evident from the analysis of ∑∆Si. However, this comparison (in absolute terms) does not allow the demonstration of the closeness between the methods, neither the relation of percentage of deviation with respect to the activity durations.
In this case study, the RAD shows that the baselines generated by the three methods have a similar robustness. Additionally, their percentage of deviation with respect to the activity durations is between 15.7 % and 16.1 %.
Then, if the decision maker considers the RAD of method C (15.7 %) acceptable, the solution of method C could be adopted as a baseline for the project. Otherwise, a new method must be developed to generate baselines evaluating the robustness again.
VI. Conclusion
In this article, an indicator to measure the solution robustness for the PSP with random duration of activities was proposed. The new robustness measure is supported in a simulation process and establishes the margin of deviation of the activities’ start times of a project in relation to its durations.
The new indicator, called Relative Average Deviation (RAD), has been applied in a case study. Then, it was necessary to develop three methods to solve the PSP with the random duration of activities and to compute and compare the RADs of the three baselines generated. All solution methods showed have taken into account the risk occurrence probability and their impacts. Each baseline was generated through an optimization process based on linear programming.
The RAD is an indicator that evaluates the deviation in the start times (planned and executed) in relative terms, which is important because it allows assess the proximity between the different methods that were applied. On the other hand, the analysis about the margin of precision of each baseline generated is easier to understand when the percentage of deviation in relation to the activity durations is computed.