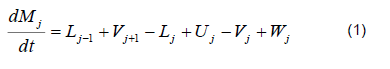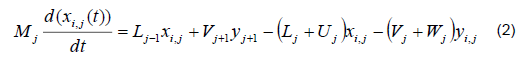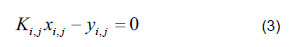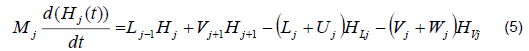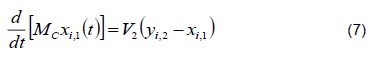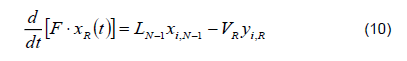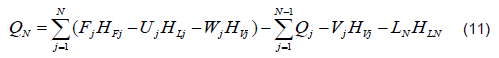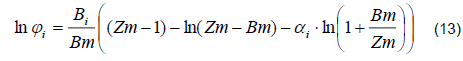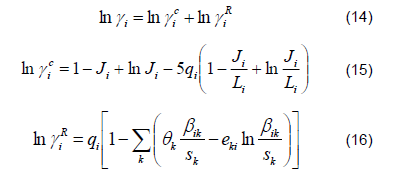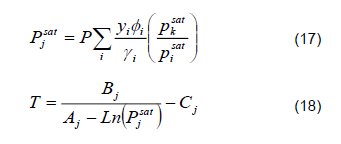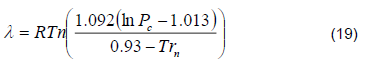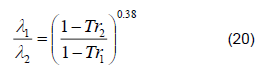1. INTRODUCTION
Distillation is one of the most widely used operations in industrial settings. Distillation by lots or batches is frequently used in the pharmaceutical industry and in several industrial processes at medium and small scales. Thus, it is of great interest to a variety of industrial sectors [1].
The simulation of distillation columns is complex because of the dynamic behavior from start-up until the time at which a defined product composition is reached. Over the course of distillation, the system is unstable and variable. At industrial scales, this variability and instability results in a large amount of wasted energy and product with many non-productive periods. Several theoretical studies have attempted to reduce the distillation start-up time, energy consumption, and product waste. Some of them use rigorous methods from one stage to the next in which they relate combined physical and geometrical properties with hydrodynamic equations and calibration models to obtain quick and reliable results [2-5].
The start-up stage is not the only inconvenient component for the modeling and simulation of rectification discontinue columns. Different solution methods have been used to predict the behavior of the distillation equipment, implementing tridiagonal matrix methods, theta convergence, and K-base methods [6]. However, temperature predictions exhibit deviations of up to 15.6% between the simulated and experimental data throughout the column.
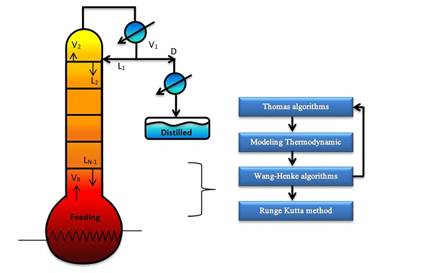
In this work, the model simulates a discontinuous rectification column operating at total reflux during commissioning to stabilize variables such as temperature and composition throughout the column while avoiding the waste product. In addition, we propose a solution method based on continuous stable states for each time tn using rigorous methods (Thomas and Wank-Henke algorithm [7]) to calculate the initial conditions. This is a novel approach to simulate discontinuous rectification columns at pilot scale and to ensure the correct prediction of the behavior on the system, including the temperature.
2. METHODS
A. Materials and Equipment
Distilled water and 96% V/V ethanol (ProQuimar) were used to prepare binary systems at different molar concentrations. A distillation column made of borosilicate glass with a nominal diameter of 2 inches with perforated plates was used at the pilot scale (Table 1). The samples were analyzed using a Spectro UV-2650 spectrophotometer.
Table 1 Specification parameters of rectification colum for pilot scale destilation.
B. Experiments
Ethanol-water solutions with the following ethanol molar concentrations were prepared: 0.15, 0.25, 0.35, and 0.40. For each initial concentration, the column was operated either with total reflux or without reflux (1 experiment per condition) during start-up until reaching a stable state (10 minutes) without wasting product. After the start-up, 5-ml samples were taken every 10 min from plates 1, 3, and 5 and from the distillate for spectrophotometric analysis.
C. Mathematical Analysis
The mathematical model was based on a system of differential and algebraic equations obtained from the calculations of mass and energy balance focusing on the equilibrium stages in the distillation column and with an approximation to MESH differential equations and continuous stable states (Figure 1) [7]. The following assumptions were made: i) the liquid and vapor phases leaving the tray are in thermodynamic equilibrium; ii) the liquid in the tray is completely mixed and non-compressible; therefore, there are no radial concentration gradients in the column (due to the MESH focus); iii) there is no vapor accumulation in the system; iv) heat loss through the column is negligible; v) vapor and liquid flows are not constant and can be calculated based on the energy balance of the column; vi) the condenser of the distillation column is absolute; vii) all of the vapor that enters the condenser is condensed, and the composition of the condensate is the same as the reflux and the distillate; vii) feeding is performed in the reboiler; viii) there is no chemical reaction or formation of tail products; and ix) the effect of accumulation "Hold-up" in the column is negligible because it is a column at scale pilot. Besides, the fluid in each tray is negligible compared to the accumulation in the boiler.
1) Equilibrium of the Generic Stage.
Total mass balance
Mass balance by component
Phase equilibrium ratio
Phase stoichiometry
Energy balance
2) Equilibrium in the Condenser. The absolute condenser implies that all vapor that enters stage 1 is converted into a saturated liquid; therefore, y1 = xD. The refrigerant used is water at an ambient temperature of 26 °C to 29 °C.
Total mass balance
Balance by component
Energy balance
3) Reboiler. The reboiler is a heating dome in which feeding occurs by batches. It is a stage of the column because there is thermodynamic liquid-vapor equilibrium on the surface of the liquid.
Total mass balance
Mass balance by component
Energy balance
4) Heat Exchanger. The column has a heat exchanger that cools the distillate from 80 °C to 29 °C. Water is used as refrigerant with an initial temperature of (28 ± 1) °C. The amount of heat needed to reduce the temperature [8] is given by:
D. Thermodynamic Model of the System
1) Vapor Phase. The distillation column with perforated plates works at a pressure of 1 atm. However, the behavior of the ethanol-water mixture is considerably different from the ideal. Therefore, a PSRK (Predictive-Soave-Redlich-Kwong) thermodynamic model was used to calculate the fugacity coefficients in the vapor phase based on the following equation [9, 10]:
The model parameters Bi, Bm, Zm, and Ai are specified in [11].
2) Liquid Phase. The ethanol-water mixture is far from ideal due to the polarity of the components, which causes the activity coefficients to deviate from unity. This behavior is described by the original UNIFAC model coupled to the PSRK [12] according to the following equations:
3) Temperature Calculation. Conventionally, predictions of the equilibrium temperature during start-up exhibit considerable deviations from dynamic distillation columns [13, 14]. To avoid discrepancies associated with the temperature, the following algorithmic structure coupled to the PSRK thermodynamic model was used to calculate the bubble point:
Start with the assumption that the fugacity coefficients are equal to 1 (ideal gas).
Compositions are calculated in the vapor phase using the equilibrium relationship (Eq. 3).
Saturated pressure is determined using equation 17.
Temperatures are determined using equation 18.
The Euclidian norm of the residual vector is calculated for the temperatures and associated errors. If the error does not meet the established restriction value, the fugacity coefficients are recalculated using the PSRK method and the molar fractions.
The stop criterion of the algorithm takes into account the normal temperatures and compositions of the vapor phase for each tray according to the following equations:
E. Solution Algorithm of the Mathematical Model
For the numeric solution of the system, it is assumed that there are continuous stable states for each step size for the Fourth Order Runge-Kutta method (RK-4). It is internally coupled for each step size to the Thomas method and the Wang-Henke algorithm [7], where the solution for time tn corresponds to the initial condition for time tn+1.
Given that the system corresponds to a dynamic model, the initialization of the variables is fundamental to guarantee the stability and correct prediction of the physical behavior of the column. The RK-4 algorithm for this type of system requires very precise initial values to guarantee the effectiveness of the solution. In this study, the initial values of the column were determined by solving the MESH equations in the stable state using the Thomas algorithm when operating with total reflux [7]. It provided valid values for the dynamic operation of the equipment.
The enthalpies of vaporization are also fundamental in the global iterative process (coupling of RK-4, Thomas, and Wang-Henke) because they influence the numerical stability of the solution.
The enthalpies of vaporization for each component in each tray was determined by Riedel’s equation. However, evaluating the global vaporization in the tray increases the computational time of the simulation. To reduce the computational times and to correctly evaluate vaporization, the enthalpies of vaporization were corrected for each component in each stage using Watson’s equation [12].
Equations to calculate enthalpy:
Riedel’s Equation:
Watson’s Equation:
The following algorithm shows the solution scheme of the system (Figure 2).
III. RESULTS
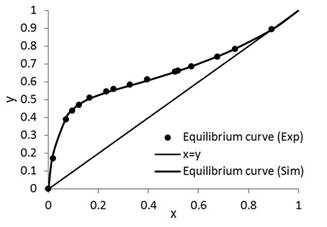
The results of this study are presented in Figures 3 to 9. Figure 3 is the representation of experimental data and simulated equilibrium curve.
Figures 4 and 5 show the responses of the distillation columns with total reflux.
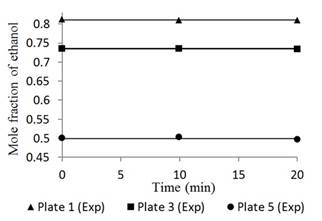
Fig. 4 Ethanol concentration profile in plates 1, 3, and 5 for a feed composition of 0.15 molar operating at total reflux.
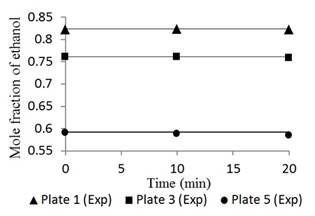
Fig. 5 Ethanol concentration profile in plates 1, 3, and 5 for a feed composition of 0.35 molar operating at total reflux.
Figures 6 and 7 reflect the dynamic experimental data behavior of the pilot scale distillation column for the distilled product and plates 1, 3, and 5.
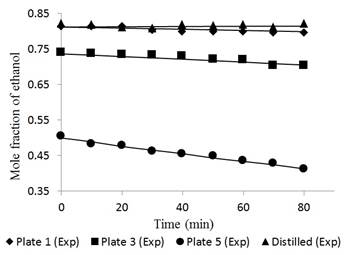
Fig. 6 Ethanol concentration profile in plates 1, 3, 5 and distilled for a feed composition of 0.15 molar operating without reflux.
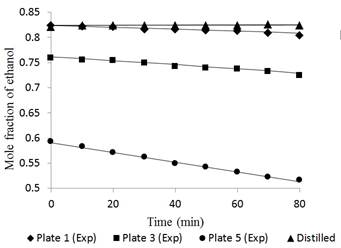
Fig. 7 Ethanol concentration profile in plates 1, 3, 5 and distilled for a feed composition of 0.35 molar operating without reflux.
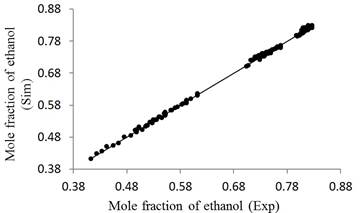
Figure 8 shows a scatter graph that relates all the experimental and simulated data from the ethanol mole fraction.
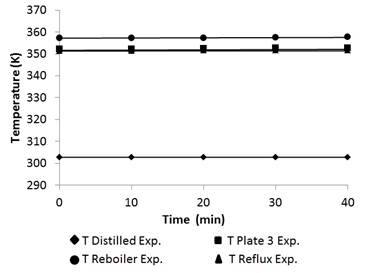
Figure 9 shows the temperature profile in the distillation column.
IV. DISCUSSION
To guarantee an efficient prediction by coupled thermodynamic modeling, simulations of the phase equilibrium curve of the ethanol-water system and the bubble point temperature were performed (Fig. 3). These were compared to experimental data reported in the literature [16]. The presented results had an average percentage error of 1.84%. Thus, the coupled UNIFAC and PSRK thermodynamic models satisfactorily predicted the liquid vapor equilibrium of the ethanol-water mixture, and also the column operating at total reflux at different initial feed conditions. These conditions guaranteed that the operation of the column was stable [17]. The experimental and simulation results showed that there were no variations in the compositions of the plates for different operation times. Therefore, we can observe that the column does not waste product and it is thermodynamically stable. In addition, the conditions guaranteed a correct estimation of the initial values of the dynamic simulation process [18].
Figures 4 and 5 had mean errors of 0.25% and 0.29% for feed compositions of 0.15 and 0.35 molar, respectively. Both the simulated and the experimental data had a constant trend with time, typical of a stationary state process [19]. This result validates the basic assumption of the mathematical model. This condition corresponds to the start-up period in which there is usually product waste due to changes and instability of the variables. However, Figures 4 and 5 show a linear behavior that indicates that operation is in the total reflux, a stable state is reached without wasted product; therefore, the Thomas method and the Wank-Henke algorithm serve to correctly predict the initial condition of the system.
In the case of dynamic performance of the tower, Figures 6 and 7 had a largest deviation between the experimental and simulated data, i.e., 1.45% and 0.95% in tray 5 for feed compositions of 0.15 and 0.35, respectively. The data at time “zero” correspond to the total reflux condition (used to feed the Fourth Order Runge-Kutta method). The separation occurs more easily in tray 5 due to the high relative volatility. However, as the ethanol concentration in the mixture increases, the volatility is reduced due to the proximity to the azeotropic point.
Figure 8 shows a scatter graph that relates all the experimental and simulated data from the ethanol mole fraction. The errors oscillated between 1.51% and 0.017% with an average deviation of 0.48%, thus demonstrating that the mathematical model satisfactorily predicts the real behavior of the column.
Finally, the temperature validation and the experimental data were taken from the reboiler, reflux, distillated, and tray 3. Data were recorded by thermocouples in the column. The maximum error was 0.18% with an average of 0.055%, thus demonstrating that the bubble point algorithm coupled to the PSRK method correctly predicts the temperature in the distillation column [20].
V. CONCLUSIONS
Mathematical modeling and simulation of a discontinuous rectification distillation column at pilot scale using MESH equations and the continuous stable states concept were conducted. The stable state approach effectively described the behavior of the dynamic distillation column, providing low deviations and minimal errors (less 0.29%) even for predicting bubble point temperatures. Coupling the bubble point algorithm with the PSRK thermodynamic model allowed us to correctly predict the compositions in the vapor phase and temperature in each stage of the distillation column at pilot scale (error less 1.45%). Coupled Thomas and Wang-Henke algorithms were used to obtain the initial conditions while guaranteeing relatively low deviations with respect to the experimental data and the effectiveness of the simulation (less 1.8%). The solution based on the Thomas method and the Wang-Henke algorithm coupled to the Runge-Kutta method made it possible to describe the behavior and variables of all stages of the distillation column. Operation at total reflux from start-up avoids wasting product and allows for the stabilization of the state variables such as temperature and molar composition.