Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ciencias
Print version ISSN 0121-1935
rev. cienc. vol.18 no.1 Cali Jan./June 2014
Sonar Sequences and Sidon Sets
Secuencias sonar y conjuntos de Sidon
Rigo Julián Osorio
Departamento de Matemáticas, Universidad del Cauca, Popayán - Colombia
E-mail: rosorio@unicauca.edu.co
Diego Fernando Ruiz
Departamento de Matemáticas, Universidad del Cauca, Popayán - Colombia
E-mail: dfruiz@unicauca.edu.co
Carlos Alberto Trujillo
Departamento de Matemáticas, Universidad del Cauca, Popayán - Colombia
E-mail: trujillo@unicauca.edu.co
Cristhian Leonardo Urbano
Departamento de Matemáticas, Universidad del Cauca, Popayán - Colombia
E-mail: cristhianleon@unicauca.edu.co
Recived: 23/10/2013
Accepted: 03/02/2014
Abstract
A is a Sidon set in an additive commutative group G if the number of representations of each non-identity element in G, as a difference of two elements in A is at most 1. An m x n sonar sequence is a function f : {1, .. . , n} → {1, .. . , m} such that its associated graph G f := {(x, f (x)) : 1 ≤x ≤ n} is a Sidon set in the group Z x Z. If G(m) denotes the maximum positive integer such that there exists an m x n sonar sequence, using additive energy and some of its properties. In this paper, we show that G(m) ≤ m + 3,78m2/3 + 4,76m1/3 + 2. Furthermore, using the construction of Sidon sets type Bose in Zq2 –1 we construct (q – 1) x q sonar sequences for all prime power q.
Keywords: Sidon sets, sonar sequences, additive energy.
Resumen
A es un conjunto de Sidon en un grupo conmutativo G notado aditivamente si el número de representaciones de todo elemento no identidad de G como diferencia de dos elementos de A es a lo sumo 1. Una secuencia sonar m x n es una función f : {1, .. . , n} →{1, .. . , m} tal que su grafo asociado Gf := {(x, f (x)) : 1 ≤ x ≤ n} es un conjunto de Sidon en el grupo Z x Z. Si G(m) denota el máximo entero positivo n tal que existe una secuencia sonar m x n, utilizando el concepto de energía aditiva y algunas de sus propiedades elementales. En este trabajo se prueba que G(m) ≤ m + 3,78m2/3 + 4,76m1/3 + 2. Además, utilizando la construcción de conjuntos de Sidon tipo Bose en Zq2 – 1 se construyen secuencias sonar (q – 1) x q, para toda potencia prima
Palabras clave: Conjuntos de Sidon, secuencias sonar, energía aditiva.
1. Introducción
En teoría de números aditiva, uno de los problemas que ha tenido gran impacto en el área de las telecomunicaciones es el de los conjuntos de Sidon, el cual data de 1930. Su nombre es en honor al analista Simon Sidon quien los introdujo con el propósito de resolver un problema en análisis armónico (Drakakis, 2006). Sidon investigaba conjuntos de enteros positivos con la propiedad que la sumas de dos elementos son todas distintas. Esta propiedad equivale a que las diferencias no cero entre cualquier par de elementos del conjunto son todas distintas. El concepto de conjunto de Sidon puede considerarse en situaciones más generales, por ejemplo en grupos conmutativos. En dimensión dos, un caso particular de los conjuntos de Sidon es el de "secuencia sonar", una función f: {1,...,n} → {1,...,m} tal que su grafo asociado
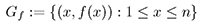
es un conjunto de Sidon en (ℤ X ℤ, +). Su nombre se debe a que tales funciones se usan en aplicaciones a dispositivos tales como el sonar, denominado así por sus siglas en inglés "Sound Navigation And Ranging", que se utiliza como medio de localización acústica. Otras aplicaciones de conjuntos de Sidon en dimensión dos se encuentran en sistemas de comunicaciones óptimos, en criptografía, en la distribución de claves en redes de celulares, e incluso en el campo militar (Taylor, 2011).
Formalmente, un conjunto de Sidon se define como sigue.
Definición 1.1. Un conjunto ![]() en un grupo abeliano G notado aditivamente es un conjunto de Sidon, si todas las diferencias a' - a' con a,a' ∈
en un grupo abeliano G notado aditivamente es un conjunto de Sidon, si todas las diferencias a' - a' con a,a' ∈ ![]() , a ≠ a', son distintas.
, a ≠ a', son distintas.
Sean a,m enteros con a < m. Mediante [a,m] se representa el conjunto {a, a + 1, a + 2,...,m}. A continuación se define el concepto de secuencia sonar como en (Moreno, 1993).
Definición 1.2. Una función f : [1, n] → [1,m] tiene la propiedad de diferencias distintas si para todos los enteros h,i,j, con 1 ≤ h ≤ n - 1, 1 ≤ i, j ≤ n - h se tiene que
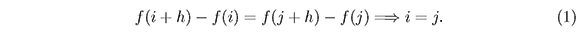
Si [1,m] se identifica con el conjunto de representantes de los enteros módulo m y la condición (1) se cambia por
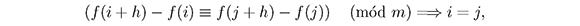
f tiene la propiedad de diferencias distintas modular.
Definición 1.3. Una función f : [1, n] → [1,m] es una secuencia sonar m × n si tiene la propiedad de diferencias distintas. Mientras que f es una secuencia sonar modular m×n si tiene la propiedad de diferencias distintas modular. En este caso se suele decir que f es una secuencia sonar módulo m con n elementos.
El siguiente lema, cuya prueba se sigue directamente de la Definición 1.1, la Definición 1.3 y del grafo asociado a una secuencia sonar Gf , establece la relación entre conjuntos de Sidon y secuencias sonar.
Lema 1.1 Una función f : [1, n] → [1,m] es una secuencia sonar si y sólo si el grafo de f, Gf , es un conjunto de Sidon en (ℤ × ℤ, +). Similarmente, f es una secuencia sonar modular m à n si y sólo si Gf es un conjunto de Sidon en (ℤ × ℤm, +).
El problema fundamental en secuencias sonar consiste en investigar el comportamiento asintótico de las siguientes funciones:
G(m) :=máx{n : existe una secuencia sonar m × n},
G(módm) :=máx{n : existe una secuencia sonar modular m × n}.
Note que G(m) ≥ G (mód m). El siguiente lema establece las cotas superiores triviales para dichas funciones.
Lema 1.2. Para todo entero positivo m, se tiene que G(m) ≥ 2m y G(módm) ≥ m + 1.
Demostración 1. Sea f : [1, n] → [1,m] una secuencia sonar. De acuerdo con el Lema 1.1, todas las parejas (1, f(i+1)–f(i)), con 1 ≤ i ≤ n–1, son distintas. Así, se tienen n – 1 enteros distintos contenidos en [–m + 1,m – 1], de donde n – 1 ≤ 2m – 1. El caso modular es similar, sólo que las n – 1 diferencias se consideran módulo m.
El Teorema 4 de (ErdÅs, 1992) establece que
G(m) < m + 5m2/3,
para m suficientemente grande. Utilizando el concepto de energía aditiva y algunas de sus propiedades elementales, en la siguiente sección se prueba que
G(m) < m+3,78m2/3 + 4,76m1/3 + 2.
En la Sección 3 se usa la construcción de conjuntos de Sidon tipo Bose para construir secuencias sonar que implican que
G(mód(q – 1)) = q,
para toda q potencia prima. Además se presentan los algoritmos correspondientes a cada construcción, los cuales han sido implementados en MuPAD Pro 4.0.
Finalmente, en la Sección 4 se presentan algunos problemas relacionados con el trabajo.
2. Energía aditiva y cota superior para G(m)
Sean (G, +) un grupo conmutativo notado aditivamente, y ![]() ,
,  ⊆ G. El conjunto suma y conjunto diferencia asociados con
⊆ G. El conjunto suma y conjunto diferencia asociados con ![]() y
y  se definen como
se definen como
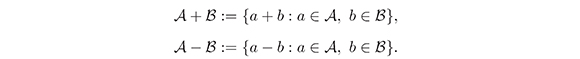
La función representación de x ∈ G con respecto al conjunto ![]() +
+  , y
, y ![]() -
-  , se define respectivamente como
, se define respectivamente como
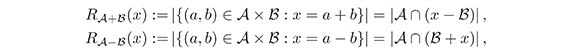
donde x -  es la reflexión de
es la reflexión de  mediante x,
mediante x,  + x es la traslación de
+ x es la traslación de  mediante
mediante
x, y |X| denota el cardinal del conjunto finito X.
Note que
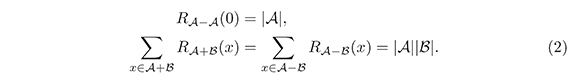
Observación 2.1. Note que ![]() es un conjunto de Sidon en G sz y sólo si RA-A(x) ≤ 1 para todo x ∈ G, x≠0.
es un conjunto de Sidon en G sz y sólo si RA-A(x) ≤ 1 para todo x ∈ G, x≠0.
Definición 2.1. La energía aditiva entre ![]() y
y  , que se denota E(
, que se denota E(![]() ,
, ), se define com:
), se define com:
E(![]() ,
, ): = |{(a,a',b,b') ∈
): = |{(a,a',b,b') ∈![]() 2×
2×  2: a + b = a' + b'}|.
2: a + b = a' + b'}|.
Note que E(![]() ,
, ) cuenta el número de soluciones de la ecuación a + b = a' + b', que es equivalente al número de soluciones de la ecuación a - b' = a' - b o de la ecuación a - a' = b' - b. Esta observación permite establecer las siguientes identidades (ver, Tao & Vu, 2006) para una prueba detallada)
) cuenta el número de soluciones de la ecuación a + b = a' + b', que es equivalente al número de soluciones de la ecuación a - b' = a' - b o de la ecuación a - a' = b' - b. Esta observación permite establecer las siguientes identidades (ver, Tao & Vu, 2006) para una prueba detallada)
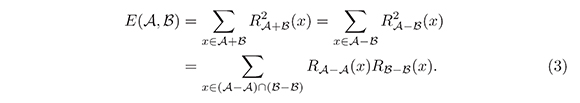
El siguiente lema, debido a Ruzsa (Ruzsa,1993), relaciona el cardinal de un conjunto de Sidon en G con el cardinal de un conjunto cualquiera en el mismo grupo.
Lema 2.1. Sea ![]() un conjunto de Sidon en G y sea
un conjunto de Sidon en G y sea  subconjunto de G. Entonces
subconjunto de G. Entonces
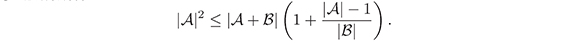
Demostración 2.1. Mediante la desigualdad de Cauchy-Schwartz y las identidades (2) y (3) se tiene que
Como ![]() es un conjunto de Sidon, entonces
es un conjunto de Sidon, entonces  para todo x ≠ 0. Por lo tanto, la suma de la desigualdad ( 4) está acotada por
para todo x ≠ 0. Por lo tanto, la suma de la desigualdad ( 4) está acotada por
lo que implica que
Utilizando el Lema 2.1 se tiene el primer resultado.
Teorema 2.1. Si f : [1,n] → [1,m] es una secuencia sonar entonces
G(m) ≤ m + 3,78m2/3 + 4,76m1/ + 2.
Demostración 2.2. Dado que es una secuencia sonar, su grafo es un conjunto de Sidon. Además se tiene que |Gf| = n y Gf ⊆ [1,n] × [1,m]. Considere el conjunto  = [0,u], donde u = [cm∝] con α,c > 0. Es claro que |
= [0,u], donde u = [cm∝] con α,c > 0. Es claro que | | = (u + 1)2. Note que Gf +
| = (u + 1)2. Note que Gf +  ⊆ [1,n + u] × [1,m + u], y por lo tanto |Gf +
⊆ [1,n + u] × [1,m + u], y por lo tanto |Gf +  | ≤ (n + u)(m+u). Así, de acuerdo con el Lema 2.1 se sigue que
| ≤ (n + u)(m+u). Así, de acuerdo con el Lema 2.1 se sigue que
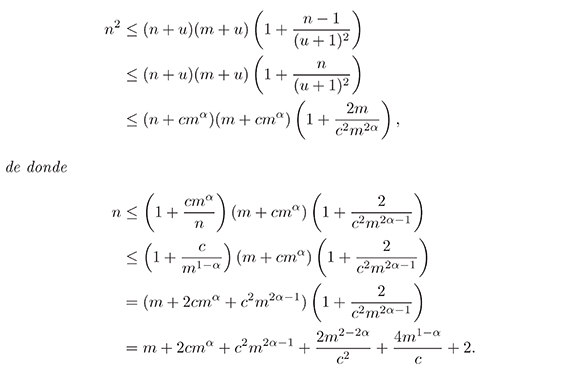
Luego, con 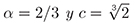 se tiene el resultado deseado.
se tiene el resultado deseado.
3. Una nueva construcción de secuencias sonar
En esta sección se presenta una nueva construcción de secuencias sonar, la cual es un caso particular de la dada en (Ruiz, 2014). Esta se basa en la construcción de conjuntos de Sidon tipo Bose y algunas propiedades que se desprenden de ella.
3.1 Conjuntos de Sidon tipo Bose
La prueba del Teorema 3.1 y de la Proposición 3.1 se presenta en (Ruiz, 2014).
Teorema 3.1. (Construcción Tipo Bose). Sean q una potencia prima, e un elemento primitivo en 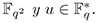 . Entonces,
. Entonces,
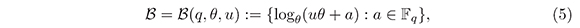
es un conjunto de Sidon con q elementos en el grupo aditivo ℤq2-1.
Proposición 3.1. El conjunto  del Teorema 3.1 satisface las siguientes propiedades.
del Teorema 3.1 satisface las siguientes propiedades.
1. Dados b, b'
, si b ≠ b' entonces b
b' (mód q + 1).
2. Para todo b ∈
b
0 (mód q + 1).
3.
(módq+1) : = {b (mód q + 1) : b ∈
} = [1,q].
El siguiente algoritmo calcula un conjunto de Sidon tipo Bose en el grupo aditivo ℤq2-1
Algoritmo 3.1. Bose:
Entrada: Un primo p y un entero positivo r.
Descripción: Mediante la función interna de MuPAD 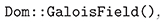 se crea el campo finito
se crea el campo finito 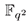 y de este se escoge al azar un elemento primitivo mediante
y de este se escoge al azar un elemento primitivo mediante 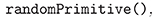 para así realizar la asignación mencionada en el Teorema 3.1.
para así realizar la asignación mencionada en el Teorema 3.1.
Salida: Una lista de enteros positivos B, que corresponde a un conjunto de Sidon tipo Base.

3.2 Construcción de secuencia sonar
Haciendo uso del Teorema 3.1 y de la Proposición 3.1 se obtiene el siguiente resultado.
Teorema 3.2. Sean q una potencia prima,  el conjunto de Sidon tipo Base, y para cada i ∈ [1,q] sea bi el único elemento de
el conjunto de Sidon tipo Base, y para cada i ∈ [1,q] sea bi el único elemento de  tal que bi ≡ i (mód q + 1). La función f : [1,q] → [0,q - 2] definida mediante f(i) =
tal que bi ≡ i (mód q + 1). La función f : [1,q] → [0,q - 2] definida mediante f(i) = 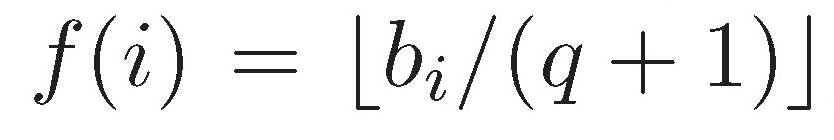 , una secuencia sonar módulo q - 1 con q elementos.
, una secuencia sonar módulo q - 1 con q elementos.
Demostración 3.1. Sean h, i, j enteros tales que 1 ≤ h ≤ q-1 y ≤ 1,j ≤ q - h. Suponga que f(i+h) - f(i) ≡ f(j+h) - f(j) (mód q-1), es decir

Dado que 0 ≤ i + h < q + 1 y 0 ≤ j + h < q + 1, de la última igualdad se tiene que bi+h - bi ≡ bj+h - bj (mód q2 - 1). Ya que  es un conjunto de Si don módulo q2 - 1 entonces i = j. Por lo tanto f es una secuencia sonar módulo q- 1 con q elementos.
es un conjunto de Si don módulo q2 - 1 entonces i = j. Por lo tanto f es una secuencia sonar módulo q- 1 con q elementos.
El siguiente algoritmo construye una secuencia sonar aplicando el Teorema 3.2.
Algoritmo 3.2. Sonar NI:
Entrada: Un primo p y un entero positivo r.
Descripción: Mediante el uso del Algoritmo 3.1 y la asignación descrita en el Teorema 3.2 se construye la secuencia sonar.
Salida: Una lista N1 la cual es una secuencia sonar módulo q-1 con q elementos.

En el siguiente ejemplo se usa el Algoritmo 3.2 para construir una secuencia sonar módulo 6 con 7 elementos
Ejemplo 3.1. Sean p = 7 y r = 1. Mediante el Algoritmo 3.1 se construye un conjunto de Sidon tipo Bose con 7 elementos sobre el grupo aditivo ℤ48.
B := Bose(7,1); B = [1, 26, 11, 5, 12, 14, 31].
Ahora, continuando con el Algoritmo 3.2 y basado en el conjunto de Sidon B se construye una secuencia sonar módulo 6 con 7 elementos.
N1 := SonarN1(7,1); N1 = [0, 3, 1, 1, 0, 1,]
4. Algunos problemas relacionados
Mediante búsqueda exhaustiva hoy se conocen valores exactos para la función G(m) (algunos se muestran en la Tabla 1).
Tabla 1. Valores exactos de G(m) y 2m – G(m), para 1 ≤ m ≤ 14.
A partir de ellos es natural preguntarse si
Problema 1. ¿G(m) ≤ 2m – 1 para todo entero m ≥ 5 Note que el resolver este problema implica una mejora en la cota superior de G(m) pequeños de m.
De otro lado, por el Lema 1.2 y el Teorema 2.1, el comportamiento de la cota superior de la función G(m), para todo m en el intervalo respectivo, es como sigue
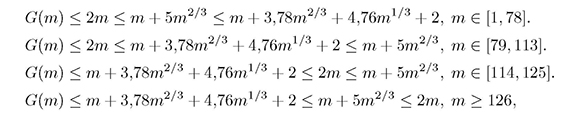
de donde se sigue el segundo problema.
Problema 2. Mejorar la cota superior para la función G(m). Relacionado con este problema, en (ErdÅs, 1992) se afirma que G(m) ≤ m + 3m2/3 + 2m1/3 + 9, con lo que se mejoraría la cota superior de G(m) para valores grandes de m. Ya que en (ErdÅs, 1992) no se presenta una prueba de este resultado, y de nuestra parte no ha sido posible establecerla, un problema específico consiste en obtener una prueba formal de dicha cota.
De la construcción presentada en la Sección 3 se infiere que G(q –1) ≥ q para toda potencia prima q. Además, de los resultados dados en (Moreno, 1993), también se observa que G(m) ≥ m para todo m ≤ 100. De este modo se presentan los siguientes problemas.
Problema 3. Probar o refutar que G(m) ≥ m para todo entero positivo m. Nuestros cálculos para otros valores particulares de m nos hace conjeturar que la respuesta es afirmativa.
Problema 4. ¿Para cúales valores de m se tiene que G (mód m) = m+1 y para cúales G (mód m) = m?
Problema 5. Finalmente, un problema que podría resolver el comportamiento asintótico de la función G(m) para valores grandes de m sería el estudio del siguiente límite
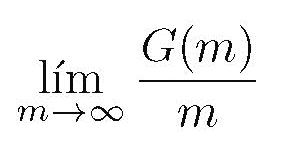
Agradecimientos
Los autores agradecen al profesor Javier Cilleruelo por la sugerencia hecha en ALTENCOA5-2012 de usar energía aditiva con el fin de lograr una mejor cota superior para la función G(m). Además, se agradece a Colciencias y a la Universidad del Cauca por el apoyo al grupo de investigación "Algebra, Teoría de Números y Aplicaciones-ALTENUA ERM" bajo los proyectos de investigación con código 110356935047 y VRI 3744, respectivamente.
Referencias
Drakakis, K. (2006). A review of Costas arrays. Journal of Applied Mathematics, 2006, 1-32 [doi:10.1155/JAM/2006/26385] [ Links ]
Erdős, P., Graham, R., Ruzsa, I. Z., & Taylor, H. (1992). Bounds for arrays of dots with distinct slopes or lengths. Combinatorica, 12(1), 39-44. [ Links ]
Moreno, O., Games, R., & Taylor, H. (1993). Sonar sequences from Costas arrays and the best known sonar sequences with up to 100 symbols. IEEE Transactions on Information Theory, 39 (6) 1985-1987. [ Links ]
Ruiz, D., Caicedo, Y., & Trujillo, C. (2014). New constructions of sonar sequences. International Journal of Basic and Applied Sciences IJBAS-IJENS, 14 (1) 12-16. [ Links ]
Ruzsa, I. (1993). Solving a linear equation in a set of integers I. Acta Arithmetica, 65 (3), 256-282. [ Links ]
Tao, T., & Vu, V. H. (2006). Additive combinatorics, Cambridge Studies in Advanced Mathematics. Cambridge, UK: Cambridge University Press. [ Links ]
Taylor, K., Rickard, S., & Drakakis, K. (2011). Costas arrays: survey, standardization, and matlab toolbox, ACM Transactions on Math. Software, 37, (4) 1-31. [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.















