Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ciencias
Print version ISSN 0121-1935
rev. cienc. vol.18 no.1 Cali Jan./June 2014
Identification of the primitive type of the Voronoi cell in 4-dimensional euclidean lattice
Identificación del tipo primitivo de la celda de Voronoi en retículos euclidianos 4 dimensionales
Juan Miguel Velásquez Soto
Departamento de Matemáticas, Universidad del Valle, Cali - Colombia
E-mail: juan.m.velasquez@correounivalle.edu.co
Received: February 6, 2014
Accepted: August 12, 2014
Abstract
We will show a mathematical algorithm in order to determine the Voronoi Type of a Euclidean lattice in dimension 4. It is an implementation of Charve's reduction theory of positive definite quadratic forms (see Charve, 1884). This algorithm helps us to recognize lattice Types in order to try to solve the general problem of finding the optimal lattice quantizer in dimension 4.
Keywords: Voronoi cell, quadratic forms.
Resumen
Basados en el trabajo de León Charve (1882), sobre reducción de formas cuadráticas cuaternarias definidas positivas, se implementa un algoritmo con el cual es posible determinar el Tipo primitivo de la celda de Voronoi que corresponde a un retículo 4 dimensional. Este resultado es esencial a la hora de calcular la constante de cuantización de un retículo arbitrario, lo que permite avances significativos al momento de abordar el problema del retículo cuantizador óptimo en dimensión 4.
Palabras clave: Celdas de Voronoí, formas cuadráticas.
1. Introducción
Un retículo euclideano es un subconjunto L de ℝn formado por todas las combinaciones lineales enteras de n vectores linealmente independientes de ℝn. En símbolos esto es: 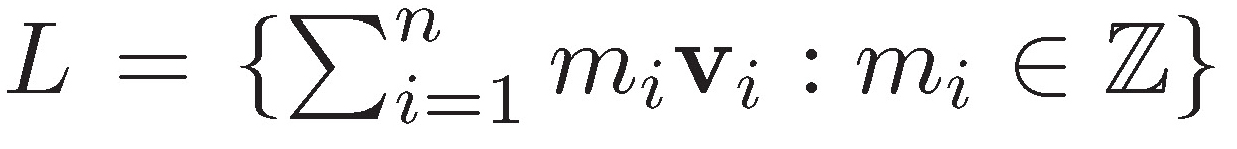 donode {v1,...,vn} constituyen una base de ℝn
donode {v1,...,vn} constituyen una base de ℝn
Son retículos euclideos: ℤ al que se le suele llamar retículo cúbico. El checkerboard lattice, o tablero de damas 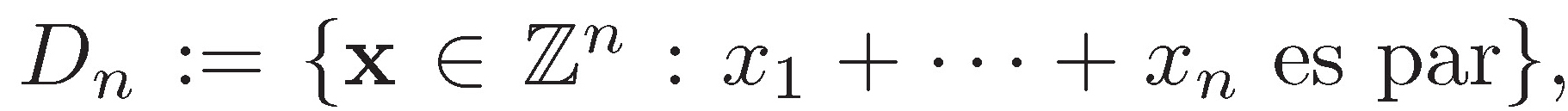 también es un retículo n-dimensional
también es un retículo n-dimensional 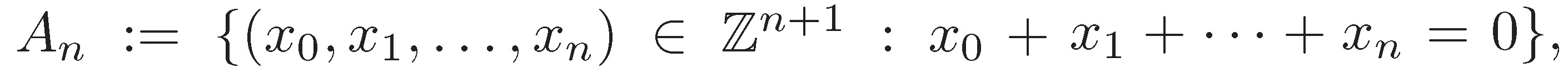 que por economía en la escritura conviene presentarlo como subconjunto de
que por economía en la escritura conviene presentarlo como subconjunto de 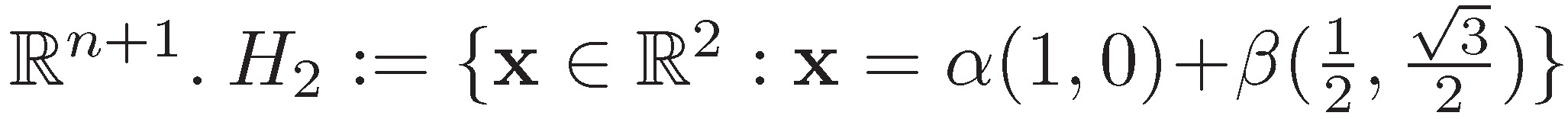 , al que comúnmente se le llama retículo hexagonal, entre otros.
, al que comúnmente se le llama retículo hexagonal, entre otros.
Alrededor de cada punto u0 de un retículo L se encuentra su celda de Voronoi S (u0), la cual se define como el conjunto de puntos del espacio euclídeo ℝn cuya distancia a u0 es menor o igual que la distancia a cualquier otro punto de L. Si N (z) = z · z, la norma al cuadrado de z, la celda S(u0) se describe como
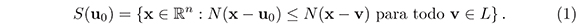
Es claro que en los retículos estas celdas son todas iguales, y producen un embaldosamiento (o tiling) del espacio ℝn. Una celda de Voronoi es primitiva si el embaldosamiento generado es tal que en cada vértice de una de las celdas concurren exactamente n + 1 de ellas, que es el mínimo número posible de celdas concurrentes. Adicionalmente, diremos que un retículo es primitivo si su celda de Voronoi asociada es primitiva.
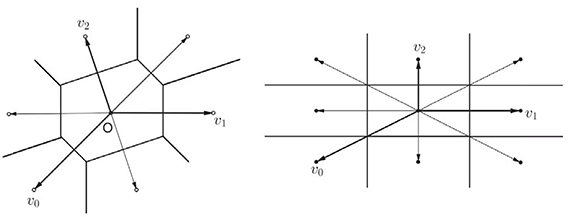
En dimensión 2 hay esencialmente dos tipos de celdas de Voronoi: una de forma hexagonal, la primitiva, y otra rectangular. La primera ocurre en el caso genérico, retículo tomado al azar. La Figura 1 muestra la forma de las celdas en dimensión 2.
Figuura 1. Celdas de Voronoi en dimensión 2
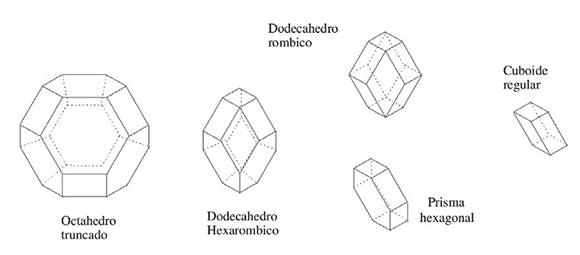
En dimensión 3 también hay una celda primitiva de la cual se desprenden 5 celdas de Voronoi distintas, salvo equivalencias combinatorias (Fedorov, 1953). La Figura 2 muestra la forma de todas las celdas en dimensión 3, En Conway y Sloane (1992) hacen una hermosa descripción de estas celdas por medio de lo que ellos llaman Vonormas y conormas.
Fugura 2. Celdas de Voronoi para retículos en dimensión 3
La celda de Voronoi es un elemento geométrico que cumple un rol fundamental en la mayoría de los problemas importantes relacionados con retículos, entre los que se destacan: The packing problem, donde se trata de empaquetar esferas del mismo tamaño de la manera más eficiente posible, es decir, disponiéndolas unas sobre otras de la forma más densa posible; The covering problem, en el que se busca cubrir el espacio con esferas del mismo tamaño, estas esferas se superponen de la manera más "económica" posible; The kissing number o número de contacto, en el que se quiere disponer el mayor número de esferas del mismo tamaño de manera que todas ellas besen â sean tangentesâ a una esfera prefijada; por último The lattice quantizer problem, donde tras un proceso de discretización, se quiere encontar la forma de la celda que minimiza el error cometido en el proceso de discretización, este problema solo ha sido resuelto en dimensiones 2 y 3. Para ampliar la información sobre estos y otros problemas relacionados, [Conway 1999, Chap 1].
En términos generales, podemos decir que se ha avanzado poco en la solución de estos problemas [Conway 1999, Chap 1]. Una de las razones es que las cuentas involucradas en ellos son muy grandes y dispendiosas aun en dimensiones bajas. Además que usan los parámetros de Selling, las vonormas o las conormas, los cuales aumentan en número muy rapidamente con relación a la dimensión del retículo. El lector puede encontrar información sobre el estado actual de estos problemas en (LATICE, s.f.).
La clasificación de las celdas de Voronoi en dimensiones bajas ha sido revisitada por varios autores en diferentes momentos de la historia, se destacan los enfoques dados por Delone [9], Conway & Sloane, con las Conormas y Vonormas [Conway & Fung, 1997; Conway & Sloane, 1992), el de Ryskov & Baranovski en (Ryskov & Baranovskii, 1978) con las llamadas L-formas, y más recientemente el de Valentin (Vallentin, 2003), por medio de formas cuadráticas semidefinidas positivas. Todas las clasificaciones usan de una u otra manera la correspondencia entre retículos y formas cuadráticas definidas positivas (FCDP). Para retículos 4-dimensionales se puede usar un método de reducción de formas cuadráticas dado por Charve (Charve, 1882) para obtener información de la celda.
Tras una lectura minuciosa del trabajo de Charve, conseguimos implementar su método de reducción de formas cuadráticas cuaternarias definidas positivas, y lo usamos para obtener el tipo primitivo que le corresponde a la celda de Voronoi del retículo asociado, información que es vital a la hora de calcular la constante de cuantización del retículo. En una investigación en curso, el autor de este artículo ha determinado que la reducción propuesta por Charve brinda información clave a la hora de calcular la constante de cuantización de un retículo 4-dimensional, problema que en la actualidad no ha sido resuelto.
2. Preliminares y conceptos básicos
Sean v1 = (v11, v21,...,vn1)tr,...,vn = (v1n, v2n,...,vnn)tr, donde tr denota el transpuesto, una base de un retículo n-dimensional L. Una matriz generadora M tiene por columnas los vectores v1, v2,...,vn. Es claro que t ∈ L si y solo si para algún x ∈ ℤn se tiene que t = Mx. Adicionalmente, A = Mtr M se conoce como matriz de Gram, y es tal que la norma cuadrado del punto t = Mx, IItII2 = t · t, se puede escribir como N(x) = xtrAx, la cual pensada en función de x, resulta ser una forma cuadrática definida positiva asociada a L.
Un punto típico t ∈ L puede describirse al menos de tres maneras distintas: En términos de sus t-coordenadas euclídeas, es decir, se lo puede ver como un punto t = (t1, t2,...,tn)tr de ℝn, o por medio de sus coordenadas enteras, que llamaremos x-coordenadas asociadas a una base v1, v2,...,vn, donde x = (x1, x2,...,xn)tr ∈ ℤn es tal que t = x1v1+x2v2+···+xnvn, equivalentemente t = Mx, o por medio de las y-coordenadas de t, definidas como y = Ax.
Hacemos notar que t · t = xtrAx = N(x), lo cual corresponde al cuadrado de la distancia entre el punto t y el origen, además t · t = ytr A−1y.
Decimos que dos retículos son equivalentes, si uno de ellos puede obtenerse del otro por medio de una rotación, y/o un cambio de escala. En formas cuadráticas, decimos que dos formas f(x) = xtr Ax, g(x) = xtrBx son equivalentes si existe una matriz entera U con determinante ±1 tal que B = Utr AU.
Hay una biyección natural entre las clases de retículos isométricos y las clases de formas cuadráticas definidas positivas aritméticamente equivalentes (Schürmann & Vallentin, 2005; Vallentin, 2003). En virtud de esta biyección, muchos aspectos de los retículos se pueden tratar desde el punto de vista de las formas cuadráticas y viceversa, con lo cual problemas de tipo geométrico asociados a los retículos se pueden tratar desde un punto de vista algebraico.
Si Φ es una forma cuadrática cuaternaria definida positiva (FCCDP), se pueden encontrar escalares fijos, pij con 0 ≤ i < j ≤ 4, a los que se les llama Parámetros de Selling, tales que si x = (x0, x1, x2, x3, x4)tr con x0 = −(x1 + x2 + x3 + x4), entonces
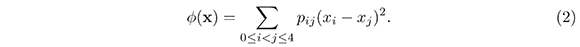
Adicionalmente, denotemos por pi|jklm a la suma pij + pik + pil + pim, y sea
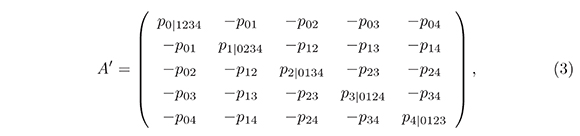
unas pocas cuentas muestran que Φ(x) = xtrA'x.
Definición 2.1. Decimos que Φ, escrita en la forma dada por (2), está reducida si satisface una de las siguientes tres condiciones:
i. Todos los coeficientes pij en (2) son no negativos.
ii. Hay un único coeficiente negativo en (2), digamos pst, todos los demás son no negativos y se cumple que |pst| ≤ pij, para {s, t} ∩ {i, j} ≠ ∅
iii. Exactamente dos coeficientes en (2) que no comparten subíndices son negativos, digamos pst y puv, los demás son no negativos y satisfacen: |pst| ≤ pij para {s, t} ∩ {i, j} ≠ ∅, |puv| ≤ pij para {u, v} â© {i, j} ≠ ∅ y |pst + puv| ≤ pij con i ∈ {s, t} y j ∈ {u, v}.
El siguiente teorema, establece que toda forma cuadrática cuaternaria definida positiva tiene una y solo una forma cuadrática aritméticamente equivalente que es reducida en el sentido de la definición anterior. La prueba del teorema es constructiva y se corresponde esencialmente con el algoritmo de reducción que presentamos en la Sección 3. El lector puede consultar dicha prueba en Charve (1882).
Teorema 2.2 (Charve). Toda forma cuadrática cuaternaria definida positiva, (FCCDP), tiene una y solo una forma cuadrática cuaternaria reducida que le es aritméticamente equivalente.
De otro lado, si L es un retículo 4-dimensional con matriz de Gram A, sabemos que N(x) = xtr Ax es una FCCDP, en virtud de la Definición 2.1, diremos que L es de Tipo I, Tipo II, o Tipo III, si su forma cuadrática asociada N(x) = xtr Ax, es aritméticamente equivalente a una forma cuadrática reducida que cumple respectivamente la condición i, ii ó iii de la Definición 2.1.
Observación 2.3. Se puede probar que un retículo 4-dimensional es primitivo si y solo si su forma cuadrática reducida asociada, escrita en la forma (2), no tiene parámetros pij nulos.
3. Algoritmo de reducción
Consideremos como antes x = (x0, x1, x2, x3, x4)tr con x0 = −(x1+x2+x3+ x4), y para 0 ≤ i < j ≤ 4 sean pij números reales tales que
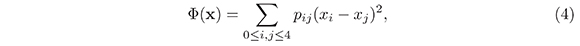
es una forma cuadrática cuaternaria definida positiva, 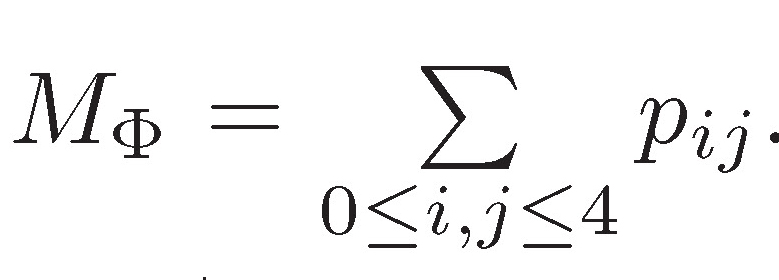 y sea Si Φ no está reducida de acuerdo con la Definición 2.1, necesariamente ocurre uno de los siguientes casos:
y sea Si Φ no está reducida de acuerdo con la Definición 2.1, necesariamente ocurre uno de los siguientes casos:
Caso 1. En (4), hay dos parámetros, pij y pit, que comparten un subíndice, tales que pij < 0 y |pij| > pit con t ≠ j. No hay pérdida de generalidad al asumir que p12 < 0 y |p12| > p13 en tal caso, al aplicarle a Φ(x) la transformación T1 dada por:
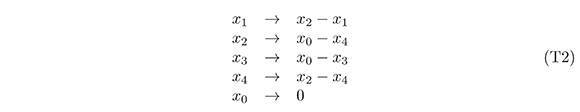
obtenemos la forma cuadrática Φ(x) = (p02+p12)(x0−x1)2+(p03+p13)(x0−x2)2+ (p12+p13+p14)(x0−x3)2+(p04−p12−p13)(x0−x4)2+p23(x1−x2)2−p12(x1−x3)2+ (p12+p24)(x1−x4)2−p13(x2−x3)2+(p13+p34)(x2−x4)2+(p01+
Caso 2. En (4) hay dos parámetros negativos, digamos pij y pkl, que no comparten subíndices, tales que |pij + pkl| > pik. No hay pérdida de generalidad al suponer que tales parámetros son p12, p34 y p13, es decir:
p12 < 0, p34 < 0, y |p12 + p34| > p13
en este caso, la transformación T2 dada por:
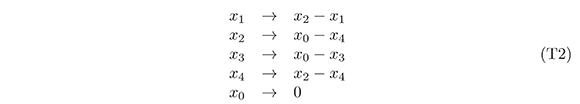
envía a Φ en la forma cuadrática Φ(x) = −(p12+p13)(x0−x1)2+(p12+p13+p24+ p34)(x0 − x2)2 + (p03 + p13 + p34)(x0 − x3)2 + (p02 + p12 − p34)(x0 − x4)2 + (p01 + p12+p13)(x1−x2)2+p13(x1−x3)2+(p12+p14)(x1−x4)2−(p13+p<(34)(x2−x3)2+(p04 − p12 + p34)(x2 − x4)2 + (p01 + p12 + p13)(x3 − x4)2, que es aritméticamente equivalente a Φ, y cuya suma de parámetros es M = (p12 + p13 + p34) +MΦ.
Hacemos notar que en cualquier caso, si una FCCDP no satisface alguna de las condiciones de reducción de la Definición 2.1, siempre es posible encontrar otra forma cuadrática aritméticamente equivalente a ella, cuya suma de parámetros sea menor, de tal manera que al aplicar este proceso repetidamente, necesariamente se obtendrá una forma cuadrática reducida que le es equivalente.
El proceso termina ya que la suma de los pij es acotada inferiormente por una constante que depende solo de los vectores de longitud mínima del retículo, y dado que estos son únicos, el proceso no se puede extender indefinidamente. Más específicamente, el algoritmo comienza con un M0 ⅀= pij , que podemos pensar asociado a una superbase del retículo correspondiente a la FCCDP, esto es: Una base aumentada en un vector para que la suma de los mismos sea cero, y el algoritmo va reduciendo estrictamente el valor de M0.
En cada paso se cambia de forma cuadrática, lo que geométricamente equivale a cambiar la superbase por una cuya suma M es menor a la anterior, pero solo hay un número finito de estas superbases, así que los posibles estados (formas cuadráticas) por los que el algoritmo puede pasar es finito, y en consecuencia el proceso de reducción no se puede extender indefinidamente.
Los pasos para aplicar el proceso de redución son los siguientes:
Paso 1. Permute los índices de manera tal que el menor parámetro sea p12 y el menor de los que comparte un índice con él sea p13.
Paso 2. Si p12 ≥ 0, entonces la forma cuadrática satisface la condición (i) de la definición de reducción, en tal caso (i) ocurre y el proceso de reducción termina.
Paso 3. Si p12 < 0, y |p12| ≤ p13 y mín{p03, p04, p34} ≥ 0 entonces la condición (ii) ocurre y el proceso de reducción termina.
Paso 4. Si p12 < 0 y |p12| > p13 entonces aplique la tranformación (T1) y regrese al Paso 1.
Paso 5. Si p12 < 0 y |p12| ≤ p13 y defina pst := mín{p03, p04, p34} < 0, entonces aplique una permutación que lleve a pst y al menor parámetro que comparte un índice con él a los parámetros p12 y p13 respectivamente.
Paso 6. Si |p12| > p13 aplique la transformación (T1) y regrese al Paso 1, en caso contrario, aplique una permutación que fije p12 y envíe al menor parámetro con índices en {0, 3, 4} a p34.
Paso 7. Si |p12 + p34| ≤ mín{p13, p14, p23, p24}, entonces se cumple la condición (iii) y el proceso de reducción términa. En caso contrario, aplique una permutación que fije a p12 y p34 y que envié en p13 al mínimo entre {p13, p14, p23, p24}, entonces aplique la tranformación (T2) y regrese al Paso 1.
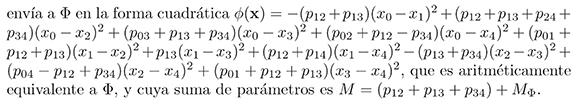
Antes de comenzar el proceso de reducción veamos primero que Φ representa una FCCDP, equivalentemente un retículo 4-dimensional, para lo cual construimos AÏ, matriz tipo Gram asociada a Φ, y verificamos si dicha matriz es definida positiva. En este caso
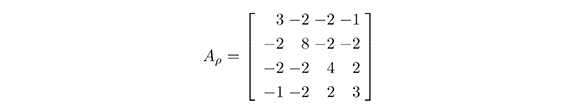
Dado que los menores principales de A&Ro; son 3, 20, 20 y 22, el criterio de Sylvester garantiza que la matriz es definida positiva, y por lo tanto &Ro; representa una FCCDP o un retículo 4-dimensional.

En una investigación sobre el problema del cuantizador óptimo en retículos euclideanos 4-dimensionales, hemos encontrado que para poder calcular el valor de la constante de cuantización de un tal retículo, es indispensable conocer su tipo primitivo, este hecho hace que los algoritmos aquí presentados jueguen un papel esencial en nuestro intento de resolver el problema del retículo cuantizador óptimo 4-dimensional.
4. Implementación
A continuación presentamos el código de una posible implementación del algoritmo de reducción arriba descrito, el mismo puede ejecutarse en el toolbox matemática simbólica de Matlab o en el sistema computacional MuPAD.
Primeroo algunos programas auxiliares
El procedimiento DP, determina si los parámetros que se ingresan representan una FCCDP equivalentemente un retículo 4 dimensional o no

Para un parámetro de Selling dado, el procedimiento aur, calcula la menor suma entre dicho parámetro y aqueññps otros parámetros en la forma cuadrática que comparten un índice con él.

El procedimiento Sel prepara los parámetros para que sea más fácil verificar las condiciones de reducción.

Referencias
Barnes, E. S., & Sloane, N. J. A. (1983). The optimal lattice quantizer in three dimensions. SIAM J. Algebraic Discrete Methods, 4 (1) 30-41. [ Links ]
Charve, L. (1882). De la réduction des formes quadratiques quaternaires positives. In, Annales scientifiques de l' Ecole normale supérieure 2, tome 11, (pp. 119-134). Paris, France. [ Links ]
Conway, J. H., & Fung, F.Y.C. (1997). The sensual (quadratic) form. Carus Mathematical Monographs, 26 Math. Washington D.C., USA: Assoc. of America. [ Links ]
Conway, J. H., & Sloane, N. J. (1992, January). Low-dimensional lattices. VI. Voronoi reduction of three-dimensional lattices. In, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, v. 436, n. 1896 (pp. 55-68). London, UK: The Royal Society. [ Links ]
Conway, J. H., & Sloane, N. J. A. (1984). On the Voronoi regions of certain lattices. SIAM Journal on Algebraic and Discrete Methods, 5 (3), 294-305. [ Links ]
Conway, J. H., & Sloane, N. J. A. (1999). Sphere Packing, Lattices and Groups (3 ed.). New York, USA: Springer-Verlag. [ Links ]
Conway, J., & Sloane, N. (1982). Voronoi regions of lattices, second moments of polytopes, and quantization. IEEE Transactions on Information Theory, 28 (2), 211-226. [ Links ]
Delone, B. N. (1929). Sur la partition r'egulière de l' espace á 4-dimensions. Izv. Akad. Nauk SSSR Otdel. Fiz.-Mat. Nauk, 1, 79-110. [ Links ]
Deza, M., & Grishukhin, V. P. (2008). More about 52 four-dimensional parallelotopes. Taiwanese J. Math., 12 (4), 901-916. Recovered 15/10/2016 http://arxiv.org/pdf/math/0307171 [ Links ]
Engel, P., & Grishukhin, V. P. (2002). There are exactly 222 L-types of primitive five-dimensional lattices. European J. Combin., 23 (3), 275-279. [ Links ]
Fedorov, E. S. (1953). Elements of the study of figures. Zap. Mineralog. Obsc. 21 (2), 1-279. [ Links ]
LATICES (s.f.) A Catalogue of Lattices. Recovered 15/10/2016 http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/ [ Links ]
Lenstra, A.K., Lenstra, H. W. Jr., & Lov'ask, L. (1982). Factoring polinomials with rational coefficients. Math. Ann., 261 (4), 515-534. [ Links ]
Ryskov, S. S., & Baranovskii, E. P. (1978). C-types of n-dimensional lattices and 5-dimensional primitive parallelohedra (with application to the theory of coverings). Proc. Steklov Inst. Math., (4), 140. [ Links ]
Schürmann, A. (2009). Computational Geometry of Positive Definite Quadratic Forms: Polyhedral Reduction Theories, Algorithms, and Applications. Providence, USA: American Mathematical Society. Recovered 15/10/2016 http://www.ams.org/books/ulect/048/ulect048-endmatter.pdf [On line] [ Links ]
Schürmann, A., & Vallentin, F. (2005/07/27). Computational Approaches to Lattice Packing and Covering Problems. Recovered 15/10/2016 http://arxiv.org/pdf/math/0403272v3 [ Links ]
Vallentin, F. (2003). Sphere covering, lattices, and tilings (in low dimensions). Ph.D. thesis, Technical University Munich, Munich, Germany. [ Links ]
Voronoi, G. F. (1909). Nouvelles applications des paramèters continus à la théorie des formes quadratiques. J. Reine Angew. Math., 133 (1908), 97-178; 134 (1908) 198-287; 136, (1909) 67-181 [2,21] [ Links ].

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.