Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ciencias
Print version ISSN 0121-1935
rev. cienc. vol.19 no.2 Cali July/Dec. 2015
Equations of Lax type with several brackets
Raúl Felipe
CIMAT, Guanajuato - Mexico
E-mail: raulf@cimat.mx
Raúl Velásquez
Instituto de Matemáticas, Universidad de Antioquia, Medellín - Colombia
raul.velasquez@udea.edu.co
Received: April 30, 2015
Accepted: December 23, 2015
Abstract
In the present paper we introduce a new hierarchy, each equation of which is defined by several brackets of two pseudodifferential operators. We deal with some algebraic properties of these equations. In particular, we show that, as in the classic case, they are related to the presence of an infinite sequence of first integrals. A new version of the Zakharov-Shabat type equations is proved. Formal solutions of this hierarchy are constructed using a "several brackets bilinear identity".
Keywords: pseudodifferential operators, Zakharov-Shabat type equations.
1. Introduction
Recently, great progress has been made in the construction of integrable systems. It has been found that integrable systems usually admit a natural extension by odd variables, and multi-dimensional and integral generalizations of soliton equation have been considered. In this paper we will concentrate on another form of construction of these systems: equations of Lax type with several brackets.
Equations with several brackets arose originally in the work of Brockett (1989; 1991), for ordinary differential equations, and then in Felipe (Felipe, 1999) for partial differential equations of Lax type with double brackets (see (Felipe & Ongay, 2001)for the super Brockett equations type).
The study of flows of the form
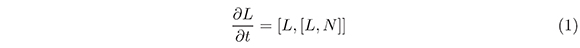
on Lie algebras of finite dimension (that is for ordinary differential equations) was first made by R. W. Brockett (see Brockett ,1989, and Brockett, 1991), who observed that this type of equations are interesting because of their relation with problems of counting and combinatorial optimization. In the case of the Toda lattices, we obtain an integral Hamiltonian system that is also a gradient flow. Also R. W. Brockett, A. Bolch and T. S. Ratiu (see Bolch et al., 1991) introduced a continuous analog of Toda Lattices (partial differential equations) that can be written as (1) and showed, in additi, that this equation has a set of functional invariants or conserved quantities.
More recently Felipe (see Felipe, 1999) introduced a hierarchy on the Lie algebra of pseudodifferential operators (the so-called hierarchy of Brockett) of the following form:
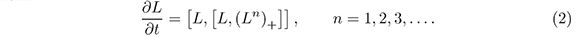
Remarkably, this hierarchy shares many properties of its finite dimensional counter part, and one of our goals is to extend this study to hierarchies defined by more brackets.
As yet another generalization, we investigate here equations of the form:
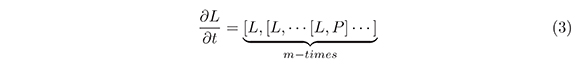
where L, P :ℝ+ → g and g is a Lie algebra. We will show that the algebraic situation is the same as the usual KP system studied in Dickey (1991), Manin (1979) and Mulase (1984) (See Mulase, 1984, for the super KP equation). In particular, that a construction of Adler gives, in this context, invariant functions.
As is well known, the definition of complete integrability in the infinite dimensional case is more subtle than in the finite dimensional one. The one we will use here is the existence of an infinite number of conserved quantities.
This paper is organized as follows. In section 2 we generalize the usual KP framework to the case of several brackets. Then, in section 3 we show that as in the classical case the equations (3) are related to the presence of an infinite sequence of first integrals. Section 4 exhibits some new integral systems. Finally, in section 5 we will emphasize the role of the Baker-Akhiezer function and one of our results will be a "several brackets bilinear identity".
2. Notations and Preliminary Results
In this section we give a brief introduction to pseudodifferential operators. Ordinary differential operators can be written as
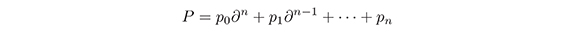
where the coefficients pi are supposed to lie in some differential algebra over ℂ of smooth functions of x, for example 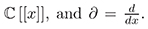 A pseudodifferential operator is a formal series of the form:
A pseudodifferential operator is a formal series of the form:
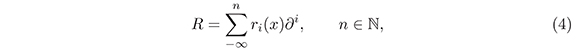
where the operator ∂1, i ∈ ℤ, acts according to the rules (see e.g. [5])
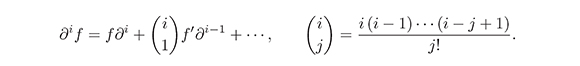
Notice that the above equation is a generalization of the well-known Leibniz rule.
We introduce the product of two operators of the form (4). First we define
∂n . ∂m = ∂n+m, ∂0 = 1 (n,m ∈ ℤ).
It is easy to see that
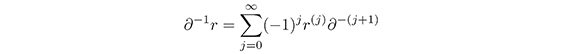
where 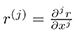 (see e.g. [5]).
(see e.g. [5]).
It is easy to check that this makes the set of all pseudodifferential operators an associative algebra, which we denote by ψDO. If 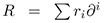 is a pseudodifferential operator, we will write R+ for the differential operator part,
is a pseudodifferential operator, we will write R+ for the differential operator part, 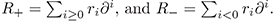
Thus R = R+ + R−. An element R ∈ ψDO has order n if
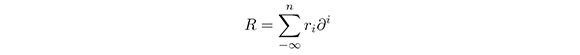
and rn ≠ 0. We denote ord(R) = n. If ord(R) = n and rn = 1, R is called a monic operator. Let E(n) be the set of all elements in ψDO of order at most n. Then, we have formally a direct sum decomposition
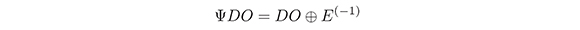
where DO is the set of all differential operators (R = R+ if R ∈ DO [R1,R2] = R1R2 − R2R(1).
We choose a subset of ψDO whose elements Φ can be expressed by:
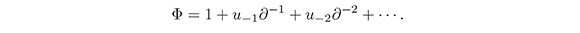
The operators belonging to this set are invertible and forms a group, denoted by (ψDO)*.
We call a first order monic operator of the form:
L = ∂ + u-1∂-1 + u-2 ∂-2 + ...
a Lax operator (u-n = u-n (x,t)). We set Ln = Ln = Ln-1. L. Then,
Ln = ∂n + qn-2 ∂n-2 + qn-ε ∂n-3 + ... .
We recall that if 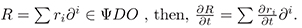
Let L be a Lax operator. An equation of Lax type with m brackets, formed from L is an equation of the form:
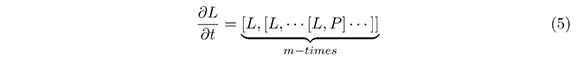
where P ∈ DO. In the rest of this paper we use the following notation of Mulase:
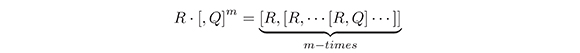
Namely, R · [,Q] = [R,Q], R · [,Q]2 = [R, [R,Q]] etc.
The possible operators P in (5) must satisfy the requirement that L · [,P]m ∈ E(−1). Hence, such a pair (P,L), where P ∈ DO and L is a Lax operator will be called admissible. If L is a Lax operator, then, as in the classical case, for n ∈ ℕ, (Ln)+ , L) is an admissible pair.
Lemma 1. Let L be a Lax operator, P ∈ DO such that [L, P] ∈ E(−1). Then, P is a linear combination of the (Ln)+, n = 0, 1,..., with coefficients in ℂ and (P,L) is an admissible pair.
Proof. This Lemma follows directly from the Lemma 3.1 of (Manin, 1979).
It should be noted that the condition [L, P] ∈ E(−1) for P ∈ DO implies that the highest order coefficient of P is a constant. On the other hand, if (P,L) is an admissible pair, then, the highest order coefficient of P is a polynomial of the form (am−1xm−1 + am−2xm−2 +···+a1x+a0), where the ai are complex numbers for i = 0, 1,···m − 1.
Lemma 2. Let L be a Lax operator, and (P,L) be an admissible pair such that the top order coefficient (am−1xm−1 + am−2xm−2 +···+ a1x + a0) of P is not constant, then, if ord(P) = n, P can be written in the following form
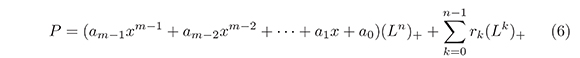
where rk ∈ ℂ [[x]] for every k.
Proof. Suppose that the Lemma is true for all admissible P ∈ DO of order less than n, such that the highest order coefficient is not constant. Let us take an admissible pair (P,L), such that, ord(P) = n and with the same property. Let (am−1xm−1 + am−2xm−2+···+a1x + a0) be the highest order coefficient of P, then, we define:
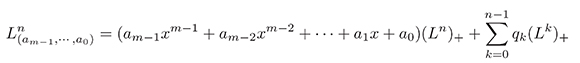

where tk ∈ ℂ[[x]]. Therefore, P can be represented as a ℂ[[x]]-linear combination of (Lk)+'s, which coincides with (6).
Definition 1. Let L be a Lax operator, then, the following system of infinitely many equations of Lax type with m brackets is called the m-brackets hierarchy
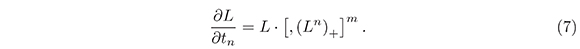
We assume that the coefficients of L in (7) are functions dependent on some additional variables t1, t2, t3,...,tn,.... We remark that L = ∂ is a trivial solution of (7).
Note that equation (7) can be interpreted as the compatibility condition for the following system of equations:
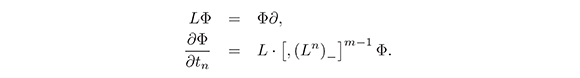
for a formal (ψDO)* -function Φ(x, t1, t2,...).
In many cases it is possible and convenient to represent the Lax operator L in a formal dressing form L = ψ ∂ Φ−1, where Φ ∈ (ψDO)* is determined up to multiplication on the right by a series in ∂−1 with constant coefficients (independents of x, but can be depend about the time variables t1, t2,....) starting with 1. In terms of Φ, the equations of the m-brackets hierarchy are:
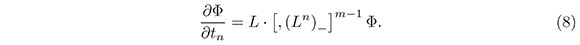
In fact, let Φ be a solution of (8), where L = Φ ∂ Φ−1 then L is a Lax operator that satisfies (7). To see this, notice that from (8) we immediately obtain the equation
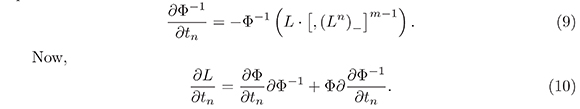
If we replace 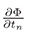 and
and 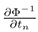 in (10) by the right hand side of (8) and (9) respectively, we have:
in (10) by the right hand side of (8) and (9) respectively, we have:
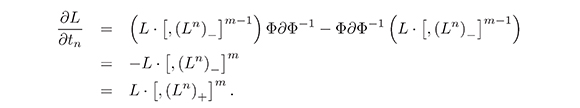
Now we can prove the following lemma:
Lemma 3. Let L = Φ ∂ Φ−1, where Φ ∈ (ψDO)*, then, (n,m ≥ 1)
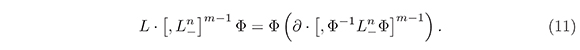
Proof. We will prove it by induction. First we prove the formula:
L · [,L_n] Φ = Φ (∂ · [Φ-1 L_n Φ]).
In fact,
Thus, the equality (11) holds. Let (11) be true for m = k, then,
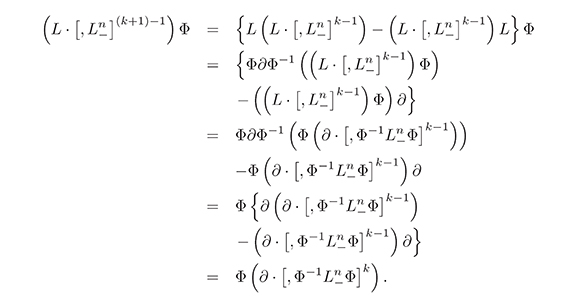
Lemma 4. The operator
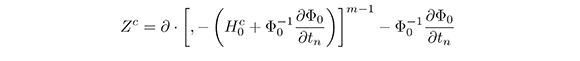
where
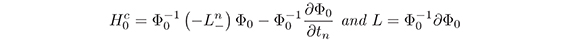
has only constant coefficients.
Proof. Lemma 4 shows that
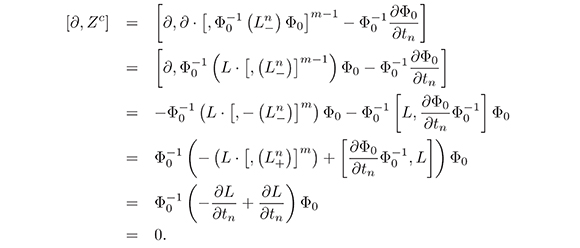
Theorem 1. Let L be a Lax operator such that L satisfies equation (7) for n fixed, then, there is an operator Φ ∈ (ψDO)*, where L = Φ ∂ Φ−1, satisfying the equation (8) for this n.
Proof. Suppose L satisfies the equation (7). Let Φ0 ∈ ()* be an operator such that L = Φ0∂ Φ−10 , then, from the Lemma 5, there is a constant element ℂ ∈ (ψDO)* (See e.g. Mulase, 1984) such that
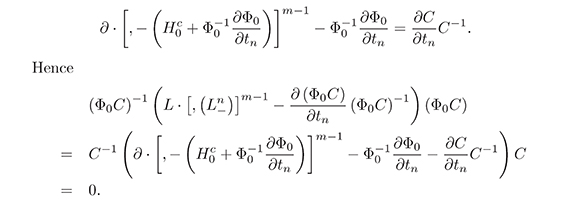
Let Φ = Φ0C. Note that Φ∂ Φ−1 = (Φ0C) ∂ (Φ0C)−1 = Φ0∂Φ−10 = L. Thus, we have found an operator Φ ∈ (ψDO)* satisfying equation (8).
3. Invariant Polynomial Functions
In this section we will work with pseudodifferential operators (4). A conservation law is an identity
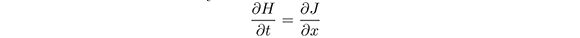
that follows formally from (5). The conserved density H and flux J are differential polynomials in u−1, u−2, u−3,... and their x-derivatives 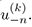 An invariant polynomial functional for (5) is a function of the form:
An invariant polynomial functional for (5) is a function of the form:
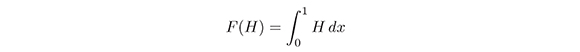
where H is a conserved density. Notice that if F is an invariant polynomial function, then, 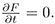
For R ∈ ψDO we define the residue as:
resR = r−1.
Next, we shall also use the Adler function
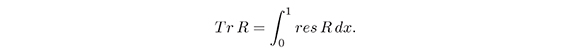
This functional has the property Tr [R1,R2] = 0, for every R1,R2 ∈ ψDO (see the proof of Theorem 8).
Lemma 5. For any k ≥ 2, by virtue of the equations (7), then,
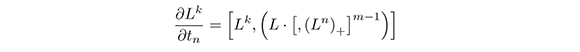
holds.
Proof. Let k = 2, then,
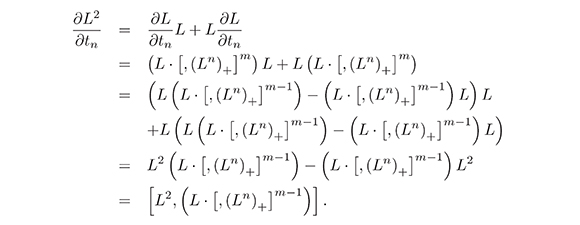
Now, we suppose that the lemma is true for k = r, i.e.
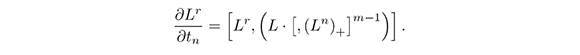
We have:
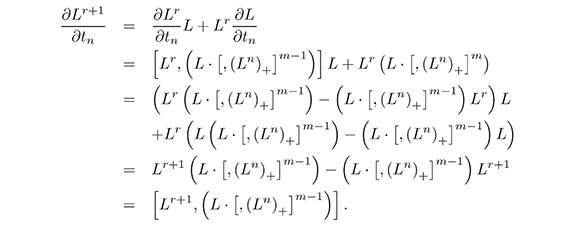
Theorem 2. The polynomial functionals
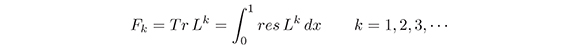
are invariant polynomial functionals.
Proof. It is well know that res [R1,R2] = ∂h (see e.g. Dickey, 1991), where h is a differential polynomial in the coefficients of R1 and R2, R1,R2 ∈ ΨDO. Hence
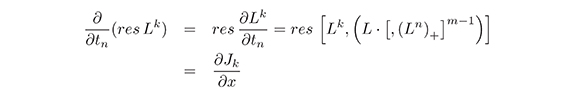
where Jk are differential polynomials in u−n, n= 1,2,3,...; and their x-derivatives 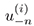 i,n = 1,2,3,....
i,n = 1,2,3,....
4. Zakharov - Shabat Type Equations and Some New Integral Systems
The purpose of this section is to show how the system (7) generates new zerocurvature type equations.
Theorem 3. Let Bq = (Lq)+, q ≥ 1. Equations (7) imply that:
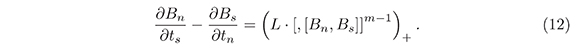
Further, every equation given by (12) is equivalent to a finite system of equations, the number of equations being equal to the number of unknown quantities, i.e. is equivalent to a closed system of partial differential equations.
Proof. It is easy to see that if q ≥ 1, then,
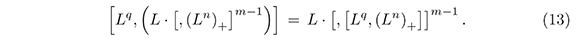
In fact, for B ∈ ΨDO we have:
Lq · [, [L,B]] = L · [, [Lq,B]] ,
(See [6] for more details). Now, this result implies (13).
¿From (13), and according to lemma 7,
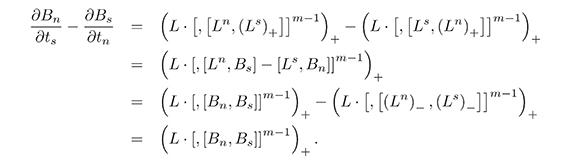
5. The Baker - Akhiezer Function
The main purpose of this section is to prove a bilinear identity with several brackets for the Baker-Akhiezer and the ad joint Baker-Akhiezer functions (the proof of the bilinear identities is essentially the same as in Felipe, 1999); they will play a crucial role in obtaining "formal solutions" of the hierarchy (7).
A formal eigen function W of L with eigenvalue z, the so-called Baker-Akhiezer function, is very important in this theory (See Cherednik, 1978). For a solution
L = ∂ + R_1∂−1 + · · ·
to the m−bracket hierarchy (8), we have, in terms of the dressing operator Φ ∈ (ψDO)*, the associated Baker-Akhiezer function:
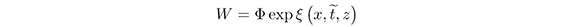
(Recall that L = Φ∂Φ−1) where 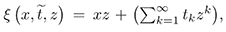 satisfying the equations:
satisfying the equations:
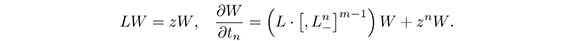
The second equation yields:
τnW = BnW (14)
where 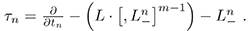 Also, the equation (18) can be written in the following form:
Also, the equation (18) can be written in the following form:
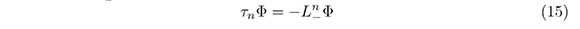
The ad joint Baker-Akhiezer function is:
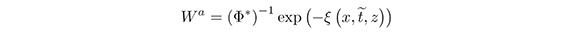
where the star means the conjugation, i.e. if 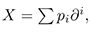 then,
then, 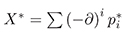 where pi* is the transpose of pi.
where pi* is the transpose of pi.
Proposition 1. Suppose we have a solution L of (7) and L = Φ∂Φ−1. Then, the following "double bracket bilinear identity"
resz (∂iτinW) · (Wa) = 0
holds for any (i, j, n) and i ≥ 0, j = 0, 1 and n ≥ 1, where 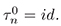 Here W and Wa are the Baker-Akhiezer and ad joint Baker-Akhiezer function respectively.
Here W and Wa are the Baker-Akhiezer and ad joint Baker-Akhiezer function respectively.
The notation resz means the coefficient of z−1. The notation res∂ means the coefficient of ∂−1.
Proof. Since τnW = BnW, it is sufficient to prove this equality for j = 0 and i ≥ 0, but in this case the proof is well known (see e.g. [5]) and therefore, it is omitted.
It is worth mentioning that if there are two expressions
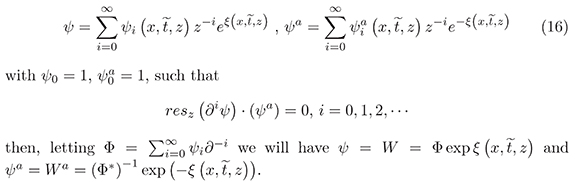

6. Open Problems
A problem for further work is to find solutions of the hierarchies using the Tau functions (see e.g. Dickey, 1991) which must exist according to the results obtained. The problem is to find what forms the Tau functions can have. For example, for the equations of the Brockett hierarchy one step to follow is to study the Tau function for the first equation of the hierarchy; i.e., find its expression in Hirota form and then calculate the explicit form of the Tau function. Furthermore, one should be able to show that similar results exist for all the hierarchy. For the existence of the Tau function, we can assume that all these hierarchies are constituted by commutative laws. In this paper we have not shown this commutability. However, good results can be obtained by showing commutability in the general case.
A very interesting problem arises here, namely to try to extend the approach of Mulase for the hierarchy KP to the hierarchies with several brackets; we do not know what results of factorization for pseudo differentials operators are lacking. In order to attack this problem one has to start with the study of the Brockett hierarchy, and in this case it consists of linearizing the hierarchy using theorems of factorization of the Birkhoff type for groups of Loops. This problem apparently is very difficult.
Another topic of investigation that could be followed is to study discrete hierarchies of equations of Lax type with several brackets using the shift matrix. This subject must have connection, as in the case of the discreet KP, with matrices of moments and orthogonal polynomials. Here, one can also consider to extend the method of Mulase in this context, as done by Felipe and Ongay (see [8]) for the discrete KP.
Acknowledgments
The second author was partially supported by CODI (Comit para el Desarrollo de la Investigación) and SUI (Sistema Universitario de Investigación), Universidad de Antioquia.
References
Bolch, A. M., Brockett, R. W., & Ratiu, T. S., (1992). Completely integrable gradient flows. Commun. Math. Phys., (147) 57-74. [ Links ]
Brockett, R. W. (1989). Least squares matching problems. Linear algebra and its applications, 122 (123-124), 761-777. [ Links ]
Brockett, R. W. (1991). Dynamical system that sort lists, diagonalize matrices and solve linear programming problems. Linear algebra and its applications, (146) 79-91. [ Links ]
Cherednik, I. V. (1978). Differential equations for the Baker-Akhiezer functions of algebraic curves. Funct. anal. appl., 12 (3), 195-205. [ Links ]
Dickey, L. A. (1991). Soliton Equations and Hamiltonians system. Advances series in Mathematical Physics, 12. [ Links ]
Felipe, R. (1999). Algebraic aspects of Brockett type equations. Physica D, (132) 287-297. [ Links ]
Felipe, R., & Ongay, F. (2001). Algebraic aspects for the discrete KP hierarchy. Linear algebra and its applications, (338) 1-17. [ Links ]
Felipe, R., & Ongay, F. (2001). Super Brockett equations: A graded grandient flow. Commun. Math. Phys, (220) 95-104. [ Links ]
Manin, Y. I. (1979). Algebraic aspects of nonlinear differential equations. J. Sov. Math., (11) 1-122. [ Links ]
Mulase, M. (1984). Cohomological structure in Soliton equations and Jacobians varieties. J. Diff. Geom., (19) 403-430. [ Links ]
Mulase, M. (1984). Complete integrability of the Kadomtsev-Petviashvili equation. Adv. Math, (54) 57-66. [ Links ]
Mulase, M. (1988). Solvability of the super KP equation and a generalization of the Birkhoff decomposition. Invent. Math, (92) 1-46. [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.














