Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ciencias
Print version ISSN 0121-1935
rev. cienc. vol.20 no.1 Cali Jan./June 2016
Talbot Non-linear Effect for a Bidimensional Network of Comparable Period to the Wavelength
Efecto Talbot no lineal para una red bidimensional de periodo comparable a la longitud de onda
Emiro Arrieta Jiménez
Departamento de Ciencias Básicas, Universidad de Córdoba, Montería - Colombia
E-mail: earrieta@correo.unicordoba.edu.co
Daladier Blanco Ávila
Estudiante, Programa de Física, Universidad de Córdoba, Montería - Colombia
E-mail: deba-09@hotmail.com
Cesar Torres Moreno
Grupo LOI, Universidad Popular del Cesar, Valledupar - Colombia
E-mail: cesartorres@unicesar.edu.co
Received: November 9, 2015
Accepted: March 16, 2016
Resumen
El efecto Talbot es un fenómeno difractivo ubicado desde su origen en la óptica Gaussiana, pero cuando la longitud de onda es comparable con el periodo del objeto se considera que este efecto entra en su régimen no lineal. En esta contribución, usando una onda plana monocromática, mostraremos analiticamente el Z-Talbot respectivo y una simulación para ubicar dos de las autoimágenes entre 0 y 10 μm generadas por una red de agujero bidimensional fabricada en pelicula de Au con periodo de 1, 9λ, que han sido reportadas de manera experimental en un articulo reciente.
Palabras clave: Z-Talbot, red, onda plana monocromática.
Abstract
The Talbot effect is a diffractive phenomenon located in the Gaussian optic field, but when the wavelength is comparable to the object period, it is considered that this effect enters in its nonlinear regime. Using a monochromatic plane wave, in this contribution, we show analytically the respective Z-Talbot and a simulation to locate two self-images between 0 and 10 microns generated by a two dimensional grating made with hole array films of Au with periodicity 1,9λ, which have been reported experimentally in a recent article.
Keywords: Z-Talbot, gratings, monochromatic plane wave.
1. Introducción
En 1836, H. Fox Talbot fue el primero en observar la periodicidad longitudinal del campo electromagnético difractado por una red de difracción en la dirección de propagación, es decir, obtuvo réplicas de esta red. Esta señal genera además otros patrones denominados imágenes Talbot fraccionales, en las que la distribución de amplitud es una versión del objeto periódico de partida con la misma celda unidad aunque con un período menor. Este último fenómeno es conocido como efecto Talbot fraccional. Por otro lado, Rayleigh demostró que la periodicidad longitudinal del campo difractado por una red de Ronchi a z = md2/λ donde d es el período espacial de la red y m un entero par) producen patrones que reproducen la entrada (Arrieta y Torres, 2015). También se tiene que, el efecto Talbot exhibe autoimagen cuando una rejilla se ilumina con una onda plana de alta coherencia espacial. Auto imágenes de la rejilla son producidas en ciertos planos detrás y en frente de la rejilla. Estas imágenes son producidas solamente por propagación en espacio libre de un campo óptico difractado (Smolyaninov & Davis, 1998). En el régimen metaxial a frecuencias ópticas, se pude usar el efecto Talbot para observar anomalías en objetos periódicos(o cuasi periódicos) que se veían perfectos en el régimen paraxial, es decir logrando "súperresolución" a esta escala (cuando el periodo del objeto periódico o cuasi periódico es menor o igual que 10 veces la longitud de la onda usada), en este caso, la posición de las autoimágenes no corresponde con la de la distancia Talbot paraxial (Huaet al., 2012). El efecto Talbot es uno de los fenómenos básicos de difracción en sistemas Gaussianos. Recientemente, imágenes Talbot producidas por un objeto periódico en un medio no homogéneo se describen teóricamente. Uno de los medios naturales en las que estas imágenes pueden ser estudiadas es en una convencional microlentes de gradiente de índice (GRIN), dando así una idea de este efecto a escala micrométrica (Flores-Arias et al., 2002). El efecto Talbot, también se ha usado en el estudio del régimen cromático y aplicación a la espectrometría 8Guérineun et al., 2003), aberraciones de las autoimágenes en el régimen pos paraxial (Ring et al., 2012), en el estudio de ondas plasmonicas (Dennis et al., 2007; Cherukulappurath et al., 2009) y cristales fotonicos no lineales [10], generación de conjunto de vórtices ópticos con el efecto Talbot fraccional (Wei et al., 2009), últimamente con red de volumen en cristales fotorrefractivos (Forte et al., 2011; Forte et al., 2011), y holografía digital (Martínez et al., 2009), entre otros. Por todo este gran volumen de aplicaciones que presenta este fenómeno y por el poco estudio que se ha realizado sobre este efecto a nivel no lineal con rejillas de difracción bidimensional de período comparable a las longitudes de onda a frecuencias ópticas, donde hasta el momento no se ha evidenciado de manera explícita una formula cuantitativa que dé cuenta de la ubicación de las autoimágenes como existe en el caso clásico (o paraxial), nosotros presentamos en este artículo, un estudio teórico de este fenómeno a escala bidimensional, de lo cual derivaremos el Z-Talbot respectivo, para lograr la ubicación de dos de las autoimagen reportadas experimental en la referencia 3 sin justificación analítica, usando una red de Au bidimensional de período 1, 9λ y una onda plana monocromática coherente de λ = 633 nm.
2. Efectoo Talbot no lineal
La teoria de las ondas escalar se utiliza tradicionalmente para el efecto Talbot en el limite paraxial, donde el patrón de luz de una matriz de agujero periódico en z = 0 (la estructura inicial) puede ser representado por una onda escalar Ψ y expandida en Fourier como una suma de ondas planas en la dirección de propagación de la luz z > 0[3]asi:
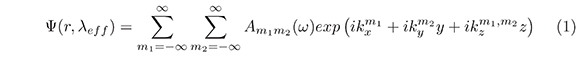
donde r =(x, y, z) es la posición espacial, λeff = λ/n es la longitud de onda efectiva en el medio con un indice de refracción 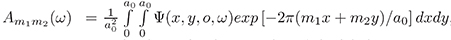 , es la amplitud compleja de la onda plana, donde a0 es el periodo del objeto propuesto, y m1, m2 números enteros.
, es la amplitud compleja de la onda plana, donde a0 es el periodo del objeto propuesto, y m1, m2 números enteros.
El vector de onda 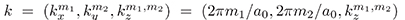 satisface lo siguiente
satisface lo siguiente 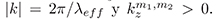 . En el limite paraxial donde a0 >> λeff , y expandiendo en Taylor para kz resulta:
. En el limite paraxial donde a0 >> λeff , y expandiendo en Taylor para kz resulta:
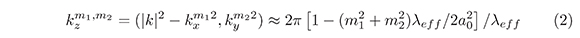
Si esta aproximación se aplica a la ecuación (1), se puede derivar la siguiente relación:
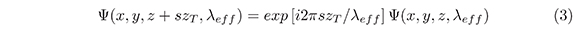
donde zT =2a02λeff es la distancia Talbot paraxial y s es un número entero. Por lo tanto, auto-imágenes exactas serán observadas a múltiplos enteros de zT por qué las intensidades satisfacen,
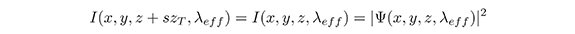
Más allá del limite paraxial, sin embargo, cuando a0/λeff se aproxima a la unidad, el desarrollo de Taylor en la ecuación (2)no es válido. Los patrones de luz todavia se pueden calcular con base a la suma de ondas planas, pero la aproximación a cerca de kz ya no puede ser utilizada. Para calcular el cambio de fase exacto de las ondas planas que se propagan (con exp(izkz)entérmino de la ecuación (1)), consideramos, más alládel limite paraxial, kz independientemente para cada plano de onda (m1,m(2). Cuando, kz es imaginario, tenemos las ondas evanescentes con 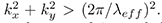 Por lo tanto, se simplifica el cálculo de xy patrones de luz en el campo lejano al despreciar las ondas evanescentes por su decaimiento exponencial. Por consiguiente, sólo las ondas planas que se propagan, representadas gráficamente como puntos de coordenadas (m1,m2) dentro del circulo con un radio de a0/λeff y k espacial, son consideradas.
Por lo tanto, se simplifica el cálculo de xy patrones de luz en el campo lejano al despreciar las ondas evanescentes por su decaimiento exponencial. Por consiguiente, sólo las ondas planas que se propagan, representadas gráficamente como puntos de coordenadas (m1,m2) dentro del circulo con un radio de a0/λeff y k espacial, son consideradas.
La condición para lograr auto-imágenes exactas requiere que todas las ondas planas estén en fase a la misma distancia. Si la frecuencia central (0, 0,kz0,0) se elige como la referencia, esta condición se puede escribir como:
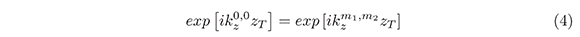
Para toda onda de propagación (m1,m2), donde zT es la distancia de la autoimagen. Debido a que los cuatro vecinos más cercanos tienen la misma componente kz, la distancia de la auto-imagen puede ser derivada fácilmente de la ecuación (4):
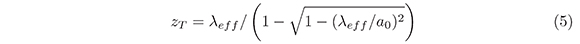
La ecuación (5), representa la distancia Talbot del régimen no lineal de Lord Rayleigh (Teng et al., 2008). El aumento de a0/λeff resulta en un incremento del número de ondas planas que se necesita considerar en la ecuación (1). Usando las mismas condiciones para la auto-imagen y tomando una componente arbitraria de onda plana con frecuencia kn1,n2 como referencia en la ecuación (4), se obtiene la expresión más general para las distancias Talbot,
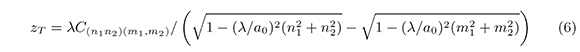
o para auto-imagen desfasadas en π,
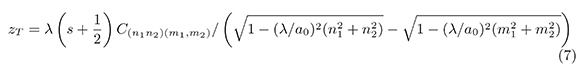
donde C(n1n2)(m1,m2) y s son números enteros.
3. Resultados y discusiones
En este caso bidimensional(2D), usando una red de oro(Au) con a0 = 1, 2μm y una onda plana de λ = 633nm, como la usada en la referencia 3. El máximo número de ondas propagantes, acorde a los valores de a0 y λ es n ≤ a0/λeff , que en este caso corresponden a los ochos primeros vecinos cercanos a (0, 0) asi, de la ecuación (2) se infiere la siguiente relación m12+ m22 ≤ (a<(0/λeff)2, la cual representa la condición básica para escoger las componentes (n1,n2) de ondas planas propagantes que intervienen en la formación de las autoimágenes de esta red de agujeros, que en este caso son: (0, 0), (1, 0), (0, 1), (−1, 0), (0, −1), (1, 1), (−1, −1), (1, −1), y (−1, 1), donde podemos notar que los cuatro vecinos más cercanos tienen la misma frecuencia espacial en magnitud. Utilizando estas ocho ondas propagantes y la relación de la ecuación (6), hallamos las siguientes distancias Talbot presentadas en la tabla 1.
Tabla 1. Calculo de las distancias Talbot, usando la ec (4) para la red de Au con periodo de 1,2 µm y λ=O,633 µm.
Cuadro 1: Calculo de las distancias Talbot, usando la ec (4) para la red de Au con periodo de 1,2 μmy λ =0, 633 μm.
Observando los resultados reportados en esta tabla, podemos notar que los valores experimentales reportados en la referencia 3 para la ubicación de las tres autoimágenes de la red de Au de 0−10μm axialmente (4μm,7, 1μm y9, 6μm), las podemos obtener con nuestros datos teóricos, usando por ejemplo, para la primera posición,elpromedio de lasdistanciasTalbotdelafila1y4;la segunda y tercera posición las ubicamos aproximadamente con las distancias Talbot presentadas en la fila 5 y 6 respectivamente. También, podemos notar que en la formación y ubicación posicional de estas autoimágenes predominan en la formula, los componentes de ondas planas de mayor frecuencia espacial y, en especial, en las dos ultimas autoimágenes.
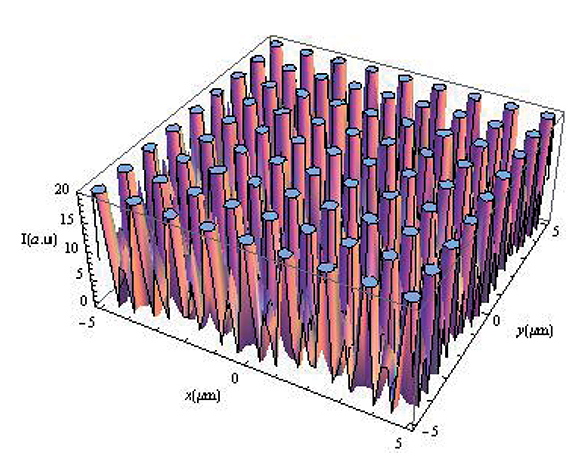
Asumiendo que la anchura de los agujeros de la red de Au, w, es w << a0 que implica que todos los coeficientes Am1,m2 de la serie son iguales, cuando se muestran los patrones de intensidad respectivos en la dirección z, usando la ecuación (1), operando las sumatorias entre −1 y 1 con la participación de los ochos primeros vecinos de ondas planas propagantes, tenemos las siguientes autoimágenes del objeto de amplitud original.
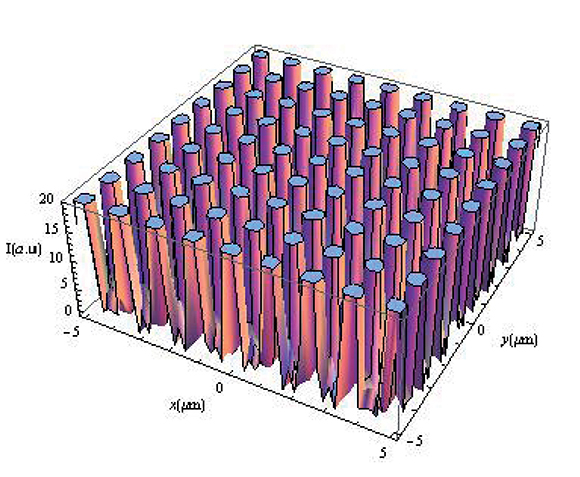
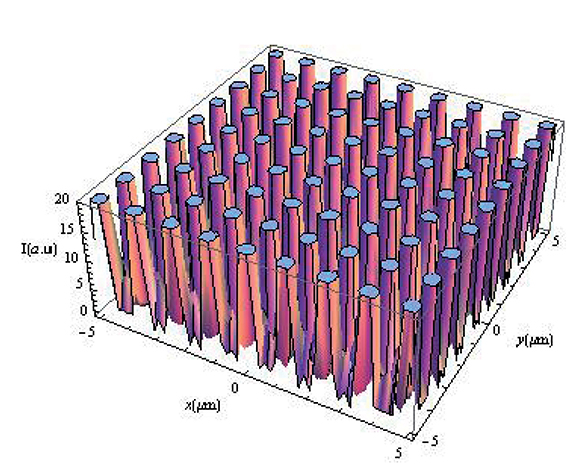
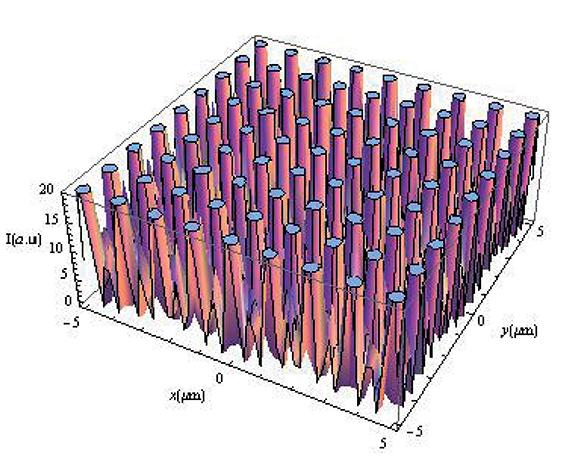
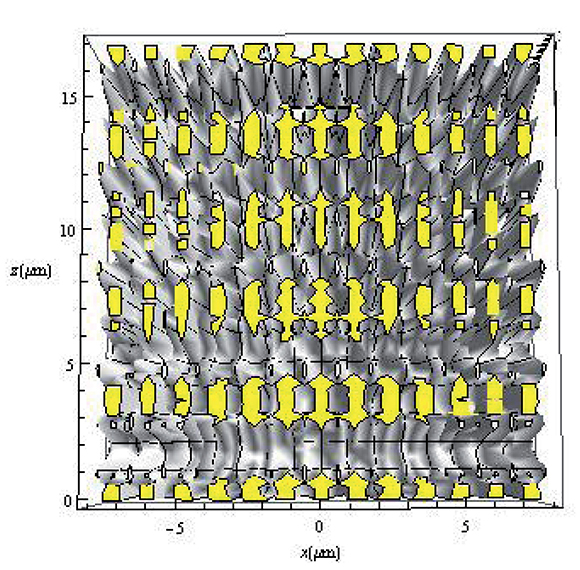
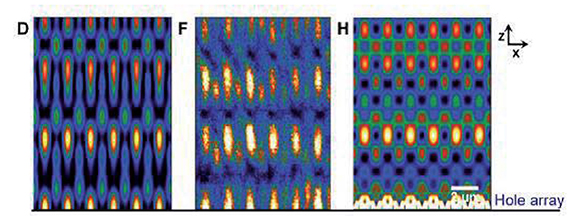
Al comparar las imágenes mostradas en las figuras 2, 3 y 4 con la del objeto original (Figura 1), vemos que en las posiciones mostradas para z se forman verdaderas autoimágenes, aunque la mostrada en la Figura 4 tiene menor contraste, tal como lo muestran los resultados experimentales de la Figura 6F, ubicada en la tercera autoimagen en el eje z a partir de la matriz de agujeros y que también se observa en la Figura 5 calculada con el modelo teórico tratado anteriormente. En esta Figura 5 podemos notar que más alláde10μm aparecen otras autoimágenes que no conservan su periodicidad axial tal como ocurrió en las tres anteriores. En la Figura 6 vemos que la formación de estas autoimágenenes se consiguen usando el cálculo de los patrones de luz con onda escalar (Figura 6D) y mediante una simulación con el método de diferencia finita en el dominio temporal (FDTD) como lo muestra la Figura 6H (Hua et al., 2012).
Figura 1. Objeto en z = 0µm.
Figura 2. Autoimagen a z = 4 µm
Figura 3. Autoimagen a z = 7,1 µm
Figura 4. Autoimagen a z = 9,6 µm
Figura 5. Autoimágenes entre 0 y 17μm para la red 2D de periodo a0 = 1, 2μm, obtenidas a partir de la teoría escalar de la difracción con ondas planas en representación del espectro angular con λeff=633nm
Figura 6. Las distancias de las Auto-imágenes del efecto Talbot no paraxial son diferentes de las distancias Talbot clásicas. Cálculos de patrones de luz de onda escalares con a0/λeff , donde a0=1, 2μmy λeff = 633nm(Fig.5D). Medidas experimentales con a0/λeff =1,9(Fig.5F). Patrones de luz a partir de simulaciones FDTD con a0/λeff = 1,9(Ver Fig.5H) [3].
4. Conclusiones
Comparando los resultados experimentales y teóricos anotados en esta contribución, podemos concluir que la teoria escalar de la difracción para campos difractados por red de Au con periodo de 1,9 λ (alta densidad) usando ondas planas monocromáticas coherentes, funciona muy bien para describir el fenómeno Talbot a nivel no lineal, como también lo avalan los resultados mostrados en el articulo de la referencia 17, utilizando rejillas metálicas unidimensionales de periodo 2 λ y4 λ. También, anotamos que uno de los aportes novedosos de este articulo, es el primer reporte en este fenómeno en el régimen no lineal, de las distancias Talbot para redes bidimensionales de periodos comparables a la longitud de la onda incidente. Finalmente, los estudios de estos objetos difractivos con este tipo de periodos, son de especial importancia, principalmente por el extenso volumen de aplicaciones que presentan, como por ejemplo, el gran poder de resolución que ofrece frente al uso como analizador de espectros atómicos, en multiplexados ópticos, entre otros, los culés vemos que por medio de este fenómeno Talbot, los podemos caracterizar en el laboratorio para sus respectivos buenos usos a esta escala.
Agradecimientos
Agradecemos al Dr. Nestor Bolognini por su valiosa colaboración en este trabajo, bajo asesorias bridadas al estudiante de VII semestre del doctorado en Ciencias Fisicas del SUE -Caribe, Emiro Arrieta Jiménez, durante una instancia de pasantia en el CIOp de La Plata, Argentina, entre julio y agosto de 2015.
Referencias
Arrieta., E. S., y Torres, C. O. (2015). Relación entre la distancia Talbot y el orden de la transformada fraccional de Fourier en medio GRIN. Revista Investigaciones Aplicadas, 9(1), 25-29. [ Links ]
Bozhevolnyi, S.I., Xiao M., & Keller. O. (1994). External-reflection Nearfield Optical Microscope with Cross-polarized Dectection. Applied Optics, 33(5), 876-880. [ Links ]
Cherukulappurath, S., Heinis, D., Cesario, J., van Hulst, N.F., Enoch, S., & Quidant, R. (2009). Local Observation of Plasmon Focusing in Talbot Carpets. Optics Express, 17(26), 23772-23784. [ Links ]
Dennis, M. R., Zheludev, N. I., & García de Abajo, F. J. (2007). The Plasmon Talbot Effect. Optics Express, 15(15), 9692-9700. [ Links ]
Flores-Arias, M. T., Bao, C., Pérez, M. V., & Fernández-Pousa, C. R. (2002). Fractional Talbot Effect in a Selfoc Gradient-index Lens. Optics Letters, 27(23), 2064-2066. [ Links ]
Forte, G., Lencina, A., Tebaldi, M., & Bolognini, N. (2011). Self-imaging by a Volume Grating. Optics Communications, 284, 2494-2499. [ Links ]
Forte, G., Lencina, A., Tebaldi, M., & Bolognini, N. (2011). Talbot effect by a photorefractive volume phase grating. Applied optics, 51(4), 479-485. [ Links ]
Guérineun, N., Di Mambro, E., & Primot, J. (2003). Talbot Experiment Reexamined: Study of the Chromatic Regime and Application to Spectrometry. Optics Express, 11(24), 3310-3318. [ Links ]
Hua, Y., Suh, J. Y., Zhou, W., Huntington, M. D., & Odom, T. W. (2012). Talbot effect beyond the paraxial limit at optical frequencies. Optics express, 20(13), 14284-14291. [ Links ]
Martínez, L., Araiza, E.M., Javidi, B., Andrés, P., Climent, V., Lancis, J. et al. (2009). Single-shot Digital Holography by Use of the Fractional Talbot Effect. Optics Express, 17(15), 12900-12908. [ Links ]
Rayleigh, L. (1880). On Copying Diï¬raction-Gratings and on Some Phenomena Connected Therewith. Philos. Mag., 11(67), 196-205. [ Links ]
Ring, J. D., Lindberg, J., Howls, C. J., & Dennis, M. R. (2012). Aberration-like cusped focusing in the post-paraxial Talbot effect. Journal of Optics, 14(7), 075702. [ Links ]
Smolyaninov, I., & Davis, C. (1998). Apparent Superresolution in Near-field Optical Imaging of Periodic Gratings. Optics letters, 23(17), 1346-1347. [ Links ]
Teng, S., Tan, Y., & Cheng, C. (2008). Quasi-Talbot effect of the high-density grating in near field. JOSA A, 25(12), 2945-2951. [ Links ]
Wei, G. X., Lu, L. L., & Guo, C. S. (2009). Generation of optical vortex array based on the fractional Talbot effect. Optics Communications, 282(14), 2665-2669. [ Links ]
Zhang, W., Zhao, C., Wang, J., & Zhang, J. (2009). An Experimental Study of the Plasmonic Talbot Effect. Optics Express, 17(22), 19757-19762. [ Links ]
Zhang, Y., Wen, J., Zhu S. N., & Xiao, M. (2010). Nonlinear Talbot Effect. Physical Review Letters, 104(18), 3901 -3904. [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.