Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ciencias
Print version ISSN 0121-1935
rev. cienc. vol.20 no.1 Cali Jan./June 2016
Ghost Dark Energy Model with Non-linear Interaction
Alexander Oliveros García
Programa de Física, Universidad del Atlántico, Barranquilla - Colombia
E-mail: alexanderoliveros@mail.uniatlantico.edu.co
Received: April 27, 2016
Acceoted: June 22, 2016
Abstract
In this paper we study a dark energy model taking into account a non-linear interaction between the dark energy and dark matter components. The non-linear interaction term, used in this work, is proportional to the square of dark energy density. Considering a FRW type flat universe, we obtain an analytical expression for the Hubble parameter H and from this quantity, the deceleration parameter q and the equation of state parameter wΛ are analyzed. We found that, in this scenario, the accelerated expansion regime of the universe in late times is possible. However, using suitable values for the coupling constant, the square of the speed of sound remains negative, therefore, the model is unstable under small perturbations.
Keywords: Dark Energy; Cosmology.
1. Introduction
The accelerated expansion of the universe was discovered in 1998 from the analysis of astrophysical information obtained from the supernovae type Ia (SNIa) (basically, from measurement of luminosity distances) (Perlmutteret al., 1998), as well as from the anisotropies observed in the cosmic microwave background (CMB) radiation (Planck Collaboration I, 2014), and the study of the large scale structure (LSS) of the universe (Tegmarket al., 2004). This accelerated expansion is consistent with the idea that the universe has an unknown form of energy density with negative pressure, so called dark energy (DE). The amount of DE in the universe is about 70% and the remaining 30% correspond to matter and radiation densities. A huge amount of DE models have been proposed in the literature (Copelandet al., 2006; Li et al., 2011; Bamba et al., 2012), but until now, there is not a satisfactory explanation of this phenomenon. In the ΛCDM model, the role of DE is played by the cosmological constant Λ (vacuum energy), but this model has two main problems: the fine tuning problem and the coincidence problem (Padmanabhan, 2003).
Recently, a different proposal has attracted considerable attention, a model which has its roots on the Veneziano ghost of QCD (Witten 1979; Veneziano, 1979; Rosenzweig et al., 1980; Nath & Arnowitt, 1981) and is known as QCD ghost dark energy (Ohta, 2011). The key ingredient of this new model is that the Veneziano ghost, which is unphysical in the usual Minkowski spacetime QFT, exhibits important physical effects in dynamical spacetime or spacetime with non-trivial topology. The Veneziano ghost is supposed to exist to solve the violation of the U(1) symmetry (the so-called U(1) problem) in the low-energy effective theory of QCD (for more details about this issue see Cai et al., 2011). The ghost has no contribution to the vacuum energy density in Minkowski spacetime, but in curved spacetime it gives rise to a small vacuum energy density. This vacuun energy density in the QCD ghost dark energy model is proportional to the Hubble parameter H and the proportional coefficient is of the order Λ3QCD, where ΛQCD is the mass scale of QCD. From this proposal, many studies in different contexts have been carried out in recent years (Ebrahimi & Sheykhi, 2011; Sheykhiet al., 2012; Sheykhi & Bagheri, 2011; Ebrahimi & Sheykhi, 2011; Rozas-Fernandez, 2012; Karami, et al., 2013; Khodam-Mohammadi et al., 2012; Malekjani & Khodam-Mohammadi, 2013; Feng et al, 2013; Honarvaryan et al., 2015). The generalization of the ghost dark energy model was carried out in (Cai et al., 2014), where the studied energy density is of the form ρΛ = αH + βH2 .
Among the vast variety of approaches to the dark energy problem, it is also considered the possibility to include an interaction term Q between the dark energy and dark matter components, usually introduced aiming to avoid the coincidence problem (Ref. Bolotin et al, 2014, offers a recent review of this topic). Recently, the authors of [26] showed that this kind of interaction is favored by current cosmological observations in an extended ΛCDM model. Due to our ignorance about the fundamental origin of dark energy, the interaction term is introduced by phenomenological considerations. This term is usually proportional either to the dark energy density, the dark matter, or to a linear combination of both. (See for instance, (Arévalo et al, 2012, and references therein). The sign in Q determines the direction of the flux of energy. If Q is positive, dark energy decays into dark matter, while if Q is negative, dark matter decays into dark energy. Some authors have also considered the possibility to have non-linear interaction terms (Arévalo et al, 2012; Mangano et al., 2003; Baldi, 2011; Ma et al., 2010; Zhang et al., 2012; Oliveros & Acero, 2015). Here we take this last idea, with a concrete selection for the interaction term Q, which allows us to find analytical and phenomenologically feasible solutions.
This article is organized as follows: in the second section, we introduce the basic equations and the cosmological evolution that arises from this model is analized. Finally, in the last section we expose some conclusions.
2. Basic Equations and Cosmological Evolution
In general, the Einstein's equations are the starting point to analyze the evolution of the universe:
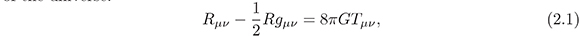
where Rμν is the Ricci tensor, R is the Ricci scalar and Tμν is the energymomentum tensor, which discribes the matter content of the universe. In this case, we consider that the universe is filled with dark matter (ρm) and dark energy (ρΛ).
The cosmological evolution of the universe that is studied from equation (2.1) needs an appropriate metric. The most general metric that satisfies the observed homogeneity and isotropy in the universe, is the Friedmann, Robertson-Walker metric (FRW) (Weinberg, 2008)
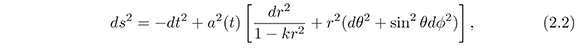
where k is the spatial curvature. The possibles values for k are +1, 0, -1. if k =1, we obtain a closed universe, k = 0 corresponds a flat universe and k = −1anopen universe. In equation (2.2) a(t) is the scale factor.
Using a flat type FRW universe in equation (2.1), it obtain the Friedmann's equations:
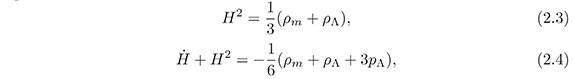
6 where we take 8πG = 1 and the dark matter pressure pm = 0 (dust); ρm is the dark matter density, ρΛ is the dark energy density and pΛ the pressure due to the dark energy component. H =˙a/a is the Hubble parameter and the dot represents the derivative with respect to time. We consider that the dark energy component is the QCD ghost dark energy density which has the form (Ohta, 2011).
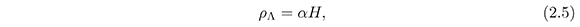
where α is positive constant with dimension [energy]3, and roughly of order of Λ3QCD where ΛQCD ∼ 100 MeV is the QCD mass scale.
When a possible interaction between dark matter and dark energy components is taken into account, the continuity equations take the form:
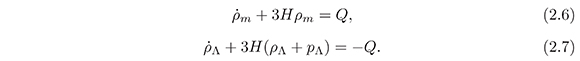
In the literature, the usual choices for Q consist of linear terms of either dark matter or dark energy or a linear combination of both. It is possible, however, to consider non-linear forms for Q. In (Arévaloet al., 2012) the cosmological evolution of the universe is analyzed, considering a non-linear interaction term of the general form:
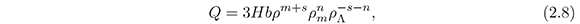
where b is a positive coupling constant, ρ = ρm + ρΛ and the powers m, n and s characterize the interaction. The Ansatz equation (2.8) contains a variety of interactions considered in the literature, for instance, for (m, n, s)=(1, 1, −1) one gets Q =3Hbρm and for (m, n, s)=(1, 0, −1) one has Q =3HbρΛ.
In order to obtain a viable model with analytical solutions, we consider that the interaction term is given by the non-linear form:
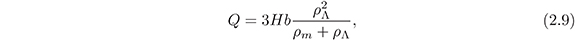
which corresponds to the choice (m, n, s)=(1, 0, −2) in equation (2.8). This term was used also in (Oliveros& Acero, 2015) in the context of holographic dark energy. Others choices are possible, but the resulting equations are more complex. For example:
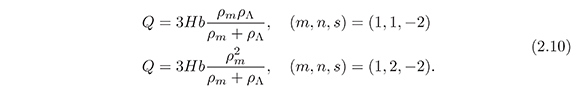
Further, from equation (2.9) it is possible to obtain an analytical expression for the Hubble parameter H which, in addition, is phenomenologically viable, as we shall show in the following:
Replacing equation (2.9) in equation (2.6), using ρm from equation (2.3), and the ghost dark energy density (2.5), we obtain the differential equation for H(x),
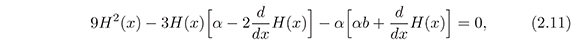
where the change of variable x =ln a has been performed. The solution of (2.11) is
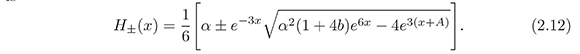
Where A is an integration constant. There are two branches: H+(x) represents an expansion solution, while H−(x) a contraction one. We neglect the latter since it goes against the observation, and for simplicity, write H+(x)as H(x)inwhat follows. The integration constant A is recovered from the initial condition:
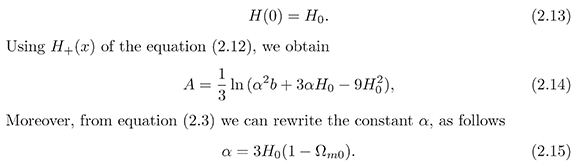
Since, the current Hubble parameter H0 and the dark matter density parameter Ωm0 are known, then, the only free parameter is the coupling constant b. Using the most recent values reported in [34]: H0 =67.8kms−1 Mpc−1 and Ωm0 =0.308 in equation (2.15), we have α ≈ 140 km s−1 Mpc−1 . This value will be considered in the next numerical calculations.
Now, we consider the behavior of the equation of state parameter w = p/ρ (p = pm + pΛ and ρ = ρm + ρΛ) in order to determine if it is possible to obtain an accelerated expansion regime for the universe at later times. Using the equations (2.3) and (2.4), the equation of state parameter w is given by:
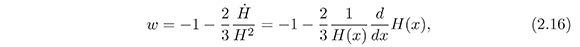
and using equations (2.12) and (2.14), we obtain
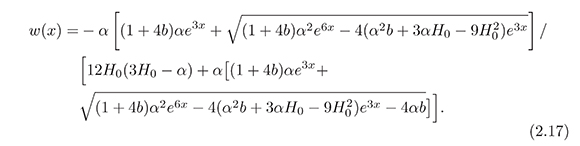
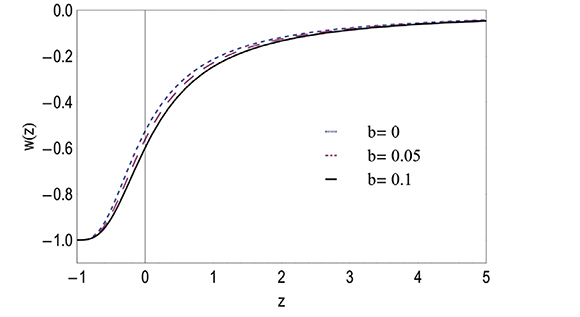
Figure 1 shows the behavior of w as a function of the redshift z for suitable values of the coupling constant b. With other choices, for example, for b << 1 not a significant change in the model is observed and for b > 1 the decaying rate of dark energy in dark matter would be very high.
Figure 1. Plot of the equation of state parameter w versus the redshift z, using suitable values for the coupling constant b
We can see that it is possible to obtain an accelerated expansion phase of the universe, since the equation state parameter w satisfies the restriction w < −1/3 at later times and a phantom phase is not observed (w does not cross the w = −1 barrier).
Another very important quantity in cosmology is the deceleration parameter q, which is given by:
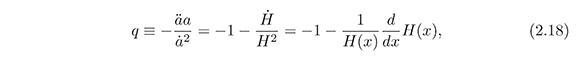
Using equations (2.12) and (2.14), we have
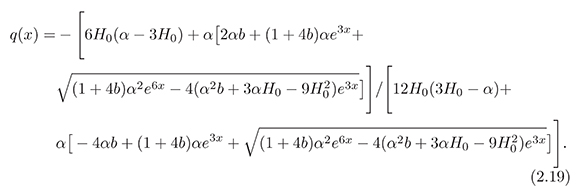
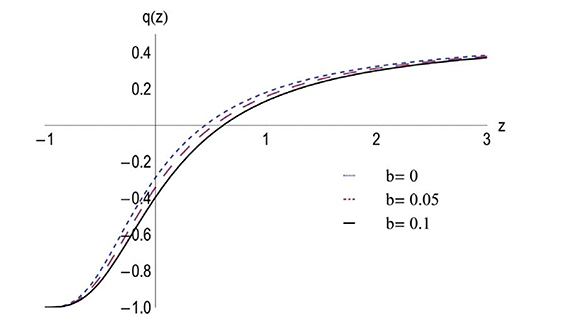
As we can see in Figure 2, the selected values for b make the transition redshift zt take values of the order of 0.5, which is consistent with the observed value (Copeland et al., 2006). In zt the universe enters an accelerating phase (q < 0)
Figure 2. Plot of the deceleration parameter q versus the redshift z, using suitable values for the coupling constant b.
In order to examine the stability of the model, we study the square of the velocity of sound (v2s) as a function of the redshift. v2s given by (Peebles & Ratra, 2003).
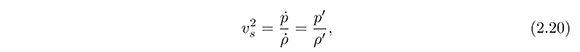
where the prime means differentiation with respect to x and from equations (2.7) and (2.9) the pressure density is given by:
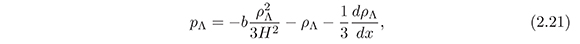
Replacing equations (2.5), (2.12) and (2.21) in (2.20), we obtain:
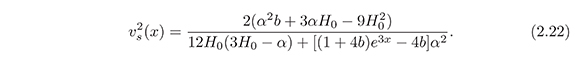
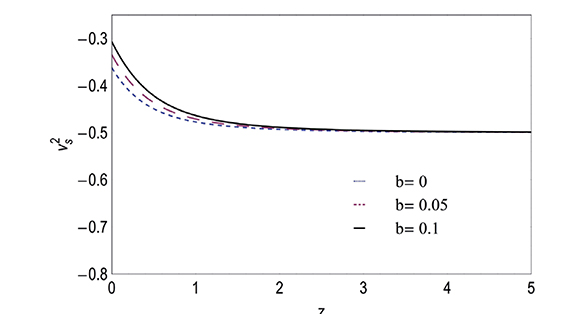
The plot of v2s versus z is shown in Figure 3. Notice that v2s remains negative for all values of z, showing that the model presented here is unstable under small perturbations. A similar result was obtained in (Ebrahimi & Sheykhi, 2011)
Figure 3. Plot of the square of the velocity of sound v2s versus the redshift z, using
suitable values for the coupling constant b
3. Concluding Remarks
In this work we studied a QCD ghost dark energy model taking into account a non-linear interaction between the dark energy and dark matter components (see equation (2.9)). Considering a FRW type flat universe, we obtained analytical expressions for the Hubble parameter (see equation (2.12)), the equation of state parameter wΛ (see equation (2.17)) and the deceleration parameter q (see equation (2.19)). It was found that, in this scenario, the accelerated expansion regime of the universe in late times is possible since the equation of state parameter w satisfies the restriction w< −1/3 at late times and a phantom phase is not observed (w does not cross the w = −1 barrier) (see Figure 1). Also, the selected values for b make zt (transition redshift) take values of the order of 0.5 (see Figure 2), which is consistent with the observed value reported in the literature. However, using suitable values for the coupling constant, the square of the speed of sound turned out to be negative, making the model unstable under small perturbations (see Figure 3). But, it is important to note that the positivity of v2s is a necessary condition but is not enough to conclude that the model is stable (Ghaffariet al., 2014).
References
Arévalo, F., Bacalhau, A. P., & Zimdahl, W. (2012). Cosmological dynamics with non-linear interactions. Class. Quant. Grav., 29, 235001. [ Links ]
Baldi, M. (2011). Time dependent couplings in the dark sector: from background evolution to nonlinear structure formation. Mon. Not. Roy. Astron. Soc., 411, 1077. [ Links ]
Bamba, K., Capozziello, S., Nojiri, Sh., & Odintsov, S. D. (2012). Dark energy cosmology: the equivalent description via diï¬erent theoretical models and cosmography tests, Astrophys. Space Sci., 342, 155-228. [ Links ]
Bolotin, Y. L., Kostenko, A., Lemets, O. A., & Yerokhin, D. A. (2014). Cosmological Evolution With Interaction Between Dark Energy And Dark Matter. Int. J. Mod. Phys. D, 24, 1530007. [ Links ]
Cai, R-C., Su Q., Tuo, Z-L. & Zhang, H-B. (2011). Notes on Ghost Dark Energy. Phys. Rev. D, 84, 123501. [ Links ]
Cai, R-G., Tuo, Z-L., Wu, Y-B. & Zhao, Y-Y (2012). More on QCD Ghost Dark Energy. Phys. Rev. D, 86, 023511. [ Links ]
Copeland, E. J., Sami, M., & Tsujikawa, Sh. (2006). Dynamics of dark energy. Int. J. Mod. Phys. D, 15, 1753-1936. [ Links ]
Ebrahimi, E., & Sheykhi, A. (2011). Instability of QCD ghost dark energy model. Int. J. Mod. Phys. D, 20, 2369-2381. [ Links ]
Ebrahimi, E., & Sheykhi, A. (2011). Interacting Ghost Dark Energy in Brans-Dicke Theory. Phys. Lett. B, 706, 19-25. [ Links ]
Feng, Ch-J., Li, X-Z., & Shen, X-Y. (2013). Latest observational constraints to the ghost dark energy model by using the Markov chain Monte Carlo approach. Phys. Rev. D, 87, 023006. [ Links ]
Ghaffari, S., Dehghani, M. H., & Sheykhi, A. (2014). Holographic Dark Energy in the DGP Braneworld with Granda-Oliveros cutoff. Phys. Rev. D, 89, 123009. [ Links ]
Honarvaryan, M., Sheykhi, A., & Moradpour, H. (2015). Thermodynamical description of the ghost dark energy model. Int. J. Mod. Phys. D, 24, 1550048. [ Links ]
Karami, K., Asadzadeh, S., Mousivand, M., & Safari, Z. (2013). QCD modified ghost scalar field dark energy models. Int. J. Mod. Phys. D, 22, 1350018. [ Links ]
Khodam-Mohammadi, A., Malekjani, M., & Monshizadeh, M. (2012). Reconstruction of modified gravity with ghost dark energy models. Mod. Phys. Lett. A, 27, 1250100. [ Links ]
Li, M., Li, X-D., Wang, Sh., & Wang, Y. (2011). Dark Energy. Commun. Theor. Phys, 56, 525-604. [ Links ]
Ma, Y-Z., Gong, Y., & Chen, X. (2010). Couplings between holographic dark energy and dark matter. Eur. Phys. J. C, 69, 509-519. [ Links ]
Malekjani, M., & Khodam-Mohammadi, A. (2013). Statefinder diagnosis and the interacting ghost model of dark energy. Astrophys. Space Sci., 343, 451-461. [ Links ]
Mangano, G., Miele, G., & Pettorino, V. (2003). Coupled quintessence and the coincidence problema. Mod. Phys. Lett. A, 18, 831-842. [ Links ]
Nath, P., & Arnowitt, R. L. (1981). The U(1) Problem: Current Algebra and the Theta Vacuum. Phys. Rev. D, 23, 473. [ Links ]
Ohta, N. (2011). Dark Energy and QCD Ghost. Phys. Lett. B, 695, 41-44. [ Links ]
Oliveros, A., & Acero, M. A. (2015). New holographic dark energy model with non-linear interaction. Astrophys. Space Sci., 357, 12. [ Links ]
Padmanabhan, T. (2003). Cosmological constant: The Weight of the vacuum. Phys. Rept, 380, 235-320. [ Links ]
Peebles, P. J. E., & Ratra, B. (2003). The Cosmological Constant and Dark Energy. Rev. Mod. Phys., 75, 559-606. [ Links ]
Perlmutter, S. et al. (1998). (Supernova Cosmology Project Collaboration) Discovery of a supernova explosion at half the age of the Universe and its cosmological implications. Nature, 391, 51-54. [ Links ]
Planck Collaboration (2015). Planck 2015 results. XIII. Cosmological parameters, arXiv:1502.01589 prepint, 1-67. [ Links ]
Planck Collaboration I (2014). Planck 2013 results. I. Overview of products and scientfic results. Astron. Astrophys, 571, A1, 1-48. [ Links ]
Rosenzweig, C., Schechter, J., & Trahern, C. G. (1980). Is the Effective Lagrangian for QCD a Sigma Model? Phys. Rev. D, 21, 3388. [ Links ]
Rozas-Fernandez, A. (2012). Kinetic k-essence ghost dark energy model. Phys. Lett. B, 709, 313-321. [ Links ]
Salvatelli, V., Said, N., Bruni, M., Melchiorri, A., & Wands, D. (2014). Indications of a late-time interaction in the dark sector. Phys. Rev. Lett., 113, 181301. [ Links ]
Sheykhi, A., & Bagheri, A. (2011). Quintessence Ghost Dark Energy Model. Europhys. Lett., 95, 39001. [ Links ]
Sheykhi, A., Sadegh Movahed, M., & Ebrahimi, E. (2012). Tachyon Reconstruction of Ghost Dark Energy. Astrophys. Space Sci., 339, 93-99. [ Links ]
Tegmark, M. et al. (2004). (SDSS Collaboration) Cosmological parameters from SDSS and WMAP. Phys. Rev. D, 69, 103501. [ Links ]
Veneziano, G. (1979). U(1) Without Instantons. Nucl. Phys. B, 159, 213-224. [ Links ]
Weinberg, S. (2008). Cosmology. New York, USA: Oxford University Press Inc. [ Links ]
Witten, E. (1979). Current Algebra Theorems for the U(1) Goldstone Boson. Nucl. Phys. B, 156, 269-283. [ Links ]
Zhang, Z., Li, S., Li, X. D., Zhang, X., & Li, M. (2012). Revisit of the interaction between holographic dark energy and dark matter. Journal of Cosmology and Astroparticle Physics, 2012(06), 009. [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.