Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista de Ciencias
Print version ISSN 0121-1935
rev. cienc. vol.20 no.1 Cali Jan./June 2016
Longitud máxima para funciones univalentes, una prueba más sencilla
Length for Univalent Functions, a Simpler Proof
Alexander Arévalo S.
Departamento de Ciencias Básicas, Institución Universitaria Antonio José Camacho, Cali - Colombia
E-mail: aarevalo@admon.uniajc.edu.co
Diana C. Giraldo M.
Departamento de Matemáticas, Universidad Autónoma de Occidente, Cali - Colombia
E-mail: dcgiraldo@uao.edu.co
Received: June 18, 2015
Accepted: August 23, 2015
Resumen
Presentaremos una prueba de la longitud de arco, de la imagen de la circunferencia |z| = r aplicando la función de Koebe definida por Yamashita en [4].
Palabras clave: Funciones univalentes, desigualdad isoperimétrica, Función de Koebe, longitud de arco.
Abstract
We will present a proof of the arc length, the image of the circumference |z| = r applying the Koebe function defined by Yamashita in [4].
Keywords: Univalent functions, isopherimetric inequality, Koebe function, arc length.
1. Introducción
La teoría de las funciones univalentes se inicia alrededor del año 1900 y actualmente sigue siendo un campo activo en la investigación. Muchos resultados en este campo, se formulan como problemas extremales, como lo es el problema que planteamos en este documento, entre otros, tales como: maximizar el módulo de los coeficientes de Taylor, áreas, longitudes y medias integrales asociadas con las funciones univalentes.
Este documento está dedicado a presentar una prueba de un problema extremal conocido en las funciones univalentes, concretamente estimar la longitud de arco de la imagen de la circunferencia |z|= r bajo la aplicación de la función de Koebe.
En este artículo se hará una estimación de esta longitud de arco, mostrando que es la mejor que se ha podido calcular para la función de Koebe y que el valor exacto de la longitud para esta función, aún no se ha podido calcular con exactitud.
En este artículo se presentará una prueba asequible a los lectores que el mismo resultado realizado por Yamashita (Yamashita, 1990).
Definición 1: Una función f analítica en un dominio D del plano complejo ℂ, se dice univalente en D,si f(z1) ≠ f(z2) para todo par de puntos z1,z2 ∈ D, con z1 ≠ z2.
Definición 2: La clase de funciones 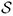 está formada por la funciones analíticas y univalentes en el disco unidad ⅅ = {z : |z|<1}, normalizadas por las condiciones f(0)=0 y f'(0) = 1.
está formada por la funciones analíticas y univalentes en el disco unidad ⅅ = {z : |z|<1}, normalizadas por las condiciones f(0)=0 y f'(0) = 1.
Cada f ∈ 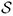 tiene una expansión en serie de Taylor de la forma
tiene una expansión en serie de Taylor de la forma
f(z)= z+ a2z2 + a3z3 + ..., |z|<1.
Algunos ejemplos de estas funciones son:
• La identidad, f(z)= z.
• l(z)= z + 2z2 + 3z3 + ... = z(1 - z)-1 .
• La función de Koebe,
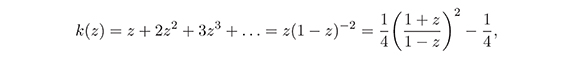
la cual envía el disco ⅅ sobre el plano entero menos la parte del eje real negativo de −1/4 al infinito, juega un papel importante como función extremal en nuestro trabajo y en una gran cantidad de problemas extremales en la clase 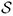 .
.
Desigualdad Isoperimétrica
Sea C una curva de Jordan rectificable con longitud L, acotando un dominio con área A, entonces se cumple que
4πA≤L2 .
Dada la función analítica f ∈ ⅅ, se calcula la longitud de arco Lr(f) de la imagen de la circunferencia |z|= r bajo la aplicación f ∈S, como
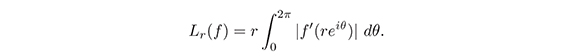
Teorema 1: Para toda f ∈ 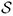 ,
,
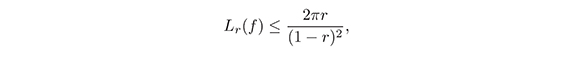
con 0 ≤ r < 1. Ver (Duren, 1983).
2. Teorema principal
Teorema 2: La longitud de arco, Lr(k) de la imagen de la circunferencia |z|= r bajo la aplicación de Koebe cumple que
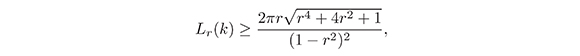
donde 0 < r < 1.
Demostración:
Para toda función f analítica en el disco ⅅ, se cumple
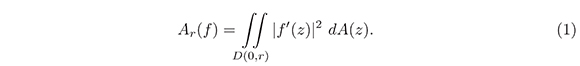
Donde Ar(f) es el área de la imagen de la circunferencia de radio r.

Luego, con base en la desigualdad isoperimétrica y empleando (2), tenemos
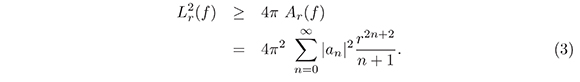
Puesto que la función de Koebe esta dada por
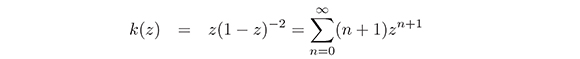
Su derivada es
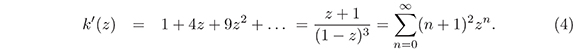
Tomando an =(n+1)2 y reemplazándolo en (3), se tiene
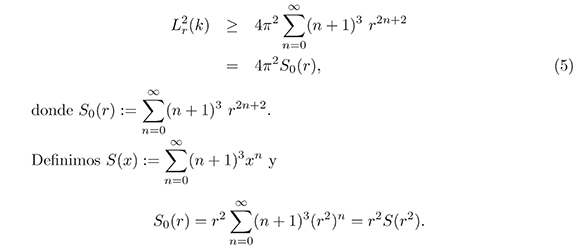 ∞
∞
Observemos que
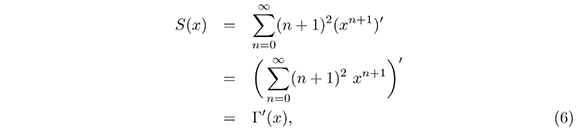
donde
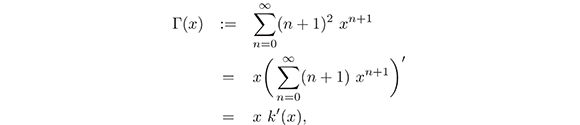
donde k(x) es la función de Koebe y por (Yamashita, 1990) 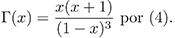

Derivando en (7) y teniendo en cuenta (6), se obtiene
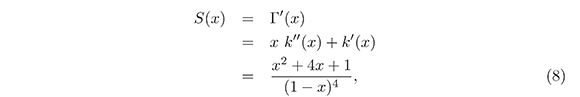
de manera que, usando (8) tenemos
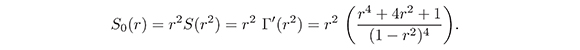
Por lo tanto, de acuerdo a (5) y teniendo en cuenta el resultado anterior, se deduce
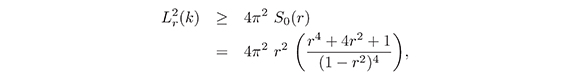
obteniendo así, el resultado deseado para la función extremal de Koebe,
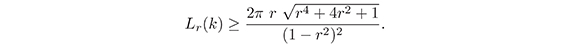
Referencias
De Branges, L. (1985). A Proof of the Bieberbach Conjecture. Acta Math., 154, 137-152. [ Links ]
Duren, P. L. (1964). An Arc Length Problem for Close to Convex Functions. Journal London Mathematical Society, 39, 757-761. [ Links ]
Duren, P. L. (1983). Univalent functions. Nueva York, USA: Springer-Verlag. [ Links ]
Yamashita, S. (1990). Area and Length Maxima for Univalent Functions. Bull. Austral. Math. Soc., 41, 435-439. [ Links ]

Revista de Ciencias por Universidad del Valle se encuentra bajo una licencia Creative Commons Reconocimiento 4.0.














