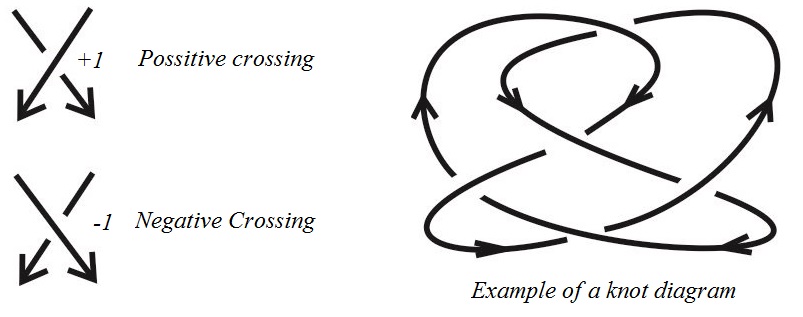
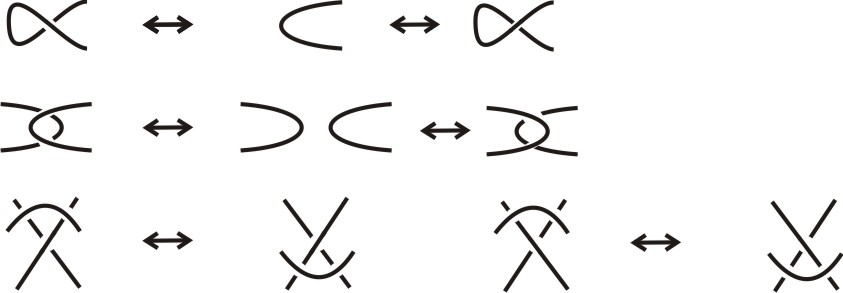
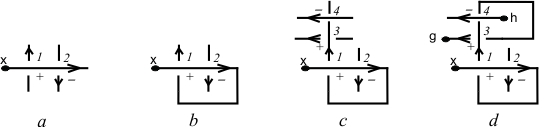
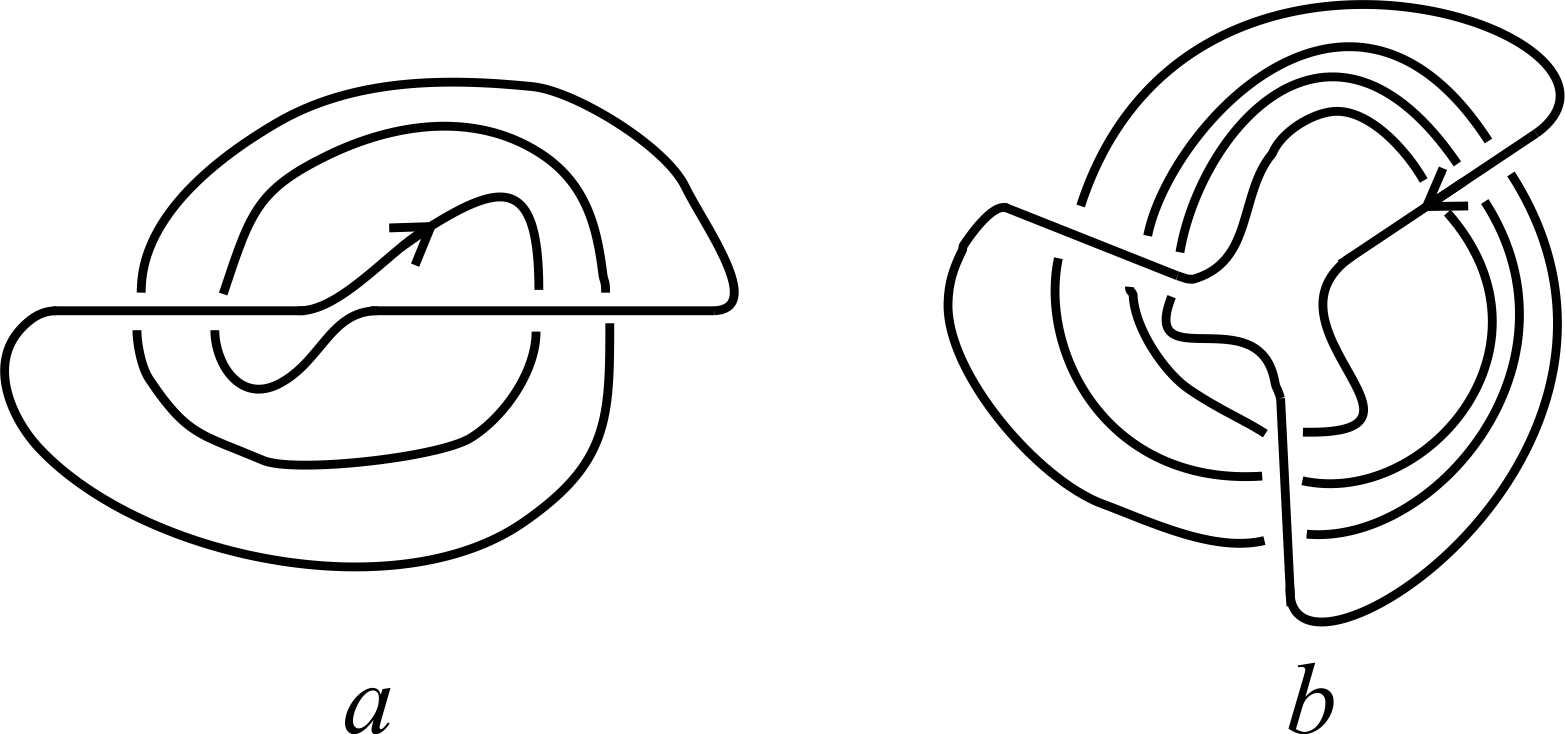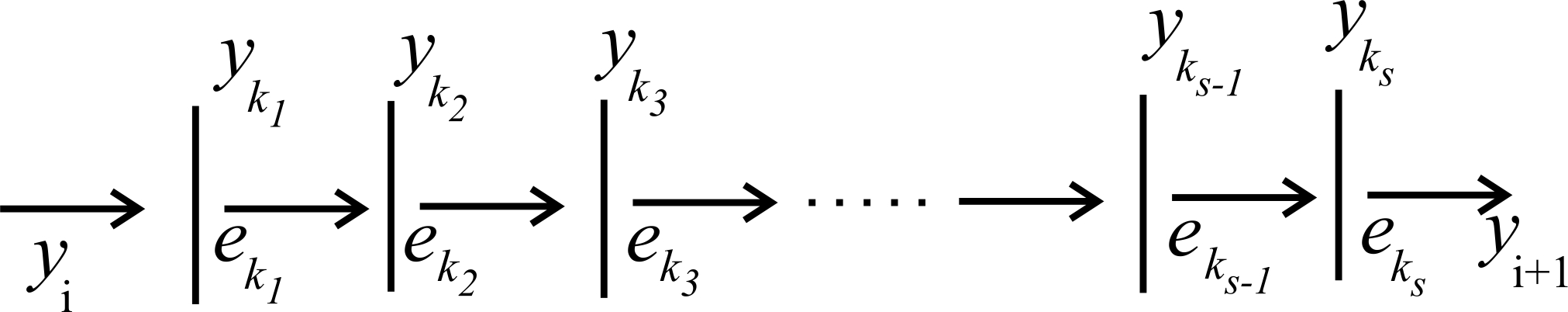1 Introducción
En la actualidad la teoría clásica de nudos es entendida como el estudio de las clases de isotopía ambiente de encajes de S 1 o copias disjuntas de S 1 en el espacio tridimensional.
A principios del siglo XX dicha teoría era considerada una pieza fundamental para algunas áreas que se encargan del estudio de propiedades químicas, atómicas y leyes de la física y no fue hasta el año 1920, cuando Alexander 1 probó que toda 3-variedad cerrada y conexa es una cubierta ramificada de S 3 con conjunto de ramificación un nudo, que se le dio un lugar privilegiado en la topología de baja dimensión, en especial al problema de clasificación de nudos.
Aunque parecería que la teoría de nudos nació como una rama de la topología de baja dimensión con los trabajos de K. F. Gauss a inicios del siglo XX, ésta realmente surgió en el área de la matemática aplicada con los trabajos de W. Thomson sobre átomos vórtices, véase 2. En la actualidad, se han encontrado nuevas aplicaciones de la teoría de nudos, por ejemplo en el empaque y desempaque del ADN, una reacción enzimática convierte las hebras de ADN en nudos, hebras enlazadas o en una forma más ordenada. La teoría de nudos puede ayudar a que los científicos descubran mecanismos mediante los cuales estas enzimas funcionen, véase 3,4 para más detalles. Las conexiones de los nudos con la física teórica pueden consultarse en 5.
Para abordar el problema de clasificación de nudos, se necesitaba un mejor entendimiento combinatorio de estos objetos. Por tanto, a lo largo de su historia, los matemáticos han usado varias aproximaciones, una de ellas y, de hecho la más fundamental, es la del concepto de “diagrama regular".
En la década de los 20's, Reidemeister 6) definió una serie de movimientos, llamados movimientos de Reidemeister, sobre el conjunto de los diagramas de nudos y probó que existe una correspondencia biunívoca entre las clases de isotopía ambiente de nudos en R3 y las clases de equivalencia, generada por los movimientos de Reidemeister e isotopías del plano de diagramas de nudos.
El teorema de Reidemeister abrió las puertas a la teoría de codificación de nudos. De esta forma, a cada diagrama de un nudo, podemos asociarle un código que lo caracterice completamente. Una de las ventajas de trabajar con códigos es que no necesitamos el uso de diagramas y las definiciones y pruebas son presentadas por medio de algoritmos, fáciles de implementar, usando programas de computación simbólica, tales como mathematica. Al codificar nudos, hay que tener cuidado debido a que al definir los movimientos de Reidemeister sobre el conjunto de códigos, pueden aparecer representantes en las clases que no correspondan a diagramas de nudos. Este hecho permitió mostrar la existencia de extensiones no triviales de la teoría clásica de nudos; por ejemplo, los nudos virtuales.
En la literatura existen varias formas de codificar nudos; por ejemplo, Toro 7) utiliza los nudos combinatorios; Kauffman 8, los códigos de Gauss y Conway 9, los tangles.
En los 90's, Kauffman definió nudo virtual, extendiendo el concepto de diagrama de un nudo. Un diagrama de un nudo virtual es una inmersión de S1 o de una unión disjunta de copias de S 1 en el plano que tiene un número infinito de puntos dobles, que son transversales. Estos puntos dobles, que llamamos también cruces, están clasificados como clásicos por encima por debajo y, virtuales, cruces encerrados por un círculo. Los movimientos extendidos de Reidemeister son una colección de movimientos, que definen una relación de equivalencia, sobre el conjunto de los diagramas de nudos virtuales.
Kauffman 8) mostró que algunos invariantes de nudos clásicos, que se pueden calcular a partir del diagrama del nudo. Pueden ser extendidos a invariantes de nudos virtuales, entre ellos, el número de puentes, el grupo fundamental, los sistemas periféricos, los quandles, el polinomio bracket, el polinomio de Kauffman y el polinomio de Jones. La forma general cómo estos invariantes de nudos clásicos pueden ser extendidos a nudos virtuales, se basa en omitir los cruces virtuales. Kauffman construyó ejemplos de diagramas de nudos virtuales, no clásicos y, por ende, no triviales, para los cuales los invariantes mencionados anteriormente tienen propiedades que no se cumplen o que aún no se han podido probar para la categoría de los nudos clásicos.
Este artículo tiene la doble finalidad de introducir y motivar el estudio de los nudos. Por un lado, damos una serie de conceptos básicos de la teoría clásica de nudos y, a través de métodos algorítmicos, llegamos a la idea de Kauffman de los nudos virtuales. Nos enfocamos en el estudio del grupo de nudos clásicos y virtuales, damos un algoritmo para hallar la presentación por encima del grupo de nudos clásicos, el cual se emula para hallar la presentación por encima en el caso virtual, además, usando este algoritmo mostramos formas de recuperar nudos virtuales a partir de ciertas presentaciones. Para más detalles, véase 10,11. Estudiamos representaciones de grupos de nudos de dos puentes, usando las técnicas de R. Riley 12) y H. Hilden, M. T. Lozano y J. M. Montesinos sobre representaciones en álgebras cuaterniónicas 13.
Este artículo está organizado de la siguiente forma: En la sección dos hacemos un estudio corto de nudos, nudos combinatorios y nudos virtuales. También damos la definición de grupo de un nudo, nudos tres coloreables y representaciones de grupos de nudos. En la sección tres, damos un algoritmo para hallar el nudo combinatorio de un nudo de dos puentes sin la necesidad de hallar primero el diagrama. Estudiamos el grupo de un nudo de dos puentes así como sus representaciones parabólicas en el grupo de las transformaciones de Möbius. Estudiamos el problema de hallar nudos combinatorios a partir de presentaciones similares de las de Wirtinger de nudos de dos puentes.
2 Conceptos básicos
En esta sección damos algunas definiciones y resultados, sin detenernos mucho en los detalles, sobre nudos, nudos combinatorios, el grupo de un nudo y nudos virtuales.
2.1 Nudos en S3
Decimos que K es un nudo (o nudo clásico) si existe una función continua e inyectiva de S 1 en S 3 (o ℝ3) cuya imagen es K. De manera intuitiva podemos imaginarnos un nudo K como un trozo de cuerda anudado en el espacio, al cual le hemos unido sus extremos.
Dos nudos K 1 y K 2 equivalentes si y sólo si existe un homeomorfismo f: S 3 → S 3, que preserva la orientación, tal que f(K 1) = K 2.
Debido a que todo homeomorfismo de S 3 en sí mismo es el extremo de una isotopía ambiente y viceversa, tenemos la prueba del siguiente teorema:
Teorema 2.1. Dos nudos K 1 y K 2 son equivalentes si y sólo si existe una isotopía ambiente {h t } tϵ [0;1] de S 3 tal que h 1(K 1) = K 2.
Una proyección regular de un nudo K consiste en proyectar el nudo sobre el plano z = 0, de tal forma que más de dos puntos no se puedan proyectar sobre uno mismo y dos segmentos no puedan tener la misma proyección.
Lo anterior motiva la siguiente definición:
Definición 2.2. Un diagrama de un nudo es un grafo planar 4-valente orientado y conexo, tal que los grados de entrada y salida de cada uno de sus vértices son iguales a 2 y pueden ser dibujados de acuerdo a laFigura 1-a.
Siguiendo la idea de la definición anterior, al dibujar las proyecciones regulares de los nudos tendremos el cuidado de dejar algunos espacios en blanco alrededor de los puntos dobles, que llamamos cruces, indicando cuál de los puntos va por encima y así poder recobrar el nudo a partir de la proyección. La Figura 1-a muestra un ejemplo de una proyección regular de un nudo.
Como podemos ver, las proyecciones regulares de nudos son diagramas de nudos. Los cruces de un diagrama de un nudo son clasificados de acuerdo a la Figura 1-b. Así que podemos hablar de cruce por debajo y cruce por encima. Entonces, a la sección del diagrama que va de un cruce por debajo al siguiente cruce por debajo se le llama arco del diagrama; en otras palabras, los arcos son los componentes conexos del diagrama del nudo.
Un nudo tiene infinitos diagramas, pero cada uno de ellos se puede transformar en el otro mediante un número finito de los movimientos de Reidemeister (véase Figura 2) e isotopías del plano.
El nudo cuya proyección regular no tiene cruces es llamado nudo suelto.
La prueba del siguiente teorema puede ser consultada en 6.
Teorema 2.3 (Teorema de Reidemeister). Dos nudos son equivalentes si y sólo si sus respectivos diagramas se pueden transformar el uno en el otro mediante un número finito de los movimientos de Reidemeister e isotopías del plano.
Por el teorema anterior, no hacemos distinción entre los diagramas de nudos y los nudos mismos. Un nudo es trivial si este es equivalente al nudo suelto.
2.2 Construcción de códigos
Sea K un diagrama de un nudo y etiquetemos sus cruces con números a
1, a
2,...,a
n
en ℤ+, donde n es el número de cruces clásicos de K. Tomemos un punto x sobre K, que no sea un cruce. Recorramos el diagrama a partir de x hasta retornar a dicho punto en el sentido de la orientación y formemos una lista con los números de los cruces que nos vayamos encontrando en el recorrido, con la convención de que si pasamos por debajo del cruce a
i
, escribimos - a
i
y si pasamos por encima del cruce a
i
, escribimos a
i
. Denotemos la lista construida anteriormente por C(K) y llamémosla lista de cruces. Construyamos la lista (e
1, e
2, …, e
m
), donde
A la pareja ordenada (C(K); S(K)) la llamamos nudo combinatorio de K. Notemos que con esta convención pueden existir enteros, entre 1 y m, que no correspondan a cruces del nudo.
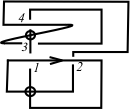
Consideremos el diagrama K mostrado en la Figura 3. Si recorremos K a partir del punto x obtenemos el código:
((-4, 6, -2, 4, -6, 2),(1, 1, 1, 1, 1, 1)).
La construcción anterior motiva la siguiente definición.
Definición 2.4.7) Un nudo combinatorio o código de n cruces es una pareja ordenada ,
((i 1, i 2,…, i 2n ); (e 1,…, e m )),
tal que, como conjuntos, {i 1, i 2,…, i 2n } = {±a 1,…, ±a n }, donde a 1,..., a n en ℕ, son llamados cruces del código, m ≥ máx {a 1, a 2, …, a n } y e j ∈ {1,-1}, j = 1, 2, …, m.
Definimos el código trivial como ((),()).
Ahora bien, dado un diagrama de un nudo K siempre existe un nudo combinatorio asociado a K, pero el recíproco no siempre es cierto; por ejemplo, el nudo combinatorio σ = ((1,2, -1, 3, -4,-3, 4,-2); (1,-1, 1,-1)) no es el nudo combinatorio de un diagrama de un nudo. La Figura 4 muestra un intento por construir un diagrama para σ. Observemos que es imposible conectar los extremos g y h sin crear un nuevo cruce.
Es claro que el proceso anterior no es una prueba rigurosa de que σ no es un nudo combinatorio asociado a un diagrama de un nudo.
De la construcción de nudo combinatorio, a partir de un diagrama de un nudo y por el Teorema de la curva cerrada de Jordan, podemos inferir la prueba de la siguiente proposición:
Proposición 2.5. Si σ = ((i 1, i 2,…, i 2n ), (e 1, …, e n )) es un nudo combinatorio asociado a un diagrama de un nudo, entonces el número de ocurrencias entre a i y -a i en (i 1, i 2,…, i 2n ), para todo i = 1, 2, …, n, es par.
De la proposición anterior, el nudo combinatorio σ del ejemplo anterior no es el nudo combinatorio de un diagrama de un nudo.
Definición 2.6. Un nudo combinatorio es geométrico si es el nudo combinatorio de un diagrama de un nudo.
Como podemos observar, a un mismo diagrama de un nudo K se le pueden asociar muchos nudos combinatorios dependiendo de la numeración de los cruces y del punto base que escojamos, sin contar con los movimientos de Reidemeister. En 7,14,15) se define una relación de equivalencia sobre los nudos combinatorios y en 15 se prueba que existe una correspondencia biunívoca entre las clases de equivalencia de nudos y las clases de equivalencia de nudos combinatorios geométricos, así que podemos suponer, sin pérdida de generalidad, que nuestros nudos combinatorios K = ((i 1, i 2,…, i 2n ), (e 1, e 2,…, e n )) satisfacen { i 1, i 2,…, i 2n } = {±1, …, ±n} y son escritos en la forma:
K = ((-1, A 1,-2, A 2,…,-n, A n ); (e 1,…, e n )), (1)
donde A i , i = 1; 2,…, n, son subsucesiones disjuntas de i 1, i 2,…, i 2n y, además, A 1 ∪ … ∪ A n = {1,2,…, n}. Es posible que algunas de las subsucesiones anteriores sean vacías. Esta forma es llamada forma normal estándar.
Si hacemos x i = (-i, A i , -(i + 1)), i = 1, 2,…,n - 1, y x n = (-n, A n , -1), entonces x i es llamado arco del nudo, i = 1,2; …, n. Más aún, si el cardinal de x i es mayor que 2, entonces x i es denominado puente. A los puentes los denotamos por y 1,...,y k y k es llamado el número de puentes de K. El mínimo número de puentes entre todos los nudos de la clase es llamado el número de puentes de la clase.
Este concepto está dado también para los diagramas de nudos. Intuitivamente un puente para un diagrama de un nudo es un “componente conexo" de éste que tiene por lo menos un cruce por encima. El número de estos componentes conexos es el número de puentes del diagrama. El número de puentes del nudo es el mínimo número de puentes entre sus diagramas asociados.
Ejemplos de diagramas de nudos de dos y tres puentes son dados en la Figura 5.
Definición 2.7. A las clases de equivalencia del nudo combinatorio K la denotamos por [K] y decimos que un nudo combinatorio [K] es clásico si y sólo si K es geométrico.
Puesto que el problema de la clasificación de nudos sigue siendo un problema abierto, muchos expertos en el área se han dedicado a clasificar ciertas familias de nudos; entre tales familias se encuentran los nudos de dos y tres puentes. La subclase de los nudos de dos puentes fue clasificada en 1956 por H. Schubert (véase 16). La clasificación completa de los nudos de tres puentes aún no se conoce, pero viene siendo desarrollada por H. Hilden, J. Montesinos, D. Tejada y M. Toro (véase 17).
2.3 El grupo de un nudo
El grupo ∏(K) de un nudo K es uno de los invariantes más antiguos y poderosos en la teoría clásica de nudos. Este grupo se define como el grupo fundamental de la 3-variedad S 3 ∖ K.
En la literatura existen métodos para calcular presentaciones del grupo de un nudo, una de ellas es conocida como presentación de Wirtinger.
Definición 2.8 (Presentación de Wirtinger). Sea G un grupo. Una presentación de Wirtinger de G es una presentación de la forma
Donde
Una presentación de Wirtinger se llama cíclica si tiene la forma
Donde
Una presentación de Wirtinger se llama realizable si
A partir de cualquier diagrama D del nudo K podemos definir una presentación de Wirtinger realizable π 1(D), en la que cada arco de D corresponde a un generador y las relaciones son definidas como se indica en la Figura 6.
Es bien sabido que la presentación π 1(D) es un invariante del nudo K. (véase 18).
Teorema 2.9.19) Si el grupo de un nudo es cíclico infinito, entonces el nudo es equivalente al nudo trivial (S 1).
El problema de determinar si un nudo es trivial o no, conocido como el problema de desanudamiento, fue uno de los primeros en ser resuelto. En 20, W. Haken da un algoritmo para determinar cuándo un nudo es trivial o no.
La prueba del siguiente teorema puede ser consultada en 21.
Teorema 2.10. El problema del desanudamiento está en NP.
Una herramienta bastante poderosa para determinar si un nudo es o no equivalente al nudo suelto, es la teoría de representaciones de grupos. Por medio de esta técnica se han podido encontrar familias infinitas de nudos no triviales.
El estudio de las representaciones de este tipo de grupos no solo se ha usado en esta dirección, también en el estudio de los problemas de geometrización de las tres variedades, en particular de los complementos de nudos en el espacio tridimensional. Por ejemplo, si tenemos una representación de ∏(K) en SL(2, ℂ), entonces, también tendríamos una en PSL(2, ℂ), el recíproco no siempre es cierto (véase 22), puesto que este último grupo es isomorfo al grupo de las isometrías, que preservan la orientación, del modelo hiperbólico del semiespacio superior, entonces, por el teorema de extensión de Poincaré (véase (2) para más detalles) podríamos definir acciones de ∏(K) en alguna de las tres variedades.
El estudio del conjunto de las órbitas para el caso de acciones fieles puede ser bastante interesante en el siguiente sentido: Si G denota la imagen de una representación no abeliana y fiel ρ y si
Por otro lado, hallar representaciones del grupo del nudo en el grupo simétrico S 3 también es una herramienta para distinguir nudos. Existe una familia de nudos cuyos grupos tienen representaciones en S 3; esta familia se llama colección de nudos 3-coloreables.
Definición 2.11. Un diagrama de un nudo es 3-coloreable si podemos pintar sus arcos con tres colores R = rojo, A = azul y V = verde, de tal forma que todos los colores sean usados y en cada cruce aparezcan o los tres colores o un solo color.
No es difícil probar que ser 3-coloreable es invariante bajo los movimientos de Reidemeister y que, además, el nudo trivial no es 3-coloreable. La Figura 5 muestra un ejemplo de un nudo 3-coloreable (a) y otro que no es 3-coloreable (b). ¿Cómo se prueba que tal nudo no es 3-coloreable?
Teorema 2.12. Si K es 3-coloreable, entonces existe una representación de ∏(K) en el grupo simétrico S 3 .
Demostración. Supongamos que K es 3-coloreable y escojamos una coloración de sus arcos. Separemos los generadores de ∏(K) en tres grupos de acuerdo a su respectivo color. Supongamos que 〈x 1, ..., x n | r 1, ..., r n 〉 es la respectiva presentación de Wirtinger de ∏(K). Consideremos el homomorfismo natural
donde
Debido a que
(12) (23) (12) = (13),
(23) (12) (23) = (13),
(13) (12) (23) = (21), (3)
entonces ker(μ) = 〈r 1, …, r n 〉, con lo que μ extiende a un homomorfismo de ∏(K) en S 3.
El siguiente algoritmo nos da una forma eficiente de calcular una presentación del grupo de un nudo. Puesto que es bien conocido y su prueba se obtiene al aplicar una sucesión adecuada de transformaciones de Tietze, omitiremos su demostración.
Algoritmo 2.13 (Algoritmo para hallar la presentación por encima). Sea D un diagrama de un nudo con puentes denotados por y 1 ,...,y k como se indica en laFigura 7. Aquí, e ki = 1 si el cruce es positivo o e ki = -1 si el cruce es negativo.
Para cada puente y i escoja un punto z i .
Recorra el diagrama D desde el punto z i en el sentido de su orientación.
Escriba una palabra w i con las etiquetas de los puentes que recorra por debajo, con la siguiente convención: escribimos y t (o y t -1 ) si el signo del cruce con respecto al cual se recorre el puente por debajo es positivo (negativo).
Termine el proceso hasta llegar al puente y i+1 .
Con la notación descrita en laFigura 7, obtenemos
Se prueba que y i W i = w i y i+1 y, además que ∏(D) = G(w 1 , ...,w k ).
De lo anterior, tenemos la prueba del siguiente teorema: (otra puede ser consultada en 11). Será que algún
Teorema 2.14. Sea D un diagrama de un nudo y sean y 1 ,...,y k sus puentes, entonces existen palabras w 1 ,...,w k en el grupo libre F(y 1 , …, y k ), tales que
La presentación anterior es conocida como presentación por encima del grupo de un nudo. Usamos la notación G(w 1 , ...,w n ) para indicar la presentación 31.
Ejemplo 2.15. Una presentación por encima del grupo del nudo, mostrado en laFigura 5-a, está dada por G(yx; xy) y para el grupo del nudo de laFigura 5-b, es G(x 2 x 3 x 1 , x 3 x 1 x 2 , x 1 x 2 x 3 ).
Definición 2.16. Sea K un nudo y σ= ((i
1, …, i
2n
), (e
1, …, e
m
)) un nudo combinatorio asociado a K. Si G(w
1, …, w
k
) es una presentación por encima del grupo de K, definimos la pareja periférica de K como el par (l
m
= w
1 ··· w
k
m
-p
,m), donde
A la palabra l m se le llama una longitud del nudo y a m, un meridiano.
Decimos que dos parejas periféricas (l m , m) y (l m' ,m') son conjugadas si existe 𝜏 ∈ G(w 1, …,w k ) tal que lm = 𝜏l m' 𝜏-1 y m = 𝜏 m' 𝜏-1. En 11, definimos la estructura periférica de un nudo como la clase conjugada en G(w 1, …, w k ) de una pareja periférica. En 11, se prueba que la estructura periférica es única, salvo la conjugación.
La tripleta (G(w 1, …, w k ); l m ,m) se llama sistema periférico. Dos sistemas periféricos son isomorfos si y sólo si existe un isomorfismo entre los grupos de los nudos que envía una estructura periférica a la otra. El teorema de Waldhausen afirma que los nudos están completamente determinados por sus sistemas periféricos. (Véase 23). Para la prueba del siguiente teorema, véanse 23 , 24.
Teorema 2.17. Si (G(w 1 , ...,w k ), l m ,m) es un sistema periférico de un nudo y l m es 1, donde 1 representa la identidad de G(w 1 , ...,w k ), entonces el nudo es trivial.
La deficiencia de una presentación es la diferencia entre el número de generadores y el número de relaciones. La deficiencia de un grupo es el máximo de las deficiencias de las presentaciones de un grupo si tal número existe. Aunque es bien sabido que la deficiencia del grupo de un nudo es 1, aquí presentamos una prueba combinatoria de este hecho, pero antes, probamos el siguiente resultado: (Su prueba fue realizada por O. P. Salazar en 25).
Teorema 2.18. Si G es el grupo de un nudo, entonces G = G' ⋊ ℤ, donde G' es el conmutador de G. Por tanto, G/ G' ≅ℤ.
Demostración. No es difícil probar que G/ G' es isomorfo a ℤ, sea t tal que ℤ = 〈t〉. Sabemos que G tiene una presentación de la forma
donde
Puesto que
Además, si definimos el homomorfismo ψ: ℤ → G, t ↦x 1, entonces, (π o ψ)(t) = t. Por tanto, la sucesión exacta (5) es escindida, por lo que G = G' ⋊ ℤ.
La prueba del siguiente teorema usa el hecho de que el grupo de un nudo tiene una presentación con deficiencia 1 (véase 18).
Teorema 2.19. La deficiencia del grupo de un nudo es 1.
Demostración. Supongamos que tenemos una presentación
〈x 1,..., x n | r 1,..., r m 〉,
Donde
Supongamos que n > 1. Dado que G/ G' es un grupo abeliano, podemos despejar a x
n
de una de las m relaciones como
Por último, cabe aclarar que en general el grupo de un nudo no es un invariante completo; es decir, existen nudos que no son equivalentes y, sin embargo, sus respectivos grupos son isomorfos. Pero, si los nudos son primos, entonces este grupo los distingue, salvo la imagen espejo e inverso. Estas definiciones pueden ser consultadas en 18. Así, tenemos el siguiente teorema:
Teorema 2.20. Sean K 1 y K 2 nudos primos. Si ∏(K 1) es isomorfo a ∏(K 2), entonces o K 1 es equivalente a K 2 o a la imagen espejo de K 2 o al inverso de K 2 o al inverso de la imagen espejo de K 2 .
2.4 La idea de Kauffman
Como habíamos visto previamente, existen nudos combinatorios que no provienen de diagramas de nudos. Entonces, ¿qué debemos hacer con estos códigos? Para resolver este interrogante, L. H. Kauffman (véase 8), permitió un nuevo tipo de cruce que él denominó cruce virtual y trabajar con el diagrama haciendo caso omiso del nuevo cruce. A ese tipo de diagramas, Kauffman los llamó diagramas de nudos virtuales.
Si completamos el proceso descrito en la Figura 4, teniendo en cuenta la idea de Kauffman, obtenemos el diagrama mostrado en la Figura 8. Así, podemos asegurar que a cada nudo combinatorio le corresponde un nudo virtual y viceversa. La prueba de esta última afirmación no es difícil de obtener. Para más detalles, véase 11.
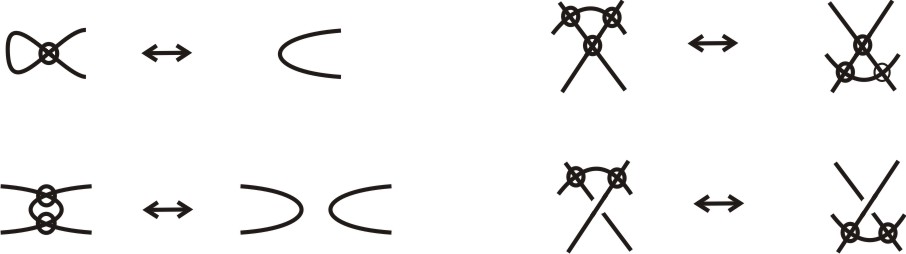
Kauffman definió una serie de movimientos, llamados movimientos extendidos de Reidemeister sobre estos diagramas, al considerar los mostrados en la Figura 9 que, junto con los movimientos de Reidemeister, definen una relación de equivalencia. Él probó, entre otras cosas, que los nudos pueden ser vistos como una subcategoría de los nudos virtuales. En 15, se prueba que existe una correspondencia biunívoca entre las categorías de los nudos virtuales y los combinatorios.
Definición 2.21. Un nudo combinatorio es clásico si es equivalente a un nudo combinatorio geométrico.
Existen condiciones necesarias y suficientes para determinar cuándo un nudo combinatorio es geométrico (véanse 15 , 26). La siguiente condición es necesaria, pero no suficiente para determinar cuándo un nudo combinatorio no es geométrico:
Proposición 2.22. Sea K = ((i 1 , i 2 , … , i 2n ), (e 1 , e 2 , … e n )) un nudo combinatorio. Aplicando permutaciones cíclicas sobre (i 1 , i 2 , · · · , i 2n ) supondremos que
donde S aj es una subsucesión de i 1 , i 2 , …, i 2n .
Si
El siguiente polinomio fue definido en 27 para diagramas de nudos virtuales. Aquí usaremos los nudos combinatorios para dar una definición alternativa:
Definición 2.23. Sea [K] la clase de equivalencia de un nudo combinatorio K con cruces a 1 ,...,a n , entonces el polinomio P [K] (t) es el polinomio
Y P [K] (t) = 0 si α ai (K) = 0 para todo i = 1, 2, ..., n.
En 15 ) se prueba que P [K] (t) es un invariante de nudos combinatorios y, por tanto, de nudos virtuales. Dicho polinomio tiene la particularidad de ser cero sobre la categoría de los nudos combinatorios clásicos.
Aunque en la literatura existen muchas técnicas (véase, por ejemplo, 8,27-29) para determinar cuándo un nudo virtual no es equivalente a un diagrama de un nudo clásico, éste sigue siendo aún un problema abierto. La técnica expuesta en 30 y en 15 parece ser una buena aproximación a resolver dicho interrogante.
La definición del grupo de un nudo virtual se hizo a nivel de diagramas, haciendo caso omiso de los cruces virtuales; es decir, que algunos arcos pasarán a través de cruces virtuales y las relaciones se obtendrán en los cruces que no sean virtuales. Usando los nudos combinatorios, podemos definir lo que es el número de puentes para los nudos virtuales y tener el siguiente teorema (para la prueba véase 11):
Teorema 2.24. Sea K un nudo virtual y sea ∏(K) su grupo. Si K tiene k puentes, y 1 ,...,y k , entonces existen palabras w 1 ,...,w k en el grupo libre 〈y 1 , …, y k |〉 tales que ∏(K) = 〈y 1 , …, y k | y i w i = w i y i+1 , i = 1, 2, …, k 〉. Las palabras w 1 ,...,w k se computan de la misma forma que la descrita en el Algoritmo 2.13.
Al permitir los movimientos virtuales de Reidemeister sobre los diagramas de nudos, podemos tener la siguiente definición alternativa de número de puentes virtuales, como sigue: sea D un diagrama de un nudo y denotemos sus clases [D] y [D] v bajo los movimientos de Reidemeister y los movimientos extendidos de Reidemeister, respectivamente. Entonces, tenemos el número de puentes virtuales, denotado b([D] v ) y el número de puentes real b([D]), como el mínimo número de puentes en las respectivas clases. Es claro que b([D] v ) ≤ b([D]). ¿Es posible tener la igualdad?
La definición de grupo de un nudo virtual de Kauffman no tiene el carácter topológico de la hecha para los nudos en S 3, sin embargo, es posible definir un grupo de esa misma forma. Para ello, debemos introducir lo que comúnmente se conoce como realización de nudos virtuales en superficies engrosadas, véase 7.
Definición 2.25. Una superficie engrosada es una 3-variedad de la forma ∑ × [0,1], donde ∑ es una superficie orientable y compacta. Un subconjunto K de ∑ × [0,1] es llamado un nudo generalizado si existe un encaje de S 1 en ∑ × [0,1], que preserva la orientación, cuya imagen es K.
En forma análoga al caso de los nudos en S 3, podemos pensar en diagramas de nudos generalizados sobre superficies orientables y compactas. Además, puesto que los movimientos de Reidemeister sólo afectan una parte del diagrama dentro de un disco pequeño, podemos pensar en los movimientos de Reidemeister para el caso de diagramas de nudos generalizados sobre superficies orientables y compactas. Sólo debemos tener cuidado de que los diagramas no intersecten la frontera de la superficie donde yacen.
Aunque no hay un teorema análogo al de Reidemeister que relacione los nudos generalizados con sus diagramas, podemos hacer la siguiente definición (véanse 8,28):
Definición 2.26. Sean D i un diagrama de un nudo sobre una superficie orientable y compacta ∑ i ,i = 1; 2. Decimos que (∑1 , D 1) es geotópico a (∑2 , D 2), denotado (∑1 , D 1) ḛ (∑2 , D 2) si existe una superficie orientable y compacta ∑ 3 y embebimientos, que preservan orientación f i : ∑ i → ∑3 , i = 1, 2 tales que, f 1(D 1) se pueda transformar en f 2(D 2) mediante un número finito de los movimientos de Reidemeister sobre ∑3 .
Al conjunto de todas las parejas ordenadas de la forma (∑, D), donde ∑ es una superficie orientable y compacta y D es un diagrama de un nudo sobre ésta, lo denotaremos por D.
Definition 2.1. (28Sean (∑, K), (∑', K') ∈ D. Estos dos elementos son establemente equivalentes, denotado por (∑, K) ~ (∑', K' ), si existen (∑ i , K i) ∈ D, i = 1, 2,..., n, tales que
(∑, K) ḛ (∑1 , K 1) ḛ ... ḛ (∑ n ,K n ) ḛ (∑', K' ).
Un ejemplo de dos diagramas de nudos generalizados establemente equivalentes se ilustra en la Figura 10.
En la Figura 11 mostramos, por medio de un ejemplo, la relación que hay entre diagramas de nudos virtuales y los nudos generalizados.
Una prueba del siguiente teorema puede ser consultada en 28.
Teorema 2.27. Existe una correspondencia biunívoca entre las clases de equivalencia de nudos virtuales y las clases de equivalencia estable de nudos generalizados.
Demostración. En la Figura 12 se da una idea intuitiva de la demostración.
Podemos, así, también definir el grupo de un nudo virtual como el grupo fundamental del complemento de una realización de éste en alguna superficie engrosada. Probablemente este grupo no sea un invariante de nudos virtuales, pero sí podemos hacernos preguntas interesantes, como por ejemplo, sobre la geometría del complemento de nudos generalizados y si ésta está conectada con representaciones de los grupos de nudos virtuales en PSL(2;ℂ) como pasa con el caso clásico.
La prueba del siguiente teorema es inmediata; por tanto, la omitiremos.
Teorema 2.28. Si K es un nudo virtual de longitud 1 y tiene un grupo no cíclico, entonces K no es equivalente a un nudo clásico.
3 Nudos combinatorios de 2 puentes
Dados α, β primos relativos, tales que 0 < α, -α < β < α y α sea impar, construimos un nudo combinatorio de 2 puentes que se puedan realizar como un nudo en S 3. Probamos que esta realización corresponde a la construcción de Schubert, véase 18.
Para los siguientes resultados, α y β son primos relativos, tales que 0 < α, 0 < β < α y α es impar.
Teorema 3.1. Para todo k ∈ {1, 2,..., α − 1},
(1) El número kβ no es congruente con t_ módulo 2α, para t = 1, 2,
(2) Existe un único t k ∈ (0, α) ∪ (α, 2α) ∩ ℤ tal que kβ≡ t k mod 2α y
(3) Como conjuntos
{|α − t k | : k = 1, 2, ..., α − 1} = {1, 2, ..., α − 1}.
Demostración (1): Probemos el caso t = 1, pues el caso t = 2 es similar. Supongamos que existe k en {1, 2, ..., α − 1} tal que kβ ≡ α mod 2α. Si β es par, entonces α sería par, que es un absurdo. Si β es impar, puesto que αβ ≡ α mod 2α, se tendría que kβ ≡ αβ mod 2α, de donde existe n ∈ ℤ+, tal que αβ - kβ = 2nα y, así, (α - k)β = 2nα y, por tanto, (α - k)β es múltiplo común de β y α. Puesto que (α, β) = 1, entonces el mínimo común múltiplo de α y β es αβ, así que, αβ ≤ (α - k)β, que es un absurdo.
(2) Si 0 < kβ < 2α, entonces t k = kβ. Por otro lado, si kβ > 2α, existen n, r enteros, tales que kβ = n(2α) + r, con 0 < r < 2α. En este caso, hacemos t k = r.
Sea k ∈ {1, 2, …, α -1} y sean
(3) Se tiene de (2).
De lo anterior, podemos definir lo que llamaremos sucesiones puentes.
Definición 3.2. Las sucesiones puente están definidas como:
A 1 = n 1 , n 2 , ..., n α−1 , A 2 = m 1 ,m 2 , ..,m α−1 ,
donde
k = 1, 2, ..., α − 1.
Con la idea de no dar una notación recargada, usamos, sin temor a confusión, la letra A i para denotar tanto a la sucesión puente A i como al conjunto ordenado {A i }, i = 1, 2.
Teorema 3.3. Las sucesiones puentes están bien definidas. Más aún,
(1) A 1 ∩ A 2 =ϕ y
(2) A 1 ∪ A 2 = {1, 2, ..., 2α − 2}.
Por tanto si B 1 = −1,−2, ...,−(α − 1), B 2 = −α,−(α + 1), ...,−(2α − 2) y e 1, e 2, ..., e 2α−2 ∈ {1,−1}, son tales que e k = −1 si t k ∈ (α, 2α) ó e k = 1 si t k ∈ (0, α), para k = 1, 2, ..., α − 1 y e α+(j−1) = e j , para j = 1, 2, ..., α − 1, entonces
K α,β = ((A 1,B 1,A 2,B 2), (e 1, e 2, ..., e 2α−2 ))
es un nudo combinatorio.
Demostración. (1): Razonemos por el absurdo, supongamos que existe b ∈ A 1∩A 2, entonces b = n x = m y para algunos x, y ∈ {1, 2, ..., α − 1}. Por Teorema 3.1, existen s, r ∈ {1, 2,..., α − 1} tal que n x = n │a-ts│ y m y = m │α-tr│ . Consideremos los siguientes casos:
Caso 1: Si s es un número par, entonces b = n x = n ((-ts( = s. Ahora bien, si r es par, m y = m ((-tr( = α + (r − 1), de donde s = b = m y = α + (r − 1) ∉ {1, 2, ..., α−1} contradiciendo la escogencia de s. Si r es impar, s = r que, tampoco es posible, ya que s es par y r es impar.
Caso 2: Si s es un número impar, entonces b = n x = n ((-ts( = α + (s - 1). Ahora bien, si r es par, m y = m((-tr(= α + (r - 1), de donde α + (s - 1) = b = m y = α + (r - 1), y así s = r que no es posible, ya que s es impar y t es par. Si r es impar, m y = m((-tr( = r, reemplazando, α + (s - 1) = r, lo que implicará que r ∉{1, 2, …, α - 1}, contradiciendo la escogencia de r.
(2) Sea r ∈ {1; 2,…, 2α - 2}. Supongamos que 1 ≤ r ≤ α - 1. Si r es par, entonces r = n ((-tr( ∈ A 1. Si r es impar, r = m((-tr(∈ A 2.
Por otro lado, si α ≤ r ≤ 2α - 2, existe k ∈ {1, 2, ..., α - 1} tal que r = α + (k - 1) (tome k = r - (α - 1)). Si k es par, r = m((-tk( ∈ A 2 y si k es impar, r = n ((-tk( ∈ A 1. De lo anterior, r ∈ A 1 ∪ A 2.
Dados α, β primos relativos tales que 0 < α, 0 < β < α, existe un diagrama de un nudo de dos puentes, denotado S(α, β), asociado a α y β , véase 8.
Teorema 3.4. El nudo combinatorio K α,β es geométrico.
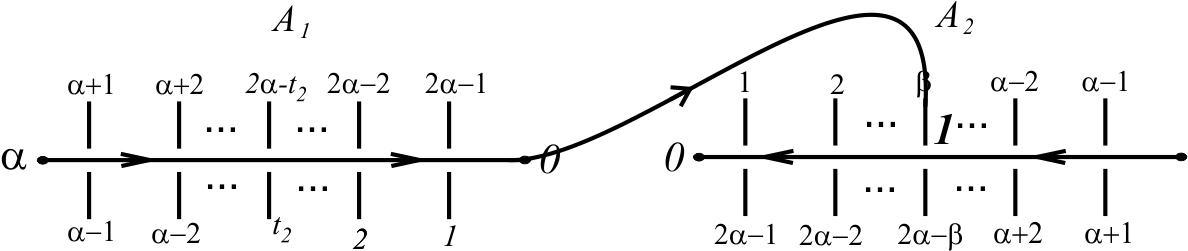
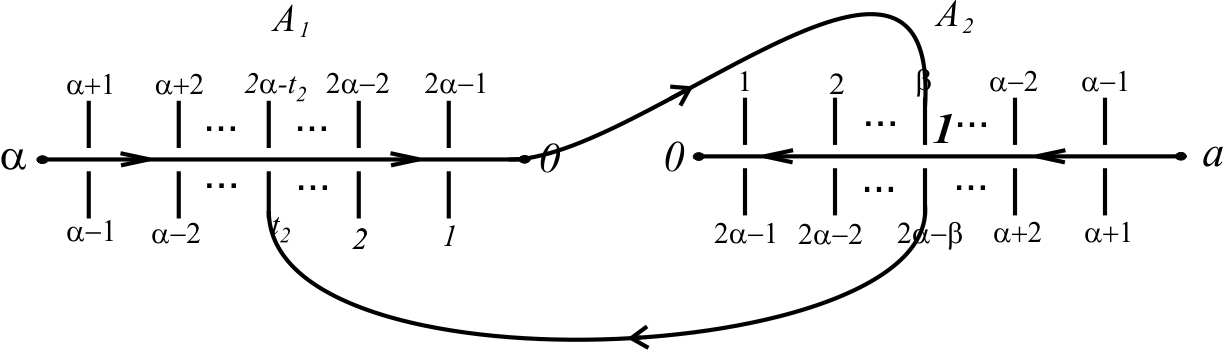
Demostración. Para probar que S(α, β) es una realización de K α,β , debemos ilustrar la construcción de Schubert, véase 18. Consideremos la Figura 13, donde A 1 y A 2 representarán los puentes del diagrama S(α, β).
Recorramos la parte A 1, desde el punto α hasta 0. Tracemos una curva desde 0 hasta el segmento etiquetado con β, en A 2 y enumeremos dicho cruce con el número 1, como se muestra en la Figura 14. Observemos que, si recorremos A 2 desde α hasta 0, la posición del 1, en dicho recorrido, es α - β.
Busquemos en A 1 el segmento etiquetado con t 2 y tracemos una curva desde el segmento etiquetado con 2α−β hasta el segmento etiquetado con t 2 y enumeremos dicho cruce con el número 2, como se muestra en la Figura 15. Observemos que, si recorremos A 1 desde α hasta 0, la posición del 2, en dicho recorrido, es |α − t 2|. En general si α < t 2 < 2α, la posición del 2 es |α − t 2|.
Repitamos el proceso anterior hasta t α-1 y tracemos una curva desde el segmento etiquetado con 2α - t α-1 hasta el punto α en A 2. Luego, recorramos A 2 desde α hasta 0 y tracemos una curva desde 0 hasta el segmento etiquetado con β en A 1 y etiquetemos ese cruce con α. Busquemos en A 2 el segmento etiquetado con t 2 y tracemos una curva desde el segmento etiquetado con 2α - β, en A 1 hasta el segmento etiquetado con t 2, en A 2 y nombremos dicho cruce con el número α +1. Repitamos este proceso hasta t α-1 .
El proceso anterior produce un diagrama de un nudo clásico de dos puentes y una enumeración de sus cruces con números enteros desde 1 hasta 2α − 2, de tal forma que si recorremos el diagrama S(α, β) a partir del punto α en A 1, se produce un código nudal de la forma
((B 1,−1,−2, ...,−(α − 1), B 2,−α, −(α + 1), ...,−(2α − 2)), (e' 1, e' 2, ..., e' 2α−2 )),
donde la posición |α − t
k
| en B
1 es k si es par entre 1 y α − 1 o es α + (k − 1) si k es impar entre 1 y α − 1. La posición |α − t
k
| en B
2 es k si es impar entre 1 y α −1 o es α + (k − 1) si k es par entre 1 y α − 1. Con lo que B
1 = A
1 y B
2 = A
2. Por ´ultimo, por la misma numeración de los cruces siempre estamos entrando por el segmento etiquetado con t
k
, con lo que
Definición 3.5. Sean α y β primos relativos α > 0, −α < β < 0 y α impar. Definimos K α,β como el nudo combinatorio dado por
((A 1,−1,−2, ...,− (α −1), A 2,− α,−(α +1), ...,−(2α −2)), (−e 1,−e 2, ...,−e 2α −2)).
La prueba del siguiente teorema puede ser encontrada en 8, Teorema 2.1.3.
Teorema 3.6. Los nudos combinatorios K α,β y K αʹ,βʹ son equivalentes si y sólo si α =αʹ y β ≡βʹ mod α ó ββʹ ≡ 1 mod α.
Teorema 3.7. Sean α y s primos relativos, tales que 0 < α − α < s < α y s es par, entonces existe β impar, con −α < β < α, tal que s β ≡ 1 mod α. Con lo que K α,s ≈ K α, β .
Demostración. Por el teorema 57 en 31, existe 0 < x < α tal que sx ≡ 1 mod α. Ahora bien, si x es impar, tomemos β = x. Si x es par, entonces β = x − α, es impar, −α < β < 0 y sβ ≡ sx ≡ 1 mod α. De lo anterior, la existencia del número β está garantizada.
Por otro lado, puesto que sβ ≡ 1 mod α., entonces (β, α) = 1 y así, K α,β es un nudo. Por el teorema 3.6, K α,s ≈ K α,β .
La siguiente proposición nos dará otra forma de calcular la lista de signos de K α,β . Su prueba puede ser consultada en 10.
Proposición 3.8. Para j ∈ {1, 2, …, α −1}, sea ê j = sign(c j ) donde −α < c j < α y j β ≡ c j mod 2α . Entonces e j = ê j , para todo j = 1,2, …, α −1.
Más aún, para
3.1 El grupo de un nudo de 2 puentes
Iniciamos esta sección con el siguiente teorema.
Teorema 3.9. Si K = K α,β , entonces la presentación por encima de ∏1(K) está dada por
∏ (K α,β ) = ⟨x, y: xw = wy, x = y⟩, (8)
donde w = y e1 x e2 ...y e2 x e1 y τ = y −e1 x −e2 ...y −e2 x −e1 .
Corolario 3.10. Dados α y β, ∏(K α,β ) ≌ ∏(K α,-β ).
Proposición 3.11. Para todo α y β existe un único s ∈{1, 2, ..., α − 1} par, tal que sβ ≡ −1 mod α ó sβ ≡ 1 mod α.
Demostración. Hacemos la prueba para el caso β > 0, ya que el caso β < 0 es similar. Puesto que (β, 2α) = 1, entonces por el teorema 57 en 31, las ecuaciones xβ ≡ (1+α) mod 2α y yβ ≡ (α −1) mod 2α tienen solución en (0, α). Probemos que tales soluciones son pares. En efecto, sea s una solución de la ecuación xβ ≡ (α +1) mod α, entonces existe n ∈ ℤ tal que sβ = α + 1 + 2nα, puesto que α + 1 + 2nα es par y β es impar, así que s debe ser par. Por otro lado, sea s una solución de la ecuación yβ ≡ (α −1) mod 2α, entonces existe m ∈ ℤ, tal que yβ = α −1+2mα, como α −1+ 2mα es par y βes impar; por lo tanto, s debe ser par. Puesto que s es par, sβ ≡ (α ± 1) mod 2α equivale a que sβ ≡ ±1 mod α.
Por último, sean s y s' ∈ {1, 2,..., α − 1} pares, tales que sβ ≡ ±1 mod α y sβ ≡ ±1 mod α ys'β ≡ ±1 mod α. Sin pérdida de generalidad, supongamos que s − sʹ > 0. Sean m y enteros, tales que sβ = ±1 + mα y sʹβ = ±1 nα, con lo que (s − sʹ)β = (m − n)α, puesto que (α, β) = 1, entonces [α, β] = αβ, donde [α, β ] denota el mínimo común múltiplo de α y β , con lo que (s − s')β ≥ αβ, que es un absurdo, ya que s − s' < α, luego s = s'.
Teorema 3.12. Sean α, β primos relativos tales que: 0 < α, −α < β < α y α impar. Sea s = s(α, β) el número par, tal que 2 ≤ s ≤ α − 1 y sβ ≡ 1 mod α(ó sβ ≡ −1 mod α), entonces, para todo β' ∈ (−α, α), tal que sβ' ≡ 1 mod α ó sβ' ≡ −1 mod α,
∏(K α,β ) ≌ ∏(K α,β' ).
Demostración. Supongamos que sβ ≡ 1 mod α, puesto que (s, α) = 1 y 0 < s < α, entonces por el teorema 3.6, K α,β ≈ K α,s . Ahora consideremos los siguientes dos casos:
Caso 1: Si sβ' ≡ 1 mod α, por el teorema 3.6, K α,s ≈ K α,β' , con lo que, K α,β ≈ K α,β' , y por la invarianza del grupo de un nudo, ∏( K α,β ) ≌ ∏(K α,β' ).
Caso 2: Si sβ' ≡ −1 mod α, entonces (−s)β' ≡ 1 mod α. Por el teorema 3.6, K α, −,s ≈ K α,β' y por la proposición 3.10, ∏( K α, −,s ) ≌ ∏( K α, ,s ).
Ahora supongamos que sβ ≡ −1 mod α, entonces (−s)β ≡1 mod α. Puesto que (−s, α) = 1, entonces, por el teorema 3.6, K α,β ≈ K α, −s .
Haciendo un procedimiento análogo al caso anterior, se muestra que ∏(K α,β ) es isomorfo a ∏(K α,βʹ ).
Algunas aplicaciones del número s se dan en los siguientes ejemplos:
Ejemplo 3.13. Para α = 7 y β = 3, ∏(K 7,3) = ⟨x, y : xw = wy, xτ = τy⟩, donde w = yxy −1 x −1 yx y τ = y −1 x −1 yxy −1x−1. Así, los relatores de ∏(K 7,3) son:
r 1: xyxy −1 x −1 yx = yxy −1 x −1 yxy,
r 2: xy −1 x −1 yxy −1 x −1 = y −1 x −1 yxy −1 x −1 y.
Por otro lado, 2 × 3 ≡−1 mod 7, de donde s = 2. Si pasamos las 2 primeras letras del lado izquierdo, en la relación r1, al derecho y pasamos las dos últimas letras del lado derecho, en la misma relación, al izquierdo, obtenemos la relación r 2 .
Ejemplo 3.14. Para 𝛼 = 13 y 𝛽 = 3, ∏(K 13,3) = ⟨x, y : xw = wy, xτ = τy⟩, donde w = yxyxy −1 x −1 y −1 x −1 yxyx y τ= y −1 x −1 y −1 x −1 yxyxy −1 x −1 y −1 x −1 .Así, los relatores de ∏(K 13,3 ) son:
r1 : xyxyxy −1 x −1 y −1 x −1 yxyx = yxyxy −1 x −1 y −1 x −1 yxyxy
r2 : xy −1 x −1 y −1 x −1 yxyxy −1 x −1 y −1 x −1 = y −1 x −1 y −1 x −1 yxyxy −1 x −1 y −1 x −1 y.
Ahora bien, 4 × 3 ≡ −1 mod 13, de donde s = 4. Si pasamos las 4 primeras letras del lado izquierdo, en la relación r 1 , al derecho y pasamos las 4 últimas letras del lado derecho, en la misma relación, al izquierdo, obtenemos la relación r 2 .
Ejemplo 3.15. Para α = 13 y β = 7, ∏(K 13,7) = 〈x, y: xw = wy, xτ = τy⟩, donde w = yx −1 y −1 xyx −1 y −1 xyx −1 y −1x y τ = y −1 xyx −1 y −1 xyx −1 y −1 xyx −1, reemplazando, encontramos que los relatores de ∏(K 13,7) son:
r1: xyx −1 y −1 xyx −1 y −1 xyx −1 y −1 x = yx −1 y −1 xyx −1 y −1 xyx −1 y −1 xy
r2: xy −1 xyx −1 y −1 xyx −1 y −1 xyx −1 = y −1 xyx −1 y −1 xyx −1 y −1 xyx −1 y.
Puesto que 2 × 7 ≡ 1 mod 13, s = 2. Si pasamos las 2 primeras letras del lado derecho, en la relación r 1, al izquierdo y pasamos las 2 últimas letras del lado izquierdo, en la misma relación, al derecho, obtenemos la relación r 2.
Ejemplo 3.16. Para α = 13 y β = 5, ∏(K 13,5) = 〈x, y : xw = wy, xτ = τy〉, donde w = yxy −1 x −1 y −1 xyx −1 y −1 x −1 yx y τ = y −1 x −1 yxyx −1 y −1 xyxy −1 x −1 . Reemplazando, encontramos que los relatores de ∏(K 13,7 ) son:
r1 : xyxy −1 x −1 y −1 xyx −1 y −1 x −1 y = yxy −1 x −1 y −1 xyx −1 y −1 x −1 yy
r2 : xy −1 x −1 yxyx −1 y −1 xyxy −1 x −1 = y −1 x −1 yxyx −1 y −1 xyxy −1 x −1 y.
Puesto que 8 × 5 ≡ 1 mod 13, s = 8. Si pasamos las 8 primeras letras del lado derecho, en la relación r 1, al izquierdo y pasamos las 8 últimas letras del lado izquierdo, en la misma relación, al derecho, obtenemos la relación r 2.
Procediendo de forma similar a lo hecho en los ejemplos anteriores, probamos en 10) el siguiente teorema:
Teorema 3.17. Para todo α y β, el relator xτ = τy es consecuencia del relator xw = wy, donde w = y e1 x e2 ... y e2 x e1 y τ = y -e1 x -e2 ... y -e2 x -e1 . Por tanto, el grupo ∏(K α,β ) tiene deficiencia 1.
3.2 Representaciones de grupo de nudos de dos puentes
En esta sección estudiamos representaciones de los grupos de nudos de dos puentes en el grupo de matrices SL(2,ℂ), dando algunas condiciones sobre las palabras w
1, w
2 para que existan tales representaciones. Para más detalles véase 32. También consideramos el caso general de representaciones en el álgebra quaterniónica
Sea z un número complejo y consideremos las matrices parabólicas
Sea F = F (x, y) el grupo libre en los generadores {x, y}. Existen homomorfismos únicos,
H: F → SL(2,ℂ) con H (y) = B, y H (x) = Az. (10)
La imagen de F bajo este homomorfismo la denotamos Г z .
___
Si w = y e1 x e2 · · · y em-1 x em ∈ F, a H (w) la denotamos genéricamente por
por lo que a, b, c y d son polinomios en la variable z, véase [Proposición 1, 32].
Para extender el homomorfismo H definido en (10) al grupo G(w), se requieren condiciones que garanticen que las relaciones se preserven.
Teorema 3.18.
Sea
Demostración. La igualdad A z W = WB es cierta si y sólo si
Resolviendo estas ecuaciones obtenemos que A z W = WB si y sólo si c = zb y a = 0.
Teorema 3.19. Sea
, α un número impar y
Demostración. Véase 12.
La prueba del siguiente teorema se hace por inducción matemática.
Teorema 3.20.
Sea
y
Demostración. Aplicamos inducción sobre α. En efecto, si α = 3, entonces
Así, grad(a) = grad(c) = 1 y grad(b) = grad(c) = 0.
Ahora bien, sea W
α
= B
e1
Az
e2
W
𝛼 -2
… B
e(-2
Az
e(-1
. Por hipótesis de inducción, en este caso tomando
Reemplazando en W α y haciendo el producto explícitamente matricial, tenemos que grad(a) = grad(c) = n y grad(b) = grad(d) = n − 1.
Del teorema anterior, podemos concluir que los grupos de los nudos de dos puentes S(α, β) siempre tienen representaciones no abelianas en SL(2;ℂ), cuando α > 2.
Un interrogante que surge es: ¿Podemos extender el procedimiento anterior a nudos de tres puentes?
Ahora, consideremos representaciones en la 𝕂-álgebra quaterniónica:
tal que i 2 = μ, j 2 = v y ij = −ji. Donde K es un campo. Para más detalles, véase 13.
Tenemos que
Es un isomorfismo.
Para A = 𝛼+ i𝛽 + j𝛾 + ij𝛿, sea A + = 𝛼 y A − = i𝛽 + j𝛾 + ij𝛿, entonces definimos T(A) como 2A + y N(A) como A(A + − A −1). No es difícil verificar que el subconjunto U1 = {A ∈ ℍ | N(A) = 1} es un subgrupo de ℍ y, además, tenemos los siguientes isomorfismos:
y si
Supongamos que G = 〈a, b | r(a, b)〉 es el grupo de un nudo de dos puentes, en este caso, r(a, b) : aw(a, b) = w (a, b)b, y sea 𝜌 : G → U 1 una representación, tal que 𝜌(a) = A y 𝜌(b)=B, entonces A + = B +.
Sea x = A +, y = −(A − B −)+ y u = 1 − x 2 = −A − A − = −B − B −. El 𝕂-subespacio vectorial Im(𝜌) de ℍ es generado por B = {1, A −, B −, (A − B −)−}, más aún, la representación ( es irreducible si y solo si ℍ es generado, como 𝕂- álgebra, por {1, A −, B − , (A − B −)−}.
Consideremos el automorfismo 𝕏 A : ℍ → ℍ, C ⟶ AC y sea m(A) la matriz del automorfismo 𝕏A con respecto a la base B, entonces
Puesto que m(A) = xII4×4 + m(A−), m(B) = xII4×4 + m(B−), m(A −1) = xII4×4 − m(A −) y m(B −1) = xII4×4 − m(B −), realicemos la sustitución a ±1 por m(A ±1) y b ±1 por m(B±1) en r(a, b) y hagamos
donde W 1(a, b) = aw(a, b) y W 2(a, b) = w(a, b)b.
Sea L G el ideal generado por los polinomios pi(x, y), i = 1, 2, 3,4 y consideremos la variedad algebraica ((L G ) correspondiente a dicho ideal.
Sea (x
0; y
0) ∈ L(L
G
) y, sean
es una representación, véase 13.
Por otro lado,
Entonces
En 10 se da una familia infinita de grupos de nudos virtuales que no corresponden a grupos de nudos clásicos. Estos grupos constituyen una subfamilia de los llamados grupos de Baumslag-Solitar. En ese artículo probamos que los grupos BS(n, n + 1) = 〈 x, y | xy n x -1 = y n+1 〉 corresponden a grupos de nudos virtuales de dos puentes y tienen la siguiente presentación:
Con las técnicas anteriores, podemos calcular los polinomios p 1(x, y),...,p 4(x, y) para el caso del grupo BS(n, n + 1) y considerar la variedad algebraica:
( (p 1(x, y),… , p 4(x + y)).
Pero, en este caso ( (p 1(x, y),…, p 4(x; y)) = Ø. La prueba de este hecho se sale de los objetivos de este artículo. Por tal motivo, la omitimos.
3.3. Construcción de nudos combinatorios a partir de ∏(K α , β )
Dado un grupo con presentación 〈x, y: xw = wy〉, donde w es una palabra en el grupo libre de dos generadores F = 〈x, y |〉, encontramos una galería de nudos combinatorios de 2 puentes K, tales que ∏(K) ≅ 〈x, y: xw = wy〉.
Teorema 3.21. Sea G(w) un grupo no cíclico con presentación:
G(w) = 〈x, y: xw = wy〉 , w = x n1 y n2 ...x nt−1 y nt , t = 2m.
Entonces, existe K; un nudo combinatorio de 2 puentes, tal que ∏(K) es isomorfo a G(w).
Demostración. Si w 1 = x n1 y n2 ...x nt−1 y nt , entonces
G(w) ≅ 〈 x, y: w1 -1 xw 1 y −1 = w2 -1 yw 2 x −1 = 1 〉 ,
donde y w 2 = y −nt x −nt−1 ...y −n2 x −n1 .
Para simplificar la prueba, sea u j = −n t−j+1 , j = 1, 2,..., t, entonces
w 2 = y u1 x u2 … y ut-1 x ut .
Consideremos los siguientes conjuntos:
Sea
Para k ∈ {1,2,…,a}definimos e
k
= siɡ(n
1) si k ∈ A
0, e
k
= siɡ(n
2j+1
) si k ∈ A
j
o e
k
= siɡ (n
2j
) si k ∈ B
j
. Sean
Consideremos las sucesiones Aσ y Bτ obtenidas, respectivamente, al dotar a los conjuntos A y B de un orden específico y despojarlos de su estructura de conjuntos. Entonces, podemos definir el siguiente nudo combinatorio:
K = ((Aσ,−1,−2, ...,−a, B τ ,−(a+1),−(a+2), ...,−2a), (e 1, ..., e a ,−e a , ...,−e 1)).
Probemos que ∏(K) ≌ G(w). En efecto, denotemos los puentes de K por x = {−2a, A,−1} y y = {−a, B,−(a + 1)}. Por teorema visto
Encontremos a ᶢ1 y ᶢ2 de forma explícita. Por definición,
ᶢ1 = (x e1 ...x e1 ) (y e2 ...y e2 ).... (xet-1 …xet-1) (yet...yet) = x n1 y n2 ... x nt-1 x nt = w 1
De forma similar se prueba que ᶢ2 = w 2. Puesto que no es un grupo cíclico, entonces K es de dos puentes.
Observación 3.22. Al nudo combinatorio encontrado en la prueba anterior lo denotamos por Kσ;τ . No es difícil probar que por cada orden A λ , B δ que le demos a los conjuntos A y B, respectivamente, obtengamos un nudo combinatorio K λ , δ tal que ∏( K λ , δ) = G(w).
Para un grupo de la forma G(w) dado, al conjunto de todos los nudos combinatorios de la forma K λ , δ tal que ∏(K λ , δ ) = G(w) lo denotamos K G (w).
Corolario 3.23. Si K ∈ K G (w), entonces K no es clásico y por tanto no trivial.
Demostración. Computemos la longitud de K. Por definición
Sean
A = {j ∈{1, 2, ..., 𝛼 − 1} : j es par} ∪ {j ∈ {𝛼 , 𝛼 + 1, ..., 2𝛼 − 2} : j es impar} y
B = {j ∈{1, 2, ..., 𝛼 − 1} : j es impar} ∪ {j ∈ {𝛼, 𝛼 + 1, ..., 2𝛼 − 2} : j es par}
conjuntos ordenados, entonces, cualquier otro orden para ellos está determinado por permutaciones σ: A →A y λ : B → B.
Sea K σ,λ el nudo combinatorio
((Aσ,−1, ...,−(𝛼 − 1), Bλ,−𝛼, ...,−(2𝛼 − 2)), (e 1, e 2, ..., e 𝛼−1, e 1, e 2, ..., e 𝛼−1)),
entonces ∏(K σ,λ) ≅ ∏(K 𝛼,𝛽 ).
Denotemos la colección de estos nudos combinatorios por K 𝛼,. Es claro que, para todo 𝛼, 𝛽, K 𝛼, ∈ K 𝛼,.
Teorema 3.24. Para todo 𝛼 y 𝛽, y σ: A → A y λ : B → B permutaciones, el nudo combinatorio
((A σ ,−1, ...,−(𝛼 − 1), B λ ,−𝛼, ...,−(2𝛼 − 2)), (e 1, ..., e 𝛼−1,−e 1, ...,−e 𝛼−1)),
satisface:
(1) Tiene grupo isomorfo a ∏( K 𝛼,𝛽) y
(2) Tiene longitud trivial, por tanto, no es clásica.
4. Conclusiones y trabajo futuro
Sabemos que hay una biyección entre clases de equivalencia de duplas de la forma (𝛼, 𝛽), donde 𝛼 y 𝛽 son números enteros positivos que satisfacen las condiciones excepcionales dadas en la sección anterior y nudos de dos puentes.
Consideremos la fracción continua (14) asociada a la dupla (𝛼, 𝛽).
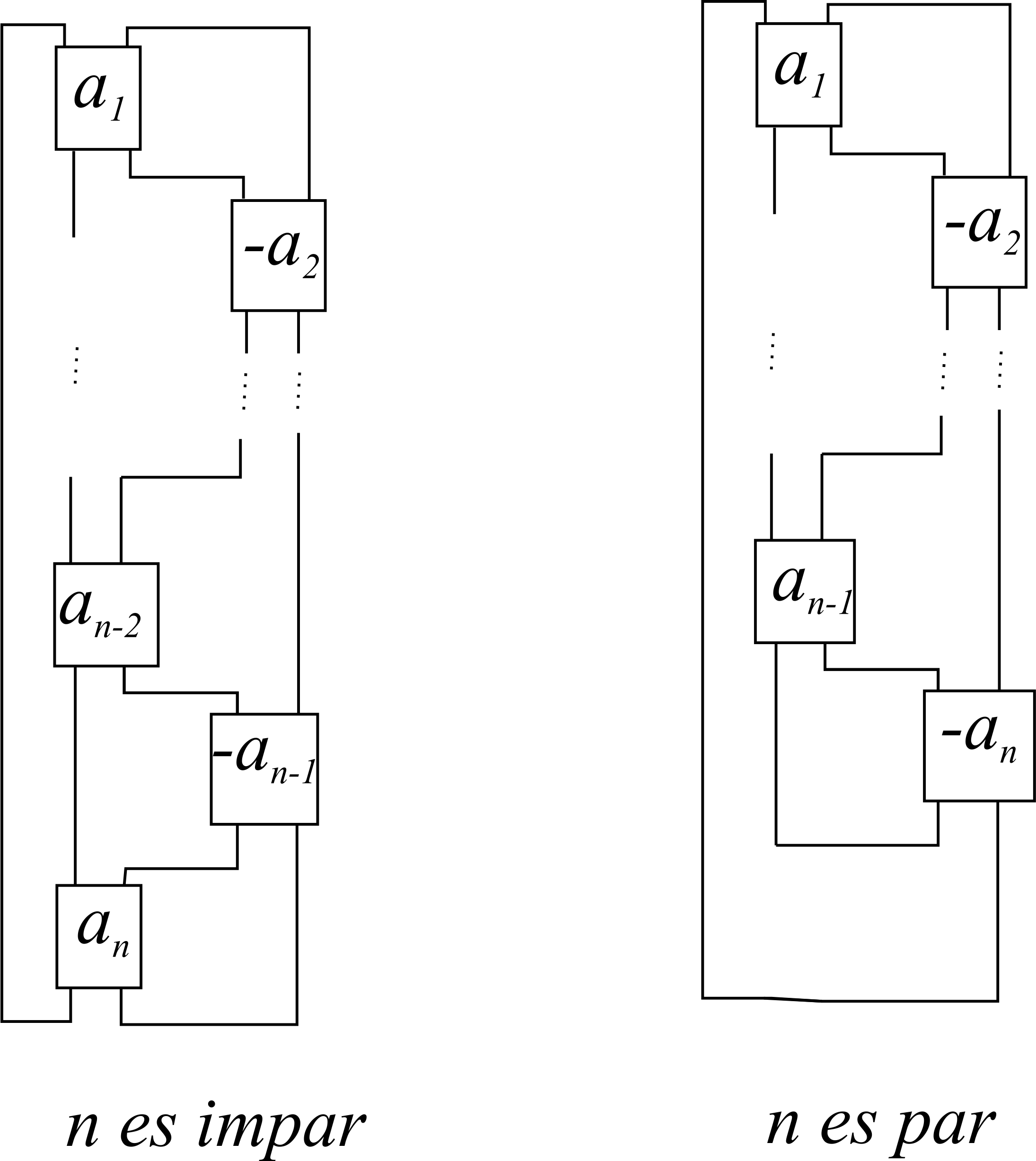
A partir de los enteros a 1, …, a n definimos el diagrama C[a 1, a 2, …, a n ] mostrado en la Figura 16.
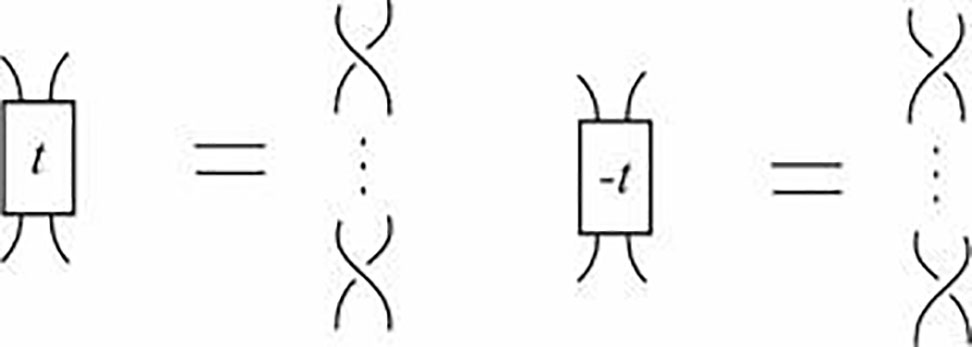
Donde los rectángulos son representaciones abstractas de sucesiones finitas de cruces de acuerdo con la notación dada en la Figura 17.
Estos diagramas fueron llamados por J. Conway 9 diagramas de nudos racionales, pues estos se obtuvieron del numerador de tangles racionales, véase 9,33 , entre otros.
Consideremos el siguiente ejemplo ilustrado que relaciona los nudos racionales con los de dos puentes.
Ejemplo 4.1. Un diagrama orientado para el nudo racional K = C [2, 2, 1] se muestra en laFigura 18. Una presentación para el grupo de este nudo está dada por
∏(K) =⟨x 1 , x 2 , x 3 , x 4 , x 5 | r 1 , r 2 , r 3 , r 4 , r 5⟩,
Donde
r 1 = x 1 x 3x1 -1 x4 -1, (15)
r 2 = x 4 x 1 x4 -1 x2 -1 , (16)
r 3 = x 3 x 4 x3 -1x5 -1, (17)
r 4 = x 5 x 2 x5 -1x3 -1 y (18)
r 5 = x 2 x 5x2 -1x1 -1. (19)
De r
1
tenemos que
Por último, de r 5 tenemos
Si hacemos
⟨x 1, x 3| x 1 w 2 = w 2 x 3, x 3, w 1 = w 1 x 1⟩. (20)
Por otro lado,
Consideremos el diagrama S(7,3) dado en laFigura 19. El grupo de este nudo tiene la presentación dada en (20), por tanto C [2, 2, 1] es un nudo de dos puentes.
Sería muy interesante tener una prueba de que los grupos fundamentales ∏(S(𝛼; 𝛽)) y ∏(C[a 1, …, a n ]) sean isomorfos. Este resultado y el hecho de que el grupo de un nudo clasifique los nudos primos probarían que los nudos racionales y los de dos puentes constituyen la misma familia. Una prueba de esta última afirmación puede ser consultada en 34.
Para el caso de los nudos de tres puentes el problema es más sutil. A estos no se les ha podido asociar una dupla pero si una séxtupla ordenada utilizando el concepto de mariposa. Este estudio está fuera de los objetivos de este artículo. Si el lector está interesado en los detalles, véase 17.