1 Introduction

Ultracold gases is a multidisciplinary field, which lies in the intersection of several physics fields such as quantum information, condensed matter, quantum mechanics, non-linear physics, and statistical mechanics with a very strong contribution of numerical methods. Ultracold gases in optical lattices constitute an extraordinary tool for the analysis of strongly correlated gases under extremely well controlled conditions ^1,2, as highlighted by the observation of the superfluid to Mott-insulator (MI) transition in ultracold bosons ³, recently followed by the realization of the metal to MI transition in two-component fermions ^4,5.

The optical lattice potential is constructed using counter propagating laser beams. These are able to trap the atoms which are already at ultralow temperatures. The most interesting feature of this kind of systems is the tunability of the interactions, making the field very promising because of its high controllability. The perfect periodic optical potential resembles the electron moving in a periodic array of ions which develops a band structure.

In the present work we concentrate on the physics of the lowest energy band.

In 1937, it was pointed out that a variety of transition metal oxides predicted to be conductors by band theory were actually insulators ⁶. About the same time, Nevill Mott and Rudolf Peierls predicted that the failure in the theoretical description can be solved by including the interactions between electrons ⁷. But it was until 1963 when Jhon Hubbard presented the simplest model for interacting electrons in a periodic potential, the nowadays called Hubbard model ⁸. This model takes into account the kinetic energy of the particles given by a hopping term and an interacting contact potential given by,

Where 𝑔= 4πℏ2a/ ma is the interaction strength. This is an isotropic pseudo-potential determined by the particle s-wave scattering length a for the alkali-like atoms and m _a is the atomic mass. Having the periodic potential one can loaded it up with fermions, bosons, spins, molecules, etc. The initial atomic cloud is in the degenerate regime and exhibits all its quantum mechanical behavior. This regime for bosons is the socalled Bose-Einstein Condensation and is achieved when the De Bloglie thermal wavefunction, λT = 2πℏ2 / kBmaT  is larger than the interparticle distance and therefore all the particles go to the lowest energy state exhibiting a giant matter-wave. For fermions, due to the Pauli exclusion principle, the fermionic cloud in this regime is broader than the bosonic cloud making the experimental realization harder but not impossible ^4,5.

It is important to emphasize how the achievement of these low temperatures had generated a boost in the experimental and theoretical techniques with such impact that the pioneers were already awarded with the Nobel Prize. In 1997, S. Chu, Cohen-Tannoudji and W. D. Phillips were awarded for the development of methods to cool and trap atoms with laser light". In 2001, E. A. Cornell, W. Ketterle and C. E. Wieman were awarded for the achievement of Bose-Einstein condensation in dilute gases of alkali atoms and for early fundamental studies of the properties of the condensates". And very recently, in 2012, S. Haroche and D. J. Wineland were awarded for ground-breaking experimental methods thatenable measuring and manipulation of individual quantum systems".

Optical traps permit the simultaneous trapping of various Zeeman sublevels, allowing for multicomponent (spinor) gases. Spinor bosons have attracted a large interest due to their internal degrees of freedom since it gives rise to rich ground-state physics and spinor dynamics ^9-12. Spinor gases in lattices are particularly exciting, since they provide unique possibilities for the analysis of quantum magnetism.

Spin-1 gases are the simplest spinor system beyond the two-component isospin-1=2. Depending on inter-particle interactions ^9,10, (given by the s-wave scattering lengths a _0,2 for collisions with total spin 0 and 2), spin-1 BECs present a ferromagnetic (FM) ground state (for a ₀ > a ₂, as in ⁸⁷Rb F = 1 ¹²) or an antiferromagnetic (AFM) one (for a ₂ > a ₀, as in ²³Na ¹¹), also called polar. The case a ₀ = a ₂ exhibits an enlarged SU(3) symmetry with a highly degenerate ground state ¹³.

The spinor system exhibits two interaction channels (given by the allowed total spins) and two collision types. Being m _i the z-component of the particle i, there is a spin preserving collision m1 + m2 = m1 + m2   where income and outcome spins have the same projections and the most interesting spin changing collision m1 + m2 = m3 + m4   where outcome differs from income spins, but always conserves the spin z-projection.

Most spin-1 species are naturally close to the SU(3) point a0 ≈ a2 . But small external perturbations as Zeeman shifts may have a large effect, reducing the system symmetry and thus, favoring different phases. Since interactions preserve the magnetization M, the linear Zeeman effect may be gauged out (although the phase diagram depends on M ^14,15. On the contrary, the quadratic Zeeman effect (QZE) plays a crucial role in spinor gases. In spite of its importance, the role of the QZE in the quantum phases of spin-1 lattice bosons remains to a large extent unexplored. We note that the QZE may be controlled by means of microwave and optical techniques ^16,17. There is a 3d mean field analysis ¹⁵, where it was shown that for finite M the QZE may lead to nematic-to-ferromagnetic (or partially magnetic) transitions and a complete phase diagram for the Mott-insulator phases of spin-1 bosons in the presence of QZE is presented in ¹⁸, where several techniques such as effective field theory (for any dimension), matrix product state (MPS) algorithm ¹⁹, (i.e. density matrix renormalization group (DMRG) ²⁰ and Lanczos diagonalization have been combined to obtain the phase boundaries and the characterization of the phase transitions. In addition, optical Feshbach resonances ^21,22, permit the modification of the ratio a ₂/a ₀, so that the full phase diagram may be explored with current techniques.

Recently, the interest on quantum entanglement in several communities has been growing ²³. This is due to the fact that in a pure bipartite state, having measured only part of the system (a subsystem), it is possible to have information of the whole quantum state if there is entanglement among the parts ²⁴. In fact, the corresponding von Neumann entropy associated to the reduced density matrix provides the entanglement entropy of the measured subsystem. Nowadays, it becomes a key tool in the many-body strongly-correlated quantum systems analysis reveling nonlocal information and therefore a suitable mechanism to study quantum phases and phase transitions ^25,26.

2 Spin-1 Lattice Bosons

In the more general case for a balance bosonic mixture, the system is described by the Bose-Hubbard-like Hamiltonian given by:

Here, the spinor operator is a three-component vector ψ^T  =  ψ^_1, ψ^0, ψ^1  involving three m _F states. Aditionaly, μ is the chemical potential, which is the energy needed to add to or extract a particle from the system. The hopping strength t measures the kinetic energy of the particles and the sum is performed over all nearest neighbors < i, j >, allowing the generalization to any dimension. V_1,2,3,4 is the on-site interaction and the last term accounts for the quadratic Zeeman effect or single ion anisotropy as it is called in the condensed matter community. At low-energy, only s-wave scattering is relevant and the interaction takes the already mentioned contact form:

Hence, the on-site interaction is expressed in terms of two interacting channels using the projector operators P^F = ∑mF=-F-F F, mf 〉〈F,mF

in each of the allowed total spins, F = F ₁ + F ₂ = 0, 2.

The Bose-Hubbard Hamiltonian exhibits two distinctive phases, the Mottinsulator or commensurate phase and the superfluid or incommensurable phase. We consider repulsively interacting ultracold spin-1 bosons in a d-dimensional hypercubic lattice, prepared in a balanced mixture (M = 0). In free space, the inter-particle interactions are characterized by the coupling constants 𝒈0,2 = 4πħ2a0,2/ma . In the presence of a lattice the onsite energies 𝒈~0,2  are proportional to 𝒈0,2  and depend as well on lattice parameters ²⁷. At integer filling, the system enters in the MI regime if the (positive) on-site energies are much larger than the hopping parameter, 𝒈~0,2 ≫t . Performing quasi-degenerate second-order perturbation theory in t using the standard Van Vleck transformation ²⁸, the low-energy physics is achieved by means of superexchange processes, being described by an effective bilinear-biquadratic Hamiltonian spin ^27,29:

where S _i are spin-1 operators at site i, the sum runs over nearest neighbors, and the coefficients are given by:

being both positive quantities. The FM case (a ₀ > a ₂ as discussed before) corresponds to J ₁ > J ₂, whereas the AFM case (a ₂ > a ₀) results in J ₂ > J ₁. Typically, a ₀ ≈ a ₂, which corresponds to the vicinity of the SU(3) point (J ₁ ≈ J ₂). The last term in Eq. (2) describes the QZE that is characterized by the externally controllable constant q = DJ and plays a crucial role in the system. In the following, a standard parameter has been used:

Where θ lies in the interval (-π+ arctan13, -π2 as the ratio 𝑔₂/𝑔₀ goes from 0 to + ∞ and uses J = J12 + J22 as the energy unit (J = 1).

This document also points out how a controlled tuning of the QZE may permit the observation of field-induced phase transitions in spin-1 lattice bosons, which are precluded by the simple use of the linear Zeeman effect due to conservation of M and thus, are absent in spin-1/2 systems.

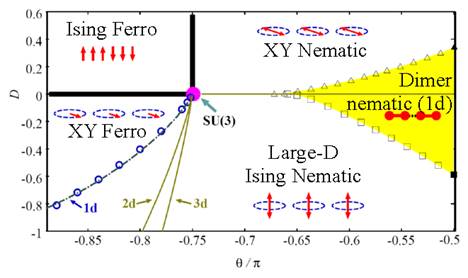
Figure 1: Phases of the spin-1 chain bosons, as a function of ( and the QZE parameter D. Solid bold lines correspond to first order phase transitions for any dimension d. Symbols represent numerical data for d = 1. Kosterlitz-Thouless transition line in the FM side (circles), and in the AFM side: the Kosterlitz-Thouless transition for D⁺ _c (triangles) and the Ising-like transition for D^- _c (squares) are the limits of the dimerized phase, filled region only in 1d. The XY-FM to large-D transition lines retrieved from the field-theory are represented by dashed line for 1d, and the solid lines correspond to 2d and 3d as it is shown. 

Spin-1 lattice bosons have attracted a strong interest, for which a wealth of quantum phases have been predicted (see Ref. ¹⁸ and references within). The phase diagram of repulsively interacting spin-1 bosons in optical lattices at unit filling in the presence of an externally induced quadratic Zeeman field obtained in Ref. ¹⁸ is shown in Figure 1. The phase diagram was obtained using the MPS method with open boundary conditions, for up to 42 sites and matrix dimension 30 correspondingly¹. For ferromagnetic interactions and negative values of D, the phase transition line between the XY-ferromagnetic and large-D phases has been done by means of the fidelity susceptibility ³⁰. The studies show that a leading finite size extrapolation of 1=L2 law ³¹ (including the cases when logarithmic correction are present ³² confirms that the transition is Kosterlitz-Thouless kind ³³ For antiferromagnetic interactions, in 2d and 3d the MI states at odd filling are nematic ^27,34, whereas in 1d quantum fluctuations lead to spontaneous dimerization ^27,35-39.

In the presence of an external field, the critical field curves Dc± have been retrieved using Lanczos diagonalizing for periodic systems of up to L = 16 sites and restricting the calculations to the different magnetization manifolds to reduce the Hilbert space dimension. In the Figure 1, the Dc+ curve (triangles) represe2ts the transition between the dimerized and the XY-nematic phases. Its finite size extrapolation follows a 1=L ² law, confirming the Kosterlitz-Thouless nature with central charge c = 1. The Dc- curve (squares) shows the transition between dimerized and large-D phases. We performed the calculations by means of the MPS method and found that this is an Ising-like transition since its central charge is c = 0.5 as it is discussed in detail in the subsection 3.1. When approaching the SU(3) point, the numerical simulations cannot recover the exponentially small dimerized region, which basically reduces to the D = 0 line.

3 Entanglement Entropy

Based on the fact that several numerical implementations lead to pure states, we restrict the discussion to pure entangled states. The aim of the present document is to discuss the entanglement entropy as a novel tool, useful to characterize phases and phase transitions in a broad set of lattice models relevant for condensed matter systems, which is the entanglement entropy.

Figure 2: A bipartite spin-chain divided in two subsystems such as a block (B) and an environment (E). 

A bipartite pure quantum state described by |Ψ〉, consisting of two subsystems a block (B) and an environment (E) as depicted in the Figure 2, is generally expressed as |Ψ〉 = ∑_ij a _ij |B _i 〉 ⊗ |E _j 〉, where {|B _i 〉}and {|E _i 〉} are the complete set of orthonormal basis vectors in their respective Hilbert subspaces. The tensor product state contains N _B N _E expansion coefficients and could be very difficult to manipulate. Here, N _B (N _E ) is the dimension of the subspace B(E).

We consider physical lattice systems made of an array with L lattice sites. Let us separate the bipartite (two-subsystem) system applying the Schmidt decomposition (SD) ⁴⁰. Following this decomposition, any arbitrary pure state of a bipartite system can be written as

where {|𝛼 _B 〉} (on the block) and {|𝛼 _E 〉} (on the environment) are two orthonormal base sets belonging to the respective Hilbert subspaces, each with at most N _B base elements when N _E > N _B . The coefficients 𝜆_𝛼 are non-negative real numbers satisfying ∑αL λα2 = 1 , known as Schmidt coefficients and α running in the reduced Hilbert subspace.

Let us recall that the density matrix operator for a pure state is written as ρ^ = ΨΨ , and the diagonalizing of ρ^ gives us ρ^ ρα = ραρα . Interestingly, the mathematics-physics connection among the Schmidt coefficients and the density matrix eigenvalues is given by λα2 = ρα .

In a pure state, there is only one density matrix eigenvalue. But the reduced density matrix for the system Block ρ^B = ∑α λα2 lnαB αB represents a mixed state where the entanglement entropy can be measured using the Von Neumann entropy.

Let us point out that the entanglement entropy is used as a resource to diagnose new quantum phases and phase transitions in condensed matter systems ⁴¹. Nevertheless, to perform a characterization of a quantum system, it is important to use several techniques to compare the behavior since different systems can present different responses to a single tool.

3.1 Central charge

For gapless or critical systems in one dimension, the quantum critical points can be described by 2d conformal field theories, there, the entanglement entropy diverges logarithmically, with the universal coefficient determined by the central charge. The latter is a measure of the number of degrees of freedom whose gap vanishes at the critical point ^42-44. Hence, the universality class of a phase transition can be determined by means of the central charge ⁴⁵. Interestingly, there exists nontrivial systems with fractional central charge, as it is the case for the Ising model where c = 1/2.

In order to classify the phase transition lying between the dimerized phase and the Ising nematic (see Figure 1), it is when D=Dc- , the central charge at D = 0, θ = -0:73𝜋 was computed. This value lies in the region where the XY-nematic and large -D phases meet each other at D = 0. Strictly speaking, this point is inside the dimerized phase, but since the correlation length is extremely large, the system can be considered as gapless.

The block entanglement entropy for a finite 1d system of size L divided into two pieces of size l (block) and L - l (environment), see Figure 2, in the context of the conformal field theory ^46-48, behaves as:

S =c6log LπsinπlL + A, (10)

where c is the central charge and A is a non-universal constant. Setting l = L2 , following Ref. ⁴⁹, and using MPS method to evaluate S for several L values, the central charge is obtained from the slope of the curve, as it is shown in Figure 3. This method had retrieved c ≃1.5. The D = Dc+ Kosterlitz-Thouless line has c = 1. Subtracting this contribution, we get c  12 for the D = Dc- line, conforming its Ising nature.

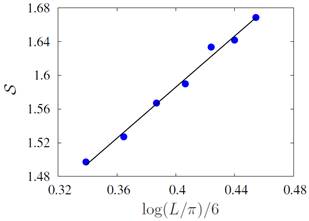
Figure 3: Central charge retrieved from the slope of the block entanglement entropy S. The calculation has been performed at ( = -0:73( for several system lengths. The fitting curve is given by f(x) = 1:51508x + 0:980015 whose slope is c = 1:515 ( 0:065. 

It is also interesting to quantify how much entanglement entropy occurs in the ground state of local and quasi-local Hamiltonians, in general, the measurement scales with L. If the entanglement between points is farther apart, some length scale ζ can be ignored. Then, the entanglement entropy should be determined by a shell of thickness ∼ ζ around the block environment boundary (having the boundary a dimension of d - 1),

S ~ Ld-1 ζ → S ~ Ld-1 as L →∞, (11)

with fixed system parameters. If there is no locality, any site in the block is likely to be entangled with a site in the environment as with another site in the block. Hence, S ∼ L ^d . This relation is known as area law. This law has been established for 1d gapped systems ⁵⁰ which are well approximated by MPS and can be simulated efficiently on a classical computer. Going beyond the area law ⁵¹ the entanglement scaling can also be used to distinguish conventional quantum critical points from non-Landau ones ⁵² and to diagnose critical phases in finite and infinite systems ^53,54,

Sn = al - cn + ... finite,Sn =al - dn lnl + ... infinte, (12)

where S _n is the Renyi entropy ⁵⁵ with a non-universal coefficient, and on the contrary c _n and d _n are universal n-dependent coefficients. In particular, the entanglement entropy S = lim _n⟶1 S _n is well defined and universal ⁵⁴.

The entanglement entropy is also useful to characterize topological phases by looking at the entanglement entropy spectrum. The later consists of the energies of the entanglement Hamiltonian block H^EB = -ln ρB^ . In the topological phase, this spectrum is expected to be two fold degenerated ^41,56,57. These topological systems are unique states of matter that incorporate long-range quantum entanglement and host exotic excitations with fractional quantum statistics. The identification of topological phases in arbitrary realistic models has been reported by accurately calculating the topological entanglement entropy ⁵⁸ using MPS. The argument is based on the fact that this algorithm systematically selects a minimally entangled state from the quasi-degenerated ground states.

4 Conclusions and outlook

In this work, we have reviewed the field-induced phase diagram of repulsively interacting spin-1 lattice bosons in the presence of the quadratic Zeeman field for both ferro and antiferromagnetic interactions, for the average filling of one boson per site.

In order to determine the nature and the precise location of the phase transitions, 1d numerical simulations must be performed. Particularly, we show the use of a novel and versatile technique based on the block entanglement entropy for 1d finite systems, to resolve the universality class of the spin Peierls and large-D transition by means of the central charge and performing finite size scaling.

The entanglement spectrum explodes also highly nonlocal properties offering the possibility of classifying 1d systems given its symmetry group ⁵⁷. Hence this technique, in principle, serves as a way to characterize from trivial to topological phases and phase transitions.