1 Introduction
Ultracold gases is a multidisciplinary field, which lies in the intersection of several physics fields such as quantum information, condensed matter, quantum mechanics, non-linear physics, and statistical mechanics with a very strong contribution of numerical methods. Ultracold gases in optical lattices constitute an extraordinary tool for the analysis of strongly correlated gases under extremely well controlled conditions 1,2, as highlighted by the observation of the superfluid to Mott-insulator (MI) transition in ultracold bosons 3, recently followed by the realization of the metal to MI transition in two-component fermions 4,5.
The optical lattice potential is constructed using counter propagating laser beams. These are able to trap the atoms which are already at ultralow temperatures. The most interesting feature of this kind of systems is the tunability of the interactions, making the field very promising because of its high controllability. The perfect periodic optical potential resembles the electron moving in a periodic array of ions which develops a band structure.
In the present work we concentrate on the physics of the lowest energy band.
In 1937, it was pointed out that a variety of transition metal oxides predicted to be conductors by band theory were actually insulators 6. About the same time, Nevill Mott and Rudolf Peierls predicted that the failure in the theoretical description can be solved by including the interactions between electrons 7. But it was until 1963 when Jhon Hubbard presented the simplest model for interacting electrons in a periodic potential, the nowadays called Hubbard model 8. This model takes into account the kinetic energy of the particles given by a hopping term and an interacting contact potential given by,
Where
It is important to emphasize how the achievement of these low temperatures had generated a boost in the experimental and theoretical techniques with such impact that the pioneers were already awarded with the Nobel Prize. In 1997, S. Chu, Cohen-Tannoudji and W. D. Phillips were awarded for the development of methods to cool and trap atoms with laser light". In 2001, E. A. Cornell, W. Ketterle and C. E. Wieman were awarded for the achievement of Bose-Einstein condensation in dilute gases of alkali atoms and for early fundamental studies of the properties of the condensates". And very recently, in 2012, S. Haroche and D. J. Wineland were awarded for ground-breaking experimental methods thatenable measuring and manipulation of individual quantum systems".
Optical traps permit the simultaneous trapping of various Zeeman sublevels, allowing for multicomponent (spinor) gases. Spinor bosons have attracted a large interest due to their internal degrees of freedom since it gives rise to rich ground-state physics and spinor dynamics 9-12. Spinor gases in lattices are particularly exciting, since they provide unique possibilities for the analysis of quantum magnetism.
Spin-1 gases are the simplest spinor system beyond the two-component isospin-1=2. Depending on inter-particle interactions 9,10, (given by the s-wave scattering lengths a 0,2 for collisions with total spin 0 and 2), spin-1 BECs present a ferromagnetic (FM) ground state (for a 0 > a 2, as in 87Rb F = 1 12) or an antiferromagnetic (AFM) one (for a 2 > a 0, as in 23Na 11), also called polar. The case a 0 = a 2 exhibits an enlarged SU(3) symmetry with a highly degenerate ground state 13.
The spinor system exhibits two interaction channels (given by the allowed total spins) and two collision types. Being m
i
the z-component of the particle i, there is a spin preserving collision
Most spin-1 species are naturally close to the SU(3) point
Recently, the interest on quantum entanglement in several communities has been growing 23. This is due to the fact that in a pure bipartite state, having measured only part of the system (a subsystem), it is possible to have information of the whole quantum state if there is entanglement among the parts 24. In fact, the corresponding von Neumann entropy associated to the reduced density matrix provides the entanglement entropy of the measured subsystem. Nowadays, it becomes a key tool in the many-body strongly-correlated quantum systems analysis reveling nonlocal information and therefore a suitable mechanism to study quantum phases and phase transitions 25,26.
2 Spin-1 Lattice Bosons
In the more general case for a balance bosonic mixture, the system is described by the Bose-Hubbard-like Hamiltonian given by:
Here, the spinor operator is a three-component vector
Hence, the on-site interaction is expressed in terms of two interacting channels using the projector operators
in each of the allowed total spins, F = F 1 + F 2 = 0, 2.
The Bose-Hubbard Hamiltonian exhibits two distinctive phases, the Mottinsulator or commensurate phase and the superfluid or incommensurable phase. We consider repulsively interacting ultracold spin-1 bosons in a d-dimensional hypercubic lattice, prepared in a balanced mixture (M = 0). In free space, the inter-particle interactions are characterized by the coupling constants
where S i are spin-1 operators at site i, the sum runs over nearest neighbors, and the coefficients are given by:
being both positive quantities. The FM case (a 0 > a 2 as discussed before) corresponds to J 1 > J 2, whereas the AFM case (a 2 > a 0) results in J 2 > J 1. Typically, a 0 ≈ a 2, which corresponds to the vicinity of the SU(3) point (J 1 ≈ J 2). The last term in Eq. (2) describes the QZE that is characterized by the externally controllable constant q = DJ and plays a crucial role in the system. In the following, a standard parameter has been used:
Where θ lies in the interval
This document also points out how a controlled tuning of the QZE may permit the observation of field-induced phase transitions in spin-1 lattice bosons, which are precluded by the simple use of the linear Zeeman effect due to conservation of M and thus, are absent in spin-1/2 systems.
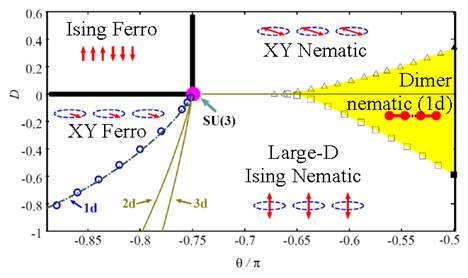
Figure 1: Phases of the spin-1 chain bosons, as a function of ( and the QZE parameter D. Solid bold lines correspond to first order phase transitions for any dimension d. Symbols represent numerical data for d = 1. Kosterlitz-Thouless transition line in the FM side (circles), and in the AFM side: the Kosterlitz-Thouless transition for D+ c (triangles) and the Ising-like transition for D- c (squares) are the limits of the dimerized phase, filled region only in 1d. The XY-FM to large-D transition lines retrieved from the field-theory are represented by dashed line for 1d, and the solid lines correspond to 2d and 3d as it is shown.
Spin-1 lattice bosons have attracted a strong interest, for which a wealth of quantum phases have been predicted (see Ref. 18 and references within). The phase diagram of repulsively interacting spin-1 bosons in optical lattices at unit filling in the presence of an externally induced quadratic Zeeman field obtained in Ref. 18 is shown in Figure 1. The phase diagram was obtained using the MPS method with open boundary conditions, for up to 42 sites and matrix dimension 30 correspondingly1. For ferromagnetic interactions and negative values of D, the phase transition line between the XY-ferromagnetic and large-D phases has been done by means of the fidelity susceptibility 30. The studies show that a leading finite size extrapolation of 1=L2 law 31 (including the cases when logarithmic correction are present 32 confirms that the transition is Kosterlitz-Thouless kind 33 For antiferromagnetic interactions, in 2d and 3d the MI states at odd filling are nematic 27,34, whereas in 1d quantum fluctuations lead to spontaneous dimerization 27,35-39.
In the presence of an external field, the critical field curves
3 Entanglement Entropy
Based on the fact that several numerical implementations lead to pure states, we restrict the discussion to pure entangled states. The aim of the present document is to discuss the entanglement entropy as a novel tool, useful to characterize phases and phase transitions in a broad set of lattice models relevant for condensed matter systems, which is the entanglement entropy.

Figure 2: A bipartite spin-chain divided in two subsystems such as a block (B) and an environment (E).
A bipartite pure quantum state described by |Ψ〉, consisting of two subsystems a block (B) and an environment (E) as depicted in the Figure 2, is generally expressed as |Ψ〉 = ∑ij a ij |B i 〉 ⊗ |E j 〉, where {|B i 〉}and {|E i 〉} are the complete set of orthonormal basis vectors in their respective Hilbert subspaces. The tensor product state contains N B N E expansion coefficients and could be very difficult to manipulate. Here, N B (N E ) is the dimension of the subspace B(E).
We consider physical lattice systems made of an array with L lattice sites. Let us separate the bipartite (two-subsystem) system applying the Schmidt decomposition (SD) 40. Following this decomposition, any arbitrary pure state of a bipartite system can be written as
where {|𝛼
B
〉} (on the block) and {|𝛼
E
〉} (on the environment) are two orthonormal base sets belonging to the respective Hilbert subspaces, each with at most N
B
base elements when N
E
> N
B
. The coefficients 𝜆𝛼 are non-negative real numbers satisfying
Let us recall that the density matrix operator for a pure state is written as
In a pure state, there is only one density matrix eigenvalue. But the reduced density matrix for the system Block
Let us point out that the entanglement entropy is used as a resource to diagnose new quantum phases and phase transitions in condensed matter systems 41. Nevertheless, to perform a characterization of a quantum system, it is important to use several techniques to compare the behavior since different systems can present different responses to a single tool.
3.1 Central charge
For gapless or critical systems in one dimension, the quantum critical points can be described by 2d conformal field theories, there, the entanglement entropy diverges logarithmically, with the universal coefficient determined by the central charge. The latter is a measure of the number of degrees of freedom whose gap vanishes at the critical point 42-44. Hence, the universality class of a phase transition can be determined by means of the central charge 45. Interestingly, there exists nontrivial systems with fractional central charge, as it is the case for the Ising model where c = 1/2.
In order to classify the phase transition lying between the dimerized phase and the Ising nematic (see Figure 1), it is when
The block entanglement entropy for a finite 1d system of size L divided into two pieces of size l (block) and L - l (environment), see Figure 2, in the context of the conformal field theory 46-48, behaves as:
where c is the central charge and A is a non-universal constant. Setting
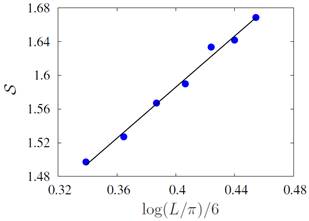
Figure 3: Central charge retrieved from the slope of the block entanglement entropy S. The calculation has been performed at ( = -0:73( for several system lengths. The fitting curve is given by f(x) = 1:51508x + 0:980015 whose slope is c = 1:515 ( 0:065.
It is also interesting to quantify how much entanglement entropy occurs in the ground state of local and quasi-local Hamiltonians, in general, the measurement scales with L. If the entanglement between points is farther apart, some length scale ζ can be ignored. Then, the entanglement entropy should be determined by a shell of thickness ∼ ζ around the block environment boundary (having the boundary a dimension of d - 1),
with fixed system parameters. If there is no locality, any site in the block is likely to be entangled with a site in the environment as with another site in the block. Hence, S ∼ L d . This relation is known as area law. This law has been established for 1d gapped systems 50 which are well approximated by MPS and can be simulated efficiently on a classical computer. Going beyond the area law 51 the entanglement scaling can also be used to distinguish conventional quantum critical points from non-Landau ones 52 and to diagnose critical phases in finite and infinite systems 53,54,
where S n is the Renyi entropy 55 with a non-universal coefficient, and on the contrary c n and d n are universal n-dependent coefficients. In particular, the entanglement entropy S = lim n⟶1 S n is well defined and universal 54.
The entanglement entropy is also useful to characterize topological phases by looking at the entanglement entropy spectrum. The later consists of the energies of the entanglement Hamiltonian block
4 Conclusions and outlook
In this work, we have reviewed the field-induced phase diagram of repulsively interacting spin-1 lattice bosons in the presence of the quadratic Zeeman field for both ferro and antiferromagnetic interactions, for the average filling of one boson per site.
In order to determine the nature and the precise location of the phase transitions, 1d numerical simulations must be performed. Particularly, we show the use of a novel and versatile technique based on the block entanglement entropy for 1d finite systems, to resolve the universality class of the spin Peierls and large-D transition by means of the central charge and performing finite size scaling.
The entanglement spectrum explodes also highly nonlocal properties offering the possibility of classifying 1d systems given its symmetry group 57. Hence this technique, in principle, serves as a way to characterize from trivial to topological phases and phase transitions.














