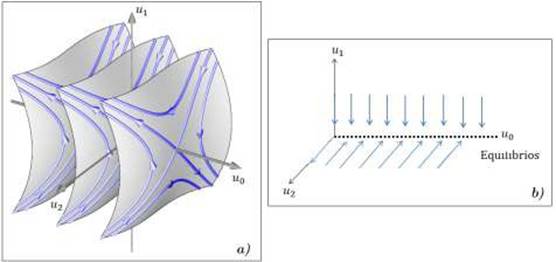
1 Introducción
Una gran variedad de fenómenos en la naturaleza se modelan a través de sistemas de ecuaciones diferenciales de la forma
donde 𝑢 ( ℝ𝑛 es el vector de estado, α ( ℝ𝑚 un vector de parámetros y 𝑓: ℝ𝑛 x ℝ𝑚 → ℝ𝑛 un campo vectorial continuo y diferenciable. Algunas variaciones en el vector de parámetros pueden ocasionar cambios en el comportamiento y estabilidad local de los puntos de equilibrio, lo que ocasiona bifurcaciones 1.
Sin embargo, cuando el vector de parámetros α ( ℝ𝑚 dado en el sistema (1) es sustituido por un vector de estados 𝑣 ( ℝ𝑚 y se analiza los cambios en el comportamiento y estabilidad en una línea de puntos de equilibrio, ocurre una bifurcación sin parámetros 2. Si dichos cambios de estabilidad se deben a un único par de valores propios imaginarios conjugados con parte real nula, calculados en la matriz jacobiana del campo vectorial en un punto que pertenece a la línea de puntos de equilibrio, se habla de una bifurcación de Hopf sin parámetro 3.
Por otro lado, existen diversos problemas presentes en la física, química e ingeniería, los cuales se pueden formular por medio de modelos matemáticos en que la cantidad total es constante a lo largo del tiempo. En este tipo de situaciones, la variable física definida en una región acotada del espacio solo puede variar debido al flujo de la variable a través de la frontera de dicha región. Esto puede traducirse en una formulación integral que, bajo ciertas hipótesis de regularidad, se convierte en un sistema de la forma,
con w =(w 0 (x,t), w 1(x,t), w 2(x,t) ( ℝ3 la variable de estado, una función de clase C 2 , 𝑓: ℝ3 → ℝ3, 𝑔 una función de clase C 2, 𝑔: ℝ3 → ℝ3, y constantes δ > 0 y ( > 0. En problemas de dinámica de fluidos, el sistema (2) representa problemas de densidad, momento o energía 4.
Un ejemplo para ilustrar el comportamiento de las soluciones para este tipo de sistemas, con condición inicial constante a trozos 5, es el siguiente: se tiene un tubo lleno con gas, inicialmente dividido en dos secciones separadas por una membrana, el gas tiene densidad y presión, en reposo, más alta en una mitad del tubo que en la otra. En 𝑡 = 0 se rompe la membrana y el gas fluye. La estructura de la solución del sistema (2) con condición inicial constante a trozos, denominada problema de Riemann, implica tres ondas distintas que separan regiones en las que las variables son constantes: La onda de choque se propaga hacia la región de más baja presión; a través de esta onda, la densidad y la presión asumen valores más altos y todas las variables son discontinuas; luego aparece una discontinuidad de contacto, a través de la cual la densidad es discontinua, pero las demás variables son constantes; la tercera es la onda de rarefacción, en la cual la densidad del gas decrece cuando esta onda pasa a través de él y tiene una estructura diferente: todas las variables son continuas y presentan una transición suave.
En este trabajo se presentan algunos elementos necesarios para identificar la existencia de una bifurcación de Hopf, con o sin parámetros, y determinar bajo qué condiciones el sistema (2) presenta una bifurcación de Hopf sin parámetros, de tipo elíptica o hiperbólica, en una línea de puntos de equilibrio. Para comprender este proceso, se desarrolla los siguientes pasos: en la segunda sección se presenta algunos conceptos y resultados importantes usados en sistemas dinámicos continuos; en la tercera sección, se plantean las condiciones en que un sistema de ecuaciones diferenciales, que depende de un vector de parámetros, presentan bifurcación de Hopf; en la cuarta sección, se explican las diferencias entre la teoría de bifurcaciones en puntos de equilibrio, línea de puntos de equilibrio y sin parámetros, de igual forma se muestra los lineamientos teóricos para la bifurcación de Hopf sin parámetros elíptica e hiperbólica. Por último, se hace el análisis respectivo de la bifurcación de Hopf sin parámetros en una línea de puntos de equilibrio para sistema (2).
2 Preliminares
La formulación matemática de un proceso determinista es un sistema dinámico , el cual permite prever cualquier estado futuro si el operador de evolución y su estado inicial son conocidos. Si el tiempo para ese operador se define en la recta real, se habla de un sistema dinámico continuo 6 .
Se observa que todo sistema de la forma
con 𝑢 ( 𝑈 y 𝑓 : 𝑈 → ℝn un campo vectorial de clase 𝐶1 definido en un conjunto 𝑈 ⊂ ℝn, es un sistema dinámico continuo y sus trayectorias φ𝑓: ℝ x 𝑈 → ℝn satisfacen:
Si 𝑓(𝑢*)=0, entonces 𝑢*( 𝑈 es un punto de equilibrio para el sistema (3). El conjunto L 0 = { e ( 𝑈: φ𝑓(t, 𝑢0)= 𝑢 para t ( ℝ} es una órbita que inicia en 𝑢0 ( 𝑈.
Una orbita L 0 que inicia en 𝑢0 ( 𝑈 es homoclínica al punto de equilibrio si 𝑢* ( 𝑈 si φ𝑓(t, 𝑢) → 𝑢* cuando 𝑡 → ±∞. Si existe otro punto de equilibrio 𝑢** ( 𝑈 en el sistema (3), la orbita L 0 que inicia en 𝑢0 ( 𝑈 es heteroclínica a los puntos 𝑢* y 𝑢** si φ𝑓(t, 𝑢) → 𝑢*
Para 𝑡 → −∞ y φ𝑓(t, 𝑢) → 𝑢** cuando 𝑡 → +∞ .
Un punto 𝑢0 ( 𝑈 es un punto ⍵ -límite de la trayectoria φ𝑓 del sistema (3), si existe una sucesión 𝑡𝑛 → +∞ de tal manera que
De manera similar, si existe una sucesión 𝑡𝑛 → −∞ tal que
y el punto 𝑢1 ( 𝑈; entonces 𝑢1 se le conoce como punto α -límite de la trayectoria φ𝑓 del sistema (3).
Al conjunto de todos los puntos ⍵-límite de una trayectoria L 0 se le llama conjunto ⍵-límite de L 0 y se denota por ⍵(L 0). De igual manera, se tiene el conjunto α-límite de L 0 y se denota por α(L 0).
Una órbita periódica L 0 es cualquier curva cerrada solución del sistema (3) que no sea un punto de equilibrio. Un ciclo límite ψ es una órbita periódica del sistema (3) el cual es el α-límite o -límite de alguna trayectoria de (3) que no sea ψ.
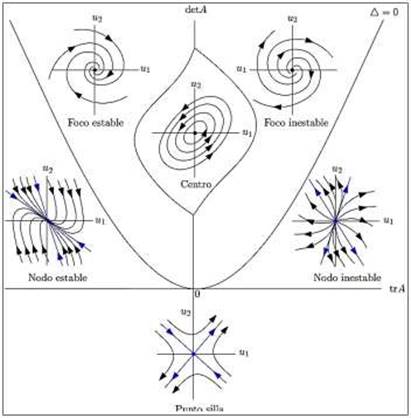
La estabilidad en un punto de equilibrio es conocido como el comportamiento cualitativo de las trayectorias de un sistema de la forma (3), con 𝑓(𝑢)= 𝐴 ∙ 𝑢 para una matriz 𝑛 x 𝑛 y punto de equilibrio 𝑢* = 0 ( ℝ𝑛 (7. Para determinar el comportamiento y estabilidad del punto de equilibrio 𝑢* = 0 ( ℝ𝑛, se debe encontrar un λ ( ℂ, tal que exista 𝑢 ( ℝ𝑛 con 𝑢 ≠ 0 que cumpla (𝐴− λI) 𝑢 = 0, con I la matriz identidad 𝑛 x 𝑛. El valor de λ es llamado valor propio asociado a la matriz 𝐴 y el vector 𝑢 ≠ (0,0) es llamado un vector propio de 𝐴 correspondiente a λ. El espacio nulo Ker (𝐴 − λI ) es llamado un espacio propio correspondiente al valor propio λ y la dimensión del espacio propio es llamada la multiplicidad del valor propio λ. Nótese que la matriz 𝐴 presenta 𝑛 valores propios λ1, λ2,…, λ𝑛 ( ℂ que son soluciones de la ecuación 𝑃(λ):det(𝐴 − λI)=0 con 𝑃(λ) el polinomio característico de 𝐴.
En particular, si 𝐴 es una matriz 2 x 2, la estabilidad del punto de equilibrio 𝑢* = (0,0) ( ℝ2 en el sistema
Los valores propios λ1, λ2, en el sistema lineal son reales y distintos:
Si λ1 < λ2 < 0, el origen es un nodo estable,
Si λ1 > λ2> 0, el origen es un nodo inestable,
Si λ1 < 0 < λ2, el origen es una silla.
Los valores propios son complejos conjugados: λ1 = 𝛼+ 𝑖𝛽, λ2 = 𝛼 − 𝑖𝛽 , con 𝛽 ≠ 0.
Si 𝛼 = 0, el origen es un centro,
Si 𝛼 < 0, el origen es un foco estable,
Si ??, el origen es un foco inestable.
Los valores propios son reales e iguales: λ1 = λ2 = λ ≠ 0.
λ posee dos vectores linealmente independientes. El origen es un nodo estrella atractor (repulsor) si λ < 0 (> 0),
λ posee un único vector propio.
En la Figura 1 resume la información geométrica sobre el retrato de fase de
Si el campo vectorial 𝑓: 𝑈→ ℝ2 de clase C 1 definido en un conjunto 𝑈 ⊂ ℝ2 no es lineal, un punto de equilibrio 𝑢* ( 𝑈 es un punto de equilibrio hiperbólico del sistema (3)
si todos los valores propios de la matriz jacobiana
Teorema 2.1. (Hartman-Grobman)9.
Sea 𝑢* ( 𝑈 un punto de equilibrio hiperbólico de
Los conjuntos
W 𝑠 (𝑢*)={𝑢 ( 𝑈: φ𝑓(𝑡, 𝑢) → 𝑢*, 𝑡→ +∞}
W 𝑢 (𝑢*)={𝑢 ( 𝑈: φ𝑓(𝑡, 𝑢) → 𝑢*, 𝑡→ −∞}
son llamados invariantes , donde W 𝑠 (𝑢*) es llamada la variedad estable del punto de equilibrio 𝑢* ( 𝑈 del sistema (3) y, W 𝑢 (𝑢*) la variedad inestable de 𝑢* ( 𝑈 .
Si
El
conjunto resolvente
El espectro discreto σ𝑝(𝐴) son valores de λ ( ℂ para el cual R λ (𝐴) no existe. Los λ ( σ𝑝(𝐴) corresponden a los valores propios de 𝐴,
El espectro continuo σ𝑐 (𝐴) es el conjunto de valores de λ ( ℂ para el cual R λ (𝐴) existe pero no es acotada,
El espectro residual σ R (𝐴) es el conjunto de los valores de λ ( ℂ para el cual R λ (𝐴) existe, es acotada, pero no está definida en un subconjunto denso en ℝ𝑛.
A partir de las definiciones, se deduce que σ𝑝(𝐴), σ𝑐 (𝐴) y σ R (𝐴) son disyuntos dos a dos y que
σ(𝐴) = σ𝑝(𝐴) ∪ σ𝑐 (𝐴) ∪ σ R (𝐴).
Por otro lado, dos sistemas de ecuaciones diferenciales de tipo (3) son topológicamente equivalentes si existe un homeomorfismo, ℎ : ℝ𝑛 → ℝ𝑛 el cual realice un mapeo de trayectorias del primer sistema en trayectorias del segundo sistema 11, preservando la dirección del tiempo, como se ilustra en la Figura 2.
Figura 2 a) Topológicamente equivalente, b) Topológicamente no equivalentes 11.
De esta manera, la teoría clásica de bifurcaciones estudia la dinámica de una familia de campos vectoriales de la forma
donde 𝑢 = (𝑢1, 𝑢2,…, 𝑢𝑛) ( ℝ𝑛 es la variable de estado, α = (α1, α2,…, α𝑚) ( ℝ𝑚 es un vector de parámetros que no depende del tiempo 𝑡 ( ℝ y, 𝑓: ℝ𝑛 x ℝ𝑚 → ℝ𝑛 un campo vectorial de clase 𝐶1; cuando aparece un retrato de fase no topológicamente equivalente en virtud a la variación del vector de parámetros α ( ℝ𝑚 del sistema (4).
3 Forma normal y teorema de la bifurcación de Hopf
Considere
con vector de estado 𝑢 = (𝑢1, 𝑢2) ( ℝ2 parámetro α ( ℝ y
El sistema (5) posee un punto de equilibrio 𝑢*=(0,0) para todo valor de α ( ℝ. La parte lineal del sistema (5) calculada en 𝑢*=(0,0) es
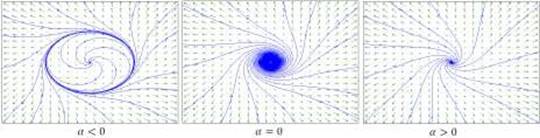
con polinomio característico 𝑃(λ)= λ2 − 2αλ + α2 + 1. Se tiene como valores propios λ1 = α + 𝑖 y λ2 = α − 𝑖. Por el Teorema 2.1, el punto de equilibrio *=(0,0) del sistema (5) es localmente un foco estable si α <0, localmente un foco inestable si α >0y, cuando α = 0 corresponde a una variación drástica del sistema (5) debido a la presencia de un par de valores propios imaginarios conjugados con parte real nula.
Para un mejor análisis del sistema (5), se convierte a un sistema equivalente en coordenadas polares. Primero se introduce la variable compleja:
donde el sistema (5) se reescribe de la siguiente manera
Si se toma
<mml:math style="font-family:'Times New Roman'"><mml:mover><mml:mi>p</mml:mi><mml:mo>˙</mml:mo></mml:mover><mml:mo>=</mml:mo><mml:mi>ρ</mml:mi><mml:mo>(</mml:mo><mml:mi>α</mml:mi><mml:mo>+</mml:mo><mml:mi>i</mml:mi><mml:mo>-</mml:mo><mml:msup><mml:mi>ρ</mml:mi><mml:mn>2</mml:mn></mml:msup><mml:mo>)</mml:mo><mml:mo>-</mml:mo><mml:mi>i</mml:mi><mml:mi>ρ</mml:mi><mml:mi>φ</mml:mi></mml:math>
Y el sistema (5) se escribe en forma polar como
La ecuación (6) tiene un punto de equilibrio en ρ = 0, para todo α ( ℝ dado que solo se considera ρ ≥ 0. El punto de equilibrio es localmente estable si α < 0, no hiperbólico si α = 0, y localmente inestable si α > 0. Por otro lado, si α > 0 existe otro punto de equilibrio
Un sistema que tiene términos no lineales con signo contrario,
presenta una bifurcación en α = 0. A diferencia del sistema (5), el sistema (7) presenta un ciclo límite inestable si α < 0 como lo observado en la Figura 4.
Por lo tanto existen dos tipos de bifurcación de Hopf: subcrítica cuando el ciclo límite inestable existe para todo α < 0 y, la supercrítica cuando el ciclo límite estable surge después de la bifurcación, es decir, cuando α > 0.
Si se considera una familia de ecuaciones diferenciales
con α ( ℝ𝑛 un vector de estados, α ( ℝ un parámetro y 𝑓 ℝ𝑛 x ℝ𝑛→ℝ un campo vectorial de clase c1, la bifurcación de Hopfse identifica por la presencia de un par de valores propios complejos conjugados con parte real nula en la matriz jacobiana de 𝑓(𝑢, α) calculada en el punto de equilibrio 𝑢* ( ℝ𝑛, esto es, λ1,2 = ±𝑖⍵0 con ⍵0 > 0, como se observa en el siguiente Teorema:
Teorema 3.1 (Forma normal de la Bifurcación de Hopf)11. Considere el sistema
con 𝑢 ( ℝ𝑛, α ( ℝ y 𝑓: ℝ𝑛 x ℝ → ℝ𝑛. Supongamos que existe (𝑢*, α0) tal que
1. 𝑓(𝑢*, α0) = 0 (Condición de Equilibrio).
2. La matriz
3.
Entonces existe un cambio invertible de coordenadas y parámetros, y una reparametrización del tiempo que trasforma el sistema en
4 Bifurcación genérica de Hopf sin parámetros
En la teoría clásica de bifurcaciones se analiza, en particular, cuando un punto de equilibrio 𝑢* ( ℝ𝑛 del sistema (4) pierde su hiperbolicidad en virtud a variaciones del vector de parámetros α ( ℝ𝑚, esto es, cuando uno de los valores propios de la matriz jacobiana de 𝑓(𝑢, α) calculada en 𝑢* ( ℝ𝑛 es cero o si la parte real de los valores propios complejos conjugados es cero, esto es, λ1,2 = ±𝑖⍵0, ⍵0 > 0 . En el segundo caso corresponde a una bifurcación de Hopf.
Si el sistema (4) presenta una línea de puntos de equilibrio de la forma
L 𝑒 = { 𝑢=( 𝑢0 0,0,…,0) ( ℝ𝑛: 𝑓(𝑢, α) = 0 para α ( ℝ𝑚}
la estabilidad en torno a la línea de puntos de equilibrio es analizada para cada punto de equilibrio. Se plantea el siguiente ejemplo 12:
Ejemplo 4.1 Considere el siguiente sistema
con 𝑢=(𝑢1, 𝑢2) ( ℝ2
, α = (α1, α2, α3) ( ℝ3, α1 ≠ 0, α2 > 0 y α3 ( ℝ. Al tomar la parte lineal del sistema (9) en torno al punto de equilibrio
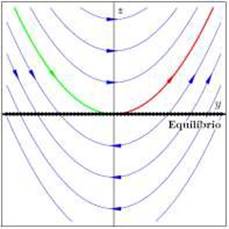
Dado α2 > 0 y α1 ≠ 0 constantes fijas, se observan en lasFigura 5,Figura 6yFigura 7los retratos fase del sistema (9) en relación a la estabilidad local de la línea de puntos de equilibrio L 𝑒 = {( 𝑢1,0) ( ℝ2: 𝑓(𝑢1,0, α3) = 0 con α3 ( ℝ} y el punto 𝑢*.
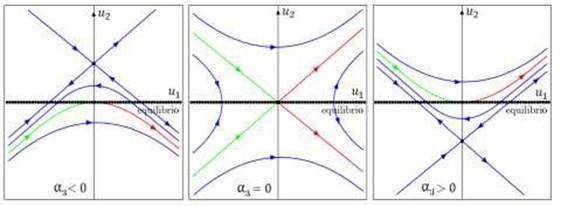
Figura 5 Bifurcación tipo silla del sistema (9). Verde: variedad estable, rojo: variedad inestable 12.
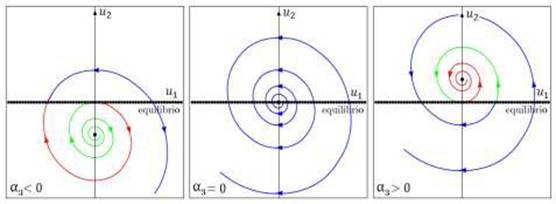
Figura 6 Bifurcación tipo foco del sistema (9). Verde: variedad estable, rojo: variedad inestable 12.

Figura 7 Bifurcación tipo nodo del sistema (9). Verde: variedad estable, rojo: variedad inestable 12.
Independientemente de las constantes fija α1 ≠ 0 y α2 > 0, si α3 < 0 el punto de equilibrio 𝑢* está por debajo de la línea de puntos de equilibrio, si α3 > 0 el punto 𝑢* está por encima de la línea puntos de equilibrio, pero, cuando α3 = 0 ocurre una variación del sistema, pues el punto de equilibrio 𝑢* está contenido en la línea de puntos de equilibrio, esto es, 𝑢* ≅ (0,0) ( L 𝑒 . Por otro lado, la línea de puntos de equilibrio es localmente estable si 𝑢1 < 0 y localmente inestable para 𝑢1 > 0. Cuando 𝑢1 = 0, el origen es un punto de equilibrio no hiperbólico que coincide con 𝑢* para 𝑢3 = 0. Así α3 = 0 corresponde a un valor de bifurcación.
La bifurcación sin parámetros se presenta al analizar, sin variar algún parámetro adicional, el sistema
donde 𝑢 = (𝑢1, 𝑢2,…, 𝑢𝑛) ( ℝ𝑛 y 𝑣 = (𝑣1, 𝑣2,…, 𝑣𝑚) ( ℝ𝑚 son las variables de estado y 𝑓𝑢, 𝑓𝑣: ℝ𝑛+𝑚 → ℝ𝑛+𝑚 campos vectoriales de clase 𝐶1. En la teoría clásica de bifurcaciones corresponde al caso cuando 𝑣 = α ( ℝ𝑚 y 𝑓𝑣 ≡ 0. En la bifurcación sin parámetros, se considera una línea de puntos de equilibrio de la forma
para todo 𝑢 ( ℝ𝑛 y 𝑣 = 0 ( ℝ𝑚. De aquí surge una fenomenología dinámica cuando el punto de equilibrio (0,0) ( ℝ𝑛+?? no es hiperbólico debido a un valor propio nulo o un par de valores propios imaginarios conjugados con parte real nula en la matriz jacobiana del sistema (10) calculada en (0,0) ( ℝ𝑛+𝑚. En particular, se hace énfasis a la presencia de un par único de valores propios complejos conjugados con parte real nula, denominada bifurcación de Hopf sin parámetros 13.
Para ello, considere el sistema (10) con 𝑓𝑢, 𝑓𝑣, ℝ2→ ℝ, 𝑓 = (𝑓𝑢, 𝑓𝑣) una función de clase 𝐶2 que satisface las siguientes condiciones genéricas,
Se observa que la primera condición en (12) representa la línea de puntos de equilibrio que coincide con el eje 𝑢 ( ℝ. La segunda condición muestra que el segundo valor propio no trivial en la parte lineal del sistema (10) se anula en 𝑢 = 0. De hecho,
Al suponer una cuarta condición, denominada condición de no degenerancia,
todo sistema de la forma (10) que satisface las condiciones (12) y (13) cumple con el siguiente resultado,
Teorema 4.113. Considere el sistema (10) y una línea de puntos de equilibrio en ℝ2 , dado en (11), que va perdiendo su hiperbolicidad a medida que se aproxima al origen de acuerdo con las condiciones (12) y (13). Entonces existe un difeomorfismo φ de clase 𝐶1 que mapea las órbitas de (10) en órbitas de la forma normal,
localmente cercano a (𝑦, 𝑧) = (0,0) ( ℝ2, verFigura 8. La orientación temporal de las órbitas se conserva.
si además, se considera un campo vectorial de clase 𝐶2 tal que 𝑓 = (𝑓𝑢, 𝑓𝑣) satisface las condiciones de simetría, esto es,
entonces
y vale el siguiente resultado.
Teorema 4.213. Considere el sistema (10) que satisface las condiciones (12), (15),(16) y una línea de puntos de equilibrio en ℝ2 dado en (11). Entonces existe un difeomorfismo ψ de clase 𝐶1 que mapea las trayectorias de (10) en trayectorias de la forma normal,
localmente cercano a (𝑦, 𝑧) = (0,0) ( ℝ2; verFigura 9. La orientación en el tiempo se preserva.
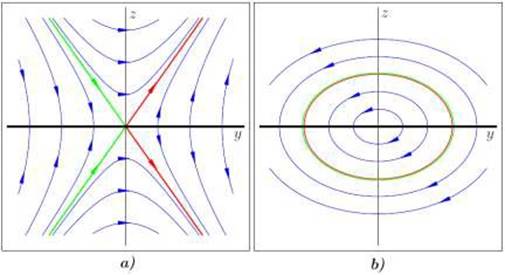
Figura 9 Retrato de fase sistema (17). Caso a) hiperbólica, η = +1; caso b) elíptica, η = −1. Roja: variedad inestable; verde: variedad estable 13.
Se pasa ahora al caso complejo para el sistema (10), con 𝑢 ( ℝ, 𝑣 ( ℝ ≡ ℂ y un par de valores propios complejos conjugados que cruza el eje imaginario a medida que se aproxima a (𝑢, 𝑣) = (0,0) en la línea de puntos de equilibrio. Se asume que (12) es sustituido por,
donde
es una matriz compleja, con valor propio α(𝑢) ( ℂ/ℝ. Se designa el laplaciano con respecto a la coordenada 𝑣 ( ℝ2 ≡ ℂ por ∆𝑣 y una condición de no degenerancia dado por
∆𝑣 𝑓𝑢 (0,0) ≠0
con
donde el punto de bifurcación en 𝑢 = 0 es hiperbólica si η = +1y elíptica si η = −1.
Por último, se pasa al caso en que el sistema es de la forma
Con 𝑢 = (𝑢1, 𝑢2,…, 𝑢𝑛) ( ℝ𝑛+1, 𝐹: ℝ𝑛+1→ ℝ𝑛+1 un campo vectorial de clase 𝐶2 y una línea de puntos de equilibrio
𝐹(𝑢0, 0,0,…,0) = 0
a lo largo del eje 𝑢0. ( ℝ. Se asume que la matriz jacobiana
Sea 𝑍 el espacio propio real bidimensional de
∆𝑍𝑃0 𝐹(0) ≠0
Al fijar la orientación a lo largo del eje 𝑢0 , se puede considerar ∆𝑍𝑃0𝐹(0) como un número real. Al depender del signo
η= sign ((Reλ´(0)) (∆𝑍𝑃0 𝐹(0)),
se dice que el punto de bifurcación en 𝑢0 = 0 es elíptica si η=−1 e hiperbólica si η=+1.
El siguiente resultado muestra el comportamiento cualitativo de las soluciones del sistema
Teorema 4.313. Se asumen que (18) y (19) se cumplen para el campo vectorial de
En el caso hiperbólico, η=+1, todas las trayectorias salen del entorno 𝑈 para un tiempo 𝑡 positivo o negativo (posiblemente ambos). Las variedades estables e inestables en 𝑢 = 0 forman conos alrededor del eje positivo 𝑢0 , con cruce asintoticamente elíptica cerca de 𝑢 = 0. Estos conos separan regiones con diferente comportamiento de convergencia como se observa en laFigura 10a).
En el caso elíptico, η=−1, todas las trayectorias fuera del equilibrio que inician en 𝑈 son heteroclínicas a los puntos de equilibrio
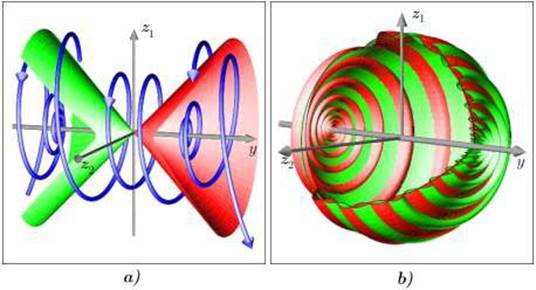
Figura 10 Líneas de puntos de equilibrio (eje ) con valores propios imaginarios. Caso a) hiperbólica, η=+1; caso b) elíptica, η=−1. Roja: variedad inestable; verde: variedad estable 13.
5 Bifurcación de Hopf en un sistema de ecuaciones diferenciales parciales
Se considera un sistema dado por:
con condición inicial constante a trozos, esto es
donde 𝑤= (𝑤0(𝑥, 𝑡), 𝑤1(𝑥, 𝑡), 𝑤2(𝑥, 𝑡)=( 𝑤1, 𝑤1, 𝑤1) ( ℝ3 es un vector de estados, 𝑓 = (𝑓0, 𝑓1, 𝑓2) un término de flujo de clase 𝐶3 con 𝑓: ℝ3, 𝑔 = (𝑔0, 𝑔1, 𝑔2) un término de reacción de clase 𝐶2 con 𝑔: ℝ3 → ℝ3, δ > 0, ( > 0 una constante de regulación; con tiempo 𝑡 real y espacio 𝑥.
Se asume que la matriz jacobiana
posee valores propios reales simples λ0 , λ1 , λ2 que pertenecen al espectro de 𝐴(𝑤), esto es σ(𝐴)={ λ0 , λ1 , λ2}.
Los contornos viscosos son soluciones de tipo onda viajera de la forma,
con velocidad de onda 𝑠. ( ℝ. Si
que aplicado en (20), da origen a un sistema de ecuaciones diferenciales de la forma
independiente de ( > 0 y 𝑠 en vez de 𝑠∙id. Para cualquier solución del sistema (22) del cual
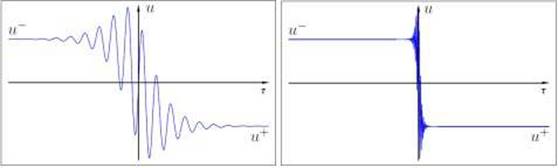
existen y genera, para (↘ 0, una solución del sistema (20) con condición constante a trozos, y los valores 𝑢 = 𝑢±, el cual viajan a una velocidad de onda 𝑠, están conectadas por una onda de choque, como lo observado en la Figura 11 para 𝑢 ( ℝ.
Se reescribe la ecuación (22) como un sistema de primer orden
con 𝑣 = (𝑣0, 𝑣1, 𝑣2) y 𝑠 en vez de 𝑠 · id. Se observa que cualquier contorno viscoso debe satisfacer
esto es, los estados asintóticos son puntos 𝑢± de equilibrio del término reactivo 𝑔(𝑢). Si 𝑔(𝑢) tiene un único punto de equilibrio, esto es 𝑢+ = 𝑢−, las ondas viajeras no existen.
Se asume que 𝑢0 no contribuye a las condiciones de reacción y los otros componentes 𝑢1 y 𝑢2 se desvanecen hacia 𝑢 = 0. Específicamente:
es independiente de 𝑢0 y satisface
el cual da origen a la línea de equilibrio
para el sistema (24).
El comportamiento asintótico de los contornos viscosos 𝑢(τ) para τ →±∞ depende de la parte lineal 𝐿δ(𝑢, 𝑣) del sistema (24) en torno a 𝑢= 𝑢±, 𝑣=0, esto es,
Donde
𝑠 ∉ σ(𝐴(𝑢))={λ0, λ1, λ2} ⊂ ℝ\{0}
De hecho, 𝑠 ∉ σ(𝐴(𝑢)) asegura que surgen ceros adicionales en el espectro real de 𝐿δ(𝑢) para 𝑢= 𝑢±, esto es,
σ(𝐿δ(𝑢))= {0} ∪ δ−1 σ(𝐴(𝑢) - 𝑠)
Para determinar la presencia de valores propios con parte real nula en 𝐿δ(𝑢) a medida que se aproxima la línea de puntos de equilibrio 𝑢=(𝑢0,0,0) y 𝑣 = 0 en 𝑢0 = 0, como se muestra en la Figura 12 se realizan unos cambios con el fin que existan valores propios imaginarios con parte real nula en 𝐿δ(𝑢) cuando δ↘0.
Específicamente, suponga:
La interacción de este flujo y la reacción es capaz de producir valores propios imaginarios puros en la parte lineal 𝐿δ(𝑢) del sistema (24), cuyo espectro es:
Proposición 5.116: Considere la parte lineal 𝐿δ(𝑢0,0,0)= 𝐿δ(𝑢0) del sistema (24). Se asume que (30) y (31) se cumplen.
A) Para δ↘0 y |𝑠|, |𝑢0| ↘0, entonces el espectro de 𝐿δ(𝑢0) se divide en dos partes:
I) Una parte no acotada σ∞ (𝐿δ(𝑢0))= δ−1 σ(𝐴−𝑠)
II) Una parte acotada σ𝑏𝑑 (𝐿δ(𝑢0))= σ(𝐴−𝑠)−1 𝑔´)
Con ´) y 𝑔 evaluados en 𝑢= (𝑢0, 0,0).
B) Para δ=0, 𝑠 = 0, |𝛾| > 1, la parte acotada σ𝑏𝑑 (𝐿δ(𝑢0) en 𝑢 = 𝑢0
posee valores propios λ0 ({0, ± 𝑖⍵0},
Tenga en cuenta que 𝐴0 y 𝑔´(0) están dadas como formas normales de Jordan, de tal manera que se produce una bifurcación cuando la velocidad de onda es 𝑠 = 0.
El siguiente teorema identifica una bifurcación de Hopf sin parámetro, elíptico o hiperbólico, para el sistema (20) bajo ciertas condiciones:
Teorema 5.116. Considere (23) - (25) para encontrar contornos viscosos con velocidad de onda 𝑠 = 0 en el sistema (20). Se asume que (26)-(28), (30), (31) se cumplen, de modo que 𝐿δ(𝑢0) con δ↘0, posee un par de valores propios imaginarios conjugados con parte real nula.
Entonces existen matrices
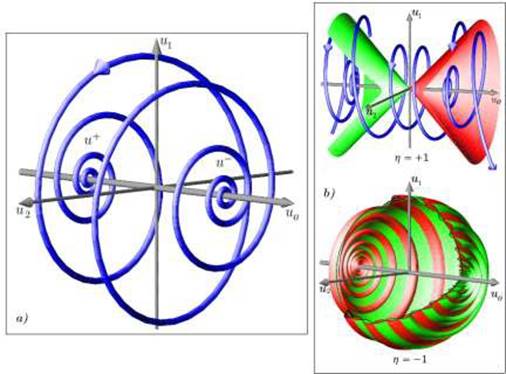
Figura 13 a) Órbita heteroclínicas cerca del punto de Hopf, b) Dinámica cerca de un punto de Hopf a lo largo de una línea de equilibrio: η =+1 Hiperbólica, η =−1 Elíptica 14.
Ya que ambas condiciones son abiertas, los resultados persisten, en particular, para pequeñas velocidades de onda 𝑠 distintos de cero, incluso cuando 𝑓, 𝑔 permanecen fijos.
Obsérvese que para el caso hiperbólico, esto es, η =+1 al menos un par de ondas débiles con colas oscilatorias, conectan los puntos 𝑢− y 𝑢+. En el caso elíptico, η =−1, los contornos viscosos salen del entorno 𝑈 y por lo tanto representan grandes choques.
Para demostrar el Teorema 5.1, se analiza la parte lineal del sistema (20) con velocidad de onda 𝑠 = 0, dado por:
con 𝐴 = 𝐴(𝑢0,0,0) y 𝑔´ = 𝑔´ (𝑢0,0,0).
Se asume que la parte lineal del término de reacción es dado por
independiente de 𝑢0 ( ℝ como lo planteado en (26).
Por la proposición 5.1, los valores propios imaginarios puros de 𝐿δ(𝑢0) surgen de una perturbación 0(δ) de la matriz
con espectro
Se observa que
en particular,
se tiene
y así
Por la perturbación 0(δ) del espectro acotado σ𝑏𝑑 (𝐿δ(𝑢)), el resultado Re λ´ (0) ≠ 0
es válida para δ↘0 y en vista del Teorema 4.3, se ha comprobado el supuesto (18).
Por otro lado, considere
con
un vector unitario en . ℝ3 x ℝ3
Nótese que el kernel y el co-kernel de 𝐿δ(𝑢0) es de dimensión uno, pues 𝐿δ(𝑢0)
posee un valor propio igual a cero. Es claro que
Ker 𝐿δ(𝑢0) = gen{ 𝑒0}
pues 𝑔´(𝑢0,0,0) 𝑒0 = 0. Para 𝑢0 = 0, el co-kernel de 𝐿δ(𝑢0) es dado por
Con
en (32) se tiene
Por el cruce transversal del valor propio en δ = 0 , se obtienen valores propios imaginarios puros ±𝑖⍵δ en el punto de equilibrio
Sea el correspondiente espacio propio. Como
con
Lema 5.116. En el ajuste y notación anterior, se tiene
en un punto de equilibrio 𝑢δ = (𝑢δ,0,0) con vectores propios complejos
En particular, considere la forma cuadrática
para δ↘0
Por el lema anterior se comprueba que condición de no degenerancia (19) es diferente de cero para δ↘0, el cual completa la demostración del Teorema 5.1. Por tanto, el sistema (20) presenta bifurcación de Hopf sin parámetros, η =+1 para el caso hiperbólico o η =−1 para caso elíptico, donde
con δ↘0. Aquí las derivadas son evaluadas en 𝑢 = 0 y se supone que δ ≠ 0 y Γ = ±1 indica el signo de
6 Conclusiones
Se ha realizado un estudio de la dinámica de un sistema de ecuaciones diferenciales ordinarias cuando esta presenta una bifurcación de Hopf, con o sin parámetros, determinar cuándo y en qué condiciones genéricas se puede presentar este tipo de bifurcaciones. Además se concluye que toda bifurcación de Hopf, sin importar que dependa o no de un vector de parámetros, presenta condiciones de equilibrio, de bifurcación y de control o transversalidad.
Por otro lado se observó que bajo ciertas condiciones un sistema de ecuaciones diferenciales parciales conlleva a una bifurcación de Hopf sin parámetros cuando es analizada a través del estudio de contornos viscosos a lo largo de una línea de puntos de equilibrio, del cual presentan órbitas heteroclínicas que conectan los puntos de equilibrio del termino reactivo formando un cono; o el modelo muestra una onda viajera el cual da origen a órbitas periódicas formando entre ellas una esfera de órbitas. A estas condiciones de perdida de estabilidad de Hopf son llamadas, respectivamente, hiperbólica o elíptica.