1 Introducción
El abastecimiento diversificado y sostenible de la energía dado el aumento en el consumo de este recurso a nivel mundial, efecto de un crecimiento progresivo de la demanda asociada a la multiplicación de las necesidades energéticas de los seres humanos y al aumento continuo de la población mundial, es uno de los desafíos críticos que enfrenta la humanidad en la actualidad, en un escenario donde el suministro de energía se garantiza principalmente mediante la utilización de fuentes de origen fósil como el petróleo, el carbón y el gas natural 1, para suplir una demanda que se contabiliza en aproximadamente 388 EJ promedio anual 2. De acuerdo con REN21- Renewable Energy Policy Network for the 21st Century3, en 2015 se reportó que alrededor del 78,4% de la energía primaria consumida a nivel mundial provino de fuentes de origen fósil, el 2,3% de la energía nuclear y el 19,3% de fuentes de energía renovable. Entre estas últimas, el 10,2% correspondió a la contribución direccionada a la generación de potencia, calor de proceso, electricidad y producción de biocombustibles; y el 9,1% restante correspondió al uso de la biomasa tradicional, principalmente para cocción de alimentos y generación de calor en zonas rurales remotas de países en vía de desarrollo. De acuerdo con lo planteado por Baruah D y Baruah DC 4, debido al continuo crecimiento de la demanda de energía y los problemas asociados a la explotación de combustibles fósiles, los estudios de investigación se han direccionado a la utilización de fuentes alternativas de energía que permitan suplir la demanda energética y a su vez mitigar el impacto al medio ambiente. Entre ellas, la implementación de tecnologías asociadas a las energías renovables se considera una alternativa que puede contribuir significativamente a que una región específica pueda alcanzar su independencia energética junto con beneficios económicos y ambientales.
Mientras se enfrentan problemas relacionados con el calentamiento global y el cambio climático, un esfuerzo substancial se ha realizado en la investigación y desarrollo dirigido hacia la utilización de la biomasa como alternativa energética respecto al uso de los combustibles fósiles. Su alta disponibilidad ha sido ampliamente reconocida ya que posee el potencial de suplir en gran proporción los requerimientos energéticos actuales con menores impactos al medio ambiente 5. Entre las fuentes de energía renovable disponibles, la biomasa es considerada una fuente de CO2 neutro, siendo la única fuente de energía renovable que puede ser transformada en un producto energético en fase sólida, líquida o gaseosa mediante múltiples procesos de conversión energética 6. De acuerdo con Long H. et al. 7, la producción de bioenergía basada en biomasa suple entre el 9-13 % del consumo total de energía a nivel mundial, lo cual supone ser una de las fuentes de energía renovable más prometedoras en el futuro; ser una fuente de energía disponible localmente 8 y ser una fuente con el potencial de reducir la dependencia existente de los combustibles de origen fósil, contribuyendo en consecuencia a la disminución de las tasas de emisión de gases de efecto invernadero y emisiones contaminantes 9.
De acuerdo con Ahrenfeldt J. et al.10, entre los procesos de transformación termoquímica de la biomasa, la gasificación ha probado ser un modo eficiente y flexible de utilizar la biomasa como fuente de energía, lo que ha atraído la atención creciente hacia el desarrollo de tecnologías relacionadas con este proceso, principalmente en la producción combinada de calor de proceso y potencia eléctrica, lo que es una tecnología prometedora. De acuerdo con Lee U et al.11, el propósito de un sistema de gasificación es el de convertir la biomasa en una forma de energía útil llamada “gas de síntesis” o “syngas” la cual está constituida principalmente por hidrógeno (H2), monóxido de carbono (CO) y metano (CH4), la cual puede ser aprovechada energéticamente en sistemas de generación de potencia. La gasificación de biomasa para la producción de hidrógeno principalmente, ha sido estudiada en la integración a tecnologías de generación de potencia tales como las turbinas evaporativas, microturbinas, celdas de combustible y motores a gas 12. Según Mahinpey N y Gomez A. 13, comparada con la incineración o la combustión directa de la biomasa, la combustión del syngas es una alternativa tecnológica eficiente y relativamente limpia debido a su alta tasa de recuperación energética y a las bajas emisiones de NOx, SOx y desechos sólidos. Por otro lado, la gasificación permite la instalación de reactores pequeños, de bajo costo de operación y eficientes en la reducción de los costos de almacenamiento y transporte de la materia prima, la recuperación de la energía disponible en los desechos de la biomasa y la reducción de los costos asociados a la disposición final de los desechos.
El presente estudio tiene como propósito analizar el comportamiento de la combustión del gas de síntesis producto de la gasificación de biomasa residual agrícola, considerando que el gas producido durante el proceso de conversión termoquímica es depurado y reformado al punto de presentar una composición mayoritaria de hidrógeno y nitrógeno. A partir de la comparación entre un modelo analítico de combustión bajo consideraciones de equilibrio químico mediante el software GASEQ y un modelo de combustión CFD de transporte de especies, se pretende caracterizar el comportamiento de la temperatura de llama adiabática y la formación de las especies químicas producto del proceso de conversión termoquímica en función de la razón de equivalencia, parámetro que permitiría la calibración de los flujos másicos de aire y gas combustible en aplicaciones de generación de potencia que involucran la hibridación entre celdas de combustible de óxido sólido SOFC y microturbinas a gas MGT.
2 Aprovechamiento energético del gas de síntesis “syngas”
Según Bang-Møller C, Rokni M y Elmegaard B 14, y en contraste a esta posibilidad, la producción distribuida de biomasa trae como consecuencia un aumento de los costos de transporte de la materia prima. Por esta razón, la conversión energética local de biomasa en electricidad y calor sería el escenario ideal mediante el cual se podría minimizar el costo asociado a su uso como recurso energético; considerando que la ubicación más cercana del usuario final a la fuente contribuye a una reducción de las pérdidas en la red de distribución eléctrica. De acuerdo con Bang-Møller C, Rokni M 15, se ha identificado que las tecnologías de generación de potencia más eficientes a pequeña escala incluyen típicamente turbinas a gas (GT), microturbinas (MGT) y celdas de combustible (FC).
De acuerdo con lo planteado por Ebrahimi M y Moradpoor I 16, las Celdas de Combustible de Óxido Sólido-SOFC poseen ventajas especiales que las hacen adecuadas para aplicaciones que involucran cogeneración a diferentes escalas. Estas pueden operar bajo un esquema de reforma de vapor tanto interna como externa para producir hidrógeno a partir de hidrocarburos. Debido a que el electrolito de la celda es sólido, es posible construirla ya sea en forma tubular, plana o monolítica. La estructura de cerámica sólida de la celda de combustible de óxido sólido permite una mayor resistencia a la corrosión e incrementa la tolerancia de la celda a las altas temperaturas. Además, las celdas de combustible de óxido sólido presentan una gran versatilidad, pueden ser utilizadas para la generación de potencia únicamente, para la generación de potencia en sistemas híbridos, para la generación de potencia, calor y enfriamiento combinados; operando con combustibles de diferente composición química; lo que las hace ideales para aprovechar el gas de síntesis proveniente de la gasificación de biomasa.
Como alternativa, según Ud Din Z y Zainal ZA 17, la gasificación de biomasa en un gasificador promete ser una estrategia más eficiente comparada con la combustión de biomasa en ciclos de potencia de vapor, particularmente a pequeña escala. Por otro lado, según Doherty W, Reynolds A y Kennedy D 18, el uso de SOFCs acopladas a sistemas de gasificación de biomasa muestra ser una alternativa de generación prometedora ya que se combinan las bondades de las fuentes de energía renovable y las características de alta eficiencia de las celdas de combustible. Estos sistemas denominados (BG-SOFC), ofrecen una configuración modular ideal en aplicaciones de generación descentralizada de calor y potencia combinada (CHP).
Según Shamoushaki M, Ehyaei MA y Ghanatir F 19, se consideran sistemas de potencia híbridos, aquellos sistemas en los cuales una máquina térmica como una micro turbina a gas es acoplada a un sistema de conversión de energía no-térmico como una celda de combustible. De acuerdo con Perna A et al.20, la Celda de Combustible de Óxido Sólido - SOFC entre las celdas de combustible disponibles, es la tecnología más atractiva para llevar a cabo la hibridación, considerando que la alta temperatura de sus gases de escape y la posibilidad de operarla a presión atmosférica o presurizada permite su acoplamiento con Ciclos Rankine Orgánicos - ORC y ciclos Brayton. Según Stambouli AB y Traversa E 21, combinando una celda de combustible de alta temperatura como una SOFC, y una microturbina a gas, pueden alcanzarse eficiencias cercanas al 65% en comparación a la eficiencia que podría alcanzar una microturbina a gas operando de manera independiente de 25-30%. Esta diferencia se debe principalmente a la contribución termodinámica favorable de la celda de combustible a la generación de potencia donde el proceso de conversión electroquímica del gas combustible utilizado no se encuentra sujeto a las limitaciones del ciclo de Carnot. A continuación, en la Figura 1, se presenta el diagrama esquemático del sistema de generación de potencia híbrido basado en una celda de combustible de óxido sólido y una microturbina a gas con recuperación de calor.
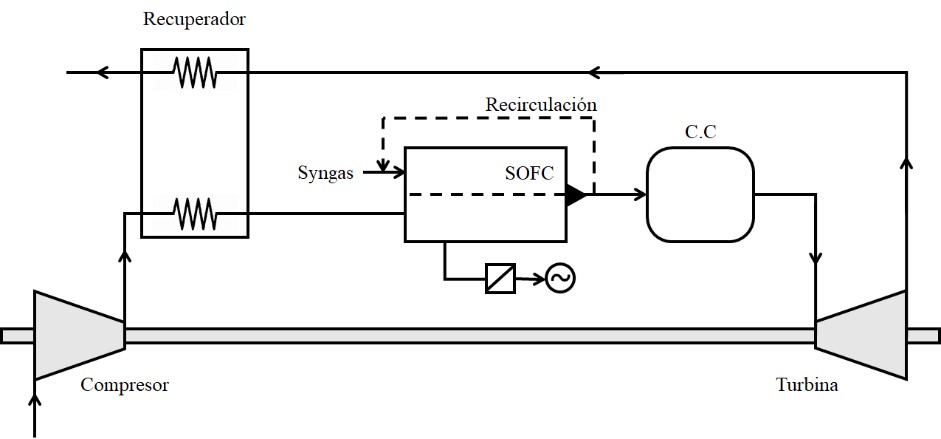
Figura 1 Sistema de generación de potencia híbrido basado en una celda de combustible de óxido sólido y una microturbina 21.
3 Modelo numérico y plan experimental
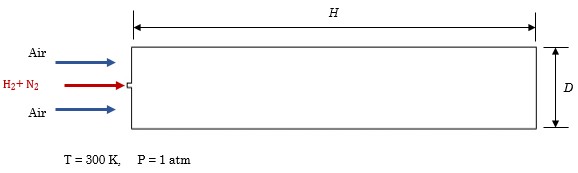
Para este estudio, se llevó a cabo la simulación de la combustión no premezclada de hidrógeno - aire para diferentes razones de equivalencia utilizando ANSYSFluent, considerando el proceso de combustión que tiene lugar en una microturbina gas de un sistema de generación de potencia híbrido SOFC-MGT. Se consideró la inyección de una mezcla de hidrógeno - nitrógeno y la inyección de aire seco al combustor a través de líneas de flujo independientes a una temperatura de 300 K y a una presión de 1 atm. La Figura 2, muestra la vista en dos dimensiones de un combustor cilíndrico en el cual tiene lugar la combustión en estado estable del gas combustible. El diámetro y longitud efectiva del combustor es D = 0,04 m y H = 0,2 m, respectivamente. El diámetro de la boquilla a través de la cual se inyecta el gas combustible en el combustor es d = 0,004 m; la distancia entre la sección transversal de inyección de combustible y la sección transversal de inyección de aire es h = 0,002 m.
Se asumió que la componente de vórtice para la velocidad es igual a cero, por lo que es posible considerar un flujo simétrico con respecto a la línea central del combustor, simplificando el modelo a un dominio en 2D. Además, asumiendo un comportamiento simétrico del flujo, fue considerado un eje de simetría axial al dominio 2D del combustor, permitiendo la división de la malla en dos partes y obteniendo como resultado, una reducción del esfuerzo computacional para la simulación. Fue seleccionado un modelo de estado estable basado en la presión y bajo la formulación de velocidad absoluta. Así mismo, se consideró un modelo adiabático, por lo que el flujo de calor a través de las paredes del combustor no fue considerada. Los efectos de la aceleración gravitacional fueron despreciados. Se destaca el hecho de que fue posible obtener una malla 2D de alta calidad (Mínima calidad ortogonal = 1,00000 e+00; Máxima distorsión ortogonal = 0,00000 e+00), de 14020 nodos, la cual fue elaborada mediante ICEM - ANSYS, utilizando la metodología de bloques. A continuación, en la Figura 3, se presenta la malla utilizada en la simulación.
Se empleó la ecuación de energía y el modelo turbulento estándar k−ε fue seleccionado un modelo de combustión por transporte de especies “Disipación de Eddy” para la interacción química turbulenta de las reacciones volumétricas de las especies, considerando la difusión de estas a la entrada del combustor para las dos líneas de flujo. Las entradas, a través de las cuales se realiza la inyección de aire e hidrógeno, fueron configuradas para una condición de frontera basada en la velocidad con valores de 70 m/s y 1,6 m/s fijos para la mezcla hidrógeno - nitrógeno y el aire respectivamente. La salida fue configurada para una condición de frontera basada en la presión con un valor de 0 kPa manométrico. Las fracciones másicas de las especies químicas; H2, O2, N2, H2O, fueron configuradas de acuerdo con las consideraciones de balance químico y la variación de la razón de equivalencia ϕ para cada uno de los casos de estudio en los que se consideraron fluctuaciones en los porcentajes de H2 en la mezcla de inyección.
Fue seleccionado el esquema SIMPLE para acoplamiento entre la velocidad y la presión. La discretización espacial de la presión fue seleccionada de segundo orden y todos los gradientes fueron computados utilizando el esquema basado en celdas por mínimos cuadrados. Igualmente, fue seleccionado el esquema de segundo orden para la solución de las ecuaciones de momento, energía cinética turbulenta, tasa de disipación turbulenta, energía y todas las especies. A continuación, en la Tabla 1 se presenta el resumen de las condiciones de frontera, las condiciones de simulación y los modelos empleados.
Tabla 1 Parámetros de simulación.
| Parámetros | Valor |
|---|---|
| Régimen de flujo | Turbulento (Simetría axial-Modelo 2D) |
| Presión de entrada [kPa] | 101.325 |
| Temperatura de entrada [K] | 300 |
| Velocidad de entrada (Aire) [m/s] | 70 |
| Velocidad de entrada (Hidrógeno) | 1.6 |
| Diámetro efectivo del combustor [m] | 0.04 |
| Diámetro de la boquilla [m] | 0.004 |
| Longitud efectiva del combustor [m] | 0.2 |
| Número de nodos | 14020 |
| Mínima calidad ortogonal | 1.000 E+00 |
| Máxima distorsión ortogonal | 0.000 E+00 |
| Condición de frontera | Basada en la velocidad |
| Esquema de acoplamiento | Simple |
| Discretización espacial de la velocidad | Segundo orden |
| Modelo de turbulencia | 𝑘−ε estándar |
| Modelo de combustión | Transporte de especies - “Disipación de Eddy” |
A continuación, se presentan las ecuaciones de continuidad, momento, energía, especies y el modelo de “Disipación de Eddy” utilizadas por ANSYS - Fluent para la solución del modelo de combustión por transporte de especies para reacciones volumétricas 22.
3.1 Ecuación de continuidad
donde, V
k,i
es la componente i - de la velocidad de difusión V
k
de las k especies, y
3.2 Ecuación de momento
donde, ƒk,j es la fuerza debida al volumen que actúa sobre las k especies en la dirección j. Debe tenerse en cuenta que la ecuación anterior no incluye términos explícitos de reacción y la combustión modifica considerablemente el comportamiento del flujo. Por ejemplo, la viscosidad dinámica varía considerablemente debido a los cambios de temperatura y la densidad cambia en la misma proporción al igual que las velocidades en el frente de llama.
3.3 Ecuación de energía
donde,
donde, el primer término representa un aporte de calor difusivo expresado en términos de la ley de Fourier, en tanto que el segundo término está asociado a la difusión de las distintas especies las cuales poseen diferentes entalpías.
3.4 Especies
donde, ℛ𝑖 es la tasa neta de producción debido a la reacción química y 𝑆𝑖 la tasa neta de creación mediante adición de la fase dispersa y otras fuentes definidas por el usuario. Esta ecuación es resuelta para un número de especies N ̶ 1 donde N es el número de especies en fase fluida presentes en el sistema. Para flujos turbulentos, Fluent computa la difusión de masa mediante la siguiente ecuación.
donde, 𝑆𝑐𝑡 es el número de turbulencia de Schmidt, con un valor por defecto de 0,7.
3.5 Modelo de disipación de Eddy
Para combustibles de combustión rápida como el hidrógeno, la reacción general es controlada por la mezcla turbulenta, por lo que la turbulencia mezcla lentamente el combustible y el oxidante dentro de las zonas donde se quema rápidamente. La tasa neta de producción de especies i debido a 𝑟, 𝑅 i, la reacción está dado por el valor mínimo entre las dos expresiones que se presentan a continuación:
donde,
𝑌𝑃, es la fracción másica de cualquier especie en los productos, 𝑃
𝑌𝑅, es la fracción másica de un reactante en particular, 𝑅
𝐴, es una constante empírica igual a 4.0
𝐵, es una constante empírica igual a 5.0
3.6 Esquema computacional
La combustión hace referencia a los procesos donde tienen lugar reacciones químicas de reducción y oxidación acompañadas de un efecto de liberación de energía térmica. Estos procesos involucran especies químicas clasificadas como combustibles y oxidantes en fase sólida, líquida o gaseosa. Los estudios de la combustión están basados en los principios de la termodinámica, la cinética química, la mecánica de fluidos, la transferencia de calor y la transferencia de masa y tiene lugar en máquinas térmicas, máquinas de combustión interna, turbinas a gas, propulsores de cohetes, quemadores y equipos de proceso como calderas, hornos, calentadores y secadores 23.
Todo proceso de combustión puede expresarse analíticamente como:
donde F y O representan el combustible y el oxidante;
donde, ø es la razón de equivalencia, 𝑊𝐹 y 𝑊𝑂 son los pesos moleculares y 𝑌𝐹 y 𝑌𝑂 las fracciones másicas del combustible y el aire respectivamente. Para la combustión de hidrógeno se tiene la siguiente ecuación que establece el equilibrio químico de las especies H2, O2, N2, H2O para una combustión estequiométrica.
2H2 + (O2 +3.76N2) → 2H2O + 3.76 N2 (11)
La razón de equivalencia es un índice comúnmente utilizado para indicar si la mezcla combustible - aire es pobre (ø < 1), es rica (ø > 1) o es estequiométrica (ø = 1). La fracción de equivalencia puede calcularse mediante la siguiente expresión 23:
Donde 𝑓 hace referencia a la relación combustible - aire de la reacción química real global y 𝑓𝑆 hace referencia a la relación combustible - aire de la reacción química estequiométrica global, es decir:
Además, para un sistema con doble alimentación, una a través de la cual fluye aire y la otra a través de la cual fluye el combustible, es posible definir una fracción másica de la mezcla 𝑍, con la cual es posible ajustar y mantener las proporciones correspondientes a una determinada razón de equivalencia. Esta fracción puede calcularse mediante la siguiente expresión:
donde, 𝑚𝑓 y 𝑚𝑂 son los flujos másicos de combustible y aire respectivamente. Dado que la inyección de hidrógeno no se realiza al 100 %, sino en diferentes proporciones junto con gas nitrógeno, se hace necesario encontrar una serie de expresiones analíticas que permitan calcular la densidad de la mezcla hidrógeno - nitrógeno en la inyección y así, establecer el flujo másico de hidrógeno 𝑚𝑓 de la mezcla no reactiva, calcular la fracción másica de la mezcla hidrógeno - aire 𝑍 y finalmente, calcular la razón de equivalencia para inyecciones de combustible con diferentes porcentajes de hidrógeno en la mezcla. Una vez se ha calculado la razón de equivalencia ø, es posible reconfigurar el balance químico para la combustión de hidrógeno. A continuación, las ecuaciones 15 y 16 permiten el cálculo de la razón de equivalencia en función del porcentaje de hidrógeno en la inyección.
para el hidrógeno la fracción másica de la mezcla en una reacción estequiométrica es 𝑍𝑠𝑡 = 0.0285. Generalmente es necesario conocer el exceso de aire (%) requerido para ajustar el flujo de inyección de aire al quemador o combustor con el propósito de permitir la transformación completa del combustible en especies químicas y energía térmica. Este valor puede calcularse como sigue:
4 Resultados y discusión
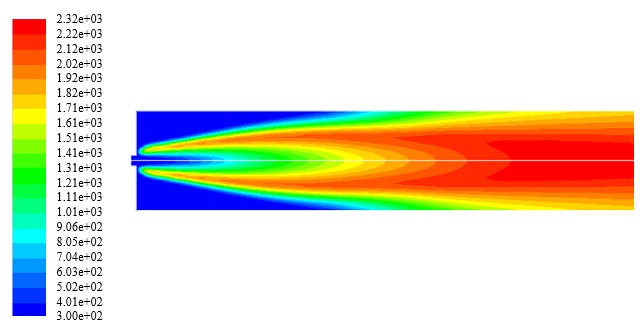
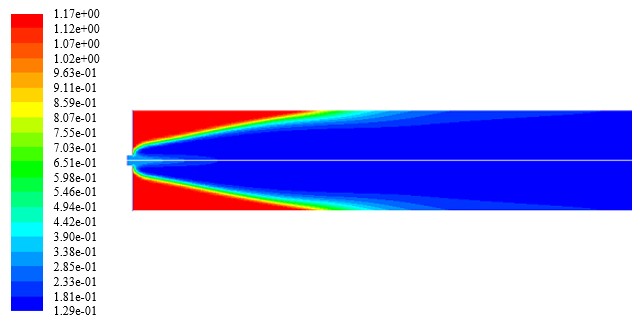
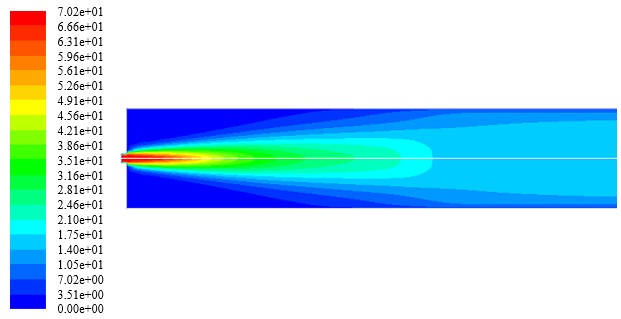
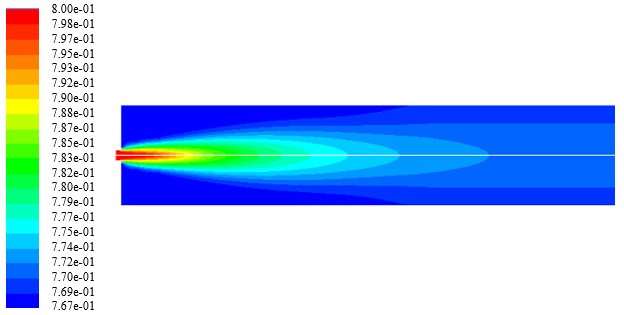
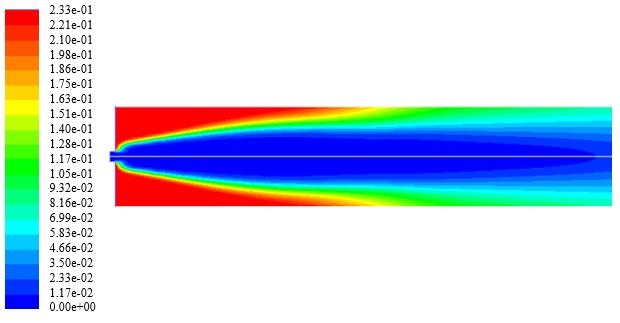
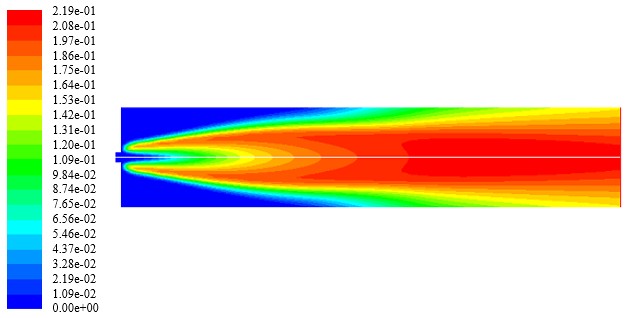
A continuación, se presentan los contornos de temperatura, densidad, velocidad y fracciones másicas de H2, O2, N2, y H2O para el caso en el que se tiene una inyección al 20% H2 con una razón de equivalencia ø = 0.814. En las Figuras 4, 5, 6, 7, 8, 9 y 10, se muestran los contornos de temperatura, densidad, magnitud de la velocidad, fracción másica de hidrógeno, fracción másica de nitrógeno, fracción másica de oxígeno y fracción másica de vapor de agua a lo largo del combustor. De estos contornos se establece que existe concordancia entre los valores teóricos y los valores obtenidos en las simulaciones para las condiciones de frontera a la entrada del combustor. Sin embargo, los valores para la temperatura adiabática de la llama y las fracciones másicas de las especies difieren a la salida del combustor. Este resultado puede ser indicativo de la necesidad de utilizar un modelo de combustión más robusto, el cual permita caracterizar de mejor manera la combustión no premezclada de la mezcla combustible considerada.
En la Tabla 2, se muestran las fracciones molares 𝑋𝑞,𝑖 obtenidas a partir del balance químico y aquellas fracciones 𝑋𝑠,𝑖 obtenidas de la simulación para el oxígeno, el vapor de agua y el nitrógeno en una combustión al 20% de hidrógeno en la inyección, con una razón de equivalencia de 0.814. En esta se observan diferencias en la predicción de las fracciones molares para el oxígeno y el vapor de agua a la salida del combustor.
Tabla 2 Fracciones molares de las especies químicas de los productos para una combustión al 20 % H2 , ø = 0.814.
| Especie Química | 𝑋 𝑠,𝑖 | 𝑋 𝑞,𝑖 | 𝑒𝑟(%) |
|---|---|---|---|
| O2 | 0.042 | 0.033 | 27.3 |
| H2O | 0.252 | 0.292 | 15.8 |
| N2 | 0.703 | 0.674 | 4.3 |
En la Tabla 3, se muestran los porcentajes de exceso de aire y la temperatura de llama adiabática en función de la razón de equivalencia para los diferentes casos de estudio. Se observa que la diferencia en la predicción de la temperatura de llama adiabática entre los valores obtenidos del balance de especies químicas y la simulación, disminuye a medida que la razón de equivalencia aumenta. Estas diferencias pueden presentarse a razón de las diferencias existentes entre los modelos analíticos utilizados por GASEQ, software que permite realizar el balance químico de especies a través de ecuaciones de balances químico y los modelos empleados por Fluent para el transporte de especies.
Tabla 3 Porcentaje de exceso de aire y temperatura de llama adiabática en función de la razón de equivalencia.
| %H 2 | ø | 𝑒 𝑎 (%) | 𝛵 𝑎,𝑏,𝑠 [ 𝐾] | 𝛵 𝑎,𝑏,𝑞 [ 𝐾] | 𝑒𝑟(%) |
|---|---|---|---|---|---|
| 8 | 0.574 | 74.2 | 2051.6 | 1797.6 | 14.1 |
| 9 | 0.607 | 64.7 | 2102.2 | 1863.4 | 12.8 |
| 10 | 0.636 | 57.2 | 2145.9 | 1919.8 | 11.7 |
| 11 | 0.663 | 50.8 | 2173.6 | 1969.9 | 10.3 |
| 12 | 0.686 | 45.8 | 2200.7 | 2012.4 | 9.3 |
| 13 | 0.708 | 41.2 | 2227.4 | 2051.9 | 8.5 |
| 14 | 0.727 | 37.5 | 2243.6 | 2086.0 | 7.5 |
| 20 | 0.814 | 22.8 | 2320.1 | 2234.7 | 3.8 |
| 30 | 0.897 | 11.44 | 2347.3 | 2369.8 | 0.9 |
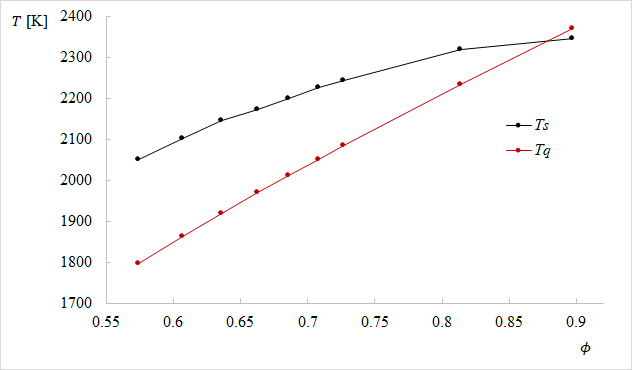
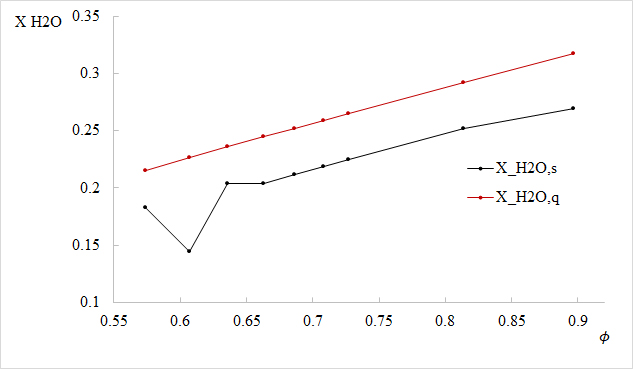
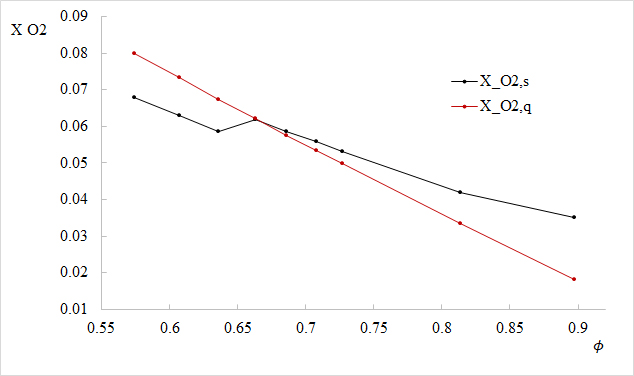
La Figura 11, muestra la variación de la temperatura de llama adiabática en función de la razón de equivalencia. De ésta se observa, que si bien la simulación predice correctamente la tendencia de decremento de la temperatura de llama adiabática ante a disminución de la razón de equivalencia, es decir, un aumento en el porcentaje de exceso de aire como lo muestra la Tabla 3; difiere de los valores calculados mediante equilibrio químico utilizando el software libre GASEQ. Las Figuras 12, 13 y 14 muestran la variación de las fracciones molares para las especies en los productos, en función de la razón de equivalencia. De éstas se puede observar que si bien la simulación predice la tendencia en la disminución de la fracción molar para el nitrógeno y el oxígeno, y un aumento en la fracción molar para el vapor de agua ante el aumento de la razón de equivalencia y la consecuente disminución del porcentaje de exceso de aire, se presentan discrepancias entre los valores; debido principal y probablemente a la diferencia entre los modelos analíticos utilizados por GASEQ y Fluent; específicamente, por los efectos de turbulencia y la fluctuación de las propiedades de flujo como la viscosidad dinámica ante las variaciones de temperatura y la velocidad del frente de llama ante la reacción química exotérmica.
5 Conclusiones
A partir de los resultados obtenidos de la simulación, se establece que el modelo de combustión seleccionado predice de forma aproximada el comportamiento de la temperatura de llama adiabática y las fracciones másicas de las especies químicas de los productos a la salida del combustor. Los valores obtenidos de la simulación difieren de los valores obtenidos por balance de especies químicas, principalmente por la contribución de los efectos de la turbulencia y la fluctuación de las propiedades de flujo debido a la reacción exotérmica. Como era de esperarse, pudo percibirse un aumento progresivo de la temperatura de llama adiabática ante el aumento de la razón de equivalencia, dado el aumento en la cantidad de aire para la combustión, lo que eleva la probabilidad de liberar la energía química contenida en el combustible en forma de calor. Por otro lado, dada la ausencia de átomos de carbono en el combustible, no se espera generación de dióxido y monóxido de carbono durante el proceso de conversión termoquímica. Sin embargo, se espera que, a partir de una razón de equivalencia de 0,708, para la cual se alcanza una temperatura de llama adiabática superior a 2000 K, sea significativa la generación de dióxidos de nitrógeno y no a una razón de equivalencia de 0,574 como predice la simulación CFD. Ante esta consideración, se identifica la falta de precisión del modelo de combustión de transporte de especies empleado para razones de equivalencia por debajo de 0,820. Por otro lado, se identifica que la combustión de hidrógeno es sumamente sensible ante cambios en la razón de equivalencia y, considerando las imprecisiones identificadas en el modelo, éste no es recomendable para el análisis de la combustión del gas de síntesis producto de la gasificación de biomasa.
Se considera el modelo presentado en este estudio como una aproximación general al comportamiento de la combustión de hidrógeno para diferentes razones de equivalencia, teniendo en cuenta que un modelo de combustión no premezclada y no un modelo por transporte de especies podría predecir con mayor fidelidad y precisión las fluctuaciones de la temperatura de llama adiabática ante cambios en el porcentaje de exceso de aire dadas las ecuaciones que el modelo emplea basada en distribuciones de probabilidad. Así, el presente modelo permite desarrollar únicamente una visión general del proceso de combustión de hidrógeno, una de las principales especies químicas en el gas de síntesis, cuyo porcentaje se intenta maximizar cuando el aprovechamiento energético del gas considera tecnologías basadas en celdas de combustible. Si bien el modelo CFD se acerca a los valores predichos por el software de equilibrio químico GASEQ para razones de equivalencia cercanas a 1, está sujeto a diferencias marcadas con respecto a la predicción realizada por éste último.