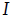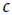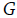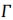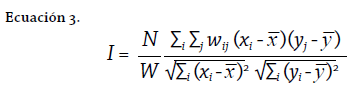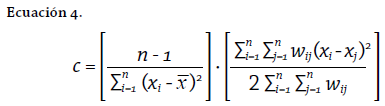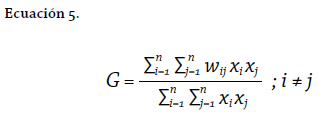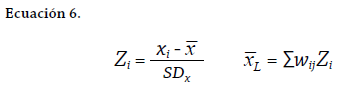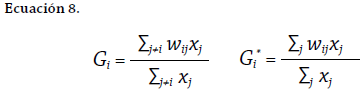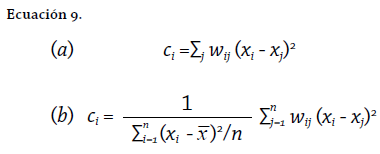Espanhol (pdf)
Artigo em XML
Referências do artigo
Tradução automática
Enviar este artigo por email
Citado por SciELO 
Citado por Google 
Similares em
SciELO 
Similares em Google 
Permalink
Contexto histórico
A partir de la década de los setenta, la geografía ha experimentado un cambio significativo gracias al desarrollo e implementación de un conjunto de metodologías de análisis espacial3 que han permitido afrontar, analizar y comprender problemas que anteriormente no se podían abordar. Entre los elementos que han aportado a este desarrollo resaltamos: (i) la econometría espacial; (ii) los aportes de Waldo Tobler con la primera ley de la geografía; y (iii) la formalización del concepto de autocorrelación espacial.
La econometría espacial se deriva de un campo especializado de la econometría general y considera específicamente los efectos espaciales -distribución y comportamiento a través del espacio geográfico- de las variables analizadas (fenómenos geográficos). Esta técnica se aplicó a inicios de 1970 en escenarios como el urbanismo, los modelos de precios hedónicos y la geografía económica. Anselin (2001, 311) indica que la econometría espacial puede ser caracterizada como “el conjunto de técnicas que considera las debilidades metodológicas derivadas de involucrar explícitamente los efectos espaciales, en específico, la autocorrelación y la heterogeneidad espacial”. Paelinck y Klaassen (1979) presentan una completa revisión sobre los inicios de la econometría espacial y Anselin (2010) muestra una perspectiva de su desarrollo.
El término autocorrelación espacial fue acuñado por Andrew Cliff y Keith Ord en 1967, durante la conferencia anual de la Regional Science Association (Cliff y Ord 1969).
Por su parte, de Smith, Goodchild y Longley (2018) indican que el término tiene su origen en el análisis de series temporales y, a su vez, en la noción de correlación de la estadística univariada.
En pocas palabras, la autocorrelación mide el grado de asociación que una variable desarrolla a través de un espacio definido como marco geográfico, esto es, el espacio de análisis propiamente dicho. El marco geográfico estará delimitado por el problema que se requiere abordar y puede ser simple o compuesto. El marco es simple si no presenta discontinuidades en el espacio geográfico, por ejemplo, al analizar los niveles de producción de sorgo en un conjunto de predios continuos localizados en una zona rural; en caso contrario, el marco es compuesto, por ejemplo, cuando se analiza la distribución de la población en el archipiélago de 7107 islas que constituye la República de Filipinas.
La esencia de la autocorrelación es analizar la variabilidad de un fenómeno a través del espacio geográfico para determinar patrones espaciales4 y describir su comportamiento, es decir, puede ser entendida como el medio para comprender cómo se distribuye el fenómeno en el espacio analizado y en qué grado los elementos locales pueden verse afectados por sus vecinos.
En este sentido, el concepto de autocorrelación espacial se deriva de y refleja la conocida primera ley de la geografía, que establece que “todo está relacionado con todo lo demás, pero las cosas cercanas están más relacionadas que las lejanas”5 (Tobler 1970, 236). Si existe una relación entre los elementos del fenómeno analizado en un marco geográfico (estructura espacial), se puede identificar un patrón espacial. También es posible afirmar que la primera ley de la geografía nos enseña, en esencia, el fenómeno de autocorrelación espacial. Al respecto, Goodchild afirma que:
Es imposible para un geógrafo imaginar un mundo en el cual la autocorrelación espacial pueda estar ausente: no podrían existir regiones de ningún tipo, ya que la variación de los fenómenos tendría que ocurrir independiente de su localización y, por tanto, lugares de un mismo vecindario serían tan disímiles como los ubicados en distintos continentes. (Goodchild 1986, 3)
Análisis espacial: autocorrelación y patrones espaciales
Inicialmente, los análisis no espaciales se enfocaban exclusivamente en los valores (medidas) de los fenómenos, sin tener en cuenta, de manera implícita, la localización espacial. En este escenario, Goodchild (1986, 3) indica que para abordar el concepto de autocorrelación espacial se requería, en primera medida, entender que el análisis espacial comprende dos tipos bien diferenciados de información: (i) los atributos de los fenómenos espaciales analizados, que incluyen medidas como el nivel de precipitación, la población desplazada, los niveles de contaminación sonora, caudal de los ríos, o también los atributos de variables cualitativas, tales como el uso del suelo o grupo religioso; (ii) cada fenómeno espacial tiene una localización, que se puede caracterizar por su posición sobre un mapa, por sistemas coordenados o por múltiples referencias geográficas6. El potencial de considerar la localización geográfica fue demostrado en 1854 por el médico inglés John Snow7, cuando combinó información base y temática para identificar focos de cólera en el distrito de Soho en Londres (para una discusión completa de este hito, véase Gilbert 1958; Cerda y Valdivia 2007; Siabato 2018a).
Con el paso del tiempo, y tras el desarrollo de nuevos métodos de análisis espacial aplicados de forma exitosa en múltiples escenarios, suelen presentarse confusiones a la hora de diferenciar los conceptos de autocorrelación y correlación espacial, debido a que algunos métodos aplican el primer concepto (ej. para la determinación de patrones espaciales y en análisis locales y globales), otros el segundo (ej. como medida de asociación de dos variables) y otros combinan los dos para complementarse y responder preguntas univariadas y multivariadas. Otra causa de esta confusión puede ser, como ya se indicó, que la autocorrelación espacial se basa en la noción de correlación de la estadística univariada. Getis (2007, 493) menciona que la autocorrelación “se puede ver como un caso especial de correlación”, tal vez este tipo de afirmaciones son mal interpretadas y son las que generan dudas. Getis de hecho aclara que “la autocorrelación espacial tiene un significado propio, mientras que las estadísticas de correlación se diseñaron para mostrar las relaciones entre variables, las estadísticas de autocorrelación se diseñaron para mostrar las correlaciones dentro de las variables, y la autocorrelación espacial muestra la correlación dentro de las variables a través del espacio.”
La diferencia fundamental entre estos conceptos es que al analizar la autocorrelación de un fenómeno geográfico no se consideran otras variables8, sino los valores observados en las zonas vecinas de la variable analizada (unidades de análisis). La autocorrelación describe el comportamiento de una única variable considerando un “plano horizontal” que está delimitado por el marco geográfico. La correlación, en contraste, identifica el grado de asociación que existe entre dos o más variables que se desarrollan en el mismo marco, aunque visto de manera vertical (véase Figura 1). Se considera una relación vertical de dos o más planos o niveles (variables) entendiendo que cada uno representa un fenómeno geográfico diferente, por ejemplo, temperatura, lluvia, remoción en masa, cobertura vegetal, tipos de suelo, etc. Nótese entonces cómo la autocorrelación espacial considera relaciones entre valores de la misma variable, pero en diferentes localizaciones (horizontal), mientras la correlación considera diferentes pares de variables en la misma localización (vertical). Los ejemplos de la Figura 1 representan este escenario.
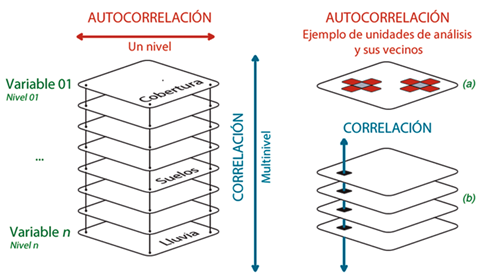
Fuente: basado en Siabato 2018b. Nota: las imágenes de la derecha muestran (a) la naturaleza univariada de la autocorrelación y (b) la multivariada de la correlación. Mientras la autocorrelación espacial relaciona una variable en diferentes espacios, la correlación relaciona múltiples variables en el mismo lugar.
Figura 1 Conceptualización de la autocorrelación espacial frente a la correlación espacial.
Como ejemplo temprano de aplicación del concepto de autocorrelación espacial, Cox (1969) demostró que en las pretensiones de voto de los ciudadanos norteamericanos existía autocorrelación espacial positiva. Si un estado tenía preferencias y votaba por el partido demócrata, se generaba una tendencia y aumentaba la probabilidad de que los estados circundantes votaran también por los demócratas (véase Jonas y Wood 2012). Este análisis se realizó considerando contigüidad espacial de primer orden entre las unidades de análisis, en este caso, entre los estados. Para cuantificar la autocorrelación espacial y poder definir si es positiva o negativa, se comparan los votos de un estado con los de sus estados colindantes. En este ejemplo, el marco geográfico de análisis corresponde a los Estados Unidos de América.
Si consideramos que la primera ley de la geografía se define por el criterio de cercanía, una pregunta válida que surge es cuánto o hasta dónde es cerca o lejos, además de plantear diferentes razonamientos sobre lo que implica estar relacionado. Miller (2004) presenta una rica discusión sobre estos conceptos y resalta además la importancia de la primera ley en el análisis espacial.
Uno de los criterios de cercanía puede ser entonces definido por aquellas unidades geográficas o unidades de análisis que tienen contigüidad física, criterio comúnmente llamado “vecindad”. Sin embargo, las relaciones de vecindad se basan en diferentes criterios geográficos tales como: la existencia de contigüidad física; la definición de relaciones de distancia; o a través de diferentes criterios de análisis como las redes de transporte, inclusive puede ser expresada en términos temporales. Por tanto, se debe utilizar el término vecindad como criterio general y comprender que la contigüidad es solo uno de los posibles tipos de vecindad que se consideran en el análisis espacial. Generalmente, la vecindad se establece a través de la matriz de contigüidad W, cuyos componentes denotaremos como wij y representan el criterio de vecindad entre las unidades de análisis i y j. Esta matriz no es solamente un criterio fundamental para el análisis de la autocorrelación espacial, sino para gran parte de los métodos de análisis de los fenómenos geográficos.
El criterio más simple de vecindad es la contigüidad física de primer orden, es decir, considerando exclusivamente los vecinos circundantes de la unidad de análisis. Los fundamentos de este criterio fueron definidos por Moran (1948). Sin embargo, el análisis espacial puede presentar limitaciones para medir el grado de asociación entre unidades que no se encuentran contiguas, es decir, en escenarios en los que el fenómeno analizado se desarrolla en un marco geográfico compuesto. Ante este problema, Cliff y Ord, en sus estudios sobre autocorrelación espacial (1972, 1973) y procesos espaciales (1981), introducen el concepto de distancia entre unidades geográficas, desarrollado como marco de análisis en Getis y Ord (1992). Moreno Serrano y Vayá (2002, 86) presentan una definición concreta de estos conceptos y de la matriz de distancia inversa, desarrollada por Anselin (1980) con el objetivo de determinar la autocorrelación espacial para aquellas unidades de análisis que carecen de contigüidad física directa. Como su nombre lo indica, la asociación entre dos unidades espaciales decrece a medida que la distancia entre ellas aumenta9.
En general, durante las últimas cuatro décadas se han desarrollado múltiples métodos para determinar con mayor precisión el concepto de vecindad entre las zonas analizadas (unidades geográficas o unidades de análisis), cada uno de ellos orientado a casos de estudio particulares que luego se convierten en procesos de aplicación general. Un ejemplo reciente es el propuesto por Ermagun y Levinson (2018), en el que proponen la matriz de pesos de red (Network Weight Matrix) para medir la dependencia espacial entre los nodos de una red considerando propiedades topológicas. Es recomendable que los analistas espaciales consideren detenidamente el tipo de matriz de vecindad que utilizarán, porque las conclusiones que se pueden derivar del análisis realizado, si consideran un tipo u otro, pueden llegar a ser opuestas. Una elección inapropiada de la matriz puede conllevar resultados imprecisos, o poco relacionados con el fenómeno analizado, que pueden generar decisiones incorrectas y la implementación de políticas con impactos adversos. El analista debería plantearse y responder, con criterio y pleno conocimiento del fenómeno analizado, esta pregunta: ¿qué tipo de matriz ayudaría a describir y representar mejor el comportamiento del fenómeno geográfico que se está analizando? Las siguientes secciones aportan elementos de juicio que ayudan a responderla. En este punto, es claro que la autocorrelación espacial marca un punto de inflexión en la geografía cuantitativa (Cliff y Ord 1969), por lo que se establece como un pilar fundamental para el análisis de la distribución y variabilidad de los fenómenos geográficos (Getis 2007).
Índices estadísticos de autocorrelación, criterios de vecindad y matriz de contigüidad
La autocorrelación espacial permite comprender la variación de UN fenómeno en UN marco geográfico de análisis. Si el fenómeno analizado tiende a agruparse en zonas uniformes, es decir, si tiende a conformar conglomerados o clústeres, entonces se evidencia la existencia de autocorrelación positiva (véase Figura 2a). Por el contrario, si las medidas de la variable en las unidades colindantes son disímiles, es decir, si el fenómeno tiende a estar disperso, entonces la autocorrelación espacial es negativa. En este caso, si un atributo está presente en un determinado lugar, este tenderá a ser diferente (±σ2) en los lugares vecinos (Figura 2b). Por último, cuando el fenómeno se comporta de forma aleatoria y no se identifica un comportamiento definido o estructurado, se dice que no existe autocorrelación espacial. En términos prácticos, este último caso implica que la presencia o ausencia de un atributo en un lugar determinado no influye, aparentemente, en la medida de dicho atributo en los lugares vecinos (Figura 2c).
Estos tres comportamientos caracterizan el fenómeno analizado en uno de los tres patrones espaciales básicos: clúster, disperso o aleatorio. La Figura 2 representa estos conceptos. Si la autocorrelación espacial de los patrones mostrados en las Figuras 2a, 2b y 2c se evaluara a través del Índice de Moran, los resultados serían 0,86, -1 y -0,17 respectivamente10. El procedimiento que lleva a estos resultados y su interpretación serán presentados más adelante.
La autocorrelación espacial se interpreta entonces como un índice estadístico descriptivo que permite medir las formas y las maneras como se distribuyen los fenómenos analizados en el espacio geográfico (Goodchild 1986). La autocorrelación espacial mide el grado en el que una variable geográfica está correlacionada con ella misma en dos puntos o zonas diferentes del área de estudio (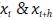
, donde h es la distancia entre los puntos), mide la similitud de la variable temática en un área determinada. Por tanto, y como se planteó al iniciar el editorial, la autocorrelación espacial permite responder la pregunta: ¿cómo varía UN fenómeno a través del espacio geográfico?
La formalización de los primeros índices para medir la similitud de un fenómeno geográfico surge a finales de la década de 1940 e inicios de los cincuenta. El Índice de Moran, uno de los más conocidos y extendidos, está fundamentado en los trabajos de Moran (1948) y Krishna Iyer (1949), y fue potenciado posteriormente por Geary (1954) 11, aunque su implementación en diferentes campos del saber, como en la economía regional, la economía urbana y los modelos de precios, requirió ajustes y complementos que permitieron su generalización y evolución dando paso a nuevos conceptos. En este escenario se deben destacar los desarrollos matemáticos, estadísticos y conceptuales planteados en los trabajos de Cliff y Ord (1969, 1972, 1973, 1981). Uno de los avances más importantes ha sido la capacidad de comprender no solamente las variaciones globales sino también las locales, esta idea marca uno de los hitos fundamentales en el desarrollo del análisis espacial puesto que los comportamientos globales suelen esconder aquellas especificidades locales a partir de las cuales se suelen resolver los problemas planteados; Anselin (1995) presenta el desarrollo y formalización de esta idea conocida como indicadores locales de asociación espacial -en adelante LISA, acrónimo de Local Indicators of Spatial Association-. Algunos conceptos aplicados y desarrollados en el seno de la econometría espacial pueden ser consultados en los trabajos de Anselin (1988), Getis, Mur y Zoller (2004) y Anselin, Florax y Rey (2004). Getis y Ord (1992) presentan el concepto de asociación por distancia, mientras que Lesage y Pace (2004, 2008) muestran cómo extender los fundamentos desarrollados en marcos de análisis espaciotemporal. De acuerdo con Getis (2007, 494), entre los índices que permiten analizar la autocorrelación espacial global y local se destacan:
de Moran (representación de covarianza global).
de Geary (representación de diferencias globales).
de Getis y Ord (representación multiplicativa global).
(representación del producto cruz).
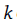de Ripley (pares acumulativos en la representación de distancia).
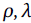(coeficientes autorregresivos en varias representaciones de regresión).
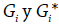de Getis y Ord (representaciones de agrupaciones locales -clústeres-).Ii y ci de Anselin (indicadores locales de asociación espacial -LISA-).
O de Getis y Ord (representación local que considera la autocorrelación global).
1/γ (el inverso del semivariograma, es decir, el correlograma).
Ck,i de Anselin (indicador local multivariado basado en el c de Geary).
Getis (2007) también lista algunos de los conceptos considerados para la definición de las matrices que describen la configuración de las unidades espaciales en las que se desarrolla el fenómeno analizado y que, en última instancia, ayudan a medir el nivel de asociación espacial del fenómeno:
wij = 1 ó wij = 0. Se considera 1 para identificar las unidades de análisis involucradas y 0 para las que no se consideran. Este es el concepto más extendido y de aplicación general.
1/dij-α. Describe el debilitamiento de la dependencia como función de la distancia, representa perfectamente el concepto de cercanía descrito en la primera ley de la geografía. El factor -α permite definir el grado de debilitamiento (distance decay representation).
s/p. Permite ponderar límites comunes. s representa la longitud del lado en común y p el perímetro de la unidad de análisis. Si existe un único límite, es claro que la relación es 1.
di - dj. Considera diferencias de distancia. En este escenario se pueden definir, por ejemplo, anillos de influencia.
Los índices de autocorrelación están determinados de forma general por la expresión de la Ecuación 1, donde Wij es el componente que determina la relación geográfica y Cij el que explica la variación temática del fenómeno analizado (Siabato 2018b). Es una técnica muy flexible que permite vincular diferentes criterios de asociación espacial a través de los distintos tipos de matriz W, como los presentados en la lista anterior. El cálculo de los índices se puede resumir en la sumatoria del producto de cada elemento Wij y su correspondiente Cij.
La definición de la matriz W = (Wij ) utiliza dos criterios básicos de vecindad: la contigüidad física y la distancia. Estos criterios se clasifican como básicos porque son los más extendidos y los que suelen estar implementados en los programas informáticos de análisis espacial, sin embargo, no se deben excluir los criterios basados en funciones de análisis y en relaciones temporales.
Para el primer caso, la matriz de contigüidad física se basa en criterios de contigüidad espacial de orden n, la Figura 3 muestra ejemplos básicos de primer y segundo orden para un marco geográfico dividido en unidades espaciales cuadradas y distribuidas uniformemente. Para determinar el primer orden, se responde a la pregunta ¿quiénes son mis vecinos? Para determinar las unidades asociadas de segundo orden, la pregunta sería ¿quiénes son los vecinos de mis vecinos? Este ejercicio se replica para cada orden n +1 que se quiera determinar. Como se indica en la Figura 3, los criterios base corresponden a los movimientos clásicos del juego de ajedrez.
Nota: nótese que se representan los órdenes de primer y segundo grado y su correspondiente integración. Los tres casos pueden ser aplicados en diferentes escenarios de análisis espacial.
Figura 3 Ejemplos de vecindad de primer y segundo orden para la definición de la matriz de contigüidad.
Por otro lado, el criterio de distancia establece quiénes son vecinos a partir de un límite máximo de vecindad determinado por una distancia d, lo importante en este escenario es definir claramente cómo se mide d. Es habitual considerar d entre los centroides de las unidades espaciales, pero también se pueden determinar otros criterios como los centros medios, los anillos de influencia, las relaciones de proporción perimetral o las proporciones entre líneas perimetrales no colindantes. La Figura 4 muestra los vecinos de la unidad central (en azul) determinados a partir de distancias de 2000 m, 3000 m, 4000 m y 5000 m entre centroides. Las unidades de análisis del ejemplo son cuadrados de 2000 m de lado. Es claro que al definir como parámetro de vecindad una distancia de 1000 m, no se encontrarían vecinos, la distancia mínima entre centroides es 2000 m.
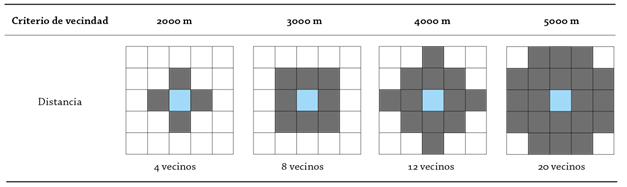
Nota: las distancias representadas consideran los centroides de las unidades de análisis.
Figura 4 Ejemplos de vecindad basados en el criterio distancia (d).
Los ejemplos muestran las claras diferencias que hay entre los criterios de vecindad. Se debe destacar que la distancia agrupa todos los elementos, mientras que la contigüidad conforma anillos según el orden determinado. Estos criterios parecen contraintuitivos, por tanto, el analista espacial debe decidir si el análisis de autocorrelación espacial debe considerar el conjunto de vecinos o solamente las franjas (anillos) definidas por el orden n de contigüidad. No obstante, se debe considerar que cada método puede tener modificaciones, por ejemplo, las matrices de contigüidad de orden dos y superiores pueden incluir los órdenes inferiores cambiando dramáticamente la definición de vecinos. Por ejemplo, si este concepto se aplicara al criterio Reina de segundo orden, los vecinos se incrementarían de 16 a 24. Nótese también que la combinación de conceptos puede llevar a resultados similares, por ejemplo, la integración del primer y segundo orden con criterio Torre mostraría el mismo resultado del criterio d = 4000 m; lo mismo sucede para los criterios Reina de primer orden y d = 3000 m. Ejemplos como los planteados en las Figuras 3 y 4 pueden ser representados para cada uno de los conceptos listados por Getis (2007, 494).
W es una matriz cuadrada n x n (véase Ecuación 1), en la que n se corresponde con el número de unidades de análisis. La Figura 5 muestra la definición de la matriz W para un marco geográfico irregular conformado por 10 unidades de análisis, considerando como criterio de vecindad Reina de primer orden (contigüidad física). La Figura 5a muestra las unidades de análisis clasificadas por área representadas con una paleta divergente para facilitar su visualización. En el ejemplo se definen los vecinos de la unidad de análisis 7, la Figura 5b resalta en tono oscuro sus cuatro vecinos: 4, 6, 8 y 9. Se podría pensar que la unidad 10 es también vecina, pero no es así. Es importante no dejarse llevar por impresiones visuales y considerar las relaciones topológicas de las geometrías que se involucran en el análisis; en este caso, la unidad 7 no comparte nodos con la 10. Una vez identificados los vecinos, se deben registrar en la matriz tal y como se muestra en la Figura 5c. Nótese que en las intersecciones de W para cada unidad de análisis (es decir, la posición ij de la matriz) se registra 1 para identificar la colindancia y 0 para establecer su ausencia. Al repetir este ejercicio para cada unidad de análisis se completa la matriz. Las filas de la matriz establecen los vectores de contigüidad y, evidentemente, el conjunto de vectores conforma la matriz, esta aclaración es importante porque los índices globales consideran la matriz, mientras que los locales utilizan los vectores para definir el índice de cada unidad. El vector de contigüidad determina la vecindad de cada unidad de análisis.
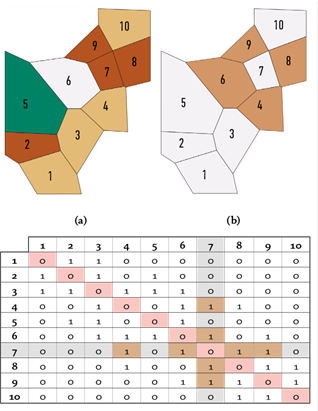
Nota: la correspondencia de colores en las figuras (b) y (c) permite integrar los criterios de selección espacial y su representación en la matriz.
Figura 5 Ejemplo de matriz de contigüidad física. Criterio de vecindad: Reina de primer orden.
Algunas propiedades de la matriz de contigüidad resultan evidentes con este ejemplo: (i) su diagonal principal se conforma de ceros, esto implica que la unidad no es vecina de sí misma; (ii) la matriz es simétrica; (iii) el número de vecinos de cada unidad de análisis está determinado por la sumatoria de cada vector, es decir, el número de vecinos de la unidad i corresponde a la suma de la i-ésima fila de la matriz; (iv) las unidades deben tener un identificador único para establecer las relaciones de forma unívoca.
Finalmente, se presenta el concepto de matriz de pesos estandarizada. A diferencia de la matriz de contigüidad, la matriz estandarizada no es simétrica, pues los pesos de cada vector varían en función del conjunto de vecinos (véase Figura 6). La sumatoria de los vectores locales o de contigüidad (filas) debe ser siempre 1. Por defecto los vectores de la matriz son equiponderados; sin embargo, resulta de gran utilidad modificar los pesos para priorizar las unidades de análisis que a priori se sabe que afectan en mayor grado la unidad central, ya sea por un criterio cuantitativo o considerando el criterio experto a partir de un conocimiento exhaustivo de la zona geográfica analizada.
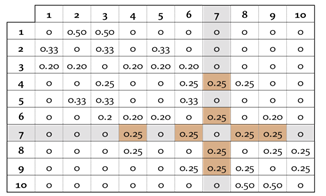
Nota: la sumatoria de cada i-ésima fila debe ser 1, tanto en el caso equiponderado como el priorizado.
Figura 6 Ejemplo de matriz de pesos estandarizada equiponderada.
Por ejemplo, la Figura 6 muestra pesos de 0,25 para los 4 vecinos de la unidad de análisis 7, valor derivado del criterio básico de equiponderancia: (1 / ∑ número de vecinos). Sin embargo, si este criterio se cambia por otro que asigne prioridades diferentes a cada zona (pesos diferentes), por ejemplo, según el área de la unidades de análisis circundantes, el vector de pesos resultante sería: [0 0 0 0,25 0 0,37 0 0,23 0,15 0], nótese cómo la unidad con mayor área (véase Figura 5a, unidad 6) obtiene el mayor peso: 0,37. En este caso, los valores serían calculados a partir de la expresión: (área de la unidad / ∑ áreas de las unidades contigüas). En este ejemplo se ha utilizado el criterio área, pero podría haber sido toneladas de producción, temperatura, pluviometría o cualquiera que sea la variable que se analice por unidad de análisis. En cualquier caso, se insiste en que la sumatoria de los pesos de cada vector siempre debe ser 1, de ahí su nombre, row-standardized spatial weighted matrix.
Índices de autocorrelación global y local
Después de definir el concepto de autocorrelación espacial y enumerar algunos delos índices que permiten cuantificar el comportamiento espacial de los fenómenos geográficos, se presentan detalles básicos para su cálculo clasificados en dos tipos: globales y locales. La diferencia principal entre ellos es que los índices globales evalúan asociaciones para el conjunto de valores del fenómeno, considerando todas las unidades de análisis como un bloque a través de la media global del fenómeno analizado (
); además, los índices globales no son sensibles a escenarios en los que se presenta heterogeneidad en el comportamiento del fenómeno geográfico12. En contraste, los indicadores locales (LISA) sí consideran escenarios específicos (de ahí su nombre), por tanto, permiten identificar subzonas en las que se presenta agrupamiento o dispersión del fenómeno. Aunque el cálculo base de los LISA también considera la media global, estos indicadores asignan medidas de autocorrelación a cada unidad de análisis y, por tanto, permiten identificar individualmente el nivel de agrupamiento o dispersión de cada unidad con relación a sus vecinos o respecto de aquellas unidades que se hayan definido a través del criterio de vecindad. En este caso, los valores o medidas de las unidades de análisis suelen ser estandarizados para que puedan ser comparados entre sí. Moreno Serrano y Vayá (2002) complementan esta discusión desde el punto de vista de la econometría espacial.
I de Moran (Moran’s I)
Es posible afirmar que tres de los índices globales más empleados por la comunidad académica son (i) el I de Moran, (ii) c de Geary y (iii) G de Getis y Ord. Como se mencionó, el I de Moran es uno de los índices más conocidos y extendidos, de hecho, es el más utilizado en gran parte de los estudios publicados en revistas de geografía y estudios ambientales (véase, por ejemplo, Wilt et ál. 2018; Yuan, Cave y Zhang 2018; Dogru et ál. 2017; Overmars, de Koning y Veldkamp 2003; Black y Thomas 1998) y, por tanto, la explicación se concentrará en este índice.
Una característica del cómputo del I de Moran es que solo se tienen en cuenta los valores de las unidades de análisis determinadas a partir del criterio de vecindad -véanse Figuras 3 y 4-, es decir, el valor de la unidad central no se considera para el cálculo; nótese que esto es consecuencia directa de la diagonal de la matriz de contigüidad de la Figura 5c, en la que se establece la restricción de que una unidad de análisis no es vecina de ella misma. Como en la mayoría de los índices, su naturaleza global se deriva de comparar de forma directa los valores de cada unidad de análisis con la media global del fenómeno (), esto es, la media de todas las medidas realizadas en el marco geográfico, tal y como se muestra en el numerador de la Ecuación 2.
Donde N es el número de unidades de análisis y
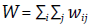corresponde al número total de vecindades. Nótese cómo el cociente entre la doble sumatoria y el número total de vecindades definen un tipo de covarianza ponderada o restricta a los vecinos. Siendo así una interpretación más sencilla de la Ecuación 2 la siguiente:
Considerando la Figura 5 como referencia, se observa que (i) el número de unidades de análisis es N = 10; (ii) el número total de vecindades, es decir, la sumatoria de los vecinos de cada unidad de análisis, es W = 36; (iii) el producto cruz estará limitado por los ceros de la matriz 5c, es claro que al resolver la expresión
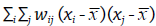, si el correspondiente wij es cero, el producto será siempre cero, este resultado es lógico si se piensa que solamente los valores vecinos sumarán al cálculo del valor I.
El dominio del I de Moran es [-1,+1]. Si se vinculan los patrones presentados en la Figura 2 con los posibles valores del dominio, se evidencia autocorrelación espacial negativa cuando I < 0. De hecho, al analizar una distribución perfecta ajedrezada como la representada en la Figura 2b a través de una matriz de contigüidad tipo Torre orden 1, resultará en un valor I = -1, indicando un comportamiento o patrón disperso del fenómeno. Si analizáramos el mismo fenómeno, pero considerando una matriz de contigüidad tipo Reina orden 1, se obtendría un I = -0,0958, indicando un comportamiento o patrón aleatorio. La Figura 7 refleja esta situación. Esto muestra que el I de Moran no es una medida universal que describe unívocamente el comportamiento de las unidades de análisis, sino que depende del criterio de vecindad W seleccionado. La implementación del tipo de vecindad define el patrón espacial que informa el índice. La decisión sobre el tipo de matriz W que será aplicada debe estar entonces definida por la interacción de las unidades de análisis que mejor describa al fenómeno analizado. En cualquier caso, siempre será necesario el buen criterio del analista espacial para interpretar el índice apropiadamente y no llegar a conclusiones equivocadas.
Nota: se evidencia cómo el cambio de criterio de vecindad afecta sustancialmente el resultado del análisis para el mismo fenómeno y distribución de las unidades espaciales. (Cálculo en GeoDa)
Figura 7 Resultado del cálculo del I de Moran para un mismo fenómeno y marco geográfico considerando los criterios de vecindad Torre y Reina.
Se evidencia autocorrelación espacial positiva cuando I > 0. El patrón clúster de la Figura 2a refleja esta situación, los valores positivos de I muestran que las unidades de análisis vecinas tienden a ser similares. Continuando con el ejemplo, una distribución agrupada como la presentada en la Figura 2a y analizada con una matriz de pesos tipo Torre, resulta en un I de Moran = 0,8645. En este caso, a diferencia del patrón disperso, al calcular I no se obtiene el límite superior del dominio; la razón principal para no obtener el valor teórico I = 1 es la franja vertical intermedia de blancos y negros, en donde claramente los vecinos son diferentes y no se conforman agrupamientos. Si este ejercicio se planteara con la matriz de contigüidad tipo Reina, el valor obtenido sería I = 0,8093. Como se puede observar, cambiar el criterio de vecindad de Reina a Torre en escenarios agrupados no representa cambios significativos en la interpretación del índice; en los dos casos se concluye que el fenómeno está agrupado (patrón clúster). Otro aspecto interesante que permite resaltar este ejemplo es que, en las condiciones presentadas, valores del Índice de Moran superiores a 0,7 corresponden a fenómenos altamente agrupados en el espacio geográfico.
Finalmente, cuando I = 0 o computa valores cercanos a cero, el fenómeno se distribuye aleatoriamente (Figura 2c). No es posible asegurar de forma concluyente rangos de aleatoriedad en el dominio del índice, pues estos varían según la distribución de las unidades de análisis y las medidas del fenómeno. No obstante, como recomendación general empírica, se sugiere pensar en aleatoriedad del fenómeno cuando el índice se encuentra en el rango -0,35 ≤ I ≤ 0,35. Los valores mayores y menores deberían llevar a pensar en patrones tipo clúster (I > 0,35) o disperso (I < -0,35), siendo clúster para valores positivos y disperso para valores negativos. La Figura 2 podría ser complementada con estos rangos, según lo indicado en la Figura 8.
Es importante aclarar que el ejercicio no es tan simple como se presenta, pues para responder la pregunta con criterio estadístico y un grado de confianza determinado se deben tener en cuenta elementos como, por ejemplo, el Z-score y la hipótesis de aleatoriedad espacial completa -en adelante, CSR-; sin embargo, estos conceptos no se discuten en este texto introductorio. Si bien el I de Moran nos presenta un valor que indica el grado de autocorrelación espacial para un conjunto de unidades de análisis considerando una variable específica, una pregunta lógica que surge es qué tan diferente de cero debe ser el índice para que realmente indique dispersión o agrupamiento, el Z-score y una prueba de hipótesis basada en la CSR ayudan a responder esta pregunta y, además, a comprender si el resultado del análisis es estadísticamente significativo dado un nivel de confianza (Siabato 2018b).
El ejemplo presentado demuestra que, al aplicar un criterio Reina o Torre, o cualquier criterio de vecindad diferente, cambia el resultado del índice y, por tanto, la conclusión a la que el analista espacial llegaría sobre la distribución del fenómeno. En el primer ejemplo (Figura 2b), el analista podría cambiar su reporte de análisis de disperso (Torre) a aleatorio (Reina); solo las condiciones del análisis y el conocimiento de la variable permitirían decir cuál es correcto. El impacto del criterio de vecindad en lattices13 uniformes o regulares como el usado en el ejemplo es muy alto (véase Figura 2); no obstante, se debe aclarar que en lattices irregulares como el mostrado en la Figura 5a no se evidenciaría un impacto alto. Un análisis de autocorrelación espacial exige que se configuren diferentes escenarios con distintos criterios de vecindad y, principalmente, interpretar los resultados con el conocimiento que se tenga de la realidad analizada, esto es, del fenómeno geográfico medido. Si el analista no conoce los pormenores de la variable o fenómeno, se debería apoyar en un experto en el tema y nunca interpretar resultados de variables geográficas que no comprende o desconoce.
I de Moran bivariado
A lo largo de este editorial se ha insistido en la naturaleza univariada de la autocorrelación espacial, por tanto, mencionar un concepto como I de Moran bivariado puede parecer contradictorio. El concepto bivariado resulta de considerar los vecinos de una variable complementaria, la Figura 9 representa esta situación. La lógica del índice bivariado se puede resumir así: (i) la unidad de análisis central está determinada por la variable 01; (ii) la unidad central ahora estará relacionada con vecinos de una variable secundaria (variable 02); (iii) el índice calculado permite identificar el patrón espacial de la variable 01; los criterios de vecindad aplicados son iguales a los que ya han sido presentados. Por supuesto, para realizar el análisis se debe mantener el mismo lattice, ya que no sería posible realizar el cálculo si se cambia la distribución espacial de cada variable.
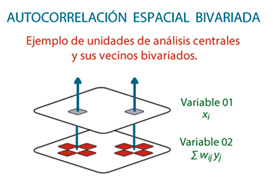
Nota: se observa cómo los vecinos determinados por uno de los criterios de vecindad ahora corresponden a una segunda variable. Para este tipo de análisis, el lattice se debe mantener constante.
Figura 9 Representación del concepto del I de Moran bivariado.
En ningún caso se debe considerar este concepto como un análisis de correlación espacial. Si se comparan las Figuras 1 y 9, se puede observar que la correlación espacial vincula las dos variables en el mismo espacio geográfico (Xi; yi ), mientras que la autocorrelación bivariada relaciona las dos variables, pero estas no coinciden en el espacio. La Figura 9 muestra cómo se vincula la unidad central (Xi) con las unidades definidas como vecinas en la segunda variable (
), es decir, la autocorrelación espacial bivariada NO tiene en cuenta la correlación espacial inherente entre las dos variables.
Un ejemplo explica mejor este concepto. Si la variable 01 representa la producción de cultivos de arroz y la variable 02 la concentración de magnesio en el suelo, entonces se puede plantear la siguiente pregunta: ¿cómo afecta la concentración de magnesio del suelo a la producción de arroz? Se puede pensar en un lattice determinado por las unidades productivas rurales de una vereda o comuna, el resultado del análisis permitiría entonces localizar los clúster (grupos de unidades) en los que la concentración del magnesio genera alta productividad de arroz o casos inversos. Si se conoce que hay zonas con alta concentración de magnesio, pero la productividad es muy baja, también es posible preguntarse si las prácticas agrícolas están afectando el potencial productivo. Este tipo de preguntas son clásicas de los indicadores locales de asociación espacial, véase Anselin (1995) para una explicación detallada.
En conclusión, el I de Moran bivariado permite conocer cómo varía un fenómeno a través del espacio geográfico, pero considerando las afectaciones que este fenómeno presenta por los cambios de una segunda variable. De manera análoga al I de Moran univariado (véase Ecuación 2), el I de Moran bivariado se define a través de la siguiente expresión:
Donde xi será la variable 01 y yj la variable 02. Nótese cómo los componentes wij determinan la relación de los valores centrales (xi) con los vecinos de la variable secundaria (yj). En el cálculo se consideran los valores (atributos) de la variable primaria (x) en el sitio “i” con los valores que asume la variable secundaria (y) en los vecinos localizados en cada sitio “j”.
Otra alternativa que vale la pena destacar de este índice es que permite analizar una variable en dos instantes t0 y t1. En este caso, se analizaría la variación de un fenómeno cualquiera en un instante base t0 versus sus cambios en el instante t1. Los cambios pueden ser analizados en el pasado o futuro, entendiendo futuro como valores conocidos de la variable en un instante t1 > t0 y no como predicciones.
Otros índices de autocorrelación espacial
El coeficiente de Geary
El coeficiente de Geary surge gracias al interés de Robert Charles Geary en crear métodos estadísticos que permitieran evaluar la asociación espacial, en particular, desarrollando el concepto de razón de contigüidad c14 para evaluar patrones espaciales (véase Unwin 1996). En su estudio base, Geary (1930) realizó el análisis de mortalidad por tuberculosis en Saorstát Éireann15, profundizando en el condado de Wexford. Este análisis sentó las bases para el futuro desarrollo y formalización del coeficiente, además dejó en claro la necesidad de establecer una medida de asociación espacial que ayudara a comprender la distribución y comportamiento de los fenómenos geográficos.
Anselin (2019) y Unwin (1996) señalan que hasta 1954 Geary formalizó su coeficiente y lo definió como medida global de autocorrelación espacial. Unwin (1996, 145) destaca que “identificar y evaluar los patrones espaciales requiere encontrar formas de modelar las relaciones espaciales. Un primer paso es construir herramientas para medir la no aleatoriedad de los datos distribuidos espacialmente”. Los autores citados presentan una completa descripción del coeficiente y sus propiedades.
A diferencia del I de Moran, el c de Geary sí incluye el valor de la unidad central en el análisis de autocorrelación. Su dominio es [0, 2]: cuando 0 ≤ c ≤ 1, existe autocorrelación positiva; por el contrario, si 2 ≥ c > 1, indica autocorrelación negativa; finalmente, si c = 1, indica ausencia de autocorrelación, es decir, aleatoriedad en la distribución del fenómeno analizado. Por tanto, mientras los valores pequeños del dominio sugieren similitud o autocorrelación espacial positiva, los valores grandes sugieren variaciones o autocorrelación negativa. Resulta interesante equiparar el dominio de Geary al de Moran, para esto basta restar el valor de c de Geary a +1, como se indica en la Tabla 1.
El c de Geary se calcula a través de la Ecuación 4. Al igual que en la expresión del I de Moran, el primer término es un factor de normalización y el numerador del segundo término es el que establece las diferencias entre la unidad de análisis y sus vecinos y, por tanto, determina en mayor grado el valor del coeficiente. Una característica que se debe resaltar de este término es que no se compara con el valor medio global, sino con el valor medido de cada vecino. Lo anterior implica que cuanto mayor sea la diferencia entre la unidad de análisis central y sus vecinos, mayor será el numerador, coincidiendo, por tanto, con la descripción previa: valores grandes c de sugieren autocorrelación negativa (valores diferentes).
Prueba de conteo de uniones
Otro método para analizar el comportamiento global de un fenómeno geográfico a través de la autocorrelación espacial es la prueba de conteo de uniones (joins count test). Este método resulta útil cuando se requiere examinar el comportamiento de variables nominales y ordinales (véase Stevens 1946). Replicando el posible comportamiento dicotómico de algunas variables nominales (ej. Hombre / mujer), se podría llevar un conjunto de datos nominales estándar a comportamiento dicotómico estableciendo un valor central de comparación y determinando si los demás valores están por debajo o por encima de la referencia de comparación (ej. mayor/menor, cumple/no cumple), y luego, a partir de esta reclasificación, aplicar la prueba de conteo. Según indican O’Sullivan y Unwin (2010, 211), “este enfoque se basa en el recuento del número de ocurrencias de pares de polígonos vecinos en las diferentes categorías”. En el caso de variables dicotómicas, y si se aplica este concepto al esquema de la Figura 2, las unidades de análisis se pueden caracterizar como “blanco” y “gris”. En este escenario, los posibles pares de polígonos vecinos son: blanco-blanco, gris-gris, blanco-gris, gris-blanco. En escenarios en los que predominen las combinaciones blanco-blanco o gris-gris se tendrá autocorrelación positiva; por el contrario, en los escenarios donde las combinaciones blanco-gris-blanco prevalezcan, presentarán tendencia a la autocorrelación negativa. Las Figuras 2a y 2b representan los dos casos. Un escenario de aplicación de este método puede ser el uso y cobertura del suelo, en el que los polígonos que conforman el lattice de análisis pueden estar clasificados en categorías como pastos, arbustos, cultivos o bosque. Cada unidad central de análisis tendrá un número determinado de vecinos de las categorías presentadas que al contarlas determinan el comportamiento dominante; por tanto, este método se puede entender como un análisis basado en frecuencias. Las relaciones de vecindad también se determinan a partir de los conceptos presentados. Los detalles de este método son presentados en Dacey (1968), Cliff y Ord (1973), Unwin (1981) y de Smith, Goodchild y Longley (2018).
G de Getis-Ord
Finalmente, y aunque su uso como indicador global es poco común, se debe incluir en esta breve descripción de medidas globales de autocorrelación el Índice G de Getis y Ord (1992). Se describe como “poco común”, porque su uso es más extendido en análisis locales (
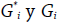), índices que se presentarán más adelante. A diferencia del I de Moran y el c de Geary, el Índice G ayuda a identificar el grado en el que las unidades de análisis con valores altos (hotspots) o bajos (coldspots) se agrupan, es decir, priorizan la conformación de clústeres. de Smith, Goodchild y Longley (2018) indican que la implementación del Índice G en el software ArcGIS (Getis-Ord General G) facilita el uso de bandas de distancia euclidiana fijas (umbrales de distancia), considerando W con ponderaciones binarias o estandarizadas, además de permitir el uso de la distancia Manhattan y otra variedad de modelos alternativos de vecindad, tales como distancia inversa, distancia inversa al cuadrado, las llamadas zonas de indiferencia (una combinación de distancia inversa y los umbrales de distancia) y matrices W ponderadas definidas por el usuario, sin excluir las matrices de contigüidad basadas en criterios Reina y Torre. Estas opciones, sin duda, fortalecen la identificación de clústeres desde diferentes puntos de vista y con la flexibilidad de la matriz W personalizada. Nótese cómo se implementan versiones de todas las opciones
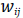listadas anteriormente (Getis 2007), aunque limitando el factor -α hasta 2. Las versiones recientes de GeoDa (Anselin, Syabri y Kho 2006) no implementan este índice. Como referencia, la Ecuación 5 muestra la expresión de cálculo del Índice G, en donde x corresponde a la medida de la variable en cada unidad de análisis. Nótese cómo en este caso la unidad central de análisis tampoco es considerada para el cálculo (i ≠ j).
Chen (2018, sección 2.1) indica que los índices de Getis-Ord son un complemento relevante de los índices de Moran y los coeficientes de Geary. Es importante resaltar el plural de esta afirmación, pues describe la naturaleza de familia de todos los índices, que incluyen las medidas globales y locales, así como de sus variaciones al incluir o excluir las medidas de la unidad central en el cálculo. El listado de Getis (2007) refleja esta diversidad. Descritas las medidas globales, ahora se presenta una descripción básica de los índices locales.
Índices de autocorrelación espacial local
Anselin (1995, 94) define los indicadores locales de asociación espacial (LISA) como estadísticos que satisfacen dos requerimientos: (i) para cada observación (unidad de análisis central), el LISA proporciona una medida del nivel de agrupamiento espacial significativo con relación a los valores que se localizan alrededor de esa observación (unidades vecinas); (ii) la suma de las medidas LISA de todas las observaciones es proporcional16 al indicador global de asociación espacial (autocorrelación espacial global), por lo que resultan útiles para medir la contribución de cada observación local al valor global. Como se mencionó, las medidas globales presentan limitaciones que no permiten identificar las especificidades del fenómeno analizado, por ejemplo, no evidencian la presencia de conglomerados zonales o locales en el marco geográfico, y es precisamente en este escenario donde los índices locales resultan de gran interés para el análisis espacial.
Aunque no es propósito de este editorial entrar en los detalles del análisis local, se requiere aclarar el concepto de análisis por asociación espacial. En la Figura 7 se hizo énfasis en la medida global y se explicaron las implicaciones de los diferentes resultados, aunque pasando por alto el hecho de que la figura está compuesta por cuadrantes. Estos son la base del análisis de asociación espacial, una versión más completa y detallada de los cuadrantes es la que se presenta en la Figura 10.
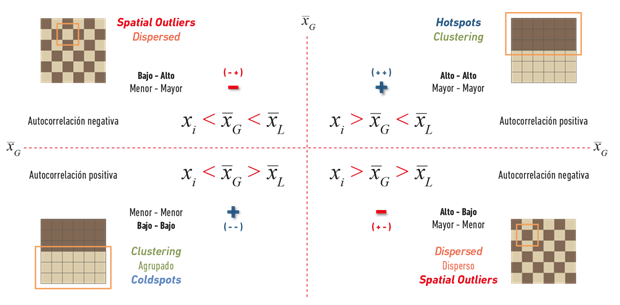
Fuente: basado en Siabato 2018b. Nota: los cuadrantes permiten identificar zonas de agrupamiento (hotspots y coldspots) y valores atípicos (spatial outliers).
Figura 10 Cuadrantes de asociación espacial. Base para el análisis de autocorrelación espacial local.
Como se puede observar en la Figura 10, los ejes están determinados por la media global (
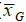), por tanto, en los cuadrantes se representan valores mayores (a derecha) y menores (a izquierda) que la media del conjunto de medidas (muestra) involucradas en el análisis. La abscisa representa las medidas xi de las unidades de análisis centrales, mientras que en la ordenada se localizan los promedios de las unidades vecinas (
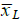). Si estos valores son MENORES a la media global (
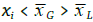), se clasificarán como menor-menor o BAJO-BAJO. Por el contrario, si son MAYORES a la media global (
), se clasificarán como mayor-mayor o ALTO-ALTO. Al combinar estas opciones en los demás cuadrantes (II y IV), resultan las opciones BAJO-ALTO y ALTO-BAJO respectivamente. Nótese la operación de la ley de signos indicada en la Figura 10, determinando positivo para los cuadrantes I y III y negativo para II y IV. Los cuadrantes y sus respectivas comparaciones son la base del análisis por asociación espacial, que permite identificar la presencia de agrupaciones (clustering) o valores atípicos (spatial outliers) en el fenómeno geográfico analizado. Las agrupaciones o clústeres pueden tener dos comportamientos: (i) la unidad central de análisis puede tener un valor por debajo de la media global y estar rodeada de vecinos que también están por debajo de la media, es decir, presenta un comportamiento BAJO-BAJO, en este escenario se configuran los llamados COLDSPOTS; (ii) en contraste, en el escenario ALTO-ALTO se determinan los HOTSPOTS. Los cuadrantes BAJO-ALTO y ALTO-BAJO determinan la presencia de valores atípicos, que espacialmente se traducen como unidades de análisis centrales que están rodeadas de valores vecinos opuestos a su valor, ya sea por encima (cuadrante II) o por debajo (cuadrante IV). Es claro que si, por ejemplo, una unidad productiva rural que genera 100 toneladas de sorgo al año está rodeada por otras unidades que producen una media de 500 toneladas en el mismo periodo, desde el punto de vista espacial este es un comportamiento atípico, no es normal que la producción de esta zona sea tan baja. En los términos presentados, este comportamiento sería clasificado como BAJO-ALTO. Esto siempre y cuando la media de producción de toda la zona analizada (
) sea por ejemplo 350 toneladas -o cualquier valor mayor a 100 toneladas-.
La Figura 11 representa la asociación espacial de las unidades de análisis mostradas en la Figura 5a asignando valores de lluvia mensuales a cada unidad -julio de 2008, datos tomados de las estaciones meteorológicas del Instituto de Hidrología, Meteorología y Estudios Ambientales; las áreas representan polígonos de Voronoi tomando como semillas las estaciones-. Se puede observar que los ejes de la gráfica no están determinados por
, sino localizados en 0, esto se debe a que los valores xi representados están normalizados considerando el valor medio
y la desviación estándar. Nótese cómo los puntos representados de los cuadrantes se corresponden con el número de unidades de análisis categorizadas17. Cada punto representa la medida estandarizada de la unidad de análisis (Zi) frente al promedio de sus respectivos vecinos; por tanto, el gráfico de asociación espacial siempre tendrá tantos puntos como unidades de análisis componga el marco geográfico (10 en el ejemplo mostrado). Las expresiones de normalización para la construcción de la gráfica de asociación espacial son las que se presentan en la Ecuación 6.
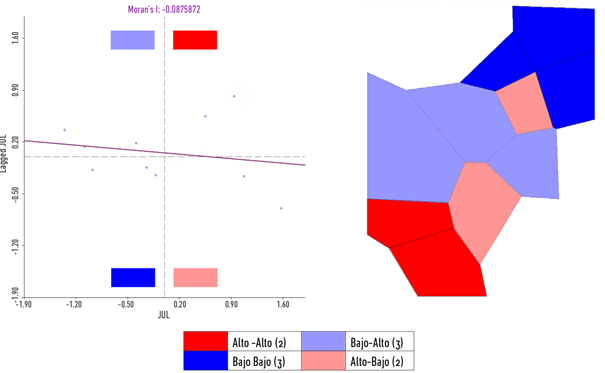
Nota: se puede observar cómo el número de unidades de análisis clasificadas en cada clase coincide con los puntos representados en los correspondientes cuadrantes. Los colores intensos representan los clústeres y los opacos las zonas atípicas (spatial outliers). (Cálculo en GeoDa)
Figura 11 Representación de los cuadrantes de asociación espacial.
Es fácil identificar cómo la Figura 11 revela la presencia de dos clústeres: un HOTSPOT (rojo intenso) y un COLDSPOT (azul intenso), sin excluir los comportamientos atípicos en la región central.
Como se ha insistido a lo largo de este editorial, el numerador de las expresiones matemáticas presentadas determina si el patrón es agrupado o disperso. O’Sullivan y Unwin (2010) y Siabato (2018b) señalan que un resultado positivo en la sumatoria implica que zonas con valores similares (altos o bajos) tienden a estar juntas. Por el contrario, un resultado negativo implicaría que valores altos están cerca de valores bajos o viceversa. En ocasiones, los resultados positivos y negativos están balanceados tendiendo a cero, lo que indica un patrón aleatorio.
Desde un punto de vista más formal, se debe resaltar nuevamente el hecho de que no basta con localizar la relación de la unidad central con sus vecinos en uno de los cuadrantes. Para definir el grado de autocorrelación del fenómeno analizado, se deben implementar pruebas de hipótesis18 (ej. CSR) con el fin de validar si la distribución espacial del fenómeno se produce aleatoriamente o no. Solo de esta forma se puede identificar, con un nivel de confianza determinado, si hay presencia de agrupaciones o zonas atípicas geográficas. Los programas informáticos para análisis espacial realizan pruebas estándar con grados de confianza del 90%, 95% y 99%. Si la hipótesis nula (H 0) de aleatoriedad espacial completa (CSR) se rechaza, entonces el fenómeno tiene una probabilidad del 90%, 95% o 99% de no haberse generado aleatoriamente. En otras palabras, es “poco” probable (0,1; 0,05 ó 0,01) que el fenómeno sea aleatorio y, por tanto, será agrupado o disperso. Considerando que la prueba de hipótesis CSR es bilateral o de dos colas, el fenómeno se clasificará como agrupado si está a la derecha (positivo); en caso contrario, el fenómeno geográfico analizado presentará un patrón disperso. Esto será verdad sólo en el nivel de confianza indicado. Nótese que el ejemplo presentado en la Figura 11 fue preparado para un nivel de confianza del 50%17. Este análisis aplica para escenarios locales y globales.
La Figura 11 representa, además, una interesante relación de los índices global y local de Moran, la pendiente (m) obtenida a partir de la regresión lineal simple que describe la recta (y = mx + b) derivada de la nube de puntos, corresponde al índice de autocorrelación global. Siendo, por tanto, los puntos la representación del índice local y la recta del global.
Breve descripción de los LISA
Los índices de autocorrelación espacial local más extendidos son: Ii de Moran, Gi* de Getis-Ord, Gi de Getis-Ord y ci de Geary. En esta sección se presentan detalles básicos y las principales diferencias entre estos índices.
El índice local de Moran (Ii de Moran) permite conocer la contribución de cada unidad de análisis a la variación global, es decir, permite medir cuánto aporta cada unidad a la autocorrelación global del marco geográfico analizado. Se debe recordar que el promedio16 de las medidas locales resulta en la medida global. Los análisis basados en el Ii de Moran son los más intuitivos y sencillos, pues su interpretación sigue sin variación los conceptos presentados sobre asociación espacial, por tanto, permiten identificar tanto clústeres positivos y negativos como valores atípicos. De los LISA presentados en esta sección es el único que permite la categorización completa y sin excepciones de las observaciones en todos los cuadrantes (véase Figura 11). La expresión que se computa para determinar las medidas individuales de cada unidad del lattice analizado es la mostrada en la Ecuación 7, nótese cómo los términos de la expresión se corresponden con los presentados en la Ecuación 6. Zi es la medida estandarizada de la unidad de análisis, mientras la sumatoria ponderada aplica las contribuciones locales de cada vecino a través de la matriz de pesos estandarizada. De los cuatro indicadores, el Ii de Moran es el más extendido.
Getis y Ord (1992) y Ord y Getis (1995) establecen que su índice mide el grado de asociación local de datos tipo punto o área ponderados. Los autores definen dos versiones: (i) una en la que, al igual que el c de Geary, se incorpora el valor de la unidad central en el análisis, este índice usa la notación Gi* de Getis-Ord; (ii) el índice Gi de Getis-Ord que no considera la unidad central. La propuesta de los autores se basa en la debilidad que muestra el Ii de Moran cuando se intentan identificar, con alto grado de confiablidad, clústeres positivos y negativos en muestras muy dispersas. Por ejemplo, al analizar datos que representan producciones agrícolas muy altas y muy bajas, y que además están muy distantes del valor medio de producción. Ord y Getis (1995) discuten esta debilidad. Por tanto, la característica principal de este índice es que permite identificar el grado en el que se agrupan los valores extremos del fenómeno analizado, señalando clústeres de medidas altas y bajas, centrándose en la identificación de coldspots y hotspots y excluyendo el análisis de valores atípicos. Las expresiones base para el cálculo de los indicadores de Getis-Ord son las que se describen en la Ecuación 8.
La versión local del c de Geary fue presentada por Anselin (1995) y mejorada en Anselin (2019). El coeficiente local de Geary (ci de Geary) está definido por las expresiones de la Ecuación 9. El primer término de la expresión b es, al igual que en las demás expresiones presentadas, un factor de normalización. Sin embargo, considerando la naturaleza del término (xi - xj ) y al no operar con la media, no se evidencian diferencias significativas si se trabaja o no con los valores originales (escala original) o con los estandarizados. Por tanto, no hay diferencia entre las expresiones presentadas, a menos que se consideren escenarios multivariados (véase Anselin 2019).
Al igual que los indicadores de Getis-Ord, el ci
de Geary se enfoca en la identificación de clústeres positivos y negativos. Aquellas zonas identificadas con el ci
de Geary, reconocidas como significativas y en las que ci es menor al valor medio
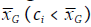, sugieren autocorrelación espacial positiva; se debe recordar que las pequeñas diferencias en el término (xi - xj
) implican similitud de la unidad central con sus vecinos19. Para las observaciones que cumplen con estos criterios y que además pueden ser clasificadas en los cuadrantes superior-derecho o inferior-izquierdo del diagrama de asociación espacial (véanse cuadrantes I y III de la Figura 10), es posible identificar, al igual que con el I de Moran, asociaciones alto-alto (hotspots) o bajo-bajo (coldspots). Sin embargo, dado que la sumatoria de las diferencias al cuadrado puede presentar comportamientos opuestos a los esperados, es decir, cruzar la media global (
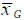) para valores bajo-bajo o ser menores en escenarios alto-alto, pueden existir observaciones para las que la clasificación por asociación no está totalmente definida, pues no es posible localizarlas unívocamente y en el cuadrante apropiado. En este caso, el análisis local de Geary implementado en GeoDa categoriza estas observaciones como Otros Positivos (Other Positive), indicando que pueden ser clúster, pero no es totalmente clara su naturaleza.
En contraste, cuando
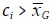la autocorrelación espacial será negativa. Anselin indica que en la autocorrelación espacial negativa (ci grandes implican disimilitud) no existe una clasificación unívoca, ya que el cuadrado de las diferencias elimina el signo de las diferencias entre la observación y sus vecinos y, por tanto, no es posible evaluar si la asociación espacial se presenta entre valores atípicos alto-bajo o bajo-alto. En principio, estos valores, que son categorizados en GeoDa como Negativos, podrían ser clasificados como spatial outliers en el análisis con Ii de Moran.
Como comentario final sobre los indicadores locales, se resalta la idea de Anselin en la que explica que
[…] los indicadores locales de Moran y Getis-Ord están fuertemente influenciados por el promedio ponderado de los vecinos, mientras que el local de Geary considera las diferencias al cuadrado. Por tanto, no hay una razón a priori por la cual los índices presentarían los mismos resultados (o similares). (Anselin 2019, 12)
La descripción completa de los indicadores locales y la comparación con sus homólogos globales puede ser consultada en Anselin (1995, 2019).
Conclusión
A manera de conclusión se puede decir que los diferentes estadígrafos locales utilizan distintos criterios para detectar las desviaciones de la unidad de análisis central con sus vecinos: (i) diferencias al cuadrado para el ci de Geary; producto cruz para el Ii de Moran; o (iii) la sumatoria en los indicadores y Gi* y Gi de Getis-Ord. El propósito principal de estas mediciones es explorar el comportamiento del fenómeno a través del espacio geográfico. Si se retoma la relación
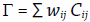presentada al inicio de este editorial y se acepta como la base para el cálculo de los indicadores de autocorrelación global y local, es posible afirmar que las mediciones enumeradas corresponden al componente general Cij que explica la variación temática del fenómeno analizado. Se ha visto cómo los diferentes Cij , tanto locales como globales, pueden ser calculados en función de los valores medios o comparando directamente las medidas de las unidades de análisis.
Gran parte de este documento se ha dedicado a explicar la naturaleza de la matriz W, que como elemento central del análisis espacial tiene la propiedad de conectar el Cij con el espacio geográfico de diversas formas -considerando diferentes criterios de vecindad y comportamientos binarios o estandarizados-, todas preparadas para resolver diferentes tipos de preguntas y para ser aplicadas al análisis de distintos fenómenos geográficos. Su versatilidad y flexibilidad es su mayor fortaleza. Se espera que, en este punto del editorial, la naturaleza de los componentes wij y Cij sea clara y los fundamentos de su aplicación en los procesos de análisis espacial prolijos.
El patrón espacial que describe la distribución de un fenómeno geográfico se define de acuerdo con la disposición espacial de las unidades de análisis y las relaciones geográficas establecidas entre ellas. Contar con medidas de autocorrelación para clasificar los comportamientos geográficos en patrones espaciales es un prerrequisito para comprender los procesos espaciales que subyacen en la distribución del fenómeno analizado. Los métodos para el cálculo de autocorrelación espacial proporcionan indicadores que permiten clasificar el fenómeno analizado en uno de los patrones espaciales (disperso, aleatorio o agrupado).
Debe ser claro que no es correcto usar de forma indistinta los términos correlación y autocorrelación espacial. El concepto de autocorrelación espacial difiere ampliamente de la noción de correlación espacial, por lo que no se deben confundir o intercambiar, cada uno de estos conceptos implica escenarios de análisis diferentes. En este editorial se han presentado los métodos estándar para el cálculo de la autocorrelación y su correspondencia con los patrones espaciales. Tampoco se deben confundir los análisis de autocorrelación bivariados o multivariados con la correlación, aunque ellos se trabajen considerando múltiples capas. La localización dispar de las unidades de análisis implicadas explica y demuestra la diferencia entre estos tres conceptos (véanse Figuras 1 y 9).
La autocorrelación espacial permite conocer el grado de asociación (influencia) que presenta un fenómeno geográfico entre las unidades de análisis definidas, considerando su vecindad y explicando el comportamiento y la distribución del fenómeno en el marco geográfico de análisis a través de los patrones espaciales. Existen diferentes estadígrafos espaciales que permiten medir el grado de autocorrelación espacial, los índices de Moran (I, Ii) NO son los únicos; sin embargo, sí son los más extendidos, tal vez debido a la interpretación directa de las asociaciones espaciales derivadas de su Cij (producto cruz) y la relación de las medidas locales y global a través de la pendiente de la recta derivada de los puntos localizados en los cuadrantes de asociación.
Aunque se ha presentado un texto amplio y descriptivo, no deja de ser introductorio y, en consecuencia, no se han descrito o tratado con rigurosidad varios temas. No se habló de los índices de autocorrelación multivariados ni se explicaron los índices diferenciales. No se presentaron las estandarizaciones basadas en Empirical Bayes ni las pruebas de significancia parametrizadas con el límite de Bonferroni o el FDR (False Discovery Rate). Tampoco se describieron las consecuencias de los comportamientos insesgados y sesgados, ni las relaciones directas de análisis con el semivariograma y el correlograma. No se presentaron los formalismos de las expresiones de cálculo, ni se detallaron las diferencias formales entre las comparaciones locales directas y las que están basadas en la media global; entre otros temas clave que permitirían una comprensión más avanzada del concepto y las medidas de autocorrelación espacial. No obstante, la discusión se acompaña con una rica lista de referencias base que amplían los conceptos presentados. Se recomienda al analista espacial que las examine poco a poco, y profundice en los conceptos a medida que avanza en su formación.
Finalmente, cabe complementar la frase de Getis y Ord (95, 287) indicando que a través de los años el interés por las de medidas de asociación espacial no solo permanece vigente, sino que ha crecido. Esto se debe a la potencia y eficiencia que los métodos descritos han demostrado para la búsqueda, identificación y análisis depatrones dispersos y agrupados. Por ejemplo, aplicados en la identificación de focosde enfermedades y el análisis de datos de maternidad (Stone 1988; Melo y de Freitas 2010), en análisis urbanos y territoriales (Cuzik y Edwards 1990; Cressie 1992; Longley y Tobón 2004; Lucero y Celemín 2008), análisis de patrones educativos (Kalogirou 2010) y económicos (Stankov y Dragićević 2015), desastres naturales (Ordóñez, Varela y Reyes 2011) o en la justa distribución de recursos naturales (Ramírez y Falcon 2015). La literatura que aplica las técnicas presentadas es amplia y prolífica.
Como colofón de este editorial, se puede afirmar que una vez aprendimos a medir el comportamiento y variación de los fenómenos geográficos a través de la autocorrelación espacial, se establecieron las bases para el surgimiento y desarrollo de la geografía cuantitativa.
