ARTÍCULO ORIGINAL

 

Método versus Cálculo en las críticas de Newton a Descartes y Leibniz*

 

Method versus Calculus in Newton's criticisms to Descartes and Leibniz

 

 

Por: Niccolò Guicciardini

Departamento de Filosofía y Ciencias Sociales

Universidad de Siena

Siena, Italia

niccolo.guicciardini@unibg.it

(Fecha de recepción: 13 de enero de 2009, Fecha de aprobación: 23 de febrero de 2009)

 

 

---

Resumen: En este artículo consideraré los puntos de vista de Newton sobre el método matemático. Newton nunca escribió en extenso sobre este tema, sin embargo, en sus escritos polémicos contra Descartes y Leibniz expresó la idea de que su método era superior a los propuestos por el francés y el alemán. Considerar estos escritos nos puede ayudar a comprender el papel que Newton le atribuyó al álgebra y al cálculo en su pensamiento matemático.

Palabras calves: Siglo XVII, Filosofía de las matemáticas, Newton, Descartes, Leibniz.

---

Abstract. In this paper I will consider Newton's views on mathematical method. Newton never wrote extensively about this issue. However, in his polemic writings addressed against Descartes and Leibniz he expressed the idea that his method was superior to the ones proposed by the French and the German. Considering these writings can help us in understanding the role attributed to algebra and calculus in Newton's mathematical thought.

Keywords. 17th Century, Philosophy of Mathematics, Newton, Descartes, Leibniz.

---

 

 

El memorándum de Newton sobre sus primeros descubrimientos.₁

Newton floreció como matemático en 1668–1666, en los llamados anni mirabilis, aproximadamente cuatro años después de haber llegado a Cambridge1. Un memorándum suyo, escrito más o menos cincuenta años después, hace un reporte que básicamente se ha confirmado por la evidencia de los manuscritos.

A principios del año 1665 descubrí el método de aproximación de series y la regla para reducir cualquier cantidad de cualquier binomio a tales series. En mayo del mismo año descubrí el método de las tangentes de Gregory y Slusius, y en noviembre tenía el método directo de fluxuiones; el año siguiente, en enero, tenía la teoría de los colores y en mayo siguiente me había adentrado al método inverso de las fluxiones. Y durante el mismo año empecé a pensar que la gravedad se extiende hasta la órbita de la luna (…) Todo esto fue durante los años de la peste de 1665–1666. Pues por esos años estaba en la principal época de mi creatividad, y pensaba en las matemáticas y en la Filosofía más que en cualquiera época después.²

Habría mucho que decir para descifrar y poner en contexto el discurso de Newton. Por ejemplo, la tarea de interpretar el significado del término "filosofía" requeriría espacio y erudición que no tengo a mi disposición.³

 

 

Figura 1. Hogar de Newton en Wollsthorpe donde —afirmó— hizo sus primeros descubrimientos en matemáticas y en filosofía natural cuando la Universidad de Cambridge fue evacuada debido a la peste de 1665–1666. De hecho, llevó a cabo un importante trabajo en matemáticas durante el periodo previo al regreso a la Universidad. Además, sus juveniles hallazgos —particularmente sobre la gravitación— habrían de desarrollarse en las décadas siguientes⁴.

Permítaseme resaltar tres cosas del anterior memorándum. El "método de series aproximadas" es el método de series de expansión a través de una prolongada división y extracción de raíz (así como otros métodos que posteriormente se fusionaron bajo técnicas más generales atribuidas a Puiseux) que le permitió a Newton ir más allá de lo que llamó "análisis común" —en el que se hacía uso de "ecuaciones finitas"— y que expresa ciertas curvas localmente en términos de potencia de series de infinitas fracciones, las cuales Newton llamó "ecuaciones infinitas". Esta "regla para reducir cualquier cantidad de cualquier binomio" es lo que llamamos el "teorema del binomio". Dichos métodos de series de expansión eran cruciales para lograr dos fines: 1. el cálculo de áreas de superficies curvilíneas y 2. la rectificación de las curvas (véase Figura 2). Nótese que Newton no habla de un teorema, sino de "métodos" y de una "regla". Este último hecho es de capital importancia y merece nuestro comentario en las Secciones 2, 3 y 4, antes de pasar en la sección 5 a los métodos directo e inverso de fluxiones que son el equivalente newtoniano al cálculo diferencial e integral leibniciano⁵.

 

Figura 2. El cálculo de las áreas de la hipérbole y las superficies circulares vía extracción de la raíz √ a + x = y Y √ a – x = y. Esta técnica de expansión de series e integración de términos similares fue básica en los primeros trabajos matemáticos de Newton y fue expuesta en un tratado que lleva por título Sobre el análisis por medio de ecuaciones infinitas (escrito en 1669, pero publicado en 1711), una extensión del "análisis común" que procede solo por medio de "ecuaciones finitas"⁶.

 

2. Pappus: sobre el método de análisis y síntesis

Newton perteneció a una comunidad matemática en la que la distinción entre teoremas y problemas se articulaba en conformidad con los criterios sancionados por la venerada tradición griega. Ello se ve de manera más notable en el trabajo del último compilador helenista, Pappus, que lleva por título Colección matemática, la cual apareció traducida al Latín en 1588. Newton —quien leyó de ávida manera esta polvorienta obra— pudo encontrar una distinción entre "análisis teoremático y problemático".

En el séptimo Libro de la Colección había una descripción de obras (la mayoría extraviada y no disponible para los primeros matemáticos modernos) que —según Pappus— tenían que ver con un método heurístico seguido por los antiguos geómetras. A menudo se cita el inicio del séptimo Libro; es un oscuro pasaje cuya decodificación era cumbre en las agendas de los primeros matemáticos europeos modernos que estaban convencidos de que ahí yacía oculta la clave del método de descubrimiento de los antiguos. Dada la importancia que este pasaje tuvo para Newton es digno de citarlo en extenso:

Aquello que se llama el Dominio del análisis, mi que querido Hermodoro, es en su totalidad un recurso que fue diseñado después de la composición de los Elementos comunes, para aquellos que quieren adquirir una destreza tal en geometría que puedan resolver los problemas que se les planteen, y solo es útil para esto. Fue escrito por tres hombres: Euclides el de los Elementos, Apolonio de Perga, y Aristeo el mayor; y su enfoque es por análisis y síntesis.

Ahora bien, el análisis es el camino desde lo que se busca, como si fuera establecido, por medio de consecuencias, a algo que se establece por síntesis. Es decir, en el análisis asumimos lo que se busca como si ya se hubiera logrado, y buscando aquello que se sigue de esto por sucesivos pasos regresivos hasta que llegamos a algo que ya se conocía, o que ocupa el rango de primer principio. A este tipo de método lo llamamos "análisis", es decir, anapalin lysis (reducción regresiva). En la síntesis, de manera inversa, asumimos como ya logrado aquello que se obtuvo en la parte final del análisis, y disponiéndolo en su orden natural, como precedentes los pasos anteriores ajustándolos entre sí, obtenemos el final de la construcción de lo que se buscaba.

Existen dos tipos de análisis: uno de ellos busca la verdad, y se llama "teoremático"; mientras que el otro trata de averiguar lo que se pide, y se llama "problemático". En el caso del teoremático, asumimos lo que se busca como hecho verdadero, y luego avanzando a través de sus consecuencias, entendidas como verdaderas según la hipótesis, a algo establecido, si lo que se establece es una verdad. En consecuencia lo que se buscaba también será verdadero, y su prueba es el reverso del análisis. Pero si se da que encontramos que algo establecido es falso, en consecuencia lo que buscábamos también es falso. En el caso del análisis problemático asumimos la proposición como algo que sabemos. Luego, procediendo a través de sus consecuencias, como verdaderas, a algo establecido, vemos que lo establecido es posible y susceptible de obtenerse, a lo cual los matemáticos le llaman lo "dado"; lo que se requiere será posible, y nuevamente la prueba será el reverso del análisis. Pero si se llega a dar que nos encontramos con algo que es imposible, en consecuencia el problema será también imposible⁷.

Pappus hace aquí una distinción entre análisis y síntesis. Aquél ("resolutio" en latín) a menudo se concebía como un método de descubrimiento o método para resolver problemas el cual, realizado en retroceso desde lo que se busca, concebido como si ya se hubiera logrado, llega eventualmente a lo conocido. La síntesis ("compositio" o "constructio") procede en sentido inverso: parte de lo que se sabe y, operando a través de las consecuencias, llega a lo que se busca. Con base en la autoridad de Pappus a menudo se sostenía que la síntesis "invierte" los pasos del análisis y provee la prueba rigurosa. De ahí provino la creencia —ampliamente difundida en Europa— según la cual los antiguos habían mantenido oculto el método del análisis y sólo habían publicado la rigurosa síntesis, bien fuera porque no consideraban el primero completamente demostrativo o porque querían ocultar el método de descubrimiento.

Otra distinción de capital importancia para los primeros matemáticos era la que había entre problemas y teoremas. Un problema demanda una construcción para su solución: parte de ciertos elementos considerados como ya construidos, bien sea por construcciones postuladas o previamente establecidas; dichos elementos son los "datos" (en latín "data") del problema. Un problema termina con "Q.E.I." o con "Q.E.F." ("quod erat inveniendum" - "lo que había que descubrir" -, y "quod erat faciendum" - "lo que había que hacer", respectivamente). Un teorema demanda una prueba deductiva, una secuencia de proposiciones cada una derivada de la anterior por reglas de inferencia aceptadas. El punto de partida de la cadena deductiva bien pueden ser axiomas o teoremas previamente demostrados. Un teorema termina con "Q.E.D." ("quod erat demonstrandum" - "lo que había que demostrar"). Según Pappus, por tanto, hay dos tipos de análisis: el primero referido a problemas, el segundo a teoremas, pero a partir de las fuentes clásicas resulta claro que el más importante, o por lo menos el más practicado, era el análisis problemático. En efecto, los primeros matemáticos de la moderna Europa estaban interesados principalmente en el análisis de los problemas geométricos.

Otra poderosa idea que empezó a circular en Europa a finales del siglo XVII era que el análisis de los griegos no era geométrico sino, antes bien, simbólico, es decir, se suponía que tuvieron una álgebra y la habían aplicado a la solución de los problemas geométricos. La evidencia de que el álgebra simbólica estaba al alcance de los antiguos estaba dada por algo muy lejano a una lectura filológica de la obra de Diofanto y partes de los Elementos de Euclides. El enfoque de la cultura del Renacimiento hacia los clásicos en escultura, arquitectura, música y filosofía estaba caracterizado por la admiración unida al deseo de restaurar las conquistas olvidadas de los antiguos. Este enfoque a menudo bordeaba la adoración; una convicción en la decadencia desde un pasado glorioso, dorado. Las obras de Euclides, Apolonio y Arquímedes eran consideradas como modelos insuperables por muchos matemáticos del Renacimiento. La pregunta que a menudo surgía era: ¿cómo pudieron haber logrado los griegos tal abundancia de resultados? En las décadas que le siguieron a la publicación de la Colección la creencia en la existencia de un "Tesoro del análisis" extraviado u oculto fue fuente de muchos esfuerzos tendientes a "restaurar" el método de descubrimiento de los antiguos. Como de costumbre, muchos promotores de la nueva álgebra simbólica estaban orgullosos de definirse a sí mismos como innovadores, antes que como restauradores. No obstante, era común, incluso en algebristas tales como François Viète, John Wallis e Isaac Newton, relacionar el álgebra simbólica con el análisis antiguo, esto es, con las técnicas ocultas de resolver problemas de los antiguos.

 

3. El método de Descartes para resolver y construir problemas

Newton estuvo profundamente arraigado en el espacio conceptual definido por Pappus y por sus lectores, intérpretes y críticos. Principalmente, sus puntos de vista sobre el método matemático los enfocó en la Géométrie (1637) de Descartes, una de las primeras fuentes de inspiración para Newton y pronto unos de los blancos de sus feroces críticas⁸. A partir de esta tradición Newton derivó la idea de que un problema, una vez analizado (resuelto), debería sintetizarse (compuesto o construido).

Pero, ¿cómo definió Descartes su canon para resolver problemas y el papel del álgebra en el análisis y síntesis de problemas geométricos? El historiador que más ha hecho para clarificar este tema es Henk Bos. Así pues, recurriremos a su trabajo⁹.

En el libro 1 de la Géométrie Descartes explicó cómo se podía traducir un problema geométrico a una ecuación. Allí pudo llevar a cabo tal cosa mediante un revolucionario distanciamiento de la tradición; de hecho, interpretó las operaciones algebraicas como operaciones cerradas sobre segmentos. Por ejemplo, si a y b representan longitudes de segmentos, el producto ab no es concebido por Descartes como si representara un área sino otra longitud. Como escribió: "debe observarse que por a², b³, y expresiones similares, entiendo comúnmente cualesquiera líneas simples", mientras que antes de la Géométrie tales expresiones representaban un área y un volumen respectivamente (Véase Figura 3).

La interpretación de las operaciones algebraicas por parte de Descartes fue, de hecho, una gigantesca innovación, pero la llevó a cabo en conformidad con el método de Pappus de análisis y síntesis, al que se refirió explícitamente. En efecto, según Descartes, se debe —siguiendo las prescripciones de Pappus— "empezar asumiendo que el problema fue resuelto y considerar una figura que incorpore la solución"¹⁰. En la figura, los segmentos dados son denotados por las letras a, b, c,…, y los desconocidos por las letras x, y, z. Las relaciones geométricas entre los segmentos se traducen luego a ecuaciones correspondientes y de esta manera se obtiene un sistema de ecuaciones que expresa simbólicamente la suposición de que el sistema está resuelto. De hecho, aquí estamos al comienzo mismo del proceso analítico: los segmentos desconocidos son tratados como si fueran conocidos y se manipulan en las ecuaciones a la par con los datos del problema. La resolución de la ecuación permite la expresión de lo x desconocido en términos de segmentos dados. De esta manera nos hemos movido desde la suposición de que el problema está resuelto (el primer paso del análisis) a la reducción de lo desconocido; se ha buscado la magnitud de los datos. Esta es la razón por la cual Descartes, y otros de los primeros promotores del álgebra, asociaron ésta con el método del análisis.

 

Figura 3. Interpretación geométrica de las operaciones geométricas de Descartes. Éste escribe: "Por ejemplo, tomemos que AB es una unidad, y supongamos que se pida multiplicar BD por BC. Solo se necesita unir los puntos A y C, y trazar DE paralela a CA. Luego, BE es el producto de BD y BC". Así, dado un segmento de unidad, el producto de dos segmentos se representa por otro segmento, no por una superficie. El segundo diagrama es la construcción de la raíz cuadrada de GH. Dados GH y un segmento de unidad FG, se traza el diámetro del círculo FG+GH y se erige GI, la raíz requerida¹¹.

 

No obstante, la resolución de la ecuación no es la solución del problema. De hecho, ésta debe ser la construcción geométrica de la magnitud buscada en términos de operaciones geométricas realizadas con base en los datos (¡Q.E.F.!). Ahora nos debemos mover desde el álgebra hacia la geometría de nuevo. Descartes entendió este proceso desde el álgebra a la geometría en los siguientes términos: las verdaderas raíces de la ecuación (para él si no hay raíces verdaderas entonces el problema no admite solución) deben construirse geométricamente. Después de Descartes este proceso fue conocido como la "construcción de la ecuación"; aquí es donde empieza la parte sintética y compositiva del proceso.

Descartes aceptó de la tradición la idea de que tales construcciones deben realizarse por intersección de curvas, es decir, las raíces verdaderas son representadas geométricamente por segmentos, los cuales han de construirse por intersección de cuervas. Efectivamente, la construcción de la ecuación le presentaba al geómetra otro nuevo problema, no siempre fácil: se tenían que elegir dos curvas, posicionarlas y escalarlas de tal manera que sus intersecciones determinaran puntos a partir de los cuales los segmentos —cuyas longitudes geométricamente representan las raíces de la ecuación— pudieran trazarse (Véase Figura 4).

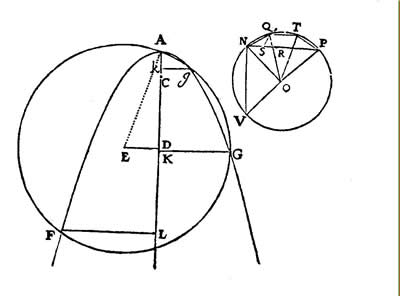
Figura 4. Construcción de una ecuación de tercer grado en la Géométrie de Descartes. El problema de trisectar el ángulo NOP se resuelve ("resolutio" es la traducción al latín de la palabra griega "analysis") con una ecuación de tercer grado. Descartes construye las raíces ("constructio" o "compositio" traducen "synthesis") por medio de la intersección del círculo y la parábola. Los segmentos kg, KG y LF representan dos raíces positivas y una negativa. La menor de las dos raíces positivas kg debe "tomarse como la longitud de la línea requerida NQ". KG es igual a NV, "la cuerda subtendida por un tercio del arco NVP"12.

 

La parte sintética del proceso de Descartes para resolver problemas hizo surgir dos preguntas: 1. ¿Cuáles curvas son admisibles en la construcción de las ecuaciones? 2. ¿Cuáles curvas, entre las admisibles, deben preferirse en términos de simplicidad? Al formularse estas preguntas Descartes continuaba un prolongado debate sobre el papel y la clasificación de las curvas en la solución de los problemas; tradición que nuevamente surge de Pappus y de las interpretaciones que de éste hicieron matemáticos como Viète, Ghetaldi, Kepler y Fermat. Su respuesta fue que sólo las "curvas geométricas" (nosotros diríamos "curvas algebraicas") son admisibles en la construcción de las raíces de las ecuaciones y que se deben elegir las curvas del menor grado posible por cuanto son las más simples. Descartes, en lugar de ello, excluyó las "curvas mecánicas" (nosotros diríamos curvas trascendentales) como herramientas legítimas de construcción.

Nótese que Descartes presentó su canon de resolución y construcción de problemas en términos agresivamente anticlasicistas; su método algebraico, sostenía, era superior a los seguidos por los antiguos. Descartes le confirió un lugar especial a un problema que se discute en la Colección matemática de Pappus que, según él, ni Euclides ni Apolonio fueron capaces de resolver. Orgullosamente les demostró a los lectores de su extensa Géométrie que mediante la aplicación del álgebra a la geometría fácilmente se podría obtener una solución que no estaba contenida en los extensos tomos de Pappus¹³.

 

4. Newton versus Descartes

Newton criticó de manera aguda el canon de Descartes del análisis y construcción de los problemas14. Su punto de vista era que las construcciones geométricas deben realizarse en términos independientes del álgebra. Sus críticas a Descartes las elaboró en sus Conferencias Lucasianas sobre álgebra que realizó antes de 1684 las cuales fueron publicadas –modificadas en cierta forma– en 1707 bajo el título de la Arithmetica Universalis. Esta obra termina con un apéndice dedicado a la "construcción de ecuaciones" en el cual abundan declaraciones muy citadas a favor de la geometría pura y en contra de los "modernos" (léase Descartes) que perdieron la "elegancia" de la geometría:

La geometría fue inventada a fin de evitar de manera expedita, mediante el trazo de líneas, lo tedioso del cálculo. Por tanto, estas dos ciencias [la geometría y el cálculo aritmético] no se deben confundir. Los antiguos los distinguieron tan diligentemente entre sí, hasta el punto de que nunca introdujeron términos aritméticos en la geometría. Y los modernos, al confundirlos, han perdido la simplicidad que constituye toda la elegancia de la geometría¹⁵.

Tales afirmaciones han puesto a cavilar a los comentaristas puesto que aparecen en un trabajo dedicado al álgebra y en el que la ventaja del análisis algebraico se despliega en una larga sección sobre la resolución de problemas geométricos. ¿Por qué Newton le estaba dando la espalda a la "aritmética"¹⁶ diciendo ahora que el álgebra y la geometría debían mantenerse separadas? Con el fin de comprender esta posición aparentemente paradójica tenemos que recordar por un momento que, según Descartes, la demarcación entre curvas admisibles e inadmisibles, como medios de construcción, era entre curvas geométricas y mecánicas. En último término, Descartes se vio forzado a recurrir a los criterios algebraicos de demarcación y simplicidad; de hecho, para él las curvas algebraicas coincidían con los lugares de las ecuaciones polinómicas, y el grado de la ecuación le permitía clasificar las curvas en términos de su simplicidad.

En cuanto a lo que tiene que ver con la demarcación, en la Arithmetica Universalis Newton sostuvo que sería erróneo pensar que una curva se puede aceptar o rechazar en términos de la ecuación que la define. Él escribió:

La descripción es lo que hace que la curva sea geométrica, no la ecuación. El círculo es una línea geométrica, no porque se puede expresar mediante una ecuación, sino porque su descripción es un postulado¹⁷.

Además, la clasificación por parte de Descartes de las curvas en función del grado de la ecuación, sostenía Newton, no es relevante para el geómetra, quien escogerá las curvas en función de la simplicidad de su descripción. Newton, por ejemplo, señaló que la ecuación de la parábola es más simple que la del círculo. No obstante, éste es el más simple y debe preferirse en la construcción de los problemas.

Lo que fundamentalmente indica que la línea debe admitirse en la construcción de los problemas no es la simplicidad de la ecuación, sino la facilidad de su descripción. (…) De hecho, la representación algebraica no tiene nada que ver con la en la simplicidad de la construcción. Lo único que aquí se reconoce es la mera descripción de las curvas¹⁸.

Newton señaló que, desde su punto de vista, una conchoide, una curva de cuarto grado, es bastante simple. Independiente de consideraciones sobre su ecuación, su descripción mecánica —afirmó— es una de las más simples y elegantes; sólo el círculo es más simple. El criterio algebraico de Descartes sobre la simplicidad es, de esta manera, considerado ajeno al estado constructivo, sintético, de la solución del problema. La debilidad de la posición de Newton es que los conceptos de simplicidad del trazado o de elegancia, a la que continuamente se refiere, son cualitativos y subjetivos. Se debe tener en cuenta que no hay ninguna razón de peso en las evaluaciones de Newton sobre la simplicidad de las construcciones que prefiere; sus criterios son ampliamente estéticos. Pese a ello, considerar esos criterios es crucial para nuestra comprensión de los puntos de vista de Newton sobre el método matemático.

En realidad, Newton —maestro de manipulaciones algebraicas— desarrolló a mediados de la década de 1670 un profundo disgusto por el simbolismo y se distanció de los matemáticos "modernos". En estos términos, pues, escribió:

A los geómetras modernos les gusta mucho la especulación de las ecuaciones. La simplicidad de éstas pertenece al ámbito de la consideración analítica. [En el apéndice a la Arithmetica Universalis] Tratamos la composición, y a la composición no se le dictan las leyes desde el análisis. El análisis, en efecto, lleva a la composición, pero no es una verdadera composición antes de ser liberada del análisis. Si llega a darse el caso de que haya algo de análisis en la composición, tal composición aún no será real. La composición es en sí misma perfecta y dista mucho de ser una mezcla de especulaciones analíticas¹⁹.

Esta posición, déjeseme reafirmarlo, no excluye el uso del álgebra en el análisis. No obstante, sí excluye de la síntesis los criterios algebraicos de demarcación y simplicidad. Como Newton habría de afirmar, en un manuscrito que data de comienzos de la década de 1690,

si se resuelve un problema (…) esto es así por el descubrimiento de la ecuación y la composición por su construcción, pero no se resuelve antes de que la enunciación de la construcción y su demostración completa sea, liberada por completo de la ecuación, compuesta²⁰.

Pero, alrededor de 1680, Newton dio un paso adelante en su oposición al método propuesto en la Géométrie; no solo la síntesis cartesiana, sino también el análisis, cayeron bajo un feroz ataque. Por esa época Newton desarrolló una profunda admiración por los antiguos matemáticos griegos, mientras criticaba en términos amargos el análisis simbólico llevado a cabo por los modernos. Asimismo, comenzó a dudar de que el análisis de los griegos fuera algebraico; más bien sospechó que Euclides y Apolonio poseyeron un análisis geométrico más poderoso desplegado en los tres libros de los Porismos atribuidos a Euclides y descritos en el Libro 7 de la Colección matemática. Así pues, no solo la composición (la síntesis) tenía que liberarse del álgebra, sino que también el cálculo algebraico tenía que evitarse por igual en el proceso de resolución (el análisis). Su blanco a menudo era Descartes; por ejemplo, a finales de la década de 1670, comentando la solución de éste al problema de Pappus, escribió vehementemente:

Con seguridad, su método [el de los Antiguos] es mucho más elegante que el cartesiano. Pues él [Descartes] obtuvo el resultado mediante un cálculo algebraico el cual, traducido a palabras (siguiendo la práctica de los antiguos en sus escritos), llegaría a ser tan tedioso y complicado que provocaría náuseas y tampoco se podría entender. Empero, ellos lo lograron mediante ciertas proposiciones simples, juzgando que nada escrito de manera diferente era digno de leerse, y en consecuencia ocultaron el análisis por el cual descubrieron sus construcciones²¹.

Newton no estaba sólo en su batalla contra los algebristas (afirmaciones similares se pueden encontrar en el trabajo de Thomas Hobbes). Pero, probablemente la influencia más profunda sobre Newton en este asunto fue ejercida por su mentor Isaac Barrow. La búsqueda de Newton del análisis no algebraico, de porismos, lo llevó a desarrollar un interés por la geometría proyectiva (Véase Figura 5).

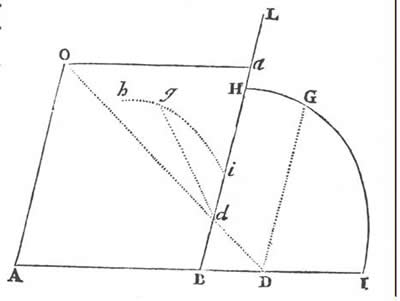
Figura 5. Newton estuvo interesado en usar transformaciones proyectivas como una herramienta heurística. Aquí se reproduce el diagrama para el Lema 22, Libro 1, de los Principia. En este Lema se nos enseña cómo "transformar unas figuras a otras de la misma clase" (a saber, curvas algebraicas del mismo grado). La figura que debe transformarse es la curva HGI. Se trazan las líneas paralelas AO y BL cortando cualquier tercera línea AB en A y B. Luego, a partir del punto O en la línea AO se traza la línea recta OD. Desde el punto d se levanta la ordenada dg (se puede elegir cualquier ángulo entre la "nueva ordenada" dg y la "nueva abscisa" ad). La nueva ordenada y la abscisa tienen que satisfacer las siguientes condiciones: AD = (AO × AB)/ad y DG = (AO × dg)/ad. Estas transformaciones son exactamente las que ocurren entre las figuras proyectadas de un plano a otro. Supongamos ahora que el punto G "se desplace a través de todos los puntos en la primera figura [HGI] con movimiento continuo; luego el punto g —también con movimiento continuo— se desplazará por todos los puntos en la nueva figura [hgi]"22.

 

Newton llegó a convencerse de que los antiguos habían usado propiedades proyectivas de las secciones cónicas a fin de lograr sus resultados: moviéndose conforme a estos lineamientos clasificó las cúbicas en cinco clases proyectivas²³.

 

5. El nuevo análisis de Newton

Ahora que sabemos más sobre los puntos de vista de Newton sobre el papel del simbolismo algebraico en el método para resolver problemas, estamos en posición de volver al memorándum sobre sus primeros descubrimientos matemáticos que he citado en la sección 1. Allí, Newton menciona los métodos directo e inverso de fluxiones. Aquél permitía la determinación de tangentes (y curvatura) para curvas planas. Newton enfocó este problema concibiendo las curvas como si fueran generadas por el continuo "flujo" de un punto; llamó "fluentes" las magnitudes geométricas generadas por movimiento, mientras que las "fluxiones" son los porcentajes instantáneos del flujo. En la década de 1690 denotó las fluxiones por medio de puntos sobre las letras de tal manera que la fluxión de x es x. Newton desarrolló una serie de estrategias a fin de determinar las tangentes. Algunas de ellas son algorítmicas, pero en muchos casos hizo uso del recurso a métodos cinemáticos. En los escritos matemáticos de Newton el algoritmo, en efecto, está profundamente ligado a especulaciones geométricas.

Al resolver el movimiento en componentes rectilíneos, Newton pudo determinar la tangente mediante la composición de los movimientos, incluso en el caso de las curvas mecánicas (Véase Figura 6). En efecto, la posibilidad de tratar con curvas trascendentales (como la espiral y la cicloide) estaba en la cúspide de la agenda de Newton; o se podía centrar la atención en el "momento del arco" generado en cada pequeño intervalo de tiempo (Newton llamó "momento" el incremento infinitesimal adquirido en un momento infinitesimal de tiempo) y establecer una proporción entre el momento de la abscisa y el momento de la ordenada y otras líneas finitas implicadas en la figura. Cuando la curva se expresaba simbólicamente mediante una ecuación, Newton tenía "reglas" que le permitían calcular la tangente (Véase Figura 7). Aquí se reconocen reglas que son "equivalentes" a las del cálculo diferencial, pero el lector debe recordar que esta equivalencia era, y aún es, objeto de debate.

El método inverso de fluxiones era la obra maestra de Newton. Por medio de este método pudo abordar el problema de "cuadrar curvas". Al concebir una superficie t como generada por el flujo de la ordenada y que se desliza en ángulo recto sobre la abscisa z, comprendió que el porcentaje de flujo de la superficie del área es igual a la ordenada (declaró ^•t/ ^•z= y/1). De esta manera nació en la mente de Newton la idea de integración como anti–diferenciación. Su enfoque consistió en aplicar el método directo a "ecuaciones que definirán la relación de t a z". Así se obtiene una ecuación para ^•t y ^•z, y así "dos ecuaciones tendrán, la última que definirá la curva, y la primera el área"²⁴. Siguiendo esta estrategia, Newton construyó un "catálogo de curvas" que pueden cuadrarse mediante "ecuaciones finitas" (Véase Figura 8). En términos leibnicianos, construyó las primeras tablas integrales en la historia de las matemáticas.

Newton le dio mucha importancia al método inverso. Con una comprensión matemática casi visionaria de lo que en verdad es revolucionario, aún estando joven, escribió:

Si dos cuerpos A & B describen por sus velocidades p & q las líneas x & y se da una ecuación que expresa la relación entre una de las líneas x, y la razón q/p de sus movimientos q & p; encontrar la otra línea y. Si esto se puede hacer, todos los problemas se podrían resolver.²⁵

 

Figura 6. Primer trabajo de Newton (noviembre de 1666) sobre las tangentes a "líneas mecánicas" (i.e. curvas trascendentales planas). Su técnica consistía en concebir las curvas como generadas por movimiento y en resolver el movimiento en componentes²⁶.

 

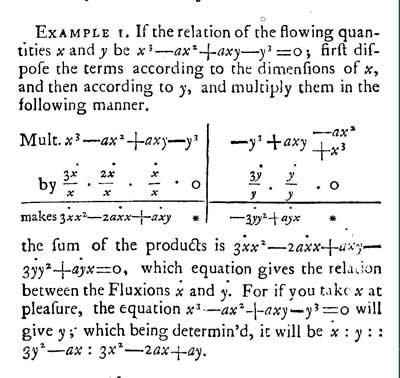
Figura 7. Algoritmo de Newton para dirigir el método de fluxiones. En este ejemplo calcula la relación entre las fluxiones (velocidades instantáneas) x y y de cantidades fluentes (magnitudes que cambian continuamente en el tiempo) x y y relacionadas por la ecuación x³ − ax² + axy − y³ = 0.²⁷

En este contexto Newton desarrolló técnicas equivalentes a la integración por partes y a la substitución.

Newton llamó "método de series y fluxiones" a las técnicas de expansión de series, determinación de tangentes y cuadraturas de curvas. Este método era, como orgullosamente afirmó, un "nuevo análisis" que se extendía a los temas que Descartes había abolido de su "análisis común" —tales como las curvas mecánicas— gracias al uso de series infinitas.

Y todo lo que el análisis común lleva a cabo por medio de ecuaciones constituidas por un número finito de términos (cuando puede ser posible), este método puede llevarse a cabo siempre mediante ecuaciones infinitas. En consecuencia, nunca he vacilado en darle también el nombre de análisis²⁸.

Según Newton, los "límites del análisis se amplían mediante […] ecuaciones infinitas: […] mediante su ayuda el análisis cubre todos los problemas"²⁹.

Figura 8. El comienzo de la tabla de curvas de Newton (tabla integral, en términos leibnicianos), obtenida gracias la comprensión de lo que llamamos el "teorema fundamental del cálculo". Aquí Newton hace una lista de los primeros cuatro "órdenes"; z es la abscisa, y la ordenada, t el área. En notación de Newton ˙t / ˙z = y/1. Nótese que d, e, f, g, h son constantes (¡d es una constante!) η es un entero o fraccionario, R significa √ e + fzⁿ o √e + fzⁿ+ gh2n.³⁰

 

6. El método sintético de Newton 6.

Se debería recordar que el "nuevo análisis" ocupaba un lugar en la agenda de Newton que, conforme al canon pappusiano, era subsidiario de la síntesis o construcción, y que ésta debería llevarse a cabo en términos independientes a los criterios algebraicos. Por ejemplo, en cuanto a la cuadratura de las curvas (en términos lebnicianos, integración) escribió:

Después de que de esta manera se haya encontrado alguna curva, se deben hacer consideraciones cuidadosas sobre realizar una demostración de la construcción que, hasta donde sea permisible, no tenga ningún cálculo algebraico, de tal forma que el teorema así embellecido sea digno de ser publicado³¹.

Newton, por tanto, dedicó grandes esfuerzos a suministrar demostraciones geométricas, algo reminiscentes de las técnicas arquimideas de exhaución, de sus cuadraturas "analíticas"; sólo tales demostraciones consideradas por él "dignas de ser publicadas".

En este contexto, Newton empezó a volver a trabajar en la década de 1670 sus primeros descubrimientos en el "nuevo análisis" en términos que consideró concordantes con los métodos constructivos geométricos de los antiguos. A este enfoque más riguroso lo llamó el "método sintético de fluxiones" y lo codificó alrededor de 1680 en un tratado intitulado Geometría curvilínea³². En este método no aparecen infinitesimales o "momentos" y tampoco se hace uso de símbolos algebraicos; todo estaba basado en procedimientos geométricos límites que Newton llamó "método de las primeras razones de las cantidades nacientes y las últimas razones de las cantidades evanescentes". Este método fue ampliamente usado en los Principia (1687) (véase Figura 9). Es un poco asombroso ver a uno de los algebristas más creativos de la historia de las matemáticas dedicarle tanto tiempo y esfuerzo a la reformulación de sus resultados analíticos en términos geométricos, pero Newton tenía argumentos persuasivos para hacerlo.

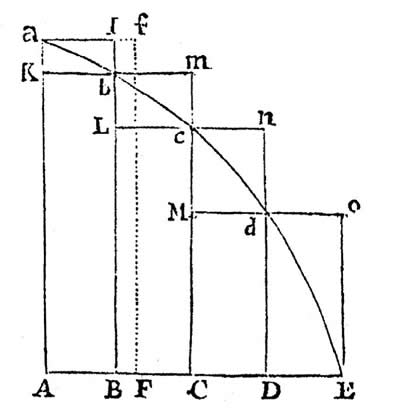
Figura 9. En la sección 1, Libro 1 de los Principia, Newton establece su "método de las primeras y últimas razones", un procedimiento geométrico límite que le permite evitar infinitesimales. En el Lema 2 Newton muestra que un área curvilínea AabcdE puede aproximarse como límite de las áreas rectilíneas inscrita AKbLcMdD o circunscrita AalbmcndoE. Cada superficie rectilínea se compone de un número infinito de rectángulos con bases iguales AB, BC, CD, etc. La prueba es magistral en su simplicidad. Su estructura aún se preserva en los libros de texto de cálculo en la definición de la integral de Riemann. Consiste en demostrar que la diferencia entre las áreas de figuras circunscritas e inscritas tiende a cero, en cuanto el número de rectángulos "se incrementa in infinitum". De hecho, esta diferencia es igual al área del rectángulo ABla la cual "debido a que su ancho AB disminuye in infinitum, deviene menos que cualquier rectángulo dado". En términos de Newton, AB es una "cantidad evanescente"³³

.

En primer lugar, en su programa de reforma a la filosofía, Newton les atribuyó un papel importante a las matemáticas como fuente de certeza. A partir de principios de la década de 1670 expresó su disgusto por el carácter probabilista e hipotético típico de la filosofía natural34 practicada en la Royal Society por gente como Robert Hooke y Robert Boyle. Su fórmula fue inyectarle matemáticas a la filosofía natural. Como afirmó:

Mediante la ayuda de filósofos geométricos y geómetras filosóficos, en lugar de conjeturas y probabilidades pregonadas por todas partes, finalmente llegaremos a tener una ciencia de la naturaleza apoyada en la más elevada evidencia³⁵.

Pero si las matemáticas habían de suministrarle evidencia a la filosofía natural, sus métodos debían estar por encima de toda disputa, y Newton era profundamente consciente, de hecho, de que el nuevo análisis estaba lejos de ser riguroso.

En segundo lugar, Newton rápidamente desarrolló un profundo anti–cartesianismo asociado a la convicción de la superioridad de los antiguos sobre los modernos. Desde su punto de vista, Descartes era el paladín de una filosofía mecánica impía que, al concebir la naturaleza como un mecanismo autónomo, negaba cualquier papel de la providencia de Dios. Newton se consideró a sí mismo como un restaurador de una filosofía antigua, olvidada, según la cual la naturaleza siempre está abierta a la intervención providencial de Dios. En efecto, pensaba que, según la teoría de la gravitación —de la cual estaba convencido que los antiguos la poseyeron—, la cantidad de movimiento en el universo estaba confinada a declinar si la intervención divina no hubiera impedido la "corrupción de los cielos". Los filósofos modernos eran peligrosos desde un punto de vista teológico y tenían que ser combatidos en todos los terrenos. Por tanto, en las matemáticas Newton también miró con admiración los antiguos modelos y se concibió a sí mismo como un restaurador de su gloria; esto no quiere decir que las anteriores razones condujeran a Newton a una condición de tensión ya que sus valores filosóficos reñían con su práctica matemática que era innovadora, simbólica y —pese a Newton— profundamente cartesiana.

Varios aspectos aún no explicados del trabajo matemático de Newton están relacionados con su condición de estrés y tensión que caracterizan sus pensamientos sobre el método matemático. ¿Por qué Newton no imprimió su método de series y fluxiones antes del surgimiento de la disputa por la prioridad con Leibniz? ¿Por qué dejó oculta su competencia en cuadraturas cuando escribió los Principia, los cuales están escritos en su mayor parte en estilo geométrico? Aunque no hay una única respuesta a estas desconcertantes preguntas, creo que la convicción de Newton de que el método analítico sintético sólo es una herramienta heurística, no "digna de ser publicada", puede explicar en parte una política de publicación que iba a tener consecuencias de capital importancia en la polémica con Leibniz.

 

7. Los puntos de vista de Leibniz

Cuando explotó la guerra contra Leibniz en 1710 Newton habría de confrontar a un oponente que no sólo llegó a resultados equivalentes a los suyos, sino que promovía un punto de vista diferente sobre las matemáticas³⁶.

La retórica sobre la novedad del cálculo domina los escritos de Leibniz. La referencia a los matemáticos antiguos por lo general tomó una forma bastante manida de tributo al "método de exhaución" de Arquímedes. En la mayoría de sus declaraciones sobre el cálculo Leibniz deseaba resaltar la novedad y carácter revolucionario de su algoritmo más que la continuidad con los antiguos modelos; este enfoque riñe bastante con el "clasicismo" de Newton. Además, Leibniz a menudo se refería al carácter heurístico del cálculo entendido como un algoritmo independiente de la interpretación geométrica. Esta independencia, exactamente, haría tan eficaz al cálculo en el proceso de descubrimiento. El cálculo, según Leibniz, debería verse también como una ars inveniendi (un arte de descubrimiento); como tal, debería ser valorado por su carácter provechoso en vez de por su contenido referencial. Podemos hacer cálculos, según Leibniz, con símbolos desprovistos de contenido referencial (por ejemplo con √ −1), con tal que el cálculo esté estructurado de tal forma que lleve a resultados correctos³⁷.

Escribiéndole a Christiaan Huygens en septiembre de 1691, Leibniz afirmó orgullosamente:

Señor, es cierto, como correctamente cree, que lo mejor y más útil de mi nuevo cálculo es que trata con verdades por medio de una especie de análisis, y sin esfuerzo alguno de la imaginación, que a veces trabaja como por azar³⁸.

 

De esta manera Leibniz estaba elogiando el cálculo como cogitatio caeca y promovía el "razonamiento ciego" entre sus discípulos. Nadie, según Leibniz, podía seguir un razonamiento largo sin liberar la mente del "esfuerzo de la imaginación"³⁹.

Leibniz se concebía a sí mismo como promotor de nuevos métodos de razonamiento, antes que como "sólo" matemático. El cálculo sólo era un ejemplo exitoso de la potencia del pensamiento algorítmico. El diplomático alemán estaba interesado en promover en Europa la formación de un grupo de intelectuales que pudieran extender un conocimiento universal logrado gracias a un nuevo algoritmo que llamó característica universal. Así ayudaba a formar una escuela de matemáticos que se distinguían por su capacidad para manipular los diferenciales y las integrales, y por su innovadora estrategia de publicación. Gracias a la recomendación de Leibniz, ellos colonizaron plazas de matemáticas en toda Europa. Se afirmaba que la eficacia de este nuevo algoritmo era independiente de cuestiones metafísicas o cosmológicas; las personas que lo practicaban tenían que ser matemáticos profesionales, antes que "filósofos geométricos", capaces de enseñar y propagar el conocimiento del cálculo.

En el contexto de la desconcertante cuestión de la existencia de los infinitesimales emerge una actitud leibniciana típica. El nuevo cálculo a menudo se atacaba ya que —se sostenía— empleaba símbolos desprovistos de significado, tales como los diferenciales organizados en una desconcertante jerarquía de órdenes. Como sabemos, Newton era particularmente sensible a estas críticas, y en su método sintético trató de prescindir de cantidades infinitamente pequeñas. Leibniz, de otra parte, repitió muchas veces que para él la cuestión de la existencia de los infinitesimales tenía que distinguirse de su utilidad en tanto recursos algorítmicos. Mientras se inclinaba, por razones filosóficas, a la negación de la existencia de los infinitesimales, también quería enfatizar que esta cuestión ontológica era algo externo a las matemáticas. Una afirmación típica, escrita a principios del siglo XVII, es la siguiente:

Tenemos que hacer un esfuerzo para preservar las matemáticas puras castas de controversias metafísicas. Esto se logrará si usamos cantidades infinitas e infinitamente pequeñas como expresión apropiada para abreviar los razonamientos, sin preocuparnos de si cantidades infinitas e infinitamente pequeñas, los números y las líneas son reales.⁴⁰

De esta forma Leibniz dejaba a sus discípulos la elección de sostener, hablando filosóficamente, enfoques diferentes sobre la cuestión ontológica de la existencia de los infinitesimales; lo que quería defender era su utilidad en cuanto símbolos en los cálculos matemáticos.

 

8. La guerra contra Leibniz: aspectos metodológicos

Cuando se tuvo que enfrentar con Leibniz en la polémica sobre la prioridad, Newton estaba interesado en construir un documento forense e histórico cuyo propósito era demostrar el plagio por parte de Leibniz. Pero no sólo hizo eso, también quería resaltar la superioridad de su método sobre el cálculo de Leibniz. El programa matemático que Leibniz estaba promoviendo sin mucho éxito reñía con los profundos valores que Newton sentía.

 

 

Figura 10. Retrato de Newton a edad madura⁴¹. Orgullosamente abre los Principia en una página dedicada a la atracción de los cuerpos extensos. Al tratar este problema Newton hizo uso de su "método inverso de fluxiones" (el equivalente al cálculo integral de Leibniz) que le permitió "cuadrar curvas". De hecho, sólo recurriendo a sus tablas de curvas ("tablas integrales"), Véase figura 8, Newton pudo resolver varios problemas en los Principia. Sin embargo, dicho métodos analíticos no eran explícitos al lector. En la polémica con los lebnicianos —quienes sostenían que la ausencia del cálculo en los Principia era una prueba positiva del desconocimiento de Newton de las técnicas de cuadratura antes de 1687— Newton se vio forzado a sostener, con cierta exageración, que "Mediante la ayuda del nuevo análisis el Sr. Newton descubrió la mayoría de las proposiciones en sus Principia Philosophiae. Pero debido a que los antiguos para establecer certezas no admitían nada en geometría antes de que se demostrara sintéticamente, demostró las proposiciones sintéticamente de tal forma que el sistema de los cielos podría estar fundado en buena geometría. Y esto hace ahora difícil, para que quienes no son diestros, ver el análisis mediante el cual se descubrieron esas proposiciones"⁴². Sobre el tema del uso por parte de Newton de técnicas analíticas en los Principia⁴³.

Por supuesto, en esta historia no solo hay matemáticas; había que oponerse a Leibniz por una serie de razones que tenían que ver con la sucesión de la casa de Hannover. De hecho, el alemán, que era empleado de la familia Hannover quería mudarse a Londres como historiador Real. La idea de tener en Inglaterra a una eminencia intelectual que defendía un punto de vista que contradecía la teología voluntarista de Newton y que promovía la unificación de las Iglesias cristianas era una anatema para Newton y sus defensores.

Para nuestros propósitos es interesante fijarnos en unos pasajes que Newton escribió en 1715 los cuales están contenidos en un "Informe" anónimo de una colección de cartas, el Commercium epistolicum, que había producido la Royal Society con el fin de demostrar el plagio por parte de Leibniz.

En el "Informe", hablando de sí en tercera persona, Newton hizo patente que Leibniz sólo había logrado la parte analítica, heurística, del método de solución de problemas. Escribió:

El método del Sr. Newton también es de mayor utilidad y certeza, pues se adaptabien sea a una proposición ya descubierta mediante tales aproximaciones para no crear error en la conclusión, o para demostrarla con exactitud. El del Sr. Leibniz es solo para descubrirla⁴⁴.

Así que, de acuerdo con Newton, Leibniz sólo obtuvo la primera fase del método pappusiano y no había logrado la demostración rigurosa, constructiva; esto, como sabemos, tenía que llevarse a cabo en términos puramente geométricos.

Además, Newton insistió en que el énfasis con que Leibniz elogiaba la fuerza de su simbolismo era excesivo. En realidad, el algoritmo es importante para Newton, pero tenía que verse sólo como un componente del método:

El Sr. Newton —escribió— no presenta el método en forma de símbolos, ni se restringe a una forma particular de símbolos⁴⁵.

Por último, Newton señaló que en su método de primeras y últimas razones no aparecen infinitesimales puesto que todo se lleva a cabo por medio de procedimientos límite. Desde el punto de vista de Newton el evitar los infinitesimales y la posibilidad de interpretar los símbolos algebraicos como magnitudes geométricas tenía la doble ventaja de hacer que su método resulte con contenido referencial y consonante con las matemáticas antiguas:

No tenemos ideas de cantidades infinitamente pequeñas y por tanto el Sr. Newton introdujo las fluxiones en su método de tal forma que pudiera proceder por medio de cantidades finitas tanto como fuera posible. Es más natural y geométrico porque se funda en primae quantitatum nascentium rationes [primeras razones de cantidades nacientes] las cuales tienen un referente en la geometría, mientras que los indivisibles en que se funda el método diferencial no tiene referente en la geometría o en la naturaleza (…) La naturaleza genera cantidades por el flujo continuo, o incremento, y los antiguos geómetras admitieron esa generación de áreas y sólidos (…). Pero la suma de indivisibles para componer un área o un sólido nunca fue admitida en la geometría⁴⁶.

La naturaleza y la geometría son dos conceptos claves; ellos le permiten a Newton defender su método debido a su continuidad con la tradición antigua así como a su contenido ontológico.

En sus escritos polémicos contra Leibniz, Newton estructuró un ataque que estaba dirigido a demostrar el plagio del alemán. Una de las prioridades de Newton era reunir evidencia que probara la culpa de Leibniz, y eso lo hizo con medios que muestran su capacidad de emplear fuentes archivísticas así como prejuicios y egotismo. No obstante, Newton defendió también posiciones sobre el método matemático que tenían profundas raíces en la prolongada oposición a Descartes y a los "matemáticos modernos" que, al confundir álgebra y geometría, "habían perdido toda la elegancia en que consiste la geometría".

 

 

---

Referencias

* Este artículo forma parte de la investigación Isaac Newton on mathematical certainty and method, Universidad de Siena, 2009. Una versión inglesa fue presentada bajo el titulo "Method versus calculus in Newton's criticisms of Descartes and Leibniz" en: Proceedings of the International Congress of Mathematicians, Madrid, Agosto 22–30, 2006, ante la Sociedad Matemática Europea, Zürich, 2006, Vol. 3, pp. 1719–1742.

1 Los lectores interesados en las matemáticas de Newton deben leer las Introducciones y comentarios de Tom Whiteside en: Newton, I. The Mathematical Papers of Isaac Newton, 8 vols. Ed. por Derek T. Whiteside. Cambridge University Press, Cambridge, pp. 1967-1981. Seguimos aquí la traducción del latín al inglés de Whiteside.

2 AddMS 3968.41 f. 85. Citado en: Westfall, R. S. Never at Rest: a Biography of Isaac Newton. Cambridge University Press, Cambridge 1980, pp. 143.

3 Sobre el programa filosófico de Newton puede leerse: Cohen, I. B. The Newtonian Revolution. Cambridge University Press, Cambridge, 1980. Smith, G. E. "The methodology of the Principia", in: The Cambridge Companion to Newton. Cambridge University Press, Cambridge 2002, pp. 137-173. Stein, H. "Newton's metaphysics", in: The Cambridge Companion to Newton. Cambridge University Press, Cambridge 2002, pp. 256-307

4 AddMS 3968.41 f. 85. Citado en: Westfall, R. S. Never at Rest: a Biography of Isaac Newton, Op. cit., pp. 54.

5 Para una evaluación de las primeras investigaciones matemáticas de Newton véase Panza M. Newton et les Origines de l' Analyse: 1664-1666. Blanchard, Paris, 2005.

6 Newton, I. The Mathematical Works of Isaac Newton, Vol. 2. Ed. Derek T. Whiteside. Johnson Reprint Corp., New York, London, 1964-1967, p. 8.

7 Jones, Alexander (ed.). Pappus de Alejandría. Libro 7 de la Colección. Sources in the History of Mathematics and the Physical Sciences. Springer–Verlag, Berlin and Heidelberg GmbH & Co. K., 1986, pp. 82–4.

8 Smith, D. E. and Latham, M. L. The Geometry of René Descartes with a Facsimile of the First Edition. Dover, New York, 1954.

9 Bos, H. J. M. Redefining Geometrical Exactness: Descartes' Transformation of the Early Modern Concept of Construction. Springer, New York, 2001.

10 Ibíd., p. 303.

11 Smith, D. E. and Latham, M. L. The Geometry of René Descartes with a Facsimile of the First Edition, Op. cit., p. 4.

12 Jones, Alexander (ed.). Pappus de Alejandria. –Libro 7 de la Colección. Sources in the History of Mathematics and the Physical Sciences, Op. cit., p. 208.

13 Dicho brevemente, el problema de Pappus requiere la determinación de puntos P tales que sus distancias d_i (i = 1, 2, 3, 4) desde cuatro líneas dadas en posición sean tales que d₁d₂ = k(d₃d₄). En la Géométrie Descartes introduce un sistema de coordenadas oblicuas, y nota que la distancia de un punto desde una línea está dada por la expresión de la forma ax + by + c. Por tanto, las 4–líneas de Pappus tienen una ecuación de segundo grado que la define: a saber, será una sección cónica. El enfoque algebraico le permitió a Descartes generalizar el problema de Pappus para cualquier número de líneas.

14 Más información sobre las críticas de Newton a Descartes se puede obtener en: Galuzzi, M. "I marginalia di Newton alla seconda edizione latina della Geometria di Descartes e i problemi ad essi collegati", in: Belgioioso, G., Climino, G., Costabel, P. and Papuli, G. (eds.) Descartes: il Metodo e i Saggi. Istituto dell'Enciclopedia Italiana, Roma 1990, 387-417.

15 Newton, I. The Mathematical Works of Isaac Newton, Op. cit., p. 228.

16 Nótese que Newton empleaba el término "aritmética universal" para el álgebra, ya que le interesaba la doctrina de las operaciones, no aplicada a los números, sino a los símbolos en general.

17 Newton, I. The Mathematical Works of Isaac Newton, Op.cit., p. 226.

18 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 5, Op. cit., pp. 425-7.

19 Newton, I. The Mathematical Works of Isaac Newton, Op. cit., p. 250.

20 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 7, Op. cit., p. 307.

21 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 4, Op. cit., p. 277.

22 Newton, I. Philosophiae Naturalis Principia Mathematica. The Third Edition (1726) with Variant Readings. Ed. Alexandre Koyré and I. Bernard Cohen con la asistencia de Anne Whitman. Cambridge University Press, Cambridge, 1972. Aquí seguimos la traducción al inglés en: Newton , I. The Principia: Mathematical Principles of Natural Philosophy. Una nueva traducción por I. Bernard Cohen y Anne Whitman con la asistencia de Julia Budenz, precedida de "A guide to Newton's Principia" por I. Bernard Cohen. University of California Press, Berkeley, Los Angeles, London, 1999, p. 162.

23 A partir de su trabajo sobre cúbicas (Newton, I. The Mathematical Works of Isaac Newton, Op. cit., pp. 137-161) Newton extrajo dos lecciones. Primera, la clasificación de curvas por grados por parte de Descartes es un criterio algebraico que poco tiene que ver con la simplicidad. En efecto, las cúbicas tienen estructuras bien complejas comparadas con las curvas mecánicas (trascendentales) como la espiral de Arquímedes. Segunda, recurriendo a la clasificación proyectiva, se logra orden y generalidad.

24 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 3, Op. cit., p. 197.

25 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 1, Op. cit., p. 403.

26 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 1, Op. cit., p. 378.

27 Newton, I. The Mathematical Works of Isaac Newton, Vol. 1, Op. cit., p. 50.

28 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 2, Op. cit., p. 241.

29 Newton, I. The Correspondence of Isaac Newton, Vol. 2. Cambridge University Press, Cambridge, 1959-1977, 39.

30 Newton, I. The Mathematical Works of Isaac Newton, Vol. 1, Op. cit., p. 105.

31 Newton, I. The Mathematical Papers of Isaac Newton, Vol. 3, Op cit., p. 279.

32 Ibíd., Vol. 4, pp. 420–521.

33 Newton, I. The Principia: Mathematical Principles of Natural Philosophy, Op. cit., p. 74.

34 Para Newton el propósito de la "filosofía natural" es deducir las fuerzas a partir de los fenómenos establecidos por la experimentación, y —una vez establecidas las fuerzas— deducir nuevos fenómenos a partir de ellas. En la actualidad llamaríamos a esta empresa "física".

35 Traducido al inglés y citado en: Shapiro, A. Fits, Passions, and Paroxysms: Physics, Method, and Chemistry and Newton'sTheories of Colored Bodies and Fits of Easy Reflection. Cambridge University Press, Cambridge 1993, p. 25.

36 Las circunstancias que rodean la controversia entre Newton y Leibniz han sido analizadas en detalle por Hall, A. R. Philosophers at War: the Quarrel between Newton and Leibniz. Cambridge University Press, Cambridge, 1980; y Newton, I. The Mathematical Papers of Isaac Newton, Vol. 8, Op. cit. En líneas generales, permítaseme recordar unos cuantos hechos: Newton formuló su método de series y fluxiones entre 1665 y 1669. Leibniz había desarrollado su cálculo diferencial e integral alrededor de 1675 y publicó una serie de artículos a partir de 1684. A partir de la evidencia manuscrita es claro que Leibniz llegó a sus resultados independientemente de Newton. Sin embargo, solo parcialmente en el Algebra de Wallis en 1685 y en Works en 1693 y 1699, y en todo un apéndice a la Opticks en 1704, Newton imprimió su método. En 1710 un matemático británico, John Keil, afirmó en las Philosophical Transactions of the Royal Society que Leibniz había plagiado a Newton. Después de la protesta de Leibniz, un comité de la Royal Society, comandado en secreto por su presidente, Isaac Newton, presentó una publicación —el llamado Commercium epistolicum (1713)— en el que se sostenía que Newton fue el "primer inventor" y que "el Método Diferencial [de Leibniz] es el mismo que el Método de Fluxiones [de Newton]". También se sugirió que Leibniz, después de su visita a Londres en 1673 y 1676, y luego de recibir dos cartas de amigos de Newton y de Newton mismo (de hecho Newton le envió dos cartas a Leibniz en 1676) había obtenido suficiente información sobre el método de Newton la cual le permitió publicar el cálculo como su propio descubrimiento, tras cambiar los símbolos. Solo después del trabajo de historiadores como Fleckenstein, Hofmann, Hall y Whiteside, tenemos pruebas de que esa acusación fue injusta. Newton y Leibniz llegaron a resultados equivalentes de manera independiente y siguiendo rutas de descubrimiento diferentes.

37 Los números complejos recibieron una interpretación geométrica solo alrededor de 1800 gracias a Jean Robert Argand, Carl Friedrich Gauss, y Caspar Wessel.

38 Leibniz, G.W. Leibnizens mathematische Schriften, Vol. 1 (2). Olms, Hildesheim, 1971, p. 104. Traducción al inglés del autor.

39 Niedersächsische Landesbibliothek (Hannover) Lh 35 VIII 21, f. 1r. Citado en: Pasini, E. Il Reale e l'Immaginario: la Fondazione del Calcolo Infinitesimale nel Pensiero di Leibniz. Sonda, Torino 1993, 149n, p. 205.

40 Ibíd.

41 AddMS 3968.41 f. 85. Citado en Westfall, R. S. Never at Rest: a Biography of Isaac Newton. Cambridge University Press, Cambridge 1980, p. 143. Esta es la mejor biografía de Newton, p. 381.

42 Newton, I. "The Mathematical Papers of Isaac Newton", Vol. 8, Op. cit., p. 599.

43 Véase Guicciardini, N. Reading the Principia: the Debate on Newton's Mathematical Methods for Natural Philosophy from 1687 to 1736. Cambridge University Press, Cambridge, 1999.

44 Citado en: Hall, A. R. Philosophers at War: the Quarrel between Newton and Leibniz. Op. cit., p. 296.

45 Citado en: Ibíd., p. 294.

46 Citado en: Ibíd., pp. 295-6.

 

 

Bibliografía

1. Bos, H. J. M., Redefining Geometrical Exactness: Descartes'Transformation of the Early Modern Concept of Construction. Springer–Verlag, New York, Berlin, Heidelberg, Tokyo, 2001.        [ Links ]

2. Cohen, I. B. The Newtonian Revolution. Cambridge University Press, Cambridge, 1980.        [ Links ]

3. Descartes, R. The Geometry of René Descartes with a Facsimile of the First Edition Ed. por D. E. Smith y M. L. Latham. Dover, NewYork, 1954.        [ Links ]

4. Galuzzi, M., "I marginalia di Newton alla seconda edizione latina della Geometria di Descartes e i problemi ad essi collegati", in: Belgioioso, G., Cimino, G., Costabel, P., Papuli, G. (eds.) Descartes: il Metodo e i Saggi. Istituto dell'Enciclopedia Italiana, Roma 1990, 387-417.        [ Links ]

5. Guicciardini, N. Reading the Principia: the Debate on Newton's Mathematical Methods for Natural Philosophy from 1687 to 1736. Cambridge University Press, Cambridge, 1999.        [ Links ]

6. Guicciardini, N. Isaac Newton on mathematical certainty and method. MIT Press, Cambridge, Mass., 2009.        [ Links ]

7. Hall, A. R. Philosophers at War: the Quarrel between Newton and Leibniz. Cambridge University Press, Cambridge, 1980.        [ Links ]

8. Jones, Alexander (ed.). Pappus de Alejandria. Book 7 of the Collection. Sources in the History of Mathematics and the Physical Sciences. Springer–Verlag Berlin and Heidelberg GmbH & Co. K., 1986.        [ Links ]

9. Leibniz, G.W. Leibnizens mathematische Schriften, 7 Vols. Olms, Hildesheim, 1971.        [ Links ]

10. Newton, I. The Principia: Mathematical Principles of Natural Philosophy. Traducción de I. Bernard Cohen y Anne Whitman con la asistencia de Julia Budenz, precedida de A guide to Newton's Principia por I. Bernard Cohen. University of California Press, Berkeley, Los Angeles, London, 1999.        [ Links ]

11. Newton, I., Philosophiae Naturalis Principia Mathematica. The Third Edition (1726) with Variant Readings. Ed. Alexandre Koyré and I. Bernard Cohen, con la asistencia de Anne Whitman. Cambridge University Press, Cambridge, 1972.        [ Links ]

12. Newton, I., The Correspondence of Isaac Newton, 7 Vols. Ed. by H. W. Turnbull et al. Cambridge University Press, Cambridge, 1959-1977.        [ Links ]

13. Newton, I., The Mathematical Papers of Isaac Newton, 8 Vols. Ed. por Derek T. Whiteside. Cambridge University Press, Cambridge, London, New York, 1967-1981.        [ Links ]

14. Newton, I., The Mathematical Works of Isaac Newton, 2 Vols. Ed. por Derek T. Whiteside. Johnson Reprint Corp., NewYork, London, 1964-1967.        [ Links ]

15. Panza, M. Newton et les Origines de l' Analyse: 1664-1666. Blanchard, Paris 2005.        [ Links ]

16. Pasini, E. Il Reale e l'Immaginario: la Fondazione del Calcolo Infinitesimale nel Pensiero di Leibniz. Sonda, Torino, 1993.        [ Links ]

17. Shapiro, A., Fits, Passions, and Paroxysms: Physics, Method, and Chemistry and Newton'sTheories of Colored Bodies and Fits of Easy Reflection.Cambridge University Press, Cambridge, 1993.        [ Links ]

18. Smith 18. , G. E., "The methodology of the Principia", in: Cohen, I. B. and Smith, George E. (eds.) The Cambridge Companion to Newton. Cambridge University Press, Cambridge, 2002, pp. 137-173.        [ Links ]

19. Stein, H. "Newton's metaphysics", in: Cohen, I. B. and Smith, George E. (eds.) The Cambridge Companion to Newton. Cambridge University Press, Cambridge, 2002, pp. 256-307.        [ Links ]

20. Westfall, R. S., Never at Rest: a Biography of Isaac Newton. Cambridge University Press, Cambridge, 1980.        [ Links ]