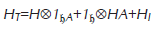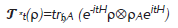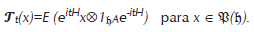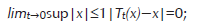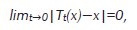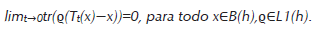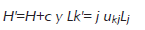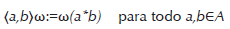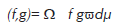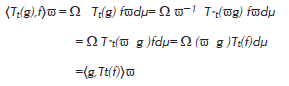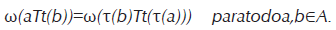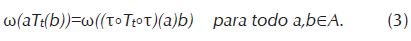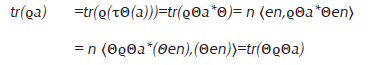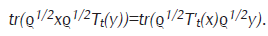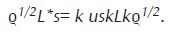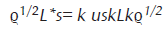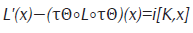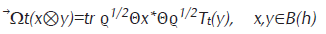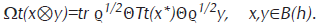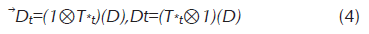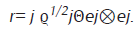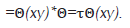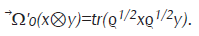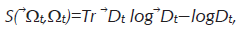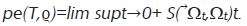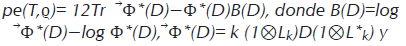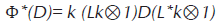Introduccion
La dinámica de un sistema cuántico abierto en la aproximación Markoviana es descrita por un semigrupo cuántico de Markov (SCM). Estos semigrupos son una extensión no conmutativa de los semigrupos de Markov definidos en probabilidad clásica y representan una evolución temporal sin memoria de un sistema microscópico acorde a las leyes de la física cuántica. Más concretamente, para la representación de la dinámica en un sistema cuántico abierto se utilizan dos espacios de Hilbert: el primer espacio de Hilbert que denotaremos por 𝔥 será el espacio del sistema y el segundo espacio denotado por 𝔥A será el espacio del ambiente, donde la dinámica total del sistema es representada sobre el espacio de Hilbert 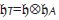 por el generador HT de un grupo unitario, siendo
por el generador HT de un grupo unitario, siendo
en el cual H es el Hamiltoniano del sistema, HA el Hamiltoniano del ambiente y HI el Hamiltoniano de interacción.
Además si se quiere analizar la dinámica reducida sobre el espacio 𝔥 es necesario conocer el estado inicial del ambiente, el cual es representado por una matriz de densidad ρA, una matriz de densidad o estado es un operador acotado positivo con traza igual a uno, definido en 𝔥A. Con esta matriz de densidad se describe la dinámica reducida sobre h en el cuadro de Schrödinger:
donde tr𝔥A es la traza parcial sobre las variables ambientales y (𝓣*t)t≥0 define un colección de aplicaciones y haciendo reescalamientos temporales y ciertos tipos de límites podemos obtener un semigrupo definido en 𝔏1(𝔥), donde 𝔏1(𝔥) es el conjunto de todas las matrices densidad. También podemos utilizar el estado ρA para determinar la esperanza condicional E definida sobre el espacio (𝔥) formado por todos los operadores acotados en 𝔥 y describir dicha dinámica en el cuadro de Heisenberg:
En este caso 𝓣t, al igual que en el cuadro Schrödinger, define un colección de aplicaciones y haciendo reescalamientos temporales y ciertos tipos de límites podemos obtener un SCM.
Más exactamente, a nivel matemático y físico el tratamiento riguroso de todo lo descrito anteriormente dió como frutos una cantidad muy variada de trabajos y conceptos entre los cuales se destaca el límite de acoplamiento débil o límite estocástico y el límite de acoplamiento singular, los cuales fueron tratados en una primera versión de manera formalizada por Davies ([11],[12],[13]), enfocándose primordialmente en la dinámica reducida y recientemente se ha trabajado la dinámica en el espacio completo ([1],[3],[14],[15],[16]).
No es el objetivo de este trabajo, discutir los métodos matemáticos para justificar la aproximación Markoviana, nuestro objetivo es distinto. Nosotros suponemos la aproximación Markoviana justificada y por ende la dinámica de nuestro sistema es descrita por un SCM (𝓣t)t ≥0. Bajo este supuesto, este trabajo se concentra en ofrecer una exposición de varios resultados básicos sobre SCM. Además discutimos aplicaciones de SCM en teoría de la información cuántica y computación cuántica.
Álgebras de operadores
Asumiremos siempre los siguientes hechos:
Todos los espacios vectoriales, espacios de Hilbert y álgebras son definidas sobe el cuerpo de escalares C de los complejos.
En un espacio de Hilbert el producto escalar / es lineal en la segunda entrada del producto y antilineal en la primera.
Cualquier espacio de Hilbert 𝔥 es separable y el conjunto de los operadores acotados sobre h será denotado por 𝔓(𝔥).
Algunas veces por comodidad utilizaremos la notación de Dirac para el producto interno, es decir, el producto interno 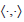 será algunas veces denotado por
será algunas veces denotado por 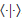 Por ejemplo dados u,v vectores en 𝔥 se define la aplicación
Por ejemplo dados u,v vectores en 𝔥 se define la aplicación  tal que para todo 𝔴
tal que para todo 𝔴 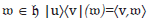 u, el cual llamaremos proyector y que en notación de Dirac su acción es escrita como
u, el cual llamaremos proyector y que en notación de Dirac su acción es escrita como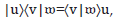 , para todo 𝔴 є 𝔥. Nótese que si v = 𝔴 obtenemos un operador proyección.
, para todo 𝔴 є 𝔥. Nótese que si v = 𝔴 obtenemos un operador proyección.
Denotaremos por (𝔥) el conjunto de los operadores clase traza, equipado con la norma traza |ϱ|1 = tr|ϱ|, donde |ϱ|=(ϱ*ϱ)1/2. En particular, el conjunto de matrices densidad o estados es denotado por 𝓛1(𝔥), donde
𝔏1(𝔥)={ϱ ∈ L;(h)ϱ ≥ 0,|ϱ|1=1}.
Proposición 1 El espacio de Banach B(h) es el dual topológico de L(h) debido a la dualidad (x,ϱ)=tr(xϱ), x∈B(h),ϱ∈L(𝔥). Además la topología débil-* en (𝔥) asociada a esta dualidad coincide con la topología σ-débil.
(Una prueba de esta proposición puede ser encontrada por ejemplo en [8], teorema 3.2, página 87). En virtud de este último teorema, en el resto de este trabajo σ-débil es denotado por 𝔴* (débil-* que traducido al inglés sería weak-*).
Semigrupos cuánticos de Markov (SCM)
Los SCMs son aplicaciones completamente positivas. A continuación discutimos sobre el concepto de aplicación completamente positiva y algunas consecuencias.
Definición Sean dos *-álgebras A,B. Una aplicación Φ:A↦B es
positiva si Φ(a*a) es un elemento positivo para todo a∈A;
n- positiva si para cualquier par de colecciones a1,…,an∈A y b1,…,bn∈B, el elemento i,j=1n b*iΦ(a*iaj)bj∈B, es positivo;
completamente positivo si Φ es npositivo para todo n≥1.
Recordemos que un elemento positivo de una *álgebra A es un elemento de la forma a*a con a∈A y que aplicación positiva es una aplicación que envia elementos positivos en elementos positivos, entonces una aplicación completamente positiva es en particular 1-positiva o positiva. Si Φ es 2positiva entonces Φ satisface la desigualdad de Schwartz Φ(a*a)≤ Φ(a)*Φ(a) ∀a∈B(h).
Para una demostración de esta última afirmación ver por ejemplo [28].
Definición Un semigrupo cuántico de Markov (SCM) en una *álgebra A con unidad 1, es una familia uniparamétrica T=(Tt)t≥0 de aplicaciones lineales de A en si mismo cumpliendo
T0(x)=x, para todo x∈A;
Cada Tt(⋅) es completamente positivo;
Tt(Ts(x))=Tt+s(x), para todo t,s≥0,x∈A;
Tt(1)=1 para todo t≥0.
De lo anterior deducimos que por la 2-positividad de Tt se sigue la desigualdad de Schwartz Tt(x*x) ≤ Tt(x)*Tt(x) para todo t ≥0 y para todo x∈A.
En este trabajo nos centraremos principalmente en SCM definidos en B(h) y siempre asumiremos que todas las *-álgebras tienen unidad 1 a menos que se diga lo contrario.
La continuidad del semigrupo es definido acorde a las diferentes topologías de B(h):
Definición Un semigrupo cuántico de Markov (Tt)t≥0 es:
El generador L del semigrupo T es definido en la topología débil-*. Esto es, su dominio D(L) consiste de elementos x del álgebra para los cuales el w*-límite of t−1(Tt(x)−x) existe cuando t→0. Este límite es denotado entonces por L(x).
El generador del semigrupo nos revela mucha información sobre el semigrupo por ejemplo, un SCM es continuo en norma si y sólo si su generador L(⋅) es un operador acotado en B(h). En este caso existe un conjunto de operadores (Lk)k∈N tal que L= k L*kLk es un operador acotado en B(h) y k L*kxLk∈B(h) cuando x∈B(h) y existe también un operador autoadjunto H=H*∈B(h) tal que L(x)=i[H,x]− 12 k (L*kLkx−2L*kxLk+xL*kLk).
Esta última representación es debida a Gorini, Kossakowski, Sudarshan y Lindblad y es llamada en forma abreviada forma GKSL de L. Para una prueba ver por ejemplo teorema 5.6 de [28]. Gorini, Kossakowski y Sudarshan encontraron la forma de L en el caso de dimensión finita, posteriormente Lindblad extendió la representación al caso de dimensión infinita.
La representación GKSL en general no es única; pero existen condiciones para aproximarse a dicha unicidad:
Teorema Sea L el generador de un SCM continuo en norma en B(h) y ϱ∈L1(h). Entonces existe un operador acotado autoadjunto H y una sucesión finita o infinita (Lk)k≥1 de elementos de B(h) tal que:
tr(ϱLk)=0 para todo k≥1,
k≥1 L*kLk es una suma fuertemente convergente,
si (ck)k≥0 es una sucesión cuadrado-sumable de escalares complejos y c01+ k≥1 ckLk=0 entonces ck=0 para todo k≥0,
la siguiente representación de L se cumple L(x)=i[H,x]− 12 k≥1 (L*kLkx−2L*kxLk+xL*kLk). Si H',(Lk')k≥1 es otra familia de operadores acotados en B(h) con H' autoadjunto y la sucesión (Lk')k≥1 es finita o infinita, entonces las condiciones (a)-(d) son satisfechas con H,(Lk)k≥1 reemplazado por H',(Lk')k≥1 respectivamente si y sólo si los tamaños de las sucesiones (Lk)k≥1,(Lk)k≥1 son iguales y para algún escalar c∈R y una matriz unitaria (ukj)kj tenemos que
Una prueba de este resultado puede ser consultada en el teorema 30.16 de [26]. Una representación GKSL de L que verifica las hipótesis del teorema anterior será llamada una representación especial. La matriz unitaria (ukj)kj obviamente puede ser vista como un operador unitario sobre un espacio de Hilbert k, llamado espacio libre de multiplicidad con dimensión igual a el tamaño de la sucesión (Lk)k≥1, la cual es también determinada en forma única por L debido al tamaño de la condición de minimalidad (c).
Como se había comentado anteriormente, el teorema 3.2 nos permite aproximarnos a la unicidad de la descomposición GKSL; más concretamente, una consecuencia inmediata de este teorema es la unicidad en la descomposición de L como la suma de una derivación i[H,⋅] y una parte disipativa L−i[H,⋅], suponiendo la representación GKSL especial. La descomposición de L en la forma L(x)=G*x+ k≥1 L*kxLk+xG es única, salvo un múltiplo imaginario puro del operador identidad sumando en G.
De lo anterior podemos ver que el suponer L(⋅) acotado no sólo nos da propiedades topológicas fuertes sino además representaciones álgebraicas del generador, las cuales como veremos más adelante serán bastante útiles para estudiar la dinámica descrita porT. Hasta el momento hemos discutido la dinámica definida en el álgebra B(h), es decir, en el cuadro de Heisenberg; pero si deseamos trabajar con los estados (en el cuadro de Schrödinger) entonces debemos usar el predual de B(h), del cual hablaremos a continuación.
Definición Sea A un álgebra de von Neumann. Llamaremos predual de A el espacio de todos los funcionales σdébilmente continuos definidos en A, y denotaremos el conjunto formado por estos como A*.
En particular B(h)*=L(h), el espacio de los operadores clase traza. Es claro que A*⊂A*. Además A* es un espacio de Banach en la norma de A*.
Definición Un funcional lineal positivo ω sobre A es normal si para toda red creciente (aα)α en A+ con envolvente superior, tenemos supαω(aα)=ω(supαaα). Un estado ω es un funcional lineal positivo tal que ω(1)=1.
Proposición Si ω es un estado en A, entonces las siguientes condiciones son equivalentes:
ω es normal;
ω es σ-débilmente continuo;
existe ϱ∈L1(h) tal que ω(a)=tr(ϱa) para todo a∈A;
ω( i∈I pi)= i∈I ω(pi) para cada colección {pi}i∈I de proyecciones ortogonales dos a dos en A.
Una prueba de lo anterior es encontrada en [9], teorema 2.4.21. En este contexto ϱ es llamado operador densidad, matriz densidad o estado. En adelante identificaremos ω con ϱ.
Ahora hablaremos sobre la evolución de los estados que nosotros manejaremos:
Definición El semigrupo predual de un SCM T* de A es el semigrupo T* de operadores en A* definido por (T*t(ω))(a)=ω(Tt(a)) para cada a∈A y cada ω∈A*. En particular, si A=B(h) entonces el semigrupo predual es definido en L1(h) por la relación tr(T*t(ϱ)x)=tr(ϱTt(x)) forallt≥0,x∈B(h),ϱ∈L1(h)
Su generador es denotado por L*.
Si T es continuo con respecto a la topología débil en B(h), el semigrupo T* es también continuo con respec to a la topología débil en el espacio de Banach L(h). Entonces por el corolario 3.1.8 en [9] , T* es un semigrupo fuertemente continuo en el espacio de Banach L(h). Además, si Tt(1)=1 para todo t≥0, entonces T* aplica estados en estados. En efecto, para cada estado nor mal ω, T*t(ω) es positivo y (Tt*(ω))(1)=ω(Tt(1))=ω(1)=1.
Una hipótesis que haremos con frecuencia es suponer que existe un estado normal fiel e invariante para el semigrupo T. A continuación aclararemos que significa este supuesto
Definición Un funcional normal ω∈A* es llamado invariante con respecto a T (o T-invariante) si (T*t(ω)) (a)=ω(a) (o equivalentemente ω(Tt(a))=ω(a)) para todo a∈A,t ≥ 0. El funcional ω es fiel si ω(a*a)>0 para todo a≠0.
Notar que si ω es un estado fiel en A entonces la forma sesquilineal definida por
es un producto interno en A.
Aplicaciones en teoría de la información cuántica y computación cuántica
En teoría de la información cuántica y en computación cuántica Tt puede ser interpretado como el paso t-ésimo de un algoritmo de un computador cuántico, teniendo ruidos que perturban la evolución de dicho algoritmo, de esta forma existe una conección natural con los objetos de estudio de teoría de la información y computación cuántica. Dado que el ruido generado por el ambiente puede alterar y afectar la evolución del algoritmo, una pregunta natural es como saber si existe una forma de elegir inputs adecuados para nuestro algoritimo descrito por Tt de tal forma que su evolución no sea alterada por este ruido. En particular, uno de los efectos del ruido que mas afecta a Tt es la decoherencia, la cual hace que rasgos cuánticos del algoritmo se pierdan, asi que nos interesaria encontrar como seleccionar inputs que no se dejen afectar por la decoherencia, para ello debemos encontrar inputs que evolucionen siempre en forma unitaria a medida que evoluciona el tiempo. La respuesta a esta pregunta es afirmativa, debemos elegir inputs que esten generados en un subespacio especial del espacio de Hilbert h, dicho espacio es llamado subespacio libre de decoherencia. A continuación precisamos matemáticamente esta situación.
Subespacio libre de decoherencia
Recordemos que un estado ω sobre B(h) es un operador positivo de traza igual a uno y que esta definido sobre h, en particular es un operador clase traza definido sobre h. El soporte de ω denotado por supp(ω) es el subespacio cerrado de h generado por vectores propios los cuales tienen valores propios estrictamente positivos.
Definición Un subespacio hf de h es libre de decoherencia (LD) si existe un operador autoadjunto K definido en hf tal que para todo estado ω con soporte en hf se tiene que
T*t(ω)=e−itKωeitK para todo t≥0. (1)
Cada vez que tengamos un operador autoadjunto K que cumple con las condiciones descritas anteriormente diremos que K es un operador asociado a hf.
Es claro que un operador autoadjunto K definido en hf siempre puede ser extendido al espacio de Hilbert h, por lo tanto, de manera equivalente, los subespacios LD pueden ser definidos con K un operador autoadjunto definido en h que deja invariante un subespacio hf. También se puede ver fácilmente que el subespacio LD es un subespacio cerrado con respecto a la topología inducida por la norma de h. Un subespacio de un subespacio LD el cual es invariante por K es a su vez un subepacio LD, por lo cual cada vez que nos refiramos a un subespacio LD estamos haciendo mención a un subespacio LD maximal.
Usando la estructura del generador del semigrupo es posible dar condiciones necesarias y suficientes para hallar los subespacios libres de decoherencia de cualquier semigrupo Markoviano cuántico. Dicho resultado es formulado tanto para el caso en que L* está dado por operadores acotados como también en el caso no acotado. A continuación recordamos el resultado para el caso acotado. (Para consultar la prueba en el caso no acotado, ver [5], proposición 7).
Teorema Un subespacio hf es un subespacio LD con operador autoadjunto asociado K, si y solo si, en cualquier representación GKSL de L* por medio de operadores Ls,G existen números complejos λs (s≥1) y un número real r tal que s 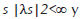
Producción de entropía para SCM
Otra aplicación interesante, principalmente enfocada en teoría de la información cuántica, se da al preguntarse por la entropía relativa, la cual es una forma de medir cuanto información se pierde o se gana en un proceso y en particular para caracterizar los estados de equilibrio de un SCM, los cuales se pueden interpretar como aquellos estados en donde la perdida de información a medida que transcurre el tiempo es despreciable. Mas exactamente, dichos estados se pueden caracterizar usando condiciones de balance detallado y usando el concepto de producción de entropía.
La noción de balance detallado que manejaremos aquí es una extensión no conmutativa de la que se emplea en probabilidad clásica, por esta razón empezamos hablando del caso clásico.
Sea (Ω,F,μ) un espacio de medida con μ medida σ-finita y sea T=(Tt)t≥0 un semigrupo de Markov clásico w*continuo formado por funciones lineales acotados sobre L∞ (Ω,F,μ)
T es el semigrupo dual de un semigrupo de contracciones fuertemente continuo sobre el espacio predual L1(Ω,F,μ)denotado por T*. Supongamos que T. admite una densidad de probabilidad 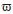 la cual es invariante por T (es decir,
la cual es invariante por T (es decir, 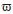 es una función no negativa de norma uno en L
1
(Ω,F,μ) tal que T*
t
(
es una función no negativa de norma uno en L
1
(Ω,F,μ) tal que T*
t
(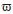 )=0 para t≥0) anulándose unicamente en elementos de Ω que tengan medida nula. Entonces es bien sabido que la forma sesquilineal
)=0 para t≥0) anulándose unicamente en elementos de Ω que tengan medida nula. Entonces es bien sabido que la forma sesquilineal
define un producto escalar sobre L∞(Ω,F,μ) que denotaremos por 〈⋅,⋅〉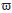 . Si denotamos por T
t
el operador adjunto de T
t
con respecto a este producto escalar, es fácil ver que
. Si denotamos por T
t
el operador adjunto de T
t
con respecto a este producto escalar, es fácil ver que
para todo t≥0 y para todo g∈L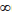 (Ω,F,μ).
(Ω,F,μ).
En efecto, si 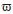 g∈L1(Ω,F,μ), como
g∈L1(Ω,F,μ), como 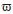 es invariante bajo T* entonces
es invariante bajo T* entonces
por lo tanto T
t
es un operador acotado bien definido en L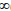 (Ω,F,μ). Además
(Ω,F,μ). Además
para todo f,g∈L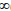 (Ω,F,μ). Claramente la aplicación T
t
también es positiva, entonces T=(T
t
)t≥0 es un semigrupo w*-continuo de aplicaciones positivas acotadas en L
(Ω,F,μ). Claramente la aplicación T
t
también es positiva, entonces T=(T
t
)t≥0 es un semigrupo w*-continuo de aplicaciones positivas acotadas en L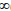 (Ω,F,μ).
(Ω,F,μ).
El semigrupo T es Markov pues T
t
(
1
)=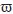 −1
T
*t
(
−1
T
*t
(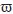 )=
1.
)=
1.
Definición Diremos que T satisface la condición de balance detallado clásica si cada operador Tt es autoadjunto con respecto a 〈⋅,⋅〉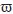 , es decir, T
t
=T
t
.
, es decir, T
t
=T
t
.
Entonces T satisface la condición de balance detallado clásica si y sólo si para todo t≥0
Nota Balance detallado es equivalente a reversibili dad en el contexto de cadenas de Markov clásicas. En efecto, si asumimos por ejemplo (por simplicidad) Ω={1,…,d} con la σ-álgebra F igual al conjunto de partes de Ω, la medida μ como la medida de conteo y además con un semigrupo de Markov al cual le asociamos una matriz de tasas de transición (qjk)1≤j,k≤d definida por q jk =limt→0t−1(T t 1{k}−1{k})(j),
siendo 1 {k} la función indicatriz del conjunto {k}. Denotando (q jk )1≤j,k≤d la matriz de tasa de transición del semigrupo de Markov (T t ) t ≥0, se sigue inmediatamente de la definición que (6) es equivalente a la condición
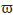 jq
jk
=
jq
jk
= kq
kj
para todo j,k∈Ω. Esta condición es conocida como reversibilidad, la cual es también conocida en cadenas de Markov a tiempo discreto.
kq
kj
para todo j,k∈Ω. Esta condición es conocida como reversibilidad, la cual es también conocida en cadenas de Markov a tiempo discreto.
En el caso cuántico, dada su naturaleza no conmutativa se tiene que varias definiciones de condiciones de balance detallado cuántico (BDC) existen en la literatura. Al parecer, historicamente, la primera fue trabajada por Agarwal (ver [4] ) y posteriormente extendida por Majewski (ver [24]), esta definición involucra una operación τ:A→A de tal forma que si a,b∈A entonces:
En este contexto, un SCM T satisface la condición de BDC de Agarwal-Majewski con respecto al estado ω y al operador reversante Ƭ, si
Si el estado ω es invariante bajo el operador reversante (ω(τ(a))=ω(a) para todo a∈A) entonces la condición BDC de Agarwal-Majewski es equivalente a
En consecuencia, si ω es fiel e invariante bajo τ, la igualdad (7) significa que bajo el producto interno definido por ω la aplicación Tt admite aplicaciones duales coincidiendo con τ∘T t ∘τ para tod t≥0; en particular las aplicaciones duales deben ser positivas dado que τ preserva la positividad.
Si A=B(h), la elección canónica para τΘ es dada por τΘ(a)=Θa*Θ donde Θ es definida sobre una base ortonormal fijada (en)n≥0 de h como
En este caso, vemos que Θ2=1 y 〈Θv,Θu〉=〈u,v〉 para todo u,v∈h (es decir, Θ es una involución y un operador antiunitario). Además, si ω es invariante bajo Θ y un estado normal es representado por ϱ∈L 1 (h) entonces
para todo a∈A, entonces ϱ=ΘϱΘ, es decir, Θ conmuta con ϱ. Es facil ver que si Θ conmuta con ϱ entonces ω es invariante bajo τΘ. Por lo tanto obtenemos:
Proposición Si ω(⋅)=tr(ϱ⋅) es un estado en B(h). ω es invariante bajo la operación reversante canónica τΘ si y sólo si Θ conmuta con ϱ.
La condición BDC más popular es debida a Alicki [6],[7] y Kossakowski, Frigerio, Gorini, Verri [23]. En este caso, BDC se cumple si existe un SCM dual T=(T t )t ≥0 (GNS-dual) en A tal que ω(aT t (b))=ω T t (a)b y la diferencia de generadores L y L es una derivación.
Cuando esta condición se cumple, todas las aplicaciones positivas T t admiten aplicaciones duales positivas con respecto al producto interno definido por la forma bilineal (a,b)→ω(ab), entonces todas las aplicaciones Tt deben commutar con el grupo modular (σωt) t ∈R asociado con el par (A,ω) (ver Prop. 2.1 en [23], Prop. 5 en [25]).
Esta restricción álgebraica es evitable, si consideramos la forma bilineal
introducida por Petz (ver [27]) entonces podemos definir un SCM dual (KMS-dual), también cuando las aplicaciones T t no conmutan con el grupo modular (ver [10], [22]).
Las condiciones BDC que surgen cuando consideramos KMS-duales en vez de GNS-duales son llamadas estándar:
Definición Sea T un SCM con SCM dual T' tal que ω(σi/2(a)T t (b))=ω(σi/2(T t '(a))b) para todo a,b∈A,t≥0. El semigrupo T satisface:
La condición de balance detallado cuántica estándar con respecto a la operación reversante τ (BDCE-τ), si T t '=τ∘T ∘τ para todo t≥0,
La condición de balance detallado cuántica estándar (BDCE), si la diferencia de generadores L−L' de T y T' es una derivación densamente definida.
Nos concentraremos en el caso A=B(h) y todos los estados serán asumidos normales e identificados con sus densidades. Entonces ω(x)=tr(ϱx) y σt(x)=ϱ it xϱ −it . En consecuencia, la definición anterior se lee
Definición Sea T un SCM en B(h) con un SCM dual T' que cumple
El semigrupo T satisface:
La condición de balance detallado cuántica estándar con respecto a la operación reversante τ (BDCE-τ), si
para todo x,y∈B(h) y para todo t≥0,
La condición de balance detallado cuántica estándar (BDCE), si existe un operador autoadjunto K tal que
para todo x∈Dom(K). Donde L es el generador de T, L' es el generador de T', y Dom(K) es denso en h.
En este caso, la condicion BDCE coincide con la condición de Agarwal-Majewski y Alicki-Gorini-Kossakowski-Frigerio-Verri respectivamente cuando el SCM Tconmuta con el grupo modular (σt)t∈R asociado con el par (B(h),ϱ) (ver, [10], [25], [21], [20]).
Supondremos adicionalmente que la aplicación canónica τΘ será una operación reversante con respecto a alguna base tal que dado un estado fiel invariante ϱ entonces ϱ conmuta con Θ. Un proceso de ortogonalización de Gram-Schmidt muestra que siempre es posible encontrar dicha base ortonormal de h conformada de vectores propios de ϱ que son también Θ-invariantes (ver proposición 7 en [18]).
Las siguientes afirmaciones describen caracterizaciones de SCM continuos en norma satisfaciendo condiciones de BDC estándar (las demostaciones pueden ser consultadas en [20], teorema 15,18 y nota 4).
Teorema Un SCM T satisface la condición de BDCE si y sólo si para cualquier representación especial GKSL del generador L por medio de los operadores G,Lk existe una matriz unitaria (u mk ) mk en k la cual es también simétrica (es decir, u mk =u km para todo m,k) tal que, para todo s≥1,
Teorema Un SCM T satisface la condición BDCE-Θ si y sólo si para cualquier representación especial GKSL del generador L por medio de los operadores G,Lk existe una matriz unitaria (umk)mk en k la cual es también simétrica tal que:
Nota La condición BDCE−Θ es más restrictiva que la condición BDCE porque esta involucra también la identidad ϱ 1/2 ΘG*Θ=Gϱ1/2 ; pero si ΘG*Θ=G and ϱ commutan con G entonces ambas condiciones son equivalentes. Esta última suposición es satisfecha por muchos SCM como por ejemplo, aquellos derivados del límite de acoplamiento débil (o límite estocástico) (ver [2], [16]).
Teorema Sea T un SCM con generador L teniendo representación especial GKSL por medio de los operadores G,Lk. Asumamos que
para todo s≥1, y para una matriz unitaria autoadjunta (umk)mk en k. Entonces
con K autoadjunto conmutando con ϱ.
La demostración de este teorema puede ser consultada en [18].
Fagnola y Rebolledo definieron el concepto de producción de entropía para SCM (ver [18]), el cual es una extensión no conmutativa del caso clásico (ver [19]) y probaron que un estado invariante con producción de entropía nula es caracterizado por condiciones de balance detallado estándar entonces la producción de entropía mide no reversibilidad y por lo tanto no equilibrio.
En esta sección, repasaremos la noción de producción de entropía en SCM. Asumiremos que es dado un SCM con un estado fiel e invariante con respecto al semigrupo, el cual es definido en B(h). La producción de entropía será definida en términos de la entropía relativa de estados de dos puntos forward y backward.
Sean V un conjunto contable y (en)n∈V una base ortonormal de h la cual da una representación diagonal del estado T-invariante ϱ.
Definición El estado de dos puntos forward es definido por
y el estado de dos puntos backward es dado por
Es claro de la definición anterior que T satisface la condición BDCE-Θ si y sólo si ⃗Ωt=Ωt para todo t≥0.
Proposición Sea ϱ= j ϱj|ej〉〈ej| una descomposición espectral de ϱ.
Los funcionales ⃗Ωt y Ωt son estados normales en B(h)⊗B(h) con densidades
respectivamente. Donde D=|r〉〈r| con
Las siguientes afirmaciones son equivalentes:
Los operadores Θx*Θ pueden ser vistos como elementos del álgebra opuesta B(h) ∘ de B(h). En efecto, recordando que B(h)∘ esta en correspondencia inyectiva con B(h) como un conjunto via la identificación trivial x→x∘, teniendo la misma estructura de espacio vectorial, la misma involución y norma pero con producto ⊚ definido por x∘⊚y∘=(yx)∘. Entonces la aplicación lineal τΘ:B(h)→B(h)∘ definida por x→Θx*Θ es un *-isomorfismo (sobreyectivo) de B(h) en B(h)∘ puesto que τΘ(x)⊚τΘ(y) =Θx*Θ⊚Θy*Θ=Θy*ΘΘx*Θ
Claramente τΘ⊗1 :B(h)⊗B(h)→B(h)∘⊗B(h) es un *-isomorfismo. Esta observación es útil para definir producción de entropía como un índice que mide desviación de la condición de balance detallado estándar sin operación reversante. En efecto, se puede definir el estado ⃗Ω'0=Ω'0 en B(h)∘⊗B(h) por
Por lo tanto, podemos definir la producción de entropía otra vez considerando la entropía relativa de ⃗Dt y Dt pero ahora visto como densidades de estados en B(h)∘⊗B(h).
Denotamos la traza sobre h⊗h por Tr(⋅). La entropía relativa de ⃗Ωt con respecto a Ωt es dada por
si el soporte de ⃗Ωt esta incluido en el soporte de Ωt, en caso contrario
Definición La tasa de producción de entropía de un SCM T y un estado invariante ϱ es definido por
Es claro que pe(T,ϱ) ≥0 y entonces pe(T,ϱ)=0 si y sólo si la condición BDCE−Θ (o la condición de BDCE, viendo ⃗Ωt y Ωt como estados en B(h)∘⊗B(h)) se cumple.
Teorema Asumamos todas las suposiciones previas dadas en esta sección. Sea T un SCM continuo en norma definido en B(h) con un estado normal, fiel e invariante ϱ. Si el soporte de ⃗D t y el soporte de D t coinciden y son de dimensión finita entonces
con L k operadores de una representación especial GKSL de L.
Adicionalmente, si G es dado en la representación especial GKSL de L tal que [ϱ,G]=[ϱ,Θ]=0 y ΘG*Θ=G entonces pe(T,ϱ)=0 si y sólo si la condición BDCE−Θ (o la condición de BDCE, viendo ⃗Ωt y Ωt como estados en B(h)∘⊗B(h)), se cumple.
Para una demostración ver teorema 5 en (18).