Introduction
String matching is one of the most useful computational primitives (Apostolico and Galil (1997). The input to the string matching problem consists of two strings defined over a given alphabet Σ: the pattern P = P1..m and the text T = T1..n. The output should list all occurrences of the pattern string in the text string, i.e. all the positions i such that Pj = Ti + j-1,1≤ j ≤ m. However, exact string matching does not support all the applications. For instance, in some areas the alphabet is drawn from a set of integer values. These integer strings are normally found in cipher text, financial data, meteorology data, image data, and music data, to name some. In such numeric strings, it would be unrealistic and ineffective to search for exact occurrences of a pattern but rather ought to search for similar instances of it. Then, some variants of the problem have been defined, including δγ-matching and order-preserving matching.
The δγ-matching problem consists of finding all the text windows in T for which: (i) the distance to the corresponding symbols in P is at most δ; and (ii) the sum of such distances is at most γ. In other words, the output of this problem is the set of positions i such that |Pj - Ti+j-1| ≤ δ,1 ≤ j ≤ m, and 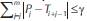 . Notice that δ bounds the individual error of each position while γ bounds the total error. Then, δγ-matching has important applications in bioinformatics, computer vision, but mainly, music information retrieval. Many kinds of algorithms have been put forward to resolve δγ-matching (see for instance Cambouropoulos et al., (2002), Crochemore et al., (2002), Crochemore et al., (2003), Clifford and Iliopoulos (2004), Cantone et al., (2004), Crochemore et al., (2005) and Lee et al., (2006). Recently, it has been used to make more flexible other string matching paradigms such as parameterized matching (see for instance Lee et al., (2008) and Mendivelso (2010), function matching (Mendivelso et al., (2012)) and jumbled matching (Mendivelso et al., (2015) and Mendivelso et al., (2014)).
. Notice that δ bounds the individual error of each position while γ bounds the total error. Then, δγ-matching has important applications in bioinformatics, computer vision, but mainly, music information retrieval. Many kinds of algorithms have been put forward to resolve δγ-matching (see for instance Cambouropoulos et al., (2002), Crochemore et al., (2002), Crochemore et al., (2003), Clifford and Iliopoulos (2004), Cantone et al., (2004), Crochemore et al., (2005) and Lee et al., (2006). Recently, it has been used to make more flexible other string matching paradigms such as parameterized matching (see for instance Lee et al., (2008) and Mendivelso (2010), function matching (Mendivelso et al., (2012)) and jumbled matching (Mendivelso et al., (2015) and Mendivelso et al., (2014)).
On the other hand, order-preserving matching considers the order relations within the numeric strings rather than the approximation of their values. In particular, the natural representation of a string is a string composed by the rankings of each symbol in such string. Then, order-preserving matching consists of finding every text window in T such that its natural representation matches the natural representation of P. Note that this problem is interested in matching the internal structure of the strings rather than their absolute values. Then, it has important applications in music information retrieval and stock market analysis. Specifically, in music information retrieval, one may be interested in finding matches between relative pitches; similarly, in stock market analysis the variation pattern of the share prices may be more interesting than the actual values of the prices (Kim et al., (2014)). Since Kim et al., (2014) and Kubica et al., (2013) defined the problem, it has gained great attention from several other researchers (Crochemore et al., (2013), Crochemore et al., (2013a), Chhabra et al., (2014), Faro et al., (2015), Crochemore et al., (2015), Hasan et al., (2015), Chhabra et al., (2015).
Notwithstanding, the only approximate variant of order-preserving matching in previous literature, to the best of our knowledge, was recently proposed by Gawrychowski et al., (2015). In particular, they allow k mismatches between the pattern and each text window. Then, they regard the number of mismatches but not their magnitude. In this paper, we propose a different approach to approximate order-preserving matching that bounds the magnitude of the mismatches through the δγ-distance. Specifically, δ is a bound between the ranking of each character in the pattern and its corresponding character in the text window; likewise, γ is a bound on the sum of all such differences in ranking. Thus, δ and γ respectively restrict the magnitude of the error individually and globally across the strings. We define δγ-order-preserving matching as the problem of finding all the text windows in T that match the pattern P under this new paradigm.
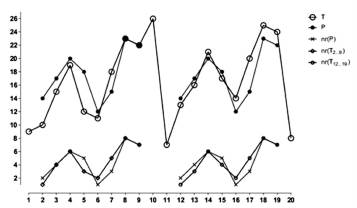
As an example of how δγ-order-preserving matching finds similarity in the order of the strings, we illustrate two substrings of a text T that are similar to a pattern P in Figure 1. The strings T=〈9,10,15,19,12,11,18, 23, 22, 26, 7, 14, 16, 21, 17, 13, 20, 25, 24, 8〉 and P = 〈14, 17, 20, 18, 12, 15, 23, 22〉 are defined over the alphabet Σ={1..26}. The X-axis and the Y-axis respectively correspond to the positions and values and rankings of both the pattern P and the substrings in T where there is two δγ-approximate order preserving matches with δ=2 and γ=6 in positions 2 and 12. Recall that δ is a bound on the distance between corresponding symbols and γ is a bound on the sum of such differences. The figure in the lower side shows the similarity between the natural representation of the pattern and the natural representation of the substrings T2..9 and T12..19. Then, with nr(P) in Figure 1, we refer to the natural representation of string P, i.e., the sequence of the rankings of the symbols in the integer string P. More formal definitions of these concepts are provided in the next section.
The motivation to define δγ-order-preserving matching stems from the observation that the application areas of order-preserving matching, mainly stock market analysis and music information retrieval, require to search for occurrences of the pattern that may not be exact but rather have slight modifications in the magnitude of the rankings. For example, let us assume that the text T presented in Figure 1 is a sequence of stock prices and that we want to determine whether it contains similar occurrences of the pattern P (also shown in this figure). Under the exact order-preserving matching paradigm, there are no matches, but there are similar occurrences at positions and 2 and 12. In particular, T2..9 and T12..19 are similar, regarding order structure, to the pattern. This similarity can be seen even more clearly if we consider natural representations of these strings (also shown in in Figure 1). These matches can be retrieved with δ=2 and γ=6.
The outline of the paper is as follows. In Section Preliminaries and problem definition, we present the preliminaries and define the δγ-order-preserving matching problem. Next, we present its solution in Section Algorithm. We evaluate the efficiency of our algorithm in Section Experimental Results. Finally, conclusions are drawn in the last section.
Preliminaries and problem definition
A string is a sequence of zero or more symbols from an alphabet Σ; the string with zero symbols is denoted by ε. The cardinality of alphabet Σ, denoted by |Σ|, is the number of characters in Σ. The set of all strings over the alphabet Σ is denoted by Σ*. Throughout the paper, we consider the numeric alphabet Σσ which is assumed to be an interval of integers from 1 to |Σ|, i.e. Σσ={1,2,..,σ}= where |Σ|=σ. T=T1...n is a string of length n defined over Σσ. Ti is used to denote the i-th element of T, Ti..j is used as a notation for the substring Ti Ti+1..Tj of T, where 1 ≤ i ≤ j ≤ n. Similarly, a pattern P = Pi..m is a string of length m defined over Σσ. For easy notation, we use Ti to denote the length-m substring of T starting at position i; thus Ti = Ti..i+m-1. Next, we present the definition of δγ-match and order-preserving match for the string comparison problem.
Definition 1: δγ-match: Let X = Xi..m and Y=Y1..m be two equal-length strings defined over Σσ. Also, let δ and γ be two given numbers (δ,γ ∈£). Strings X and Y are said to δγ-match, denoted as. 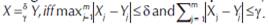 Note that the operator
Note that the operator 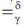 is conmutative.
is conmutative.
Example 1: There is a δγ-match, for δ=2 and γ=7, between the strings X=〈1,3,1,3,6,3,3,4,1,2〉 and Y=〈2,2,1,3,4,3,4,5,2,2〉 defined over Σ6 as |X-Y|=〈1,1,0,0,2,0,1,1,1,0〉. Note that the maximum difference between corresponding characters is 2 and takes place at the fifth position. Similarly, the sum of all differences is 7.
Now, some important concepts for the definition of order-preserving match are introduced. Let X=X1..m be a string defined over Σσ. The rank of Xi in X is defined as RankX(i)=1+| {j ∶ Xj < Xi,1 ≤ j < i }|. Furthermore, the natural representation of X is nr(X)=Rankx (1)Rankx (2)…Rankx (m). For simplicity of the description, we assume that all the characters appear at most once in X; however, the extension to the general case is straightforward. For example, if X = 〈10,15,19,12,11,18,23,22〉, then nr(X) = 〈1,4,6,3,2,5,8,7〉.
Definition 2: Order-Preserving Match: Let X=X1..m and Y = Y1..m be two equal-length strings defined over Σσ. Strings X and Y are said to order-preserving match, denoted as X↭Y iff nr(X) = nr(Y).
Example 2: Given integer strings X = 〈10, 15, 19, 12, 11, 18, 23, 22〉 and Y = 〈12,18,22,15,13,20,30,23〉, we conclude that X↭Y as nr(X) = nr(Y) = 〈1, 4, 6, 3, 2, 5, 8, 7〉
Next, we define order-preserving match for the string comparison problem and then generalize it to the associated pattern matching problem.
Definition 3: δγ-order-preserving match: Let X = X1..m and Y=Y1..m be two equal-length strings defined over Σσ. Also, δ and γ be two given numbers (δ,γ ∈£). Strings X and Y are said to δγ-order-preserving match, denoted as X↭  iff nr(X)=
iff nr(X)=  nr(Y). Note that the operator ↭ is conmutative.
nr(Y). Note that the operator ↭ is conmutative.
Example 3: Given δ = 2, γ = 6, X = 〈10,15,19,12,11,18,23, 22〉 and Y = 〈14,17,20,18,12,15,23,22〉, we conclude that X↭ Y, as nr(X) = 〈1,4,6,3,2,5,8,7〉, nr(Y) = 〈2,4,6,5,1,3,8,7〉 and nr(X) =  nr(Y).
nr(Y).
Problem 1: δγ-order-preserving matching: Let P = P1..m be a pattern string and T = T1..n be a text string, both defined over Σσ. Also, let δ and γ be two given numbers (δ,γ ∈£). The δγ-order-preserving matching problem is to calculate the set of all indices i, 1 ≤ i ≤ n - m + 1, satisfying the condition P↭  Ti.
Ti.
Algorithm
The input of the algorithm is the text T = T1..n and pattern P = P1..m, both defined over integer alphabet Σσ, and the integer bounds δ,γ∈£. We begin by creating a linear list with the length-m substring that starts at position 1 of the text, i.e. T1; this list is denoted by 𝒯. Furthermore, we create a sorted linear, called 𝒮, with the same characters. Other two (unsorted) lists are created: 𝒯nr and 𝒫nr; they contain the natural representations of 𝒫 and 𝒯1, respectively. Then, the δγ- conditions are evaluated: the maximum difference between corresponding characters of 𝒫nr and 𝒯nr is compared with δ and the sum of such differences is compared with γ. If there is a δγ-order-preserving match (see Definition 3), position 1 is reported. After this, the natural representation of the other text windows is compared with the natural representation of the pattern. Specifically, our strategy is updating 𝒯nr in O(m) time so that it contains the natural representation of the next text window to consider.
Let us assume that 𝒯nr contains the natural representation of the text window Ti, for 1 ≤ i < n - m + 1. Then, in order to transform 𝒯nr so that it contains the natural representation of Ti+1, we update the ranks in 𝒯 that are greater than the rank of 𝒯1 (the element that must be removed from the text window) by reducing them in one unit; note that the ranks that are less than 𝒯1nr remain the same. Then, we remove the element at the first position of 𝒯 and 𝒯nr. Also, the corresponding element must be removed from 𝒮, but it may be in any position of the list as it is sorted. After this step, the new character in the text window, namely 𝒯i+m, is inserted at the end of 𝒯. It is also inserted in 𝒮 but at the correct position according to the order. Such position corresponds to its rank in the text window, so it is added at the end of 𝒯nr. Finally, the ranks of the elements in the text window that are greater than or equal to 𝒯 are incremented in 1 due to the arrival of Ti+m.
The pseudocode of this algorithm, which we call δγ-OPM, is presented in section Algorithm 1: δγ-OPM algorithm. The elements of the lists are indexed from 1 to m. The methods of the lists are specified as follows:
add(x): For unsorted lists, X is inserted at the end of the list. For sorted lists, X is inserted in the correct position according to the order.
remove(i): The i-th element is removed from the list.
indexOf(x): It returns the index at which X occurs in the list.
The time complexity analysis of the algorithm is derived as follows. Line 1 takes constant time. Lines 2 and 4 take O(m log m) resulting from the sorting operation. The total cost of filling 𝒯 and 𝒮 is θ(m) as all of the insertions are done at the end of the lists (see line 3). Next, the operations within the loop of lines 5-12 are analysed for a single iteration. Evaluating the δγ- conditions takes θ(m) time (see line 6). Updating the rankings of 𝒯nr takes θ(m) (see lines 7-8 and 11-12). Deletions from the first positions take constant time (see line 9). Even the removal from S can be done in constant time if we use doubly linked lists and keep pointers from the elements in 𝒯 to the corresponding elements in 𝒮. The insertions at the end of the list take O(1) (see line 10); however, the insertion in the sorted list 𝒯nr takes linear time to find the correct position according to the order if doubly linked lists are used. Notice that if arrays were used to represent the linear lists, it would cost O(log m) to find the correct position of an element; however, the movement entailed by an insertion or deletion increases this cost to O(m).
Then, the total cost of the loop is O(nm) as the cost of each iteration is O(m) and there are O(n) iterations. Then, the total time complexity of δγ-OPM algorithm is O(nm + m log m). Since this is the first algorithm for the δγ-order-preserving matching problem, we compare it with a naive algorithm. In particular, a naive algorithm would calculate the natural representation of each text window and compare it with the natural representation of the pattern. Calculating the natural representation of each text window takes O(m log m) so the total time complexity is O(n m log m). The proposed algorithm improves this complexity to O(nm+m log m). It is important to remark that further improvements to this complexity are not easy to achieve since the updates on the considered text window may change all the rankings in it. Specifically, the removal of an element and the insertion of a new element in the window may greatly change the rankings. Furthermore the alignment of the pattern changes. Thus, it is necessary to evaluate the δγ- condition, which takes O(m).
Algorithm 1: δγ-OPM algorithm
Input: P = P1..m,T = T1..n, δ, γ, Σσ
Output: {i∈{1..n-m+1}: P ↭ Ti}
Ti}
Create: 𝒯, 𝒯 nr , 𝓟 nr as Lists, and 𝒮 as a Sorted List.
W ← T1..m.sort()
for j = 1→ m do 𝒯.add(Tj ), 𝒮.add(Wj)
𝒯 nr ← calculateNR(T1..m) ), 𝓟 nr ← calculateNR(P)
for j =1→ m do
if isAMatch (𝓟 nr , 𝒯 nr , δ, γ) then report i
for j = 2→ m do
if 𝒯j nr < 𝒯1 nr then 𝒯j nr ← 𝒯j nr -1
𝒮.remove(𝒮.indexOf(𝒯nr)), 𝒯 nr .remove(1),𝒯.remo ve(1)
𝒮.add(𝒯 i+m ),𝒯.add(𝒯i+m),𝒯 nr .add(𝒮.indexOf(T i+m))
for j = 1→m -1 do
if 𝒯j nr ≥ 𝒯m nr then 𝒯j nr ← 𝒯j nr + 1
if isAMatch( 𝒫 nr , 𝒯 nr , δ, γ) then report n-m +11
Example 4: Given δ=2, γ=6, and strings P=〈14,17,20, 18,12,15,23,22〉 and T = 〈9,10,15,19,12,11,18,23,22,26, 7,14,16,21,17,13,20,25,24,8〉, defined over Σ30, the output of the δγ-order-preserving matching problem is {2,12} because P↭ T2 and P↭ T12 (see Figure 1). Notice that P↭ T2 was shown in Example 3 by taking P as Y and T2 as X. On the other hand, P ↭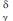 T12 since T
12
= 〈14,16,21,17,13,20,25,24〉, as nr(P) = 〈1,4,6,3,2,5,8,7〉, nr(T12) = 〈2,3,6,4,1,5,8,7〉 and nr(X)
T12 since T
12
= 〈14,16,21,17,13,20,25,24〉, as nr(P) = 〈1,4,6,3,2,5,8,7〉, nr(T12) = 〈2,3,6,4,1,5,8,7〉 and nr(X) 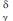 nr(Y).
nr(Y).
Experimental results
In this section, we describe the experimental setup we designed to evaluate the performance of the algorithm proposed. We compare it against the naive algorithm which processes each length-m text window separately. The time complexity of our solution is O(nm+m log m), while the time complexity of the naive algorithm is O(nm log m). In this section, we experimentally verify these theoretical bounds. Particularly, in section Experimental setup we present the experimental framework, while we describe the data generation in Section Random data generation Then, in Section Experimental results and analysis, we discuss the results obtained.
Experimental setup: In section Hardware and software, we describe the hardware and software used for the experiments. Then, we show how we vary the input parameters in Section Parameters.
Hardware and software : Both algorithms, the nai ve algorithm and our solution, were implemented using C++. The computer used for the experiments was a Lenovo ThinkPad with a processor Intel(R) Core(TM) i7 4600u CPU @ 2.10GHz 2.69 GHz and installed RAM memory of 8GB. The computer was running 64-bit Linux Ubuntu 14.04.5 LTS. The C++ compiler version was g++ (Ubuntu 4.8.4-2ubun tu1~14.04.3) 4.8.4.
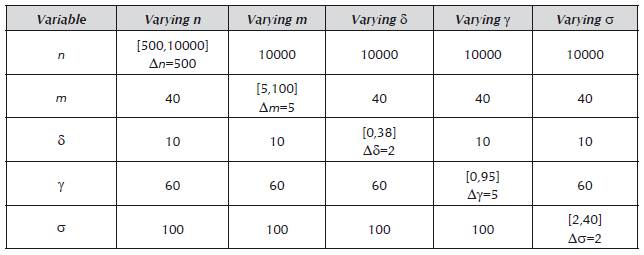
Parameters : It is clear that the defined problem of Order Preserving Matching under δ and γ distances has several parameters. They may change depending on the area of study in which the problem and pattern searching algorithms are applied. To show how our solution behaves with different configuration of the given parameters, we perform five types of experiments. In each experiment, we vary one of the given parameters n,m,δ,γ and Σ, and let the other four parameters fixed at a given value. For each experiment type, we performed five different experiments and took the median as the value to plot. The variation of the parameter values for each experiment type is presented in Table 1.
Random data generation: An experiment consists of two stages. The first stage is the pseudo-random generation of a text T of length n and the pattern P of length m. The second stage is the execution of both algorithms (naive and the proposed algorithm) on the generated strings P and T. The random generation of each character of both the pattern P and the text T is done by calling a function that pseudo-randomly selects a number between 1 and Σσ with the same probability for each number to be selected.
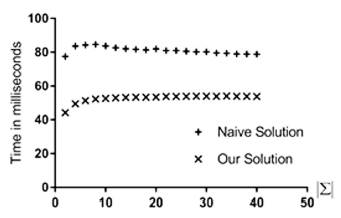
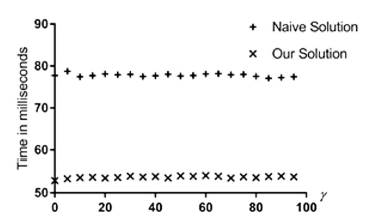
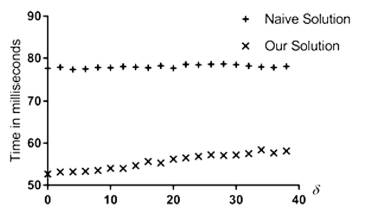
Experimental results and analysis: The first result to highlight is the fact that, in every experiment, our solution has lower execution time than the naive solution. The results shown in Figure 2 and Figure 3 show that the size of the alphabet and the parameter γ have no impact on the execution time of any of the algorithms. The result shown in Figure 4 shows no effect of the parameter δ on the naive algorithm. However, increasing δ yielded a small increase in the execution time of the experiments with our algorithm. That behavior motivated the setup of more experiments with varying values of the parameter δ; notwithstading, despite the small increase of the execution time in our algorithm, our solution outperformed the naive solution in all the experiments.
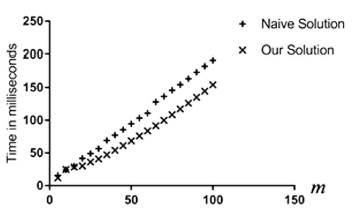
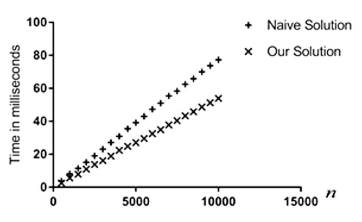
Figures 5 and Figure 6 verify the theoretical complexity analysis that states that n and m are the parameters that really determine the execution time of both algorithms. In particular, the time complexity of the naive algorithm is O(nm log m) while ours is O(nm + m log m).
In Figure 6, m is a constant and n is a variable while in Figure 5, n is a constant and m is a variable. Notice that, under these conditions, the graphs are expected to be linear and the experiments verify that. Morever, the log m extra factor of the naive algorithm's time complexity can be seen in the graphs as our solution always outperforms the naive solution in all the experiments. This also applies to the cases where both n and m are constant (see Figure 2, Figure 3 and Figure 4).
Conclusions and future work
In this paper, we propose an approximate variant of order-preserving matching that permits an individual error between the ranking of corresponding characters, and a global error across all the positions. The former is bounded by δ and the latter by γ. We present a O(nm+m log m) algorithm to solve this new problem. We verified its efficiency through experimental results. In particular, we clearly showed that the proposed algorithm outperforms the naive solution. To the best of our knowledge, it is the first approximate version of the problem that takes into account the magnitude of the rankings.
The question about the lower bound of an algorithm for the Order Preserving Matching under δ and γ distances remains open; it is left to see if there is an algorithm of better asymptotic complexity than O(nm+m log m).