Teoría euclidiana de la proporción en la construcción de los números reales: ¿un asunto útil para un profesor?

Euclidean Theory of Proportion in the Construction of Real Numbers: A Useful Subject for a Teacher?

Edgar Alberto Guacaneme Suárez^*

Artículo recibido: 30-08-2010. aprobado: 04-05-2012

Resumen:

Desde la época dorada griega, la teoría euclidiana de la proporción, expresada en el Libro V de Elementos, se constituyó en esquema para la formulación de relaciones entre magnitudes, sin interesar si estas eran o no conmensurables y, en consecuencia, sin recurrir a los valores numéricos de sus medidas para establecer tanto las razones entre magnitudes, como la proporción entre razones. Cerca de veinte siglos después, esta manera de tratamiento independiente de una estrategia aritmética parece ser precisa y, paradójicamente, el acicate y guía para la constitución del conjunto de números reales. Los historiadores de las Matemáticas han discutido la relación entre estas teorías y conjeturamos que el estudio de sus posturas puede traer beneficios a la educación del profesor de Matemáticas. Estos beneficios se refieren, entre otros aspectos, a visiones alternas de la actividad matemática de estudio de una teoría y a la ampliación de la mirada sobre los objetos matemáticos implicados en las teorías.

Palabras clave: Razón, proporción, número real, Euclides, Dedekind, Frege, conocimiento del profesor.

Abstract:

From the Greek Golden Age, the Euclidean theory of proportion, stated in Book V of Elements, was established as an outline for the formulation of relations between magnitudes, were they or not measurable and, therefore, without resort to numerical values of its measurements to establish both the ratios of magnitudes as the proportion between ratios. Nearly twenty centuries later, this way of independent treatment of arithmetic strategy seems to be accurate and, paradoxically, the incentive and guidance for the establishment of the set of real numbers. Historians of mathematics have discussed the relationship between these theories and we conjecture that the study of their positions can bring benefits to the mathematics teacher education. These benefits relate with alternative visions of the mathematical study of a theory and the extension of the look on the mathematical objects involved in theories.

Keywords: Ratio, proportion, real number, Euclid, Dedekind, Frege, teacher's knowledge.

Introducción

En el intento de hacer una aproximación a la historia de los conceptos de razón y proporción, desde nuestra posición de aprendices de la historia - y no de historiadores -, hemos llevado a cabo una búsqueda bibliográfica que nos ha conducido a identificar más de un centenar y medio de escritos de historiadores de las matemáticas y filósofos de las ciencias, que versan sobre dicho asunto. Aun sin haber hecho un estudio profundo de todos esos documentos, nos atrevemos a afirmar que la gran mayoría de ellos tratan momentos y hechos específicos del desarrollo de estos conceptos y exhiben análisis diversos sobre los mismos; esta especificidad contrasta con la ilusión -ingenua y hasta romántica- que teníamos al iniciar la búsqueda bibliográfica de encontrar una historia de la evolución de los conceptos de razón y proporción.

A través del estudio de algunos de los documentos identificados, hemos podido perfilar varios hitos que, de manera secuencial, describen varias épocas de la historia de los conceptos de razón y proporción, a saber:

a. La época de la escuela pitagórica, en la cual existía una teoría de las proporciones que, según la tradición hegemónica¹, entra en crisis por el "descubrimiento" de la inconmensurabilidad;

b. la época dorada de los griegos (fundamentalmente de Eudoxo, Euclides y Apolonio) en la que se "crea" una teoría de las proporciones, se adapta a la versión hipotético-deductiva y se usa en la descripción de las cónicas;

c. la época del surgimiento de lo que hoy se llama álgebra -y particularmente de la geometría analítica- en la que se hace uso de la teoría de las proporciones en la solución de problemas geométricos, a través de procedimientos analíticos;

d. la época del Renacimiento, en la que la clásica teoría de proporciones griega se transforma y reformula para ampliar su ámbito de aplicación a magnitudes no geométricas y su empleo en las ciencias naturales y médicas;

e. la época de creación del Cálculo y del Análisis, en la que el lenguaje de las funciones sustituye el clásico lenguaje de las proporciones empleado por varios siglos, cayendo este último en un estado de aletargamiento;

f. la época de desarrollo de los trabajos del matemático alemán Julius W.R. Dedekind y del matemático y filósofo alemán Gottlob Frege, relativos a la construcción del conjunto de los números reales, en la que de manera un poco intempestiva, la teoría euclidiana parece renacer en cuanto a su protagonismo, como acicate en dichas construcciones.

De estos hitos hemos estudiado, con entusiasmo y relativa intensidad, varios resultados de la investigación y reflexión de la historia de la Matemática acerca de la teoría euclidiana de la proporción presentada en el Libro V de Elementos (Guacaneme, en prensa), y actualmente investigamos sobre el potencial formativo que algunos de tales resultados tendrían en la educación del profesor de Matemáticas.

Colateralmente -y mediado por un interesante planteamiento de Grattan-Guinness (2004a, 2004b) acerca de la posibilidad de estudiar las "consecuencias históricas" de objetos matemáticos, desde al menos dos maneras de aprehender las matemáticas del pasado- hemos abordado el estudio de una problemática vinculada al último de los hitos reseñados antes. Esta se expresa en diversos documentos de la bibliografía consultada, a través de textos que aluden a una cierta analogía entre la definición 5 del Libro V de Elementos y la definición de los números reales expresada por Dedekind. Varias de las referencias presentan esta analogía como una cierta identidad de la razón de dos magnitudes con un número; veámoslas a través de la traducción que hemos hecho al español, cuando ha sido necesario:

La razón de una magnitud A a otra magnitud B de la misma clase es un número real, racional o irracional, determinado de la manera como se explican en lo que sigue. Este se denota por el símbolo A:B. (Hill, 1912, p. 360)

Estos seis resultados suministran una regla para determinar si la razón A:B es mayor que, o igual a, o menor que, cualquier número racional; consecuentemente, en concordancia con la definición de Dedekind, la razón A:B es considerada como un número. (Hill, 1928, p. 44)

Esto significa que la definición de número real propuesta por Richard Dedekind es la misma que la presentada por Eudoxio. (Zubieta, 1991, p. 478)

Otras, por su parte, presentan esta analogía como una correspondencia, interpretación o equivalencia:

...existe una correspondencia exacta, casi una coincidencia, entre la definición euclidiana de identidad de razones y la teoría moderna, debida a Dedekind, de los números irracionales. (Heath, 1956, p. 124)

Esta nota presenta la definición de número real atribuida a Dedekind como una interpretación de la definición de proporción de Eudoxio, tal como la enuncia Euclides al principio de su Libro V. (Zubieta, 1991, p. 477)

Como es bien sabido, las definiciones euclidianas son un equivalente de la técnica de Dedekind (a través de «cortes» en los racionales) para investigar la propiedad de los números reales. (Knorr, 1992, p. 3)

Otras, sencillamente, exhiben un tipo de relación de dependencia:

Después de más de dos milenios, la teoría de las proporciones de Eudoxio llegó a ser la base de la teoría de los números reales de Dedekind (que data de los años 1870). Aproximadamente, la teoría de las proporciones de Eudoxio corresponde a la teoría de los números reales (positivos) bajo multiplicación (Shenitzer, 1995, p. 286).

A continuación recapitularemos algunos asuntos que hemos explorado y estudiado sobre la relación entre la teoría euclidiana de la proporción y la construcción de los números reales. Inicialmente presentaremos algunos aspectos relevantes del Libro V de Elementos de Euclides, enfatizando en la idea de que en la teoría allí expuesta no es pertinente concebir las razones como números, ni la proporción como igualdad entre razones, ni operaciones entre razones. Luego, expondremos una mirada a la discusión en torno al uso que, al parecer, Dedekind hizo de la teoría euclidiana de la proporción; igualmente, a modo de hipótesis, arriesgaremos una interpretación de la manera como Frege pudo atender a aspectos de tal teoría. Finalmente, exhibiremos algunas conclusiones respecto de la intervención de la teoría euclidiana en la construcción de los números reales y presentaremos algunas reflexiones respecto de una posible utilidad de incorporar un estudio similar al presentado, en el marco de la educación de un profesor de Matemáticas.

Algunos aspectos de la teoría de la proporción en el Libro V de Elementos

Si bien varios de los trece libros que componen Elementos, magistral obra de Euclides, abordan cuestiones sobre las razones de magnitudes geométricas o números y sobre las proporciones, hemos centrado nuestra atención en el Libro V, debido a que en este se exhibe la reelaboración euclidiana de la teoría de la proporción eudoxiana, que plantea un tratamiento general para las magnitudes geométricas y ha sido ampliamente estudiada por los historiadores y filósofos; además, es esta teoría -y no precisamente a la de la proporción numérica tratada en los Libros VII, VIII y IX- la que se puede vincular con los trabajos sobre los números reales de Dedekind y Frege.

Al explorar la configuración del Libro V, en la versión de Puertas (1994, pp. 9-54), se distinguen: un grupo de dieciocho definiciones, veinticinco proposiciones -ninguna de ellas construcción

o problema- y dos porismas o corolarios. A continuación nos referiremos primero a algunas de las definiciones y posteriormente a una clasificación de las proposiciones.

Interpretación de algunas definiciones del Libro V

En su orden, las dieciocho definiciones procuran caracterizar y nominar las ideas de: parte, múltiplo, razón, guardar razón, guardar la misma razón, magnitudes proporcionales, razón mayor, menor proporción, razón duplicada, razón triplicada, magnitudes correspondientes, razón por alternancia, razón por inversión, composición de una razón, separación de una razón, conversión de una razón, razón por igualdad y proporción perturbada. El contenido de algunas de las definiciones contempla otras ideas no definidas en Elementos, tales como: magnitud, medir (o ser medido), tamaño, magnitudes homogéneas, equimúltiplo, comparación de magnitudes, antecedente, consecuente, extremos, medios, adición de magnitudes y diferencia de magnitudes.

Ahora bien, la historia de la teoría euclidiana de la proporción ha prestado especial atención a las definiciones de razón, guardar la misma razón [proporción] y razón mayor [desproporción] (definiciones 3, 5 y 7, respectivamente). Veámoslas y discutámoslas brevemente una a una.

Definición 3: una razón es determinada relación con respecto a su tamaño entre dos magnitudes homogéneas. (Puertas, 1994, p. 9)

Existe un cierto consenso en que la definición 3 presenta un carácter general y vago, respecto de la intención de definir la idea de razón. Desde nuestra perspectiva, este carácter no constituye una falencia en la teoría y, por el contrario, devela que en el conjunto de la teoría euclidiana de la proporción, no es pertinente precisarla más.

No obstante esta postura, advertimos conveniente reseñar que las ideas de tamaño y magnitudes homogéneas, implicadas en la definición 3, ameritan ser clarificadas, incluso a través de una referencia a la intuición. Respecto del tamaño de una magnitud, se puede señalar que es una característica intrínseca del objeto geométrico, de orden cuantitativo, no numérico, y no de este en relación con otro; así, por ejemplo, el tamaño de un segmento es la cantidad de longitud del mismo, pero no la medida² de la cantidad de su longitud, o bien, el tamaño de una región es la cantidad de superficie de esta, pero no su área.

Respecto de la idea de homogeneidad entre las magnitudes, basta con señalar que ello refiere a que las dos magnitudes involucradas en una razón no pueden ser de diferente naturaleza (i.e., no se puede establecer una razón entre el tamaño de un segmento y el tamaño de una superficie, así como tampoco entre el tamaño de un ángulo y el tamaño de un volumen, entre otros).

Bajo esta perspectiva la definición 3, más allá de definir la idea de razón y aún sin precisar la idea de relación, condiciona parcialmente³ la posibilidad de su existencia y apuntala aspectos respecto de su naturaleza; particularmente descarta la posibilidad de entenderla como una relación entre números (pero sí entre tamaños de magnitudes) e incluso como un número.

El papel aparentemente secundario de la definición 3, contrasta con el papel central en la teoría que le adjudican los historiadores y filósofos a la definición 5:

Definición 5: se dice que una primera magnitud guarda la misma razón con una segunda que una tercera con una cuarta, cuando cualesquiera equimúltiplos de la primera y la tercera excedan a la par, sean iguales a la par o resulten inferiores a la par, que cualesquiera equimúltiplos de la segunda y la cuarta, respectivamentey tomados en el orden correspondiente. (Puertas, 1994, p. 11)

Su interpretación en primera instancia se dificulta, desde nuestra perspectiva y experiencia, por la falta de apropiación del lenguaje retórico en que está escrita -o la carencia de un lenguaje simbólico o gráfico que la acompañe y represente-, por la vaguedad de la idea de equimúltiplo y por la generalidad implicada en la condición que se tiene que satisfacer para todos los equimúltipos (o mejor, para todas las parejas de equimúltiplos).

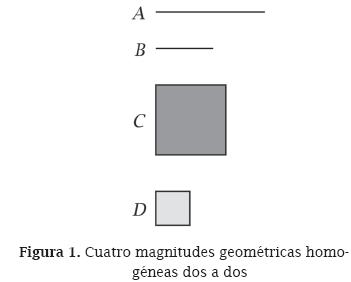
Para contrarrestar tal dificultad, recurramos al lenguaje gráfico a través de unos dibujos que representen las magnitudes implicadas, así: sean A y B segmentos, y C y D cuadrados, de los tamaños indicados en la Figura 1:

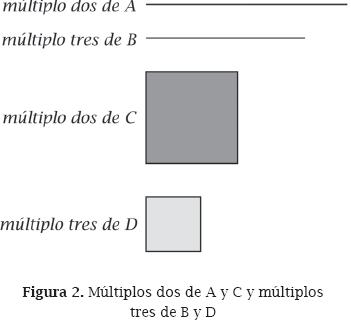
Atendiendo a la particularidad connatural de los dibujos, construyamos los múltiplos dos de A y C así como los múltiplos tres de B y D, obteniendo los dibujos que se muestran en la Figura 2⁴.

Comparando ahora los tamaños del múltiplo dos de A con el del múltiplo tres de B y a la vez el tamaño del múltiplo dos de C con el múltiplo tres de D, se establece que el múltiplo dos de A "es menor" que el múltiplo tres de B y a la vez el múltiplo dos de C "es menor" que el múltiplo tres de D, existiendo entonces la posibilidad de que A guarde con B la misma razón que C guarda con D. Si la comparación de los múltiplos de A y B arroja siempre el mismo resultado que la comparación de C y D (para los respectivos equimúltiplos), entonces se confirmará que A guarda con B la misma razón que C guarda con D.

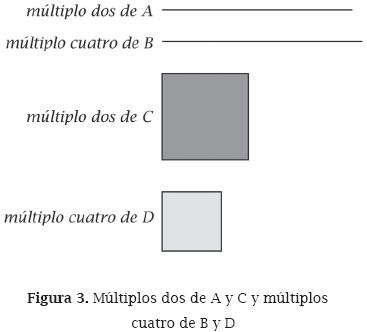
Para el ejemplo en cuestión se comprueba que las cuatro magnitudes no satisfacen la definición 5 o, en otras palabras, se verifica que A no guarda con B la misma razón que C con D, pues luego de construir los múltiplos dos de A y C y los múltiplos cuatro de B y D se verifica que, si bien el múltiplo dos de A "es menor" que el múltiplo cuatro de B, el múltiplo dos de C "es mayor" que el múltiplo cuatro de D, como se observa en la Figura 3.

Notemos desde ya que en el ejemplo no se requirió saber o precisar cuál era la relación (o razón) entre A y B, o cuál la relación (o razón) entre C y D para establecer que no guardan la misma razón.

Otra estrategia para intentar clarificar la interpretación de la definición 5, es recurrir a la traducción simbólica del contenido de la definición a través de expresiones lógicas y algebraicas. En esta dirección, en los textos de los historiadores se reportan varias versiones simbólicas (no euclidianas, por supuesto); por ejemplo, Puertas (1994) reseña dos de tales versiones en las cuales a, b, c, d son unas magnitudes del dominio de la teoría y m y n unos números naturales cualesquiera; en estas, respectivamente, se establece que se da una proporción

a:b :: c:d si y solo si:

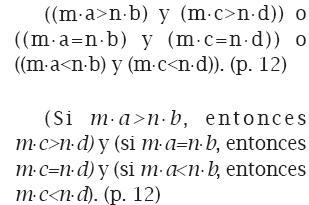
Como se puede observar, la primera se formula como disyunción de conjunciones, en tanto que la segunda es expresada como conjunción de condiciones (o conjunción de implicaciones)⁵. Más allá de la observación hecha por Puertas (1994, p. 12) sobre la no equivalencia lógica entre las dos fórmulas anteriores, resaltemos que en las expresiones simbólicas solo se incorporan relaciones entre múltiplos, pero no la razón entre dos de tales magnitudes.

Probablemente la interpretación de la definición 5 que se ha logrado a través de las representaciones gráfica y simbólica, expuestas antes, contrasta -y eventualmente se complementa- con la sugestiva interpretación que hace Fine (1917) y que hemos traducido al español:

Ya que según la Definición 5 la condición para que A, B, X, Y sean proporcionales es que: si los múltiplos A, 2A, 3A, ... y B, 2B, 3B, ... son dispuestos en un arreglo en una sola secuencia en el orden de tamaño, y de la misma manera se disponen los múltiplos X, 2X, 3X, ... y Y, 2Y, 3Y, ..., la ley de distribución de los múltiplos de A entre aquellos de B debe ser la misma que la de los múltiplos de X entre aquellos de Y. De ahí que «la identidad» de las razones

A:B y X:Y significa la identidad de estas dos leyes de distribución, y la razón A:B en sí misma significa la relación de tamaño entre A y B que es indicada por la manera en que los múltiplos de A están distribuidos entre aquellos de B.(p. 73)

Como se aprecia, esta interpretación alude a una correspondencia entre dos sucesiones ordenadas de múltiplos, cada una compuesta por los múltiplos de las dos magnitudes de una razón. Además, Fine sostiene que para una teoría general de la proporción no se requiere una definición de razón, en singular, aunque sí se exigen sendas definiciones de igualdad y desigualdad entre razones, las cuales son respectivamente proveídas en las definiciones 5 y 7 (guardar la misma razón y razón mayor). Veamos esta última.

Definición 7: entre los equimúltiplos, cuando el múltiplo de la primera excede al múltiplo de la segunda pero el múltiplo de la tercera no excede al múltiplo de la cuarta, entonces se dice que la primera guarda con la segunda una razón mayor que la tercera con la cuarta. (Puertas, 1994, p. 13)

Haciendo uso de la Definición 7 para el ejemplo gráfico que planteamos antes como interpretación de la Definición 5, se tendría que la razón que guarda C con D "es mayor" que la razón que guarda A con B, en tanto que, como señala Fine (1917, p. 73) al parafrasear la Definición 7, se logró encontrar m y n tal que

m·A<n·B pero m·C >n·D.

Con respecto a lo planteado por los historiadores sobre la Definición 7, resaltemos que Knorr (1992) establece que:

Uno de los defectos conocidos de la teoría euclidiana en el Libro V es que no prueba que «no tener la misma razón» sea equivalente a «tener una razón mayor o menor razón»(p. 8)

Sin embargo, al explorar el uso que se hace de esta definición en la teoría (por ejemplo, en el Libro V, proposiciones 9 y 10), se corrobora que Euclides sí supone tal equivalencia, con lo cual dispone de una herramienta potente para la demostración de la proporción o desproporción de cuatro magnitudes; en otras palabras, si se supone que tener una razón mayor que otra equivale a afirmar que no es cierto que exista proporción entre tales magnitudes, se dispone de una herramienta para demostrar por reducción al absurdo.

En el marco de las interpretaciones y observaciones relatadas antes para las definiciones consideradas, hemos querido dejar claro, desde nuestra perspectiva e interpretación, en la teoría euclidiana de la proporción contenida en el Libro V:

a. Las razones son relaciones, pero no son números ni se establecen entre números, sino entre tamaños de magnitudes geométricas homogéneas dos a dos.

b. La proporción no es una igualdad entre razones (y por tanto no es igualdad entre números) ni depende de estas, sino fundamentalmente del comportamiento relativo y correspondiente de los múltiplos de las magnitudes implicadas.

Una clasificación de las proposiciones y porismas del Libro V

Las veinticinco proposiciones y los dos porismas se pueden clasificar en cinco grupos de propiedades: cuatro de ellos atienden a los diferentes dominios que relaciona cada proposición (v.g., magnitudes y magnitudes, magnitudes y proporciones, proporciones y magnitudes, proporciones y proporciones) en tanto que el quinto ubica una proposición que no establece relación entre ninguno de tales dominios.

Así, en un primer grupo estarían las proposiciones que se refieren a las magnitudes y sus múltiplos, pero que no aluden a las razones ni a las proporciones. En este grupo hemos clasificado las proposiciones 1, 2, 3, 5 y 6. Las expresiones simbólicas [m(A1+A2+...+An)= mA1+mA2+...+mAn], [(m-n)A=mA+nA], [m(nA)=(mn)A], [m(A-B)=mA-mB] y [(m+n)A=mA- nA] constituyen una interpretación simbólica de cada una de las proposiciones aludidas. Como se ve a través de estas -aunque también en la retórica enunciación euclidiana- no se incluye alusión alguna a la razón ni a la proporción, aunque sí a los múltiplos de las magnitudes, a la suma o diferencia de magnitudes, o a la adición, diferencia y multiplicación de los números ligados a los múltiplos. En cierto sentido, este conjunto de proposiciones caracteriza parcialmente el dominio de magnitudes con la operación suma.

En un segundo grupo ubicamos dos proposiciones (7 -sin su porisma 7'- y 8), que se pueden representar con sendas expresiones: [Si A=B, entonces A:C::B:C y C:A::C:B] y [Si A<B, entonces A:CA<B:C; y C:A>C:B], respectivamente. Una interpretación de estas expresiones permitiría reconocer que las proposiciones aluden a propiedades "de orden" de las razones a partir de propiedades "de orden" en las magnitudes; en otras palabras, estas proposiciones expresarían cómo la igualdad o desigualdad de las magnitudes se refleja o trasmite a algunas de las razones en que ellas están implicadas.

El tercer grupo está integrado por proposiciones (9, 10, 14, 20, 21 y 25) que describen cómo las relaciones entre razones determinan relaciones u operaciones entre magnitudes. Sus expresiones simbólicas respectivamente son: [Si A:C::B:C, entonces A=B. Y, si C:A::C:B, entonces A=B], [Si A:C<B:C, entonces A<B. Y si C:A<C:B, entonces A>B], [Si A:B::C:D y AC, entonces BD], [Si A:B::D:E y B:C::E:C y AC, entonces DC], [Si A:B ::E:C y B:C::D:E y AC, entonces DC], [Si A:B::C:D y A>B y A>C y B>D y C>D, entonces A+D>B+C]. Una interpretación semejante a la hecha para el segundo grupo referiría que las proposiciones aluden a propiedades "de orden" de las magnitudes a partir de propiedades "de orden" de las razones.

El cuarto grupo contiene el mayor número de proposiciones (4, 7', 11, 12, 13, 16, 17, 18, 19, 19', 22, 23 y 24) e incluye propiedades de las proporciones o desproporciones, es decir, de las razones en sí mismas. Sus enunciados simbólicos respectivamente son: [Si A:B::C:D, entonces para todo m y n, mA:nB::mC:nD], [Si A:B::C:D, entonces B:A::D:C], [Si A:B::C:D y C:D::E:F, entonces A:B::E:F], A₁:B₁::A₂:B₂:: ... ::A_n:B_n, entonces (A₁+A₂+...+A_n):(B₁+B₂+...+B_n) ::A_i:B_i, para todo i=1,...,n], [Si A:B::C:D y C:D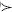E:F, entonces A:B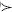E:F], [Si A:B::C:D, entonces A:C::B:D (a condición que las cuatro magnitudes sean homogéneas)], [Si (A+B):B::(C+D):D, entonces A:B::C:D], [Si A:B::C:D, entonces (A+B):B::(C+D):D], [Si ( A + B ):( C + D ):: A : C, entonces (A+B):(C+D)::B:D], [Si (A+B):(C+D)::B:D, entonces (A+B):(C+D)::A:C], [Si A₁:A₂::B₁:B₂, A₂:A₃::B₂:B₃, ... , y A_n1:A_n::B_n1:B_n, entonces A₁:A_n::B₁:B_n], [Si A:B::E:F y B:C::D:E, entonces A:C::D:F], [Si A:B::C:D y E:B::F:D, entonces (A+E):B::(C+F):D]).

El último grupo contiene únicamente a la proposición 15, la cual solo alude a una proporción. Su expresión simbólica es simplemente [A:B‰nA:nB].

Entre otros aspectos importantes, la anterior clasificación permite reconocer que no existen proposiciones que establezcan operaciones entre razones, a pesar de que sí se admitan operaciones entre las magnitudes implicadas en las razones. Este punto será trascendental en la argumentación que adelante explicitaremos respecto de la imposibilidad de reconocer en la teoría euclidiana una estructura para las razones, similar a la que se tendría para los números reales⁶.

Dedekind y la teoría de la proporción

En la mayoría de los tratamientos encontrados en los documentos de donde proceden las citas presentadas en la introducción de este documento -y en otras que no hemos referenciado-, se encuentra la siguiente traducción simbólica⁷ de la definición 5 del Libro V de Elementos:

A:B=C:D si y solo si para cualesquiera enteros positivos n, m,

Si nA = mB entonces, nC = mD

Si nA>mB entonces, nC>mD

Si nA<mB entonces, nC<mD

Haciendo transformaciones algebraicas en las expresiones anteriores -sin necesariamente considerar su viabilidad y rigurosidad-, normalmente se obtienen las sentencias siguientes⁸:

Si A/B = m/n entonces, C/D = m/n

Si A/B>m/n entonces, C/D>m/n

Si A/B<m/n entonces, C/D<m/n

Al interpretar tales sentencias, se puede argüir que, para el primer caso (i.e., cuando las magnitudes A y B son conmensurables) la razón A/B (o el número racional m/n, dado que son iguales) fragmenta al conjunto de los racionales en dos clases definidas, respectivamente, por los racionales mayores o menores que m/n, donde este pertenece a alguna de ellas. Para el segundo y tercer caso, la razón A/B fragmenta al conjunto de los racionales en dos clases de números estrictamente mayores o menores que esta, en tanto que esta se da entre magnitudes inconmensurables y no puede ser expresada como un número racional. Desde una perspectiva general, la anterior interpretación es en esencia análoga a la que se puede hacer de la construcción de los reales presentada por Dedekind y recapitulada al español en una obra de divulgación de la historia de las Matemáticas (Dedekind, 1968).

Sin embargo, como lo menciona Leo Corry (1994, p. 8)⁹, existen historiadores de las matemáticas que rechazan la existencia de una correspondencia o equivalencia entre la teoría euclidiana de las proporciones y la teoría de los números reales de Dedekind, bajo la idea que la interpretación de los textos griegos debe hacerse en el marco de las restricciones en que estos fueron producidos.

Una de tales restricciones se refiere al lenguaje; en este sentido, no se acepta la traducción o formulación simbólica de las definiciones, ni las interpretaciones y deducciones que a partir de ellas se hacen. Otra de las restricciones obedece a la radical diferencia entre la idea de número de la obra griega y la del número del siglo XIX; la idea griega reconoce a los números y las magnitudes como cantidades no abstractas asociadas respectivamente al contar y medir, en tanto que la idea moderna se refiere a la cantidad como abstracta y general. En Elementos se establece una clara diferencia entre el contexto de las magnitudes geométricas (o cantidades continuas) y el de los números (o cantidades discretas), al punto que hay una formulación específica de teoría de la proporción en cada uno de ellos.

Más allá de la discrepancia interpretativa entre los historiadores, debemos reseñar que también se presentó entre el matemático alemán Rudolph Otto Sigismund Lipschitz y, precisamente, Julius Wilhelm Richard Dedekind. Lipschitz, en su correspondencia con Dedekind¹⁰, le manifestó que su teoría de las cortaduras difería tan solo en formulación, pero no en contenido matemático, de la concepción griega de número. De manera específica, Lipschitz rechazaba la afirmación de que tal teoría fuera la primera en demostrar legítimamente que √2·3=√6.