Reflexiones sobre la enseñanza de la geometría en primaria y secundaria ^*

Reflections on the Teaching of Geometry in Primary and Secondary Schools

Ángel Gutiérrez^*
Adela Jaime^**

^*Universidad de Valencia. Valencia, España. www.uv.es/Angel.Gutierrez, angel.gutierrez@uv.es
^**Universidad de Valencia. Valencia, España. adela.jaime@uv.es

Recibido: 15/01/12, aprobado: 15/11/12

Resumen

En este artículo presentamos introducciones a algunos modelos didácticos centrales de la enseñanza de la geometría en los diferentes niveles educativos desde infantil hasta la universidad. En primer lugar introducimos el modelo de Van Hiele, que es el marco más efectivo para organizar la enseñanza de la geometría en los diferentes niveles educativos. Nos centramos en uno de sus componentes, las fases de aprendizaje, que sugiere cómo organizar los contenidos de los temas de enseñanza de las matemáticas escolares. Luego, prestamos atención al modelo de Vinner de aprendizaje de conceptos matemáticos con un fuerte apoyo gráfico. Se trata de una propuesta más específica que el modelo de Van Hiele, si bien son plenamente compatibles, centrada en describir el aprendizaje de conceptos que admiten representaciones gráficas potentes, basada en la distinción entre las imágenes conceptuales y las definiciones conceptuales, para mostrar el papel crítico que pueden cumplir los ejemplos y los contraejemplos en la comprensión y el aprendizaje por los estudiantes. Por último, reflexionamos sobre la necesidad de que los profesores tengan en cuenta las representaciones gráficas, tanto físicas como mentales, utilizadas en la enseñanza y el aprendizaje de la geometría. Describimos los principales elementos que forman parte de las imágenes, procesos y habilidades de visualización presentes en el trabajo con elementos geométricos.

Palabras Clave Educación matemática, Didáctica de la geometría, Van Hiele, modelo de Vinner, visualización.

Abstract

In this paper we introduce some important educational models relevant to the teaching and learning of Geometry in every educational level, from kindergarten to university. First, we describe the Van Hiele model, that currently is the most effective framework to organize the teaching of Geometry in any educational level. We will focus on one of its components, namely the phases of learning that proposes teachers a way to organize the contents of the lessons of Mathematics. Next, we will pay attention to the Vinner model of learning of mathematical concepts having strong graphical support. This model is more specific than the Van Hiele model, although they are fully compatible. The Vinner model describes the learning of concepts with graphical support based on the distinction among concept images and concept definitions, showing the role examples and counterexamples may play in students' understanding and learning. Lastly, we will raise the need for teachers to take into consideration graphical representations, both physical and mental, used in teaching and learning Geometry. I will describe the main components of the images, processes and abilities of visualization present when working with geometric elements.

Keywords Mathematics education, Geometry education, Van Hiele, model of Vinner, visualization.

Introducción

Existe un acuerdo generalizado entre didáctas de las matemáticas y profesores de matemáticas en que la enseñanza de la geometría en los niveles de Primaria y Secundaria debe basarse en metodologías que faciliten la actividad de exploración y descubrimiento por los estudiantes. Fruto de la actividad de los investigadores en educación matemática, existen varios modelos teóricos que identifican y organizan diversos elementos intervinientes en los procesos de enseñanza y aprendizaje de la geometría, con el fin de facilitar a los profesores la tarea de planificar y gestionar sus clases para que sean activas y participativas. En este texto se presentan reflexiones sobre algunos de tales marcos teóricos, aparentemente desconectados pero que, en realidad, presentan estrechas relaciones que pueden ayudar a los profesores a tener una visión más global y conexa de la geometría, su enseñanza y su aprendizaje.

El modelo de razonamiento de Van Hiele (1986) es, en la actualidad, el marco más provechoso para organizar la enseñanza de la geometría y realizar una correcta evaluación del aprendizaje comprensivo de los estudiantes. En este artículo,también, se presentan las fases de aprendizaje, el componente del modelo relacionado de manera más directa con la actividad cotidiana de profesores y estudiantes.

Por su parte, S. Vinner (1991) ha definido un modelo que explica cómo se produce el aprendizaje de conceptos matemáticos con fuerte contenido gráfico o visual, y propone a los profesores formas de prevenir o corregir aprendizajes erróneos. En la segunda parte del artículo, se exponen las líneas maestras del modelo de Vinner.

No es posible analizar adecuadamente la enseñanza y el aprendizaje de la geometría sin tener en cuenta la influencia de las formas de presentar la información gráfica en la comprensión por los estudiantes de los contenidos estudiados. En la tercera parte del artículo se muestra un modelo de interpretación del uso de elementos visuales por parte de un estudiante, cuando realiza actividades de aprendizaje, resolución de problemas, etcétera, de contenidos geométricos.

Las fases de aprendizaje de Van Hiele

Existen diversas publicaciones que presentan muestras de cómo utilizar el modelo de Van Hiele (1986), tanto organizaciones curriculares completas de toda la enseñanza no universitaria (NCTM, 2003), como organización de unos contenidos matemáticos enseñados a lo largo de los años (Jaime, 1993; Jaime y Gutiérrez, 1996) u organización de un tema específico de un grado particular (Corberánet al., 1994). Un elemento del modelo de Van Hiele son las fases de aprendizaje. Estas constituyen una propuesta metodológica para los profesores que les indican cómo organizar los diferentes tipos de contenidos de un tema específico, secuenciándolos para que faciliten el progreso de los estudiantes y gradúen su aprendizaje.

Como indican Jaime y Gutiérrez (1990), Van Hiele caracteriza el aprendizaje como un resultado de la acumulación de la cantidad suficiente de experiencias adecuadas; por tanto, existe la posibilidad de alcanzar niveles más altos de razonamiento fuera de la enseñanza escolar si se consiguen las experiencias apropiadas. No obstante, esas experiencias, aunque existen y no deben despreciarse, generalmente no son suficientes para producir un desarrollo de la capacidad de razonamiento completo y rápido, por lo que la misión de la educación matemática escolar es proporcionar experiencias adicionales, bien organizadas para que sean lo más útiles posible. La función de las fases de aprendizaje propuestas por Van Hiele consiste en sugerir al profesor cómo realizar dicha organización. Las fases de aprendizaje son unas etapas en la graduación y organización de las actividades que debe realizar un estudiante para adquirir las experiencias que le lleven al nivel superior de razonamiento. A lo largo de estas fases, el profesor debe procurar que sus alumnos construyan una red mental de relaciones entre los diferentes contenidos matemáticos que tiene que aprender, incluyendo en esta red las formas de razonamiento propias del nivel de razonamiento al que deben acceder. Es necesario conseguir, en primer lugar, que los estudiantes adquieran de manera comprensiva los conocimientos básicos necesarios (nuevos conceptos, propiedades, vocabulario, etcétera) con los que tendrán que trabajar, para después centrar su actividad en aprender a utilizarlos y combinarlos. Las fases de aprendizaje propuestas por Van Hiele son cinco (Jaime y Gutiérrez, 1990):

Primera fase: información

Se trata de una fase de toma de contacto. El profesor debe informar a los estudiantes sobre el campo de estudio en el que van a trabajar, qué tipo de problemas se van a plantear, qué materiales van a utilizar, etcétera. Así mismo, los alum-nos aprenderán a manejar el material y adquirirán una serie de conocimientos básicos imprescindibles para poder empezar el trabajo matemático propiamente dicho.

Ésta es también una fase de información para el profesor, pues sirve para que éste averigüe los conocimientos previos de los estudiantes sobre el tema que se va a abordar. Como se mencionaba, la experiencia extraescolar no debe despreciarse, sino que puede aprovecharse como fuente de motivación; además, es conveniente evitar hacer un trabajo repetido o tratar de "enseñar" cosas que los alumnos ya saben. Por otra parte, muchas veces tendremos que trabajar en un tema que no es absolutamente nuevo para los estudiantes, que ya lo han estudiado en algún curso anterior, por lo que, para una buena utilización del modelo de Van Hiele, es imprescindible que el profesor sepa qué grado de conocimiento de los contenidos del tema tienen sus alumnos y, sobre todo, qué nivel de razonamiento son capaces de mostrar.

Segunda fase: orientación dirigida

En esta fase los estudiantes empiezan a explorar el campo de estudio por medio de investigaciones basadas en el material que les ha sido proporcionado. El objetivo principal de esta fase es conseguir que los estudiantes descubran, comprendan y aprendan cuáles son los conceptos, propiedades, figuras, etcétera, principales en el área de la geometría que están estudiando. En esta fase se construirán los elementos básicos de la red de relaciones del nuevo nivel. Con respecto a esta fase, Van Hiele (1986) afirma: "las actividades, si son escogidas cuidadosamente, forman la base adecuada del pensamiento del nivel superior" (p. 97).

Obviamente los estudiantes, por sí solos, no podrían realizar un aprendizaje eficaz (en cuanto a los resultados obtenidos y al tiempo empleado), por lo que es necesario que las actividades propuestas estén convenientemente dirigidas hacia los conceptos, propiedades, entre otros, que deben estudiar. El trabajo que vayan a hacer estará organizado para que los conceptos y estructuras característicos se les presenten de manera progresiva.

Tercera fase: explicitación

Una de las finalidades principales de la tercera fase es hacer que los estudiantes intercambien sus experiencias, comenten las regularidades que han observado, y expliquen cómo han resuelto las actividades; todo ello dentro de un contexto de diálogo en grupo. Es interesante que surjan puntos de vista divergentes, ya que el intento de cada estudiante por justificar su opinión hará que tenga que analizar con cuidado sus ideas (o las de su compañero), además de ordenarlas y expresarlas con claridad. Este diálogo hace que sea en el transcurso de esta fase cuando se forma parcialmente la nueva red de relaciones.

En esta fase se tiene también el objetivo de conseguir que los estudiantes terminen de aprender el nuevo vocabulario, correspondiente al nuevo nivel de razonamiento que están empezando a alcanzar. En algunos casos, especialmente con niños de enseñanza Primaria, no es conveniente, desde el punto de vista didáctico, introducir al mismo tiempo nuevos conceptos, nuevo vocabulario y nuevos símbolos. Una técnica utilizada por los maestros para reducir este problema consiste en permitir que, al principio, los niños denominen las nuevas figuras o propiedades a su gusto, hasta que hayan adquirido un dominio suficiente de las mismas. En la fase de explicitación se fomentará el paso del vocabulario de los niños al término matemático usual.

La tercera fase no hay que entenderla como un periodo de actividad entre las fases 2 y 4, sino que se trata de una fase transversal, que se superpone a las demás fases, pues hay que aprovechar cualquier momento propicio para pro-mover el diálogo entre los estudiantes (con participación o no del profesor, según interese).

Cuarta fase: orientación libre

Este es el momento en el que los alum-nos deberán aplicar los conocimientos y lenguaje que acaban de adquirir a otras investigaciones diferentes de las presentadas anteriormente. El campo de estudio ya es, en gran parte, conocido por los alumnos, pero estos todavía deben perfeccionar su conocimiento del mismo. Esto se consigue mediante el planteamiento por el profesor de problemas que, preferiblemente, puedan desarrollarse de diversas formas o que puedan llevar a diferentes soluciones. En estos problemas se colocarán indicios que muestren el camino a seguir, pero de forma que el estudiante tenga que combinarlos adecuadamente, aplicando los conocimientos y la forma de razonar que ha adquirido en las fases anteriores.

Queremos remarcar que el núcleo de esta fase está formado por actividades de utilización y combinación de los nuevos conceptos, propiedades y forma de razonamiento. Los problemas que hay que plantear en la fase 4 no tienen nada que ver con los ejercicios de "aplicación", tan frecuentes en nuestros libros de texto de enseñanza primaria y secundaria, para cuya solución solo hace falta recordar algún hecho concreto y utilizarlo directamente; por el contrario, algunos de los problemas de esta fase deben presentar situaciones nuevas, ser abiertos, con varios caminos de resolución. Este tipo de actividad es la que permitirá completar la red de relaciones que se empezó a formar en las fases anteriores, dando lugar a que se establezcan las relaciones más complejas e importantes.

Quinta fase: integración

A lo largo de las fases anteriores, los estudiantes han adquirido nuevos conocimientos y habilidades, pero todavía deben adquirir una visión general de los contenidos y métodos que tienen a su disposición, relacionando los nuevos conocimientos con otros campos que hayan estudiado anteriormente; se trata de condensar en un todo el dominio que han explorado sus pensamientos. En esta fase, el profesor puede fomentar este trabajo proporcionando comprensiones globales, pero es importante que estas no les aporten ningún concepto o propiedad nuevos a los estudiantes: solamente deben ser una acumulación, comparación y combinación de cosas que ya conocen.

En Corberán et al. (1994) se presenta una secuencia de actividades para la enseñanza de polígonos organizada de acuerdo con los niveles y las fases del modelo de Van Hiele. Por otra parte, en Jaime (1993) y Jaime y Gutiérrez (1996) se ofrece una propuesta de enseñanza de las traslaciones, giros y simetrías del plano para estudiantes desde educación Primaria hasta la universidad, organizada a partir de las directrices de los niveles y las fases del modelo de Van Hiele. A continuación, a modo de ejemplo del modelo de Van Hiele, se presenta un pequeño fragmento de las actividades incluidas en esta propuesta para la enseñanza de los giros a estudiantes situados en el nivel 2 de razonamiento.

Las actividades tienen como objetivo general la enseñanza de las propiedades características de los giros, para que los estudiantes puedan enunciar, a continuación, la definición de giro, el producto de giros del mismo centro, y algunas propiedades básicas de los giros como el cálculo del centro o la amplitud de un giro a partir de otros datos.

1. Actividades de la primera fase. Sus objetivos son obtener información de los conocimientos que tienen los estudiantes sobre ángulos, manejo del transportador y el compás para realizar construcciones relacionadas con los giros.

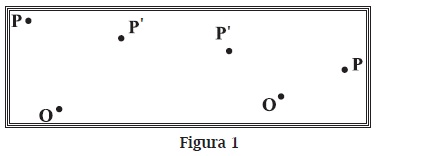
a. El punto P' es la imagen del punto P por un giro con centro en el punto O (figura 1). Marca el ángulo que se forma y mídelo.

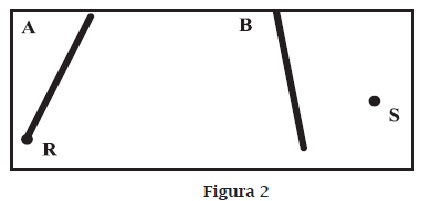
b. Sin utilizar ningún instrumento de medida, gira el segmento A de la figura 2 un ángulo de aproximadamente -45°; toma como centro del giro el punto R. Comprueba luego el resultado con un instrumento de medida.

Repite la actividad con ángulos de +90°, -120°, +30°, -270°, +60°, y -200°. Repite toda la actividad con el segmento B y centro de giro S.

2. Actividades de la segunda fase. Sus objetivos son ayudar a los estudiantes a descubrir las propiedades características de los giros, para que puedan llegar a formular la definición de giro, y que aprendan a calcular de manera exacta imágenes de puntos y figuras por giros. Estos objetivos estarán siempre apoyados en la visualización de los movimientos y en la actividad inductiva. A continuación solo se presentan parte de las actividades de este bloque.

Estas actividades son de la segunda fase, porque su objetivo es el descubrimiento de algunas propiedades elementales y centrales de los giros, que es necesario conocer para poder profundizar en el aprendizaje de los giros.

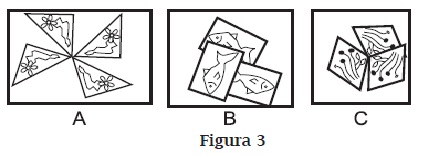
a. Determina la posición exacta del centro de giro en cada grupo de figuras iguales. Explica cómo lo has obtenido.

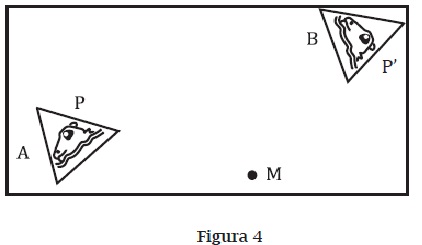
b. Al aplicarle a la figura 4A un giro con centro M, hemos obtenido la figura 4B. La imagen del punto P es P'. Dibuja el arco de circunferencia recorrido por P y los lados del ángulo <PMP'. Mide el ángulo <PMP'.

Elige dos puntos más de la figura 4A y haz lo mismo con ellos. ¿Qué sucede con las medidas de los ángulos?

Generaliza lo que acabas de observar: "Cuando giramos una figura, el ángulo girado por todos sus puntos...".

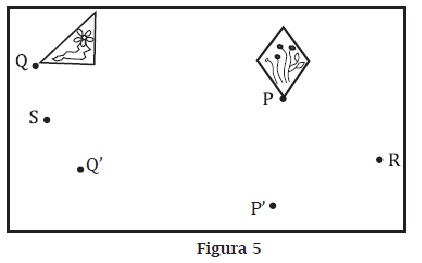
c. P' es la imagen de P por un giro con centro en R. ¿Puedes colocar la imagen del rombo directamente, sin hacer más cálculos? Para no resolverla actividad por tanteo, determina el ángulo de giro (<POP') y halla las imágenes de otros puntos del rombo.

Utiliza el mismo procedimiento para calcular la imagen del triángulo por un giro con centro de giro en S, sabiendo que Q' es la imagen de Q.

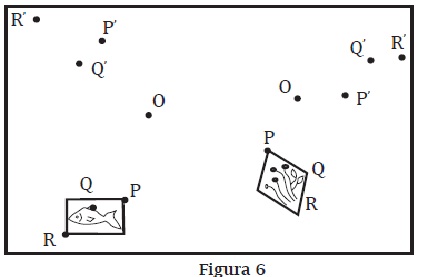
d. ¿Pueden ser los puntos P', Q' y R' las imágenes de P, Q y R, respectivamente, por medio de un mismo giro de centro O? Justifica tu respuesta.

3. Actividades de la tercera fase. Como se indicaba en la descripción teórica de la fase 3, ésta debe estar siempre presente. Todas las actividades hechas hasta ahora deben incorporar algún momento para que los estudiantes dialoguen, expliquen qué han hecho y por qué lo han hecho, planteen sus dudas, etcétera. Por tanto, en nuestras unidades de enseñanza no hay actividades específicas de la tercera fase.

4. Actividades de la cuarta fase. Sus objetivos son el aprendizaje de la equivalencia de giros y del producto de giros con el mismo centro, tanto en su aspecto manipulativo, de construir imágenes de productos de giros, como en su aspecto matemático abstracto, de generalizar los resultados de los ejemplos calculados para formular los enunciados teóricos de los resultados del producto de varios giros del mismo centro. El estudio del producto de giros de distintos centros es más complejo, y hay que esperar a que los estudiantes estén en el nivel 3. Pero en el nivel 2 pueden realizar actividades para descubrir que los centros de los giros que relacionan dos puntos dados están en la mediatriz entre dichos puntos.

Estas actividades son de la fase 4 porque utilizan los conocimientos adquiridos en la fase 2 para resolver problemas nuevos y más complejos.

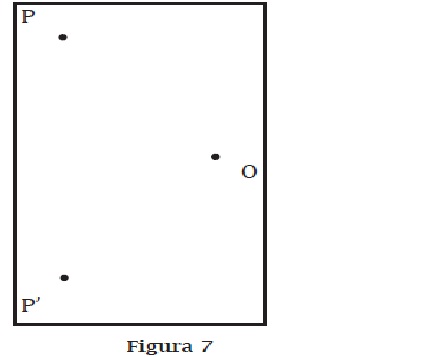
a. Un giro con centro en O mueve el punto P hasta el punto P'. Dibuja el recorrido de P hasta P'.

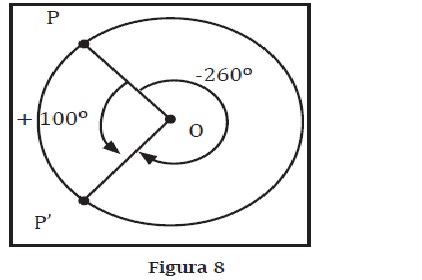
El profesor debe buscar dos alumnos que hayan dibujado los dos recorridos diferentes y pedirles que dibujen sus soluciones en el tablero, para que se vea que hay dos soluciones. La figura 8 debe servir para que los estudiantes entiendan que el giro de ángulo de 100° y el giro de ángulo de 260° son equivalentes, ya que producen el mismo resultado, pues el punto P acaba llegando al mismo lugar en ambos casos. El profesor introducirá la notación de grados positivos y negativos y el convenio de considerar positivos los ángulos en sentido contrario a las manecillas del reloj y negativos los ángulos en sentido de las manecillas del reloj.

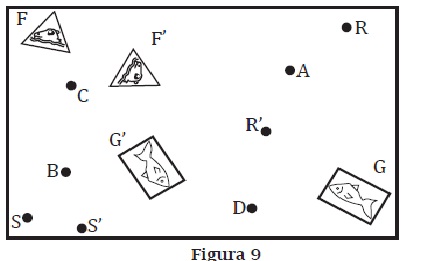
Traza los dos posibles recorridos de los giros de los puntos R (con centro en A) y S (con centro en B) de la lámina inferior. Escribe los ángulos de giro orientados (con signo) correspondientes. Haz lo mismo con las figuras 9F y 9G, que han girado alrededor de los centros C y D respectivamente.

¿Qué relación existe entre los ángulos de dos giros equivalentes? Identifica los giros equivalentes a los siguientes: G(A,90°), G(B,-100°), G(C,+70°), G(D,+180°).

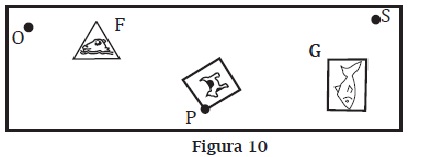
b. Aplícale a la figura 10F el giro G(O,+45°). A la figura imagen de este giro, aplícale el giro G(O,+100°). Identifica un movimiento simple que permita pasar directamente desde la figura 10F hasta la última imagen obtenida, e indica las características de dicho movimiento.

El profesor explicará el concepto de producto de dos giros basándose en la analogía de un viaje de varias etapas. También introducirá la notación de producto de giros: G(O,+100°)×G(O,+45°) y el convenio de que se realiza primero el movimiento escrito más a la derecha.

Repite la actividad con las otras figuras de la lámina y los productos G(P,-30°)×G(P,-60°) y G(S, 110°)×G(S,-50°).

Generaliza el resultado que has obtenido: "El resultado del producto de dos giros con el mismo centro es...".

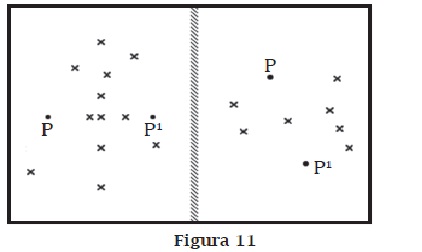
c. Busca los puntos de la lámina que pueden ser centros de giros que transformen P en P'. Busca otros puntos, no dibujados en la lámina, que también puedan ser centros de giro. ¿Hay más posibilidades?

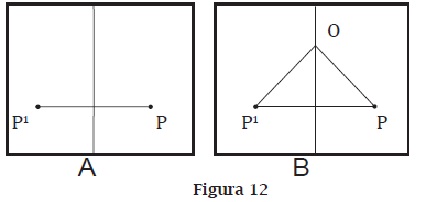
d. Busca, en la figura 12A, el centro de un giro de -80° que transforme P en P'.

Si no se te ocurre otro procedimiento mejor, prueba por tanteo y después fíjate en la figura de la derecha: ¿Qué tipo de triángulo es POP'? ¿Cuánto miden sus ángulos <O, <P y <P'?

e. Da centros de giros que lleven el punto A hasta el A'.

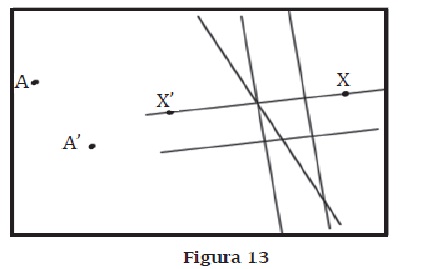
Justifica cuál(es) recta(s) de la lámina contiene(n) el(los) centro(s) del (de los) giro(s) que lleva(n) X hasta X'.

5. Actividades de la quinta fase. Esta fase debe servir para que los estudiantes lleguen a elaborar una síntesis de lo que han aprendido sobre giros y a integrar estos nuevos conocimientos con los que pudieran tener antes. No se plantean actividades concretas para esta fase porque dependen de cada caso en particular. Si se trata de un grupo de estudiantes que no había estudiado antes ninguna isometría, en la quinta fase el profesor hará un resumen de las definiciones y propiedades estudiadas y los guiará para que verbalicen las relaciones descubiertas. Si, por el contrario, es un grupo con el que ya se había estudiado contenidos más elementales de giros, el profesor, además del resumen mencionado, planteará a sus alumnos cuestiones que les hagan relacionar los conocimientos anteriores sobre giros con los nuevos. Si la clase ha estudiado otras isometrías (normalmente traslaciones y simetrías), el profesor puede plantear actividades que relacionen los giros con las otras isometrías. Por ejemplo, puede plantear productos mixtos de giros y simetrías o traslaciones, o puede plantear un producto de giros de distintos centros cuyos ángulos sumen 0º, para descubrir que el resultado es una traslación.

Aprendizaje de conceptos geométricos elementales

En geometría, como en las demás partes de las matemáticas escolares, los estudiantes deben entender y aprender conceptos, propiedades de estos conceptos y relaciones entre unos y otras. En contextos matemáticos en los que hay un importante soporte gráfico y visual, los procesos de aprendizaje están muy condicionados por el uso de objetos físicos, figuras, diagramas, etcétera. De manera general, se aprecia un desajuste entre los componentes gráficos y verbales de las actividades y respuestas de los estudiantes. Este desajuste se puede entender gracias a los resultados de las investigaciones del didacta S. Vinner (citado por Gutiérrez y Jaime,1996).

Cuando los profesores y libros de texto españoles presentan por primera vez a los estudiantes un concepto nuevo de geometría elemental, suelen recurrir a uno de estos dos métodos de enseñanza: i) enunciar una definición matemática de dicho concepto (más o menos formal, según el curso) y, a continuación, plantear ejercicios de memorización y de reconocimiento de algunas figuras concretas, ii) presentar ejemplos de figuras que representan ese concepto, haciendo una descripción de sus características matemáticas (y, a veces, físicas), a continuación, enunciar una definición matemática del concepto y, por último, plantear ejercicios de memorización de la definición y de reconocimiento de otras figuras concretas.

En ambos casos, los profesores suelen poner más énfasis en las definiciones que en los ejemplos, sin darse cuenta de que son los últimos los que impactan más en los estudiantes y los que producen un efecto mental más duradero y profundo. Según Vinner (1991), cuando leemos o escuchamos el nombre de un concepto conocido, se estimula nuestra memoria y se evoca algo, que raramente es la definición del concepto, sino un conjunto de representaciones visuales, imágenes, impresiones o experiencias. Este "algo" es lo que Vinner llama la imagen del concepto (o imagen conceptual). En el caso de conceptosgeométricos, la imagen conceptual que se crea en la mente de los estudiantes está compuesta por las diversas figuras, dibujos o representaciones que recuerdan los estudiantes como ejemplos de dicho concepto, junto al conjunto de las propiedades que el estudiante asocia al concepto. Según esto, una imagen de un concepto es correcta cuando le permite al estudiante discriminar sin errores todos los ejemplos de ese concepto y cuando las propiedades que lleva asociadas son todas relevantes. Dichas propiedades no son necesariamente matemáticas puesto que, especialmente en estudiantes situados en el primer o segundo niveles de Van Hiele, también pueden ser propiedades irrelevantes de tipo físico. Por ejemplo, la imagen del concepto de rectángulo que se for-man muchos estudiantes de enseñanza primaria está compuesta por una serie de rectángulos concretos colocados en posición estándar (el par de lados más largos horizontales) y por algunas propiedades derivadas de estas figuras, como tener los ángulos rectos, los lados opuestos iguales, los lados verticales y horizontales, siendo los horizontales más largos que los verticales, etc.

Por otra parte, fruto de los métodos de enseñanza que se mencionaban antes, los estudiantes memorizan una cierta definición, que repiten cuando el profesor les pregunta pero que no utilizan cuando les pide que pongan en acción dicho concepto para resolver un problema. Vinner y Hershkowitz (1983) llaman definición de un concepto a la definición verbal que un estudiante tiene en su memoria y que recita cuando se le pide. La definición de un concepto expresada por un estudiante no tiene por qué estar ligada operativamente a su imagen de ese concepto en el momento de la realización de tareas. Por ejemplo, Gutiérrez y Jaime (1996) reportan que muchos estudiantes, al preguntarles qué es un polígono regular, recitan: "un polígono regular es un polígono que tiene todos los lados iguales", aunque parte de estos estudiantes son capaces de reconocer sin errores todos los ejemplos de polígonos regulares e irregulares que se les presentan. Inversamente, también es frecuente encontrar estudiantes de todos los niveles educativos que, aunque escriben la definición correcta de polígono regular, identifican como tales los rectángulos "porque tienen los ángulos iguales". Ambas discrepancias ponen en evidencia la diferencia que, para los estudiantes, hay entre la imagen y la definición de un concepto y los diferentes usos que hacen de ambas, situación que explica el modelo de Vinner, como se verá más adelante.

Una de las aplicaciones del modelo de Vinner es dar pautas concretas sobre cómo analizar y mejorar las imágenes de los conceptos geométricos de los estudiantes. El modelo de Vinner es una herramienta interesante para los profesores al preparar sus clases de geometría pues, como afirma Vinner (1991), en la formación de la imagen de un concepto que tiene una persona, desempeñan un papel básico la propia experiencia y los ejemplos que se han visto o utilizado tanto en el contexto escolar como extraescolar. Con frecuencia, estos ejemplos son pocos y con alguna característica visual peculiar, convirtiéndose en prototipos y en los únicos casos de referencia con los que el estudiante puede comparar casos nuevos. Por tanto, una manera de mejorar la calidad de las imágenes conceptuales consiste en ofrecer a los estudiantes mayor variedad de ejemplos, tratar de detectar los defectos de sus imágenes del concepto y hacer especial incidencia en los ejemplos directamente relacionados con esos errores. Una presentación cuidada de ejemplos y contraejemplos a los estudiantes les ayudará a formar una mejor imagen conceptual y a discriminar con eficacia los ejemplos de los contraejemplos. Para ello, los profesores deben dar la oportunidad a sus alumnos:

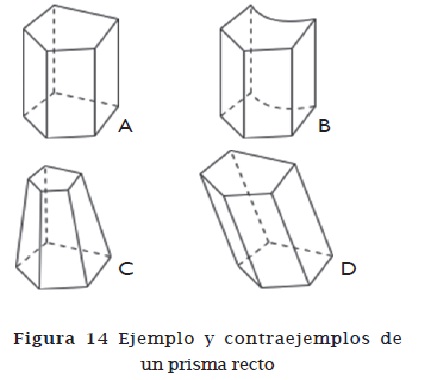
-De comparar ejemplos y contraejemplos para identificar sus diferencias más significativas. La contraposición entre un ejemplo y un contraejemplo pondrá de relieve la existencia de una propiedad que tiene el ejemplo pero no el contraejemplo, y mostrará a los alumnos que se trata de una propiedad necesaria del concepto que están estudiando. La figura 14 muestra cómo al comparar el ejemplo A de prisma recto con cada uno de los contraejemplos B, C y D se pone de relieve una propiedad necesaria de esta familia (todas las caras deben ser polígonos; las dos bases deben ser congruentes; las aristas laterales deben ser perpendiculares a las bases o las caras laterales deben ser rectángulos).

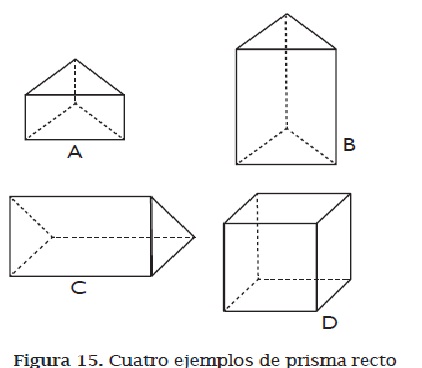
-De comparar ejemplos diferentes para identificar sus diferencias más significativas. La contraposición entre uno y otros ejemplos pondrá de relieve la existencia de una propiedad que tiene un ejemplo pero no el otro y mostrará a los alumnos que se trata de una propiedad innecesaria del concepto que están estudiando. La figura 15 muestra cómo al comparar el ejemplo A de prisma recto con cada uno de los ejemplos B, C y D se pone de relieve una propiedad irrelevante (no necesaria) de esta familia (la longitud de la altura; la posición; la cantidad de lados de las bases).

En cuanto a la utilización, por parte de los estudiantes, de las imágenes y las definiciones de los conceptos, está muy extendida entre los profesores de los diferentes niveles educativos la creencia (casi siempre errónea) de que los estudiantes basan sus razonamientos principalmente en las definiciones verbales (formales) de los conceptos y que sus imágenes del concepto tienen, como mucho, un papel secundario, de apoyo. Sin embargo, la actividad de los estudiantes está, en una mayoría de casos, basada solo en sus imágenes conceptuales, pues hay un elevado número de estudiantes cuya definición del concepto es inactiva (la saben recitar pero no la usan cuando resuelven problemas) o no existe (olvidaron o nunca aprendieron la definición enseñada por su profesor). Un ejemplo de esto es la investigación presentada en Gutiérrez y Jaime (1996), en cuyos resultados se observa que los estudiantes cometen los mismos tipos de errores, tanto si pueden leer la definición de altura mientras contestan al cuestionario, como si no pueden leerla, con una frecuencia de comisión de errores que solo es un poco inferior entre los estudiantes con acceso a la definición que entre los otros estudiantes.

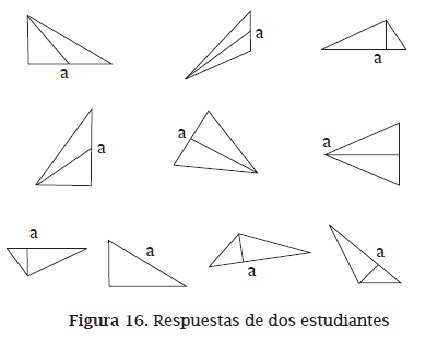
El análisis de las respuestas de los estudiantes a determinadas actividades puede permitir a los profesores ver cómo de ricas, correctas y completas son las imágenes conceptuales de sus alumnos. En esas respuestas se puede observar que, cuando hay errores en las imágenes conceptuales de los estudiantes, estos suelen ser sistemáticos. Por ejemplo, en Gutiérrez y Jaime (1996) se ofrecen algunas respuestas de dos estudiantes a la tarea de dibujar las alturas de varios triángulos sobre el lado marcado con la letra a. La fila superior de la figura 16 muestra a un estudiante cuya concepción de altura de un triángulo es incorrecta pues en los triángulos cuya altura no es interior dibuja la mediana en vez de la altura. La fila inferior muestra a un estudiante cuya concepción de altura de un triángulo es correcta pero incompleta, pues en los triángulos obtusángulos dibuja una altura diferente de la pedida.

Las reacciones del profesor ante estos estudiantes deben ser diferentes, pues en el primer caso debe modificar la concepción de altura que tiene el estudiante para eliminar la confusión entre altura y mediana, mientras que en el segundo caso debe completar la concepción del estudiante para que incorpore las alturas exteriores de los triángulos obtusángulos.

La visualización espacial en el aprendizaje de conceptos geométricos

La percepción visual es un elemento importante en infinidad de actividades de la vida, no solo en las relacionadas con el aprendizaje escolar o con la geometría. Esto hace que, como apunta Gutiérrez (1992, 1996) diferentes grupos de investigadores, con objetivos y contextos diversos, se hayan preocupado de estudiar este campo, al que se suele dar diversos nombres como "percepción espacial", "imaginación espacial", "visión espacial" o "visualización". El término elegido por una persona suele dar indicios de la posición concreta que ha adoptado y del significado que le da a ese término, aunque ésta no es una regla general. Para aludir a este tipo de habilidades, en Didáctica de las Matemáticas, cuando nos centramos en el estudio de la geometría 3-dimensional, se emplean generalmente los términos equivalentes de "visualización","visualización espacial" o "imaginación espacial".

El elemento básico central en todas las concepciones de percepción visual son las imágenes mentales, es decir, las representaciones mentales que las personas podemos hacer de objetos físicos, relaciones, conceptos, etcétera. En el contexto de las matemáticas, Presmeg (1986) ha encontrado diversos tipos de imágenes mentales:

• Imágenes concretas pictóricas: se trata de imágenes figurativas de objetos físicos.
• Imágenes de fórmulas: consisten en la visualización mental de fórmulas o relaciones esquemáticas de la misma manera como se las vería, por ejemplo, en el libro de texto.
• Imágenes de patrones: son imágenes de esquemas visuales correspondientes a relaciones abstractas. A diferencia del tipo anterior, no se visualiza la relación propiamente dicha (una fórmula generalmente), sino alguna representación gráfica de su significado.
• Imágenes cinéticas: se trata de imágenes en parte físicas y en parte mentales, ya que en ellas cumple un papel importante el movimiento de manos, cabeza, etcétera.
• Imágenes dinámicas: son imágenes mentales en las que los objetos o algunos de sus elementos se desplazan.

Una determinada imagen puede ser de dos tipos diferentes pues, normalmente, su clasificación como cinética o dinámica es independiente de su clasificación como pictórica, patrón o de fórmula.

De acuerdo con la distinción que hace Bishop (1989), las imágenes visuales (físicas o mentales) son los objetos que se manipulan en la actividad de visualización, manipulación que se realiza según dos tipos de procesos:

• Procesamiento visual (VP): es el proceso de conversión de información abstracta o no figurativa en imágenes visuales y también el proceso de transformación de unas imágenes visuales ya formadas en otras.
• Interpretación de información figurativa (IFI): es el proceso de comprensión e interpretación de representaciones visuales para extraer la información que contienen. Por tanto, este proceso puede verse como el inverso del anterior.

El tercer componente diferenciado de la visualización son las habilidades de visualización utilizadas por los individuos para la creación y procesamiento de imágenes visuales. Aunque Bishop no diferencia claramente entre procesos y habilidades, otros investigadores sí han hecho esa distinción. Una relación bastante detallada de las habilidades que pueden integrar la percepción espacial de un individuo es la que proporciona Del Grande (1990), obtenida uniendo las propuestas de diversos autores y que se refiere a un contexto más amplio que el de la geometría:

• Coordinación motriz de los ojos: es la habilidad para seguir con los ojos el movimiento de los objetos de forma ágil y eficaz.
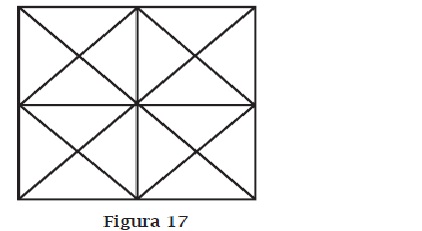
• Identificación visual: es la habilidad para reconocer una figura aislándola de su contexto. Se utiliza, por ejemplo, cuando la figura está formada por varias partes, como en los mosaicos, o cuando hay varias figuras superpuestas. Por ejemplo, ¿cuántos cuadrados hay en la figura 17?



• Conservación de la percepción: es la habilidad para reconocer que un objeto mantiene su forma aunque deje de verse total o parcialmente, por ejemplo, porque haya girado o se haya ocultado.
• Reconocimiento de posiciones en el espacio: es la habilidad del obsevador para relacionar su propia posición (o la de un objeto que actúa como punto de referencia) con la de otro objeto.
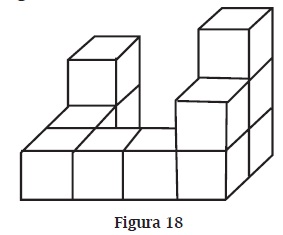
• Reconocimiento de las relaciones espaciales: es la habilidad que permite identificar correctamente las características de relaciones entre diversos objetos situados en el espacio. Por ejemplo, que están girados, son perpendiculares, simétricos, etcétera. Esta habilidad es necesaria para construir con cubos Multilink el cuerpo de la figura 18.



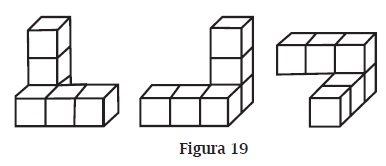
• Discriminación visual: es la habilidad que permite comparar varios objetos identificando sus semejanzas y diferencias visuales. Por ejemplo: calcular la cantidad de módulos iguales que hay en la figura 19.



• Memoria visual: es la habilidad para recordar las características visuales y de posición que tenían en un momento dado un conjunto de objetos que estaban a la vista pero que ya no se ven o que han sido cambiados de posición.

Se pueden definir otras habilidades interesantes y que merece la pena estudiar, pero casi siempre se trata de combinaciones de las habilidades indicadas antes. Por ejemplo, la habilidad de "conservación de las relaciones espaciales", que permite reconocer que las posiciones relativas de varios objetos no varían cuando se les somete al mismo movimiento (giro o traslación), sería una combinación de las habilidades de reconocimiento de las posiciones espaciales y de conservación de la percepción.

Si se realiza una clasificación conjunta de imágenes, procesos y habilidades visuales, se tendrá que, aunque todos ellos tienen relación con la actividad de los estudiantes de matemáticas, algunos tienen una relación más estrecha con el contexto del aprendizaje de la geometría espacial. En concreto, son importantes las imágenes pictóricas, cinéticas y dinámicas, los procesos VP e IFI (cuando intervienen en la obtención o análisis de los tres tipos anteriores de imágenes) y las habilidades de identificación visual, de reconocimiento de posiciones o de relaciones en el espacio y de discriminación visual (también cuando se usan con los tres tipos de imágenes mencionados). Esta mayor relación con el contexto de la geometría-dimensional implica, por una parte, que los estudiantes los utilizan directamente al realizar actividades o resolver problemas en los que intervienen objetos geométricos espaciales y, por otra parte, que la capacidad de los estudiantes para usarlos puede ser mejorada mediante una instrucción específica centrada en la resolución de actividades geométricas.

Referencias

Bishop, A. (1989). Review of research on visualization in mathematics education. Focus on Learning Problems in Mathematics, 11(1), 7-16.         [ Links ]

Corberán, R.; Huerat, M.; Jaime, A.; Margarite, J.; Peñas, A. y Ruíz, E. (1994). Diseño y evaluación de una propuesta curricular de aprendizaje de la geometría en enseñanza Secundaria basada en el modelo de razonamiento de Van Hiele. Madrid: Ministerio de Educación.         [ Links ]

Del Grande, J. (1990). Spatialsense. ArithmeticTeacher, 37(6), 14-20.         [ Links ]

Gutiérrez, A. (1992). Procesos y habilidades en visualización espacial. En A. Gutiérrez (ed.), Memorias del Tercer Simposio Internacional sobre Investigación en Educación Matemática. Geometría (pp. 44-59). México D.F.: Secc. de Matemática Educativa, CINVESTAV.         [ Links ]

Gutiérrez, A. (1996). Visualization in 3-dimensional geometry: In search of a framework. Proceedings of the 20th PME International Conference, 1, 3-19.         [ Links ]

Gutiérrez, A. y Jaime, A. (1996). Uso de definiciones e imágenes de conceptos geométricos por los estudiantes de Magisterio. En: J. Giménez; S. Llinares y M.V. Sánchez (eds.), El proceso de llegar a ser un profesor de prima-ria. Cuestiones desde la educación matemática (pp. 143-170). Granada, España: Comares.         [ Links ]

Jaime, A. (1993). Aportaciones a la interpretación y aplicación del modelo de Van Hiele: La enseñanza de las isometrías del plano. La evaluación del nivel de razonamiento (tesis doctoral). Valencia, España: Universidad de Valencia.         [ Links ]

Jaime, A. y Gutiérrez, A. (1990). Una propuesta de fundamentación para la enseñanza de la geometría: El modelo de van Hiele. En S. Llinares y M.V. Sánchez (eds.), Teoría y práctica en educación matemática (pp. 295-384). Sevilla, España: Alfar.         [ Links ]

Jaime, A. y Gutiérrez, A. (1996). El grupo de las isometrías del plano. Madrid: Síntesis.         [ Links ]

NCTM (2003). Principios y estándares para la educación matemática. Reston, VA, EE.UU.: N.C.T.M.         [ Links ]

Presmeg, N.C. (1986). Visualization in high school mathematics. For the Learning of Mathematics, 6(3), 42-46.         [ Links ]

Van Hiele, P.M. (1986). Structure and insight. A theory of mathematics education. Londres, G. Bretaña: Academic Press.         [ Links ]

Vinner, S. (1991). The role of definitions in the teaching and learning of mathematics. En D. Tall (ed.), Advanced mathematical thinking (pp. 65-81). Dordrecht, Holanda: Kluwer.         [ Links ]

Vinner, S. y Hershkowitz, R. (1983). On concept formation in geometry. Zentralblattfür Didaktik der Mathematik, 83(1), 20-25.         [ Links ]