Producción de teoremas con estudiantes en extraedad: la justificación de una conjetura

Production of theorems in adult students: the proof of a conjecture

A produção de teoremas com alunos em idade avançada: a justificativa de uma conjectura

Oscar Molina^*
Carolina Luque^**
Alejandro Robayo^***

^*Profesor Universidad Pedagógica Nacional. Bogotá, Colombia. ojmolina@pedagogica.edu.co
^**Egresada Maestría Docencia de la Matemática Universidad Pedagógica Nacional. Bogotá, Colombia carolina.luque@live.com
^***Egresado Maestría Docencia de la Matemática Universidad Pedagógica Nacional. Bogotá, Colombia luisalejandroleon@yahoo.com

Artículo recibido el 31-01-2013 y aprobado el 10-06-2014

Resumen analítico

El presente artículo es el resultado de un trabajo de grado de maestría asociado al grupo Didáctica de la Matemáticas en la línea de investigación Aprendizaje y Enseñanza de la Geometría (Æ•G) de la Universidad Pedagógica Nacional. Dado que la enseñanza de la demostración no es una práctica habitual en la educación básica, específicamente se pretende mostrar un ejemplo de la posibilidad de abordarla en el contexto escolar. En tal sentido, se presenta información sobre las acciones de un grupo de tres estudiantes en edad extraescolar que reflejan un involucramiento en los procesos de conjeturación y justificación de la actividad demostrativa —constructo propuesto por el grupo Æ•G¬— en una clase de geometría donde se usa el software de geometría dinámica Cabri. Para precisar tal involucramiento, se tuvo en cuenta la práctica de demostrar como proceso y las fases propuestas por Boero (1999) para la construcción de un teorema. Particularmente, estas fases son base de las categorías de análisis que permitieron interpretar la actividad de los estudiantes cuando se enfrentan a una situación geométrica particular.

Palabras clave: Actividad demostrativa, geometría dinámica, teorema, hecho geométrico.

Abstract

This paper is a partial result of a research project associated to a Mathematics Didactics research group at Universidad Pedagógica Nacional. It has to do with the Learning and Teaching of Geometry field. The paper shows an example of the possibility to address the proof in the school context. In this sense, it presents information on the actions of a group of three-school-adult students involved in conjecturation and proof process of proving activity –a didactical construct by the Æ • G group– in a geometry class in which Cabri -a dynamic geometry software- is used. To describe that involvement, both the proof process and the phases proposed by Boero (1999) were considered for the production of a theorem. Finally, it is said that the categories of analysis to interpret the students' activity when they face a geometric problem, are based on these phases.

Keywords: Proving activity, dynamic geometry, theorem, geometric statement.

Resumo

O presente artigo é resultado de um trabalho de mestrado ao grupo "Didáctica de la Matemática" na linha de investigação "Aprendizaje y Enseñanza de la Geometría (AEG)" da Universidade Pedagógica Nacional. Tendo em vista que o ensino por demonstração não é uma prática habitual na educação básica, se pretende mostrar um exemplo de possibilidade para abordá-la no contexto escolar. Neste sentido, são apresentadas informações sobre as ações de um grupo de três alunos fora da idade escolar, refletindo um envolvimento nos processos de fazer conjecturas e justificativas da atividade demonstrativa – construção proposta pelo grupo AEG – em uma aula de Geometria que se usa o software de geometria dinâmica Cabri. Para aprimorar este envolvimento, foi considerada a prática de mostrar o processo e as fases propostas por Boero (1999) para a construção de um teorema. Particularmente, estas suas fases são as bases das categorias de análise que permitiram interpretar as atividades dos alunos quando confrontados com uma situação geométrica particular.

Palavras-chave: Atividade demonstrativa, geometria dinâmica, teorema, fato geométrico.

Un tema de constante debate en Educación Matemática es la pertinencia de la enseñanza y aprendizaje de la demostración en el ámbito escolar. Existen quienes piensan que enseñar a demostrar en la escuela es un fracaso y los que, por el contrario, señalan que la demostración es fundamental para comprender las matemáticas (Perry, Camargo, Samper y Rojas, 2006). El grupo Aprendizaje y Enseñanza de la Geometría (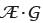) de la Universidad Pedagógica Nacional (upn) es uno de los grupos de investigación, en Colombia, interesados en indagar sobre la importancia de la demostración en clase de matemáticas. Desde el año 2006, el grupo 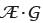ha adelantado sus investigaciones solo en educación superior, apoyados en su experiencia y bajo la hipótesis de la posibilidad del aprendizaje de la demostración en cualquier contexto escolar, los miembros de tal grupo han decidido mirar hacia la escuela y cuestionarse sobre la posibilidad de aprender y enseñar a demostrar en los niveles de básica y media de educación formal. La inquietud por enseñar y aprender a demostrar en la escuela no solo es consecuencia del interés del grupo por hacer que su innovación curricular impacte en los niveles de básica y media de educación formal, también es fruto de la necesidad de afrontar una problemática reconocida por la comunidad internacional de educadores interesados en el tema: el abandono de la demostración en el ámbito escolar. Según Healy, Holyes y Dreyfus (1998; 1999, citados por Perry et al., 2006), el currículo de secundaria ha optado por dejar de lado actividades de carácter demostrativo o por incluirlas en el contexto escolar presentando la demostración como un producto acabado, lo cual ha conducido al fracaso de su enseñanza y a abandonar los intentos de involucrar la demostración en el currículo escolar.

Tal abandono está arraigado en la práctica docente y no en las disposiciones del Ministerio de Educación Nacional. En el contexto colombiano, tanto los Lineamientos Curriculares de Matemáticas (men, 1998) como los Estándares Básicos de Competencias Matemáticas (men, 2006) evidencian una posición en pro de enseñar a demostrar en la escuela, manifestando que en la enseñanza de las matemáticas la demostración no debe verse como mecanismo de validación, sino que debe constituirse en una práctica fundamental.

El estudio que aquí se reporta es el resultado de un trabajo de grado de maestría asociado a la línea de investigación Argumentación y Prueba en Geometría, el cual buscó contribuir a la producción científica del grupo 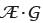de la upn y de manera parcial responder a asuntos que tanto sus integrantes como las políticas educativas se han planteado alrededor del aprendizaje de la demostración en el contexto escolar. Dado que la enseñanza de la demostración no es una práctica habitual en educación básica y que compartimos la posición del grupo frente a esta situación, consideramos pertinente realizar un estudio que aportara información sobre las acciones de estudiantes en edad extraescolar que reflejan un involucramiento en los procesos de conjeturación y justificación de la actividad demostrativa en una clase de geometría donde se usa Cabri. Hacemos referencia a estudiantes en edad extraescolar porque la población cuyas acciones fueron objeto de estudio correspondió a un grupo de 35 estudiantes cuyas edades están fuera del rango (entre los 24 y 57 años) de las personas que están en aulas de secundaria usuales. Para describir el trabajo realizado, en este artículo se dan a conocer los siguientes aspectos del estudio: antecedentes bibliográficos sobre (i) enseñanza y aprendizaje de la demostración y (ii) estudios de educación matemática con estudiantes en edad extraescolar; referentes teóricos que orientaron el diseño de las categorías de análisis y que reflejan nuestra posición en relación con la actividad de demostrar en la escuela; diseño metodológico enfocado en las categorías de análisis; ejemplo del análisis de la actividad de los estudiantes y resultados parciales del mismo. Finalmente, se plantean algunas conclusiones derivadas del trabajo realizado.

Antecedentes bibliográficos

La revisión de antecedentes estuvo centrada en dos aspectos, la enseñanza y aprendizaje de la demostración y estudios relativos a educación matemática cuya población fuera de estudiantes en edad extraescolar. En relación con el primer aspecto, los antecedentes estuvieron guiados por los reportes de investigación y las producciones escritas del grupo de investigación 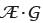y por la búsqueda de literatura que estuviera en correspondencia con la postura del grupo de investigación referenciado, frente al aprendizaje de la demostración.

Perry et al. (2006) manifiestan que la demostración proporciona a los estudiantes comprensión y conocimiento del quehacer matemático. Sin embargo, lograr que los estudiantes demuestren de manera formal no es algo instantáneo. Para el grupo 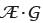aprender a demostrar no es algo inmediato, es un proceso. Los miembros de este grupo manifiestan que la práctica de demostrar la constituyen dos procesos: conjeturación y justificación. El primer proceso busca que un sujeto reconozca el contenido geométrico y las propiedades que subyacen en una situación geométrica de manera tal que sean reportados en enunciado condicional de índole matemático (i.e., una conjetura); el segundo proceso se presenta cuando el sujeto se enfrenta a la justificación matemática de tal enunciado. Es la visión de la demostración como proceso la que marca las directrices de este trabajo. Tal visión se concreta en el constructo "actividad demostrativa", el cual se define a partir de los dos procesos citados y se constituye en uno de los referentes teóricos de este estudio.

Existen investigadores internacionales que reportan estudios con intereses similares a los del grupo 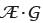. Investigaciones como las de Mariotti (1997) y Boero (1999) exploran, cada uno bajo su propuesta, la manera de llevar la demostración al ámbito escolar.

El estudio de Mariotti (1997; 2006) presenta una recopilación de investigaciones realizadas en contexto escolar, que señalan la importancia del uso de software de geometría dinámica en la creación de un entorno favorable para aprender a demostrar. Mariotti (1997) resalta que los estudiantes en dicho entorno muestran una actividad matemática centrada en la producción de teoremas. La noción de teorema propuesta por Mariotti es de interés para este estudio, ya que proporciona una perspectiva para señalar lo que significa la producción de teoremas en la escuela. La viabilidad de producción de teoremas en el contexto escolar es algo que ratifica Boero (1999) al señalar que es posible involucrar a los estudiantes en una cultura de construcción de teoremas. Dicha cultura se enmarca en el desarrollo de competencias inherentes a la producción de una conjetura y su posterior comprobación. Según este autor, cuando los estudiantes están inmersos en una cultura de producción de teoremas dan indicios de aspectos relevantes de las actividades matemáticas que desarrollan. Tales aspectos los enuncia en seis fases: (i) producción de una conjetura,(ii) formulación de un enunciado de acuerdo con convenciones culturales compartidas, (iii) exploración del contenido (y los límites de validez) de la conjetura, (iv) selección y encadenamiento de argumentos teóricos coherentes en una cadena deductiva, (v) organización de la cadena de argumentos en la forma de una prueba que es aceptable desde el punto de vista de los estándares matemáticos vigentes, y (vi) aproximación a la prueba formal. Estas fases son la base de las categorías de análisis que permitieron interpretar la actividad de los estudiantes en el marco del estudio reportado.

En relación con estudios que reportaran trabajos relativos a estudiantes en edad extraescolar, la revisión de la literatura condujo a identificar una carencia de estudios centrados en población de adultos. Según Ávila (1999), no es necesario realizar una investigación que dé cuenta de la cantidad de estudios en educación matemática con este tipo de población, dado que existen indicadores que permiten estimar que la cantidad es mínima. Un ejemplo de estos indicadores es la poca producción en artículos de revistas o memorias de congresos que reporten trabajos con estudiantes en edad extraescolar. No obstante la percepción anterior, se encontraron dos investigaciones sobre la enseñanza de las matemáticas que involucran población adulta en un contexto escolar, una realizada por Bastán y Elguero (2005) y otra hecha por Barrio de la Puente J., Barrio de la Puente M. y Quintanilla M. (2006). Bastán y Elguero (2005) señalan que aunque los estudiantes en edad adulta tienen las mismas capacidades de aprendizaje que un adolescente, la heterogeneidad del grupo y sus deberes como adulto (ocupaciones laborales y familiares, experiencias previas, expectativas a futuro) afectan su proceso de aprendizaje. Esto implica que las estrategias metodológicas de clase deben contemplar características específicas (que no se describen en el documento)y deben también promover la abstracción, generalización y resolución de problemas. Estas acciones permiten que los estudiantes adultos amplíen sus expectativas respecto a lo educativo y logren superación desde el punto de vista cognitivo. Por otro lado, Barrio de la Puente et al. (2006) proponen el uso de software educativo para la enseñanza de algunos temas de geometría y estadística mostrando que los estudiantes en extraedad, con su uso, tienen una actitud positiva y más receptiva hacia las matemáticas.

Referentes teóricos

La actividad demostrativa en el ámbito escolar

Uno de los referentes teóricos que sustentan el estudio realizado es el constructo "actividad demostrativa" elaborado por el grupo de investigación 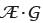de la upn. Este constructo abarca dos procesos de ninguna manera independientes, conjeturación y justificación. Estos se componen de acciones que no se consideran secuenciales. Específicamente, en el proceso de conjeturación están presentes acciones de tipo heurístico tales como: visualizar, explorar, generalizar y verificar. Tales acciones permiten a los estudiantes reconocer el contenido geométrico y las propiedades que subyacen en un enunciado matemático o en una figura geométrica, y contribuyen al planteamiento de conjeturas y a la verificación empírica de las mismas (Perry, et al. 2006). La visualización es la acción por medio de la cual el estudiante identifica, percibe o evoca propiedades geométricas de una representación gráfica dada o construida. Cuando la indagación del estudiante involucra otros modos de actuación distintos a la observación, que conducen a la manipulación de la figura, su proceder tiene el carácter de exploración. Tanto en la visualización como en la exploración, el estudiante tiene la oportunidad de encontrar regularidades en las figuras geométricas, que posteriormente se constituyen en una generalización. Tal generalización se cristaliza en el enunciado de una conjetura a manera de proposición condicional. Según Perry et al. (2006), la satisfacción y el convencimiento personal cuando plantea una conjetura conducen a la necesidad de generar una justificación de la misma. Los estudiantes, para asegurarse de la validez de su conjetura, pueden empezar por estudiar los posibles casos en los que esta puede no cumplirse, realizando comprobaciones empíricas sobre la representación gráfica. Estas comprobaciones son actuaciones de verificación, que se dan cuando surge un cuestionamiento que suscita duda frente a la conjetura planteada o cuando se quiere ratificar una propiedad enunciada en esta.

Cuando existe la plena seguridad de la veracidad de una generalidad planteada (una conjetura), los estudiantes pueden proponer diversas vías de justificación (segundo proceso de la actividad demostrativa) de la misma: la explicación, la prueba o la demostración formal. La explicación se constituye en una acción de carácter empírico por medio de la cual se hace alusión a una figura para mostrar lo que en ella se ve y señalar posibles invariantes o propiedades observadas durante la exploración. En este modo de justificación, los argumentos de los estudiantes se apoyan en la evidencia. A diferencia de la explicación, la prueba se constituye en un modo de justificación en el que los resultados no se sustentan a través de una figura. Desde el punto de vista de la prueba, se realizan afirmaciones basadas en propiedades geométricas generales. Según Perry et al. (2006), las afirmaciones que pueden dar los estudiantes y que son indicios de la acción de probar, son aquellas fundamentadas en el conjunto de referentes estudiados o en las nuevas relaciones de dependencia encontradas en la figura, es decir, los estudiantes pueden hacer uso de afirmaciones que no hacen parte del contenido geométrico estudiado en la clase. El uso de propiedades o definiciones no estudiadas previamente y la ausencia de una organización deductiva es lo que hace que este modo de justificación no se constituya en una demostración formal. La demostración formal, como su nombre lo indica, es una acción mucho más rigurosa que las otras dos vías de justificación. Este tipo de justificación presenta una secuencia lógica de afirmaciones y razones, sustentadas en el referente teórico de la clase.

Producir teoremas en la escuela y las fases que conllevan a tal producción

Boero (1999) manifiesta que aprender a demostrar es involucrarse en una cultura de teoremas y teorías matemáticas, lo cual implica el desarrollo de competencias específicas inherentes a la producción de conjeturas y pruebas para las mismas con base en elementos del saber teórico. En este sentido, Boero, al igual que el grupo 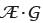, atiende a una visión de la demostración como proceso, cuyo aprendizaje está ligado a la producción de conjeturas y justificaciones, y en particular a la producción de teoremas.

Hablar de teoremas no solo es referirse a enunciados que tienen el estatus de verdad matemática. Según Mariotti (1997) un teorema es la articulación de tres elementos en el campo teórico de las matemáticas: afirmación o enunciado, demostración y teoría. Para esta autora, un teorema matemático se caracteriza por estar inscrito en una teoría de referencia que contempla un conjunto de principios y reglas de deducción que permiten validar el enunciado mediante el cual se formula el teorema. Desde el punto de vista matemático, se demuestran "verdades" que adquieren validez en relación con una teoría especifica. Esta validez se obtiene de aceptar tanto la veracidad de las hipótesis como de los axiomas y reglas de inferencia establecidas (Mariotti, 2006). En este sentido, la definición propuesta por Mariotti es inherente a una construcción axiomática, rigurosa y formal de las matemáticas, la cual es afortunada en una comunidad de matemáticos pero no en una comunidad de principiantes, es decir, de personas que se están iniciando en el estudio de las matemáticas en un nivel no profesional.

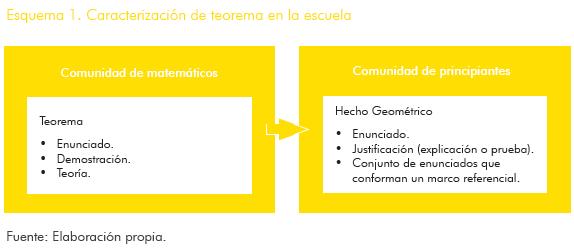
Con respecto a lo anterior, Mariotti (2006) señala que para los estudiantes inexpertos no es espontáneo llegar a una perspectiva teórica de las proposiciones matemáticas, lo que para los matemáticos es incuestionable y tácito (existencia y fiabilidad de un marco teórico en el que subyace la demostración de una afirmación), para los principiantes no lo es. Por tanto, la idea de una verdad como teoría puede ser difícil de comprender. Esta afirmación no implica aceptar la imposibilidad de aproximar a los estudiantes al estudio de la demostración en un nivel de educación básica, más bien es una invitación a ser conscientes de tal complejidad y a repensar la idea de teorema para aterrizarla al contexto escolar. En el esquema 1 planteamos una analogía entre los elementos que componen la definición de teorema propuesta por Mariotti (1997) y los elementos que están inmersos en el constructo de actividad demostrativa y que consideramos son próximos a la comprensión de teorema en el contexto escolar.

Es claro que en la escuela no formamos matemáticos, por tanto, no construimos teorías matemáticas ni demostraciones formales y rigurosas como las que elaboran los expertos de esta ciencia. Pero sí formulamos conjeturas que se pueden justificar con base en un sistema teórico local (conjunto de enunciados alrededor de un concepto, los cuales pueden estar conectados o aislados en el mundo de las matemáticas escolares) o en reglas sociomatemáticas que determinan los modos de validación en la clase; la diferencia entre la actividad de los matemáticos y la de los estudiantes a nivel escolar es la que, consideramos, motiva la propuesta de una analogía como la del esquema anterior. El reconocer que en la escuela no se producen teorías y demostraciones a un nivel formal, nos permite señalar que en el campo de la educación básica en matemáticas, en general, no es posible hablar de teorema en el sentido estricto de Mariotti, lo cual no implica el abandono de la enseñanza de la demostración en este nivel de formación, más bien supone el reconocimiento de la proximidad teórica de las matemáticas que pueden hacer los estudiantes en la escuela: enunciado o conjetura, justificación y conjunto de enunciados que conforma un marco referencial.

El reconocimiento de dicha aproximación teórica a las matemáticas en el contexto escolar nos conduce a no adoptar el término teorema para hacer referencia a aquellos enunciados que adquieren el estatus de verdad matemática dentro del aula sino más bien a utilizar la expresión hecho geométrico. En vista de que a nivel escolar se hace una aproximación teórica a las matemáticas a partir de una conjunto de enunciados que no necesariamente pertenecen a un sistema teórico explícito para los estudiantes, consideramos conveniente no precisar un estatus teórico para las proposiciones matemáticas estudiadas en el aula; es decir, no discriminar entre aquellas proposiciones que serían teoremas y aquellas que serían postulados sino optar por denominarlas todas como hechos geométricos. La razón de esta decisión es de carácter didáctico y está asociada a la construcción del marco referencial. Así y en correspondencia con el grupo 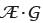existen solo dos tipos de enunciados en dicho marco: hechos geométricos y definiciones. Distinguir entre postulado y teorema implica establecer su diferencia y respetar su estatus en el proceso de construcción de tal marco referencial, lo que conduciría a tener que demostrar todo aquello a lo que se denomine teorema; no obstante, ello no siempre es posible en un contexto escolar, dado que hay justificaciones de proposiciones matemáticas que requieren de elementos teóricos con los que aún no cuentan los estudiantes que se están iniciando en el proceso de aprender a demostrar. Se espera que cuando los estudiantes ya tengan una mayor experiencia y cuenten con un marco referencial más amplio puedan distinguir y decidir cuándo es teorema o postulado un hecho geométrico. En este sentido, el hecho geométrico será un enunciado que puede tener una justificación con carácter de explicación, prueba o demostración (lo que usualmente sería teorema) o no tener justificación teórica (lo que sería un postulado). La aceptación de alguno de estos modos de validación dependerá de la reglas sociomatemáticas establecidas en la clase, del alcance del marco referencial construido y de la complejidad teórica que tenga la justificación del hecho geométrico para el grupo particular que lo estudia.

Adoptar el término de hecho geométrico para referirnos a las verdades a nivel escolar y ser partidarios de los planteamientos de Boero (1999) nos permite señalar que aprender a demostrar está ligado a iniciar a los estudiantes en una cultura de hechos geométricos, es decir, a involucrarlos en la producción de conjeturas y justificaciones (actividad demostrativa) en el contexto escolar. Según Boero (1999), en tal involucramiento es posible distinguir algunos aspectos relevantes de las actividades matemáticas concernientes a la producción de hechos geométricos (en palabras de Boero, teoremas). Este autor enuncia estos aspectos como fases en la producción de conjeturas y pruebas matemáticas. Tales fases son:

1. Producción de una conjetura, lo cual incluye la exploración de la situación problema, identificación de "regularidades", reconocimiento de condiciones bajo las cuales estas ocurren, etc.
2. Formulación del enunciado de acuerdo con convenciones culturales compartidas.
3. Exploración del contenido (y los límites de validez) de la conjetura; elaboraciones heurísticas, semánticas (y aun formales) acerca de las relaciones entre hipótesis y tesis; identificación de argumentos apropiados para la validación, relacionados con la teoría de referencia y ponderación de relaciones posibles entre ellos.
4. Selección y encadenamiento de argumentos teóricos coherentes en una cadena deductiva, frecuentemente bajo la guía de la analogía o en casos específicos y apropiados, etc.
5. Organización de la cadena de argumentos en la forma de una prueba que es aceptable desde el punto de vista de los estándares matemáticos vigentes. Esta fase conduce a la producción de un texto para publicación.
6. Aproximación a la prueba formal.

De acuerdo con Boero (1999), las seis fases mencionadas están interconectadas de manera no lineal en el trabajo de los matemáticos y son útiles para destacar momentos en la actividad matemática de los mismos. Dada la correspondencia entre el constructo actividad demostrativa del grupo 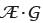y las fases de Boero, hemos escogido estas fases como nuestras categorías de análisis para describir el involucramiento de los estudiantes en un ambiente de actividad demostrativa.

La geometría dinámica como herramienta que favorece el aprender a demostrar

En los últimos años diversas investigaciones sobre el tema de la demostración han coincidido en la elección de ambientes de geometría dinámica como entornos favorables para el desarrollo del razonamiento geométrico (Mariotti, 2006). Según Hanna (2000), la capacidad gráfica de este tipo de software no solo ha impulsado la exploración en matemáticas y la inclusión de las nuevas tecnologías en la enseñanza de las mismas, sino que también ha alentado a los estudiantes a conjeturar y justificar en geometría.

Motivados por el potencial que diferentes autores le atribuyen al software de geometría dinámica en la enseñanza y el aprendizaje de la geometría y en particular de la demostración (Perry, Samper, Camargo, Echeverry y Molina, 2008; Hanna, 2000; Mariotti, 1997; Gutiérrez, 2005), se optó por utilizar este tipo de software en el estudio que se reporta. Esto con la finalidad de identificar cómo la geometría dinámica contribuye a que estudiantes en edad extraescolar se involucren en los procesos de la actividad demostrativa. Específicamente, se utilizó el software de geometría dinámica Cabri Geometry II plus (Cabri).

Según Mariotti (1997) son dos las características que se le atribuyen a Cabri en relación con la geometría euclidiana: (i) preserva correspondencia entre las herramientas del software y las propiedades geométricas básicas de las figuras, y (ii) permite interactuar con los objetos geométricos a través de la herramienta arrastre dotando de dinamismo a la geometría. En relación con la primera característica, Perry et al. (2008) manifiestan que los principios que se utilizaron en el diseño de Cabri se corresponden con los postulados de la geometría euclidiana, hecho que crea un vínculo entre las herramientas utilizadas en la construcción de una figura y sus propiedades geométricas. En cuanto al dinamismo que proporciona Cabri al estudio de la geometría euclidiana, Laborde (2000, citada por Mariotti, 2006) señala que esta es una característica que hace que este software se convierta en una herramienta que potencia el aprendizaje de la geometría por encima del lápiz y el papel, debido a que permite articular acciones de visualización y conjeturación a través de la herramienta "arrastre". El arrastre permite modificar los objetos geométricos de una figura construida en Cabri y evidenciar que tales objetos conservan todas sus relaciones geométricas, algo que no sucede con la geometría estática de lápiz y papel, en la que los objetos geométricos se representan a través de la experiencia perceptual y de hechos que visualmente no se relacionan (Laborde 2000, citada por Mariotti, 2006). Además de las posibilidades de movimiento y transformación que ofrece la herramienta arrastre, Cabri cuenta con herramientas que permiten tomar medidas exactas y obtener representaciones precisas de los objetos geométricos, lo cual amplía su potencial frente a la geometría estática.

Las características atribuidas a este tipo de software permiten a los estudiantes experimentar y explorar, a través del arrastre, múltiples ejemplos o casos particulares de objetos que se construyen haciendo uso de las herramientas del software; la exploración de casos particulares, les permite, a su vez, visualizar distintas representaciones gráficas de una misma figura geométrica con miras a identificar e inferir propiedades invariantes de la misma y establecer generalidades (Christou, Mousoulides, Pitallis, Pitta-Patanzi, 2004). En términos de la generalización, se considera que la geometría dinámica favorece el reconocimiento y la producción de conjeturas en tanto que permite reconocer el antecedente y el consecuente de las mismas. Mariotti (2006) señala que las relaciones declaradas en la construcción se constituyen en las hipótesis, y las propiedades derivadas de ellas, que aparecen como invariantes ante el modo de arrastre, se convierten en las posibles tesis. En conclusión, las conjeturas en un ambiente de geometría dinámica emergen de la interpretación de dependencia entre las propiedades que se utilizan en la construcción y los invariantes identificados mediante la acción de arrastre.

Además de la exploración y reconocimiento de patrones invariantes, la herramienta arrastre posibilita la emergencia de argumentos y justificaciones en el marco de la práctica de aprender a demostrar. Según Mariotti (2006), en un entorno como Cabri, el arrastre ofrece a los estudiantes una fuerte evidencia perceptual de la veracidad de una propiedad y aunque esto no asegura que los alumnos se vean inmersos en una perspectiva teórica de la demostración, en términos pragmáticos proporciona un contexto para una cultura de preguntas acerca de por qué una construcción funciona. En otras palabras, Cabri puede generar un espacio propicio para la emergencia de justificaciones ya sean empíricas (explicación) o teóricas (pruebas o demostraciones) en el aula. Aunque existen dudas en relación con la contribución de la geometría dinámica a la producción de justificaciones matemáticas, en la literatura se encuentran investigaciones que aluden al uso de este tipo de software para vincular a los estudiantes en el mundo teórico de la geometría. Por ejemplo, Jones (2000) señala que en el entorno de la geometría dinámica es posible motivar a los estudiantes a generar explicaciones sobre la base de las relaciones lógicas entre propiedades. Siguiendo con la misma idea, Hadas, Herschkowitz y Schwarz (2000; citados por Mariotti, 2006) manifiestan que en ambientes de geometría dinámica la dialéctica entre los datos empíricos y la conjetura pueden conducir a los estudiantes a experimentar contradicción e incertidumbre, abriendo el camino hacia la necesidad de explicaciones que superen la evidencia empírica. Ahora bien, se debe tener presente que la emergencia de justificaciones no sucede solamente con el uso de Cabri; es necesario generar un ambiente de clase en el que se dé el espacio para que los argumentos surjan. Laborde (2000; citada por Mariotti, 2006) afirma que se necesita organizar un entorno adecuado que provoque la necesidad de la prueba. Es aquí donde adquiere significado uno de los elementos del enfoque metodológico del grupo : la interacción social en la clase. Para Mariotti (1997), la evolución de la evidencia empírica a las justificaciones dentro de un sistema teórico se da cuando se exige explicar el razonamiento seguido en la solución de una tarea a los demás miembros de la clase y cuando las discusiones en el aula se direccionan a la búsqueda de razones que justifiquen por qué una conjetura o construcción es aceptable bajo unas reglas que en el marco de la clase se reconocen como válidas.

Aspectos metodológicos

El interés por identificar las acciones de estudiantes en edad extraescolar que reflejan la emergencia de un ambiente de actividad demostrativa en el aula de matemáticas, enmarca nuestro estudio en una metodología de carácter cualitativo, descriptivo e interpretativo, que corresponde a un estudio de caso en la modalidad estructurada y no participante (Cohen y Manion, 1990). Específicamente buscamos describir las acciones que realiza un grupo de tres estudiantes cuando se enfrentan a una situación que indaga sobre las propiedades de los triángulos. Los estudiantes, en el momento de la implementación, se encontraban nivelando los grados octavo y noveno de educación básica en jornada nocturna. Vale la pena mencionar que los estudiantes no contaban con conocimientos en geometría ni habían usado algún tipo de software en clase de matemáticas.

El estudio de caso se estructura con base en la aproximación metodológica del grupo con miras a involucrar a los estudiantes en un ambiente de clase específico en el que se desea observar la manera en la que los estudiantes interactúan y dan soluciones a situaciones particulares que se les proponen. En cuanto que nosotros como investigadores no nos involucramos en la actividad de los estudiantes, este estudio es no estructurado. Por otro lado, las acciones de los estudiantes fueron interpretadas y analizadas a la luz de las categorías de análisis cuyo proceso de construcción a continuación describimos:

Categorías de análisis

Como señalamos anteriormente, la construcción de las categorías de análisis están basadas en las seis fases de Boero (1999); específicamente cada una de ellas fue complementada con indicadores y acciones que nos permitieron dar cuenta de la actividad demostrativa de los estudiantes en el marco de cada fase. Los indicadores y las acciones de las tres primeras categorías se definieron con base en la propuesta que realizaron Parra y Piñeros (2011) en su trabajo de grado de licenciatura en matemáticas (upn). Para la elaboración de los indicadores y acciones de las tres categorías restantes tomamos algunas ideas planteadas por Camargo (2010) en su tesis doctoral en relación con los procesos de argumentar, demostrar y sistematizar. Es de resaltar que a pesar de haber tomado como base el trabajo de los autores citados realizamos algunas modificaciones y/o ampliaciones a su propuesta con base en las observaciones preliminares del trabajo de los estudiantes y en la revisión de la literatura especializada, por tanto, tales categorías se constituyen en uno de los productos de este estudio.

A continuación presentamos, a modo de ejemplo, los indicadores y acciones establecidos para la categoría tres. Es de resaltar que para efectos del análisis de los datos del estudio, decidimos codificar cada categoría, indicador y acción. La codificación asignada aparece al final de la categoría, indicador o acción en paréntesis. Tal codificación, en cada caso, se ha asignado de la siguiente manera:

• Para el caso de las categorías, la codificación será denotada por C seguido por un número romano. La numeración romana indica la categoría a la cual estamos haciendo alusión y se corresponde con el orden propuesto por Boero (1999).
• Para los indicadores, la codificación será: C seguido de un número romano, "i" seguida de un número en su escritura induarábiga, por ejemplo (CIII, i1).
• Para las acciones, en la codificación denotamos el indicador añadiendo la letra a seguida de un número en su escritura induarábiga, por ejemplo, (CIII, i1, a1).

Indicadores y acciones fueron numerados para ser distinguidos dentro de una misma categoría, tal numeración no representa un orden jerárquico de los mismos, sólo sugiere una organización.

Exploración del contenido de la conjetura y los límites de validez de la misma (CIII)

En esta categoría se hace referencia a los argumentos elaborados con miras a explorar el contenido de la conjetura y los límites de validez de la misma. Abarca acciones que le permiten al estudiante generar argumentos para justificar la relación entre hipótesis y tesis, la plausibilidad y validación de la conjetura en relación con la teoría de referencia. En esta categoría los estudiantes pueden evocar argumentos, generalmente empíricos, o eventualmente teóricos sin producir cadenas deductivas.

Los indicadores que proponemos para esta categoría son: exploración del contenido de la conjetura, búsqueda de argumentos para la plausibilidad de la conjetura y reconocimiento de argumentos para explicar la validez de la conjetura. Tales indicadores se explican a continuación:

Exploración del contenido de la conjetura (CIII, i1)

Este indicador hace referencia a identificar con base en la exploración de la figura, las circunstancias bajo las cuales la conjetura se cumple (CIII, i1, a1). Estas circunstancias están relacionadas con las condiciones impuestas en la situación y la determinación de cual cuantificador universal y existencial; los estudiantes aluden a la relación de dependencia entre hipótesis y tesis. En el marco de este indicador surgen explicaciones (en el sentido de la actividad demostrativa) de carácter heurístico que buscan argumentar en qué casos y bajo qué condiciones es válida la conjetura.

Adicional a la acción de explicar, en este indicador, también están inmersas las acciones de exploración y visualización de la actividad demostrativa, dado que es a través de la manipulación y observación de representaciones gráficas que los estudiantes identifican las circunstancias bajo las cuales se cumple la conjetura propuesta.

Búsqueda de argumentos para la plausibilidad de la conjetura (CIII, i2)

En el marco de este indicador, el interés de los estudiantes se centra en la búsqueda de argumentos que justifiquen la validez de la conjetura. Es de resaltar que en este momento de la actividad de los estudiantes aún no hay certeza frente a los argumentos que pueden justificarla sino inquietud frente a la veracidad de la conjetura y las razones que podrían justificarla (CIII, i2, a1). También pueden llevar a cabo acciones como: esgrimir razones o puntos de vista en pro o en contra de una afirmación con el objeto de dar cuenta de la plausibilidad del enunciado (CIII, i2, a2); sugerir una construcción auxiliar para enriquecer una representación que le permitan encontrar ideas para la justificación (CIII, i2, a3).La búsqueda de argumentos refleja la necesidad del estudiante de convencerse a sí mismo y a los demás de la validez de la conjetura.

Selección de argumentos para explicar la validez de la conjetura (CIII, i3)

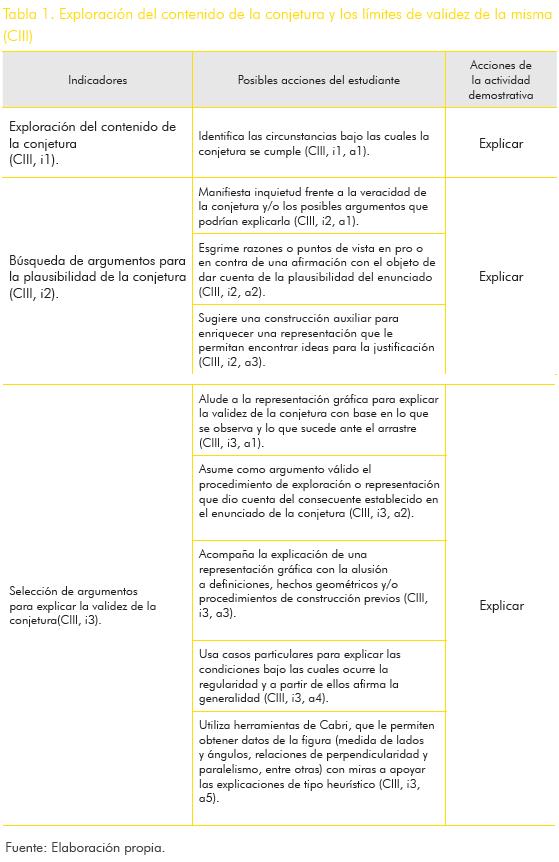
Luego de buscar argumentos que puedan justificar la conjetura, los estudiantes pueden seleccionar algunos de ellos para plantear una justificación de la conjetura. Bajo este indicador, el estudiante puede señalar argumentos empíricos o teóricos que justifiquen la validez de la conjetura. Las posibles acciones de los estudiantes en el marco de este indicador son: aludir a la representación gráfica para explicar la validez de la conjetura con base en lo que se observa y lo que sucede ante el arrastre (CIII, i3, a1); asumir como argumento válido el procedimiento de exploración o representación que dio cuenta del consecuente establecido en el enunciado de la conjetura (CIII, i3, a2); acompañar la explicación de una representación gráfica con la alusión a definiciones, hechos geométricos y/o procedimientos de construcción previos (CIII, i3, a3); usar casos particulares para explicar las condiciones bajo las cuales ocurre la regularidad y a partir de ellos afirma la generalidad (CIII, i3, a4); utilizar herramientas de Cabri, que le permitan obtener datos de la figura (medida de lados y ángulos, relaciones de perpendicularidad y paralelismo, entre otras) con miras a apoyar las explicaciones (CIII, i3, a5). En todas las acciones de este indicador está presente la acción de explicar de la actividad demostrativa, ya que en estas primeras justificaciones los estudiantes plantean sus argumentos con base construcciones dinámicas.

En la tabla 1 se sintetizan las ideas relacionadas con la tercera categoría (CIII), sus indicadores, posibles acciones del estudiante y acciones de la actividad demostrativa.

Población del estudio

El estudio se llevó a cabo durante el segundo semestre de 2010, en el Colegio Gabriel Echavarría de Madrid (Cundinamarca), con un grupo de 35 estudiantes, quienes se encontraban nivelando los grados octavo y noveno de educación básica secundaria, en jornada nocturna. El rango de edades del grupo de estudiantes oscilaba entre los 24 y 57 años de edad. Su ocupación, en la mayoría de los casos, estaba relacionada con oficios operarios en empresas de flores, vidrios y panadería. Estos estudiantes estaban terminando sus estudios de secundaria porque las empresas en las que laboraban así lo exigían. Tal exigencia no implicaba un desinterés por parte de ellos en relación con su formación académica; más bien, como lo manifestaban ellos mismos, se constituía en una oportunidad para aprender, mejorar su calidad de vida e incluso para postularse a un ascenso laboral. En particular, se mostraban dispuestos e interesados en aprender matemáticas. Durante su experiencia escolar en dicho semestre, los estudiantes no habían abordado temas de geometría ni tampoco habían incorporado el uso de las tecnologías en el aula de matemáticas; además, la clase de matemáticas estaba enmarcada en un modelo de enseñanza tradicional, en la que los estudiantes atendían explicaciones de la profesora y posteriormente realizaban los ejercicios propuestos por ella. En la dinámica de la clase no existía un espacio para que los alumnos comunicaran sus ideas y aportaran al conocimiento que se abordaba en el aula.

Un ejemplo de análisis

Durante la implementación de la propuesta, se propuso a los estudiantes varias situaciones encaminadas a descubrir mediante el uso de la geometría dinámica propiedades de los triángulos. En principio, se plantearon situaciones para definir y clasificar los triángulos según sus ángulos; posteriormente, situaciones con miras a indagar sobre hechos geométricos relacionados las propiedades de los triángulos. El siguiente ejemplo de análisis de la producción de los estudiantes (basado en la categorización presentada en la tabla 1) muestra sus acciones frente a una situación que implica indagar sobre la suma de las medidas de los ángulos de un triángulo. Vale la pena precisar que el ejemplo que se ilustra se basa en la producción de un grupo de tres estudiantes (Sandra, Miguel y Diego.); este grupo fue escogido con unos criterios previamente establecidos que se fundamentaron en su disposición para comunicar sus ideas y en la estabilidad como grupo (i.e., no faltar a clase).

En una de la sesiones de clase, la profesora propuso a los estudiantes abordar el siguiente problema: ¿Para qué tipo de triángulo la suma de la medida de sus ángulos es menor que 120 grados? El grupo de estudiantes escogido para este estudio, empezó construyendo un triángulo con la herramienta correspondiente de Cabri. Posteriormente, tomaron las medidas de sus ángulos y lados; manifestaron que estas últimas no eran necesarias porque la tarea solo implicaba medir los ángulos. La observación de las medidas de los ángulos permitió al grupo hacer una primera estimación de la suma de las mismas, apreciando que la adición era mayor que 120. Esta primera estimación condujo a los alumnos a centrarse en la búsqueda de un triángulo específico en donde se cumpliera la propiedad establecida en la situación. Indagar por un triángulo particular encaminó la actividad de los estudiantes hacia la exploración de posibles estrategias de solución. Las estrategias utilizadas por los estudiantes fueron: someter el triángulo construido a la acción de arrastre para cambiar su tamaño y verificar si la medida de sus ángulos dependía de la longitud de sus lados; construir triángulos específicos (rectángulo, equilátero) para comprobar si alguno de ellos cumplía con la condición requerida; arrastrar un vértice del triángulo con miras a modificar la medida de uno de los tres ángulos, buscando mantener la medida de los otros dos ángulos cuyo vértice no se sometía al arrastre; y sumar las medidas de los ángulos. La adición de las medidas de los ángulos la realizaron utilizando lápiz y papel debido a que no conocían la herramienta "calculadora" de Cabri.

La estrategia de la suma de medidas de ángulos (no la estimación de la suma de las medidas de los ángulos), fue sugerida por la profesora al grupo de estudiantes desde el principio, pero ellos inicialmente no la aceptaron porque no les permitía encontrar el tipo triángulo para el cual la suma de las medidas de sus ángulos era menor que 120. Luego de descartar las demás estrategias citadas, por intervención de la profesora, los alumnos decidieron retomar la estrategia de la suma de las medidas de los ángulos del triángulo. En esta ocasión dicho método cobro sentido para ellos dado que observan que sin importar el triángulo construido la suma de las medidas de sus ángulos siempre es 180. Reconocer el invariante llevo a la solución de la situación, dado que uno de los integrantes del grupo manifiesta que no hay triángulo que satisfaga la condición del problema propuesto.

El reconocimiento y la aceptación del invariante por parte del grupo de estudiantes se apoyaron en la observación que hizo uno de sus integrantes del comportamiento de las medidas de los ángulos del triángulo cuando este se sometía al arrastre. Específicamente, Sandra identificó que el resultado de la suma era invariante porque al tratar de disminuir la medida de uno de los ángulos del triángulo a través del arrastre, por lo menos una de las medidas de los otros dos ángulos aumentaba, lo cual implicaba conservar el valor de la suma de las medidas de los ángulos del triángulo.

Luego de haber identificado el invariante y haber solucionado la situación planteada, la profesora pidió a los estudiantes escribir el hecho geométrico correspondiente. La formulación del hecho geométrico estuvo guiada por la intención de los estudiantes de hacer explícito el antecedente y el consecuente de la situación en el formato condicional "si...entonces..." y por señalar que la propiedad era válida para todo triángulo. Finalmente, el hecho geométrico formulado por el grupo de estudiantes fue: "Si sumamos la medida de los ángulos de un triángulo entonces el resultado va a ser siempre 180".

La manera en la que los estudiantes abordaron la situación propuesta nos condujo a tener en cuenta sus estrategias de solución como punto de partida para el análisis de su actividad, en este sentido, el trabajo de los estudiantes se describió y analizó atendiendo a los siguientes momentos de su actividad:

• Momento 1. En la búsqueda de un triángulo particular: Interpretan la situación como la búsqueda de un triángulo específico que cumpla con la condición propuesta.
• Momento 2. Suman la medida de los ángulos: Utilizan una estrategia de solución sugerida por la profesora sin apropiarse de tal sugerencia.
• Momento 3.¿Cómo disminuir la medida de los ángulos?: Plantean y verifican hipótesis buscando disminuir la medida de los ángulos del triángulo.
• Momento 4.El triángulo rectángulo y equilátero: Exploran e identifican la regularidad luego de generar y descartar varias estrategias de solución de la tarea.
• Momento 5. Nuevamente suman la medida de los ángulos: Identifican la regularidad luego de haber generado y descartado varias estrategias de solución de la tarea.
• Momento 6. ¿Pero por qué siempre da 180?: Justifican por qué es válido el invariante encontrado.
• Momento 7. ¿Cómo escribimos el hecho geométrico?: Formulan el hecho geométrico correspondiente a la suma de las medidas de los ángulos de un triángulo.

De los momentos mencionados, tomaremos como ejemplo de análisis el momento 6, puesto que nos permite evidenciar el uso de la categoría antes referenciada, es decir la III.

¿Pero por qué siempre da 180?: justifican por qué es válido el invariante encontrado

Después de encontrar un patrón invariante en la suma de las medidas de los ángulos de un triángulo, Sandra se pregunta en dos ocasiones el porqué de la ocurrencia de tal patrón.

En la intervención 115 se evidencia la intención de buscar una explicación que justifique por qué la suma de las medidas de los ángulos del triángulo da 180, lo cual es una evidencia de la acción CIII, i2, a1. Pensar que el patrón es propio de un triángulo particular direcciona las acciones de la estudiante hacia la verificación del patrón en otros triángulos, buscando identificar a través del arrastre en qué casos se cumple que dicha suma sea 180. El estudio de casos particulares se constituye en una acción encaminada a la búsqueda de argumentos basados en invariantes de las figuras construidas, las cuales ayudan a justificar una regularidad [125]. Esta búsqueda de argumentos pone en evidencia la acción CIII, i3, a1, dado que se alude a una representación gráfica para explicar la veracidad de una conjetura. Es de señalar que cuestionarse acerca del porqué del invariante es iniciativa de Sandra, dado que en ningún momento la profesora solicitó que justificaran su respuesta.

Indagar sobre el porqué del patrón condujo a Sandra a identificar argumentos basados en las figuras construidas que le permitieran justificar la regularidad encontrada. El estudio de casos particulares, a partir de la acción de arrastre, le permitió a Sandra observar cómo variaba la medida de los tres ángulos cuando se arrastraba uno de los vértices del triángulo.

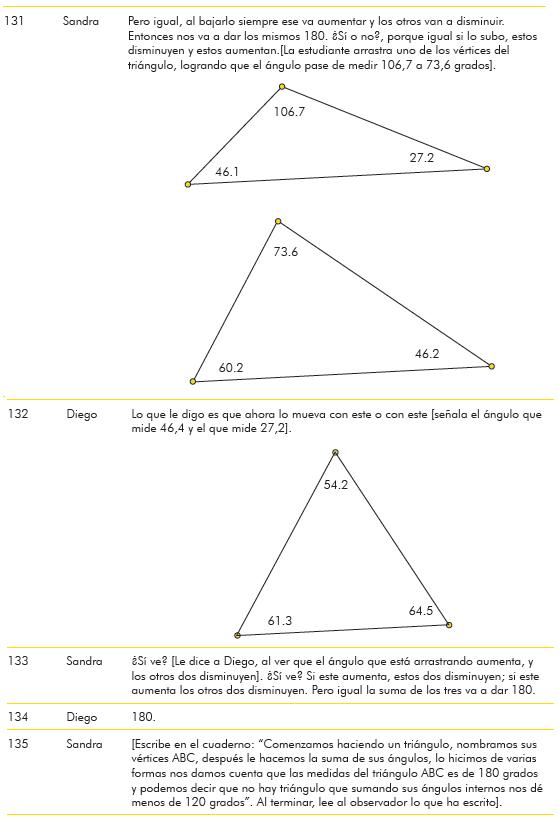
Mencionar que al disminuir la medida de uno de los ángulos del triángulo se aumenta la medida de por lo menos uno de los otros dos ángulos [131], se constituye en una acción de visualización y exploración que le permite a Sandra observar una variación conjunta en la medida de los ángulos e identifica que lo que se resta a uno de los ángulos se la suma a los otros para mantener invariable la suma de las medidas de los mismos [133]. En las intervenciones 131y 133 de la estudiante, se ve reflejada la acción: CIII, i3, a1, puesto que explica la propiedad invariante asociada a la suma de las medidas de los ángulos de un triángulo a través de la acción de arrastre.

Vale la pena resaltar, que la variación conjunta de la medida de los ángulos del triángulo es una observación que Sandra había realizado previamente sin otorgarle la relevancia de las intervenciones 131 y 133. Es decir, a pesar de notar la variación de los ángulos, en un primer momento, no se percató de la importancia que tenía dicha observación para la solución de la tarea propuesta. Específicamente, Sandra observó la variación conjunta de los ángulos en el momento en que estaban verificando si el triángulo construido era equilátero. Por tanto, la justificación planteada por Sandra se gesta en la exploración de casos particulares que en un momento de la actividad de los estudiantes se postularon como posible solución.

En la intervención 132 de Diego, el estudiante, de manera implícita, le manifiesta a Sandra no estar convencido del argumento que ella ofrece para validar la propiedad invariante. Por ello le sugiere someter nuevamente el triángulo a la acción de arrastre, pero esta vez considerando otro vértice. Dicha sugerencia señala la importancia de la arrastre para verificar la propiedad invariante. La intervención de Diego motiva a Sandra a repetir su explicación, aludiendo nuevamente a la representación gráfica para explicar a partir esta la recurrencia del patrón, lo cual evidencia dos acciones sujetas al reconocimiento de argumentos para explicar la validez de una conjetura: el uso de representaciones gráficas para sustentar explicaciones (CIII, i3, a1)y el uso de casos particulares para explicar las condiciones bajo las cuales ocurre la regularidad y exponer una generalidad(CIII, i3, a4).

La intervención 132 de Diego, resulta afortunada en términos de la aceptación de la regularidad dentro del grupo, dado que por un lado le permite a Sandra ratificar y convencerse del patrón descubierto [133] y por el otro lo lleva a él a aceptar la explicación de Sandra y la validez del invariante que ella propone. Esto se ve reflejado en la intervención 134, donde Diego afirma que la suma de las medidas de los ángulos de un triángulo es 180. La aceptación de la propiedad invariante se ve reflejada en la intervención 135 de Sandra, en la que decide escribir lo encontrado, luego de repetir la explicación a su compañero. Al parecer la escritura del invariante está motivada por la afirmación de Diego en la intervención 134, dado que Sandra pudo haberla tomado como una aceptación a su explicación.

Es de resaltar que Sandra da respuesta a la tarea solo hasta que ha encontrado un argumento que le permite justificarla y persuadir a su compañero. El texto que escribe esta estudiante y que luego lee al observador evidencia su convencimiento de que no existe triángulo que cumpla con la condición impuesta en la situación y que además la suma de la medida de los ángulos de un triángulo es siempre 180.

Resultados del análisis ejemplificado

Es de resaltar que el uso de las categorías, específicamente de la codificación de las acciones de los estudiantes, permitió identificar que ellos realizaron acciones tanto del proceso de conjeturación como de justificación a lo largo de toda su actividad. Tal codificación también puso en evidencia el uso de la geometría dinámica en la exploración, generalización y explicación de propiedades invariantes.

En relación con las acciones de la actividad demostrativa, el ejemplo citado permitió evidenciar, en particular, acciones de: visualizar, explorar, verificar y explicar. Los estudiantes visualizaron al identificar los elementos constitutivos del triángulo (vértices, lados y ángulos). En relación con la exploración, los estudiantes hicieron acciones en el entorno Cabri tales como arrastrar para identificar invariantes y tomar medidas para identificar relaciones entre los objetos involucrados en la situación en la situación. En términos de la verificación, los estudiantes se motivaron a corroborar el invariante encontrado haciendo uso de casos particulares, bajo la posibilidad de encontrar algún tipo de triángulo en el que el invariante encontrado no se cumpliera. Aunque no esperábamos que los estudiantes justificaran el hecho geométrico de la suma de las medidas de los ángulos, por motivación propia ellos decidieron aludir a la representación gráfica construida en Cabri para argumentar por qué era cierto que la suma de las medidas de los ángulos de un triángulo es 180, manifestando que dicha suma era constante porque al tratar de disminuir la medida de uno de los ángulos del triángulo aumentaba la medida de alguno de los otros dos. Tal motivación no solo refleja una participación genuina por parte de los estudiantes sino también la acción de explicar de la actividad demostrativa y la utilidad del arrastre en la producción de justificaciones que permitan validar un invariante encontrado. Consideramos que haber propuesto a los estudiantes una situación que no tenía solución, dado que no es posible encontrar un triángulo donde la suma de la medida de sus ángulos sea menor que 120, contribuyó para que ellos se inquietaran por el resultado obtenido y buscaran justificarlo.

Conclusiones

El análisis de la actividad de los estudiantes permitió evidenciar el potencial de la geometría dinámica en la solución de las situaciones, particularmente en la exploración de las mismas; en el reconocimiento de propiedades invariantes; en la verificación de propiedades invariantes, conjeturas, construcciones e hipótesis de solución; y en la búsqueda de argumentos para la validación de los invariantes encontrados. En particular, tal análisis nos condujo a percibir que el arrastre ofrece evidencia perceptual de la veracidad de una propiedad geométrica. Mariotti (2006) menciona que dicha herramienta proporciona un contexto para una cultura de preguntas acerca del por qué una construcción funciona, con base en el análisis de la actividad de los estudiantes, añadiríamos que también proporciona un espacio propicio para la emergencia de cuestiones relativas al porqué de un invariante en una situación geométrica particular.

En relación con el aprendizaje de la demostración en la escuela, consideramos que el trabajo reportado señala una nueva concepción de teorema al proponer la producción de hechos geométricos en el contexto escolar; tal concepción no implica aceptar la imposibilidad de aproximar a los estudiantes al estudio de la demostración en un nivel de educación básica sino, más bien, es una invitación a ser conscientes de la complejidad de la producción de teoremas en el sentido estricto de Mariotti (1997). En este marco, planteamos una analogía entre los elementos que componen la definición de teorema propuesta por dicha autora y los elementos que están inmersos en el constructo "actividad demostrativa" y que consideramos son próximos a la comprensión de teorema en el contexto escolar. Es claro que en la escuela no formamos matemáticos. Por tanto, no construimos teorías matemáticas ni demostraciones formales y rigurosas como las que elaboran los expertos de esta ciencia, pero sí formulamos conjeturas que se pueden justificar con base en un sistema teórico local (conjunto de enunciados alrededor de un concepto, los cuales pueden estar conectados o aislados en el mundo de las matemáticas escolares) o en reglas sociomatemáticas que determinan los modos de validación en la clase.

En términos del diseño de las categorías de análisis, si bien tomamos a Boero (1999), Parra y Piñeros (2011) y Camargo (2010) como referentes para la construcción de las mismas, es de destacar que nosotros hicimos un aporte en su elaboración, en cuanto que las complementamos con indicadores y acciones emergentes del análisis de los datos del estudio y propusimos una codificación. La construcción de tales categorías se constituye en un primer intento por caracterizar la actividad de los estudiantes en edad extraescolar en términos de la actividad demostrativa; por ello consideramos que estas pueden ser estudiadas y enriquecidas en el marco de futuros estudios relacionados con la posibilidad de actividad demostrativa en un contexto escolar particular. Es de resaltar que dichas categorías están construidas teniendo en cuenta el uso de Cabri para la solución de las situaciones propuestas a los estudiantes, por ello consideramos que podrían ser útiles en estudios que contemplen el uso de la geometría dinámica para su realización.

Los resultados obtenidos mediante el análisis de la actividad de los estudiantes, nos ha llevado a considerar que en relación con este tipo de estudios aún hay cuestiones por solucionar, que eventualmente podrían convertirse en el foco de indagación de futuros estudios. En particular, nos ha surgido una pregunta: los estudiantes han hecho explicita la importancia de Cabri en su actividad y nosotros hemos identificado en el uso del software un elemento importante para la generación de un ambiente de actividad demostrativa. De no utilizarse dicho software sino otro tipo de herramienta diferente a la geometría dinámica ¿se darían cambios en la producción de los estudiantes relacionados con los dos procesos de la actividad demostrativa? ¿Cuáles y en qué sentido?

Referencias bibliográficas

Ávila A. (1999). Una tarea necesaria. (La investigación en educación matemática de jóvenes y adultos). Recuperado el 26 de octubre de 2011 de http://descartes.ajusco.upn.mx/varios/piem/publicaas.html.         [ Links ]

Barrio de la Puente, J., Barrio de la Puente, M., y Quintanilla, M. (2006). Tecnología y educación en las matemáticas. Revista Complutense de Educación,18(1), 113-132.         [ Links ]

Bastán, M. y Elguero, C. (2005). El escenario socio-cultural en la formación matemática del sujeto adulto. Una indagación en alumnos de nivel medio. Premisa (Revista de la sociedad argentina de educación matemática), 7(27), 23-25.         [ Links ]

Boero, P. (1999). Argumentation and mathematical proof: A complex productive, unavoidable relationship in mathematics and mathematics education. International Newsletter on the teaching and learning of mathematical proof [Traducción realizada por Patricio Herbst].Genova: International Newsletter on the Teaching and Learning of Mathematical Proof.         [ Links ]

Camargo, L. (2010). Descripción y análisis de un caso de enseñanza y aprendizaje de la demostración en una comunidad de práctica de futuros profesores de matemáticas de educación secundaria (Tesis doctoral). Universitat de Valéncia, Valencia, España.         [ Links ]

Christou, C., Mousoulides, N., Pitallis, M. y Pitta-Patanzi, D. (2004). Proofs through exploration in dynamic geometry environments. International Journal of Computers for Mathematical Learning, 2(3), 339-352.         [ Links ]

Cohen, L. y Manion, L. (1990). Métodos de investigación educativa. Madrid: La muralla.^o        [ Links ]

Gutiérrez, A. (2005). Aspectos metodológicos de la investigación sobre aprendizaje de la demostración mediante exploraciones con software de geometría dinámica. En A. Maz, B. Gómez, M. Torralbo (eds.). Noveno Simposio de la Sociedad Española de Educación Matemática SEIEM, 27-44. Córdoba: Sociedad Española de Investigación en Educación Matemática, SEIEM.         [ Links ]

Hanna, G. (2000). Proof, explanation and exploration: An overview. Educational Studies in Mathematics, 44(1), 5-23.         [ Links ]

Jones, K. (2000). Providing a foundation for a deductive reasoning: students' interpretation when using dynamic geometry software and their evolving mathematical explanations. Educational Studies in Mathematics, 44(1 y 2), 55-85.         [ Links ]

Larios, V. (2002). Demostraciones y conjeturas en la escuela media. Revista Electrónica de Didáctica de las Matemáticas, 3, 45-55.         [ Links ]

Mariotti, A. (1997). Justifying and proving in geometry: the mediation of a microworld. En M. Hejnyy J. Novotna (eds.).Proceedings of the European Conference on Mathematical Education (pp. 21-26). Prague: Prometheus Publishing House.         [ Links ]

Mariotti, A. (2006). Proof and proving in mathematics. En A. Gutierrez y P. Boero (eds.), Handbook of Research on the Psychology of Mathematics Education: Past, Present and Future (pp. 173-204). Genova: Sensepublishers.         [ Links ]

Ministerio de Educación Nacional (MEN) (1998). Matemáticas. Lineamientos curriculares. Serie Lineamientos Curriculares. Dirección general de Investigación y desarrollo pedagógico. Bogotá, Colombia.         [ Links ]

Ministerio de Educación Nacional (MEN) (2006). Estándares básicos de calidad. Bogotá, Colombia.         [ Links ]

Molina, O.; Luque, C. y Robayo A. (2014). Producción de teoremas con estudiantes en extraedad: la justificación de una conjetura. Tecné, Episteme y Didaxis: TED. Num 35. p.39-61.         [ Links ]

Parra, D. y Piñeros, A. (2011). Elaboración de conjeturas: El caso de una pareja de estudiantes en una clase de geometría plana (Tesis de Licenciatura en Matemáticas). Universidad Pedagógica Nacional. Bogotá         [ Links ].

Perry, P., Camargo, L., Samper, C. y Rojas, C. (2006). Actividad demostrativa en la formación inicial del profesor de matemáticas. Bogotá: Universidad Pedagógica Nacional.         [ Links ]

Perry, P., Samper, C., Camargo, L., Echeverry, A., y Molina, O. (2008). Innovación en la enseñanza de la demostración en un curso de geometría para formación inicial de profesores. En A. Cano; F. Contreras y E. Olvera (eds.), Libro electrónico del XVII Simposio Iberoamericano de Enseñanza de las Matemáticas: "Innovando la enseñanza de las matemáticas" (pp. 1-18). Toluca: Universidad Autónoma del Estado de México.         [ Links ]