Since the pioneering work of Darwin (1872), emotion has been a key topic in psychology. In this regard, two predominant theoretical conceptions have guided research on the structure of affective states (Watson & Clark, 1997). From the first perspective, affective states are organized in different categories, such as anger, fear and happiness (Lazarus, 2000). From the second perspective, they are categorized into higher-order dimensions (e.g., positive and negative) based on the relationships among discrete emotions (Watson et al., 1988). From this latter approach, Watson et al. (1988) developed the Positive and Negative Affect Schedule (PANAS). This self-reported measure contains two 10-item subscales designed to measure positive and negative affect as state (e.g., present moment), moods (e.g., past week) or traits (e.g., last month). Positive Affect (PA) reflects the extent to which one is experiencing positive emotions, while Negative affect (NA) represents the occurrence of negative emotions. Watson et al. (1988) showed, based on exploratory factor analyses (EFA), that PA and NA represent orthogonal dimensions of affective experience.
The PANAS scale is widely used in studies related to emotions. For instance, Seib-Pfeifer, Pugnaghi, Beauducel, and Leue (2017) found that 465 published articles used PANAS in diverse research projects within the past twelve years. Although numerous studies scored the scale according to the two dimensions (PA and NA) as Watson et al. (1988) proposed, the structural validity of the PANAS has been under debate since the late '80s (Seib-Pfeifer et al., 2017). Numerous studies investigated the factor structure of the PANAS by means of EFA, showing that two-factor (with oblique and orthogonal rotation) and three-factor models offer a good fit to data (see e.g., Moriondo, De Palma, Medrano, & Murillo, 2012; Villodas, Villodas, & Roesch, 2011).
The factor structure of the PANAS has also been investigated by confirmatory factor analysis (CFA). Numerous studies provided evidence for the two-factor model, where PA and NA were either proposed to be correlated or uncorrelated factors. For example, Crawford and Henry (2004), using robust maximum likelihood (ML), found that a model with correlated factors provided a good fit to data. Although, Tuccitto, Giacobbi, and Leite (2010), using ML, observed that an orthogonal two-factor model provided the best fit. In both cases, covariance between errors was allowed (Zevon & Tellegen, 1982). In addition, Vera-Villarroel et al. (2017) evidenced that a model with uncorrelated factors presented an adequate fit, using the weighted least squares means and variance adjusted, and without correlated error.
Recent studies have provided evidence for a bifactor model. For instance, Leue and Beauducel (2011) found a good fit for a bifactor model with NA and PA with uncorrelated factors as well as an additional general factor (labeled Affective Polarity, AP). Also, Ortuño Sierra, Santarén-Rosell, Pérez de Albéniz and Fonseca-Pedrero (2015) and Seib-Pfeifer et al. (2017) revealed that a bifactor model provided the best fit to the data. However, the structure of the PANAS might be more complex (e.g., Gaudreau et al., 2006). Some researchers have reported that a three-factor model showed a better fit; for instance, Gaudreau et al. (2006) showed that a three-factor model with cross-loadings provided a better fit to the data than a two-factor model. They observed that the NA factor was divided into two factors, named as NA-Afraid and NA-Upset. NA-Afraid included the items afraid, scared, nervous, distressed and jittery, while NA-Upset incorporated the items upset, hostile, guilty, ashamed and irritable. On the other hand, Mehrabian (1997) tested two models for the PANAS: a two-factor model and a three-factor model with PA constituting a first order factor and NA constituting a second-order factor, with two factors (NA-Afraid and NA-Upset). Mehrabian found that NA-Afraid comprised the items afraid, scared, nervous, guilty, ashamed and jittery; while NA-Upset included the items upset, distressed, irritable and hostile. Although the three-factor model was better, both models showed a poor fit.
Until now, four examinations of the PANAS have been carried-out in Argentina, three of them consisting of exploratory analyses with general population (Moriondo et al., 2012), university students (Medrano, Flores Kanter, Trógolo, Curarello, & González, 2015), and children (Schulz de Begle, Lemos, & Richaud de Minzi, 2009), while only one study performed confirmatory analyses. Flores Kanter and Medrano (2016) conducted CFA with students from the National University of Cordoba. They compared one, two, and three-factor structures, both in their oblique and orthogonal variants. They found good indexes for all the models examined, except for the one with only one factor.
Flores Kanter and Medrano's (2016) results are relevant in order to understand the structure of the PANAS but, we believe that due to the frequent use of this instrument in the local context, a deeper examination of its structure is needed, including other samples. Specifically, we consider there are four main aspects to consider. First, there is lack of CFA of the structure of the PANAS with general population and there is no evidence whatsoever regarding this instrument with athletes. The affective configuration of athletes has been found to differ from the general population, mostly because the former tends to show a higher proportion of positive emotions, compared to the latter (Borges Hernández, De la Vega Marcos & Ruiz Barquín, 2016). Also, psychological factors in general present patterns considered unique to athletes, due to the characteristics of the sportive environment. In effect, they experience a wide range of emotions during their practice and competitions which varies even across pre-, mid- and post- performance event (Barrios, 2007; Latinjak, 2011). In fact, sports are considered an ideal field for studying emotional reactions to stressful and competitive situations (Barrios, 2007). These characteristics make it inadequate to employ instruments adapted to the general population for measuring athletes' states or traits (García-Más, Estrany Bonnín, & Cruz Feliu, 2004), and therefore, highlights the need to specifically evaluate instruments designed to assess emotional factors in athletes. On the other hand, students are the most employed sample in local psychological studies, followed by general population. As a consequence, it is essential to have a deep and complete understanding of the instruments used to inquire about their characteristics. Furthermore, to know the properties of the PANAS on these populations is relevant due to the potential predictive and explicative role of affection on several variables such as attention, depression, anxiety and stress (Crawford & Henry, 2004).
Second, Flores Kanter and Medrano (2016) employed an online version of the PANAS. There is evidence of differences in the properties of the scale between paper-and-pencil and online versions. Specifically, Seib-Pfeifer et al. (2017) could not find measurement invariance across those presentation forms and concluded that online presentations of the PANAS should be considered cautiously. It is particularly important to count on evidence for the paper-and-pencil version, especially for general population, because some subsamples of the general population are not accessible through online channels.
Third, although Flores Kanter and Medrano (2016) provide useful information about the three-factor model proposed by Mehrabian (1997), it is still necessary to consider the model proposed by Gaudreau et al. (2006). The further testing of these models could help to shed light on the structural ambiguity of the PANAS in the local population. This is especially necessary due to the inconclusive results obtained by Flores Kanter and Medrano, who found good indicators for different models.
Fourth, there are two items, alert and excited, that have been found to cross-load (e.g., Tuccitto et al., 2010), and although Flores Kanter and Medrano (2016) theoretically discussed these items, they did not conduct any analysis excluding them. To explore these items is especially relevant for our population, due to their characteristics in the Spanish language. On one hand, the word excited in Spanish is polysemic, being equally related to sexual arousal, nervousness, enthusiasm, anger, and joy (Real Academia Española, 2001). Also, in sports, it can be interpreted as a positive state related to readiness and activation or as a negative state, signaling anxiety and lack of control (Hanin, 2000). Similarly, although the meaning of the word alert seems clear, it has been pointed out that this adjective can be perceived as positive (e.g., facilitative) by some people, while negative (e.g., debilitative) by others (Gaudreau et al., 2006).
In these sets of studies, we aimed to perform CFA to evaluate the original two-factor model (Watson et al., 1988) and two three-factor models, one proposed by Mehrabian (1997) and another by Gaudreau et al. (2006), as well as a bi-factor model (Leue & Beauducel, 2011), all of them in their oblique and orthogonal variants, with Argentinean samples of university students, general population, and athletes. We expect that the two-factor model proposed by Watson et al. (1988) would be replicated. However, it is important to highlight that the samples were obtained as part of four different and broader studies. In fact, there are slight variations; for example, in the order of presentation of the items, and the version used (paper-and-pencil or online). Extended details about each of the broader studies can be found in the Appendix (see Supplementary materials). Consequently, our aim is not to make comparisons, but to present the independent examination of the proposed models for the selected samples.
Method
The ethical guidelines for human research recommended by the American Psychological Association (APA, 2017) were respected. Informed consent forms and information sheets were used. The participation in the studies was voluntary and anonymous. Studies did not imply any risk for the participants and protocols did not require the approval from an ethics committee. The use and analysis of the data were confidential.
Study 1
This study was carried out in 2016, with the aim to validate the instruments Difficulties in Emotion Regulation Scale (DERS; Gratz & Roemer, 2004) and Difficulties in the Regulation of Positive Emotions Scale (DERS-P; Weiss, Gratz, & Lavender, 2015) in an Argentinian sample.
Participants
A convenience sample of 392 college students from the National University of Córdoba and the National Technological University of Córdoba in Argentina, aged 18 to 28 years (M = 21.40, SD = 2.24; 253 females, 64.5%) was evaluated.
Instrument
This study was based on the Spanish version of the PANAS used in Moriondo et al. (2012). It is composed of 20 adjectives of emotional states measuring positive (10 items) and negative (10 items) affect. Participants indicated to what extent they generally experienced each emotion. Each item was scored on a 5-point Likert-type scale (1 = very little or nothing, 5 = extremely).
Study 2
This study was carried out in October 2012, in the framework of a major study about psychometric properties of different instruments, measuring decision-making and/or emotional processes.
Participants
A convenience sample of 395 students from 18 to 57 years (M = 23.42, SD = 5.51; 252 females, 63.8%) studying different degrees at the National University of Córdoba and the National Technological University of Córdoba was constituted.
Study 3
This study was carried out in July 2012, in the framework of a major study about psychometric properties of different instruments, measuring decision-making and/or emotional processes.
Participants
A convenience sample of 316 adults from Cordoba in Argentina, aged 18 to 65 years (M = 32.67, SD = 10.66; 178 females, 56.3%) was evaluated. A total of 36 (11.4%) participants had only primary education studies, 59 (18.7%) had secondary studies, and 130 (41.1%) were tertiary or university students, whereas 39 (12.34%) had already completed tertiary studies, and 52 (16.46%) had completed university studies.
Study 4
The study was carried out in 2017 in order to test the role of motor self-efficacy, competitive state anxiety, mood, risk perception and risk taking on sport injuries.
Previously, an instrumental study of the PANAS was developed in order to validate it. In this research we used the dataset of the main study.
Participants
A convenience sample of 533 sports athletes from Córdoba, Argentina (173 female, 32.5%) completed the PANAS 1 to 72 hours prior to competing (M = 34.9, SD = 20.51). The sample was made up of soccer players (n = 197), hockey players (n = 184), basketball players (n = 46), handball players (n = 52), indoor soccer players (n = 22) and martial arts practitioners (n = 32), from 14 to 50 years old (M = 21.22, SD = 5.71). On average they trained 4.20 days per week (SD = 1.21), between 3 and 10 hours per day. Athletes overall averaged 10 or more years practicing their respective sports and they had all competed at province to international levels at least three times a year.
Instruments
Similar to Study 1, although participants had to indicate the extent to which they were experiencing each adjective at the moment of taking the questionnaire, just before competing, using a 5-point Likert-type scale (1 = very little or nothing, 5 = very much).
Procedure
After initial contacts, data collection was done on the last training day before competition. All other procedures were like Study 2. The questionnaires were collectively administered in the locker room, but each participant completed the questionnaire individually.
Statistical analyses
Each dataset was analyzed separately. First, the pattern of missing data was explored. Second, a preliminary data analysis was conducted. Univariate and multivariate outliers were identified. Skewness and kurtosis values in the range of ±1 were considered excellent, and those in the range of ±1.5 were acceptable. In order to achieve a more parsimonious presentation throughout this paper we decided to report only the results excluding outliers. Nevertheless, it is worth noting that similar results were obtained in the CFAs using the full sample of each study. Third, several CFA were conducted at the item level in order to evaluate the models exposed in the next section. Considering the ordinal nature of the data, we used the weighted least squares means and variance adjusted (WLSMV) estimator and the polychoric correlation matrix. For bi-factor models, we used theta parameterization. The following goodness-of-fit indices were considered: Root Mean Square Error of Approximation (RMSEA and 90% confidence interval; < .08 reasonable fit, < .05 good fit), Comparative Fit Index (CFI) and Tucker-Lewis Index (TLI) (> .90 acceptable, > .95 preferred) (Hu & Bentler, 1999), and Weighted Root Mean Square Residual (WRMR, near to 1.0 adequate model fit). Finally, the internal consistency of each factor was analyzed for the models that presented a better fit. Following the procedures used in previous studies of the scale, Cronbach's alpha coefficient (α) was calculated. Moreover, McDonald's omega coefficient (ω) was estimated. Additionally, the composite reliability was estimated with the Raykov's rho coefficient (p), which considers the factorial weights, the residual variance, and the r 2 of each item, which generates less variation of the error. SPSS 19 (IBM SPSS), Mplus 6 (Muthén & Muthén, 1998-2011) and R 3.5.1 (R Core Team, 2018) were employed.
Specification of CFA models
Seven models were examined: (1) Two-factor orthogonal model (PA and NA); (2) Two-factor oblique model; (3) Three-factor model based on Gaudreau et al. (2006), NA split into two correlated factors (Upset and Afraid), which were both uncorrelated with PA; (4) Like model 3, but with correlated factors; (5) Three-factor model based on Mehrabian (1997), NA split into the two correlated factors (Upset and Afraid), which were both uncorrelated with PA; (6) Like model 5, but with correlated factors; (7) Bi-factor model with a three-factor solution, in which PA and NA were un-correlated factors and the loadings of all items on a third uncorrelated more general factor AP (Affective Polarity) were freely estimated (Leue & Beauducel, 2011). For each model presented above, four variants were analyzed: (a) Model with all items; (b) Model with all items, allowing for covariance between errors; (c) Model with all items except alert and excited items, and (d) Model with all items except alert and excited items and allowing for covariance between errors. We add covariance between errors that were comprised in Zevon and Tellegen's (1982) proposal, considering modification index suggested by the software. The items alert and excited were eliminated from the analysis because they presented low factorial loadings (≤ .40) or cross-loadings between factors.
Results
Study 1
After preliminary analysis, the sample was comprised of 390 college students (M = 21.40, SD = 2.24; 252 females, 64.6%). All items presented excellent skewness and kurtosis values.
Table 1 shows the goodness-of-fit indices estimated for each model. The oblique solutions presented a better fit than the orthogonal solutions. Moreover, models excluding the items alert and excited (2b, 4b, and 6b) presented a better fit than the models with all items. In fact, models (2d, 4d, and 6d) which also permitted covariance between errors showed the best goodness-of-fit indices. The standardized factor loadings were greater than .40. Despite the bi-factor model, 7d showed the best fit, the factor AP presented negative or far below .40 factor loadings (see Appendix in Supplementary materials).
Table 1 Goodness-of-Fit Indices of the PANAS models estimated by Confirmatory Factor Analysis - College students (n = 390).

Note. df = degrees of freedom; RMSEA = root mean square error of approximation; CI = confidence interval; CFI = Comparative Fit Index; TLI = Tucker-Lewis index; WRMR = weighted root mean square residual. CE = Covariance between errors. PA = Positive Affect; NA = Negative Affect; Af = Afraid; Up = Upset.
The models that showed better fit are presented in bold.
1. All models presented statistically significant X 2 values (p < .001).
*p ≤ .05.
Notoriously, very high correlations between Upset and Afraid were observed in models 4d (.864) and 6d (.931), which suggest an underlying common dimensionality. Additionally, the correlations between PA-NA (or Upset or Afraid) were negative and moderate (between -.271 and -.402) in models 2d, 4d and 6d.
Table 2 Goodness-of-Fit Indices of the PANAS models estimated by Confirmatory Factor Analysis - College students (n = 387).
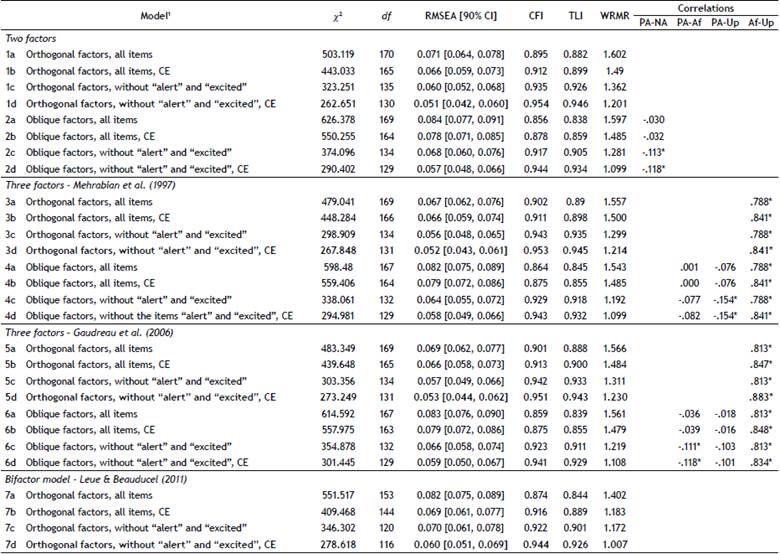
Note. df = degrees of freedom; RMSEA = root mean square error of approximation; CI = confidence interval; CFI = Comparative Fit Index; TLI = Tucker-Lewis index; WRMR = weighted root mean square residual. CE = Covariance between errors. PA = Positive Affect; NA = Negative Affect; Af = Afraid; Up = Upset.
The models that showed better fit are presented in bold.
1. All models presented statistically significant X 2 values (p < .001).
* p ≤ .05.
Table 3 Goodness-of-Fit Indices of the PANAS models estimated by Confirmatory Factor Analysis - Youth and Adults (n = 300).
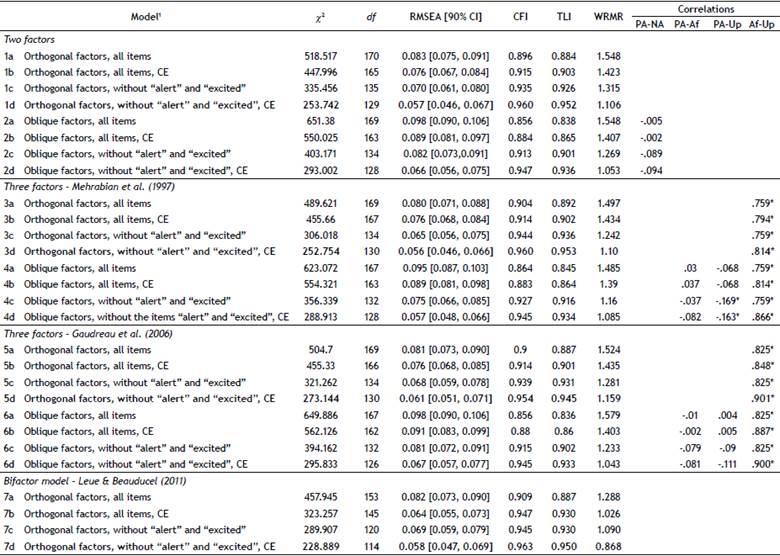
Note. df = degrees of freedom; RMSEA = root mean square error of approximation; CI = confidence interval; CFI = Comparative Fit Index; TLI = Tucker-Lewis index; WRMR = weighted root mean square residual. CE = Covariance between errors. PA = Positive Affect; NA = Negative Affect; Af = Afraid; Up = Upset.
The models that showed better fit are presented in bold.
1. All models presented statistically significant X 2 values (p < .001).
*p ≤ .05.
Table 4 Goodness-of-Fit Indices of the PANAS models estimated by Confirmatory Factor Analysis - Athletes (n = 469).
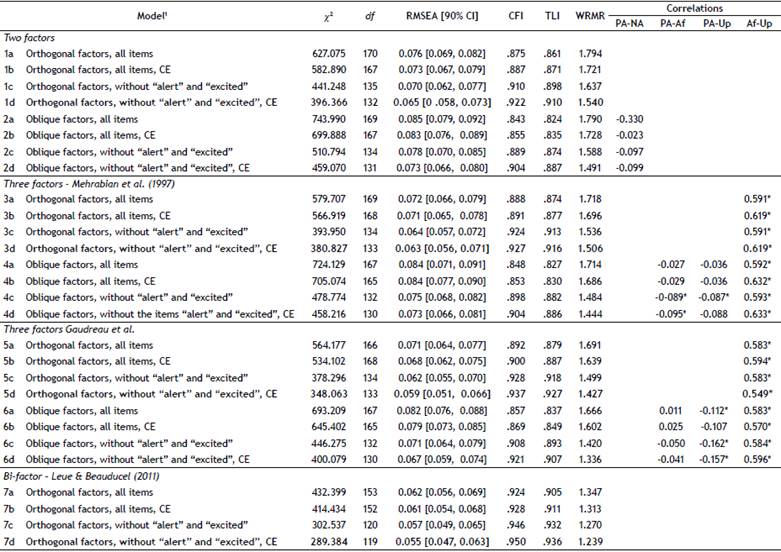
Note. df = degrees of freedom; RMSEA = root mean square error of approximation; CI = confidence interval; CFI = Comparative Fit Index; TLI = Tucker-Lewis index; WRMR = weighted root mean square residual. CE = Covariance between errors. PA = Positive Affect; NA = Negative Affect; Af = Afraid; Up = Upset.
The models that showed better fit are presented in bold.
1. All models presented statistically significant X 2 values (p < .001).
*p ≤ .05.
Table 5 shows internal consistency results. Composite reliability values of the best models were between .80 and .89, whereas the omega values were between .78 and .85. The Upset dimension of the model 4d showed the lowest omega coefficient.
Study 2
The final sample included 387 students (M = 23.47 years old, SD = 5.54; 63.3% females). All items presented acceptable skewness and kurtosis values.
The goodness-of-fit indices estimated for each model are presented in Table 2. In general, the orthogonal solutions presented a better fit than the oblique solutions, although it was not optimal. Models excluding items alert and excited and allowing covariance between errors showed the best fit. In those models, the standardized factor loadings were greater than .40. Even though differences in the global adjustment of the four best models are practically indistinguishable, it is worth dwelling on the correlations between the factors of the negative dimension that is tested in three-dimensional models. In both models 3d (grouping of items proposed by Mehrabian, 1997) and 5d (Gaudreau et al., 2006), very high correlations were observed between Upset and Afraid (.816 and .811, respectively), which is indicative of the underlying common dimensionality. In general, very low and negative correlations were observed between PA-Upset, while non-significant relations were observed between PA-NA, and PA-Afraid. Regarding bifactor models, the model 7d offered the best fit. In this case, the Polar Affectivity factor did not offer an easy interpretation (see Appendix in Supplementary materials).
In terms of internal consistency, Cronbach's alpha and omega values were between .70 and .83, while p values were between .76 and .86 (Table 5).
Study 3
The final sample included 300 participants (M = 32.74 years old, SD = 10.66; 56% females). All items presented acceptable skewness and kurtosis values.
The goodness-of-fit indices of the models under analysis are presented in Table 3. Similar to what was observed in Study 2, the orthogonal solutions presented a better fit than the oblique solutions. Specifically, models excluding items alert and excited and allowing covariance between errors showed the best fit. In those models, the standardized factor loadings were greater than .40, except for item 1 (interested) which presented loads between .35 and .40. We found high correlation indices between Upset and Afraid in the three factor models, model 3d = .794, and model 5d = .848. PA was negatively related to Upset, but the magnitude of the relation was very low. Moreover, the relationships between PA-NA and PA-Afraid were, in general, non-significant. The model 7d offered the best fit. The AP factor also fails to offer an easy interpretation (see Appendix in Supplementary materials).
With respect to internal consistency, Cronbach's a values were between .67 and .84, omega values between .68 and .85, while rho values were between .71 and .86 (Table 5).
The Upset dimension of the model 5d showed the lowest Cronbach's a coefficient.
Study 4
The final sample included 469 athletes (M = 21.30 years old, SD = 5.8; 31.2% females). The presence of several outliers (48 univariate and 17 multivariate) produced poor indices of goodness-of-fit, so 65 cases were discarded from the final sample. All items presented acceptable skewness and kurtosis values.
The goodness-of-fit indexes for each assessed model are presented in Table 4. In general, orthogonal solutions presented a better global fit than the oblique solutions, and bi-factor models showed better goodness-of-fit indices than the other two. In all models, goodness-of-fit indexes increased when covariance between errors were allowed and the items alert and excited were excluded. Standardized factor loadings of two and three factor models were greater than .40, except item 8 (hostile) which presented a load of .352. The AP factor showed loadings oscillating between -.014 and .666.
Regarding the correlation indexes, we found moderate to high correlations between Upset and Afraid throughout all the models (.570 to .633), suggesting an underlying common dimension between those factors. Additionally, low and negative correlations were observed between PA-Upset (models 4c, 6a 6c, and 6d) and PA-Afraid (models 4c and 4d), while PA was not significantly related to NA.
Regarding the internal consistency, Cronbach's a index oscillated between .55 and .82, composite reliability indices were between .67 and .87, and omega index between .55 and .82. The model 1d showed best reliability indexes.
Discussion
The PANAS is widely used across different samples, developmental stages, and cultural contexts. However, its use is not free of controversy (e.g., Seib-Pfeifer et al., 2017). In Argentina, several studies had been conducted using the PANAS, but much remains to be understood about its structure. Thus, we combined four independent studies measuring the PANAS in order to examine its structure and provide evidence about its validity and reliability. We carried-out a confirmatory analysis of the two-factor model, originally proposed as the structure of the PANAS (Watson et al., 1988), the three-factor model proposed by Mehrabian (1997), the three-factor model proposed by Gaudreau et al. (2006), and a bi-factor model (Leue & Beauducel, 2011). In all cases we included oblique and orthogonal variants and explored these attributes with university students, general population, and athletes.
In line with previous findings (e.g., Crawford & Henry, 2004), we observed that more than one model had an optimal fit. Specifically, two-factor as well as three-factor and bi-factor models showed a good fit. Moreover, in all cases fit improved when correlated errors were permitted (Zevon & Tellegen, 1982) and the items alert and excited were excluded. Regarding the internal consistency of the PANAS, Cronbach's alpha coefficients and composite reliability and omega indexes oscillated between .55 and .89. The result is consistent with previous studies in which optimal values of alpha coefficients (Crawford & Henry, 2004) as well as composite reliability (Estevez et al., 2016; Tuccitto et al., 2010) were observed.
Our findings show that the PANAS comprises a complex factor structure. In the two studies with college student samples, we found opposite results with respect to the relationship between PA and NA. In Study 1 they were correlated, but not in Study 2. Previous researchers have also reported inconsistencies in factor structure of the PANAS with samples of college students. For example, Merz and Roesch (2011) found that an oblique two-factor model presented the best fit to data. Whereas Gargurevich and Matos (2012), using two samples of Peruvian college students, reported that orthogonal and oblique two-factor models provided a good fit to data. What's more, Mehrabian (1997) found that a hierarchical model of three-factors showed a better fit than an orthogonal two-factor model. In Study 3, using a sample of adults, we observed that orthogonal two-factor and three-factor models showed the best fit, similar to what was observed in previous studies (e.g., Vera-Villarroel et al., 2017). Also, employing a sample of athletes, in Study 4 we observed that PA and NA were uncorrelated factors, similar to what was observed by Gaudreau et al. (2006).
Orthogonal and oblique structures of the PANAS have been under debate for a long time and there is evidence for both the former (e.g., Crawford & Henry, 2004) and the latter structures (e.g., Merz et al., 2013; Estevez et al., 2016). The structures reflect the theoretical assumptions about negative and positive emotions. Originally, it was suggested that these two subscales were unrelated, due to their nature as opposite emotions, which reside at the end of one of two opposing poles (Watson et al., 1988). In fact, in some cases, only one dimension of the PANAS correlates with other constructs, which indicates independence between the two factors of the scale (e.g., Watson et al., 1988). However, based on empirical evidence about the correlation of negative and positive emotions, some authors have argued that it is counterintuitive to consider them as unrelated (Crawford & Henry, 2004). In this regard, for example, Estevez et al. (2016) described them as alternative models in which theoretically independent PA and NA factors are also negatively associated. According to Crawford and Henry (2004), this overlap deeply questions such original independence. Whereas, Merz et al. (2013) argue that it is possible to consider that this structure of affect is composed of "separate dimensions on which a person can simultaneously experience PA and NA at low or high levels" (p. 947).
When using the PANAS to explore affective traits (Studies 1, 2 and 3) we observed that PA and NA were correlated in some cases, but in other cases they were not. In the local context, Flores Kanter and Medrano (2016) reported that oblique solutions presented a better fit than the orthogonal version. However, for the same version of the PANAS, Allan, Lonigan and Phillips (2015) provided evidence that PA and NA were uncorrelated factors. In our studies, we believe that the differences found in the structure of the PANAS, in addition to the application format (Study 1: online; Studies 2 and 3: paper-and-pencil), may be related to what they are measuring. Specifically, Gaudreau et al. (2006) point out a difference between mood and trait. In this sense, Ekkekakis (2012) proposed that moods last longer than emotions, but are usually temporally remote. In Studies 2 and 3 we asked participants to indicate the extent to which they had experience each adjective during the past weeks. Therefore, it remains unclear whether in these studies we measure mood or trait. Regarding state version of the PANAS (Study 4), we found that PA and NA were uncorrelated factors, like Flores Kanter and Medrano.
Some specific items of the PANAS have shown limitations due to cross-loading or ambivalence in the interpretation that participants make of them. Specifically, the items alert and excited have been found to cross-load between factors (e.g., Moriondo et al., 2012). In fact, several authors argue that these items can be interpreted as having facilitative or debilitative effects on behavior (e.g., Gaudreau et al., 2006). The ambivalence on interpretation could explain the cross-loading of such items. Consequently, we carried-out further exploration of the load of the items alert and excited and we evaluated alternatives without them. The reason for us choosing this path instead of allowing cross-loading, as is more commonly done, resides in the higher importance we place on the usefulness of the PANAS for applied research. The admission of cross-loads may provide a better fit for some models, but it does so at the cost of obscuring the interpretation for a singular person in a single factor, which is fundamental for studies using the PANAS as a predictor or a mediational variable. However, we found that models without the items alert and excited showed a better fit.
Our work presents some major limitations that we would like to highlight. First, as explicitly stated through the manuscript, the measurements and samples came from different and independent studies. In effect, these set of studies were not designed with the aim of examining the PANAS exclusively. Thus, they (a) were presented before or after other measurements that may have influenced participant's answers to the PANAS; (b) contained different orders and ways of presenting the items (e.g., the presentation of the word proud or the presentation of the phrase to feel proud); and (c) all were carried-out at different times and places. Although the PANAS has been found to be stable (e.g., Crawford & Henry, 2004) and these differences were rather small, one should not discard the possibility of an influence on the data collected.
Second, we could not identify the model with the best fit. Because the estimation method we used was not able to calculate comparison indices such as AIC and BIC, and models were not necessarily nested. And last, we did not analyze gender or education differences. In this sense, future research should test the structural equivalence of PA and NA scores in men and women. In summary, we found that our models for the PANAS with two and three factors presented adequate loads. However, considering current theories of emotions and its practical applications, we favor the two-factor model.
As a side note, and far from the proposed objectives for this manuscript, we consider that this study provides information about the properties of the online version, and draw attention on the need to further explore this form of the PANAS. We presented two studies with college students, using the online (Study 1) and paper-and-pencil (Study 2) presentation forms, and observed differences regarding the structure of the PANAS. Specifically, in the online application, oblique structures fitted better, whereas on paper-and-pencil presentation, all the models with an acceptable fit where orthogonal. To our knowledge, only one study (Seib-Pfeifer et al., 2017) examined the invariance between the paper-and-pencil and the online forms and found that both presentation forms differed substantially for models of one, two and three factors. Although, here we are just making exploratory and observational comparisons, it serves as an indicator that further exploration is needed in order to understand the invariance of the PANAS for different presentation forms.
Multiple approaches and perspectives must be integrated across all levels of analysis in order to understand emotion (see, for instance, Hamann, 2018). Even more, when considering the growing body of evidence that reveals great variation among human populations in many domains (Henrich, Heine, & Norenzayan, 2010), especially regarding emotion (e.g. Gendron, Crivelli, & Feldman Barrett, 2018). In this sense, to have validated instruments for different populations is fundamental. Therefore, despite the mentioned limitations, the present work contributes to this effort, offering a deeper understanding of the structure of the PANAS for different Argentinean populations.















