Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Momento
Print version ISSN 0121-4470
Momento no.54 Bogotá June 2017
BASES FOR QUANTUM ALGEBRAS AND SKEW POINCARE-BIRKHOFF-WITT EXTENSIONS
BASES PARA ALGEBRAS CUANTICAS Y EXTENSIONES TORCIDAS DE POINCARE-BIRKHOFF-WITT
Armando Reyes1, Héctor Suárez2
1 Departamento de Matemáticas, Universidad Nacional de Colombia, Bogotá, Colombia.
2 Escuela de Matemáticas y Estadística, Universidad Pedagógica y Tecnológica de Colombia, Tunja, Colombia.
Armando Reyes: mareyesv@unal.edu.co
(Recibido: Septiembre/2016. Aceptado: Diciembre/2016)
Abstract
Considering quantum algebras and skew Poincaré-Birkhoff-Witt (PBW for short) extensions defined by a ring and a set of variables with relations between them, we are interesting in finding a criteria and some algorithms which allow us to decide whether an algebraic structure, defined by variables and relations between them, can be expressed as a skew PBW extension, so that the base of the structure is determined. Finally, we illustrate our treatment with examples concerning quantum physics.
Keywords: Quantum algebras, skew Poincare-Birkhoff-Witt extensions, diamond lemma.
Resumen
Para las álgebras cuánticas y las extensiones torcidas de Poincare-Birkhoff-Witt definidas por un anillo y un conjunto de variables con relaciones entre ellas, estamos interesados en establecer un criterio y algunos algoritmos que nos permitan decidir si una estructura algebraica, definida en términos de generadores y relaciones, puede expresarse como una extensión torcida de Poincare-Birkhoff-Witt, de manera que se determine la base de la misma. Ilustramos nuestro tratamiento con diversas algebras de la física cuántica.
Palabras clave: Álgebras cuánticas, extensiones torcidas de Poincare-Birkhoff-Witt, lema del diamante.
Introduction
Historically, the importance of quantum algebras has been considered for several authors in the context of quantum mechanics, see [1] and [2]. For instance, in [3] it was presented a purely algebraic formulation of quantum mechanics which does not require the specification of a space of state vectors; rather, the required vector spaces can be identified as substructures in the algebra of dynamical variables (suitably extended for bosonic systems). As we can see, this formulation of quantum mechanics captures the undivided wholeness characteristic of quantum phenomena, and provides insight into their characteristic nonseparability and nonlocality. In fact, and like the authors say in [3], "the formalism we present fulfils Dirac's aim of working with the algebra of quantum mechanics alone. Furthermore, this approach addresses Dirac's interpretational difficulty, since it can be interpreted in terms of a "process" approach to quantum theory".
Now, from a philosophical point of view, it is very important the new relationships between physics and mathematics that emerge with Heisenberg's discovery of matrix mechanics and its development in the work of Born, Jordan, and Heisenberg himself. Precisely, this is the Einstein's view of "the Heisenberg method", as "a purely algebraic method of description of nature". In [4], chapter 4, it is examined the shift from geometry to algebra in quantum mechanics as a reversal of the philosophy that governed classical mechanics by grounding it mathematically in the geometrical description of the behavior of physical objects in space and time (Heisenberg's matrix mechanics abandons any attempts to develop this type of description and instead offers essentially algebraic machinery for predicting the outcomes of experiments observed in measuring instruments).
One of the fundamental objects in quantum theory is the Heisenberg algebra (see [5] for a detailed exposition ofthis quantum algebra). This algebra and its generalizations - deformations -have recently become of interest in both theoretical physics and mathematics, where it is regarded as a fundamental object and as a suitable model for checking various physical and mathematical ideas and constructions (c.f. [6-15], and others). For example, in [15] it is discussed representations of the Heisenberg relation in various mathematical structures; in [12], it is investigated the structure of two-sided ideals - a key concept in noncommutative algebra - in the q-deformed Heisenberg algebras and the relationships of this algebra with the quantum plane, and its realizations are of primary importance to studying the dynamics of a q-deformed quantum system (see [11] for an exposition of the q-deformed Heisenberg algebra and its relation with the origin of q-calculus).
Actually, and following [14], "algebraic methods have long been applied to the solution of a large number of quantum physical systems. In the last decades, quantum algebras appeared in the framework of quantum integrable one-dimensional models and have ever since been applied to many physical phenomena [... ] It was found that it could be generalized leading to the concept of deformed Heisenberg algebras [16], that have been used in many areas, as nuclear physics, condensed matter, atomic physics, etc". Indeed, the algebraic approach in theoretical physics has been also considered in a possible reconciliation of the quantum mechanics with general relativity theory, where the gravity does not need to be quantized [17].
With this in mind, several families of algebras have been defined with the purpose of studying mathematical and physical properties of different algebraic systems. One of them are the skew Poincare-Birkhoff-Witt extensions (PBW for short) introduced in [18]. These extensions have been studied in several papers ([18-28], and others), and the PhD Thesis [29], where the first author studied ring and module theoretical properties of these algebras.
Skew PBW extensions are defined by a ring and a set of variables with relations between them, (analogously to the definition of several quantum algebras, see [6,8-10,13, 30-32], and others). In the study of these algebras it is important to specify one basis for every one of them, since this allows us to characterize several properties with physical meaning. This can be appreciated in several works: in [33] it was considered the PBW theorem for quantized universal enveloping algebras; in [34] it was established the quantum PBW theorem for a wide class of associative algebras; in [35], it was studied the PBW bases for quantum groups using the notion of Hopf algebra, and in [36] it was considered this theorem for diffusion algebras. Following this idea, in this article we present a criteria and some algorithms which decide whether a given ring with some variables and relations can be expressed as a skew PBW extension with a basis in the sense of Definition 2.1. With this objective, our techniques used here are fairly standard and follow the same path as other text on the subject (see [37] and [29]). The results presented are new for skew PBW extensions and all they are similar to others existing in the literature (cf. [12, 15, 33, 35], and others).
The paper is organized as follows. Section 1 contains the criteria and algorithms of our treatment. Section 2 is dedicated to definition and some properties of skew PBW extensions. Section 3 presents two examples of quantum algebras which illustrate the results established in Section 1 (other examples can be found in [29]). Finally, we present some conclusions about this topic and a future work.
1. Diamond Lemma and PBW Bases
Bergman's Diamond Lemma [37] provides a general method to prove that certain sets are bases of algebras which are defined in terms of generators and relations. For instance, the Poincare-Birkhoff-Witt theorem, which appeared at first for universal enveloping algebras of finite dimensional Lie algebras (see [30] for a detailed treatment) can be derived from it. PBW theorems have been considered several classes of commutative and noncommutative algebras (see [33-36], and others). With this in mind, and since skew PBW extensions are defined by a ring and a set of variables with relations between them (Definition 2.1), in this section we establish a criteria and some algorithms which decide whether a given ring with some variables and relations can be expressed as a skew PBW extension. This answer is obtained following the original ideas presented in [37] and the treatment developed in [29].
Definition 1.1. (i) Let X be a non-empty set and denote by 〈X〉 and R〈X〉 the free monoid on X and the free associative R-ring on X, respectively. A subset Q ⊆〈X〉×R〈X〉 is called a reduction system for R〈X〉. An element σ =(Wσ,fσ) ∈ Q has components Wσ a word in 〈X〉 and fσ a polynomial in R〈X〉. Note that every reduction system for R〈X〉 defines a factor ring A = R〈X〉/IQ, with IQ the two-sided ideal of R〈X〉 generated by the polynomials Wσ − fσ, with σ ∈ Q.
(ii) If σ is an element of a reduction system Q and A, B ∈〈X〉, the R-linear endomorphism rAσB : R〈X〉→ R〈X〉, which fixes all elements in the basis 〈X〉 different from AWσB and sends this particular element to AfσB is called a reduction for Q. If r is a reduction and f ∈ R〈X〉, then f and r(f) represent the same element in the R-ring R〈X〉/IQ. Thus, reductions may be viewed as rewriting rules in this factor ring.
(iii) A reduction rAσB acts trivially on an element f ∈ R〈X〉 if rAσB(f)= f. An element f ∈ R〈X〉 is said to be irreducible under Q if all reductions act trivially on f. Note that the set R〈X〉irr of all irreducible elements of R〈X〉 under Q is a left submodule of R〈X〉.
(iv) Let f be an element of R〈X〉. We say that f reduces to g ∈ R〈X〉, if there is a finite sequence r1,...,rn of reductions such that g =(rn ··· r1)(f). We will write f →Q g. A finite sequence of reductions r1,...,rn is said to be final on f, if (rn ··· r1)(f) ∈ R〈X〉irr.
(v) An element f ∈ R〈X〉 is said to be reduction-finite, if for every infinite sequence r1,r2,... of reductions there exists some positive integer m such that ri acts trivially on the element (ri−1 ... r1)(f), for every i > m. If f is reduction-finite, then any maximal sequence of reductions r1,...,rn such that ri acts non-trivially on the element (ri−1 ··· r1)(f), for 1 ≤ i ≤ n, will be finite. Thus, every reduction-finite element reduces to an irreducible element. We remark that the set of all reduction-finite elements of R〈X〉 is a left submodule of R〈X〉.
(vi) An element f ∈ R〈X〉 is said to be reduction-unique ifit is reduction-finite and if its images under all final sequences of reductions coincide. This value is denoted by rQ(f).
Proposition 1.2 ([29], Lemma 3.1.2). (i) The set R〈X〉 un of reduction-unique elements of R〈X〉 is a left submodule, and rQ : R〈X〉 un → R〈X〉irr becomes an R-linear map. (ii) If f, g, h ∈ R〈X〉 are elements such that ABC is reduction-unique for all terms A, B, C occurring in respectively f, g, h, then fgh is reduction-unique. Moreover, if r is any reduction, then fr(g)h is reduction-unique and rQ(fr(g)h)= rQ(fgh).
Proof. (i) Consider f, g ∈ R〈X〉un,λ ∈ R. We know that λf + g is reduction-finite. Let r1,...,rm be a sequence of reductions (note that it is final on this element), and r := rm ··· r1 for the composition. Using that f is reduction-unique, there is a finite composition of reductions r' such that (r'r)(f)= rQ(f), andin a similar way, a composition of reductions r'' such that 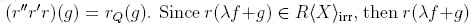
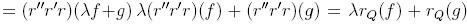 . Hence, the expression r(λf + g) is uniquely determined, and λf + g is reduction-unique. In fact,
. Hence, the expression r(λf + g) is uniquely determined, and λf + g is reduction-unique. In fact, 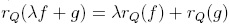 , and therefore (i) is proved.
, and therefore (i) is proved.
(ii) From (i) we know that fgh is reduction-unique. Consider 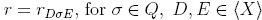 . The idea is to show that fr(g)h is reduction-unique and rQ(fr(g)h)= rQ(fgh). Note that if f, g, h are terms A, B, C, then rADσEC(ABC)= ArDσE(B)C, that is, ArDσE(B)C is reduction-unique with rQ(ABC)= rQ(ArDσE(B)C).
. The idea is to show that fr(g)h is reduction-unique and rQ(fr(g)h)= rQ(fgh). Note that if f, g, h are terms A, B, C, then rADσEC(ABC)= ArDσE(B)C, that is, ArDσE(B)C is reduction-unique with rQ(ABC)= rQ(ArDσE(B)C).
Now, more generally, 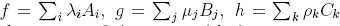 where the indices i, j, k run over finite sets, with λi,µj,ρk, and where Ai,Bj,Ck are terms such that AiBjCk is reduction unique for every i, j, k. In this way,
where the indices i, j, k run over finite sets, with λi,µj,ρk, and where Ai,Bj,Ck are terms such that AiBjCk is reduction unique for every i, j, k. In this way, 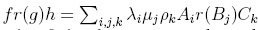 . Finally, since
. Finally, since 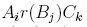 is reduction-finite for every i, j, k, and we have
is reduction-finite for every i, j, k, and we have 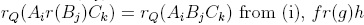 is reduction-unique and
is reduction-unique and 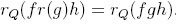 .
.
Proposition 1.3 ([29], Proposition 3.1.3). If every element f G R(X) is reduction-finite under a reduction system Q, and Iq is the ideal of R(X) generated by the set (Wσ - fσ | σ ε Q} then R(X) = R(X)irr ⊕ IQ if and only if every element of R(X) is reduction-unique.
Proof. Suppose that 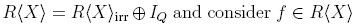 . Note that if
. Note that if 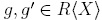 are elements for which f reduces to g and g', then
are elements for which f reduces to g and g', then 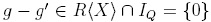 , that is, f is reduction-unique. Conversely, if every element of R(X) is reduction-unique under Q, then tq : R(X) → R(X)irr is a R-linear projection. Consider f G ker(rQ), that is, rQ(f) = 0. Then f G Iq, whence the ker(rQ) C Iq, but in fact, ker(rQ) contains Iq: for every a G Q,A,B G (X), we have
, that is, f is reduction-unique. Conversely, if every element of R(X) is reduction-unique under Q, then tq : R(X) → R(X)irr is a R-linear projection. Consider f G ker(rQ), that is, rQ(f) = 0. Then f G Iq, whence the ker(rQ) C Iq, but in fact, ker(rQ) contains Iq: for every a G Q,A,B G (X), we have 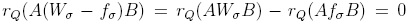 from Proposition 1.2, when r = r1σ1.
from Proposition 1.2, when r = r1σ1.
Under the previous assumptions, A = R(X)/IQ may be identified with the left free R-module R(X)irr with R-module structure given by the multiplication f * g = rQ(fg).
Definition 1.4. An overlap ambiguity for Q is a 5-tuple of the form 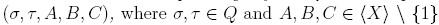 such that Wσ- = AB and WT = BC. This ambiguity is solvable if there exist compositions of reductions r, r' such that r(fσC) = r'(AfT τ). Similarly, a 5-tuple (σ, τ, A, B, C) with σ ≠ τ is called an inclusion ambiguity if Wτ = B and Wσ = ABC. This ambiguity is solvable if there are compositions of reductions r, r' such that r(AfτB) = r'(fσ).
such that Wσ- = AB and WT = BC. This ambiguity is solvable if there exist compositions of reductions r, r' such that r(fσC) = r'(AfT τ). Similarly, a 5-tuple (σ, τ, A, B, C) with σ ≠ τ is called an inclusion ambiguity if Wτ = B and Wσ = ABC. This ambiguity is solvable if there are compositions of reductions r, r' such that r(AfτB) = r'(fσ).
Definition 1.5. A partial monomial order ≤ on (X) is said to be compatible with Q if fσ is a linear combination of terms M with M < Wσ, for all σ ∈ Q.
Proposition 1.6 ([29], Proposition 3.1.6). If ≤ is a monomial partial order on (X) satisfying the descending chain condition and compatible with a reduction system Q, then every element f ∈ R(X) is reduction-finite. In particular, every element of R(X) reduces under Q to an irreducible element.
Let ≤ be a monoid partial order on (X) compatible with the reduction system Q. Let M be a term in (X) and write YM for the submodule of R(X) spanned by all polynomials of the form A(Wσ - fσ)B, where A, B ∈ (X) are such that AWσB < M. We will denote by VM the submodule of R(X) spanned by all terms M' < M. Note that YM ⊆ VM.
Definition 1.7. An overlap ambiguity (σ, τ, A,B,C) is said to be resolvable relative to < if foC - AfT ∈ YABC. An inclusion ambiguity (σ, τ, A,B,C) is said to be resolvable relative to < if AfτC - fσ ∈ YABC.
If r is a finite composition of reductions, and f belongs to VM, then f - r(f) ∈ YM. Hence, f ∈ YM if and only if r(f) ∈ YM ([19], Proposition 3.1.8).
Proposition 1.8 (Bergman's Diamond Lemma [37]; [29], Theorem 3.21). Let Q be a reduction system for the free associative R-ring R(X), and let ≤ be a monomial partial order on (X), compatible with Q and satisfying the descending chain condition. The following conditions are equivalent: (i) all ambiguities of Q are resolvable; (ii) all ambiguities of Q are resolvable relative to ≤; (iii) all elements of R(X) are reduction-unique under Q; (iv) R(X) = R(X)irr ⊕ IQ.
1.1. Algorithms
Throughout this section we will consider the lexicographical degree order :≤deglex to be defined on the variables x1,... ,xn. For more details about these orders, see [18], section 3.
Definition 1.9. A reduction system Q for the free associative R-ring R(x1,..., xn) is said to be a ≤deglex-skew reduction system if the following conditions hold: (i) 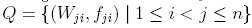 ; (ii) for every
; (ii) for every 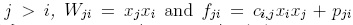 , where ci;j ∈ R \ {0} and pji ∈ R(x1,..., xn); (iii) for each j > i, lm
, where ci;j ∈ R \ {0} and pji ∈ R(x1,..., xn); (iii) for each j > i, lm 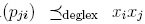 . We will denote (Q, ≤degiex) this type of reduction systems.
. We will denote (Q, ≤degiex) this type of reduction systems.
Note that if 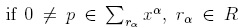 , we consider its Newton diagram as
, we consider its Newton diagram as 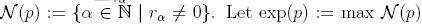 . In this way, by Proposition 1.6 every element f ∈ R(x1,...,xn) reduces under Q to an irreducible element. Let Iq be the two-sided ideal of R(x1,... ,xn) generated by Wji - fji, for 1 ≤ i < j ≤ n. If xi + Iq is also represented by xi, for each 1 < i < n, then we call standard terms in A. Proposition 1.11 below shows that any polynomial reduces under Q to some standard polynomial and hence standard terms in A generate this algebra as a left free R-module.
. In this way, by Proposition 1.6 every element f ∈ R(x1,...,xn) reduces under Q to an irreducible element. Let Iq be the two-sided ideal of R(x1,... ,xn) generated by Wji - fji, for 1 ≤ i < j ≤ n. If xi + Iq is also represented by xi, for each 1 < i < n, then we call standard terms in A. Proposition 1.11 below shows that any polynomial reduces under Q to some standard polynomial and hence standard terms in A generate this algebra as a left free R-module.
Proposition 1.10 (29], Lemma 3.2.2). If (Q, ≤deglex) is a skew reduction system, then the set R(x1,..., xn)irr is the left submodule of R(x1,... ,xn) consisting of all standard polynomials f ∈ R(X1,. . . ,Xn).
Proof. It is clear that every standard term is irreducible. Now, let us see that if a monomial M = λxj1 ... xjs is not standard, then some reduction will act non-trivially on it. If s < 2 the monomial is clearly standard. This is also true if jk ≤ jk+1, for every 1 ≤ k ≤ s - 1. Let s ≥ 2. There exists k such that jk ≤ jk+1 and M = CxjxiB = CWjiB where j = jk, i = jk+1 and where C and B are terms. Then CWjiB -q CfjiB acts non trivially on M.
Proposition 1.11 ([29], Proposition 3.2.3). If (Q, ≤deglex) is a skew reduction system for the set R(x1,..., xn), then every element of R(x1,... ,xn) reduces under Q to a standard polynomial. Thus the standard terms in A = R(x1,..., xn)/lQ span A as a left free module over R.
Proof. It follows from Proposition 1.10 and Proposition 1.6.
Next, we present an algorithm to reduce any polynomial in R(x1,... ,xn) to its standard representation modulo Iq. The basic step in this algorithm is the reduction of terms to polynomials of smaller leading term. In the proof of Proposition 1.10 we can choose k to be the least integer such that jk > jk+1, thus yielding a procedure to define for every non-standard monomial λM a reduction denoted red that acts non-trivially on M. In this way, the linear map red : R(xi,..., xn) → R(xi,..., xn) depends on M. However, the following procedure is an algorithm.

An element f ∈ R(x1,... ,xn) is called normal if deg(Xt) ≤deglex deg(lt(f)), for every term Xt # lt(f) in f. (In Definition 2.4 we will see that elements of skew PBW extensions are normal).
Proposition 1.12 ([29], Proposition 3.2.4). Let (Q, ≤deglex) be a skew quantum reduction system. There exists a R-linear map stredQ: R( x1 , . . . , xn ) → R( x1 , ..., xn)irr satisfying the following conditions: (i) for every f ∈ R(x1 ,...,xn), there exists a finite sequence r1,..., rm of reductions such that stredQ(f) = (rm ... r1)(f); (ii) if f is normal, then mdeg(lm(f)) = mdeg(lm(stredQ(f))).
From the proof of Proposition 1.12 we obtain the next algorithm. Remark 1.13 and Theorem 1.14 are the key results connecting this section with skew PBW extensions.

Remark 1.13. A free left R-module A is a skew PBW extension with respect to ≤deglex if and only if it is isomorphic to the quotient R(x1,..., xn)/IQ, where Q is a skew reduction system with respect to ≤deglex.
By Proposition 1.8, the set of all standard terms forms a R-basis for A = R(x1,..., xn)/Iq. We have the following key result:
Theorem 1.14 ([29], Theorem 3.2.6). Let (Q, ≤deglex) be a skew reduction system on R(x1,... ,xn) and let A = R(x1,..., xn)/Iq. For 1 < i < j < k < n, let gkji, hkji be elements in R(x1,... ,xn) such that xkfji (resp. fkjxi) reduces to gkji (resp. hkji) under Q. The following conditions are equivalent:
(i) A is a skew PBW extension of R;
(ii) the standard terms form a basis of A as a left free R-module;
(iii) gkji = hkji, for every 1 ≤ i < j < k ≤ n;
(iv) stredQ(xk fji) = stredQ(fj xi), for every 1 ≤ i < j < k ≤ n.
Moreover, if A is a skew PBW extension, then stredQ = rQ and A is isomorphic as a left module to R(x1, . . . , xn)irr whose module structure is given by the product f * g := r-Q(fg), for every f,g ∈ R(x1,...,xn)irr.
Proof. The equivalence between (i) and (ii) as well between (i) and (iii) is given by Proposition 1.8. The equivalence between (i) and (iv) is obtained from Proposition 1.8 and Proposition 1.12. The remaining statements are also consequences of Proposition 1.8.
Theorem 1.14 gives an algorithm to check whether the algebraic structure R(x1,... ,xn)/Iq is a skew PBW extension since stredQ(xkfji) and stredQ(fkjxi) can be computed by means of Algorithm "Reduction to standard form algorithm".
Remark 1.15. In [38], it was also investigated the problem of determining if one quantum algebra have a PBW basis, and more especifically, if the algebra is a skew PBW extension, using different tools. In this sense, our Theorem 1.14 establishes an analogous result to [38], Theorem 2.4.
2. Skew Poincare-Birkhoff-Witt extensions
Skew PBW extensions introduced in [18] include many algebras of interest for modern mathematical physicists. As examples of these extensions, we mention the following: (a) the enveloping algebra of any finite-dimensional Lie algebra; (b) any differential operator formed from commuting derivations; (c) any Weyl algebra; (d) those differential operator rings V(B,L) where L is a Lie algebra which is also a finitely generated free B-module equipped with a suitable Lie algebra map to derivations on B; (e) the twisted or smash product differential operator ring involving finite-dimensional Lie algebras acting on a ring by derivations together with Lie 2-cocycles; (f) group rings of polycyclic by finite groups; (g) Ore algebras of injective type; (h) operator algebras; (i) diffusion algebras; (j) some quantum algebras; (k) quadratic algebras in 3 variables; (l) some types of Auslander-Gorenstein rings; (m) some skew Calabi-Yau algebras; (n) quantum polynomials, (o) some quantum universal enveloping algebras. A detailed list of examples of skew PBW extensions is presented in [29], [20] and [24].
Definition 2.1 ([18], Definition 1). Let R and A be rings. We say that A is a skew PBW extension of R (also called a a-PBW extension of R), if the following conditions hold:
(i) R ⊆ A;
(ii) there exist elements x1 , . . . , xn ∈ A such that A is a left free R-module, with basis the basic elements Mon(A) 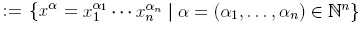 .
.
(iii) For each 1 ≤ i ≤ n and any r ∈ R \ {0}, there exists an element ci,r ∈ R \ {0} such that xir - ci,rxi ∈ R.
(iv) For any elements 1 ≤ i, j ≤ n, there exists ∈ R \ {0} such that xjxi - xixj ∈ R + Rx1 + ... + Rxn.
Under these conditions, we write A := σ(R)(x1,... ,xn).
Proposition 2.2 ([18], Proposition 3). Let A be a skew PBW extension of R. For each 1 ≤ i ≤ n, there exists an injective endomorphism σi : R → R and an σi-derivation δi : R → R such that xir = σi(r)xi + δi(r), for each r ∈ R.
Two particular cases of skew PBW extensions are considered in the following definition.
Definition 2.3 ([18], Definition 4). Let A be a skew PBW extension of R. (a) A is called quasi-commutative if the conditions (iii) and (iv) in Definition 2.1 are replaced by (iii'): for each 1 ≤ i ≤ n and all r ∈ R \ {0} there exists ci,r ∈ R \ {0} such that xir = ci,rxi; (iv'): for any 1 ≤ i, j ≤ n there exists ci,j ∈ R \ {0} such that xj xi = ci,jxixj; (b) A is called bijective if σi is bijective for each 1 ≤ i ≤ n, and ci,j is invertible for any 1 ≤ i ≤ j ≤ n.
Definition 2.4 ([18], Definition 6). Let A be a skew PBW extension of R with endomorphisms σi, 1 ≤ i ≤ n, as in Proposition 2.2.
(i) 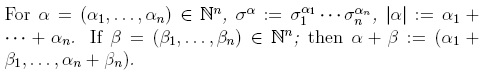
(ii) For X = xα ∈ Mon(A), exp(X) := α and deg(X) := |α|. The symbol 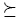 y will denote a total order defined on Mon(A) (a total order on Nq1 ). For an element xα ∈ Mon(A), exp(xα) := α ∈ Nq1. If xa y but xa = , we write xa y . Every element f e A can be expressed uniquely as f - Ü0 + 01X1 + ... + amXm, with ai E R \ {0}, and Xm y ... y X1. With this notation, we define lm(f) := Xm, the leading monomial of f; lc(f) := am, the leading coefficient of f; lt(f) := amXm, the leading term of f; exp(f) := exp(Xm), the order of f; and E(f) := {exp(Xi) | 1 < i < t}. Note that deg(f) := max{deg(Xi)}*=1. Finally, if f = 0, then lm(0) := 0, lc(0) :=0, lt(0) := 0. We also consider X y 0 for any X E Mon(A). Again, for a detailed description of monomial orders in skew PBW extensions, see [18], Section 3.
y will denote a total order defined on Mon(A) (a total order on Nq1 ). For an element xα ∈ Mon(A), exp(xα) := α ∈ Nq1. If xa y but xa = , we write xa y . Every element f e A can be expressed uniquely as f - Ü0 + 01X1 + ... + amXm, with ai E R \ {0}, and Xm y ... y X1. With this notation, we define lm(f) := Xm, the leading monomial of f; lc(f) := am, the leading coefficient of f; lt(f) := amXm, the leading term of f; exp(f) := exp(Xm), the order of f; and E(f) := {exp(Xi) | 1 < i < t}. Note that deg(f) := max{deg(Xi)}*=1. Finally, if f = 0, then lm(0) := 0, lc(0) :=0, lt(0) := 0. We also consider X y 0 for any X E Mon(A). Again, for a detailed description of monomial orders in skew PBW extensions, see [18], Section 3.
3. Examples
In this section we present two examples of skew PBW extensions which illustrate the results of Section 1.1. Our aim is to show that several rings have a PBW basis in the sense of Definition 2.1. Other well known examples for quantum physics (Weyl algebras, quantum Weyl algebras, dispin algebras, Woronowicz algebra, skew polynomial rings, q-Heisenberg algebra, etc) can be realized following the ideas presented in this paper (see [29] for a detailed description of each one of these algebras).
Hayashi algebra
With the purpose of obtaining bosonic representations of the Drinfield-Jimbo quantum algebras, Hayashi considered in [39] the 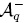 algebra. Let us see its construction (we follow [34], Example 2.7.7). Let us be the algebra generated by the indeterminates
algebra. Let us see its construction (we follow [34], Example 2.7.7). Let us be the algebra generated by the indeterminates  , with the relations
, with the relations
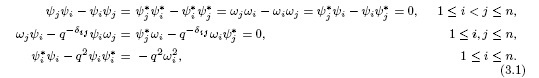
Let 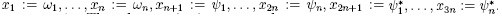 The relations (3.1) are equivalent to
The relations (3.1) are equivalent to
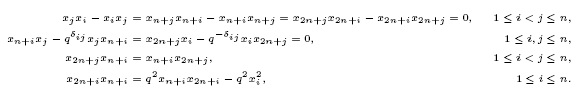
Again, consider 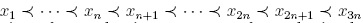 . Then
. Then 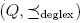 is a skew reduction system, and we obtain the following cases:
is a skew reduction system, and we obtain the following cases:
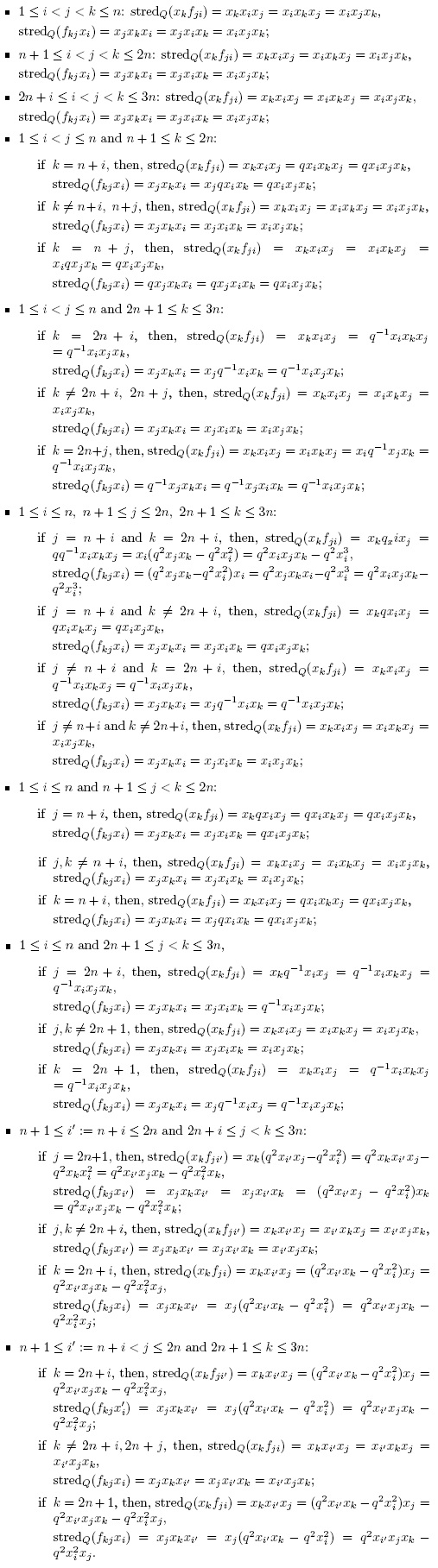
As we have seen, 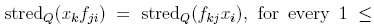
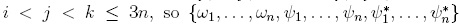 form a k-basis of U. Now, to obtain the Hayashi algebra
form a k-basis of U. Now, to obtain the Hayashi algebra 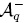 , we take the field of the complex numbers and consider the multiplicative monoid S generated by ωl,..., ωn. Since S is a regular Ore set and the localization S-lU exists, then
, we take the field of the complex numbers and consider the multiplicative monoid S generated by ωl,..., ωn. Since S is a regular Ore set and the localization S-lU exists, then 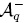 is S-lU modulo the ideal generated by
is S-lU modulo the ideal generated by 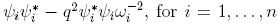 (see [20], section 3.8, for localizations in skew PBW extensions).
(see [20], section 3.8, for localizations in skew PBW extensions).
Non-Hermitian realization of a Lie deformed, non-canonical Heisenberg algebra
In [6], it was studied the non-Hermitian realization of a Lie deformed, a non-canonical Heisenberg algebra, considering the case of operators Aj, Bk which are non-Hermitian (i.e., 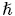 =1)
=1)
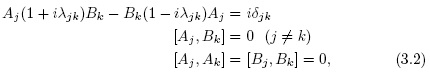
and,
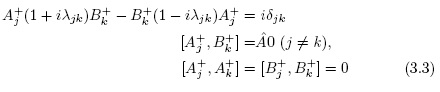
where 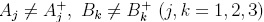 . If the operators Aj, Bk are in the form
. If the operators Aj, Bk are in the form 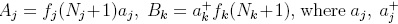 , are leader operators of the usual Heisenberg-Weyl algebra, with Nj the corresponding number operator
, are leader operators of the usual Heisenberg-Weyl algebra, with Nj the corresponding number operator 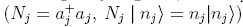 , and the structure functions fj(Nj + 1) complex, then it is showed in [6] that Aj and Bk are given by
, and the structure functions fj(Nj + 1) complex, then it is showed in [6] that Aj and Bk are given by
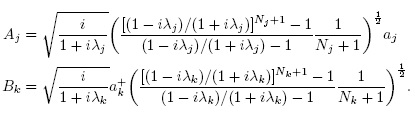
Next, we show that this algebra is a skew PBW extension of a field 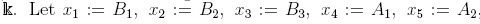 . and x6 :=A3. Under these identifications, the relations (3.2) are equivalent to the following:
. and x6 :=A3. Under these identifications, the relations (3.2) are equivalent to the following:
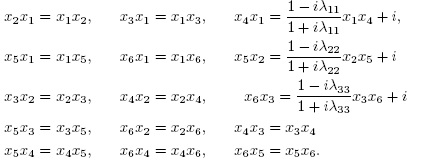
Then,

Since stredQ 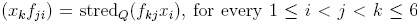 , then the elements
, then the elements 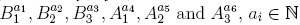 , for every i, form a basis of the Lie-deformed Heisenberg algebra, and from (3.2), we can see that this algebra is a skew PBW extension over the complex numbers.
, for every i, form a basis of the Lie-deformed Heisenberg algebra, and from (3.2), we can see that this algebra is a skew PBW extension over the complex numbers.
Conclusions and future work
In this paper, we have presented a criteria to determine whether an algebra defined by generators and relations can be expressed as a skew PBW extension. Nevertheless, since the limited size of the paper, there are a lot of remarkable algebras of the theoretical physics which are skew PBW extensions and were not illustrated here (see [29] for more examples). As a future work, we will investigate a theory of PBW bases for another kinds of quantum algebras more general than skew PBW extensions over fields. The techniques to be used will concern noncommutative differential geometry (see [27]) with the aim of characterizing algebras arising in geometries of noncommutative spaces and their interactions with quantum physics, in the sense of [40], [41], and others.
Acknowledgment
The first author is supported by Grant HERMES CODE 30366, Departamento de Matemáticas, Universidad Nacional de Colombia, Bogotá.
References
[1] P. A. M. Dirac, Proc. Camb. Phil. Soc. 23, 412 (1926). [ Links ]
[2] H. Weyl, Gruppentheorie und Quantenmechanik (English Edition) (Dover, 1932). [ Links ]
[3] N. A. M. Monk and B. J. Hiley, Found. Phys. Lett. 11, 371 (1998). [ Links ]
[4] A. Plotnitsky, Epistemology and Probability. Bohr, Heisenberg, Schródinger, and the Nature of Quantum-Theoretical Thinking. Fundamental Theories of Physics 161 (Springer, 2010). [ Links ]
[5] V. S. Varadarajan, Reflections on Quanta, Symmetries, and Supersymmetries (Springer, 2011). [ Links ]
[6] A. Jannussis, A. Leodaris, and R. Mignani, Phys. Lett. A 197, 187 (1995). [ Links ]
[7] A. Turbiner, Funct. Anal. Appl. 29, 291 (1995). [ Links ]
[8] M. Pillin, Commun. Math. Phys 180, 23 (1996). [ Links ]
[9] H. Y. Pan and Z. S. Zhao, Phys. Lett. A 282, 251 (2001). [ Links ]
[10] H. Y. Pan and Z. S. Zhao, Phys. Lett. A 312, 1 (2003). [ Links ]
[11] P. Narayama, Physica A 328, 145 (2003). [ Links ]
[12] L. Hellstrom and S. Silvestrov, Expo. Math. 23, 99 (2005). [ Links ]
[13] J. Douari, Int. J. Theor. Phys 45, 893 (2006). [ Links ]
[14] E. M. F. Curado, Y. Hassouni, M. A. Rego-Monteiro, and L.M. C. S. Rodrigues, Phys. Lett. A 372, 3350 (2008). [ Links ]
[15] L. Zhe, Sci. China Math. 541, 2427 (2011). [ Links ]
[16] M. Arik and D. D. Coon, J. Math. Phys. 17, 524 (1976). [ Links ]
[17] D. A. Slavnov, Theoret. Math. Phys. 171, 848 (2012). [ Links ]
[18] C. Gallego and O. Lezama, Commun. Algebra 39, 50 (2011). [ Links ]
[19] A. Reyes, Rev. Col. Mat. 47, 95 (2013). [ Links ]
[20] O. Lezama and A. Reyes, Commun. Algebra 42 (1200-1230). [ Links ]
[21] A. Reyes, Rev. Col. Mat. 48, 79 (2014). [ Links ]
[22] A. Reyes, Rev. Integr. Temas Mat. 33, 173 (2015). [ Links ]
[23] O. Lezama, J. P. Acosta, and A. Reyes, Rev. Un. Mat. Argentina 56, 39 (2015). [ Links ]
[24] H. Suáarez, O. Lezama, and A. Reyes, Ciencia en Desarrollo 6, 205 (2015). [ Links ]
[25] A. Reyes and H. Suáarez, Bol. Mat. 23, 71 (2016). [ Links ]
[26] A. Reyes and H. Suaárez, Rev. Integr. Temas Mat. 34, 147 (2016). [ Links ]
[27] A. Reyes and H. Suáarez, Ciencia en Desarrollo 7, 99 (2016). [ Links ]
[28] H. Suáarez and A. Reyes, Far East J. Math. Sci. (FJMS) 101, 301 (2017). [ Links ]
[29] A. Reyes, Ring and Module Theoretical Properties of Skew PBW Extensions, Ph.D. thesis, Universidad Nacional de Colombia, Bogotá - Colombia (2013). [ Links ]
[30] J. Dixmier, Enveloping Algebras (Graduate Studies in Mathematics, American Mathematical Society, 1996). [ Links ]
[31] H. Gausterer, H. Grosse, and L. E. Pittner, Geometry and Quantum Physics, Lecture Notes in Physics, Proceedings, Schladming, Austria (Springer-Verlag, 2000). [ Links ]
[32] M. Rosenbaun and J. D. Vergara, Gen. Relativ. Gravit. 38, 607 (2006). [ Links ]
[33] H. A. Yamane, Publ. RIMS Kyoto Univ. 25, 503 (1989). [ Links ]
[34] R. Berger, Comm. Math. Physics 143, 215 (1992). [ Links ]
[35] C. M. Ringel, J. Reine Angew. Math. 470, 51 (1996). [ Links ]
[36] O. Hinchcliffe, Diffusion Algebras, Ph.D. thesis, University of Sheffield, Sheffield, South Yorkshire - England (2005). [ Links ]
[37] G. M. Bergman, Adv. Math. 29, 178 (1978). [ Links ]
[38] J. P. Acosta and O. Lezama, Alg. Dis. Math. 20, 1 (2015). [ Links ]
[39] T. Hayashi, Commun. Math. Phys 127, 129 (1990). [ Links ]
[40] H. Gausterer, H. Grosse, and L. E. Pittner, Geometry and Quantum Physics, Lecture Notes in Physics, Proceedings of the 38. Internationale Universitatswochen fór Kern-und Teilchenphysik, Schladming, Austria, January (Springer-Verlag Berlin Heidelberg, 200). [ Links ]
[41] M. Marcolli and D. E. Parashar, Quantum Groups and Noncommutative Spaces, Perspectives on Quantum Geometry (Springer-Verlag Berlin Heidelberg, 2011). [ Links ]














