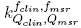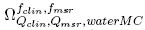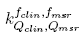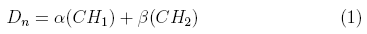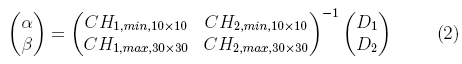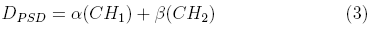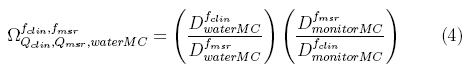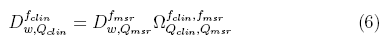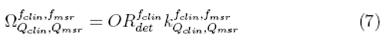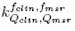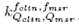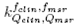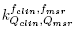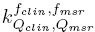Introduction
Small photon fields have been increasingly used in the last few years due to the introduction of new treatment techniques. [1] Stereotactic radiosurgery has used small photon fields since many years ago, in malignant tumors and benign pathologies. High radiation doses have been prescribed for small planning target volumes but the dosimetry of sub-centimeter radiation fields is still a subject of controversy and alerts.
Many stereotactic detectors have been designed and tested for dosimetry of small photon fields such as air-filled or liquid-filled ionization microchambers [2-4], shielded or unshielded silicon diodes, [5,6] plastic scintillation detectors (PSD), [7,8] radiochromic films, [9,10] micro MOSFET detectors, [11] thermoluminescent dosimeters (TLD), [12] optically stimulated luminescent dosimeters (OSL),[13,14] micro- diamonds, [5] Alanine gel and Fricke gel dosimeters. [15] However, there are significant differences among these dosimeters when output factors of small radiation fields are measured.
Multiple variables affect the accuracy of small photon field dosimetry. Including the density and atomic composition of the detector, [16,17] the source occlusion effect and its volume averaging errors, [18] the peak-shaped dose profiles, the volume of the detector itself, the changes of the energy spectrum caused by beam hardening and the lack of lateral equilibrium of secondary charged particles. [19]
On this regard, this work calculates the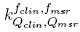 correction factors for different stereotactic detectors, considering the use of the linac jaws and the micro-multileaf collimator to conform the small photon fields.
correction factors for different stereotactic detectors, considering the use of the linac jaws and the micro-multileaf collimator to conform the small photon fields.
Materials and Methods
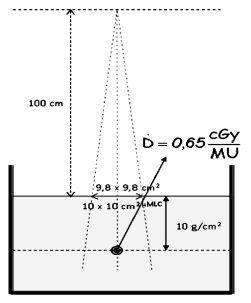
A Varian Clinac iX linear accelerator with the BrainLab m3 micro-multileaf collimator attached to its gantry was simulated for the energy of 6 MeV photons with a TPR20/10 of 0.666 (Figure 1).
The experimental and Monte Carlo setup consisted on positioning each detector at 10 cm depth in a water phantom or its equivalent. The source surface distance was set at 100 cm where the sizes of the set of radiation fields were defined. The absolute dose rate for the calibration radiation field of 10 cm X 10 cm jaws and 9.8 cm X 9.8 cm micro multileaf collimator was measured by a semiflex PTW 31010 ionization chamber and found to be 0.65 cGy/MU.
The W1 Exradin Plastic Scintillation Detector:
The Exradin W1 Plastic Scintillation Detector manufactured by Standard Imaging was used in the present study. The W1 is the first commercially available radiation detector using organic scintillators. It comprises a small cylinder of 1 mm diameter and 3 mm length corresponding to a circular cross section of 0.79 mm2. The scintillator is composed by a core of scintillating fiber of polystyrene surrounded by an acrylic cladding. The effective atomic number (Ze f f ) of the plastic scintillating detector is reported as 5.7. [20]
This piece of scintillator material is optically coupled to another acrylic optical fiber of 1 mm diameter and 3 m length. When the scintillating fiber is irradiated by a high-energy beam, a scintillation signal is produced. Electrons set in motion by primary photons gain high enough energies to travel through the optical fiber at relativistic velocities, so generating a Cherenkov radiation spectrum in the optical fiber. [21]
The signals produced are guided to a photodiode enclosure that generates two charge signals which can be measured by a dual channel electrometer specially designed to work efficiently with the system.
The spectral discrimination was chosen as the method for dose calibration purposes. [22] Such a method is supported on the fact that the Cherenkov spectrum must be invariant under irradiation configuration. [21]
The dose at a pre-defined condition n was measured by means of a PTW semiflex 31010 ionization chamber with absolute calibration and expressed by a linear combination of the readings in the two channels (CHi) of the electrometer in the following way:
where α and β are calibration constants which can be found by irradiating the plastic scintillator under two different conditions of Cherenkov-light ratio. The virtual water slab that is shown in Figure 2 allows to irradiate a minimum and maximum amount of optical fiber so that the next matrix equation can be solved:

Figure 2 Pictures of the two different configurations of irradiated optical fiber used in this work.
where CH1,min,10x10 corresponds to the reading of the first channel of the electrometer for a 10 cm x 10 cm radiation field with the minimum amount of optical fiber exposed to radiation and so forth for the other variables.
Once the calibration coefficients were found, the dose for any field size was obtained with the Plastic Scintillation Detector using the equation:
To avoid Cherenkov spectrum variations, all the measurements were done following the same calibration setup namely at 10 cm depth and at a source to surface distance of 100 cm.
The orientation of the plastic scintillator was chosen perpendicular to the beam central axis both in solid and liquid water. The effective point of measurement in liquid water was set by means of a plastic cap supplied by the manufacturer. The positioning in solid water was done using the carved plastic slab. When the scintillator is oriented parallel to the beam central axis, the volume averaging effect reduces significantly in comparison to the perpendicular orientation. However, since the calibration of the Exradin W1 was done for the perpendicular positioning by means of the solid water slab, we consider to keep as invariant as possible the Cerenkov effect generated in the optical fiber in comparison to the calibration condition.
The electrometer used was the Standard Imaging dual channel SuperMax especially designed to improve the signal to noise ratio.
Dosimetry Diode E PTW 60017:
The p-type unshielded silicon diode is a well-recognized stereotactic dosimeter. Its small circular area of 1 mm2 gives it a high spatial resolution that reduces the averaging effect making it ideal for the measurement of output factors for very small fields. However, silicon is not water-equivalent. Its atomic number (Z=14) is higher than the effective atomic number of water.
In this study, the diode was coupled to a MP3 PTW motorized water phantom and the output ratios, depth dose curves and profiles were measured with the stem of the detector parallel to the central beam axis. The reference point was set at 0.8 mm taken from the detector tip, corresponding to 1.3 mm water equivalent.
Pinpoint 3D Ionization Chamber PTW 31016:
The PTW 31016 is an air-filled ionization chamber with a measuring volume of 16 mm3. Its wall is made of 0.57 mm of PMMA (1.19 g/cm3) and 0.09 mm of graphite (1.84 g/cm3). The output ratios, percent depth dose curves and dose profiles were obtained with the chamber set at 10 cm depth in water with 100 cm source to surface distance. The stem of the chamber was aligned perpendicular to the beam central axis. The reference point was set at 2.4 mm taken from the ion chamber tip at the geometrical center of the cross section. The effective atomic number (Ze f f ) of the air inside the sensitive volume is 7.8 as calculated with equation 7 .26 in [23].
Monte Carlo Simulations:
The BEAMnrc[24] and DOSXYZnrc[25] codes of the EGSnrc Monte Carlo system[26] were used to simulate the linear accelerator Varian Clinac iX with the m3 mMLC attached to the linac gantry.
The BEAMnrc code does not have a specific module for the Monte Carlo simulation of the BrainLab m3 mMLC but some previously published works[27] have proven good results with the use of the VARMLC module from the standard distribution of the BEAMnrc code. The actual three-faceted shape of the leaf is approximated to a circular edge and the three tongues and grooves of the original micro leaf is replaced by only one pair to fit the VARMLC module parameters. This was the method followed in the present study.
The simulation was made in two steps. First, by means of the BEAMnrc code, the linac gantry was simulated by considering the following elements: target, primary collimator, flattening filter, linac ionization chamber, mirror, secondary Y and X collimators, 120 MLC, m3 micro- multileaf collimator and air to an extent of 100 cm. Second, phase space files corresponding to many combinations of jaws and micro leaves were obtained and the DOSXYZnrc code was used as a voxelized water phantom for each phase space file. The volume of the voxels was 1 mm3 at the beam central axis up to the depth of 5 cm and 2 mm3 beyond. The materials and dimensions of the linac parts were taken from the Monte Carlo simulation package supplied by Varian® under a policy of confidentiality.
Following the method of Cranmer-Sargison, [28] where different configurations of incident electron beam energy and focal spot sizes were studied, an energy of 6.2 MeV for the incident beam energy and 0.11 cm for circularly symmetric Gaussian FWHM were chosen in this work to model the electron beam source at the target. With these values, the simulated percent depth dose curves and profiles matched the measured data for the linac calibration radiation field, endorsing the selection of parameters.
The Directional Bremsstrahlung Splitting technique (DBS), [29] was used to reduce the variance and improve both the photons and electrons fluence.
The number of histories simulated for the first step was 108 to obtain an average uncertainty on the dose calculation of less than 0.7%.
The equation used for the calculation of the Monte Carlo output factors[30] is given by:
where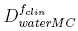 is the dose calculated by the DOSXYZ Monte Carlo code for the different clinical field sizes simulated and presented in this work,
is the dose calculated by the DOSXYZ Monte Carlo code for the different clinical field sizes simulated and presented in this work,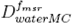 is the dose calculated by the same Monte Carlo code for the machine specific reference field set in this work by 9.8 cm x 9.8 cm jaws and 10 cm x 10 cm micro MLC.
is the dose calculated by the same Monte Carlo code for the machine specific reference field set in this work by 9.8 cm x 9.8 cm jaws and 10 cm x 10 cm micro MLC.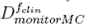 is the Monte Carlo dose accumulated in the linac ion chamber at the time the clinical fields are virtually irradiated.
is the Monte Carlo dose accumulated in the linac ion chamber at the time the clinical fields are virtually irradiated.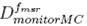 is also the Monte Carlo dose accumulated in the linac ion chamber for the machine specific reference field.
is also the Monte Carlo dose accumulated in the linac ion chamber for the machine specific reference field.
Detector Specific Output Ratio Measurements:
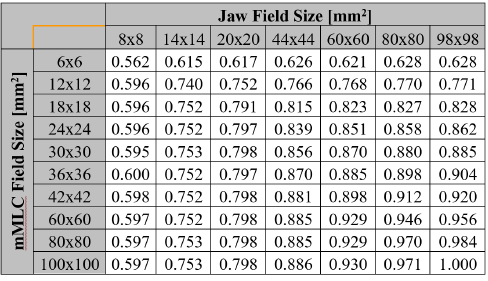
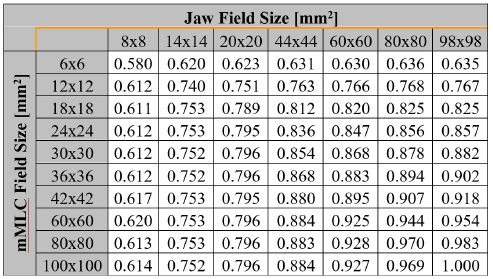
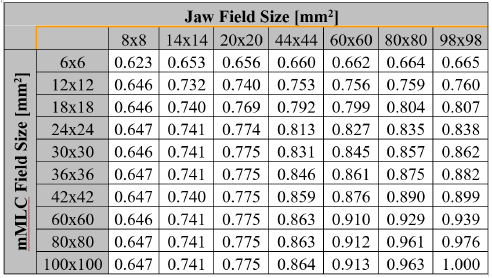
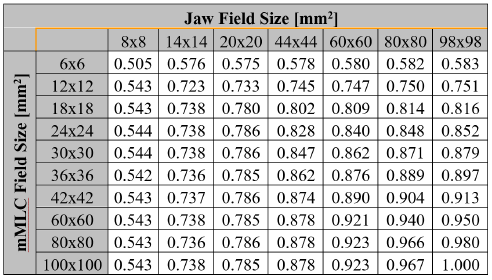
The direct ratio of the readings for the clinical field and the machine specific reference obtained by the different detectors with the measurement setup is presented in tables II to VI. This magnitude is called the output ratio and it is expressed by the equation:
where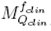 is the direct reading of each detector for the different clinical field sizes and
is the direct reading of each detector for the different clinical field sizes and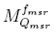 is the direct reading for the machine specific reference field.
is the direct reading for the machine specific reference field.
Calculation of the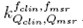 Correction Factors:
Correction Factors:
From the formalism for reference dosimetry of small and non-standard fields proposed by the International Atomic Energy Agency, [31] it is stated that the absorbed dose to water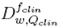 at a reference point in a phantom for a clinical field f
clin
of quality
Qclin
in the absence of the chamber is given by:
at a reference point in a phantom for a clinical field f
clin
of quality
Qclin
in the absence of the chamber is given by:
where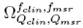 is the field output factor that converts the absorbed dose to water
is the field output factor that converts the absorbed dose to water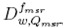 for a machine specific reference field f
msr
to the absorbed dose to water for the clinical field /c1ira. The product of the output ratio
for a machine specific reference field f
msr
to the absorbed dose to water for the clinical field /c1ira. The product of the output ratio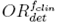 and the correction factor
and the correction factor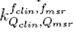 gives the field output factor:
gives the field output factor:
from which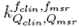 correction factors were obtained in this work for different radiation fields and detectors, using the Monte Carlo calculated field output factors
correction factors were obtained in this work for different radiation fields and detectors, using the Monte Carlo calculated field output factors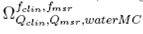 and the measured values of
and the measured values of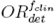
Profiles and Percentage Depth Dose Curves:
For obtaining dose profiles, the W1 Exradin PSD was coupled to a PTW MP3 water tank by means of a homemade holder. The graphical interphase of the PTW Mephysto mc2 software showed Cerenkov and scintillation signals with a wedge-shaped profile for each channel but once the signals were composed point by point by means of equation (3), became the final dose profiles. The micro ionization chamber and the Dosimetry Diode were also coupled to the PTW MP3 water tank. The chamber was set with its axis perpendicular to the beam central axis and the diode was set parallel to it.
Regarding the the Monte Carlo simulations, a program called STATDOSE for analyzing 3-dimensional dose distributions generated by DOSXYZnrc was used to obtain curves of the percentage depth dose distributions and dose profiles.
Results
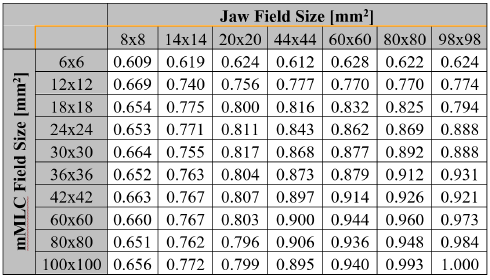
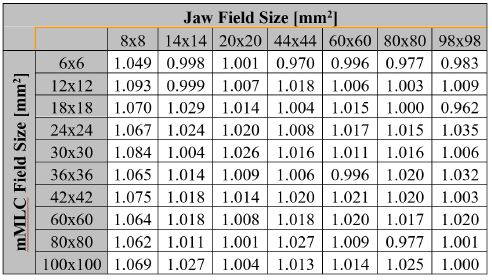
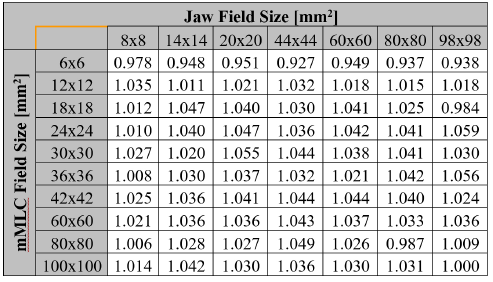
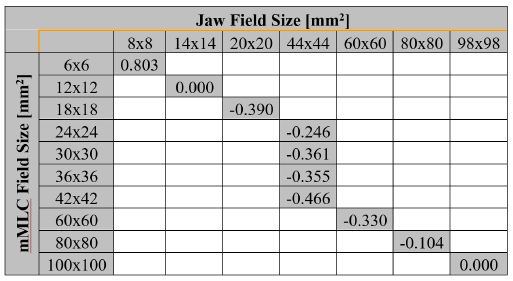
Theoretical calculations of the field output factors found with the BEAMnrc and DOSXYZnrc Monte Carlo codes are shown in Table 1. The output ratios table for the different combinations of jaws and mMLC openings measured by the set of stereotactic detectors used in this work are presented in Tables 2, 3, 4 and 5. Calculations of the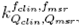 correction factor by means of the Equation (7) for the set of different detectors used in this work are presented in Tables 6, 7, 8 and 9.
correction factor by means of the Equation (7) for the set of different detectors used in this work are presented in Tables 6, 7, 8 and 9.
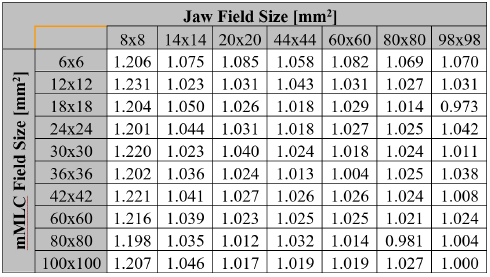
Figure 3 shows the Monte Carlo dose profiles calculated at 10 cm depth for the sub-centimeter radiation fields along the first row of the table.
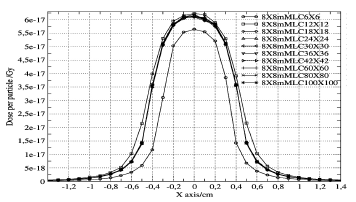
Figure 4 shows the Monte Carlo dose profiles calculated at 10 cm depth for the sub-centimeter radiation fields along the first column of the table.
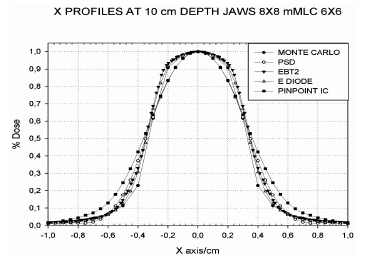
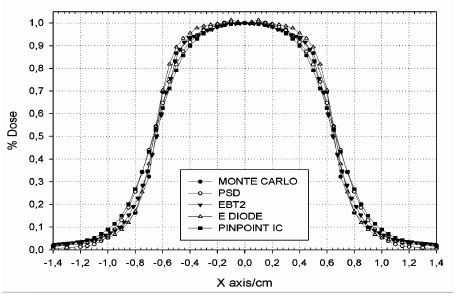
Figures 5 shows the comparison of dose profiles calculated by Monte Carlo and measured with the set of detectors for the smallest sub-centimeter field of the table.
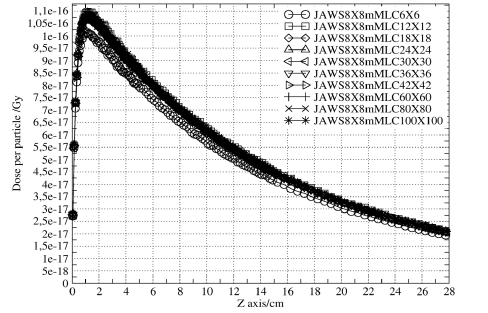
Figure 6 shows the percent depth dose curves calculated by Monte Carlo for the sub-centimeter fields along the first row of the table.
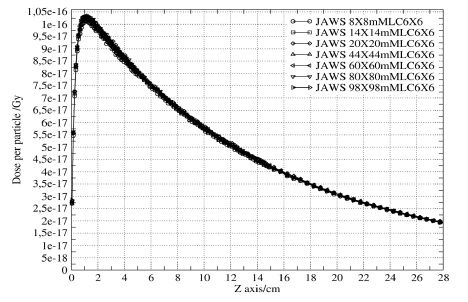
Figure 7 shows the percent depth dose curves calculated by Monte Carlo for the sub-centimeter fields along the first column of the table.
Figure 8 shows the comparison of dose profiles calculated by Monte Carlo and those measured by the set of detectors for small fields with sizes just larger than the range of secondary charged particles.
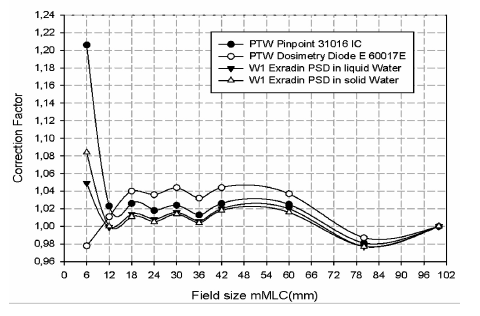
Figure 9 shows the influence of radiation field size on the magnitude of the correction factor. Also from the graph, it can be seen a threshold below which, detectors show large discrepancies among themselves.
Discussion
The observation of the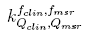 correction factor tables for the group of stereotactic detectors studied in this work shows that for radiation field sizes with radius larger than the range of secondary charged particles, regions where lateral charged-particles equilibrium exists, all the correction factors are lower than 7% compared to Monte Carlo calculations. However, for sub-centimeter radiation fields, the
correction factor tables for the group of stereotactic detectors studied in this work shows that for radiation field sizes with radius larger than the range of secondary charged particles, regions where lateral charged-particles equilibrium exists, all the correction factors are lower than 7% compared to Monte Carlo calculations. However, for sub-centimeter radiation fields, the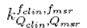 correction factors reach values with differences relative to Monte Carlo results of up to 23% for the PTW Pinpoint ionization chamber 31016, 12% for the W1 PSD in solid water, 9% for the W1 PSD in liquid water and 4% for the PTW 60017E diode. This fact is endorsed by the Figure 9 where some radiation fields have been selected to illustrate the behavior of correction factor
correction factors reach values with differences relative to Monte Carlo results of up to 23% for the PTW Pinpoint ionization chamber 31016, 12% for the W1 PSD in solid water, 9% for the W1 PSD in liquid water and 4% for the PTW 60017E diode. This fact is endorsed by the Figure 9 where some radiation fields have been selected to illustrate the behavior of correction factor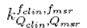 versus the size of the radiation field.
versus the size of the radiation field.
The more affected detector by the lack of lateral equilibrium in sub-centimeter radiation fields is the micro ionization chamber because of its sensitive volume composed by air which increases the perturbation factor and the volume averaging effect.
Although, the unshielded diode shows low correction values for the sub-centimeter field sizes compared to the Monte Carlo calculations, the high atomic number of its sensitive volume made of silicon of 14 in comparison to water with an effective atomic number of 7.5 increases the absorption of low energy photons and hence compromises the accuracy of the dosimeter. The density of the Plastic Scintillation Detector nearly equivalent to water and its small size are factors that decrease the averaging errors in the measurement and in general the perturbation of the dosimeter. The correction factors for both solid and liquid water were lower than 12% for sub-centimeter fields but less than 3% for the rest of the radiation fields. The volume of the scintillation fiber of about 2.36 mm3 used in the present study is still large compared to the volume of other noncommercial experimental plastic scintillators like those reported in the literature[32] with volumes of 0.196 mm3 and 0.785 mm3.
The under-response of the plastic scintillation detector along the first column of the tables may be related to the refractive index of PMMA which is higher for shorter wavelengths. [21] The broad penumbra in sub-centimeter fields containing low energy photons produces changes in the Cherenkov spectrum in comparison to the calibration condition, which contributes to the error in the measurements. Despite of the 23% error found with the pinpoint ionization chamber for the radiation fields with radius smaller than the range of secondary charged particles, corrections of about 2% are found for the larger radiation fields. This fact confirms that ionization chambers continue to be one of the most accurate radiation detectors but not indicated for the dosimetry of sub-centimeter radiation fields.
Figure 3 shows the Monte Carlo cross dose profiles for different configurations of sub-centimeter radiation fields delimited by multiple apertures of jaws and effective field size of 6 mm determined by the mMLC. Each graph corresponds to a different Monte Carlo simulation but the similar behavior of the set, endorses the reproducibility of the Monte Carlo BEAMnrc and DOSXYZnrc codes used in this work.
Figure 4 shows the Monte Carlo cross dose profiles for sub-centimeter radiation fields but this time the effective field size of 8 mm is determined by the jaws of the linac apart from the (8 mm jaws, 6 mm mMLC) field which is one of the Figure 3. The behavior of the (8 mm jaws, 12 mm mMLC) field at the penumbra region is different from the rest of its equivalent radiation field sizes. The presence of larger number of low energy photons at the vicinity of the measuring point increases the penumbra. This is one of the reasons why a stereotactic detector with high resolution to discriminate multi-energetic spectrums is required for the dosimetry of small photon fields.
Figure 5 shows differences in the penumbra region for the cross profile of the smallest radiation field calculated by Monte Carlo and measured by the pinpoint ionization chamber. The 31016-pinpoint chamber over responds due to the low density of its sensitive volume. This fact points to the importance of the selection of the appropriate detector when doing the commissioning of treatment planning systems dedicated to stereotactic treatments. Figures 6 and 7 show the percentage depth dose curves calculated by Monte Carlo for different configurations of sub-centimeter fields which were found in good agreement with the ones measured with the set of detectors.
Figure 8 shows that for radiation fields with radius larger than the range of the secondary charged particles, the cross-dose profiles calculated by Monte Carlo match the profiles measured with the set of stereotactic detectors. This fact endorses the concept that the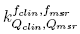 correction factor tends to unity as the radiation field size gets larger beyond the electrons lateral equilibrium radius and that the
correction factor tends to unity as the radiation field size gets larger beyond the electrons lateral equilibrium radius and that the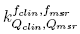 correction factor is related directly with variations with the incident energy spectrum.
correction factor is related directly with variations with the incident energy spectrum.
A published study[33] has used several detectors to measure output and correction factors of some linear accelerators equipped with micro-multileaf collimators. Table 10 shows the percentage difference of that results compared to those obtained in this work, for the same detector PTW 60017E, the same field sizes and under the same experimental conditions.
Another study[6] selected a group ofetectors dedicated to dosimetry of small fields to determine the correction factors due to the volume of the detectors. The work used the BrainLab® micro-multileaf collimator to determine the radiation fields but did not specify the setting of the collimator jaws. The reported corrections agree to the ones obtained in this work.
Conclusions
Stereotactic detectors show large discrepancies among themselves when they are used to measure output factors and dose profiles for sub-centimeter radiation fields. The measurements obtained by the plastic scintillation detectors show good agreement in comparison with the Monte Carlo simulation results. Improvements on the calibration method and developments of smaller volumes of scintillating fibers will increase the accuracy of the system to measure sub-centimeter radiation fields.
The unshielded diode PTW 60017E is a very accurate tool for the measurement of output factors and dose profiles of sub-centimeter radiation fields. However, its higher density in comparison to water induces an over-response when photoelectrons are crossing the detector.
It is important to include Monte Carlo simulations when doing the commissioning of treatment planning systems, when these systems are used to plan radiosurgery treatments. Air volume ionization chambers are not recommended for the commissioning of stereotactic treatment planning systems. Especially for sub-centimetric radiation fields.
This work has presented tables of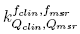 correction factors for the set of detectors studied that may be applied to adjust the measurements of output factors and dose profiles required by the commissioning of treatment planning systems. However, it is important to continue the search of the dosimeter with negligible corrections that may be recommended in calibration protocols of sub-centimeter fields. The plastic scintillation detector seems to be a good candidate.
correction factors for the set of detectors studied that may be applied to adjust the measurements of output factors and dose profiles required by the commissioning of treatment planning systems. However, it is important to continue the search of the dosimeter with negligible corrections that may be recommended in calibration protocols of sub-centimeter fields. The plastic scintillation detector seems to be a good candidate.
Recently, companies developing treatment planning systems for stereotactic radiation treatments have informed about the discrepancies between the irradiation time predicted by their planning systems and the actual dose prescribed to the patients when the size of the radiation fields are on the order of sub-centimeters and new solutions of software are being offered to the radiotherapy facilities to improve the accuracy of their planning systems but better detectors are still required.