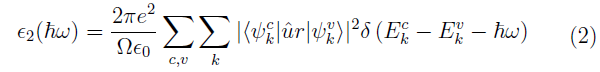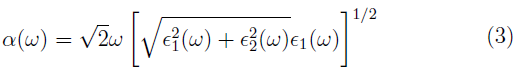Introducción
El dióxido de Titanio (TiO2) es muy importante en lo que respecta a celdas fotovoltaicas [1,2]. Debido al agotamiento de energías no renovables, el desarrollo de materiales fotovoltaicos es de alta trascendencia y por ello TiO2 es idóneo por su abundancia y precio bajo.
El dióxido de Titanio es un material de cualidades tan singulares que, ya ha sido objeto de estudio para aplicaciones en la production de hidrógeno a partir de energía solar, baterías de litio, celdas solares y purification de agua, entre otros [3-5]. Es aceptado para fases puras que la fase anatasa exhibe mayor actividad fotovoltaica comparada con TiO2 rutilo [6]. A pesar del intenso estudio de TiO2 no hay una explicación generalmente aceptada para las diferencias de las distintas actividades fotovoltaicas de los diferentes polimorfos. Aun así, ha sido reportado que el dopado con diferentes elementos para otras fases como rutilo, también en mejora significativamente la actividad fotovoltaica, en específico, Amraoui et al [7] estudiaron la fase rutilo de TiO2 dopada con Ni y Ce, y reportaron una apreciable actividad fotovoltaica en el espectro visible. Este trabajo se enfoca en el sistema anatasa por su predisposición a una mejor actividad fotovoltaica en comparación con las otras fases.
Lamentablemente, TiO2 anatasa tiene un band gap (banda prohibida, en ingles) ancho (de aproximadamente 3.2 eV), que corresponde a una absorción de radiación en la región UV del espectro. Ya que la mayor parte de la radiación que proviene está en la región visible, se pierde una gran energía. Para mejorar la fotorespuesta de TiO2 se usa el dopado por sustitución con metales y no metales [8].
Xuechao et al [9] investigaron las propiedades ópticas de TiO2 anatasa dopado con Fe y B por medio de cálculos DFT. En su estudio, concluyeron que el dopado con un solo elemento era menos eficiente para incrementar la actividad fotovoltaica. Justificaron la absorción mós intensa del caso codopado afirmando que los estados de impureza se acoplan con la parte superior de la banda de valencia lo cual se traduce en una considerable reducción del band gap, y também debido a la reducción de la recombinación lo cual justifican con la casi completa ocupación de los estados gap (de la banda prohibida, en inglés). Este comportamiento de los sistemas codopados es continuamente reportado por varias investigaciones [10-12].
Los beneficiosos efectos del dopado con N han sido observados en sistemas dopados y codopados [13-16]; en especifico: Wu et al [17] indicaron en su estudio para diferentes concentraciones de N que en el caso de un dopaje de alta concentración la banda de valencia crece disminuyendo el band gap y que los dopajes de baja concentración no afectan significativamente el VBM (máximo de la banda de valencia en inglés) o el CBM (mínimo de la banda de conducción en inglés).
En este trabajo se realizan cálculos de primeros principios para estudiar las propiedades ópticas y los cambios en el gap de TiO2 anatasa dopado con N y/o F. Además se analiza el caso de codopado N-F, para entender el efecto sinérgico, y asó corroborar lo reportado en previas investigaciones de sistemas codopados. El objetivo es encontrar un material dopante que reduzca efectivamente el band gap y que a la vez brinde un coeficiente de absorción alto en la región visible.
1. Detalles computacionales y modelos estructurales
La fase anatasa de TiO2 posee una estructura tetragonal (espacio grupal I41/amd) y tiene los siguientes parámetros de red: a=3.7842 Å, b=3.7842 Å, c=9.5146 Å [2]. La celda unitaria tiene cuatro átomos de Ti y ocho átomos de O.
Las optimizaciones de estructura asó como los cálculos de energía total de TiO2 bulk fueron realizados en el marco de la Teoría del Funcional de la Densidad implementada en el código Wien2k [18]. La aproximación de gradiente generalizado (GGA) de Perdew-Burke-Ernzerhof (PBE) [19] fue usada para el potencial de correlación-intercambio, en todos los sistemas. Es importante usar el potencial de intercambio-correlación adecuado para obtener los mejores resultados para el band gap. La aproximación GGA da mejores resultados que LDA (Aproximación de densidad local en inglés) en este aspecto [20,21], sin embargo subestima el valor del gap con respecto a resultados experimentales. Esto es por efectos no locales que aparecen por intensas repulsiones de Coulomb. Recientemente el potencial modificado de Tran y Blaha de Becke-Johnson (TB-mBJ), ha demostrado dar excelentes resultados para el gap y la estructura de bandas [22]. Sin embargo TB-mBJ puede ser computacionalmente muy exigente. Ya que la aproximación PBE y TB-mBJ describen adecuadamente y casi con el mismo grado de precisión la estructura de bandas [23], se adoptó la aproximación GGA-PBE con una corrección scissor para el cálculo de propiedades ópticas.
Para modelar a TiO2 dopado se aumentó el tamaño de la celda en 2x2x1. El dopado se realizó reemplazando, uno, tres, y cinco átomos de oxígeno por nitrógeno o flúor, que corresponden a concentraciones de 2.08%, 6.25%, y 10.4%. Para los sistemas codopados se reemplazaron 3 átomos de oxígeno por dos átomos de F y uno de N correspondientes a una concentración de 6.25 %, y 5 átomos de oxígeno por 4 átomos de F y uno de N correspondientes a una concentración de 10.4%. Se ha adoptado el dopado sustitucional por que la energía de formación es menor que para el dopado intersticial [20].
La constante Rmt.Kmax usada, que es un indicador del tamaño de la base de ondas planas, fue de 6.5, luego del análisis de la convergencia correspondiente. Se realizó un barrido de los puntos k para obtener la malla adecuada en la zona irreductible de Brillouin, la cual fue de 60. Sin embargo, para el cálculo de propiedades ópticas se usó una malla de puntos k más densa de 250. La energía de corte, que es la separación de energía entre estados de core y valencia, fue de -6.0 Ry.
Se realizó un relajación de estructura por medio del cálculo de fuerzas para garantizar la estabilidad de la estructura. La relajación atómica se detuvo cuando las fuerzas sobre los átomos eran menores que 1 mRy/ua. Luego se realizó la optimización de volumen considerando la razón c/a y se obtuvieron los parámetros de red a=b=7.6115 Å, y c=9.5182 Å, para la supercelda de TiO2 anatasa. Se usaron las simetrías de la estructura cristalina para reducir el tiempo computacional. Después de la optimización de los demás sistemas, los parámetros de red no presentaron cambios considerables.
Los estados de valencia usados para los elementos fueron los siguientes: Ti (4s23d2), O (2s22p4), N (2s22p3) y F (2s22p5). Los radios de las esferas de Muffin-Tin (Rmt) usados para Ti, O, N y F fueron de 1.76, 1.63, 1.59 y 1.68 bohr, respectivamente. El valor Lmax para los armónicos esféricos fue de 10. El ciclo autoconsistente se considero convergente para una precisión de 0.000 1 Ry. Ya que TiO2 anatasa no presenta momento magnético apreciable [24], y tampoco N o F (diamagnéticos), no se consideró magnetismo en los cálculos de estructura electrónica.
Las propiedades ópticas son causadas por la interacción de fotones con electrones en el material, es decir la transición entre estados ocupados y desocupados, de los electrones, por absorción o emisión de fotones. La función dieléctrica compleja es utilizada para el cálculo de propiedades ópticas [25]:
Donde e! es la parte real y e2 es la parte imaginaria. Cuando se trata de un material con estructura tetragonal como TiO2 las propiedades ópticas se calculan experimentalmente aplicando campos eléctricos paralelos y perpendiculares al eje c. Una vez que se obtiene la función dieléctrica habremos hallado con ella, la polarizabilidad (parte real) y la absorción electrónica (parte imaginaria). Esta parte imaginaria viene dada por [26]:
donde Ω es el volumen de la celda elemental, v y c representan las bandas de valencia y conducción respectivamente, k es el vector que define la polarización del campo eléctrico y ω es la frecuencia de la luz incidente.
A partir de Є1 y Є2 se obtienen conductividad óptica, el coeficiente de absorción, el índice de refracción, etc. En este trabajo nos enfocamos en el coeficiente de absorción que viene dado por [20,25]:
2. Resultados y discusión
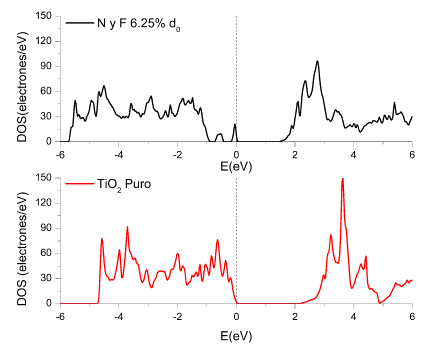
Luego de las optimizaciones de estructura se han obtenido parâmetros de red en concordancia con cálculos previos [20,27], lo cual implica que nuestros cálculos son razonablemente confiables. Para comprender mejor la estructura electronica, en específico, para obtener el band gap, se calculo la densidad de estados para los sistemas puro, y dopados. Nuestros resultados se muestran en las Figuras 1(a), 1(b), y 2 donde se ven la densidad de estados totales de TiO2 dopado con N, con F, y el codopado con N y F, donde la separación entre N y F es de 7.2051 bohr (d0), para este último. También se analizaron las densidades de estados parciales en las Figuras 3(a), 3(b).
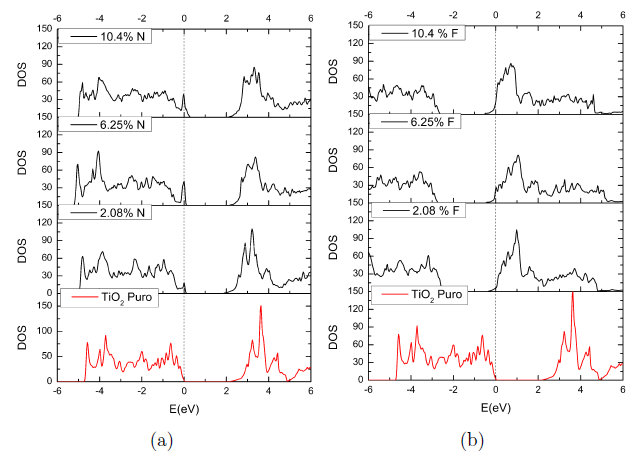
FIGURA 1 Densidad de estados calculados mediante DFT del TiO 2 dopado con diferentes concentraciones (a) de N y (b) de F.
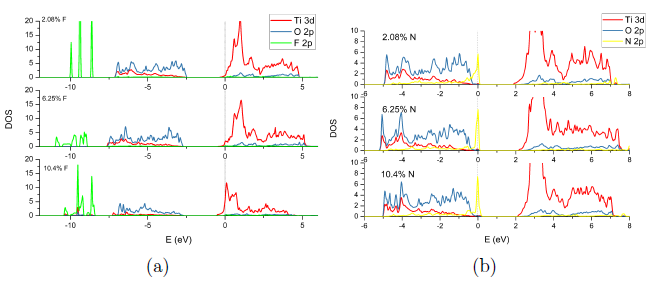
FIGURA 3 Densidad de estados parcial calculada mediante DFT de TiO 2 dopado con diferentes concentraciones (a) de N y (b) de F
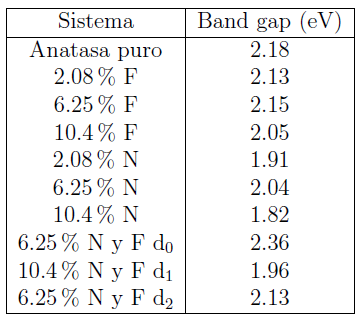
Los band gap obtenidos para cada sistema se muestran en el cuadro 1. Se analizaron también los sistemas codopados NF con separación entre N y F de d1=10.2156 bohr y d2=4.7292 bohr, para comprender mejor por qué la absorción óptica es menor en el caso de codopado.
A partir de las densidades de estado totales para los sistemas monodopados en las Figuras 1(a) y 1(b), donde la línea vertical a 0 eV representa el nivel de Fermi, se observa que el dopado con F resulta ser del tipo-n pues el nivel de Fermi pasa de la parte superior de la banda de valencia a la parte inferior de la banda de conducción y que el dopado con N es de tipo-p, pues el nivel de Fermi está cerca de la banda de valencia.
Se puede notar en la Figura 1(a) y en el cuadro 1 que el gap de los sistemas dopados con N, es apreciablemente reducido para una concentración de 10.4%. Esto corresponde a una disminución de 17% respecto del sistema puro. Wu et al [17] ya habían reportado que el dopado con N a altas concentraciones (TiO2-xNx, x=0.3125) produce variaciones significativas del VBM y CBM en TiO2, que inducen corrimiento al rojo en el borde del rango de absorción óptica. Nuestros resultados están en acuerdo con lo afirmado con Wu et al.
En la Figura 2 se aprecia el sistema codopado para elementos dopantes separados a una distancia de 7.2051 bohr, el gap es mayor comparado con los sistemas monodopados a la misma concentración. Esto último no está en concordancia con los estudios previos [10-12].
En el caso del dopado con F, como se puede observar en la Figura 3(a), la contribución de la impureza a la BV y la BC es extremadamente baja, comparada con O 2p y Ti 3d. En todas las concentraciones de monodopaje estudiadas, F solo introduce estados apreciables, con picos muy altos a una concentración de 2.08%, y localizados siempre por debajo de la BV en los tres sistemas monodopados. Para una concentración de 10.4 % los estados de impureza de F forman una banda que hibridiza ligeramente con O 2p y Ti 3d, la separación de los estados F 2p con la parte inferior de la BV se hace menor conforme aumenta la concentración de F. Se observa además un ensanchamiento de la BV para la concentration de 6.25% comparada con el sistema a 2.08 % y TiO2 puro.
A partir de la Figura 3(b) se observa que las impurezas de N introducen estados 2p en la parte superior de la banda de valencia (VBM). Hay hibridización de N 2p con Ti 3d y O 2p en la BV y la BC en un amplio rango de energías. En los tres casos de monodopado se observa un pico cerca de la energía de Fermi, correspondiente a estados de impureza N 2p. Para una concentración de 10.4 % esto induce una reducción apreciable del gap (cuadro 1). Nuestros resultados están en concordancia con los estudios previos para N. [13-15,17].
Ya que el band gap de TiO2 puro está 1.09 eV por debajo del band gap experimental (3.2 eV) para TiO2 anatasa, se agregó una corrección scissor de 1.09 eV [20].
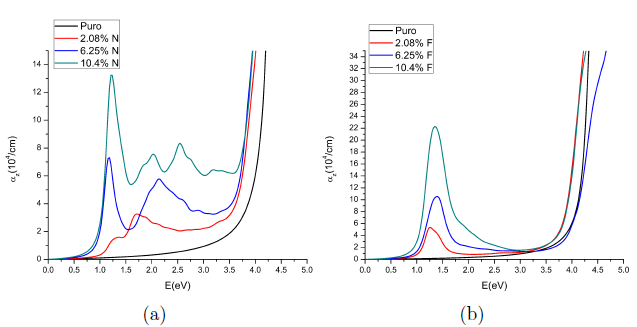
El coeficiente de absorción de los modelos puros y dopados a diferentes concentraciones de N y F se muestran en las Figuras 4(a) y 4(b).
En la Figura 4(a) se muestra el coeficiente de absorción de TiO2 puro y para diferentes concentraciones de dopaje con N. TiO2 dopado con N muestra absorción muy alta en la región UV (>3.30 eV) que corresponde a excitaciones desde estados O 2p en la banda de valencia a estados Ti 3d en la banda de conducción. El mismo patrón en la región UV es observado para TiO2 dopado con F en la Figura 4(b). El incremento de la intensidad de absorción en la región visible con el aumento en la concentración de dopado con N o F se puede observar en la Figura 4(a) y 4(b), estos resultados coinciden con los resultados experimentales y cálculos teóricos previos [15,17,28]. Para los sistemas monodopados; todas las concentraciones de dopaje con N y F estudiadas muestran absorción, en la región UV como en la visible. En la Figura 5 se aprecia la absorción óptica para las concentraciones más altas estudiadas de N y F, asá como para el codopado NF con una separación entre N y F de d0=7.2051 bohr. Se puede observar que la absorción es muy baja para este último caso, aunque hay un incremento de la absorción a partir 2.0 eV. El dopado con N con una concentración de 10.4 % presenta la absorción más alta en el espectro visible.
Meili Guo y Jiulin Du [29] estudiaron el codopado con C y N en TiO2 anatasa y señalan que el enlace covalente entre los átomos de C y O, que dificulta la transferencia de carga, se hace más intenso conforme se reduce la distancia entre C y N, y recomiendan que la distancia entre los átomos C y N debe ser lo más alta posible. Debido a esto, se analizó como afecta la distancia entre los átomos de N y F a la absorción, y se hizo el cálculo para el sistema codopado NF con dos separaciones adicionales.
En la Figura 5, d1 corresponde a una separación entre los átomos de N y F de 10.2156 bohr y d2 a 4.7292 bohr, y concentraciones de 10.4% (donde hay 4 átomos de F y 1 de N) y 6.25% (donde hay 2 átomos de F y 1 de N) respectivamente. Se aprecia que la absorción en la zona visible del espectro es notable para d1=10.2156 bohr, que es la mayor separación de los sistemas estudiados para codopado, aunque baja comparada con los sistemas monodopados. Además la absorción se incrementa para energías más altas en la parte visible a partir de 2.0 eV, el codopado a 6.25% tiene este mismo comportamiento. Asá, se puede deducir que la mayor concentración de F (sistema d1) y mayor separación de los átomos, está asociada a una mejor absorción en la zona visible para el sistema codopado NF. La absorción menos intensa del sistema codopado comparada con el monodopado no era esperada en este estudio, pues contradice los resultados previos de codopado hallados en la literatura [10-12].
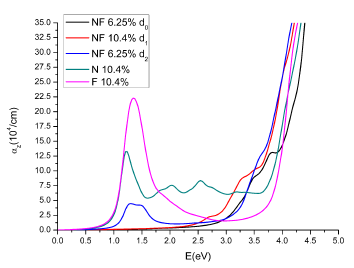
FIGURA 5 Coeficiente de absorción para TiO 2 dopado con N, dopado con F, y codopado con NF separados en 7.2051, 10.2156 y 4.7292 bohr
Cabe resaltar que a partir de 3.14 eV el codopado a 10.4 % presenta mayor absorción que el monodopado con N a 10.4% en la región violeta del espectro visible, y menor que el sistema codopado a 6.25 % en la región energética comprendida entre 1.65 eV y 2.5 eV, aun asá la absorción de los sistemas monodopados predomina en esta región.
Guo y Jiulin Du [29] argumentan que la gran disminución del gap para el sistema codopado se debe al efecto sinérgico; ya que el dopado C genera un mayor reducción del gap que N, y el dopado con N genera un absorción más intensa, el codopado con estos elementos presenta ambos beneficios. En nuestro estudio N presenta la mayor absorción óptica en la zona visible del espectro y también la mayor disminución del gap. No hubo mejora en la absorción para el caso codopado NF, tampoco se observa una mayor reducción del gap para este sistema comparado con el monodopado. Para comprender mejor lo que está sucediendo se calculó la densidad de estados parcial para los sistemas d0, d1 y d2.
En la Figura 6 se observa el sistema codopado a 6.25% con una separación entre F y N de 7.2051 bohr, donde hay un átomo de Ti entre los átomos N y F. Aquí, los estados de impureza se ubican encima del VBM y están compuestos principalmente de estados N 2p, con una baja concentración de estados O 2p y Ti 3d. En la Figura 7(a) se observa el sistema codopado a 10.4 % con una separación entre F y N de 10.2156 bohr, donde no hay átomos de Ti u O entre los átomos de N y F. Aquí, los estados de impureza también se ubican encima del VBM y están compuestos principalmente de estados N 2p, O 2p y Ti 3d contribuyen muy poco pero abarcan un rango más amplio de energías que en el sistema previo, al igual que N 2p. La banda de conducción se desplaza hacia regiones menos energéticas.
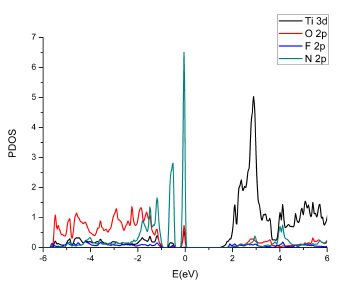
FIGURA 6 Densidad de estados parcial para el sistema codopado NF con una separación d 0 =7.2051 bohr entre N y F y una concentración 6.25 %
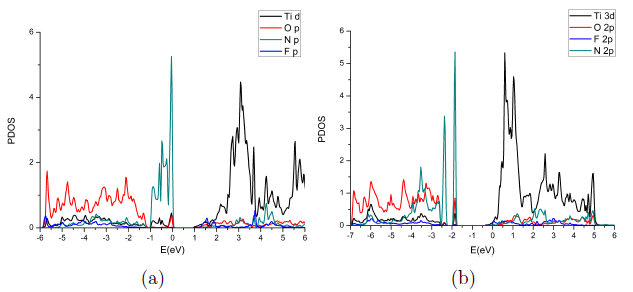
FIGURA 7 Densidad de estados parcial para el sistema codopado NF con una separación entre N y F de (a) d 1 =10.2156 bohr, concentración de 10.4% y (b) d 2 =4.7292, concentración de 6.25%
De la Figura 7(b) se observa el sistema codopado a 6.25 % con una separación entre F y N de 4.7292 bohr, donde no hay átomos de Ti u O entre los átomos de N y F, los estados de impureza se ubican encima del VBM y están compuestos principalmente de estados N 2p. Los estados O 2p y Ti 3d contribuyen muy poco en esta zona.
Las transiciones a los niveles energéticos de impureza facilitan la excitación de los electrones al CBM por radiación electromagnética, en los tres sistemas.
Conclusiones
Se realizaron cálculos GGA, basados en primeros principios implementados en el código WIEN2k para el sistema TiO2 anatasa dopado con F y N y se compararon con la literarura. Con una corrección scissor adecuada basada en resultados experimentales, se concluye que el codopaje con N y F reduce el band gap en 10.1 %, para una concentración de 10.4% y una separación de 10.2156 bohr entre N y F, mientras que el monodopado con F y N en una concentración de 10.4 % lo reducen a 5.96 % y 17 % respectivamente. El corrimiento de la energía de Fermi para el dopado, muestra la naturaleza de dopaje tipo-n de F, y la tipo-p de N. Luego del análisis del coeficiente de absorción para todos los sistemas, se observó que TiO2 dopado con N a 10.4% muestra la más intensa absorción en la región visible debido a la disminución del gap provocada por la presencia de estados N 2p en la parte superior de la banda de valencia, sin embargo, el codopado a una concentración de 10.4% de este estudio manifiesta una mayor absorción en la región visible del espectro que el monodopado con N a la misma concentración a partir de 3.14 eV. El espectro de absorción muestra también que los picos se mueven hacia regiones más energéticas conforme la concentración de dopado aumenta, lo cual implica que existe un límite en el beneficio de la concentración de dopado. El incremento de la distancia entre las impurezas de N y F en el sistema codopado y la mayor concentración de F, facilita la absorción en el espectro visible. Los resultados de esta investigación proveen una base teórica importante para futuro trabajo experimental y teórico.