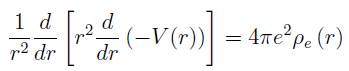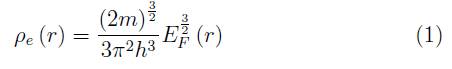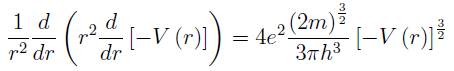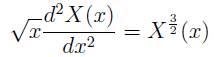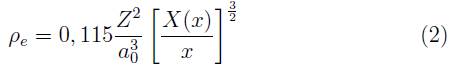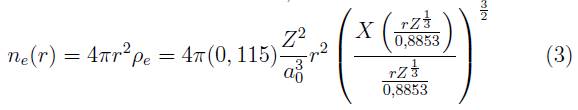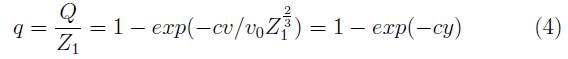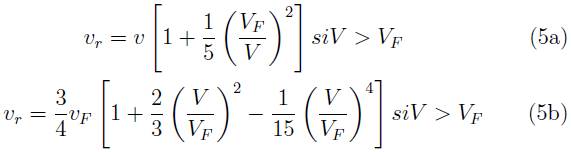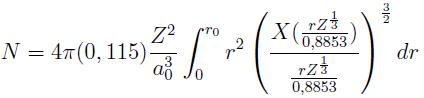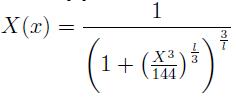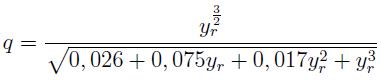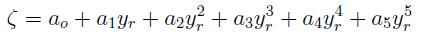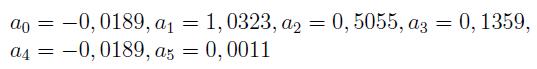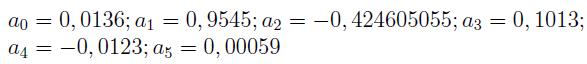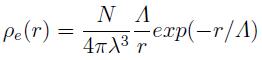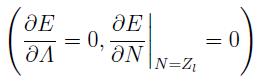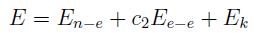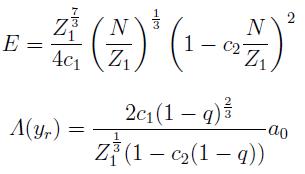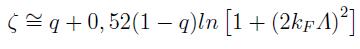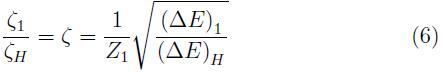Introducción
El proceso de parametrización de valores experimentales de frenado de proyectiles atómicos iniciado por T. Hall en 1950, ha visto dos periodos de discusión intensa en torno a la carga efectiva que poseen los iones livianos en un medio material. La evidencia experimental recopilada durante mas de dos décadas en el rango de energías altas e intermedias apuntaba a la imposibilidad de que el proton ligara electrones en el jellium 1, afirmación que extendía al rango de las energías bajas un cálculos teórico realizado por Rogers et al. en 1970. La polemica que ocupo esa década, de si el hidrogeno intersticial mantenía siempre el valor de carga +1 o manifestaba una carga variable, vino a resolverse en 1982, año en el que Brandt y Kitagawa (B-K) formulan la Teoría de Carga Efectiva basada en la afirmación fuerte de que el hidrogeno intersticial siempre interactúa con la materia como protón desnudo, asignando a este elemento el papel de referencia. Para dar soporte a la teoría, en el mismo año F. Schulz [1] llevó a cabo mediciones de precisión lanzando iones de Ar, Ne, N y He contra blancos de C, Al y Au. Los resultados satisfactorios excluían al helio al considerarse que no era un átomo de Thomas-Fermi. En un segundo periodo (1994-2008), nuevas mediciones de frenado en He y H en metales alcalino-térreos, de los que la teoría de la funcional de densidad (DFT) no pudo dar cuenta, y desarrollos teóricos paralelos achacan las dificultades a la pérdida de la simetría esférica del potencial efectivo que sufre una carga en movimiento: el dipolo de Landauer [2].
Anteriormente [3] se había discutido el cociente de frenados del helio y el hidrogeno en metales, en relación con DTF. En contraste, el presente artículo describe una adaptación del modelo de carga efectiva de Brandt y Yarlagadda, quienes en 1978 levantaron la restricción de protón no ligante, en razón de que sólo así se predecía correctamente dicho cociente de frenados. Nuestros cálculos en átomos livianos distintos al helio muestran resultados del mismo grado de concordancia a los datos de Schulz, que aquellos deducidos con la teoría de B-K, pero con la virtud de acertar el cociente de frenados de He, lo que BK no hace. De hecho, esta versión del modelo de carga efectiva nunca fue revaluada, simplemente se abandonó quizás por su carácter semiclásico, ante el formalismo, en apariencia riguroso de DFT, que a la postre mostro serias. Limitaciones. Incluso se considera hoy que la teoría del hidrógeno en el jellium es aún incompleta en el sentido de forzar la hipótesis ad hoc de una ocupación parcial del orbital 1S que esta teoría predice.
El Átomo de Thomas y Fermi
Aunque el modelo atómico de Thomas y Fermi (T-F) para el estado base de átomos de muchos electrones (Z ≥ 18) se desarrolla casi en cualquier texto de Física Moderna o introduction a la Mecánica Cuántica [4], se resumen aquí los pasos esenciales. La idea subyacente al modelo es que la nube de electrones confinada por el núcleo atómico se gobierna por las leyes de la electrostática y las propias del gas de Fermi. Se plantea entonces la ecuación de Poisson del sistema electrostático con simetría esférica:
En el gas de Fermi el conteo de estados (número de electrones) en el gas 3-dimensional se realiza teniendo en cuenta que cada estado (2 electrones) ocupa un volumen h 3 del espacio de fase de momentum, por lo que la densidad electrónica en el espacio real es:
Que la profundidad del pozo de potencial sea igual a la energía de Fermi en cada entorno (E F (r) = - V(r)), asegura que la energía del estado base sea mínima, por lo que la ecuación de Poisson se transforma en la expresión auto-consistente:
Con la sustitución 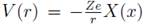 , donde X es la función de apantallamiento de Thomas-Fermi y eligiendo
, donde X es la función de apantallamiento de Thomas-Fermi y eligiendo 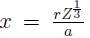 con α = 0, 8853α0 y α
0
el radio de Bohr, como una variable adimensional reducida, se fija una escala para los tamaños atómicos al tiempo que la ecuación de Thomas y Fermi alcanza una expresión universal:
con α = 0, 8853α0 y α
0
el radio de Bohr, como una variable adimensional reducida, se fija una escala para los tamaños atómicos al tiempo que la ecuación de Thomas y Fermi alcanza una expresión universal:
Ecuación diferencial no lineal que requiere de métodos numéricos de solución para X, función universal que ha sido tabulada en numerosas referencias (ver por ejemplo [4,7]). Resulta ahora sencillo calcular las diferentes variables atómicas de interés como tamaño, velocidad, energía, ya que resultan ser funciones algebraicas de Z, cuyos exponentes son números enteros pequeños o fracciones simples. Por ejemplo la densidad electrónica (electrones en la unidad de volumen) es:
Y aprovechando la simetría radial de la distribution de carga, la densidad electronica radial se escribe,
Aunque en el modelo T-F la densidad electronica diverge en el origen, la densidad radial crece de cero hasta un valor máximo para luego decrecer monótonamente.
La curva universal de ionización
Representa el grado de ionización que sufre el átomo de Thomas-Fermi al enfrentar el "viento electrónico" que se produce por el movimiento relativo entre átomo y jellium.
Modelo exponencial de la curva universal
Al incidir un electrón libre contra un átomo a velocidad relativa v el criterio de ionización de Bohr establece que los electrones atómicos que posean velocidades orbitales u > v permanecerán ligados al átomo (condición adiabática), mientras que en el caso contrario (u < v), los electrones son forzados a abandonar el átomo y la ionización ocurre. El modelo estadístico de Thomas-Fermi reduce el átomo de muchos electrones a una suerte de átomo hidrogenoide cuyo único electrón orbita a la velocidad representativa dada por el promedio de las velocidades de todos los electrones, es decir, 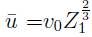 (vo, la velocidad de Bohr; Z
1
, el numero atómico) por lo cual, la comparación de velocidades que exige el criterio de Bohr para determinar el grado de ionización atómico se logra mediante la variable adimensional
(vo, la velocidad de Bohr; Z
1
, el numero atómico) por lo cual, la comparación de velocidades que exige el criterio de Bohr para determinar el grado de ionización atómico se logra mediante la variable adimensional 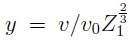 , definida como el cociente entre la velocidad v y la velocidad electrónica media del átomo de Thomas-Fermi.
, definida como el cociente entre la velocidad v y la velocidad electrónica media del átomo de Thomas-Fermi.
En términos de la nueva variable se establece la ley exponencial que aproximadamente cuantifica el grado de ionización q, que en términos generales 2 se identifica con la carga efectiva fraccional o fracción de carga efectiva ζ, de un proyectil atómico (o impureza atómica) en un medio material, como función de la velocidad relativa entre los electrones del medio y los del átomo,
en donde Q simboliza la carga neta de un átomo de carga nominal Z y c, un parámetro de ajuste a los valores experimentales 3.
En realidad, la intensa agitación electrónica que representa la velocidad de Fermi del medió, vF, es causa de ionización inclusive para una impureza estática (interesa a las técnicas de dopado e implantación de iones en materiales) por lo que mas que la velocidad de proyectil, importa es la velocidad de este relativa a la distribución de velocidades promediada de los electrones del blanco vr, la que se expresa en términos de v así 4:
Pese al acuerdo satisfactorio que alcanza (ecuación 4) en el rango de velocidades medias y bajas (0, 4 < y < 2) en el que se encuentra el grueso de los reportes experimentales, resulta insuficiente para y < 0, 4, en cuyo caso se debe mejorar el modelo de aproximación exponencial.
Modelo de dos plasmas de la curva universal
El modelo T-F otorga calidad de gas de Fermi a la nube de electrones confinada por el núcleo atómico, quede antemano la tiene el plasma metálico del blanco: Aluminio5. Para el gas de electrones, uno cualquiera de los siguientes parámetros define completamente sus características: n, EF , kF, vF, rs, ω0 (respectivamente: densidad, energía de Fermi, momento y velocidad de Fermi; radio por electrón, frecuencia del plasma). Para Al algunos de los valores (en unidades atómicas) son: EF, = 0, 43; kF = vF = 0, 91; rs = 2,12 y la frecuencia de plasma ωο = 2, 4x1016 rad/s. Por motivos didácticos, hemos elegido a vF como parámetro para describir el modo de encontrar la condición de equilibrio entre el gas de Fermi atómico y el jellium. El procedimiento equivale al originalmente seguido por Brandt para generar la "Curva Universal de Ionización" [6] en base a igualar las frecuencias de resonancia de plasma atómico y del metal huesped, con los resultados que aparecen en la Tabla 1.
TABLA 1 Fracción de carga efectiva calculada por el procedimiento de Brandt. q es una función universal de (1/b)(vr/v0 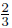 ). Se recomienda usar b = 1, 26 para proyectiles livianos (Z < 18) y velocidades altas, mientras que b = 1, 33 es mas apropiado para proyectiles pesados y velocidades bajas.
). Se recomienda usar b = 1, 26 para proyectiles livianos (Z < 18) y velocidades altas, mientras que b = 1, 33 es mas apropiado para proyectiles pesados y velocidades bajas.
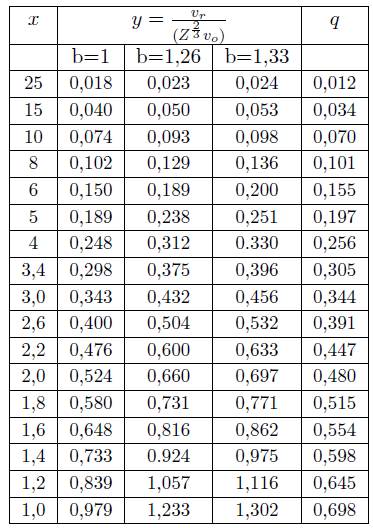
En el modelo T-F del átomo el criterio de ionización de Bohr se escribe, bvF(x) = vr, ecuación en la que el parámetro b ≈ 1 sirve de ajuste a los datos experimentales, vF(x) representa la velocidad local de Fermi a la distancia reducida x del núcleo; el valor x0 (y correspondiente r0) que soluciona la ecuación, fija la frontera del ahora ion atómico.
A continuación se ilustra el procedimiento para el caso de un atomo de hidrogeno estático en aluminio:
- Inicialmente se determina la velocidad media de los electrones en el metal huesped (ec. 5b con ν = 0), con el resultado vr = 0, 6825v0, el cual es también el valor de vF(x0) si b =1.
- De la ecuación (1) vF = (3π2ρ) 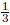 , que relaciona la velocidad de Fermi con la densidad, se despeja y evalúa ρ obteniendo,
, que relaciona la velocidad de Fermi con la densidad, se despeja y evalúa ρ obteniendo,  en unidades de
en unidades de 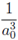 .
.
- Mediante un cálculo inverso se determina de la ecuación (2) el valor de x que hace p(x) = 0, 01074, se encuentra que x0 ≈ 1, 46 ó r0 ≈ 1, 29α0.
- Se calcula la carga electrónica encerrada por el ión atómico de radio r0, integrando para ello la función de densidad radial ne(r) ecuación (3) hasta la frontera del ion r0, es decir,
Para facilitar el cálculo de la integral tal que pudiera ejecutarse en una calculadora corriente (en este caso una calculadora gráfica HP - 48G+) se empleo la siguiente aproximación analítica de la función de apantallamiento [7]:
con 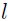 = 0, 8034. El valor hallado es N = 0, 403.
= 0, 8034. El valor hallado es N = 0, 403.
En general se resta de Z el valor N para obtener la carga efectiva neta Q y en el caso presente q = 1 - N ≈ 0, 6 es la fracción de carga efectiva.
Resumiendo, q ≈ 0, 6 es la fracción de carga o grado de ionización del H en Al, de acuerdo a la hipótesis de que en la frontera r0 de estos dos sistemas de Fermi, la velocidad y también la densidad electrónica del ión, decreciente con la distancia, se hace igual a la del aluminio. Finalmente, se compara esta fracción de carga con aquella obtenida por Brandt en base a las resonancias del plasma (tabla 1). La interpolación lineal en x = 1, 46 da por resultado, q = 0, 585.
La concordancia es aceptable a pesar de las interpolaciones realizadas y que la función X es apenas aproximada a la función de pantalla de Thomas-Fermi. En consecuencia, aprovechamos el cálculo numérico ya realizado por Brandt y acogemos la tabla 1 para subsiguientes evaluaciones de fracciones de carga.
Debido a su naturaleza estadística la universalidad de la curva de ionización se restringe al rango Z > 18. En un intento por explicar el comportamiento anómalo que presentan los átomos livianos, Brandt y Kitagawa, invocando un efecto de incremento de la carga efectiva que observa un electrón en colisión cercana con el ión atómico, se apartan de la curva universal postulando la Teoría de Carga Efectiva. Para que ésta funcione es necesario que el hidrogeno intersticial no de lugar a este efecto, por lo que debería interactuar como protón desnudo, es decir, su carga efectiva debe ser siempre + 1, asunto de álgida discusión por muchos años. Se logró así un acuerdo satisfactorio con los experimentos de alta precisión de Schulz con Z1 ≥ 6. En este artículo mostramos como la aparente discrepancia creciente al descender en Z1, observada en la relación de frenados con el hidrógeno, no es otra cosa que la confirmación de la universalidad de dicha curva.
El modelo de carga efectiva de Brandt y Yarlagadda [8]
El método de cálculo mediante el cual Brandt obtuvo la curva universal de ionización implica una integración numérica, por lo que se cuenta sólo con los valores que da la tabla 1 y no se dispone en la literatura de una ecuación de ajuste para el rango completo. En este trabajo se empleó la ecuación de ajuste [9].
la cual muestra un buen ajuste (desviación < 5 %) en el rango yr < 0, 2; el que corresponde a la data de Schulz para Ar y Ne (en N se subió el límite a yr ≈ 0,3; esperando no exceder las tolerancias y sin mas justificación que la consistencia de los resultados). Se empleó el valor de parámetro b = 1,33 que permite comparar en igualdad de condiciones con Schulz (además en correspondencia con los lineamientos de Brandt de la tabla 1. Para y- > 0, 2 (el rango correspondiente a los y- del hidrógeno) se empleó un ajuste polinomial de grado 5,
donde el juego de coeficientes del polinomio para b = 1, 26 es:
Para mantener la concordancia con Schulz el parámetro de ajuste utilizado para helio es b = 1, 33 (b = 1, 26 o inclusive el ajuste exponencial (ecuación 4) no hace mayor diferencia en el He). Los coeficientes correspondientes a este caso son:
El rango de los ajustes polinomiales se extiende hasta y- = 1, 2.
La teoría de carga efectiva de Brandt y Kitagwa [10]
La idea de esta teoría es corregir el apartamiento de la curva universal de ionización que muestran los átomos livianos, argumentando por ejemplo que un electrón en trayectoria frontal hacia el átomo penetra profundamente la nube de apantallamiento, alcanzando mayor cercanía a la carga nuclear Z, en contraste a aquel electrón de parámetro de impacto p grande, que "observa" una carga nuclear reducida. Con Q = Z - N, la carga iónica (correspondientemente, q =1 - N/Z, el grado de ionización); N, número de electrones que permanecen ligados al ión. La teoría distingue carga efectiva ζ del grado de ionización q y se afirma que por efecto de las colisiones cercanas, Z* > Q (correspondientemente ζ < q).
La elaboración detallada del modelo sigue el siguiente procedimiento:
Esquema básico de la teoría B-K
-Supone una dependencia radial para la densidad electrónica del ión apantallado de la forma:
Λ : Parámetro variacional de apantallamiento.
-Se minimiza la energía E del ión con respecto al parámetro de pantalla Λ, y al número de electrones N:
lo que determina el valor de dos parámetros cl y c2 además de Λ:La energía total interna del ion E se compone de la energía de interacción núcleo-electrón, la interacción electrón-electrón y energía cinética electronica, de modo que:
c2: parámetro variacional para incluir de forma promediada el efecto de correlación electronica. El procedimiento arroja los siguientes resultados:
• Se construye un modelo analítico que aproxima de forma satisfactoria la distribution de carga del modelo T-F. La energía y longitud de pantalla resultan dadas respectivamente por:
con c1 = 0, 240 y c2 = 0,143
• Finalmente se halla también el coeficiente fraccional de carga, que en primera aproximación es 6:
En consecuencia se trazan las curvas de círculos solidos pequeños, rotuladas B-K en las figuras 1 a 4, siguiendo las indicaciones de la siguiente sección de representación gráfica.
Representación de las fracciones de carga y de los valoresexperimentales de frenado en la gráfica ζ vs. yr
La ecuación que conecta la teoría con el experimento es la regla de escalamiento,
A la izquierda, las fracciones de carga del átomo Z1 y de la referencia (hidrogeno) que calculan las teorías de carga efectiva; a la derecha, las respectivas pérdidas de energía sufridas al atravesar el medio (determinadas a una misma velocidad y de preferencia en un mismo blanco).
El procedimiento para generar un punto cualquiera de la curva de fracción de carga ζ vs. yr de un átomo determinado es entonces como sigue:
-En el modelo Yar se evalúa la abscisa yr y el valor se substituye en el polinomio de ajuste a q mas apropiado 7 (respetando los criterios indicados en la tabla 1, de número atómico y rango de velocidad); el resultado es el valor de q1. De la exigencia de determinación a igual velocidad, la misma evaluación para el átomo de referencia significa subsituir el valor 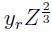 en el ajuste polinomial de q que corresponda al hidrogeno según su velocidad, siendo éste es el valor de ζH. De este modo se consigue el par ordenado (yr, ζ) que se registra como un punto de la curva. Por ejemplo, para un átomo de helio que transita a una velocidad media v = 8V0; su velocidad relativa reducida es yr 63 ,0־. Así que ζΗε se evalúa en el valor de abscisa 0,63, mientras que ζΗ se evalúa en el valor 1. Y las coordenadas del punto son (0,63; 0,72).
en el ajuste polinomial de q que corresponda al hidrogeno según su velocidad, siendo éste es el valor de ζH. De este modo se consigue el par ordenado (yr, ζ) que se registra como un punto de la curva. Por ejemplo, para un átomo de helio que transita a una velocidad media v = 8V0; su velocidad relativa reducida es yr 63 ,0־. Así que ζΗε se evalúa en el valor de abscisa 0,63, mientras que ζΗ se evalúa en el valor 1. Y las coordenadas del punto son (0,63; 0,72).
Los valores experimentales de frenado se procesan de manera similar aunque, es decir, con pérdidas de energía de Z1 y H evaluadas a la misma velocidadH. Las curvas de la predicción de Brandt-Kitagawa se elaboran a partir de la ecuaciíon (6) también del mismo modo, aunque con ζ Η 1 ־ y ζ Η e calculado de la ecuación 31 de la referencia [10].
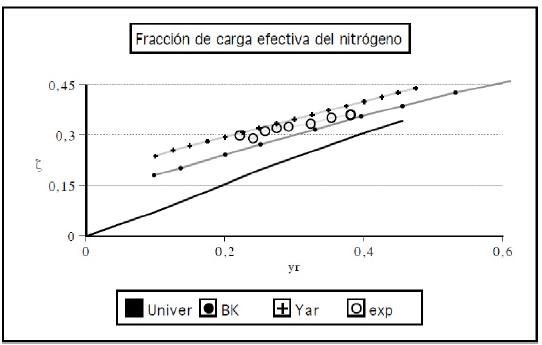
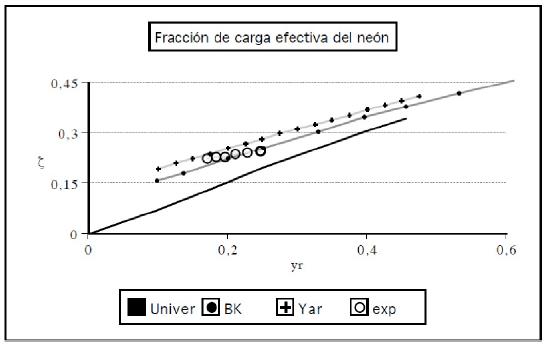
A continuación se condensan de modo gráfico las predicciones de las fracciones de carga efectiva de iones de argón, neón, nitrógeno y helio, con velocidades entre moderadas y bajas (v < 1, 7v0), en aluminio. Con pequeñas cruces se señalan las curvas correspondientes al modelo de Yarlagadda, los pequeños círculos sólidos para la teoría de Brandt y Kitagawa. Círculos grandes sin rellenar para los valores que se desprenden de las mediciones de frenado de F. Schulz (las mismas que se utilizaron para dar soporte experimental a la teoría de carga efectiva que aquí se cuestiona) y en el caso específico de la figura 1, se incluyen también las mediciones de G. Martínez et al. [11]; estas últimas con proyectiles lentos de He e H, cumpliendo la indicación de hacer la medición en un mismo blanco 8. Por último, en trazo continuo la curva universal de ionización. Nótese que no hay mayores diferencias entre la data de uno y otro autor.
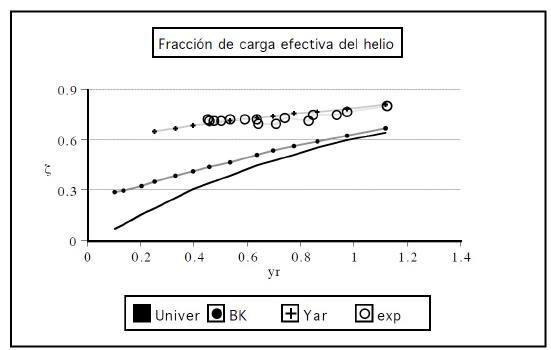
FIGURA 1 Fracción de carga efectiva para Z 1 = 2 en Al en función de la velocidad relativa reducida. La teoría B-K colapsa frente a los valores experimentales.
Un análisis preliminar de las figuras 1 a 4 revela la convergencia monótona hacia la curva universal al crecer en Z, tal como se espera de un modelo estadístico como T-F. El apartamiento de las fracciones de carga teóricas y experimentales de la curva universal no debe ser motivo de preocupación. Simplemente, en el modelo Yar es consecuencia de la definición de ζ como un cociente de fracciones de carga, cada una de las cuales sigue la curva de ionizaciíon. En el modelo B-K se debe al incremento de la fracción de carga de Z1 por colisiones próximas (ya que ζH 1 ־).
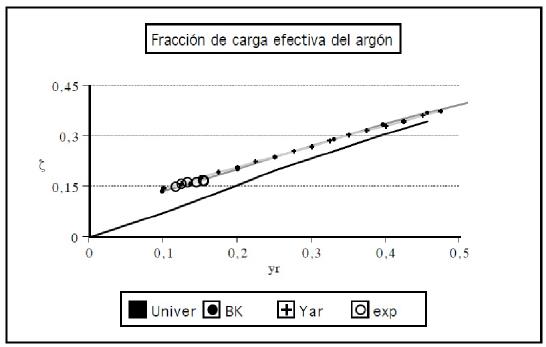
FIGURA 4 Fracción de carga efectiva para Z1=18 en Al en función de la velocidad relativa reducida. Las predicciones de Yar y B-K prácticamente se superponen entre sí y con los valores experimentales.
En esencia importan las diferencias entre teoría y experimento, y en este aspecto los cálculos de B-K y Yar discrepan levemente y prácticamente por igual (la primera por defecto y la segunda por exceso) de los valores experimentales para N y Ne (en Ar prácticamente coinciden entre sí). No sorprende el resultado en B-K, por ser los valores experimentales que en su momento sirvieron para comprobar la teoría para Z > 5. Lo notable es que Yar predice además las fracciones del helio (figura 1), logrando así el cometido en el rango completo sin hipótesis distinta a suponer que todos los elementos, incluido el hidrogeno, siguen razonablemente la curva universal de ionización.
Conclusiones
■ Se evidencia un comportamiento estadístico de Thomas-Fermi por parte de los átomos livianos, facilitado por el intercambio de electrones entre átomo y jellium.
■ Se verifica la validez de la regla de escalamiento
, con ζh variable dada por la curva universal de ionización de Brandt. Se refuta así la hipótesis de que el hidrogeno intersticial solo interactua como protón desnudo (q = +1).
■ Se extiende el rango de validez de la Curva Universal de Ionización a la totalidad de la tabla periódica, honrando ahora sí el nombre originalmente dado por cubrir solamente el rango de los átomos de muchos electrones.
■ En base a los mismos valores experimentales que originalmente se esgrimieron como prueba de la teoría de Brandt-Kitagawa, los dos modelos discrepan moderadamente de los resultados experimentales, BK por defecto y Yarlagadda por exceso. Pero la "prueba de fuego" que representa el helio sólo la supera el modelo de Yarlagadda.
■ La distinción entre Z* y Q que suponen Brandt y Kitagawa no parece tener lugar, no tanto porque no pueda haber un efecto de colisiones próximas, sino tal vez porque los parámetros empíricos de ajuste b y c implícitamente ya contenían esta información.
■ Llama la atención el valor de carga efectiva del helio cercano a
. La regla de partición del frenado,
sostiene que en el régimen de velocidades altas de Bethe, las colisiones próximas y las distantes contribuyen aproximadamente por igual al frenado del átomo, tal que para un átomo neutro (q = 0) la fracción de carga efectiva toma el valor
. Al respecto, el hecho de que la energía de ionización del helio sea con creces la más alta de la tabla periódica sugiere esta posibilidad de permanencia en estado neutro (el hidrógeno continuaría manifestándose como protón desnudo), lo que salvaría la teoría de Brandt y Kitagawa. Sin embargo, una tendencia similar (incremento de ζ) no parece ocurrir en los otros dos átomos raros estudiados, el neón y el argón; además, en el régimen de velocidades bajas es dudosa la validez de la regla. En todo caso, esta discusión está por fuera de la teoría B-K, pues para el helio neutro en Al, ζ es tan solo 0,238. Con fines didácticos valdría la pena ahondar en este aspecto.
■ Finalmente, el buen desempeño del modelo semiclásico de Yarlagadda lo hace una referencia útil para la prueba de modelos de cálculo más sofisticados.