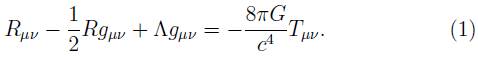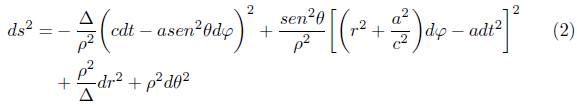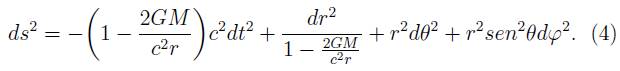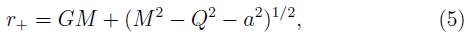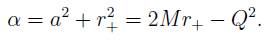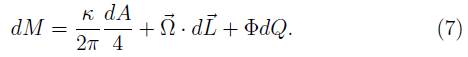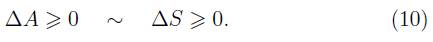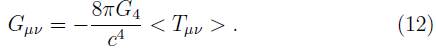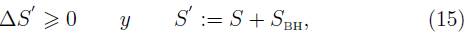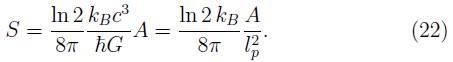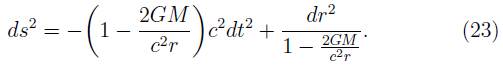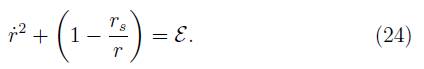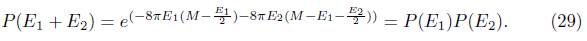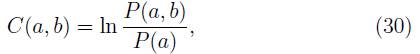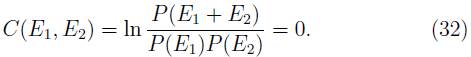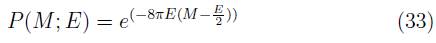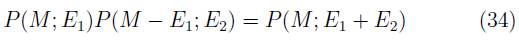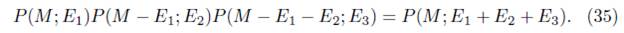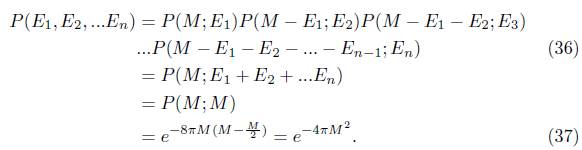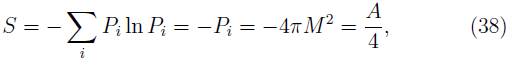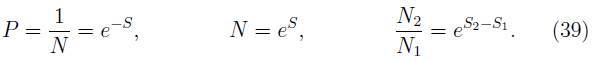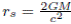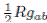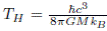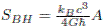I. Introducción
Uno de los aspectos más importantes en la física de agujeros negros es la similitud formal entre las leyes de la mecánica de los agujeros y las leyes de la termodinámica, donde se establece una correspondencia entre la gravedad superficial con la temperatura y el área del horizonte con la entropía. Los primeros trabajos que surgen en el contexto de la termodinámica de agujeros negros comienzan con Bekenstein y Hawking [1-6] con el descubrimiento de la evaporación de los agujeros y la formulación de la segunda ley generalizada de la termodinámica donde se considera que la entropía Bekenstein-Hawking SBH es una entropía térmica. Avanzando un paso más en la similitud formal, al igual que la termodinámica usual tiene una descripción microscópica bien establecida, se espera que la entropía Bekenstein-Hawking esté relacionada con un número de estados microscópicos que den cuenta de los fundamentos de lo que sería una teoría cuántica de la gravedad [7].
El trabajo pionero de Hawking plantea la idea en la cual un agujero negro emite una radiación de cuerpo negro que tiene una temperatura dada por la masa del agujero. Esta radiación térmica no transmite ninguna información la cual está en un estado cuántico mezclado. Un objeto cayendo al agujero negro aporta información la cual se representa por un estado cuántico puro. Así surge la pregunta natural, ¿qué sucede con la información?. En el límite cuando el agujero negro se evapora por completo, el estado cuántico puro ha evolucionado a un estado cuántico mezclado lo cual está prohibido por la mecánica cuántica, cuya unitariedad exige que un estado cuántico puro debe permanecer en un estado cuántico puro para así mantener la conservación de la información. Por tanto, la idea de renunciar a la unitariedad de la mecánica cuántica o de la conservation de la information, es lo que establece la paradoja de la perdida de información [8].
En este contexto se hace una revisión de la termodinámica de agujeros negros en la sección II para esbozar el escenario en el cual se establece la paradoja de la pérdida de información en la sección III. En esta sección se exponen las ideas seminales de Bekenstein y Hawking para la formulación de la paradoja y sus posibles soluciones desde que fue enunciada hasta la actualidad. Finalmente, en la sección IV se establecen a manera de comentarios algunas conclusiones.
II. Termodinámica de agujeros negros
Al establecerse una analogía formal entre las leyes mecánicas de los agujeros negros con la termodinámica, surge toda un área de estudio de la física teórica denominada termodinámica de los agujeros negros en la cual el teorema de las áreas de Hawking encuentra su equivalencia con la entropía termodinámica, y la aceleración gravitacional en la superficie del agujero con la temperatura. Esta analogía se formalizó cuando se estableció una conexión profunda con la mecánica cuántica.
A. Aspectos generales
Desde un punto de vista formal, un agujero negro es un espacio-tiempo que posee un horizonte (horizonte de eventos), que actúa de tal manera que el exterior del horizonte está incomunicado en relación con el interior, y además tiende a ser asintóticamente una variedad plana donde los efectos gravitatorios son nulos, y el espacio-tiempo adopta la métrica de Minkowski. Para caracterizar un agujero negro existen tres parámetros: la masa M, la carga Q y el momento angular L. Este resultado está demostrado por los trabajos de W. Israel, B. Carter, S.W. Hawking y D.C. Robinson [9]. El contenido de estos trabajos es el denominado teorema del no pelo, donde la palabra "pelo" hace referencia a cualquier parámetro necesario para describir al agujero que no sea la masa, la carga o el momento angular. Las ecuaciones de Einstein de la relatividad general que determinan la métrica sobre la variedad espacio-tiempo (M,g) son 1:
Al solucionar las ecuaciones de Einstein, se describe el espacio-tiempo en torno a un agujero negro teniendo en cuenta los tres parámetros anteriores. La solución mas general está establecida por la métrica de Kerr-Newman la cual describe el espacio-tiempo en torno a un agujero negro cuyos parámetros fundamentales son la masa, la carga y el momentum angular que está dada por2
Donde
siendo M: Masa, 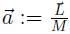 : momentum angular por unidad de masa y Q:carga eléctrica.
: momentum angular por unidad de masa y Q:carga eléctrica.
Si Q = 0 se obtiene la métrica de Kerr. Si α = 0y Q = 0se obtiene la métrica de Reissner-Nordstrom y si Q = α = 0 se obtiene la métrica de Schwarzschild3
J.M. Bardeen, B.Carter y S.W. Hawking desarrollaron sistemáticamente leyes de la mecánica de agujeros negros, análogas de las leyes de la termodinámica [5].
Para el agujero negro de Kerr-Newman se tiene el horizonte de eventos en4
donde el área del agujero negro corresponde a la superficie constante a una distancia r+ dada por
Definiendo el área racionalizada α = A/4π, se tiene
Diferenciando la ecuación anterior se obtiene
siendo
B. Aspectos termodinâmicos
Se puede establecer una correspondencia entre la ecuación (7) y la primera ley de la termodinámica
donde la gravedad superficial κ en (7) que es la aceleración gravitacional producida por el agujero en el horizonte de eventos, se identifica con la temperatura T en (9), y el área A con la entropía S. Los términos 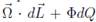 es el correspondiente a -PdV que representa el trabajo hecho sobre el agujero por un agente externo que incrementa el momentum angular del agujero negro y la carga por dL y dQ, respectivamente. Sin embargo, para que la correspondencia sea consistente es necesario introducir efectos cuánticos.
es el correspondiente a -PdV que representa el trabajo hecho sobre el agujero por un agente externo que incrementa el momentum angular del agujero negro y la carga por dL y dQ, respectivamente. Sin embargo, para que la correspondencia sea consistente es necesario introducir efectos cuánticos.
La ley cero de la termodinámica postula que la temperatura es constante en un sistema en equilibrio termodinámico. Es decir un sistema físico en equilibrio completo posee la misma temperatura en todas sus partes. De la misma manera para cualquier agujero negro en equilibrio, la gravedad superficial es una constante sobre el horizonte de eventos. En otras palabras, todos los puntos del horizonte de eventos de un agujero negro en equilibrio poseen la misma gravedad superficial.
La primera ley de la termodinámica manifiesta el hecho de que la energía se conserva en un sistema aislado. Si se consideran los agujeros negros como sistemas aislados lo anterior tiene validez. Esta ley permite relacionar el aumento de energía interna con el aumento de la entropía.
La segunda ley de la termodinámica se puede postular como la no disminución de la entropía en cualquier proceso termodinámico aislado. Esta encuentra su análogo en los agujeros negros en lo que Hawking denomino la ley de las áreas, en la cual, el área del horizonte de un agujero negro nunca disminuye, porque este no radía nada al exterior. Es decir,
En lo relacionado con la tercera ley, κ > 0 en (8), debido a que Q2 + α2 > M2 no es una solution física debemos tener en cuenta la carga eléctrica y el momentum angular, específicamente sus posibles valores máximos [10]. De (5) encontramos que a cumple la siguiente desigualdad
Lo anterior implica que en caso de ser violada la anterior desigualdad el horizonte desaparecería y obtendríamos una singularidad desnuda, lo cual está en total desacuerdo con el principio de la censura cósmica5, sin embargo existen evidencias numéricas sobre su violación. La imposibilidad de alcanzar la temperatura del cero absoluto en la termodinámica encuentra su analogía en los agujeros negros al establecer que la gravedad superficial en un agujero negro nunca es nula, esto es que al menos clásicamente tal desigualdad nunca se satura.
Sin embargo, las analogías anteriormente mostradas no son completas en el sentido de que si el agujero negro tiene entropía, entonces debe tener temperatura y por lo tanto debe emitir radiación. Pero de acuerdo con la física clásica nada puede escapar de un agujero negro. Además, al ser aplicada a un agujero negro la primera ley de la termodinámica (9), conlleva a que si la temperatura es cero, la entropía del agujero debe ser infinita.
C. Aspectos cuánticos
No existe una teoría completa para tratar los campos cuánticos sobre variedades curvas, sin embargo, se trabaja con un método semiclásico de la gravedad cuántica. Este método, denominado aproximación semiclásica, considera la presencia del campo gravitacional ignorando los efectos cuánticos de la gravedad sobre los campos cuánticos de materia. La aproximación de tratar cuánticamente los campos de materia sobre un espacio curvo y clásico es una buena aproximación en regiones donde el radio de curvatura es mucho mayor que la longitud de Planck [6]. Es decir, reexpresando la ecuación (1) se tiene 6
Al introducir efectos cuánticos cuyo origen se establece en la teoría de campos cuánticos sobre variedades curvas (ver sección III-B), Hawking descubrió [6] que los agujeros negros emiten radiación como si fueran un cuerpo negro en equilibrio termodinámico total, con temperatura 7κ
La temperatura de esta radiación se conoce como radiación Hawking, y le dio un sentido termodinámico formal y matemático al estudio de los agujeros negros.
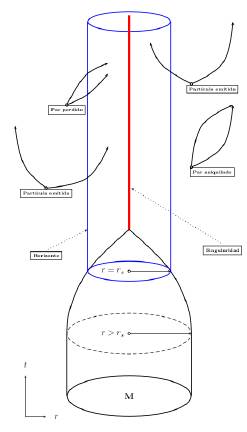
Al comparar (7), (9) y (13), se define la entropía Bekenstein-Hawking 8
A partir del descubrimiento de Hawking, se generalizo la segunda ley de la termodinámica (10) discutida en la sección anterior, definiendo una entropía generalizada S’ [11], donde
así, S representa la entropía de la materia y la radiación externas al agujero negro. Luego si el agujero negro radía, la consecuente disminución del área y de la entropía se compensa por el aumento de entropía en el medio que rodea al agujero negro, debido a la radiación emitida.
D. Un caso especial: el agujero negro extremal
Uno de los casos más estudiados en el contexto de la termodinámica de agujeros negros es el del agujero negro extremal definido a partir de la condición
es decir la saturación total de la desigualdad definida en (11). Lo anterior implica que en (8)
Tenemos un agujero negro con gravedad superficial cero justo sobre el horizonte y llevando a cabo la analogía termodinámica, de temperatura cero.
Este tipo de solución se interpreta clásicamente como el estado final de un agujero negro que se ha estado evaporando debido a la continua emisión de radiación, con temperatura cero no hay emisión entonces son absolutamente estables.
Sin embargo a partir de esta interpretación surge un problema, ¿cual es la entropía asociada a este tipo de agujero negro?, una posible respuesta ha sido planteada por Carroll et.al al mostrar que en el límite extremal la solución de agujero negro predice dos regiones totalmente desconectadas, una de ellas corresponde al agujero negro extremal y la otra a una geometría tipo AdS e interpretar esto como que la entropía de la solución extremal es cero mientras que la de la otra solución es diferente de cero [12]. Otra solution se da en teoría de cuerdas donde la entropía se calcula a partir de las cargas supersimétricas asociadas a la solución de agujero negro, este cálculo fue realizado por Strominger y Vafa [13], donde muestran que mientras el área asociada al horizonte de una solución extremal es
su entropía resulta ser
Recuperando la fórmula del cuarto del área, aquí Q H es la carga asociada a los estados de cuerda heterópicos y QF la carga eléctrica. La geometría de estas soluciones extremales y las cercanas a la extremalidad también han sido objeto de estudio por sus implicaciones en la unicidad de soluciones, análisis de estabilidad de solucione y aplicaciones en el contexto de la supersimetría [14].
III. Agujeros negros y teoría de la información
En el contexto de la información un agujero negro se asemeja bastante a un sistema termodinámico, en el cual, a diferencia de un sistema físico, como un cubo de azúcar, donde se requiere una infinidad de parámetros para tener un conocimiento completo, para un observador ubicado en el exterior de un agujero negro, este se presenta como un sistema relativamente simple. La descripción total del sistema está dada si se conocen los parámetros de masa, momentum angular y carga eléctrica (también en algunos casos se puede incluir la magnética) como se señaló en la sección A. Esta simplicidad representa tal vez la característica más fundamental de los agujeros negros. La emisión de ondas gravitacionales que acompaña a la formación del agujero barre la complejidad estructural de la materia, es decir, esta afeita al agujero negro (debido a esto se adopta el termino de no pelo) para solo ser identificado por su masa, momentum angular y carga eléctrica 9 El resto de información se pierde, aumentando asá la entropía.
Así, al considerar que gran cantidad de información se pierde tras del horizonte de eventos cuando el agujero negro se forma, se puede pensar en relacionar la entropía del agujero con esta información.
A. Bekenstein y el origen de la relación entropía-información
Desde el punto de vista de la teoría de la información, supongamos un sistema físico en el cual todo lo que es conocido acerca de la configuration interna de este es que el sistema puede ser encontrado en alguno de un número de estados con probabilidad Pn para el n - esimo estado. Se define la entropía
la cual mide la falta de información acerca de la configuration interna del sistema 10 Por tanto, se puede pensar en la información I que se puede tener acerca del sistema, tal que cuando S sea máxima I sea mínima y viceversa. De manera que se cumple
Definiendo el bit como la unidad convencional de información disponible cuando la respuesta a una pregunta de si o no se conoce con precisión se tiene que S = 0. De acuerdo con la expresión (16), un bit también es numericamente igual a la máxima entropía que puede estar asociada con la pregunta de si o no, es decir, la entropía cuando ninguna información se puede obtener acerca de la respuesta. Luego, por definición 1 bit= ln 2. Cuando se notó la analogía evidente entre entropía y área del horizonte de eventos no se sabía cómo relacionar esto matemáticamente a los agujeros negros. Bekenstein notando que información considerable se perdía tras del horizonte cuando se formaba el agujero, sugirió que la entropía del agujero podría estar relacionada con esta información. De esta manera se iniciaba el sentido físico de la analogía entre termodinámica y mecánica de los agujeros negros.
Así, al suponer que el área del agujero negro puede ser descrita en términos de pequenas celdas de área 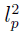 , siendo lp la longitud de Planck, y asociando a cada una de ellas un bit de información podemos expresar la entropía del agujero negro como:
, siendo lp la longitud de Planck, y asociando a cada una de ellas un bit de información podemos expresar la entropía del agujero negro como:
B. Hawking y el descubrimiento de la radiación de los agujeros negros
A mediados de los años setenta Stephen Hawking se encontraba investigando el comportamiento de la materia en las proximidades de un agujero negro con base en la mecánica cuántica, descubriendo que el agujero negro emitía partículas de manera uniforme, y que estás partículas tenían un espectro térmico [6]. La manera de entender la emisión desde el contexto de la mecánica cuántica, es que el espacio está lleno de pares de partículas y antipartículas "virtuales" que se materializan constantemente en parejas alejándose y acercándose para aniquilarse de nuevo entre ellas. La etiqueta de virtuales a diferencia de las reales, se basa en el hecho que estas no pueden observarse directamente. Sin embargo, pueden medirse sus efectos indirectos, y su existencia se ha confirmado por un pequeno corrimiento que se produce en el espectro de la luz de los atómos de hidrogeno excitados (efecto Lamb). En presencia de un agujero negro, un componente del par de partículas virtuales puede caer en el interior del mismo, dejando al otro componente sin pareja con la cual aniquilarse (figura 1). La partícula o antipartícula abandonada puede caer en el agujero después de su compañera, pero también puede escapar al infinito, donde aparecerá como radiación emitida por el agujero negro. Otra manera de ver el proceso de emisión es observar al componente de la pareja de partículas que cae en el agujero, supongamos por ejemplo la antipartícula, como si realmente fuera una partícula que estuviera viajando hacia atrás en el tiempo. De esta manera, la antipartícula que cae en el agujero puede observarse como una partícula que sale del agujero negro y viaja hacia atrás en el tiempo. Cuando la partícula alcanza el punto en el que la pareja partícula-antipartícula se materializo originalmente, se difunde por el campo gravitatorio y viaja en el sentido del tiempo. De esta manera, se ve como la mecánica cuántica ha permitido que una partícula escape desde el interior de un agujero negro, cosa que no es permitida en la mecánica clásica. Así desde el punto de vista cuántico las partículas pueden vencer una especie de potencial que las confina a permanecer dentro del agujero negro, esto es lo que se conoce como el fenómeno tunelamiento.
C. La paradoja de la pérdida de información
La paradoja es el planteamiento que la información no se conserva tanto en el regimen clásico como en el semiclásico. Desde que fue propuesta se ha buscado la manera de conservar la información en el régimen semiclásico, pero lo mías probables es que sólo se tenga conservation de información en el regimen netamente cuántico. Supongamos que lanzamos una revista a un agujero negro a un angulo definido, lo cual implica un aumento de masa del agujero debido a la masa de la revista y una modification de su momentum angular por el impulso angular de la revista. Suponiendo que la revista tiene carga elétrica el agujero modifica su carga en la misma cantidad. Así, desde el contexto clásico a medida que la revista desaparece en la singularidad la información de la revista se pierde para siempre puesto que nada escapa del agujero. Desde el punto de vista semiclásico a partir del descubrimiento de la radiación térmica de Hawking, se evidencia que no hay información que se pueda obtener, a parte de la temperatura del agujero (dada por 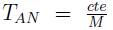 [1-4](1973)) la cual solo nos da la masa de la revista, lo que coincide con el tratamiento clásico, en donde de nuevo se pierde información. Así, un estado cuántico puro cae en el agujero y un estado cuántico mezclado es emitido, donde el cálculo semiclásico indica que un estado puro evoluciona a un estado cuántico mezclado. Lo anterior viola la unitariedad, una de las piedras angulares la mecánica cuántica. Por lo tanto, tenemos dos opciones:
[1-4](1973)) la cual solo nos da la masa de la revista, lo que coincide con el tratamiento clásico, en donde de nuevo se pierde información. Así, un estado cuántico puro cae en el agujero y un estado cuántico mezclado es emitido, donde el cálculo semiclásico indica que un estado puro evoluciona a un estado cuántico mezclado. Lo anterior viola la unitariedad, una de las piedras angulares la mecánica cuántica. Por lo tanto, tenemos dos opciones:
Aceptar como válido el resultado del cálculo semiclásico y renunciar a la unitariedad admitiendo pérdida de información.
Tratar de encontrar un cálculo totalmente cuántico donde la unitariedad se preserve y se admita la conservación de información.
Dentro de los defensores de la opción 1 encontramos a Hawking como su principal representante, y en la opción 2 se encuentran: la teoría de cuerdas, los modelos de probabilidad de tunelamiento y el modelo de la pared de fuego entre los más relevantes. En resumen, la paradoja de la pérdida de información se describe por la siguientes características [16]:
Violation de la evolución en el tiempo unitaria. II. Grandes valores para la entropía del agujero negro.
Lo que sucede con la entropía (información) después de la evaporación del agujero (como la radiación lleva solo una fracción de la entropía inicial).
Violation de leyes de conservación (conservación del número leptónico y bariónico).
D. La paradoja y sus "soluciones"
A la pregunta: ¿Se pierde la información en el proceso de evaporación de los agujeros negros?, se resaltan las siguientes soluciones:
1. Las soluciones de Preskill
Un primer conjunto de soluciones fue dado por Preskill las cuales se resumen a continuación [17].
■ La información se transmite por la radiación del agujero. Si se admite que la radiación del agujero no es totalmente térmica, lo cual se consigue sumando un espectro discreto adicional al espectro de cuerpo negro continuó, se podría tener un estado cuántico puro para la radiación emitida que posee la información con lo cual el agujero negro debe estar en un estado cuántico único. Luego si se consigue un análisis cuántico total, se debería encontrar la manera de enviar información en la radiación del agujero, asumiendo un modelo en el cual la radiación no es térmica. Este modelo debería explicar que la entropía de un agujero negro es el logaritmo del número de estado internos accesibles para un agujero de masa M, es decir, su temperatura.
■ La información se retiene por un agujero negro estable remanente. Cuando el agujero se evapora se hace cada vez mas pequeno. Cuando llega a la escala de Planck, las fluctuaciones cuánticas dominan y los cálculos semiclásicos ya no serían válidos. Luego, tal vez el agujero nunca se evapore completamente, lo cual implicaría que un remanente permanecería el cual llevaría toda la información del agujero. Sin embargo, aquí surge un problema. Debido a que un agujero puede tener cualquier masa desde un valor finito M 0 hasta el infinito, tanto el área del horizonte, como la entropía (y a su vez la información) es proporcional a la masa al cuadrado 11,el agujero remanente tendría que almacenar una cantidad grande de información lo que exigiría un número infinito de clases de remanentes lo cual es difícil de integrar en teoría cuántica de campos. Además el modelo de remanente no explicaría el origen de la entropía del agujero.
■ La información sale al final . En este punto se considera que la radiación en verdad es térmica para un tiempo muy grande y el agujero se evapora hasta que este alcanza la escala de Planck. En este instante el cálculo semiclásico diverge, haciendo que en lugar de crear un remanente estable, en este modelo, la información es emitida como correlaciones entre los cuantos térmicos emitidos antes y los cuantos térmicos emitidos al final. Sin embargo cuando se tiene un agujero negro muy masivo, este tiene bastante información almacenada, por lo que toma bastante tiempo emitir esta información. Así, se tiene una gran cantidad de posibilidades para agujeros remanentes de larga vida, lo que originaría los mismo problemas planteados en el párrafo anterior.
■ La información es codificada en el pelo cuántico . Desde el punto de vista de la teoría semiclásica se tiene que el exterior del horizonte es independiente de lo que ha colapsado en el horizonte, lo que significa que la radiación Hawking no esta correlacionada con el estado del cuerpo colapsante. Lo anterior significa que ninguna información se envia por la radiación térmica. Si la radiación lleva información, el agujero negro debe tener algún mecanismo que le permite conocer cómo y de que fue formado, y qué cuantos o partículas ha emitido en realidad. Luego, la idea es ver si se cumple el teorema de no pelo (sección A-II), un efecto cuántico de este teorema permitiría que el agujero recuerde mías información de la que se espera en primer lugar.
■ La información escapa a un universo bebé. Para este modelo, se tiene que la gravedad cuántica impide que el agujero negro produzca una verdadera singularidad, originando así un universo bebé cerrado en el cual toda la materia que cae dentro del agujero va dirigida a este universo junto con la información asociada. Para un observador en nuestro universo no hay conservación de la información puesto que nuestro universo estaría desconectado del universo bebé. Pero para un observador universal que ve ambos universos al mismo tiempo, la información se conserva. Sin embargo, en este punto aún no se conoce por qué mecanismo el agujero negro recuerda su estado inicial por el cual "sabe" como evaporarse.
De las soluciones propuestas por Preskill se puede concluir de manera parcial que si se acepta la pérdida de información, se necesita una mejor comprensión de lo que se entiende por pérdida de información. Se necesita una teoría cuántica de campos generalizada que sería la teoría cuántica de campos actual en el límite de bajas energías. Es decir, se necesita una teoría cuántica de la gravedad que preserve la unitariedad. Es aquí donde entra la teoría de cuerdas a lidiar con la paradoja.
2. La teoría de cuerdas
La teoría de cuerdas es una de las candidatas mías sería a convertirse en una teoría cuántica de la gravedad y unificar todas las fuerzas. Con el fin de tener una comprensión completa de los agujeros negros y los procesos físicos que tienen lugar en ellos, se necesita de una teoría cuántica de la gravedad. Por lo tanto, se debe esperar que la teoría de cuerdas reproduzca correctamente las características semiclásicas de los agujeros negros y que también solucione los problemas relacionados con su naturaleza térmica y la conservación de la información.
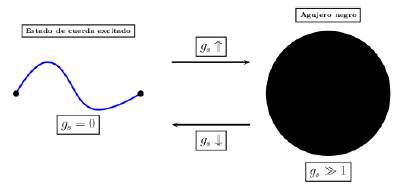
Una aproximación interesante para estudiar agujeros negros en teoría de cuerdas fue propuesta por Susskind en 1993 [18]. Partiendo del hecho de que la constante de acople de las cuerdas gs es una cantidad variable, se puede considerar un estado de cuerda libre altamente excitado (gs = 0). Si se incrementa el acoplamiento de la cuerda, la gravedad entrara en juego y la cuerda reducirá su tamaño debido a la relación que se establece entre la constante de Newton y la constante de acople de las cuerdas dada por 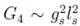 . Si la masa de la cuerda Ms es lo suficientemente grande, se debe esperar que a medida que se incrementa el acople, la longitud de la cuerda decrecería por debajo de su radio de Schwarschild, así se tiene la imagen de una cuerda como un agujero negro (figura 2). Si por el contrario, se parte de un agujero negro (gs >> 1) y se disminuye el acople, el radio del agujero negro r0 = 2G4Ma también disminuirá y eventualmente llegaría a ser mías pequeño que la longitud de la cuerda. En la imagen de Susskind se debe pensar en este estado final como un estado de cuerda altamente excitado.
. Si la masa de la cuerda Ms es lo suficientemente grande, se debe esperar que a medida que se incrementa el acople, la longitud de la cuerda decrecería por debajo de su radio de Schwarschild, así se tiene la imagen de una cuerda como un agujero negro (figura 2). Si por el contrario, se parte de un agujero negro (gs >> 1) y se disminuye el acople, el radio del agujero negro r0 = 2G4Ma también disminuirá y eventualmente llegaría a ser mías pequeño que la longitud de la cuerda. En la imagen de Susskind se debe pensar en este estado final como un estado de cuerda altamente excitado.
Posteriormente en 1996 [19], Gary Horowitz en un intento por ver donde está la información del cuerpo colapsado pone de manifiesto que la información del agujero negro no está localizada cerca del horizonte o cerca a la singularidad, sino que abarca todo el espacio entre ellas. Así, en 1997 Horowitz muestra en el contexto de la teoría de cuerdas que se puede identificar y contar los estados cuánticos asociados con los agujeros negros. De esta manera, la radiación Hawking puede preservar su unitariedad en lugar de ser térmica, incluso en el régimen de bajas energías tanto para agujeros negros extremales y no extremales (sección II-A) [20]. Con lo anterior y buscando la conservación de la energía, el agujero se transforma en una cuerda que lleva toda la información del cuerpo colapsante que lo originó y de todo lo que ha caído en este, y por interacción de cuerdas la información sería devuelta a nuestro universo.
En 1997 Marshkevich [16] propuso un modelo que preserva la conservación de los números bariónicos y leptíonicos, contrario a lo que fue planteado originalmente por Hawking, donde sugirió un nuevo canal de pérdida de energía en el cual se plantea una disminución del número de partículas conservadas y no conservadas de la no conservación de los números bariónicos y leptónicos. Más adelante de nuevo Horowitz en el 2003 [21], sugiere que se necesita imponer una condition de frontera al estado final en la singularidad del agujero, en lugar de cambiar toda la mecánica cuántica, para así preservar la unitariedad.
Una visión más optimista del problema, ha surgido en los últimos años en el contexto de las dualidades establecidas en teorías de cuerdas y el principio holográfico como se expone a continuación.
3. El principio holográfico
Basados en la idea de complementariedad de Bohr, que acompañó el descubrimiento de la mecánica cuántica con la dualidad onda-partícula para la luz, Susskind, Thorlacius y Uglum enunciaron un principio según el cual ningún observador ve una violación de las leyes de la naturaleza denominado "complementariedad de horizontes" o de manera divulgativa complementariedad de agujero negro [22]. La complementariedad del agujero negro es un nuevo tipo de complementariedad que resulta de combinar la mecánica cuántica con la gravedad. Esta establece que no hay una única respuesta a la pregunta ¿quién tiene razón: el observador que permanece fuera del agujero negro el cual ve que toda la información se irradía desde el horizonte, o el observador que lo cruza con los bits que se dirigen hacia la singularidad?. Cada uno tiene razón desde su propio marco de referencia, es decir, son descripciones complementarias de dos experimentos diferentes.
Para ilustrar lo anterior consideremos la trayectoria de una partícula que cae radialmente desde un punto r0 > rs. De la metrica de Schwarzschild (4), para una partícula en movimiento radial se tiene
La ecuación para la geodésica radial está dada por12
si se considera una partícula de prueba que se deja caer libremente desde un punto r = R, la ecuación de movimiento radial toma la forma
al integrarse en forma paramétrica (28) se obtiene el tiempo propio finito dado por
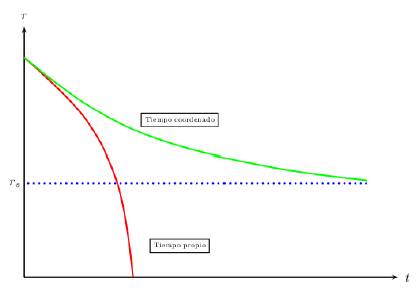
luego, para un reloj que viaja con la partícula, esta llega a la singularidad en un tiempo finito. Ahora el tiempo coordenado, que corresponde al medido por un observador situado en una región lejos de la masa (observador asintótico) esta dado por
con K una constante. Así, se tiene que la partícula requiere de un tiempo infinito (el fenómeno de dilatation temporal) para llegar a r = rs para el observador asintótico (figura 3). Retomando la complementariedad, por un lado, el experimentador se queda fuera del agujero. De manera heurística puede arrojar cosas dentro (como la revista de la sección II-C), recoger fotones cuando salen, dejar caer sondas hasta una distancia por encima del horizonte, y observar los efectos de las trayectorias de las partículas que pasan cerca del agujero. De otro lado, el experimentador prepara su laboratorio, y luego con laboratorio y todo, se lanza al agujero cruzando el horizonte mientras realiza el experimento.
Las descripciones complementarias de los dos experimentos son tan radicalmente diferentes que dificilmente parece creíble que ambas pudieran ser correctas. El observador externo (mide el tiempo coordenado) ve que la materia cae hacia el horizonte, se frena y queda suspendida exactamente por encima del mismo. La temperatura inmediatamente por encima del horizonte es elevada y reduce toda la materia a partículas, que finalmente son radiadas hacia el exterior. Es decir, el observador externo, que controla al observador en caída, lo ve vaporizado y reemitido como radiación Hawking. En cambio, el observador en caída libre (mide tiempo propio) atraviesa el horizonte sin siquiera notarlo ni detectar ninguna temperatura, es decir, ninguna incomodidad hasta que llega al corazón del agujero negro donde las fuerzas de marea se hacen finalmente tan fuertes que lo destruyen. Así se tiene que para el observador asintótico, el agujero negro consiste en un enorme vertedero de materia plana congelada en su horizonte. Lo anterior es un ejemplo del holograma óptico usual en el cual una superficie bidimensional codifica información sobre la forma tridimensional de un objeto. Una idea parecida fue propuesta hace ya algunos años por G. 't Hooft y L. Susskind [23], que sugirieron que el número de grados de libertad que describen una región en una teoría de gravedad es proporcional al íarea de esa región recordando la relación entre la entropía y el área del agujero negro.
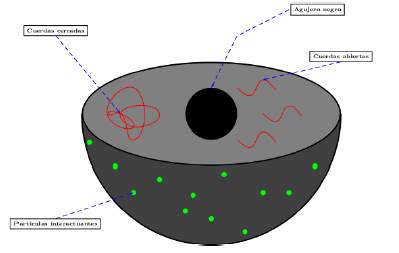
Maldacena encontro una realización explícita de esta propuesta en la teoría de cuerdas. Pudo describir el interior de un espacio-tiempo particular (llamado Anti-de Sitter) en términos de una teoría en la frontera de ese espacio-tiempo, que tiene una dimensión menos 13 Según esta idea, las partículas que viven en el borde del espacio-tiempo describen un objeto que está en el interior. Los agujeros negros en el interior se describen mediante un gran número de partículas en el borde. La física gravitatoria en el interior, cuando resulta muy complicada, se puede describir de manera alternativa mediante partículas interactuantes en el borde (figura 4). La teoría de la frontera es una teoría de partículas relativamente sencilla. Entonces, hay dos descripciones equivalentes de la misma física. Cuando una de ellas resulta incapaz de resolver un problema, se apela a la otra, que permite abordar las preguntas sin respuesta en la primera formulación. Una teoría de partículas relativamente sencilla en el borde puede describir objetos muy complicados del interior. El espacio-tiempo emerge dinámicamente en este esquema, a partir de la interacción de las partículas que viven en la frontera. Y en esta formulation no hay perdida de información porque la teoría cuántica de las partículas del borde es una teoría unitaria que respeta los postulados de la mecánica cuántica.
4. Pared de Fuego
Al seguir el principio de complementariedad planteado en la sección anterior, Susskind et.al se dieron cuenta que la información podía ser codificada en el estado cuántico de la radiación en su conjunto si las partículas llegasen a tener estados entrelazados, de tal forma que las mediciones llevadas a cabo sobre una de ellas influiría inmediatamente en su pareja sin importar lo lejos que se encuentren [25]. Sin embargo, Polchinski et.al, se percataron de que si esto sucediese se tendría que clonar información debido a que el principio de complementariedad plantea dos enredamientos: el de las partículas emitidas con las partículas que caen en el agujero, y la de las partículas emitidas con toda la radiación Hawking [26]. Para solucionar esta dificultad, se decide eliminar una de las posibles relaciones de enredamiento que plantea Susskind por el principio de complementariedad. Al romper este enredamiento se libera una gran cantidad de energía, que el horizonte de eventos se convertiría en un anillo de fuego en el cual cualquier objeto que lo atraviese sería quemado, es decir nada entra al agujero y toda la información quedaría incinerada en su horizonte. Lo anterior confirma de nuevo el principio holográfico. Luego, para salvaguardar el principio de equivalencia todo observador en caída libre hacia un agujero negro debe encontrar una pared de fuego (firewall) que lo destruye evitando que realice mediciones al interior de este 14 Lo anterior involucra los siguientes principios físicos:
Principio de complementariedad para agujeros negros (sección 3-D-III)
Principio de equivalencia
Imposibilidad de clonación de un estado cuántico
La evolución de un agujero negro puede darse en términos de la emisión de entropía, así que puede caracterizarse por un tiempo medio conocido como el tiempo de Page al cabo del cual un agujero negro ha emitido la mitad de su entropía inicial [27]. Esto genera tres regiones diferentes donde los modos (estados asociados a las partículas emitidas) emitidos pueden estar:
Al analizar las tres regiones de acuerdo con Susskind se encuentra que [25]:
■ Un observador lejano encuentra enredamiento entre los modos lejos del horizonte y los que están fuera
■ Un observador en caída libre encuentra enredamiento entre las partículas fuera del horizonte y las del interior.
Lo anterior implica que un conjunto de modos esta clonado para que ambos observadores puedan verlo, violando así el principio (c). También desde la perspectiva del observador lejano es posible el transporte de enredamiento debido a la emisión por parte del agujero negro.
En términos de complementariedad las dos versiones deberían ser correctas, sin embargo, como se ve, esto rompe principios básicos y fundamentales de la teoría de la relatividad general y la mecánica cuántica, y para los teóricos que analizan este problema este principio es inquebrantable debido a que renunciar a él implicaría renunciar a uno de los fundamentos del trabajo de Maldacena (sección 3-D-III). Al final, las preguntas más simple que surgen son: ¿Esta mal aplicada la mecánica cuántica para los dos tipos de observadores?, ¿el principio de equivalencia se rompe debido a efectos termicos?, y ¿es de verdad la complementariedad un principio básico de la física de lo agujeros negros?.
5. Probabilidad de tunelamiento
Como Kraus y Wilczek demostraron de una idea original de Parikh [28-30], si el back-reacción de la radiación Hawking a la geometría de fondo se toma en cuenta, la probabilidad de que un agujero negro de Schwarzschild de masa inicial M emitiendo un quantum de energía ω esta dada por
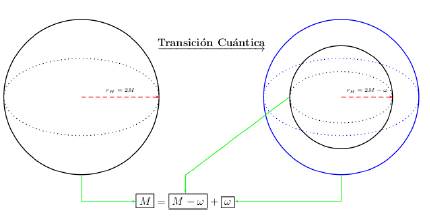
El sistema físico contempla un agujero negro de Schwarzschild de masa M supermasivo, donde se modela la radiación Hawking como un proceso de evaporación por efectos de tunelamiento cuántico (sección B-III), y además se considera la emisión de partículas escalares de energía ω, descritas como cascarones con simetría esférica. La figura 5 esquematiza el proceso para la primera emisión: en la parte izquierda de la figura se presenta un agujero de Schwarzschild de masa M y radio 2M (ecuación 4). En la parte derecha se representa la emisión de un cascarían ω con simetría esférica y radio exterior re, donde la masa debido al proceso de emisión se reduce a M - ω, y su radio a 2(M - ω).
No obstante de acuerdo con Parikh, este resultado no muestra correlaciones entre emisiones [31]
En general, se define el coeficiente de correlación C(α,b) entre dos eventos α y b como
donde P(a, b) es la probabilidad conjunta, y P(b) = Σa P(a, b). La probabilidad condicional de b dado que α a ocurrido es
Luego de acuerdo con Parikh, (24) no muestra las correlaciones
Zhang et.al [32] han señalado recientemente que la desviación de la termalidad pura derivada por Parikh y Wilczek muestra una correlación entre las emisiones. Ellos encontraron que la ultima ecuación de (24) no es correcta y debe ser reemplazada por la probabilidad condicional. Es decir, que la radiación Hawking correlaciona eventos sucesivos, lo cual implica que la recuperación de información es posible. Por lo tanto, se puede expresar (23) como
Asi, de la probabilidad de tunelamiento (23) se tiene
Además
Lo anterior muestra que todas la posibles combinaciones de emisiones de energía P(E1, E2,...En) son igualmente probables. La probabilidad de tunelamiento resultante es independiente de cómo cada emisión infinitesimal (que es pequeña comparada con la energía de radiación total E) son diferentes son diferentes la una de la otra. Luego si se interpreta la entropía del agujero negro microscópicamente como todas las posibles combinaciones de energía emitida, entonces de la ecuación (15) se tiene
donde se ha usado el hecho de que todas las posibles combinaciones de emisión de energía P(E1, E2...En) son igualmente probables. La ecuación (33) muestra que la entropía llevada por la evaporación es la misma que la entropía del agujero negro. De la ecuación (33) se tiene
Esta transition de probabilidad equivale a un factor estadístico 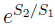 , el cual es igual a la razón del numero de estados final e inicial. Luego, los grados de libertad en la radiación emitida igualan la capacidad de información del agujero, como medidos por la entropía Bekenstein-Hawking. Por lo tanto se tiene una evidencia, fundamentada sobre la base del conteo, de que la unitariedad se preserva y que la información se puede recuperar. Un construcción completa de este modelo, la justification de los detalles técnicos (asignación de las probabilidades) y una discusión completa puede encontrarse en [33].
, el cual es igual a la razón del numero de estados final e inicial. Luego, los grados de libertad en la radiación emitida igualan la capacidad de información del agujero, como medidos por la entropía Bekenstein-Hawking. Por lo tanto se tiene una evidencia, fundamentada sobre la base del conteo, de que la unitariedad se preserva y que la información se puede recuperar. Un construcción completa de este modelo, la justification de los detalles técnicos (asignación de las probabilidades) y una discusión completa puede encontrarse en [33].
IV. Conclusiones
Del trabajo de Hawking se evidencia que si se siguen los principios básicos de la relatividad general y la mecánica cuántica hasta el final se concluye que un estado puro evoluciona en un estado mezclado, lo cual viola los principios de la mecánica cuántica. Es decir, podemos formar un agujero negro de distintas maneras, pero siempre se evapora de la misma forma, aunque los principios de la mecánica cuántica impliquen que debería haber una descripción precisa de los agujeros negros y que no todos los agujeros negros deberían evaporarse dejando los mismos residuos, indistinguibles unos de otros. Debería haber diferencias sutiles en lo que queda cuando el agujero negro se evaporó, según cómo se formó. Pero Hawking mostró que la evaporación del agujero negro es un fenómeno diferente de los procesos físicos ordinarios; la información que cae detrás del horizonte de eventos de un agujero negro se perderá para siempre, permaneciendo oculta aún después de que el agujero negro se evapore completamente y desaparezca. Durante cerca de 30 años Hawking afirmó que los agujeros negros pueden destruir información cuántica. Este tipo de destrucción de información viola los principios de la mecánica cuántica. Por lo tanto Hawking sugirió que esta teoría debía ser abandonada o por lo menos modificada lo cual era una posición revolucionaria. Pero en julio de 2004 Hawking presentó esquematicamente un argumento que, según dijo, sustenta la conclusión de que no hay pérdida de información [34]. Su propuesta no satisfactoria para la mayoría de la comunidad de físicos está fundamentada en la idea de suma de historias de Feynman sobre los múltiples universos en los cuales un agujero destruye y no destruye información.
Asó, a traves de los trabajos de Preskill hasta Parikh y Wilczek se evidencia que la solución a la pregunta ¿Se pierde la información en el proceso de evaporación de los agujeros negros? es una cuestión que aún se puede tomar como no resuelta, debido a que no se tiene un conocimiento claro de lo que sería una teoría cuántica de la gravedad.
Debido la dependencia de los detalles técnicos los resultados obtenidos por la teoría de cuerdas, no son claros. Al apelar a una aparente dualidad impuesta por el régimen de acoplamiento débil-fuerte y viceversa, se pierde toda signification en cuanto a la física del sistema termodinámico a estudiar, es decir, el agujero negro y su termodinámica asociada. La descripción y no localización de los grados de libertad (relacionados con la entropía del agujero) hace que la teoría no sea universal y dependa del modelo sobre el cual se obtienen los resultados. Lo anterior es una consecuencia de que la aparente dualidad está apoyada por un principio holográfico subyacente que no está comprobado y que se postula como principio universal.
El modelo de la pared de fuego señala que la complementariedad sobre la cual se fundamenta la holografía traía consigo una complicación más y es la violación del principio de equivalencia. Luego, si salvaguardamos el principio de equivalencia, el principio de complementariedad no se cumple de manera total y el trabajo de Maldacena y todo lo que implican las dualidades de la teoría de cuerdas se vendría abajo. Por lo tanto se llega a un punto en el cual tal vez se pueda concluir que Hawking desde el principio tenía razón. Sin embargo, la comunidad científica apuesta por el trabajo de Maldacena y todas sus implicaciones [35].
Tal vez una solución no tan ostentosa y más viable sea la que se obtiene con el modelo de probabilidad de tunelamiento de Parikh-Wilczek. Este modelo plantea la idea de correlación de estados desde un modelo de probabilidad, es decir, se presenta un método de solución para un problema de pérdida de información apoyado en un cálculo de probabilidad. La manera como se obtiene el resultado (32) evidencia que el modelo de probabilidad da cuenta del sistema físico a estudiar, lo que no sucede con los demás. Sin embargo, debe señalarse que este modelo plantea la correlación de emisión de partículas y no de estados. Pero es un buen punto de partida.
En enero del 2017 Hawking, Perry y Strominger [36] publicaron un artículo en el cual argumentan que es posible dar cuenta de la pérdida de información si tenemos en cuenta las supertraslaciones definidas a traves del grupo BMS [37,38]. Sin embargo el artículo no es concluyente y se espera más trabajo en esta línea.