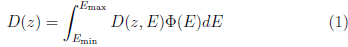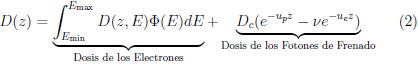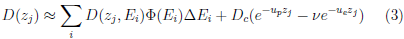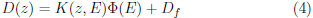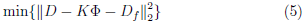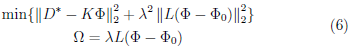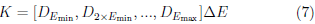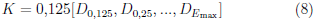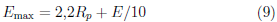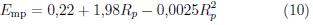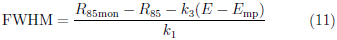Introducción

El conocimiento del haz clinico de radiación es esencial en dosimetría ^[1], en la planificación del tratamiento ^[1,2], en garantía de calidad, en el diseno de un acelerador lineal ^[3] y en simulaciones realistas del haz ^[4]. La planificación del tratamiento del cáncer puede ser elaborada correctamente solo si las características del haz son conocidas. La calidad del haz influye tanto en los efectos físicos, químicos y radiobiologicos como en la respuesta de varios detectores ^[3].

Los haces clínicos de electrones están constituidos por una mezcla de electrones primarios, electrones secundarios y fotones contaminantes de frenado ^[5]. Las interacciones inelósticas de los electrones primarios del haz con las estructuras internas del cabezal del acelerador dan origen a fotones de frenado y electrones secundarios, mientras que interacciones elásticas producen dispersión angular de algunos de los electrones que impactan en la superficie del fantoma de agua ^[5-7].

El espectro de energía y la distribución angular de los electrones así como la dosis de los fotones contaminantes son las características más importantes de un haz clínico de electrones ^[1,3,8]. El componente mías crítico para cualquier modelo de haz de electrones en radioterapia, cuyo propósito sea el cálculo de la dosis, es el espectro de energía ^[8], puesto que afecta significativamente el patrón de la distribución de dosis ^[9,10].

Existen tres maneras para determinar el espectro de energía de un haz de electrones: I) Simulación del cabezal del acelerador por vía el metodo Monte Carlo. A pesar de ser un metodo exacto ^[11], no es comúnmente utilizado en la clínica dado que exige un conocimiento preciso de la geometría y de la composición de los componentes del cabezal del acelerador; un alto nivel de manejo de Monte Carlo y mucho tiempo para generar el espacio de fases ^[9]. II) La medición directa consiste en la determinación experimental del espectro a partir de aparatos como el espectrómetro magnético de electrones ^[4,12]. Si bien es un abordaje exacto ^[13], tampoco suele usarse en la clínica ^[11] dada la complejidad del proceso de medición ^[9]. III) La reconstrucción inversa es un abordaje práctico, simple y confiable que deriva el espectro de energía a partir de distribuciones de dosis utilizando un apropiado modelo matemático ^[6,14]. Su fundamento consiste en que mucha de la información sobre el espectro de energía se encuentra envuelta en la distribución de dosis ^[6]. Pese a no ser el estándar de oro, es considerado como un método mías atractivo pues: a) no necesita de un equipo suplementario (medición directa) o del conocimiento exacto de la geometría y composición de las estructuras del cabezal (simulación de la fuente); b) todos los equipos que miden distribución de dosis están disponibles en cualquier centro de radioterapia y c) es computacionalmente rápido ^[9].

La reconstrucción inversa requiere resolver limitaciones matemáticas y físicas para producir un resultado útil y confiable. Las limitaciones físicas se asocian a la determinación de los fotones contaminantes y la dispersión angular. Las limitaciones matemáticas se relacionan con el mal condicionamiento del modelo matemático ^[9].

En este trabajo se propone reconstruir inversamente el espectro de energía de un haz clínico de electrones usando un criterio estricto de aceptación del índice gamma ^[15]. Por tanto, será utilizado el metodo de regularización de Tikhonov a fin de superar el mal condicionamiento de la ecuación integral de Fredholm de primer tipo. Se hará uso del código PENELOPE 2008 ^[16] para simular las distribuciones de dosis monoenergéticas y aquellas de los espectros reconstruidos (distribuciones de dosis reconstruidas), suponiendo una incidencia divergente del haz de electrones sobre la superficie del fantoma.

Materiales y Métodos

La reconstrucción inversa del espectro de energía de electrones incidente en la superficie del fantoma de agua, Φ(Ε), se basa en la solución numérica de la ecuación integral de Fredholm de primer tipo,

donde D(z) es la distribución o porcentaje de dosis en profundidad (PDP) medida en el eje central y D(z,E) es la matriz de distribuciones de dosis en profundidad del eje central para haces monoenergéticos de energía E variando entre la energía mínima E _min y la energía maxima del haz E _max.

Dado que todo haz clínico de electrones posee cierta cantidad de fotones de frenado, producidos antes y después de colisionar con la superficie del fantoma de agua, la Ec. 1 debe ser modificada, adicionando la dosis de los fotones de frenado modelada mediante la fórmula semiempírica de Brahme & Svensson ^[17],

en que D _c es una constante de normalización, u _p es el coeficiente de atenuación de los fotones primarios y dispersados de alta energía, u_e es el coeficiente de atenuación de los electrones secundarios generados por los fotones primarios y de los fotones de baja energía y ν es una constante relacionada con la dosis superficial.

Discretizando la Ec. 2 en la profundidad de medición de la distribución de dosis, z, se tiene que,

donde i = [1, 2, ...n] es el i-esimo haz monoenergetico de energía E _i; j = [1, 2, ...m] es la j-esima caja en que el vector profundidad es seccionada ubicada a la profundidad z _j y ∆E _i es el i-esimo intervalo de energía entre dos haces monoenergéticos consecutivos E _i y E _i+1.

Así, la Ec. 3 puede ser reescrita como un sistema lineal de ecuaciones,

donde K = D(z, E)∆E es la matriz kernel y D _f es la dosis de los fotones de frenado. Dimensionalmente, K Є ℝ ^mxn , D(z) Є ℝ ^m , Φ Є ℝⁿ y D _f Є ℝ^m.

Como la ecuación integral de Fredholm de primer tipo, representada por la Ec. 1, es generalmente mal definida ^[6,18], la Ec. 4 derivada de ella, también lo será. Usualmente, la Ec. 1 es mal definida por ser mal condicionada. El mal condicionamiento de un problema significa que su solución es extremadamente sensible a los errores incluidos en los datos de entrada ^[19]. Por esta razón, los métodos algebraicos comunes no son capaces de resolver adecuadamente problemas mal definidos como los representados por la Ec. 1 ^[6].

Para corregir el mal condicionamiento de la Ec. 4, sería aplicado el metodo de regularización de Phillips-Tikhonov ^[6,20], más conocido como regularización de Tikhonov ^[21].

Este método de regularización tiene por objeto transformar la ecuación integral de primer tipo (mal definida) en la ecuación integral de segundo tipo, (bien definida) ^[20], pretendiendo amortiguar los errores contenidos en los datos de entrada ^[22] y así alcanzar una solución útil y estable.

Con esto, la regularización de Tikhonov, en vez de minimizar la norma euclidiana de la Ec. 3,

propone la minimización de la Ec. 6 adicionando una función de restricción, Ω, a la Ec. 5 tal que,

donde la dosis de los electrones es D* = D - D _f .El parametro de regularización, λ, permite un balance entre el tamaño de las dos normas euclidianas. La matriz de regularización, L, es una matriz de operadores derivada y Φ_ο es la tentativa inicial de solución del espectro. La matriz L Є ℝ ^(n-d)xn, donde d Є ℕ N es el orden del operador derivada. La función Ω amortigua las fluctuaciones en Φ debidas a los errores introducidos en K y D a través de una elección apropiada de λ y L ^[23].

La minimización de la Ec. 5 requiere del conocimiento previo de las variables involucradas, a fin de posibilitar el hallazgo de Φ. Para ello, se describirá la forma en que D, K, D _f , λ, L y Φο son determinados.

La metodologia de minimización es descrita como sigue:

Regularmente, el valor de E_min coincide con el de ΔΕ, cuyo valor fue establecido en 0,125 MeV, de modo que,

El valor de E_max es aproximado como siendo una función del valor de la energía nominal de haz, Ε, y del rango práctico de D, R_p, así,

con R _p localizado, aproximadamente, a la profundidad del 10% de D ^[24].

Los haces monoenergéticos fueron modelados como siendo una fuente puntual de haz divergente ubicada 100 cm encima del fantoma de agua, dibujando un campo cuadrado de 10 x 10 cm² en la superficie del mismo. El código Monte Carlo usado en la simulación de los haces fue PENELOPE 2008. El fantoma de agua fue supuesto como siendo un cubo de 20 x 20 x 15 cm³.

con anchura de pico (FWHM) encontrada a partir de la expresión general del rango terapéutico de un haz degradado [17], es decir,

donde k ₁ y k ₃ son constantes, R _85mon es el rango terapeutico de la distribución de dosis en profundidad correspondiente al haz monoenergetico de energía nominal de 6 MeV y R ₈₅ es el rango terapeutico de D*.

Una vez descifrado el espectro de energía, se utiliza PENELOPE para encontrar la distribución de dosis del eje central asociada, bajo las mismas condiciones de irradiación de los haces monoenergéticos. De este modo, la distribución de dosis reconstruida es comparada con la distribución de dosis medida, mediante el índice gamma. El criterio clínico del índice gamma exigido para aprobar la distribución de dosis reconstruida es tal que el 95 % de los puntos de la distribución de dosis reconstruida queden dentro de una distancia de 1 %/1 mm respecto de la distribución de dosis medida. El índice gamma se computa mediante la función calcgamma desarrollada por Geurts ^[25].

Los cálculos involucrados en el proceso de reconstrucción fueron realizados con MATLAB®2015a (Microsoft Windows 10 Home, CPU: 2.3 GHz, RAM: 4 Gb). El tiempo de cálculo conjunto del espectro y la dosis de los fotones de frenado fue menor a 20 s.

Resultados y Discusión

En la Fig. 1 se muestra el espectro de energía de electrones reconstruido utilizando el valor del parámetro de regularización óptimo dado por l_curve.

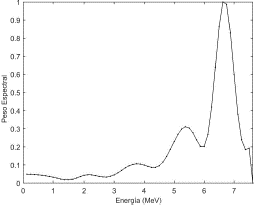
Figura 1 Espectro de energía de electrones en la superficie del fantoma. Energía nominal del haz de electrones, E = 6 MeV; orden de la matriz de regularización, d = 1 y parametro de regularización, λ = 0,039. 

El patrón del espectro de energía de un haz de electrones consiste en una amplia región de baja energía y poca ponderación seguida por una corta región de pico altamente ponderada, centrada en la energía maíz probable.

El espectro de energía de la Fig. 1 muestra las fluctuaciones propias del mal condicionamiento del problema. Reflejando asimismo, que el parámetro de regularización óptimo no consigue amortiguar tales desperfectos.

La energía mas probable del espectro de energía se localizo en 6,625 MeV mientras que la anchura a media altura del pico fue de 0,76 MeV.

En la Fig. 2 se ilustra el espectro de energía de electrones reconstruido utilizando un valor del parámetro de regularización 10 veces superior al anterior.

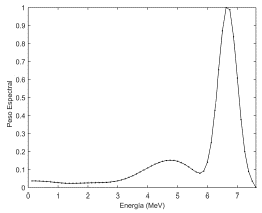
Figura 2 Espectro de energia de electrones en la superficie del fantoma. Energia nominal del haz de electrones, E = 6 MeV; orden de la matriz de regularización, d = 1 y parametro de regularizacion, λ = 0,39. 

Respecto al espectro de energía de la Fig. 1, el espectro de la Fig. 2 mantiene el valor de la energía mías probable. Contrariamente, el valor de la anchura de pico cambió levemente para 0,77 MeV.

Como era de esperarse, el cambio mas significativo es el amortiguamiento de las fluctuaciones o irregularidades en el espectro de energía de la Fig. 2 respecto al de la Fig. 1. Ciertamente, ello obedece al aumento en el valor del parámetro de regularización que hace las veces de filtro.

Esto demuestra que el parámetro de regularización óptimo dado por l_curve no siempre es adecuado para conseguir una solución útil. De hecho, en la practica, la escogencia del parametro de regularización optimo suele darse mediante un proceso de prueba y error ^[21], tal como se ha realizado.

Un factor del espectro que auxilia en la evaluación de la reconstrucción es el cociente entre la anchura de pico y la energía media del pico, FWHM/E_med, con E_med = 2,33R₅₀ y siendo R50 la profundidad a la cual la distribución de dosis cae al 50 % de su máximo valor.

Björk et al ^{[ 11]}, reportaron valores de dicho cociente entre 8% y 22 % para varias energías de un acelerador lineal Phillips SL25. Entre tanto, Deng et al ^{[ 10]} reportaron valores entre 5.3% y 3.9% para energías entre 6 y 20 MeV de la simulación Monte Carlo de un acelerador lineal Varian Clinac 2100C.

Nosotros hemos encontrado cocientes de 8,35 % y 8,45 % para los espectros de la Fig. 1 y Fig. 2, respectivamente. Luego, el cociente para ambos espectros de 6 MeV es consistente con la franja de Bjöork et al ^{[ 11]}. Sin embargo, sus valores sobreestiman los reportados por Deng et al _[10] .

Es posible que el cociente FWHM/E_med sea exclusivamente dependiente del acelerador dado que la energía media y la anchura de pico dependen fuertemente de las características intrínsecas del mismo (tipo de onda aceleradora, metodo de inyección, afinamiento de la guía de onda, geometría y composición de estructuras modificadoras, etc.) ^[11]. El tamaño del intervalo de energía en la reconstrucción también incide en el valor del factor ^[10].

En la Fig. 3 se muestra la dosis de los fotones contaminantes para el haz de energía nominal de 6 MeV. Su forma es parecida a la de haces de fotones de rayos-X de alta energía: una región de build-up seguida por una región de caída lenta.

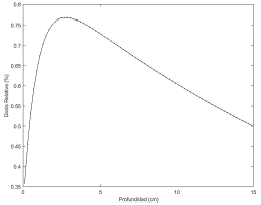
Figura 3 Dosis de los fotones de frenado relativa al valor máximo de la distribución de dosis en profundidad (electrones + fotones) del haz de energía nominal de 6 MeV. 

Los valores de los parámetros de reconstrucción de la dosis de los fotones de frenado fueron D _c = 0,009, up = 0,038 cm^-1, ν = 0,659 y ue = 1,102 cm^-1. El valor medio de la dosis de los fotones fue de 1.1 %. Entre tanto, el valor máximo de la dosis fue de 1,34 %, a 2,5 cm de profundidad.

En la Fig. 1 también se nota que la región de caída de la dosis de los fotones de frenado es la que mías aporta a la distribución de dosis en profundidad D, particularmente, mías allá del rango práctico. Por esta razon, a la parte final de la distribución de dosis en profundidad se le llama región de bremmstralung ^[12]. En efecto, en un artículo anterior ^[26], aprovechamos el método de extrapolación lineal de la región de bremmstralung para determinar la dosis de los fotones contaminantes.

Como el cálculo de la dosis de los fotones de frenado no depende de la función de restricción, Ω, su valor permanece invariable para los espectros de la Fig. 1 y Fig. 2.

En la Fig. 4 se presenta la comparación entre la PDP reconstruida a partir de la simulación Monte Carlo del espectro reconstruido, utilizando el parámetro de regularización óptimo, y la PDP medida en el fantoma de agua.

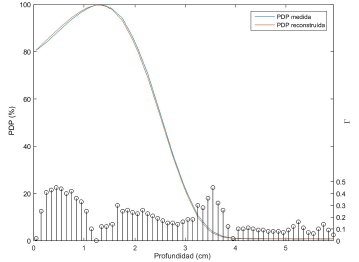
Figura 4 Comparación entre la PDP reconstruida y la PDP medida utilizando el índice gamma, Γ. La PDP reconstruida se obtuvo por simulación Monte Carlo del espectro de energia reconstruido a partir del parametro de regularización óptimo dado por la funcion l_ curve.  

Se observa que el índice gamma, para todos los puntos de la PDP reconstruida con respecto a la medida, fue menor a 1 lo que se traduce en que el porcentaje de aceptación de la PDP reconstruida es 100%, considerando Γ = 1%/1mm. Las mayores discrepancias suceden en el final de la región de caída de la PDP y en la región de build-up cerca a la superficie, donde Γ alcanza valores alrededor de 0,4.

En la Fig. 5 se compara la PDP reconstruida, utilizando el parametro de regularizacion elegido manualmente, y la PDP medida en el fantoma de agua.

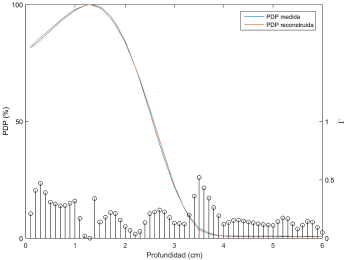
Figura 5 Comparación entre la PDP reconstruida y la PDP medida utilizando el índice gamma, Γ. La PDP reconstruida se obtuvo por simulación Monte Carlo del espectro de energia reconstruido a partir del parametro de regularizacion escogido manualmente como siendo 10 veces el valor del parametro optimo. 

En la Fig. 5, se percibe que todos los puntos evaluados de la PDP reconstruida están dentro del criterio de aceptación gamma previamente establecido (i.e., >95% en 1 %/1 mm), ya que en cada uno de ellos Γ < 1.

A pesar de que el espectro de energía de la Fig. 2 esta más regularizado (suavizado) que su par de la Fig. 1, el efecto clínico de ambos en el fantoma, expresado en la PDP reconstruida, es bastante similar. En efecto, esto se refleja en que el porcentaje de aprobación, en ambos casos, fue 100%.

Las mayores diferencias entre las PDP de la Fig. 5 se encuentran en el final de la región de caída. Las discrepancias en la región superficial son menores a las encontradas en la Fig. 4.

Se destaca que la coincidencia en la regkín de la cola de bremsstrahlung entre las PDP, para ambos espectros reconstruidos, es excelente dado que Γ ≤ 0,2 en todos los puntos evaluados. Esto indica idoneidad en la reconstrucción de la dosis de los fotones de frenado.

No obstante el resultado de ambos espectros reconstruidos haya sido el mismo en términos del índice gamma, el espectro de energía de la Fig. 2 tiene mayor sentido físico pues la apariencia usual de cualquier espectro es continua o suave. De hecho, el error medio absoluto entre las PDP de la Fig. 4 fue de 0,52 % mientras el asociado a la Fig. 5 fue de 0,41 %, indicando un mejor ajuste con la PDP correspondiente al espectro de la Fig. 2.

Se ha demostrado que el método de regularización es efectivo para reconstruir el espectro de energía y la dosis de los fotones de frenado de un haz clínico de electrones de 6 MeV.

Conclusiones

La reconstrucción inversa del espectro de energía de un haz clínico de electrones es un problema mal definido ya que perturbaciones en la distribución de dosis clínica y las distribuciones de dosis monoenergéticas pueden provocar fluctuaciones indeseadas en el espectro.

La regularización de Tikhonov se mostro efectiva para reconstruir el espectro de energía de electrones a partir de distribuciones de dosis en profundidad bajo un criterio de índice gamma bastante restrictivo como 1 %/1mm. Además, se constató que no siempre el parámetro de regularización óptimo produce el mejor resultado, siendo a menudo, recomendable, hacer una escogencia manual del mismo.

La rapidez y efectividad del método de reconstrucción inversa fundamentado en la regularización de Tikhonov hace de este una herramienta interesante para simulaciones realistas en radioterapia 1D.