Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.20 no.35 Bogotá July/Dec. 2001
EL PROBLEMA DE LA VARIACIÓN DE LOS PRECIOS: LOS LÍMITES DE LA TEORÍA WALRASIANA
Carlo Benetti *
* Universidad de París X-Nanterre (FORUM-CAESAR) 200, Avenue de la République, 92001, Nanterre Cedex, Una primera versión de este artículo se ha beneficiado de los comentarios de Jean Cartelier, Antaine Rebeyrol y Michel Rosier, a quienes agradezco profundamente. Traducción de Edith Klimovsky. Este artículo inédito se recibió el 3 de agosto de 2001 y fue aprobado por el Comité Editorial el 27 de agosto de 2001.
Resumen
Este artículo propone un modelo de equilibrio general idéntico en todo al modelo walrasiano, salvo que incorpora un mecanismo endógeno de variación de los precios. Este modelo permite eliminar al subastador walrasiano, lo que resuelve el problema de K. Arrow sin que sea necesario introducir la competencia imperfecta. Muestra también que la regla simple y determinista de variación de los precios según la ley de la oferta y la demanda, exógena en la teoría estándar, está lógicamente relacionada con la noción walrasiana de agentes tomadores de precio. Estas dos propiedades del modelo walrasiano sólo se verifican en condiciones particulares, exageradamente restrictivas.
Palabras clave: subastador walrasiano, variación de precios, equilibrio.
Abstract
This paper propases a general equilibrium model in all respects identical to the Walrasian one, except that it includes a mechanism by which prices change endogeneously. In this model the Walrasian auctioneer is eliminated and, consequently the problem put forward by K. Arrow is sol ved without introducing imperfect competition. This model also shows that the simple and deterministic rule of price change according to the law of supply and demand, which is exogeneous in the standard general equilibrium theory, is logically related to the Walrasian price taker individual behaviour. These two properties of the Walrasian model depend on particular and very restrictive conditions.
Key words: Walrasian auctioneer, price change, equilibrium.
INTRODUCCIÓN
En la teoría del equilibrio general competitivo, la variación de los precios es la única expresión social del grado de mútua. compatibilidad de las decisiones individuales, de la que se deriva la noción de equilibrio: un estado de la economía en el cual los precios no varían. Se explica así el vínculo estrecho entre la noción de equilibrio y la teoría de la variación de los precios. En la tradición walrasiana, esta última se identifica con la "ley de la oferta y la demanda" .
Esta ley es omnipresente en la teoría del equilibrio. Es constantemente invocada como interpretación o justificación económica de las correspondencias utilizadas en la demostración de la existencia del equilibrio general.1 Ocupa un lugar central en la teoría de la estabilidad hasta el punto que se está más dispuesto a admitir el fracaso de ésta, pese al reconocimiento unánime de que se trata de un golpe grave para la teoría walrasiana, que a dudar de la regla de variación de los precios según la oferta y la demanda2.
Desde hace más de 40 años (antes de que se comprobara el fracaso de los modelos de estabilidad), la teoría walrasiana de la variación de los precios es objeto de una profunda insatisfacción. Le corresponde a T. Koopmans [1957] hacer hincapié en la dificultad que K. Arrow [1959] presenta en su formulación definitiva: la hipótesis de individuos "tomadores de precios" implica la atribución de la variación de los precios a un "subastador". Por consiguiente, éste sólo puede ser eliminado si, fuera del equilibrio, los individuos no están en una situación de competencia perfecta: es la competencia imperfecta que se encarga de explicar la variación de los precios. Este argumento ha sido unánimemente aceptado. No conocemos ninguna objeción, ni de los partidarios de la teoría del equilibrio general, ni de sus opositores.3 La conclusión de K. Arrow ha sido ulteriormente reforzada por la crítica que F. Fisher [1983] dirige a la noción de agente tomador de precios que, fuera del equilibrio, se comporta como si estuviera en equilibrio. La competencia imperfecta es invocada nuevamente, esta vez para suprimir la incoherencia.
La importancia tanto de la ley de la oferta y la demanda en la teoría del equilibrio como de las críticas que le han sido dirigidas justifican, en nuestra opinión, que se vuelva a examinar el problema en su conjunto. En este artículo, sugerimos una solución a la dificultad de la teoría walrasiana de la variación de los precios considerada en sí misma, sin interrogarnos sobre las demostraciones de existencia del equilibrio, ni sobre la estabilidad de los procesos de ajuste que se derivan de dicha teoría. Esto es legítimo ya que el estudio de la regla de variación de los precios difiere lógicamente del análisis de la estabilidad y lo antecede. La sección 1 muestra que la dificultad central de la teoría walrasiana reside en su incapacidad para determinar los precios fuera del equilibrio. Esta dificultad se elimina en un esquema de formación de los precios, cuyo origen se encuentra en los escritos de antiguos economistas (sección 2). Una vez incorporadas las modificaciones necesarias para adaptarlo al marco walrasiano, se obtiene un modelo que tiene todas las propiedades walrasianas y en que la variación de los precios es endógena (sección 3). Este modelo permite resolver los problemas planteados por T. Koopmans, K. Arrow y F. Fisher. El subastador es eliminado (sección 4) y los límites comunes a la noción walrasiana de agente tomador de precios y a la ley de la oferta y la demanda son puestos en evidencia (sección 5).
Nos limitamos a la economía de intercambio e identificamos en lo sucesivo el subastador con su función esencial de cambiar los precios, dejando de lado sus otras atribuciones.
Las principales conclusiones de este estudio son las siguientes:
(i) El subastador walrasiano no se origina en la hipótesis de agentes tomadores de precios sino en la indeterminación de los precios fuera del equilibrio. Es eliminado en un esquema de variación endógena de los precios en competencia perfecta, lo que resuelve el problema de T. Koopmans y K. Arrow sin que sea necesario introducir la competencia imperfecta.4
(ii) En una economía competitiva, la variación de los precios no obedece, en general, a la ley de la oferta y la demanda. Esta regla simple y determinista sólo se verifica en condiciones particulares, exageradamente restrictivas. Dicha regla está ligada lógicamente a la noción walrasiana de agente tomador de precios, que depende de esas mismas condiciones. Esta noción no proporciona, por lo tanto, la definición general de la competencia perfecta y el problema de F. Fisher se soluciona sin introducir la competencia imperfecta.
Estos resultados pueden contribuir al estudio de la economía competitiva fuera del equilibrio, que ha desembocado en un callejón sin salida cuando ha sido emprendido en el marco walrasiano.
1. LA INDETERMINACIÓN DE LOS PRECIOS FUERA DEL EQUILIBRIO
La teoría walrasiana se apoya sobre el esquema de base siguiente:
 | (1) |
donde el signo "→" designa la respuesta de los individuos al vector de precios p dados, y el signo "⇒;" indica la reacción de los precios ante las decisiones de los individuos, expresadas por el vector de las demandas excedentes z(p).5 La primera relación es explicada por la teoría de la elección individual. La segunda representa la variación de los precios de p a p' conforme a la ley de la oferta y la demanda.
Hace más de un siglo, Walras afirmó, triunfante, que él había por fin descubierto la "formulación científica de […] la ley de la oferta y la demanda, ley fundamental que hasta ahora ha sido formulada con expresiones carentes de sentido o erróneas" [Walras 1900, 312]. Pero, ni Walras, ni ninguno de sus sucesores, han establecido una relación cuantitativa únivoca entre las demandas excedentes asociadas al vector p y la variación de los precios, es decir, el vector p. De las dos relaciones que figuran en la relación [1], sólo la primera está determinada. La teoría microeconómica atribuye al individuo la información y los instrumentos matemáticos que le permiten calcular con precisión las cantidades ofrecidas y demandadas a los precios p. Pero la ley de la oferta y la demanda no dice nada acerca de la importancia de la variación del precio, que resulta de las demandas excedentes cuantitativamente determinadas. Dicha ley sólo indica el sentido de esta variación. Así, el vector p está indeterminado: la variación del precio relativo Pij está siempre cuantitativamente indeterminada, cualquiera que sea el signo de las demandas excedentes de las mercancías i y j, y si ambas son del mismo signo, también está indeterminada cualitativamente.
La indeterminación del vector p (o de la variación de los precios relativos) es, en nuestra opinión, la causa de las dificultades de la teoría walrasiana:
(i) La consecuencia directa es la inevitable presencia del subastador. Si p estuviera determinado por el modelo, sería razonable admitir que es constatado por los individuos, y el subastador perdería su razón de ser. Pero en la teoría walrasiana, con tal que se respete el signo de las demandas excedentes, la variación de los precios es exógena: la ecuación que la representa es simplemente una hipótesis, ajena al modelo que, por esto no puede proporcionar la más mínima justificación de ella.v6 Se deduce que la crítica de T. Koopmans y K. Arrow se justifica únicamente si la indeterminación de los precios fuera del equilibrio se origina en la hipótesis de agente tomador de precios. En la sección 4 mostramos que éste no es el caso.
(ii) Sin embargo, el artificio del subastador no basta para eliminar la dificultad. Precisemos este punto que parece no estar suficientemente claro. Según F. Hahn, el subastador "announces p and agents send back messages which allow him to calcu1ate z(p) […] In this light he calculates a new vector p as follows:
La ambigüedad de esta presentación se debe a que los vectores z(p) y p aparecen como el resultado de dos "cálculos" sucesivos efectuados por el subastador. No es para nada así. Sólo el primero es un cálculo propiamente dicho: la suma de las demandas netas individuales para cada mercancía.
La naturaleza de la segunda operación es totalmente diferente. El subastador no puede limitarse a aplicar pasivamente la ley de la oferta y la demanda. él debe, además, fijar un nuevo vector p . Pero no tiene ninguna manera de "calcularlo" a partir de la única información que posee, z(p), ya que existe una infinidad de precios pi que verifican las desigualdades anteriores. Por consiguiente, el vector p (o la variación de los precios) es necesariamente arbitrario.8
(iii) Se deduce que los precios sólo están determinados en el equilibrio, es decir, cuando el vector p no resulta de una variación de los precios fijada por el subastador. El privilegio exclusivo acorde a las situaciones de equilibrio no se explica solamente por el fracaso de la teoría de la estabilidad. Su origen es más profundo e independiente de este último: la teoría walrasiana no tiene nada que decir acerca de los precios fuera del equilibrio.
Pero las dificultades persisten, en una forma diferente, porque el concepto de equilibrio elaborado en este marco resulta frágil. Este punto es raramente notado. Una excepción notable es F. Hahn:
[…] the behaviour postulated for the auctioneer will irnplicitly define what we are to mean by an equilibrium: a state of affairs when the rules tell the auctioneer to leave prices where they are. But the auctioneer's pricing rules are not derived from any consideration of the rational actions of agents on which the theory is supposed to resto Thus the equilibrium notion becomes arbitrary and unfounded. If, on the other hand, we had a theory of price formation based on the rational calculations of rational agents then the equilibrium notion would be a natural corollary of such a theory [Hahn 1987,66].
Es este tipo de teoría de la formación de los precios en una economía competitiva que vamos a esbozar a continuación.
2. COMPETENCIA Y FORMACIÓN DE LOS PRECIOS
En una economía en que la actividad económica está descentralizada, cada individuo actúa en la ignorancia de las acciones de los otros y, de ese modo, de los precios de mercado (a los cuales se realizan los intercambios) que resultan de la interacción del conjunto de las acciones individuales. A través de estos precios, que pueden ser diferentes de los precios anticipados a partir de los cuales se toman las decisiones individuales, las actividades privadas son evaluadas socialmente (o sancionadas, en la terminología de Marx).
Llamemos mecanismo de mercado al algoritmo que permite calcular los precios de mercado y las asignaciones que resultan de un conjunto dado de decisiones individuales. Se pueden sin duda considerar diferentes mecanismos de mercado. Una regla natural es propuesta por Cantillon (y retomada por Smith): Los precios van fijándose en el mercado conforme a la proporción de los artículos que se ofrecen en venta y del dinero dispuesto a comprarlos.9
En una economía con n mercancías (i = 1, 2, … , n), existen [n(n-1)]/2 lugares de intercambio, que suponemos organizados: en el lugar de intercambio (i, j) se presentan todos los oferentes dei (y también de j), y todos los demandantes de j (y también de i). Sea shij la cantidad de i utilizada por el agente h para la compra de j. La tasa de cambio vij (precio de i en términos de j) es igual a (Σh Shji) / (Σh Shij). Cualquiera que sea la manera en que se calculan las ofertas y demandas, en este sistema de trueque generalizado, los intercambios engendran precios incoherentes, en el sentido de que la condición vik vkj vij = 1, en general, no se verifica. Cada mercancía recibe una evaluación diferente según el lugar en que es intercambiada. La supresión de esta incoherencia implica la unicidad del medio de cambio, como lo indica Cantillon.
Hay que introducir aquí un sistema monetario. Se supone que no existe ninguna restricción de origen monetario: los individuos disponen siempre de la moneda necesaria para el financiamiento de su demanda y restituyen la cantidad obtenida gracias a sus ventas. 10 Este tipo de moneda es por lo tanto un simple medio de cambio.
La regla de formación de los precios de mercado es independiente de la teoría del valor adoptada,11 del comportamiento de los individuos y de la estructura competitiva o no de la economía. Dado el objeto de este artículo, la presentaremos en el marco de la economía de mercados competitivos. Las únicas decisiones de los individuos conciernen a las cantidades que están dispuestos a intercambiar y la única información que necesitan para decidir es la anticipación de los precios de mercado que resultan del conjunto de las acciones individuales en conformidad con la regla de Cantillon. Por hipótesis, se excluye todo poder individual, directo o indirecto, sobre los precios anticipados y de mercado. Los individuos consideran que sus propias decisiones sobre las cantidades no tienen efecto sobre los precios que anticipan y, de ese modo, sobre los precios de mercado. En este sentido, la economía se compone de agentes tomadores de precios.
Sean shi(ph) y dhi(ph) las cantidades de i ofrecidas y demandadas, respectivamente, por el agente h, y ph el vector de precios anticipados y utilizados por este último para calcularlas. La elección de la teoría del cálculo individual es remitida a la sección siguiente debido a que no es necesaria aquí. En virtud de la hipótesis acerca de la organización monetaria, la cantidad de moneda de la que dispone el agente h está dada por mh(ph) = Σi phi dhi(ph). El precio de mercado v¡ que resulta del conjunto de las acciones individuales está determinado por el cociente: Σh mhi(ph)/ Σh Shi(ph), donde mhi = phi dhi(ph)es la cantidad de moneda que el agente h gasta en el mercado i. Los individuos actúan en la ignorancia de los precios monetarios que se forman en los mercados, de los que se derivan los precios relativos.
Como consecuencia de los intercambios, al cierre de los mercados aparecen desequilibrios individuales a la vez reales y monetarios. Los primeros, que conciernen únicamente a las cantidades demandadas, son medidos por la diferencia entre mhi (ph) / phi (la cantidad deseada de i) y mhi(ph) / vi (la cantidad de i obtenida a través del intercambio). La restricción de presupuesto, necesariamente respetada en el momento del cálculo al precio ph, es generalmente violada en el intercambio al precio v. Aparece un déficit o un excedente monetario en el balance individual de los agentes que intercambian, medido por la diferencia Σi vi shi(ph)- mh(ph).
En virtud del mecanismo de formación de los precios de mercado, la suma algebraica para todos los agentes es igual a cero: Σh Σi vi shi(ph)- Σh mh (ph) = 0.
El equilibrio, si existe, es un vector de precios de mercado tal que ph = v, para todo h. A estos precios, los saldos monetarios son nulos.
Como el desequilibrio es a la vez real y monetario, el proceso de ajuste depende, por una parte, del comportamiento de la autoridad monetaria en cuanto a la liquidación de los saldos individuales y, por la otra, de las funciones de anticipación ph = φh(V)que representan la interpretación individual de las diferencias entre los precios anticipados y los precios de mercado, a partir de la cual se forman las anticipaciones de los precios de mercado para el periodo siguiente, ph. Estos precios anticipados son utilizados para el cálculo de las acciones individuales cuya confrontación engendra un nuevo vector (único) de precios de mercado (v). Es cierto que actualmente no existe ninguna teoría satisfactoria de las anticipaciones de los precios fuera del equilibrio. Esta laguna no molesta aquí porque las anticipaciones individuales sólo afectan a las trayectorias de los precios de mercado. éstos están siempre determinados por el mecanismo de mercado, excepto si los precios monetarios anticipados son nulos o infinitos.12
Todo esto está sintetizado en el siguiente esquema:
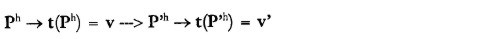 | (2) |
donde Ph y Ph son las matrices de los precios anticipados, t(Ph) y t (Ph) son los vectores que representan las transacciones según la regla de Cantillon, de dimensión n, cuyos i-ésimos componentes son, respectivamente, Σh phi dhi(ph) / si(ph) y Σh phi dhi(ph)/ si(ph).El signo → designa la respuesta de los individuos ante los precios anticipados Ph, en forma de ofertas de bienes y de gastos monetarios en los diferentes mercados; el signo → indica las anticipaciones de los precios según las funciones φh(v).
Este modelo permite tratar las situaciones de equilibrio y de desequilibrio en una economía competitiva en que la variación de los precios es endógena y tiene lugar en ausencia de todo subastador.13 Aunque breve, este esbozo es suficiente para nuestro propósito.
3.LA ADAPTACIÓN AL MARCO WALRASIANO: UN MODELO DE TANTEO SIN SUBASTADOR
El modelo arriba mencionado es demasiado general. Debe ser adaptado al marco walrasiano, lo que se hace introduciendo las tres especificaciones siguientes.
Las dos primeras son evidentes.
(i) La primera se refiere al comportamiento maximizador de los individuos: las cantidades ofrecidas y demandadas son el resultado de un cálculo individual de maximización de una función objetivo bajo la restricción de presupuesto. ésta es la base de las funciones Shi(P) y dhi(p) (para todo i y h) Σh Shi(p)= si(p) y Σh dhi(p) = di(p).
(ii) La segunda concierne al tanteo: un acuerdo general se establece entre todos los participantes en el mercado, estipulando que el intercambio efectivo se suspende hasta que los precios no sean de equilibrio. 14
(iii) La tercera es más compleja. Se trata de traducir en el modelo precedente la hipótesis walrasiana de agente tomador de precios y la regla de variación de los precios según la ley de la oferta y la demanda. Comencemos por la segunda.
Como lo ilustra el esquema [1] p → z(p) ⇒ p, esta ley prescribe una regla determinista de variación de los precios, desde el vector p al que se calculan las ofertas y las demandas individuales, hacia el vector p, en función únicamente del signo de las demandas excedentes agregadas. La dificultad es que p es a la vez exógeno y arbitrario (ver la sección 1). En el esquema [2], se determinan los precios. Pero como ofertas y demandas individuales se calculan a los precios anticipados ph, las variaciones de los precios) sean paramétricos o de mercado, escapan a la ley de la oferta y la demanda. De ahí la necesidad de introducir, en este esquema, hipótesis acerca de las anticipaciones.
La hipótesis según la cual todos los individuos tienen la misma anticipación de los precios, ph = p, '∀h, conduce al esquema siguiente:
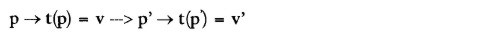 | (3) |
donde t(p) y t(p) son los vectores, de dimensión n, cuyos i-ésimos componentes son, respectivamente, pi di(p) / si(p) y pi di(p) / si(p). No obstante, al igual que en el esquema [2] la variación de los precios, paramétricos o de mercado, no sigue la ley walrasiana de la oferta y la demanda. Todo sucede, en efecto, como si un subastador anunciara los precios v que los agentes no adoptan para calcular sus ofertas y demandas. Todos ellos los interpretan de la misma manera y utilizan como parámetros de sus cálculos los precios que resultan de esa interpretación. El único resultado nuevo del esquema [3] es la existencia de una ley de la oferta y la demanda particular, limitada a las diferencias entre los precios de mercado y los precios paramétricos, v y p, y v y p (lo que no era el caso en el esquema [2] donde los primeros son un vector y los segundos una matriz).
La hipótesis de anticipaciones estáticas, p' = v elimina estas dificultades. Se obtiene:
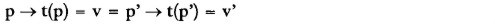 | (4) |
La variación de los precios es medida indistintamente por el cambio del precio anticipado o del precio de mercado. Para todo i, el precio pi (o vi) aumenta o baja según que di(p) / si(p) (o di(p) / si(p)) sea superior o inferior a 1, es decir, según que zi(p) (o zi(p)) sea posrtrva o negativa. En este modelo, los precios se determinan y varían de manera endógena según la ley walrasiana de la oferta y la demanda.
Se llega al mismo resultado si se introduce en el modelo [2] la noción walrasiana de agente tomador de precios según la cual, por una parte, la "ley del precio único" se verifica incluso fuera del equilibrio, pues todos los individuos se confrontan al mismo vector de precios (el subastador anuncia los precios en numerario), y por la otra, dichos precios son interpretados como si fueran de equilibrio. La primera característica implica que el vector ph de los precios anticipados es único, es decir que todos los individuos anticipan los mismos precios: ph = p, ∀h. La segunda implica que el vector único de los precios futuros anticipados es igual al vector de los precios de mercado del periodo corriente: p = v. De esta forma se obtiene el esquema [4] anteriormente mencionado.
Estas dos condiciones acerca de las anticipaciones no son independientes entre sí. Puesto que el vector de los precios de mercado v es único, si se verifica la segunda condición también se verifica la primera (no siendo verdadera la proposición inversa).
Se deduce que la elasticidad unitaria de las anticipaciones individuales de los precios es la condición suficiente de la que dependen, a la vez, el comportamiento walrasiano tomador de precios y la variación de los precios conforme a la ley de la oferta y la demanda. La equivalencia lógica entre estas dos proposiciones, ajenas una a la otra en la teoría walrasiana, puede sorprender; este punto se desarrolla en la sección 5.
El modelo de tanteo sin subastador, obtenido introduciendo las hipótesis (i) - (iii), es idéntico al modelo walrasiano, salvo que incorpora un mecanismo de mercado que suprime la indeterminación de los precios fuera del equilibrio.15 Esta propiedad permite resolver el problema de T. Koopmans y K. Arrow (sección 4) y poner en evidencia los límites del enfoque walrasiano (sección 5)
4.UNA SOLUCIÓN PARA EL PROBLEMA DE T. KOOPMANS Y K. ARROW
Tomemos como punto de partida un vector de precios anunciados p que los individuos adoptan como parámetros para calcular sus ofertas y sus demandas. ¿Cuáles son los nuevos precios que resultan? Comparemos los esquemas [1] y [4].
En el primero, p es a la vez el vector de los precios paramétricos y de los precios de mercado a los cuales se realizan los intercambios, virtuales en la hipótesis del tanteo. Como vimos, la teoría walrasiana no proporciona ninguna respuesta a la cuestión planteada: el vector p está indeterminado. Debe ser fijado de manera exógena mediante una nueva intervención, arbitraria, del subastador y así sucesivamente.
En cambio en el esquema [4] las dos nociones de precios paramétricos y de mercado son distintas. Esto permite suprimir la dificultad. La teoría estándar de la elección individual determina las ofertas y las demandas a los precios p y, de esta manera, los gastos en cada mercado. Se puede aquí imaginar un sistema de bonos a la Walras que indican las cantidades de mercancías ofrecidas y de moneda gastada en los diferentes mercados [Walras 1900, 309]. La confrontación de estos bonos según la regla de Cantillon permite deducir los precios de mercado v. Si diferen de p, se suspenden los intercambios. Las ofertas de mercancías y los gastos monetarios resultan virtuales y los compromisos expresados en los bonos se anulan. Los individuos constatan el vector v e infieren los nuevos precios anticipados p, es decir, los parámetros de sus cálculos para el periodo siguiente. Este tanteo describe un proceso determinista y endógeno de variación de los precios en competencia perfecta, que tiene lugar en ausencia de cualquier subastador. Lo hemos acogido inicialmente, pero inmediatamente después él desaparece pura y simplemente. Queda así resuelto el problema de T. Koopmans y K. Arrow.
T. Koopmans se pregunta: "If, for instance, the net rate of increase in price is assumed to be proportional to the excess of demand over supply, whose behavior is thereby expressed? And how is that behavior motivated?" [Koopmans 1957, 179]. La respuesta es inmediata. La proporcionalidad entre la variación de los precios y la demanda excedente no es una hipótesis puesto que: Δpi/pi = [di(p) / si(p)]-l, ∀i. En segundo lugar y sobre todo, la variación del precio es el resultado del comportamiento racional como demandantes y oferentes de todos los individuos que intervienen en el mercado considerado. Dicha variación no es decidida por nadie. Por consiguiente, no se plantea la cuestión de las motivaciones de quien decide las variaciones de los precios.
Al igual que T. Koopmans, K. Arrow sitúa la dificultad en la hipótesis de agente competitivo: ld It is not explained whose decision it is to change prices […] Each individual participant in the economy is supposed to take prices as given and determine his choice as to purchases and sales accordingly; there is no one left over whose job it is to make a decision on price" [Arrow 1959, 43]. Y unos años después: Si decidimos que los términos de intercambio a que se enfrenta cualquier unidad de decisión serán independientes del curso de acción que esa unidad podría desear proseguir, decididamente es ridículo que imaginemos a cualquiera unidad de decisión cambiando los precios bajo ‘presión del mercado [Arrow y Hahn 1971, 380]. Esta observación, evidentemente justa, no se dirige al modelo de tanteo sin subastador (esquema [4]) en el cual, bajo la presión del mercado, los individuos no modifican los precios sino únicamente sus propias cantidades de mercancías ofrecidas y de moneda gastada, es decir, las únicas variables que controlan. De lo que resulta la formación endógena de otros precios.
Según K. Arrow y F. Hahn: having decided on one idealization (perfect competition), we run into what must be taken to be logical difficulties unless we import a further idealization: the auctioneer .16 Es verdad que en la teoría del equilibrio general competitivo existe una "dificultad lógica". Pero, contrariamente a lo que se afirma, ella no deriva ni de la hipótesis de competencia perfecta (ver el esquema [1]), ni de la hipótesis más restrictiva de agente walrasiano tomador de precios (ver el esquema [4]). La dificultad lógica se origina en la indeterminación de los precios fuera del equilibrio, que está a su vez ligada a la identificación del precio parámetrico con el precio de mercado. La introducción de un mecanismo de formación de los precios permite distinguir estas dos nociones. Se obtiene entonces un modelo de tanteo en el que se puede aceptar la idealización que son la competencia perfecta y el agente walrasiano tomador de precios, y al mismo tiempo rechazar la idealización adicional, el subastador.
Esto conduce a examinar nuevamente la solución de K. Arrow, aceptada únanimemente desde entonces, según la cual el subastador es eliminado suprimiendo la hipótesis de competencia perfecta fuera del equilibrio y confiando la variación de los precios a los individuos en situación de competencia imperfecta.17 Esta salida no nos parece satisfactoria. La competencia imperfecta es sólo una condición suficiente para la eliminación del subastador. Otra condición suficiente es la que hemos sugerido: la introducción de un mecanismo de formación de los precios en una economía que sigue siendo competitiva. Dado que el problema planteado es el de la variación de los precios en competencia perfecta, esta segunda solución nos parece ampliamente preferible. La proposición de K. Arrow evita la dificultad en lugar de resolverla.
5.LOS LÍMITES DE LA NOCIÓN WALRASIANA DE AGENTE TOMADOR DE PRECIOS Y DE LA LEY DE LA OFERTA Y LA DEMANDA
Una característica propia de la teoría walrasiana es la disociación completa entre los comportamientos individuales y la regla de variación de los. precios. Dado que esta última es admitida como una hipótesis exterior al modelo, todas las situaciones, incluso las más extravagantes, son a priori concebibles. Según la hipótesis retenida, para cambiar los precios el subastador puede ajustarse a la ley de la oferta y la demanda, pero también podría seguir cualquier otra regla, o incluso ninguna regla y establecer los precios al azar: los individuos walrasianos aceptarán siempre esos precios, cualesquiera que sean, como parámetros de sus cálculos de las ofertas y demandas.
Se llega a una concepción evidentemente muy insatisfactoria de la competencia que en la teoría ortodoxa se singulariza como la única estructura de mercado en que la regla de variación de los precios no guarda ninguna relación con los comportamientos individuales. Esta anomalía tiene efectos negativos sobre la propia noción de equilibrio competitivo [Hahn 1987, 66]. Es eliminada en el esquema [2] que describeuna economía de competenciaperfecta donde, a través de las funciones φh(v), la regla de variaciónde los precios se vincula estrechamente con los comportamientos de los agentes:las interpretaciones individuales de los precios de mercado corrientes dan como resultado los precios paramétricos, de los que se derivan las ofertas y las demandas y, de esa forma, los nuevos precios de mercado. Es la razón por la cual, a fin de obtener la regla determinista de variación de los precios dictada por la ley de la oferta y la demanda, es necesario imponer un principio de interpretación particular según el cual los individuos adoptan los precios de mercado corrientes como parámetros de sus cálculos de las ofertas y demandas futuras. De lo que se infiere, como hemos visto, que la misma hipótesis de anticipaciones estáticases la condición suficientea la vez para el comportamiento walrasiano tomador de precios y para la variación de los precios según la ley de la oferta y la demanda.
Siendo lógicamente equivalentes, estas dos reglas están sujetas a los mismos límites. La hipótesis de anticipaciones estáticas es excesiva y sobre todo incompatible con la racionalidad atribuida a los individuos. éstos constatan precios de mercado diferentes de los que han anticipado y, sin embargo, los adoptan sistemáticamente como parámetros de sus cálculos, interpretándolos como precios de equilibrio.
(i) La ley walrasiana de la oferta y la demanda
Dos razones explican, sin duda, el atractivo de la idea según la cual el precio varía en función de la ley de la oferta y la demanda: por una parte, la referencia a las prácticas muy conocidas de pujas a la alza o a la baja en los mercados, y por la otra, la búsqueda de una regla simple y determinista a la que podía reducirse la complejidad de la variación de los precios, siguiendo en esto el ejemplo de la física clásica.
Según Walras, lo que hasta entonces sólo era una intuición adquiere en su teoría el estatus de una ley económica general. Pero en el tanteo walrasiano la ley de la oferta y la demanda es una prescripción impuesta desde el exterior y no una regla económica obtenida como resultado de la teoría. El modelo del tanteo sin subastador, esquema [4], muestra que esta ley sólo existe si se imponen condiciones restrictivas y económicamente inaceptables en cuanto a las anticipaciones individuales. Si estas condiciones no se verifican, ninguna regla simple y determinista de variación de los precios en competencia perfecta puede deducirse partiendo únicamente de las ecuaciones de oferta y demanda. En el caso general, estas ecuaciones sólo sirven para determinar los precios de equilibrio.18
Esto tiene consecuencias notables sobre el análisis de la estabilidad. El estudio de la variación de los precios es la etapa lógicamente anterior a cualquier análisis dinámico. Si la explicación de la regla de variación de los precios es insatisfactoria, los procesos dinámicos que ella engendra también lo son. El fracaso del tanteo walrasiano no se reduce, en nuestra opinión, a la imposibilidad de demostrar la estabilidad del equilibrio en condiciones económicamente aceptables. Incluso si este resultado se hubiese obtenido, habría tenido un alcance liniitado porque en el tanteo walrasiano la regla de variación de los precios es, o bien arbitraria cuando es exógena al modelo, o bien sólo es válida bajo hipótesis restrictivas y económicamente inaceptables.
(ii) La noción walrasiana de agente tomador de precios
En la teoría del equilibrio general, la competencia perfecta es no sólo una abstracción sino también una noción contradictoria. Al ser definida a partir del agente walrasiano tomador de precios, ella implica que los individuos son a la vez racionales (en sus cálculos de las ofertas y demandas) e irracionales (en su interpretación de los precios). Se concluyó de lo anterior que la eliminación de esta contradicción exige la supresión de la hipótesis de competencia perfecta y su reemplazo por la de la competencia imperfecta [Fisher 1983, cap. 6].
Nuestro análisis conduce a un resultado totalmente distinto. El comportamiento walrasiano tomador de precios no proporciona la definición general de la competencia perfecta porque corresponde al caso particular y económicamente poco significativode anticipaciones estáticas.Esta hipótesis sólo es útil si se desea obtener trayectorias donde los precios varían de manera determinista de acuerdo con la ley de la oferta y la demanda. Ella puede ser desechada.Se vuelve entonces al sistema [2]. Los individuos perciben el desequilibrio al anticipar precios diferentes de los que constatan. Utilizando los términos de F. Fisher, ellos pierden su ingenuidad y recobran su memoria. Siguen siendo competitivos o tomadores de precios porque consideran que sus decisiones en cuanto a las cantidades no tienen efecto sobre los precios anticipados (y así, sobre los precios de mercado). Sobre esta base se obtiene, nos parece, una definición no contradictoria de la competencia perfecta. El precio que se determina en el mercado competitivo es concebido como un puro hecho social, en el sentido preciso y más fuerte de que no depende de nadie. Ningún agente, aunque sea consciente de las situaciones de desequilibrio, no toma decisiones (o no tiene poder) acerca de los precios. Esta noción de competencia está presente en la teoría del mercado de Smith, en la teoría del valor de Marx y es compatible con la teoría del equilibrio general, con tal que se abandone la noción walrasiana de agente tomador de precios.
NOTAS AL PIE
1 La lista de las referencias sería demasiado larga. Comprende tanto a los fundadores de la teoría contemporánea del equilibrio general como a los autores de manuales. Limitémosnos a mencionar, entre los primeros a Nikaido (1956, 139) y entre los segundos a Starr (1997, 101).
2 En efecto, el fracaso de la teoría de la estabilidad no significa que no se haya encontrado ningún proceso estable de variación de los precios en condiciones suficientemente generales y compatibles con el comportamiento racional de los individuos. Dicho fracaso consiste en la demostración según la cual no existe, en el caso general, un proceso estable de variación de los precios tal que ésta esté regida por la ley de la oferta y la demanda. Un buen ejemplo es el "método de Newton" que ha dado un notable resultado de estabilidad. No se trata evidentemente de sostener que es un método adecuado. Lo que nos interesa es el principal argumento (no único) utilizado para rechazarlo. Según Arrow y Hahn, un subastador que cambia los precios según el método de Newton se olvida "de la simulación de procedimientos de mercado […] Es importante advertir que éste no es un proceso que imite a la mano invisible; por ejemplo, el precio de un bien puede aumentar aunque su oferta sea excedente"(Arrow y Hahn 1971, 355 Y 357). Ver también Hahn (1987, 64). Es su incompatibilidad con la ley de la oferta y la demanda que descalifica a esta formalización del proceso de ajuste de los precios.
3 Estos últimos han insistido en la inadecuación de la representación centralizada del mercado competitivo. Esto es cierto pero insuficiente pues, como mostraremos, el problema es más profundo que lo que sugiere la crítica de Arrow. En este punto, la única posición original que conocemos es la defendida por Rebeyrol (1999) en su interpretación del tanteo de Walras como "metáfora" de una negociación generalizada en la que el intercambio está sujeto a la condición de equilibrio general (el acuerdo de todos los participantes) que garantiza así la justicia conmutativa. Esta interpretación nos parece importante y merece una amplia discusión. Mientras tanto, en este artículo nos conformamos al uso que se impuso a partir de la crítica de K. Arrow que califica de ‘walrasiano al agente tomador de precios de la teoría actual del equilibrio general.
4 Esta solución es sugerida en Benetti(1996).
5 El esquema es exactamente el mismo si se tiene en cuenta la crítica de Patinkin y Clower según la cual la medida apropiada del desequilibrio del mercado, en virtud del cual los precios cambian, se obtiene agregando las demandas netas efectivas y no las demandas netas nocionales. Sobre esta base se construye el modelo de no tanteo. Ver Arrow y Hahn (1971, cap. 13). Este esquema es empleado tanto en la teoría de la existencia como en la de la estabilidad del equilibrio. La primera afirma la existencia, en ciertas condiciones, de un vector p* de precios no negativos tal que z(p*) ⇒ p*. El estudio de la estabilidad tiene por objeto las propiedades de la trayectoria de los precios. A fin de evitar algún malentendido, repitamos que el problema aquí planteado es totalmente ajeno a estas dos cuestiones. Dicho problema concierne únicamente a la determinación de p, o a la variación de los precios, y no a su tendencia asintótica, ni a la existencia de un equilibrio.
6 Arrow y Hahn (1971 313). No vemos lo que autoriza a Hahn a decir, al inicio de su importante artículo sobre la estabilidad: "We are concerned with endogeneous processes operating in an economy which may bring about an equilibrium […]. The most famous and most discussed is "the law of supply and dernand" (Hahn 1982, 745). Pero en la teoría walrasiana esta leyes exógena. No existe ningún proceso "endógeno" susceptible de ser estudiado.
7 Hahn (1987,63).
8 Es lo que señala Hahn: … we have no theory to help in this rnatter (Hahn 1982, 769) Parece haberlo olvidado en su artículo de 1987.
9 Cantillon (1755, 19). Esta regla reaparecerá en los modelos de juegos estratégicos de mercado. Para una presentación general, ver Shubik (1990).
10 En estas condiciones, el equilibrio si existe, es walrasiano. Ver Dubey y Shapley (1994).
11 En Benetti y Cartelier (1998) se muestra que es compatible con la teoría marxista. En este artículo se encontrarán precisiones que completan las indicaciones arriba mencionadas.
12 En cambio, la ausencia de una teoría de las anticipaciones de los precios en desequilibrio es un obstáculo evidente para el estudio de la estabilidad del equilibrio, que es excluido aquí.
13 La necesidad del medio de cambio se deduce directamente como condición para la coherencia de los precios. Esta propiedad, que no utilizamos aquí, es importante para la teoría monetaria.
14 La hipótesis de tanteo suprime, por definición, el problema del intercambio voluntario fuera del equilibrio, que plantea la regla de Cantillon, Por otro lado, la moneda sólo es medio de cambio en las transacciones a los precios de equilibrio, como en la teoría estándar. Fuera del equilibrio, se reduce a la unidad de cuenta abstracta en términos de la cual se calcula el valor de las demandas Pi di.
15 Como se supone que las funciones de utilidad son estrictamente casi-cóncavas, continuas y monótonas, las funciones si(p) y di(p) son continuas, homogéneas de grado 0 en p y respetan la ley de Walras. Los precios de mercado de equilibrio son también los precios de equilibrio walrasiano.
16 Los autores se refieren al no tanteo, pero el argumento es el mismo para el tanteo (ver la nota 6). En el mismo sentido: La ficción de un subastador es muy seria, ya que sin ella tendríamos que encarar el problema paradójico de que un competidor perfecto cambia precios que se supone toma como dados (Arrow y Hahn 1971,377).
17 Es interesante señalar que la solución de Arrow es de la misma naturaleza que la que Sraffa propone en los años 20 en vista de superar las dificultades que él ha identificado en la teoría marshalliana [Sraffa 1926]. En ambos casos se supone que la competencia imperfecta resuelve las dificultades lógicas de la teoría del valor en competencia perfecta.
18 Contrariamente a la afirmación de Walras, para quien la ley de la oferta y la demanda resulta de la reunión de la ley de variación de los precios de equilibrio y de la ley de fijación de los precios de equilibrio (Walras 1900, 213), la ley de la oferta y la demanda se reduce en realidad a la segunda.
REFERENCIAS BIBLIOGRÁFICAS
[1] Arrow, K. (1959). "Toward a theory of price adjustment", The Allocation of Economic Resources. M. Abramovitz (ed), Stanford University Press, 41-51. [ Links ]
[2]Arrow, K. y Hahn, F. (1971). Análisis general competitivo, Fondo de Cultura Económica, México,1977. [ Links ]
[3] Benetti, C.(1996). "La regla "Cantillon-Smith' de formación de los precios y la teoría del equilibrio general", Análisis Económico, vol. XIII, n. 28. [ Links ]
[4] Benetti, C. y Cartelier, J. (1998). "Money, form and determination of value" , Marxian Economics: A Reappraisal. Essays on the Volume III of Capital, Method, Value and Money, Riccardo Bellofiore (ed.), vol. 1, Macmillan. Londres. [ Links ]
[5] Cantillon, R.(1755). Ensayo sobre la naturaleza del comercio en general. Fondo de Cultura Económica. México, 1978. [ Links ]
[6] Dubey, P. y Shapley, L. (1994). "Noncooperative general exchange with a continuum of traders. Two models", Journal of Mathematical Economics, vol. 23, 253-293. [ Links ]
[7] Fisher, F.(1983). Disequilibrium Foundations of Equilibrium Economics, Cambridge, Cambridge University Press. [ Links ]
[8] Hahn, F. (1982)"Stability", Handbook of Mathematical Economics, North Holland, 62-67. [ Links ]
[9] Hahn, F.(1987)."Auctioneer", The New Palgrave, General Equilibrium, Macmillan, 745- 793. [ Links ]
[10]Koopmans, T. C. (1957) Three Essays on the State of Economic Science, McGraw Hill, Nueva York. [ Links ]
[11] Nikaido, H.(1956). "On the Classical Multilateral Exchange Problem", Metroeconomica 8, agosto, 135-145. [ Links ]
[12] Rebeyrol, A. (1999).La pensée économique de Walras. Dunod., Paris. [ Links ]
[13] Shubik, M. (1990)."A Game Theoretic Approach to the Theory of Money and Financial Institutions", Friedman, B. M. y Hahn, F. H.(eds), Handbook of Monetary Economics, vol 1, cap. 5, Elsevier Science Publishers, 171-219. [ Links ]
[14] Sraffa, P.(1926). "The Laws of Returns under Competitive Conditions", Economic Journal 36, diciembre, 535-550. [ Links ]
[15] Starr, R. (1997). General Equilibrium theory. An Introduction. Cambridge University Press. [ Links ]
[16] Walras, L.(1900).Elementos de economía política pura, Alianza Editorial, Madrid, 1987 [ Links ]