Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.21 no.37 Bogotá July/Dec. 2002
EL MODELO DE CICLO Y CRECIMIENTO DE RICHARD GOODWIN. UNA EVALUACIÓN EMPÍRICA PARA COLOMBIA
Álvaro Martín Moreno R. *
* A. Moreno es profesor asistente de la Escuela de Economía, Universidad Nacional. El autor agradece el interés y las discusiones informales con el profesor Homero Cuevas y con Julián Libreros, así como también los comentarios de un árbitro anónimo. Los errores que aún persistan en el documento son responsabilidad del autor. Artículo recibido el 15 de marzo de 2002 y aprobado por el Consejo Editorial el 27 de septiembre de 2002.
Resumen
El objetivo del presente trabajo es exponer y evaluar la hipótesis del crecimiento cíclico de Richard Goodwin. Se utilizan datos colombianos para contrastar los supuestos del modelo. Se encontró que a nivel cualitativo, la dinámica de las variables de estado en el espacio de fases muestra cierta correspondencia con las predicciones teóricas, al menos para dos períodos: 1957-1966 y 1968-1974. Los resultados cuantitativos rechazan los supuestos del modelo y los modelos empíricos no describen el verdadero proceso generador de los datos.
Palabras clave: dinámica no lineal, ciclo límite, ciclo endógeno, crecimiento, curva de Phillips. JEL: B5, E30, O54
Abstract
The purpose of the present work is to expose and evaluate the hypothesis of cyclical growth of Richard Goodwin. Colombian data are used to contrast the ideas of the model. It was found that at a qualitative level, the dynamic of the state variables in the space of phases shows certain correspondence with the theoretical predictions, at least for two periods: 1957-1966 and 1968-1974. The quantitative results reject the suppositions of the pattern and the empiric models do not describe the true generator process of the data.
Key words: Nonlinear dynamic, limit cycle, endogenous cycle, growth, curves of Phillips. JEL: B5, E30, O54
Solamente las ecuaciones diferenciales no lineales son interesantes para la dinámica
Morris Hirsch
Es más fácil ser un conservador, que un rebelde competente
G. Myrdal
La dinámica de las economías capitalistas se caracteriza por una superposición de ciclos irregulares acotados sobre una tendencia de crecimiento del producto a largo plazo. Si bien los economistas carecen aún de una descripción completa de los dos fenómenos, existe una gran variedad de teorías y modelos parciales que buscan explicarlos. Al parecer la estrategia seguida por la mayor parte de los estudiosos del tema ha sido ´dividir para vencer´. En efecto, los economistas que han alcanzado cierto reconocimiento mundial tienen, entre su lista de creaciones teóricas, un modelo canónico de crecimiento o de fluctuaciones de la actividad económica. Sin embargo, muy pocos han tomado el riesgo de embarcarse en un programa de investigación que integre de manera rigurosa y sencilla los dos hechos estilizados.1
De hecho, como lo reconoce Robert Solow [ 1987], la teoría neoclásica no sólo carece de un tratamiento adecuado de las desviaciones de la actividad productiva de su ruta de equilibrio, sino que además los más recientes modelos de ciclos reales fallan al pretender hacernos creer, sin mucho fundamento, que "lo que solíamos llamar ciclos económicos –o por lo menos auges y recesiones- deberán interpretarse ahora como parpadeos óptimos en rutas óptimas, en respuesta a fluctuaciones aleatorias de la productividad y el deseo de ocio". Es decir, la teoría actual niega la posibilidad de la existencia de problemas de demanda efectiva, asumiendo que los mercados siempre se vacían y que el sistema se mueve sobre una senda de equilibrio que garantiza el pleno empleo de los recursos.
Mientras la enseñanza de la nueva economía neoclásica se repliega sobre sus viejos dogmas, sin mayores cambios sustanciales para describir la dinámica económica de las economías capitalistas, se olvida que en la historia del análisis económico se conserva a manera de stock, añejas tradiciones que con el paso de los años demuestran su vigor y riqueza analítica. Sin lugar a dudas, el trabajo de Richard Goodwin, un pensador marxista que se mantuvo firme hasta el final de su vida, es uno de los mejores ejemplos de rigurosidad y tenacidad del pensamiento no convencional en este campo. Pasinetti [1996] uno de sus discípulos en la Universidad de Cambridge recordó que con su muerte, acaecida el 6 de agosto de 1996, la profesión perdió a uno de los más "notables, originales, enigmáticos y no conformista de los economistas".
No es para menos, pues estaba convencido de que la evolución de la economía capitalista sólo podría entenderse en el contexto de las ecuaciones y los sistemas no lineales. Como él mismo decía:
El capitalismo se encuentra casi siempre en estados inestables, la explicación de ello es que es un juego jugado simultáneamente por millones de jugadores quienes no pueden tener la información necesaria para jugarlo bien, es decir, óptimamente. El resultado es un sistema que se bifurca entre estados estables e inestables: un estado de crecimiento inestable es de puro interés teórico, puesto que es una trayectoria del sistema que nunca permanecerá. (Citado por M. Desai y Ormenod [1998]).
Esta visión compleja y no lineal del mundo se forjó y se consolidó a lo largo de los años. Por supuesto, las influencias fueron muchas. Entre ellas, cabe mencionar, sin lugar a dudas, las siguientes: la de sus grandes profesores en Harvard (Haberger, Currie y Schumpeter); la crisis de los años treinta y la bancarrota de su padre que lo llevaron hacia la teoría de Marx cuando apenas era estudiante de ciencias políticas en la Universidad de Harvard; el ambiente y las discusiones del Cambridge de Inglaterra, donde tuvo la oportunidad de conocer a Joan Robinson, Piero Sraffa y Roy Harrod; sus estudios en Oxford donde asistió al seminario de Jacob Marschak. En Cambridge Mass tuvieron una enorme influencia el matemático Phillippe Le Corbellier -el gran matemático de las oscilaciones-, Wassily Leontief sobre todo con su esquema de insumo-producto -tan olvidado en la enseñanza ortodoxa actual- y de Norbet Wiener del Mit [Pasinetti 1996].
En sus últimos años, como profesor de la Universidad de Siena, leyó con entusiasmo los trabajos del matemático francés René Thom sobre teoría de catástrofes y las nacientes teorías de la dinámica caótica. Esta época fue de gran producción intelectual y de síntesis teóricas. Como lo anota G.C. Harcourt:
Sus ideas de toda la vida se unieron en una espléndida síntesis. Previamente, sus pensamientos habían evolucionado en dos líneas separadas, de un lado, la naturaleza del proceso cíclico en modelos agregados, y del otro, la naturaleza interdependiente de la producción en modelos multisectoriales. Ahora los dos habían sido integrados dentro de un todo impresionante [Harcourt 1985].
Dicho resultado fue la consecuencia de una vida no lineal, irregular y en muchos sentidos plural.2
Al respecto, no puedo dejar de citar esta bella e implacable frase del viejo y entrañable Stevenson: "Nuestra misión en este mundo no consiste en triunfar sino continuar fracasando, de buen ánimo". Dick Goodwin no fue un economista exitoso socialmente hablando, tampoco recibió medallas y se le negó el nombramiento como profesor titular en Harvard. Durante el período mccarthyista en los Estados Unidos se le persiguió por sus simpatías con el partido comunista y su orientación de izquierda. En Cambrigde Inglaterra se ganó la enemistad de los miembros más conservadores de la universidad, sin embargo, continuó... de buen ánimo.
El objetivo del presente trabajo es modesto. En primer lugar, se presentará el desarrollo del modelo de R. Goodwin de crecimiento y ciclo de 1967 en el cual hace uso del conocido sistema de Lotka y Volterra que describe la dinámica biológica de la presa y el rapaz. En segundo lugar, se evalúa la pertinencia del modelo con datos de la economía colombiana. Se realizan dos tipos de pruebas: una cualitativa y otra econométrica [Harvie 2000]. Finalmente se presentan las conclusiones.
UN MODELO DE CRECIMIENTO Y CICLO ENDÓGENO NO MONETARIO
Aunque Richard Goodwin había trabajado en economía aplicada y monetaria en su monografía de Oxford y en su tesis doctoral en Harvard, estaba convencido de que se podía desarrollar un modelo que integrara el crecimiento y las fluctuaciones del producto (empleo) de su equilibrio, sin necesidad de introducir choques aleatorios o monetarios. En efecto, hacia finales de los sesenta se sabía que era posible derivar oscilaciones regulares e irregulares a partir de sistemas y ecuaciones diferenciales (o en diferencia) lineales de manera exógena. Por el contrario, Goodwin consideraba que era imprescindible incorporar relaciones no lineales en los modelos para captar la idea genial de Marx sobre la naturaleza endógena y contradictoria de la dinámica de las economías capitalistas. Sin embargo, como anota Michele Boldrin:
Su esfuerzo de investigación hacia una explicación endógena de las fluctuaciones económicas motivó a unos pocos economistas dentro de la tradición keynesiana y del Cambridge de Inglaterra, pero nunca fue capaz de extenderse a toda la profesión. En realidad, entre finales de los sesenta y los setenta se atestigua una casi completa unanimidad sobre el uso de modelos lineales estocásticos para comprender los ciclos de los negocios [Boldrin 1988].
Las cosas parecen haber cambiado desde mediados de los ochenta. El interés de los economistas por la dinámica no lineal, la teoría de catástrofes, la emergencia del caos y la complejidad no sólo se ha incrementado durante los últimos años sino que además ha dado origen a una abundante literatura en las áreas de la macroeconomía y las finanzas. En realidad, gran parte de los modelos no lineales recientes que se inscriben en la literatura de los sistemas dinámicos complejos y caóticos son una reescritura discreta de los primeros modelos de ciclos y crecimiento en tiempo continuo [Sordi 1996].
Lo curioso de esta literatura es que restablece cierto interés por métodos olvidados, desprestigiados y catalogados como metafísicos. Un ejemplo interesante es el de la dialéctica hegeliana. Como lo muestra Rosser [2000] los tres principios del método dialéctico, adoptados por los hegelianos de izquierda, como la transformación de la cantidad en cualidad y viceversa, la interpenetración de los contrarios y la negación de la negación encuentran su expresión formal en la teoría de catástrofes, la teoría del caos, la dinámica compleja y la termodinámica del no equilibrio de la escuela de Bruselas.
De otra parte, la llamada dinámica compleja que implica la existencia de trayectorias erráticas cuya génesis endógena -causas inherentes al sistema- llevan necesariamente a la imposibilidad de la predicción y por ende la negación de la formación de expectativas racionales, ha permitido encontrar un vínculo entre la literatura postkeynesiana, que asume el axioma de no ergodicidad e incertidumbre radical y los modelos postwalrasianos o del llamado neokeynesiano duro, mientras revela el carácter blando y convencional de toda la literatura neokeynesiana de Harvard y Stanford [Rosser 1999].
En este orden de ideas, la lectura de un autor que se anticipó a los más importantes desarrollos de la ciencia moderna y que en medio del aislamiento y el desinterés de sus colegas, logró desarrollar una visión heterodoxa de la dinámica económica haciendo uso del análisis matemático y de los métodos topológicos más sofisticados, nos permite inclinar un poco la balanza a favor de un pequeño gueto de académicos que, aunque cuentan con recursos escasos, mantienen una resistencia rigurosa en busca de una nueva y diferente interpretación de la vida económica.
Como dice Richard Rorty:
Perder esa diferencia es, supongo, lo que todo poeta –todo hacedor, cualquiera que se propone crear algo nuevo- teme. Cualquiera que pasa su vida intentando formular una respuesta a la pregunta acerca de lo que es posible e importante, teme la extinción de esa respuesta. Pero eso no quiere decir meramente que uno tema que sus obras se pierdan o sean ignoradas. Porque ese temor se combina con el temor de que, aun cuando se conserven y se les preste atención, nadie encuentre allí nada distintivo. Las palabras (o las formas, los teoremas, los modelos de la naturaleza física) sometidas al gobierno de uno pueden parecer meramente artículos de stock, ordenados del modo acostumbrado. Uno no habrá dejado impresa su huella en el lenguaje sino que, en lugar de ello, habrá pasado la vida arrojando monedas ya acuñadas [Rorty 1991].
En el tributo que le hizo Pasinetti a su maestro, escribe: "¿Una vida finalmente plena? Quizás". El modelo clásico de crecimiento y ciclo que se presenta a continuación es, sin lugar a dudas, una prueba de que sus ideas no sólo dejaron huella en el lenguaje de los economistas sino que pueden convertirse en el punto de partida para desarrollar un proyecto disidente de la dinámica económica.
Las fluctuaciones económicas en el modelo de Goodwin se derivan del conflicto distributivo entre los trabajadores y los capitalistas. Las contradicciones entre las dos clases sociales, "en parte complementarias, en parte hostiles", se resuelven a espaldas de los actores. Cuando las variables distributivas (participaciones de salarios y ganancias en el producto) no corresponden a su nivel de equilibrio, la fuerza de negociación de los trabajadores durante el boom (alto nivel de empleo) o la implacable disciplina del mercado durante la recesión (desempleo rampante) determina el ritmo de crecimiento de los salarios, la tasa de ganancia y de crecimiento económico. Sin embargo, en el largo plazo, las participaciones de los ingresos de los asalariados y capitalistas permanecen constantes.
Esto sugiere una explicación de la paradoja de cada sindicalista que piensa que puede aumentar los salarios a expensas de las ganancias y está seguro que así ha sucedido en la realidad, mientras las escasas pruebas disponibles sugieren que esta distribución no ha cambiado significativamente durante un período de aumento del poder sindical [Goodwin 1967].3
Se asume que los trabajadores "gastan todo lo que ganan" y los capitalistas invierten todos sus beneficios. Todas las variables del modelo están expresadas en términos reales y en unidades netas. El dinero no juega ningún papel en la dinámica de corto y largo plazo de la economía, es un simple velo. No existen problemas de demanda efectiva, de hecho, Joan Robinson, reprendió a Goodwin cuando en una comunicación informal le dijo: "tú has cometido el mismo error de Marx, no pudiste escapar de la ley de Say". Efectivamente, el modelo asume implícitamente el postulado de que la oferta siempre crea su propia demanda, sin embargo, el mercado de trabajo no se vacía.
Mucho después, Goodwin [1983] retomó la crítica de su vieja amiga de Cambridge. En esta oportunidad encontró que cuando el nivel de producto está determinado por la demanda efectiva, las ganancias de los capitalistas son independientes de los salarios, más aún, la relación inversa entre los ingresos laborales y del capital desaparece en el corto plazo. Curiosamente, al final de esta breve nota aclaratoria, Goodwin reconoció que los resultados de su modelo sólo eran validos cuando la economía se encontraba cerca del pleno empleo.
[ ] es en la región de pleno empleo donde surge el problema de la relación inversa entre salarios y beneficios, puesto que con escasez de trabajo, el salario real tiende a incrementarse abruptamente. Este es el concepto marxista de fluctuación del ejército industrial de reserva [Goodwin 1983].
Es decir que la idea de Marx de la existencia de un ejército industrial de reserva de trabajadores presenta cierto isomorfismo con el concepto de tasa natural de desempleo -más conocido como NAIRU- presente en todos los modelos de la escuela de la nueva macroeconomía clásica. Goodwin nunca negó ser un keynesiano en el corto plazo, pero adoptó una posición clásica en el largo plazo. Sobre este mismo tema, Solow [1990] señaló las grandes dificultades analíticas de integrar el ciclo, el crecimiento y la demanda efectiva en el modelo de R. Goodwin, por ejemplo, afirmaba que "cualquier abandono de la Ley de Say tiene que iniciar con la provisión de un objeto de deseo no producible que sea un vehículo para el ahorro de las personas, diferente del capital real. El dinero fiat es una elección tradicional, pero quizás no sea la mejor". Una economía monetaria de producción es, por supuesto, la otra alternativa [Keynes 1936].
El modelo de Goodwin consiste en un sistema de ecuaciones diferenciales no lineales las cuales determinan, simultáneamente, la evolución de la tasa de empleo y de la participación de los salarios en el producto. El sistema de ecuaciones es el siguiente:
Se supone que la productividad del trabajo crece a una tasa constante. Siendon α la tasa de crecimiento de la productividad, la expresión se define como:
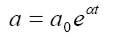 |
La tasa de crecimiento de la población se considera exógena y constante a lo largo del tiempo. Siendo β la tasa de crecimiento de la fuerza de trabajo, la ecuación es la siguiente:
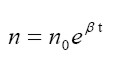 |
Se supone una razón capital-producto constante (σ). Siendo k el stock de capital y q el nivel de producto, la ecuación es la siguiente:
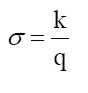 |
Sea l el nivel de empleo de la economía, es decir, la demanda de trabajo, y a la productividad media del trabajo, la relación se expresa como:
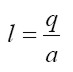 |
La participación de los ingresos de los trabajadores en el producto se puede definir como u, donde w es la tasa de salarios:
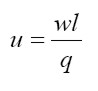 |
Utilizando la expresión para el nivel de empleo, se obtiene que:
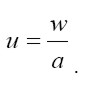 |
La tasa de empleo se define como v, donde l es la población ocupada y n la oferta laboral:
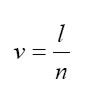 |
Se supone la existencia de una versión lineal de la curva de Phillips,4 que relaciona la tasa de crecimiento de los salarios reales y la tasa de empleo, tenemos entonces:
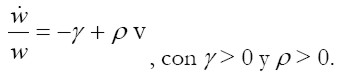 |
A partir del supuesto de que los beneficios se invierten en su totalidad, podemos escribir la expresión para la tasa de acumulación: 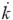 = ( 1 - u) q, si dividimos esta expresión por el stock de capital (k) tendremos la expresión para la tasa de ganancia, esto es:
= ( 1 - u) q, si dividimos esta expresión por el stock de capital (k) tendremos la expresión para la tasa de ganancia, esto es:
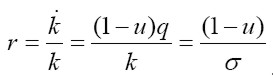 |
Como la razón capital-producto es constante, entonces es fácil mostrar que la tasa de crecimiento del producto es igual a la tasa de ganancia, así:
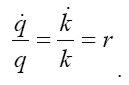 |
Las ecuaciones del sistema dinámico se derivan de la diferenciación con respecto al tiempo de las expresiones de la participación de los salarios en el ingreso (u) y de la tasa de empleo (v). Tomando logaritmos a ambos lados de las ecuaciones y derivando con respecto al tiempo tenemos:
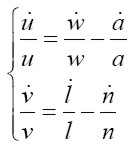 | [1] |
Este sistema está escrito en términos de las tasas de crecimiento de las variables de interés. Utilizando las definiciones anteriores, se puede llegar finalmente a nuestro modelo canónico de crecimiento y ciclo:
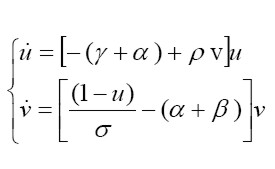 | [2] |
La solución de este sistema de ecuaciones no lineales es tediosa y complicada, de hecho, la mejor manera de resolverlo es por medio de métodos de linealización que se aplican a las expresiones anteriores. Sin embargo, Goodwin siguió la elegante solución cualitativa del modelo de Lotka y Volterra, que consiste en integrar el sistema por medio de la eliminación del factor dt, lo que permite igualar du y dv. Siguiendo el método presentado en Simmons [1972], tenemos:
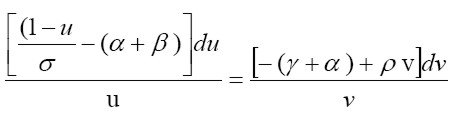 | [3] |
Integrando a ambos lados y agregando la constate de integración a la derecha se puede llegar a la siguiente igualdad en términos de funciones exponenciales:
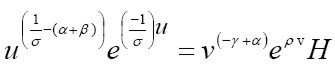 | [4] |
Donde, H es la constante de integración y depende de las condiciones iniciales del sistema. Esta última expresión se puede representar de una manera más sintética así:
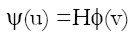 | [5] |
Las funciones ψ(u) y Φ(v) son no lineales respecto a sus argumentos (u y v respectivamente), tomado la primera y la segunda derivada de las funciones mencionadas, se puede mostrar que ψ(u) tiene un máximo y Φ(v) tiene un mínimo. Utilizando estas propiedades de las funciones y construyendo un sencillo diagrama de cuatro cuadrantes, podemos mostrar que la solución del sistema es una curva cerrada o ciclo límite. Ahora bien, el sistema posee un equilibrio de estado estacionario, el cual se encuentra igualando a cero las derivadas con respecto al tiempo del sistema [2], el cual además es el centro de todas las curvas cerradas que se pueden constituir como soluciones del sistema dadas las condiciones iniciales. En efecto, haciendo 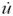 = 0 y
= 0 y 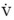 = 0, obtenemos los niveles de equilibrio para la participación de los ingresos de los trabajadores en el producto, para la tasa de empleo en el estado estacionario y el período del ciclo. Las expresiones son las siguientes:
= 0, obtenemos los niveles de equilibrio para la participación de los ingresos de los trabajadores en el producto, para la tasa de empleo en el estado estacionario y el período del ciclo. Las expresiones son las siguientes:
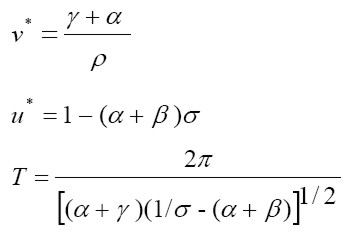 | [6] |
El diagrama se presenta a continuación. En el primer cuadrante se muestra una curva cerrada cuyos puntos (u,v) son una solución al sistema de ecuaciones. En el segundo cuadrante se dibuja la función Φ(v), en el tercer cuadrante se presenta una función lineal con pendiente H, y finalmente en el cuarto cuadrante la función ψ(u).
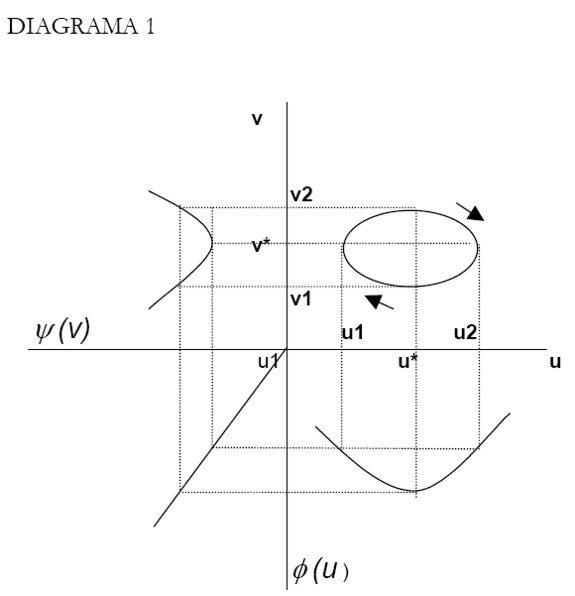 |
La familia completa de curvas cerradas que son la solución del modelo se pueden obtener mediante cambios en el valor de H, es decir, variando las condiciones iniciales. La dirección del movimiento sigue la trayectoria señalada por las flechas exteriores a la curva del primer cuadrante.
Así las cosas, una vez se defina una condición inicial, esta determina la curva cerrada sobre la cual el sistema se moverá eternamente. De otro lado, para valores iniciales definidos de u y v el sistema determina el punto de partida. Es claro que la tasa de empleo oscilará entre v1 y v2, mientras que la participación del ingreso de los trabajadores vibrará entre u1 y u2. "Así pues, podemos clasificar nuestro modelo como un oscilador conservador no lineal, afortunadamente de tipo soluble" [Goodwin 1967]. Si bien el modelo no presenta choques exógenos, cualquier evento que logre sacar a la economía de su ciclo límite original, lo hará de manera indefinida, es decir, la economía oscilará sobre otra curva cerrada, dejando para siempre su equilibrio inicial [Harvie 2000].
Supongamos que partimos de un punto en el cual la tasa de ganancia está por encima de su nivel de largo plazo (puntos a la izquierda de u*), en ese caso los capitalistas consideraran que la situación amerita aumentar el ritmo de inversión, por supuesto, esta percepción es consistente con el programa óptimo del empresario individual. Sin embargo, no contempla el efecto del aumento de la inversión sobre la tasa de ganancia de la economía, "esto significa que puede surgir una divergencia entre la optimización individual y colectiva, y que el resultado de la conducta colectiva de los capitalistas puede ser algo diferente de lo que buscaba el capitalista individual" [Medio 1975].
Ahora bien, dada la relación capital-producto constante, el mayor ritmo de acumulación incrementa la demanda de trabajo, lo que se refleja en incrementos de la tasa de empleo y en aumentos de los salarios reales por encima de la tasa de crecimiento de la productividad media del trabajo. Los mayores salarios reducen paulatinamente la tasa de ganancia, lo que reduce el ritmo de acumulación de capital y la tasa de crecimiento económico. Después de cierto punto, la tasa de empleo empieza a reducirse, el ejército industrial de reserva se expande nuevamente y los salarios disminuyen, creciendo a tasas menores que la productividad, ello permite que los beneficios se recuperen, que la tasa de ganancia aumente, iniciándose un nuevo ciclo, con mayores ritmos de acumulación, de empleo y de crecimiento económico. En palabras de Goodwin:
El progreso se traduce primero en ganancias, pero las ganancias conducen a la expansión, y la expansión impone el ascenso de los salarios y el descenso de las ganancias. Tenemos así una ley de hierro de las ganancias malthusiana. Esto se debe a la tendencia del capital, aunque no de los capitalistas, a crecer excesivamente [Goodwin 1967].
EVALUACIÓN EMPÍRICA DEL MODELO: UNA APROXIMACIÓN
La evaluación de los modelos teóricos requiere, entre otras cosas, información consistente de las principales variables económicas, criterios metodológicos rigurosos que permitan estimar los parámetros de interés con base en las relaciones causales que establece la teoría y las propiedades estadísticas del verdadero proceso generador de los datos. Si bien en la actualidad se cuenta con un acervo de datos confiable sobre un conjunto importante de magnitudes económicas, lo cierto es que aún se carece de series de tiempo lo suficientemente largas -infinitas- que permitan determinar las propiedades del proceso generador de los datos y especificar el modelo econométrico más adecuado.
De otro lado, el quehacer de los macro-econometristas se ha reducido a una mera aplicación mecánica y ateórica de pruebas econométricas que evalúan la presencia o no de raíces unitarias en las series de tiempo. Sin embargo, es muy bien conocido que las pruebas estadísticas son poco potentes ante cambios leves en la especificación de los test. De hecho, para poder saber si una serie es estacionaria en diferencia (raíz unitaria) o estacionaria en tendencia (no tiene raíz unitaria) se requiere de un número infinito de datos. Recientemente, Chumacero [2001] ha logrado diseñar una interesante metodología para construir test de raíz unitaria indirectos a partir de la teoría económica. Aplicando estos procedimientos para variables como el PIB y el consumo en Chile -que tradicionalmente se consideraban como series no estacionarias aplicando los procedimientos convencionales-, encuentra que realmente son estacionarias en tendencia.
La lección que surge de este apasionante debate es sencilla: la econometría sin teoría es poco útil, en muchos casos engañosa, y casi siempre intrascendente. Solow manifiesta lo siguiente:
El verdadero test de un simple modelo es el que nos ayuda a darle sentido al mundo. Una correspondencia razonable con los hechos es, sin duda, una condición para que el modelo sea útil para interpretar el mundo. Pero la clase usual de sistemas de ecuaciones sobre identificados o vectores autoregresivos, acompañados por una inapropiada batería de test de significancia, no parece ofrecer alguna guía [Solow 1990].
En este orden de ideas, se presentan las especificaciones econométricas que se utilizaron para evaluar la pertinencia del modelo de R. Goodwin para Colombia. Por supuesto, las ecuaciones econométricas respetan el supuesto de estacionariedad explícito en las ecuaciones del modelo. El procedimiento sigue el trabajo de Harvie [2000] en el cual se realiza el mismo ejercicio para diez países de la OCDE. En dicha investigación se ofrecen dos tipos de pruebas. En primer lugar, se presenta una prueba cualitativa en el espacio de fase (u,v) la cual muestra que la hipótesis de los ciclos límite tiene cierto respaldo en los datos, de allí la importancia de mejorar el modelo, mediante un proceso de refinamiento y flexibilización de los supuestos.
Al respecto, vale la pena comentar que el modelo de Goodwin no es muy interesante cuando se cambia marginalmente su especificación, pues al carecer de estabilidad estructural, las propiedades de su simple y bella solución pueden desaparecer [Medio 1980]. En segundo lugar, las pruebas econométricas rechazan la hipótesis central del modelo. En efecto, los parámetros estimados predicen pobremente los valores del centro del ciclo límite, mientras que los datos invalidan los principales supuestos restrictivos del modelo. Una explicación del pobre ajuste econométrico del modelo para las variables estado de economías como la de Estados Unidos puede ser la supuesta existencia de una curva de Phillips nominal y no real [Solow 1990].
En la Gráfica 1 se presenta el espacio de fases para las variables (u,v) con datos de la economía colombiana entre 1951 y 1995. Aunque la dinámica de las variables no muestra una correspondencia nítida con el modelo de Goodwin, es decir, no describen una curva cerrada cuya dirección sigue las manecillas del reloj, se pueden observar, por lo menos, dos ciclos que constatan, débilmente, la teoría del crecimiento cíclico. En efecto, entre 1957 y 1966, la evolución de la tasa de empleo y de la participación de los salarios en el ingreso siguió la trayectoria que predice el modelo. El otro período en el cual se encuentra una dinámica favorable con la teoría de Goodwin es 1968-1974, sin embargo, en este período la relación es más débil.
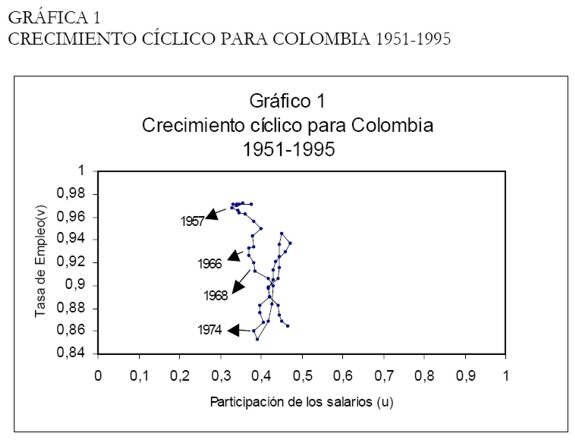 |
Si bien esta evidencia cualitativa es frágil, sugiere que el conflicto distributivo puede ser una de las causas que originan el movimiento oscilante e irregular de la actividad económica No obstante, se debe aceptar que no necesariamente es la única fuente que genera el crecimiento cíclico. Ahora bien, este resultado era de esperarse, pues el modelo –como Goodwin reconoció– es una drástica simplificación de la realidad, cuyo objetivo central era evaluar las consecuencias de la lucha distributiva sobre la dinámica de las economías capitalistas contemporáneas.
Los valores de equilibrio de u* y v* se determinaron a partir de los promedios de las series colombianas entre 1951 y 1995. En efecto, u* = 0.40 y v* = 0.91. Los parámetros (α, β, γ, ρ, σ) se estimaron por métodos econométricos. Posteriormente, se utilizaron las expresiones en [6] para obtener las estimaciones de las variables de interés:
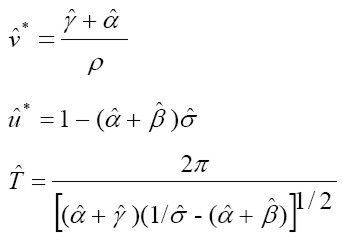 | [7] |
Los resultados de las estimaciones econométricas y las pruebas estadísticas se comentan a continuación. En el cuadro 1 se presentan las regresiones realizadas para determinar los parámetros del sistema de Goodwin.
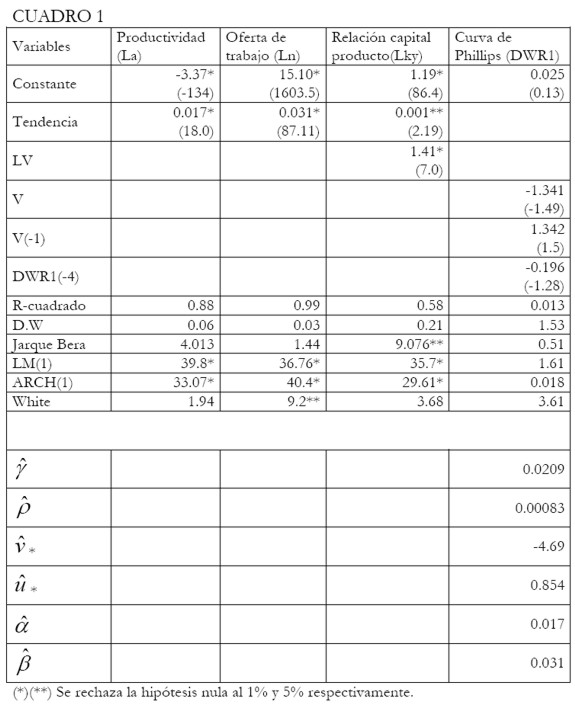 |
Como se puede constatar, los resultados cuantitativos rechazan la hipótesis central del modelo de crecimiento cíclico. Los parámetros de la curva de Phillips lineal no son los esperados y ninguno es significativo a los niveles convencionales de significancia estadística. La constante tiene signo positivo y el valor del coeficiente de largo plazo de la tasa de empleo es prácticamente cero. De allí que el valor predicho de v* sea absurdo (-4.1). De otra parte, la predicción sobre la participación de los ingresos de los trabajadores en el Pib prácticamente duplica el promedio que se obtiene de los datos.
Finalmente, no se puede asumir que la relación capital-producto se mantuvo constante durante el período de estimación. Los coeficientes sobre LV y la tendencia son significativamente diferentes de cero a los niveles convencionales del 95% de confianza estadística. Se realizó adicionalmente una prueba econométrica para evaluar si la curva de Phillips es real o nominal, se rechazó la hipótesis de trabajo de Goodwin de la existencia de una relación entre la tasa de crecimiento del salario real y la tasa de empleo únicamente.5
Al respecto, vale la pena comentar que en el país se han estimado versiones no lineales de la curva de Phillips. Los trabajos más interesantes al respecto son Birchenall [1999] y Gómez y Julio [2000]. Por supuesto, al incorporar estos resultados en el modelo junto con algunas características específicas del caso colombiano, como la estabilidad de la inflación y la indexación de los salarios,6 podrían mejorar las estimaciones de los parámetros del modelo.
CONCLUSIONES
El objetivo del presente trabajo fue exponer y evaluar la hipótesis del crecimiento cíclico de R. Goodwin. Se utilizaron datos colombianos para contrastar las ideas del modelo. Se encontró que a nivel cualitativo, la dinámica de las variables de estado en el espacio de fases muestra cierta correspondencia con las predicciones teóricas, al menos para dos períodos: 1957-1966 y 1968-1974. Los resultados cuantitativos rechazan los supuestos del modelo y los modelos empíricos no describen el verdadero proceso generador de los datos. En efecto, la relación capital-producto no se mantuvo constante a lo largo del período de estimación y la curva de Phillips real no encuentra soporte en los datos. Aquí podemos traer a colación el comentario de Solow:
En una economía con curva de Phillips nominal, la participación de los salarios será afectada por fuerzas tales como la rapidez y el vigor con que los precios nominales responden a los desequilibrios de la oferta y la demanda (la conducta de los mark-up sobre costos) y la conducta cíclica de la productividad en sí misma (ignorada en el modelo formal) [Solow 1990].
Este trabajo es sólo un ensayo preliminar, y por tanto, un fracaso parcial. Como dice Koyre un hecho para ser científico requiere ser verificado teóricamente. En este sentido, el trabajo futuro reside en ampliar y refinar el modelo de crecimiento cíclico, integrar hipótesis y relajar condiciones. Por supuesto, inventar nuevos métodos. Al fin y al cabo, "el riesgo de la razón debe, por otra parte, ser total. Todo o nada. Si la experiencia triunfa, sé que cambiará completamente mi mente. Hago una experiencia física para cambiar mi mente. Qué haría yo, en efecto, con una experiencia que sólo confirmara lo que sé y, por consiguiente, lo que soy" [Bachelard 1972].
NOTAS AL PIE
1 Kalecki es una notable excepción.
2 Goodwin fue un gran pintor moderno y gran maestro. Durante su estadía en Inglaterra aprovechó para estudiar y mejorar sus técnicas de pintura. Algunos de sus discípulos cuentan que les otorgaba, sin reparo y con generosidad, una gran cantidad de su tiempo para discutir sus ideas y trabajos. Fue un hombre modesto, afirmaba de sí mismo: “siempre sufrí de una inhabilidad para comprender y desarrollar la matemática pura. Mi esfuerzo inicial, bajo la guía del eminente matemático Marston Morse fue penoso.” (citado por Velupillai [ 1990a])
3 Sordi [1999] extiende el modelo de Goodwin asumiendo que los trabajadores ahorran, ello permite comprender mejor los determinantes de la distribución del ingreso siguiendo los trabajos clásicos de Kaldor y Pasinetti
4 Una especificación más general y no lineal para la tasa de crecimiento de los salarios fue propuesta recientemente por Anwar Shaikh [2002].
5 La prueba no se reporta. Se siguió el trabajo de Harvei [2000]. El test F(3.40) = 3.2 es mayor que el nivel crítico al 95% de confianza 2.84.
6 Agradezco esta sugerencia del profesor Mario García.
REFERENCIAS BIBLIOGRÁFICAS
1. Bachelard, Gaston. 1972. El Compromiso Racionalista, Siglo XXI ed., México. [ Links ]
2. Birchenall, Javier A. 1999. "La Curva de Phillips, la Crítica de Lucas y la persistencia de la inflación en Colombia", Archivos de Macroeconomía, n. 102. DNP. [ Links ]
3. Boldrin, Michele. 1988. "Persistent oscillations and Chaos in Dynamic Economic models: Notes for a Survey", en Philip W. et al. [1998]. [ Links ]
4. Chumacero, Rómulo. 2001. "Testing for Unit Roots Using Economics", Universidad de Chile, julio, mimeo. [ Links ]
5. Desai, Meghnad y Ormenod, Paul. 1998. "Richard Goodwin: a short appreciation", The Economic Journal, 108, septiembre, 1431-1435. [ Links ]
6. Gómez, J. y Julio, J. M. 2000. "An Estimation of the Non Linear Phillips Curve in Colombia", Borradores Semanales de Economía, n. 160. [ Links ]
7. Goodwin, Richard. 1967. "Un ciclo de crecimiento", en Hunt y Schwartz [1967]. [ Links ]
8. Goodwin, Richard. 1983. "A note on wages, profits and fluctuating growth rates", Cambridge Journal of Economics, 7, 305-309. [ Links ]
9. Harcourt, G. C. 1985. "A twentieth-century eclectic: Richard Goodwin", Journal of Post Keynesian Economics, v. 7, n. 3, 410-421. [ Links ]
10. Harvie, David. 2000. "Testing Goodwin: growth cycles in ten OECD countries", Cambridge Journal of Economics, 24, 349-376. [ Links ]
11. Hunt y Schwartz, editores. 1967. Crítica de la teoría económica. Lecturas del Trimestre Económico, Fondo de Cultura Económica (FCE), 1977, México. [ Links ]
12. Keynes, J. M. 1936. Teoría general de la ocupación, el interés y el dinero, FCE, 1986. [ Links ]
13. Medio, Alfredo. 1980. "A classical model of business cycles", en Nell [1980]. [ Links ]
14. Nell. Editor. 1980. Growth, Profits and property, Cambridge University Press. [ Links ]
15. Pasinetti, Luigi. 1996. "Richard Murphey Goodwin (1913-1996): a pupil´s tribute to a great teacher", Cambridge Journal of Economic, 20, 645-649. [ Links ]
16. Philip, Anderson, Arrow, Kenneth, y Pines, David (editores). 1998. The Economy as an Evolving complex system, Santa Fe Institute, Addison-Wesley. [ Links ]
17. Rorty, Richard. 1991. Contingencia, ironía y solidaridad, Piados. Barcelona. [ Links ]
18. Rosser, J. Barkley Jr. 1999. "Complex Dynamics in New Keynesian and Post Keynesian economics", http://csf.colorado.edu/pkt/seminars/rosser/rosser.htm [ Links ]
19. Rosser, J. Barkley Jr. 2000. "Aspects of Dialectics and Non-linear Dynamics", Cambridge Journal of Economics, 24, 311-324. [ Links ]
20. Shaikh, Anwar. 2002. "Nonlinear Dynamics and Pseudo-Productions Functions", http://homepage.newschool.edu/AShaikh/ [ Links ]
21. Simmons, F. 1972. Ecuaciones diferenciales con aplicaciones y notas históricas, McGrawHill, 1977. [ Links ]
22. Solow, Robert. 1987. La Teoría del Crecimiento. Editorial FCE, México. [ Links ]
23. Solow, Robert. 1990.Goodwin´s Growth Cycle: Reminiscence and Rumination", en Velupillai [1990]. [ Links ]
24. Sordi, Serena. 1996. "Chaos in Macrodynamics: an Excursión through the Literature", Universidad de Siena, mimeo. [ Links ]
25. Sordi, Serena. 1999. "Persistent and irregular growth cycles when workers save: A reformulation of Goodwin´s model along Kaldorian-Pasinettian lines", Quaderni, Università degli Studi di Siena, n. 263. [ Links ]
26. Velupillai K Vela. Editor. 1990. Nonlinear and Multisectorial Macrodinamics: Essays in Honour of Richard Goodwin, New York University Press, Washington Square. [ Links ]
27. Velupillai K Vela. 1990a. "The (Nonlinear) life and (Economic) Times of Richard Goodwin", en Velupillai [1990] [ Links ]
28. Velupillai K. Vela 1998. "Richard Goodwin 1913-1996", The Economic Journal, 108, septiembre,. 1436-1449. [ Links ]














