Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.22 no.39 Bogotá July/Dec. 2003
APLICACIÓN DE LA TEORÍA DEL PORTAFOLIO EN EL MERCADO ACCIONARIO COLOMBIANO
Luis Ángel Medina*
* Economista de la Universidad Nacional de Colombia y Especialista en Estadística de la misma Universidad. Enviar los comentarios al correo: luis1000@lycos.com. Artículo recibido el 12 de mayo de 2003 y aprobado el 20 de octubre del mismo año.
Resumen
Este artículo emplea la teoría del portafolio de Harry Markowitz para construir dos portafolios, cada uno compuesto por cinco acciones de la Bolsa de Valores de Colombia. Estos portafolios se elaboran pensando en dos inversionistas con aversión al riesgo pero con distinto nivel de tolerancia al mismo.
Palabras clave: cartera, inversiones, acciones, optimización.JEL: G100, G110, C610, C600.
Abstract
This article uses Harry Markowitz’s portfolio theory to construct two portfolios, each made up of five shares on the Colombia stock-exchange. These portfolios have been drawn up bearing in mind the idea of two investors who whilst having an aversion to risk do have a distinct level of tolerance towards it.
Key words: portfolio, investments, shares, optimization. JEL: G100, G110, C610, C600.
Résumé
Cet article utilise la théorie du portefeuille d´Harry Markowitz pour créer deux portefeuilles, chacun des deux composé par cinq actions de la Bourse de Valeurs Colombienne. Ces portefeuilles ont été réalisés en pensant à deux investisseurs hostiles au risque mais ayant un niveau différent de tolérance à celui-ci.
Mots clés: portefeuille, investissements, actions, optimisation. JEL: G100, G110, C610, C600.
INTRODUCCIÓN
Markowitz [ 1952] desarrolló una teoría en la cual los inversionistas construyen portafolios basados exclusivamente en el riesgo y en el rendimiento esperado. Aquí el riesgo es entendido como la variabilidad del retorno de la inversión, y los inversionistas –en este modelo– prefieren lograr rendimientos con la menor variabilidad posible, es decir, que tienen aversión al riesgo. Cuando se invierte un capital en un portafolio se logra conseguir un rendimiento particular con menor riesgo que el de invertir todo el capital en un solo activo. Este fenómeno es conocido como "diversificación".
Es común pensar que a mayor número de activos, mayor diversificación del portafolio. Por ejemplo, si se invierte un capital en n activos en iguales cantidades, es posible ver que el riesgo de esta inversión disminuye a medida que n se hace más grande. Este tipo de diversificación se conoce como "diversificación ingenua". El modelo de Markowitz no está basado en esta clase de diversificación, sino en las correlaciones de los activos de riesgo. La diversificación basada en la correlación, y no en el número de activos, es llamada "diversificación eficiente".
El artículo inicia con la presentación de los conceptos de riesgo y rendimiento esperado, tanto para un activo individual como para un portafolio. Luego se expone la función de utilidad esperada de un inversionista. La siguiente sección se trata de cómo se compone un conjunto eficiente de portafolios de activos de riesgo que contenga las mejores combinaciones de riesgo y rendimiento esperado (R-R). Más adelante se muestra que al incluir un activo cuyo retorno no es aleatorio es posible construir portafolios con mejores combinaciones de R-R. Bajo la existencia de este activo, además de otras condiciones, es posible mostrar que el portafolio de activos de riesgo es independiente de las preferencias. Esto último se conoce como el "teorema de la separación". Finalmente, se construyen dos portafolios eficientes con cinco acciones de la bolsa de Valores de Colombia (BVC), uno para un inversionista conservador y otro para un inversionista emprendedor, ambos aversos al riesgo.
RENDIMIENTO ESPERADO Y RIESGO
Dado que el rendimiento futuro de los activos financieros es incierto, éste es considerado como una variable aleatoria. Así, la incertidumbre hace que además de los rendimientos esperados, los analistas deban tener en cuenta el riesgo de los activos financieros. Por este motivo, la teoría moderna de la inversión hace uso de distribuciones de probabilidad para estimar el rendimiento futuro de los activos financieros y el riesgo asociado.
La teoría del portafolio considera que en las decisiones de inversión sólo se tienen en cuenta el retorno esperado y el riesgo. El primer momento de la distribución del retorno es usado como estimación del retorno esperado, y la varianza (o la desviación estándar) del retorno es empleada como medida del riesgo. En el área financiera, la desviación estándar es conocida como la volatilidad.
Estimación del rendimiento y riesgo de un activo individual
El retorno esperado de un activo de riesgo es calculado con el primer momento de la distribución de los retornos:
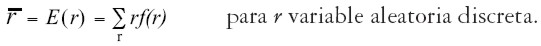 | [1] |
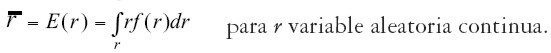 | [1'] |
Donde f(r) representa la función de probabilidad del retorno, la cual puede ser continua o discreta. El segundo momento de esta distribución, con respecto a la media, constituye el riesgo del activo:
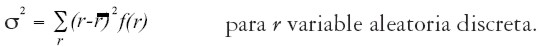 | [2] |
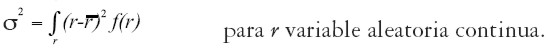 | [2'] |
Adicional al riesgo y al rendimiento esperado, la teoría requiere el cálculo de las relaciones entre los rendimientos de estos activos. Para este cálculo se puede emplear la covarianza o el coeficiente de correlación1. La covarianza entre retornos de las parejas de activos A y B se determina como:
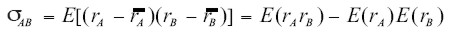 | [3] |
y el coeficiente de correlación de los retornos de esta pareja como:
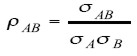 | [4] |
El coeficiente de correlación ρ es una medida que varía en el intervalo [ -1, 1] . Un valor ρ = -1 indica una perfecta relación lineal negativa, mientras que un valor de ρ = +1 indica una perfecta relación lineal positiva entre los retornos de A y B.
Estimación del rendimiento y del riesgo de un portafolio
Un portafolio constituido por n activos individuales se puede representar mediante un vector de n elementos: [ w1, w2,...,wn] T tal que 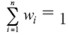 . El elemento wi indica la tasa de participación del activo individual i en el portafolio.
. El elemento wi indica la tasa de participación del activo individual i en el portafolio.
La esperanza matemática del rendimiento de un portafolio resulta ser el promedio de los n rendimientos esperados individuales, ponderados por la participación de cada activo individual en el portafolio:
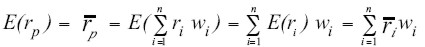 | [5] |
Este también se puede expresar como el producto entre el vector transpuesto de w y el vector de rendimientos esperados individuales 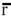 :
:
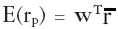 | [5'] |
De otro lado, la varianza del portafolio se determina a partir de:
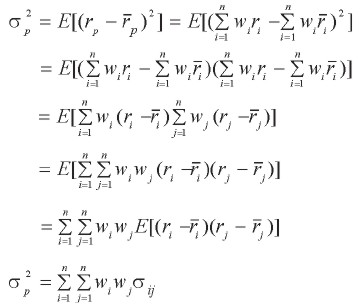 | [6] |
donde i y j representan dos activos individuales del portafolio, wi y wj sus participaciones en el portafolio, y σij la covarianza entre sus retornos. En la expresión [ 6] la varianza del portafolio está en función de las participaciones de los activos individuales dentro del portafolio, y de las covarianzas (o correlaciones) entre los retornos medios individuales. Se observa que entre más baja sea la covarianza (o correlación) entre los retornos de los activos individuales, menor será la variabilidad (riesgo) del portafolio. Así, el poder de diversificación de un portafolio está en la correlación. Los portafolios que incluyan activos con la menor correlación posible (especialmente negativa) presentarán menor volatilidad –menor riesgo– que aquellos que incluyan activos altamente correlacionados.
La varianza del portafolio también puede representarse matricialmente como:
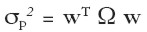 | [6'] |
donde Ω representa la matriz de varianzas y covarianzas de los retornos de los activos del portafolio.
ESTRUCTURA DE PREFERENCIAS BAJO INCERTIDUMBRE
Bajo incertidumbre, la estructura de preferencias difiere del enfoque tradicional, en el cual, a partir de ciertos axiomas se construye una función de utilidad que depende de la cantidad de bienes no inciertos. La utilidad que deriva un consumidor o inversionista de un activo incierto puede ser tratada por la función de utilidad propuesta por Neumann y Morgenstern [ 1944] . Estos autores definen el concepto de "utilidad esperada" como la utilidad de un activo incierto o variable aleatoria. Tomemos el caso en que la utilidad de un inversionista se representa por una función que está en términos del rendimiento cierto: u = u(r). Al adquirir un activo incierto cuya función de probabilidad del retorno es f(r), la utilidad esperada de este inversionista será:
 | [7] |
 | [7'] |
De este modo, la utilidad esperada queda en términos de la función de utilidad del retorno bajo certeza y de la función de probabilidad del retorno. Markowitz propone que la anterior función de utilidad esperada sea resumida por los dos primeros momentos de la distribución de probabilidad del retorno:
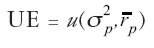 | [8] |
Adicionalmente, Markowitz supone que el inversor es racional y averso al riesgo, es decir, que el inversionista prefiere mayor a menor retorno y, a su vez, menor a mayor riesgo. Asumiendo que 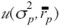 es diferenciable, entonces:
es diferenciable, entonces:
 |
Alternativamente, podemos formalizar este argumento con el siguiente axioma:
Axioma Media-Volatilidad (M-V): sean dos portafolios factibles, A y B, con combinaciones media-volatilidad: 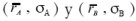 , respectivamente. El portafolio A se prefiere al portafolio B si se cumple que:
, respectivamente. El portafolio A se prefiere al portafolio B si se cumple que:
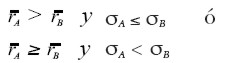 |
Si los principales criterios de inversión son el riesgo y el rendimiento esperado, resulta conveniente representar todos los portafolios en un espacio P generado por la media y la volatilidad: 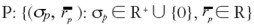 . Ver Gráfica 1
. Ver Gráfica 1
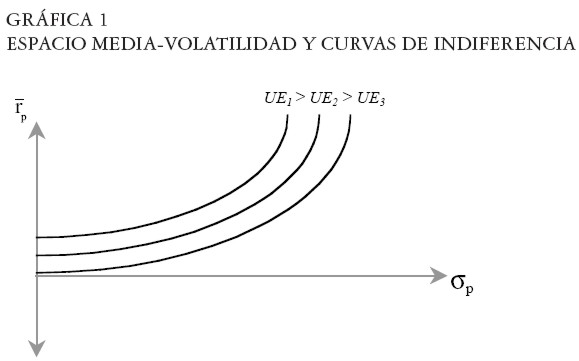 |
En el espacio Media-Volatilidad se grafican las curvas de indiferencia de los inversionistas. Cada una de estas curvas representa un nivel de utilidad esperada –razón por la cual son paralelas– y entre más hacia el noroeste se localicen, mayor utilidad esperada representan. Las curvas de indiferencia son de pendiente positiva por el axioma M-V, ya que el riesgo es un mal y el retorno esperado es un bien. Por lo tanto, partiendo de un portafolio inicial, si existe otro con mayor rendimiento esperado, éste debe contener mayor riesgo para que pertenezca al conjunto de indiferencia del portafolio inicial. Adicionalmente, se asume convexidad de las curvas de indiferencia, lo cual implica que el inversor tiene aversión creciente al riesgo con respecto al nivel de riesgo asumido.
En síntesis, el modelo de preferencias propuesto por Markowitz implica que los inversionistas sólo se fijan en el retorno medio y en el riesgo de la inversión. James Tobin [ 1958] muestra las condiciones bajo las cuales tal argumento es válido. Si la función de utilidad en términos del retorno es cuadrática o el retorno se distribuye normalmente, este modelo de preferencias propuesto por Markowitz es adecuado.
EL MODELO DE DIVERSIFICACIÓN DE MARKOWITZ
De las ecuaciones [ 5] y [ 6] se desprende que la información necesaria para el análisis de portafolio requiere la siguiente información: n medias (o valores esperados), n varianzas (o desviaciones estándar) y n(n-1)/2 covarianzas (o coeficientes de correlación). Adicionalmente, se requiere conocer la función de utilidad esperada del inversionista, la cual está expresada exclusivamente en términos de los dos primeros momentos del retorno.
Un modelo de diversificación eficiente considera óptimo el portafolio que maximiza la función de utilidad esperada del inversionista dentro de un conjunto factible de portafolios. El conjunto factible de portafolios es el conjunto de vectores w tales que la suma de sus elementos sea igual a uno: 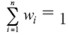 . Esta restricción indica que el inversionista gasta exactamente un capital disponible. Dado que el conjunto factible es extenso, conviene determinar un subconjunto de este conjunto tal que esté constituido exclusivamente de portafolios eficientes en el sentido del axioma M-V. La representación gráfica de este conjunto se denomina "frontera eficiente de portafolios". En la frontera eficiente, los portafolios cumplen dos requisitos de eficiencia del axioma M-V:
. Esta restricción indica que el inversionista gasta exactamente un capital disponible. Dado que el conjunto factible es extenso, conviene determinar un subconjunto de este conjunto tal que esté constituido exclusivamente de portafolios eficientes en el sentido del axioma M-V. La representación gráfica de este conjunto se denomina "frontera eficiente de portafolios". En la frontera eficiente, los portafolios cumplen dos requisitos de eficiencia del axioma M-V:
1. Son de mínimo riesgo entre portafolios de igual rendimiento esperado.
2. Son de máximo rendimiento entre portafolios de igual riesgo.
La forma de la frontera eficiente de portafolios depende de la correlación entre los retornos de los activos del portafolio. A continuación se analizan tres casos para portafolios constituidos por sólo dos activos o portafolios cuando: (i) el coeficiente de correlación entre los retornos de estos activos es +1, (ii) el coeficiente de correlación es –1; y (iii) el coeficiente de correlación toma un valor general en el intervalo (-1, 1).
Correlación perfectamente positiva, r = +1
Consideremos una inversión en sólo dos acciones, A y B, con combinaciones de media-volatilidad 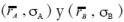 , respectivamente. Por conveniencia, supongamos que:
, respectivamente. Por conveniencia, supongamos que: 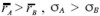 , y que el coeficiente de correlación de rendimientos A y B es uno: ρAB= +1.
, y que el coeficiente de correlación de rendimientos A y B es uno: ρAB= +1.
Las combinaciones R-R que se obtienen a partir portafolios formados con estas dos acciones, se representan por la ecuación:
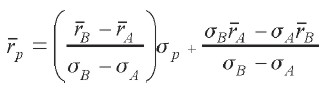 |
Gráficamente estos portafolios se localizan en el segmento lineal AB de la Gráfica 2.
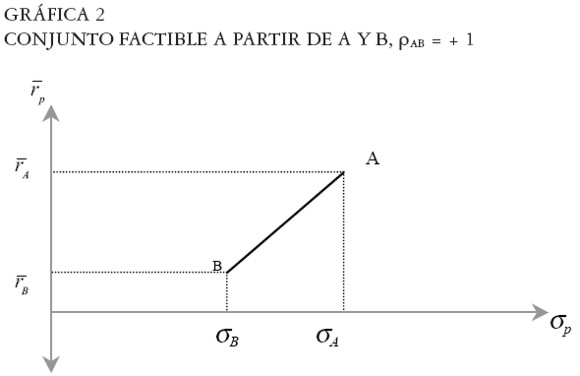 |
Correlación perfectamente negativa, ρ = -1
Sea ahora el caso en el cual la correlación entre los activos A y B es -1. Las combinaciones de R-R que se obtienen a partir de portafolios constituidos con A y B se representan mediante la expresión:
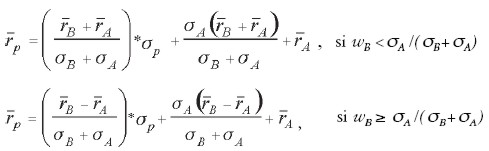 |
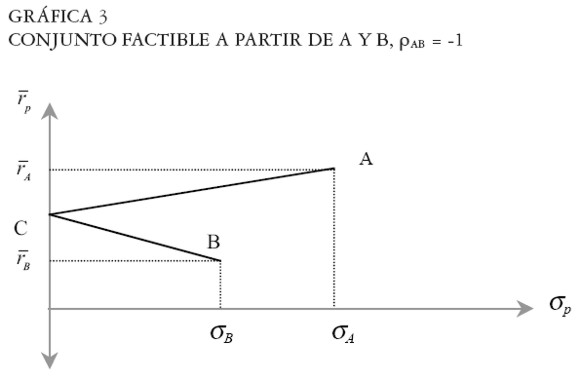
donde wB es la proporción del portafolio invertida en el portafolio B. En este caso, la forma del conjunto factible se parte en dos (ver Gráfica 3), una con pendiente positiva (segmento AC) y otra de pendiente negativa (segmento CB), dependiendo del valor que tome wB.
En el caso de correlación negativa perfecta encontramos diversificación útil, puesto que existen portafolios del conjunto factible con menor riesgo y mayor retorno que el del activo B. Por ejemplo, el portafolio de mínimo riesgo es el de desviación estándar nula, localizado en el punto C de la Gráfica 3. Este portafolio se obtiene cuando wB= σA /(σB+σA). Este caso particular de inversión sin riesgo sólo ocurre cuando la correlación entre los portafolios es perfectamente negativa.
 |
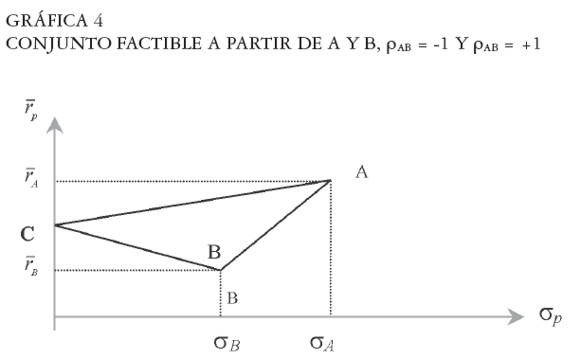
La Gráfica 4 resume los dos casos extremos de correlación (ρ= 1 y ρ= -1). Los portafolios comprendidos entre A y B corresponden al primer caso extremo (ρ = 1), y los comprendidos entre A y C, y C y B corresponden al caso de correlación negativa perfecta (ρ= -1). En la práctica no es común encontrar activos con rendimientos perfectamente correlacionados; siendo más frecuente encontrar activos con correlación en el intervalo (-1, +1).
 |
Correlación entre -1 y +1, r 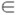 t(-1, 1)
t(-1, 1)
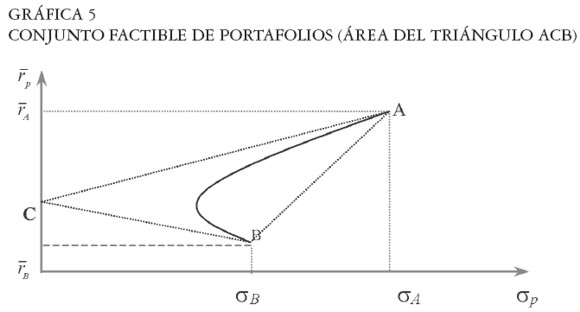
En general, para cualquier valor específico del coeficiente de correlación entre -1 y +1, los portafolios se localizarán dentro del triángulo ACB de la Gráfica 4. Con excepción de los dos casos extremos de correlación, la forma del conjunto factible es una hipérbola localizada dentro del triángulo ACB, como muestra la Gráfica 5.
En la Gráfica 5 se ilustra la forma general del conjunto factible cuando el coeficiente de correlación se encuentra entre -1 y +1. Así, para cualquier valor de ρ, el conjunto factible de portafolios comprenderá toda el área del triángulo ACB. Cuando el número de activos que compone el portafolio es mayor que dos (n > 2), la forma del conjunto factible es el área comprendida entre A, C, B, A de la Gráfica 6, la cual tiene forma de sombrilla.
 |
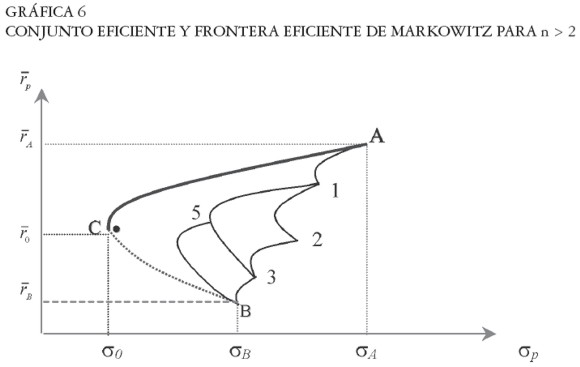 |
El portafolio de máximo y mínimo rendimiento es el constituido únicamente con el activo de mayor y menor retorno esperado entre los n activos del portafolio, respectivamente (puntos A y B). El portafolio de mínimo riesgo corresponde al punto de inflexión de la frontera del conjunto factible (punto C). Lo anterior es válido cuando los portafolios son legítimos (wi > O, para i = 1,2,...,n).
El conjunto factible tiene forma de sombrilla, puesto que entre los activos A y 1, por ejemplo, se pueden formar todos los portafolios comprendidos entre la hipérbola que une a A con 1. Igual ocurre entre los activos 1 y 2, 2 y 3, 1 y 3, etc. También se pueden combinar diferentes portafolios para formar otros, como sucede en el caso del portafolio 5 con el activo B. En general, se obtendrán infinitas combinaciones de activos y portafolios, generando como conjunto factible un área con forma de sombrilla. Los portafolios eficientes corresponderán a la frontera izquierda de dicha área, puesto que representan el mínimo riesgo para cada nivel de rendimiento. Sin embargo, los portafolios ubicados entre los puntos C y B, sin incluir al portafolio C, no hacen parte de la frontera eficiente, puesto que son dominados, de acuerdo con el axioma M-V, por los portafolios comprendidos entre C y A. De igual forma, los portafolios ubicados entre A y B son dominados. Como resultado, la frontera eficiente corresponde a la curva entre A y C (curva gruesa de la Gráfica 6). En adelante, esta frontera se denomina Frontera Eficiente Markowitz (E-M).
Determinación de la frontera eficiente de Markowitz (E-M)
Para determinar matemáticamente la frontera eficiente de Markowitz (E-M) se debe resolver el siguiente problema, para diferentes niveles de rendimiento esperado 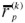 :
:
 | [9] |
donde el vector 1n representa un vector cuyos n elementos son todos unos. Aquí se busca un portafolio w de mínima varianza (wT Ωw), para un nivel particular de rendimiento requerido del portafolio 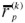 (primera restricción), en el conjunto factible de portafolios (vectorialmente, los portafolios tales que: wT1n =1, segunda restricción). Asumiendo la posibilidad de realizar ventas en corto2, el problema [ 9] puede resolverse por el método de Lagrange:
(primera restricción), en el conjunto factible de portafolios (vectorialmente, los portafolios tales que: wT1n =1, segunda restricción). Asumiendo la posibilidad de realizar ventas en corto2, el problema [ 9] puede resolverse por el método de Lagrange:
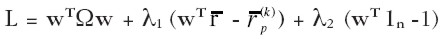 | [10] |
Las condiciones de primer orden son:
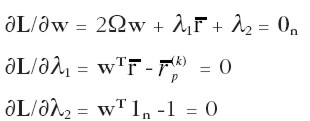 |
Estas condiciones constituyen un sistema de n+2 ecuaciones con n+2 incógnitas. Multiplicando por ½ a ambos lados de la primera ecuación matricial y despejando los términos independientes en las dos últimas ecuaciones, el sistema puede representarse matricialmente como:
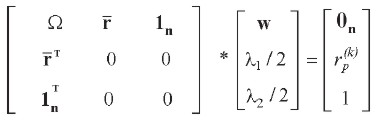 |
Despejando matricialmente el anterior sistema:
 | [11] |
La solución anterior constituye la combinación ponderacional óptima w (portafolio eficiente) para un nivel particular de rendimiento esperado del portafolio 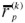 . Este rendimiento constituye la variable exógena del sistema de ecuaciones [ 11] . Entonces, para construir la frontera E-M se debe resolver [ 11] para distintos valores particulares de
. Este rendimiento constituye la variable exógena del sistema de ecuaciones [ 11] . Entonces, para construir la frontera E-M se debe resolver [ 11] para distintos valores particulares de 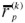 . El sistema tiene solución única (a un nivel particular
. El sistema tiene solución única (a un nivel particular 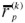 ) si la matriz Ω aumentada es semidefinida positiva.
) si la matriz Ω aumentada es semidefinida positiva.
La solución al problema [ 9] arroja algunos portafolios ineficientes de acuerdo con el axioma M-V, puesto que no siempre el portafolio de mínima varianza a cada nivel de rendimiento esperado es el de máximo rendimiento esperado a cada nivel de riesgo (varianza). Para obviar esto, se debe dar valores a 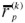 por encima del rendimiento del portafolio de mínimo riesgo puesto que este portafolio es el punto de inflexión en la frontera E-M. En la Gráfica 6 se aprecia esta particularidad. El punto de inflexión localizado en el punto C corresponde al portafolio de mínimo riesgo global, y separa los portafolios eficientes (arriba de C) de los portafolios ineficientes (debajo de C). Arriba de C, todo portafolio de mínimo riesgo a cada nivel de rendimiento esperado es el de máximo rendimiento a cada nivel de riesgo. Este portafolio de mínimo riesgo global se determina eliminando la restricción 1 del problema [ 9] . Así, el portafolio de mínimo riesgo se determinará resolviendo:
por encima del rendimiento del portafolio de mínimo riesgo puesto que este portafolio es el punto de inflexión en la frontera E-M. En la Gráfica 6 se aprecia esta particularidad. El punto de inflexión localizado en el punto C corresponde al portafolio de mínimo riesgo global, y separa los portafolios eficientes (arriba de C) de los portafolios ineficientes (debajo de C). Arriba de C, todo portafolio de mínimo riesgo a cada nivel de rendimiento esperado es el de máximo rendimiento a cada nivel de riesgo. Este portafolio de mínimo riesgo global se determina eliminando la restricción 1 del problema [ 9] . Así, el portafolio de mínimo riesgo se determinará resolviendo:
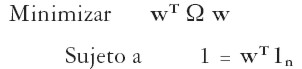 | [12] |
La función de Lagrange queda como:
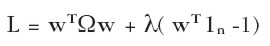 | [13] |
Las condiciones de Lagrange son:
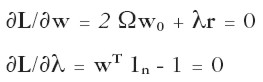 |
Resulta un sistema de n+1 ecuaciones con n+1 incógnitas (n ponderadores y el multiplicador de Lagrange). Multiplicando ambos lados de la primera ecuación matricial por ½ y despejando 1 en la segunda, el sistema se representa matricialmente como:
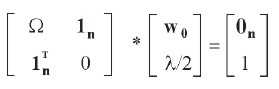 |
Despejando para w0 se obtiene:
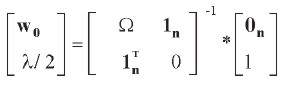 | [14] |
Asumiendo que la matriz Ω aumentada tiene inversa, el vector solución w0 será único (portafolio de mínimo riesgo global). Entonces, el riesgo y el rendimiento del portafolio de mínimo riesgo (w0) están dados por:
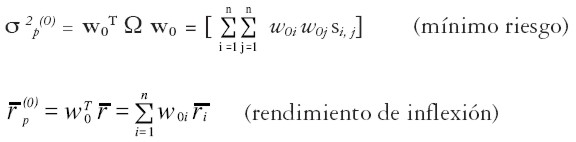 |
donde w0i denota el i-ésimo elemento del portafolio de mínimo riesgo global w0. De esta forma, para la construcción de la frontera E-M, al dato exógeno 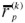 deben darse valores por encima de
deben darse valores por encima de 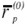 , para evitar incluir los portafolios ineficientes que están por debajo del punto de inflexión C de la Gráfica 6.
, para evitar incluir los portafolios ineficientes que están por debajo del punto de inflexión C de la Gráfica 6.
Vender en corto o en descubierto
Es muy probable que al determinar la frontera E-M y el portafolio óptimo se obtengan algunos ponderadores negativos (wi< < 0). Cuando ocurre esto, el modelo indica que se deben adquirir unidades negativas del activo. La venta en corto o venta en descubierto se considera como la adquisición de unidades negativas del activo. Una venta en corto consiste en tomar en préstamo una o varias unidades de un activo con el fin de venderlas al precio actual de mercado, y posteriormente adquirirlas a un precio supuestamente más bajo para devolverlas a su dueño. Así, un agente vende en corto cuando cree que el precio futuro del activo va a caer, de tal forma que obtenga una ganancia en la diferencia entre el precio actual y el precio futuro. No obstante, existe el riesgo de que el precio del activo suba en lugar de caer, y el agente obtenga pérdidas.
Determinación de la frontera E-M con restricciones a la venta en corto
Cuando no es posible realizar ventas en corto se introduce una nueva restricción al problema [ 9] : wi > O, para i = 1,2,...,n. Dado que la restricción es de desigualdad, la solución no puede determinarse por el método de Lagrange. El problema [ 9] con restricción a la venta en corto se puede resolver a través de la programación cuadrática; un método de optimización para funciones objetivo cuadráticas con restricciones de desigualdad y/o igualdad. El problema queda expresado como:
 | [15] |
La tercera restricción w > On indica que cada componente del portafolio no debe ser negativo. El problema [ 12] debe ser desarrollado por algún algoritmo que busque iterativamente un vector de ponderadores tal que arroje las soluciones.
La maximización de la utilidad esperada con un portafolio de sólo acciones
El problema de encontrar un portafolio óptimo que haga máxima las preferencias puede plantearse como:
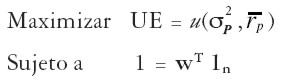 | [16] |
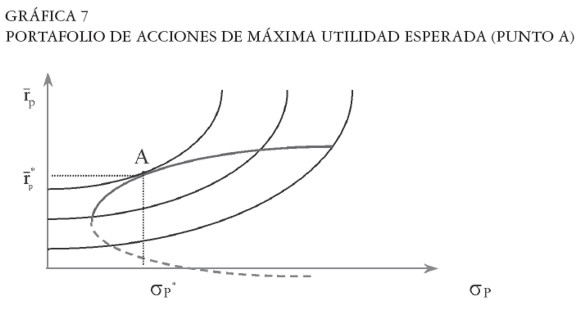
La solución al problema de maximización de la utilidad esperada se ilustra en la Gráfica 7. La máxima utilidad esperada se logra en el punto de tangencia de la frontera E-M con la curva de indiferencia del inversor3.
 |
En la solución del problema [ 16] se debe especificar una función de utilidad esperada del inversionista 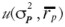 , tal que sea consistente con el axioma M-V.
, tal que sea consistente con el axioma M-V.
Maximización de una función de utilidad esperada
Si el retorno accionario tiene distribución normal, podemos representar las preferencias de forma similar a la de Sharpe [ 1970] :
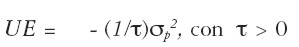 | [17] |
Esta expresión indica que la utilidad esperada está en relación directa con el rendimiento esperado del portafolio, y en relación inversa con el riesgo del mismo, lo cual es consistente con el axioma de Media-Volatilidad, en el cual el inversor es racional y averso al riesgo. En general, se asume que todos los inversores tienen este comportamiento, pero lo que los diferencia es su tolerancia al riesgo, es decir, la cantidad de riesgo que está dispuesto a aceptar por una unidad porcentual de rendimiento adicional. En la expresión [ 17] τ denota la tolerancia al riesgo, la cual determina el grado de inclinación de la recta de indiferencia en el espacio de Media-Varianza. Un mayor valor de τ indica mayor tolerancia al riesgo y, por lo tanto, menor pendiente. La ecuación [ 17] es una función cuadrática si se expresa el riesgo en volatilidad (desviación estándar), lo cual implica curvas de indiferencia convexas en el espacio Media-Volatilidad.
Empleando la ecuación [ 17] , el problema [ 16] queda expresado como:
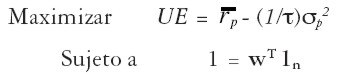 | [18] |
El anterior problema de maximización de la utilidad es equivalente al problema de minimizar su valor negativo:
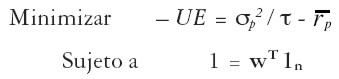 | [18'] |
donde σp 2 = wTΩ w , y 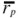 = wT
= wT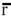
El problema sin restricción a vender en corto puede resolverse mediante el método de Lagrange:
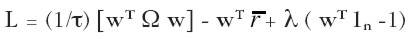 | [19] |
Las condiciones de primer orden son:
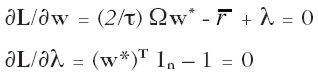 |
Este sistema tiene n+1 incógnitas (los n ponderadores wi y λ) y n+1 ecuaciones. Multiplicando a ambos lados de la primera ecuación matricial por τ/2 y despejando 1 en la segunda, el sistema puede expresarse matricialmente como:
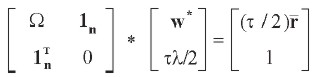 |
La solución al sistema anterior resulta de calcular:
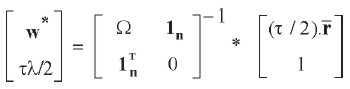 | [20] |
Tobin [ 1958, 80-85] muestra que bajo ciertas condiciones, la decisión de inversión puede dividirse en dos fases: (i) elegir un portafolio óptimo de activos de riesgo (como acciones), y (ii) una elección separada que consiste en asignar fondos en el portafolio de acciones de la fase uno y otra en un activo sin riesgo (o simplemente en dinero en efectivo). Con esta estrategia, la maximización de la utilidad esperada se lleva a cabo en la fase dos y no en la fase uno. Esto implica que el portafolio óptimo de acciones no depende de las preferencias, lo cual hace ineficiente el portafolio de la ecuación [ 20] . Lo anterior es cierto para un inversionista averso al riesgo que pueda invertir su capital sin restricciones a la venta en corto y si en el mercado existe un activo sin riesgo. Esta importante aseveración se conoce como el Teorema de la Separación.
INCLUSIÓN DE UN ACTIVO SIN RIESGO: EL TEOREMA DE LA SEPARACIÓN
Se conoce como activo sin riesgo al activo que ofrece un rendimiento nominal pactado de antemano y cuyo emisor se considera lo suficientemente confiable como para garantizar el cumplimiento de las obligaciones del título. En la práctica son muy pocos los emisores que ofrecen esta confianza a los inversores. Son ejemplo de estos títulos son los bonos del Tesoro Americano o, en Colombia, los títulos de tesorería (TES). Técnicamente, un activo sin riesgo es aquél cuya varianza o volatilidad del retorno esperado es cero. Esto es, el retorno de este activo no es variable aleatoria y, por tanto, la covarianza de su retorno con la del retorno de cualquier activo de riesgo x es nula.
Cuando se incluye un activo sin riesgo en el portafolio y se construye una nueva frontera eficiente, ésta dominará a la frontera eficiente de portafolios constituida exclusivamente con activos de riesgo (acciones), es decir, a la frontera E-M. De este modo, el portafolio óptimo –el punto A de la Gráfica 7– deja de ser eficiente con la inclusión del activo sin riesgo.
Sea un portafolio global todo portafolio constituido por n+1 activos, así: un activo de libre riesgo y un portafolio de n activos de riesgo (acciones). Si denotamos Φ como la proporción invertida en el portafolio de acciones W, y (1-Φ) como la proporción invertida en el activo sin riesgo F, podemos expresar el rendimiento esperado y el riesgo del portafolio global como:
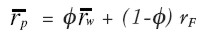 | [21] |
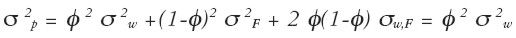 | [22] |
donde rF denota el rendimiento del activo sin riesgo F; 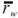 y σ 2 w el rendimiento esperado y el riesgo del portafolio W, respectivamente; y
y σ 2 w el rendimiento esperado y el riesgo del portafolio W, respectivamente; y 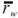 y σ 2 p denotan, en su orden, el retorno medio y la varianza del portafolio global. En la ecuación [ 22] la varianza del portafolio global sólo depende de la varianza del portafolio W, puesto que por definición, la varianza del activo sin riesgo F es cero y, por tanto, σ w, F = O.
y σ 2 p denotan, en su orden, el retorno medio y la varianza del portafolio global. En la ecuación [ 22] la varianza del portafolio global sólo depende de la varianza del portafolio W, puesto que por definición, la varianza del activo sin riesgo F es cero y, por tanto, σ w, F = O.
Cuando Φ =1, el portafolio global es el portafolio de acciones W, cuando Φ = 0, el portafolio global es el activo de libre riesgo. Cuando Φ >1, el portafolio global está apalancado; en este caso, el inversor está tomando prestado una fracción (Φ - 1) del presupuesto de la inversión a la tasa rF para invertir más fondos en el portafolio W. Esto es cierto si el inversor puede endeudarse a la tasa rF , supuesto algo irreal porque generalmente la tasa de rendimiento que un inversor particular paga por un préstamo es mayor a la tasa de rendimiento de libre riesgo rF. Este hecho también puede interpretarse como una venta en corto del activo sin riesgo, para invertir mayores fondos en el portafolio de acciones. Cuando Φ< O, se vende en corto el portafolio de acciones W y se invierten más fondos en el activo sin riesgo. En síntesis, cuando Φ 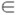 [ 0, 1] no hay ventas en corto, y en otro caso se está vendiendo en corto ya sea el portafolio de acciones (Φ < 0) o el activo sin riesgo (Φ > 1).
[ 0, 1] no hay ventas en corto, y en otro caso se está vendiendo en corto ya sea el portafolio de acciones (Φ < 0) o el activo sin riesgo (Φ > 1).
En la Gráfica 8 se observa que todas las combinaciones R-R en el espacio Media-Volatilidad de una inversión compuesta por un portafolio de acciones W con un activo sin riesgo F, se representan por dos rectas con vértice en el punto (O, rF ). Esta relación es lineal antes que hiperbólica porque la covarianza del activo F con el portafolio W es cero. Para observar esto, despejamos Φ en la expresión [ 22] , teniendo en cuenta que las volatilidades, por definición, no pueden ser negativas: |Φ |=σp /σw. Reemplazando esta ecuación en [ 21] se tiene:
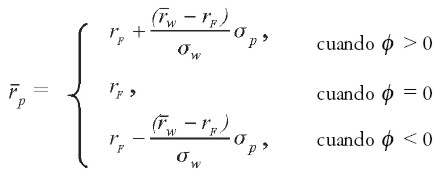 | [23] |
 |
Obtenemos así que las combinaciones R-R a partir de F y W se representan por dos rectas con vértice en rF en el espacio Media-Volatilidad, una con pendiente positiva: (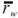 - rF) / σw, cuando Φ> 0, y otra con pendiente negativa: (rF -
- rF) / σw, cuando Φ> 0, y otra con pendiente negativa: (rF - 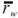 ) / σw cuando Φ< O.
) / σw cuando Φ< O.
¿Con qué portafolio de la frontera E-M debe combinarse el activo sin riesgo F? Observemos que la recta que hace tangencia en la Gráfica 9 (la del punto T) representa cualquier nivel de retorno la menor volatilidad sobre las demás rectas que interceptan a la frontera E-M. La respuesta entonces es con el portafolio T, puesto que esta recta allí domina a todas las demás al presentar menor volatilidad del nivel de retorno requerido. Esta recta eficiente tiene dos características particulares: (i) hace tangencia con la frontera E-M y, por tanto, (ii) es la recta con mayor pendiente que logra tocar la frontera E-M. En adelante, esta recta eficiente de portafolios se llamará "la frontera eficiente de Tobin" (E-T), la cual está compuesta por portafolios globales, mientras que la frontera E-M sólo está compuesta por portafolios de activos de riesgo (acciones)4.
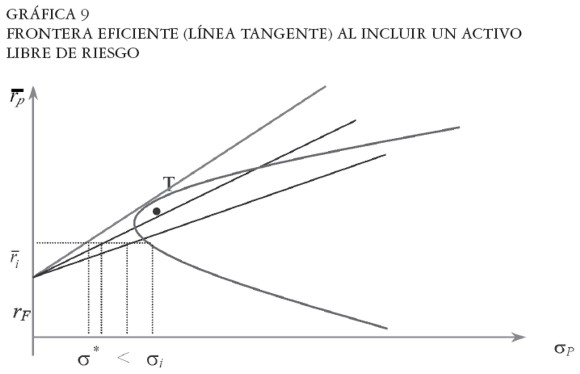 |
En la Gráfica 9 es importante observar que la frontera E-T domina de acuerdo con el axioma M-V en todos los puntos, a excepción del punto de tangencia T. Para cualquier nivel de rendimiento esperado de portafolio 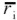 , la frontera E-T (la que incluye el activo sin riesgo: recta tangente) presenta menor riesgo –desviación estándar– que el que presenta la frontera E-M (que incluye sólo acciones: hipérbola), esto es: σ* < σi. Esto se cumple para cualquier rendimiento esperado excepto para el del portafolio tangente T:
, la frontera E-T (la que incluye el activo sin riesgo: recta tangente) presenta menor riesgo –desviación estándar– que el que presenta la frontera E-M (que incluye sólo acciones: hipérbola), esto es: σ* < σi. Esto se cumple para cualquier rendimiento esperado excepto para el del portafolio tangente T: 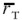 , en cuyo caso, ambas fronteras presentan el mismo portafolio.
, en cuyo caso, ambas fronteras presentan el mismo portafolio.
En el área del triángulo de la Gráfica 10 se ilustra el conjunto factible, el cual contiene todas las rectas que se pueden formar entre el activo de libre riesgo F y cualquier portafolio de acciones.
Determinación del portafolio de acciones óptimo y de la frontera E-T
La característica fundamental del portafolio T de la Gráfica 9 –el portafolio óptimo de acciones– es que pertenece a la recta eficiente, la cual presenta la mayor pendiente que logra tocar la frontera E-M (tangente a E-M). A partir de la ecuación [ 23] podemos expresar matricialmente la pendiente de la recta de portafolios globales como:
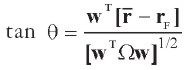 | [24] |
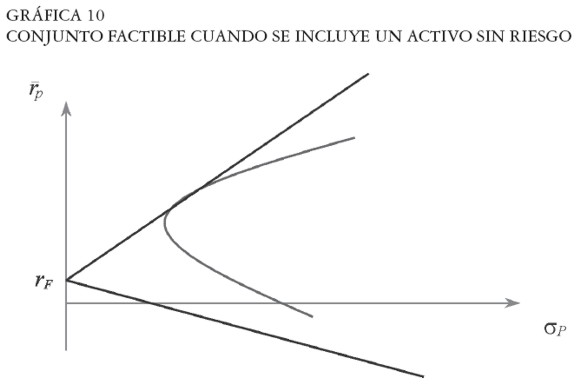 |
donde rF representa un vector cuyos n elementos son rF y θ el ángulo de la pendiente máxima. Entonces, el portafolio de acciones óptimo es el vector w que hace máxima la pendiente (tan θ) de la ecuación [ 24] . El problema a resolver es:
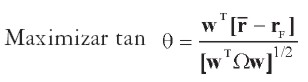 | [25] |
La condición necesaria y además suficiente [ Lintner 1965, 21] para el máximo de θ es que la primera derivada de la función q con respecto al vector w sea igual a cero:
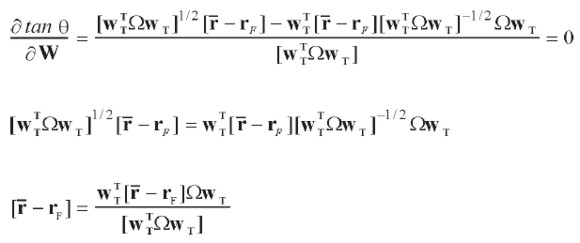 |
donde wT T es el portafolio óptimo de acciones. Entonces:
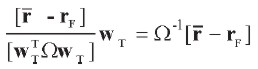 | [26] |
El término 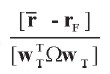 es un escalar que denotamos como γ. Entonces [ 26] también puede expresarse como:
es un escalar que denotamos como γ. Entonces [ 26] también puede expresarse como:
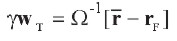 | [26'] |
El vector γwT cumple la propiedad según la cual la suma de todos sus elementos es igual al mismo escalar γ, puesto que:
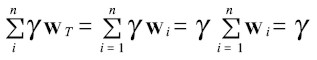 |
Entonces, la suma de todos los elementos del vector del lado derecho de la ecuación [ 26’] también debe ser igual al escalar γ:
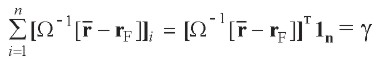 | [27] |
Reemplazando [ 27] en [ 26’] y despejando wT:
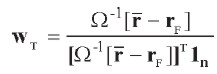 | [28] |
Esta última es la ecuación del portafolio óptimo de acciones. Una vez hallado éste podemos calcular su retorno esperado 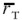 y su volatilidad σT. Reemplazando la ecuación [ 28] en la [ 23] , la ecuación de la frontera E-T en el espacio Media-Volatilidad se determina por:
y su volatilidad σT. Reemplazando la ecuación [ 28] en la [ 23] , la ecuación de la frontera E-T en el espacio Media-Volatilidad se determina por:
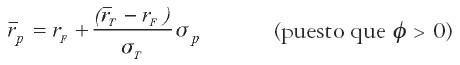 | [29] |
Ahora la variable exógena es σp, es decir, cada punto de la frontera eficiente se determina dando distintos valores particulares de σp. Una vez elegido un nivel particular de riesgo global σp, la participación del portafolio de acciones óptimo wT en ese portafolio global es:
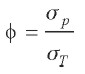 | [30] |
y la participación del activo sin riesgo F en este mismo portafolio global será 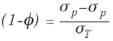 .
.
Otra forma de determinar la frontera S-T consiste en dar distintos valores a Φ y encontrar cada punto de esta recta directamente a partir de las ecuaciones [ 21] y [ 22] .
Determinación del portafolio de acciones tangente y de la frontera E-T sin ventas en corto
Cuando no es posible realizar ventas en corto los ponderadores de los activos individuales no pueden ser negativos. Esto implica que w > On, así que el problema de calcular el portafolio tangente de acciones queda expresado como:
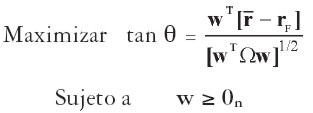 | [31] |
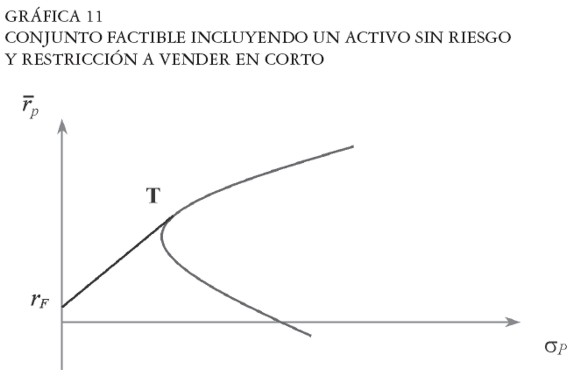
Dado que el problema [ 31] presenta restricciones de desigualdad, se aplica el programa cuadrático para encontrar el conjunto eficiente E-T. El portafolio tangente obtenido al resolver [ 31] no siempre es el portafolio óptimo de acciones puesto que al restringir la venta en corto se viola uno de los supuestos del teorema de la separación. Este portafolio es útil para determinar la frontera E-T a la izquierda del punto tangente (punto T en la Gráfica 11), es decir, cuando O < Φ > 1. A la derecha del punto tangente la frontera E-T coincide con la frontera E-M cuando hay restricciones a la venta en corto. Además, la frontera estará acotada superiormente por el mayor retorno en los n retornos de los activos de riesgo.
Maximización de la utilidad esperada al incluir el activo sin riesgo: el teorema de la separación de Tobin
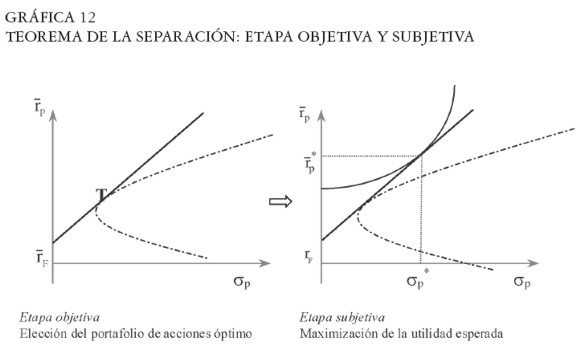
El principal problema del inversor es elegir el portafolio que contenga la combinación R-R que haga máxima su función de utilidad esperada. Suponiendo que existe un activo libre de riesgo y que no hay restricciones a la venta en corto, el teorema de la separación afirma que para llevar a cabo este objetivo el inversor debe maximizar en dos etapas5:
 |
1. Elegir el portafolio de acciones óptimo wT (el cual es independiente de las preferencias).
2. Elegir una combinación entre el portafolio de acciones óptimo y el activo sin riesgo (o mantener efectivo). En otras palabras, elegir un valor particular Φ que haga máxima las preferencias.
La primera etapa es independiente de las preferencias puesto que se escoge el portafolio de acciones tangente a la frontera E-M (portafolio T), de acuerdo con la ecuación [ 28] . En la segunda etapa el inversor debe combinar ese portafolio de acciones wT con el activo sin riesgo –elige un Φ– a fin de alcanzar la curva de indiferencia más alta. Esto implica que la elección de wT es una elección objetiva, mientras que la elección de Φ es subjetiva o particular para cada inversionista.
 |
La Gráfica 13 muestra que al incluir el activo sin riesgo se logra alcanzar una curva de indiferencia más alta que la alcanzada al invertir exclusivamente en acciones. El nivel de utilidad logrado al incluir el activo sin riesgo UEF* es mayor al nivel de utilidad obtenido con un portafolio constituido por sólo acciones UE*.
La elección subjetiva de Φ debe estar en función de las preferencias de cada inversionista particular:
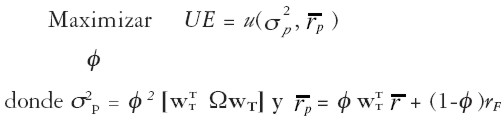 | [32] |
Naturalmente, el problema [ 32] está planteado suponiendo que se conoce el portafolio tangente wT, el cual se obtiene a partir de las ecuaciones [ 28] o [ 31] . Si se desconoce el portafolio de acciones óptimo wT es posible hallar directamente el portafolio global óptimo resolviendo el problema:
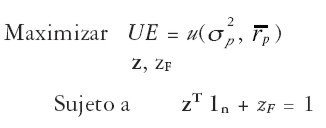 | [32'] |
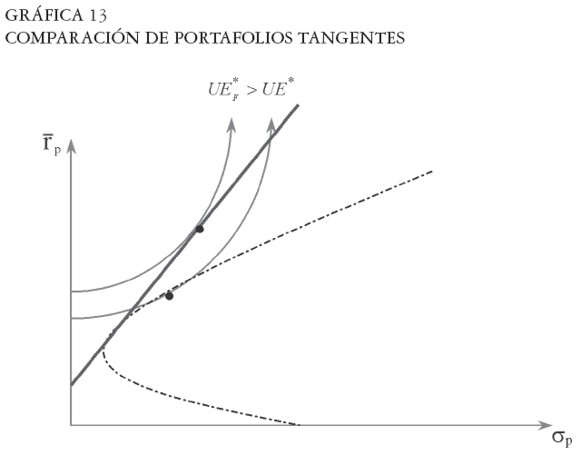 |
donde zF representa la ponderación del activo sin riesgo en el portafolio global zn+1, y z es el vector que contiene las participaciones de cada una de las n acciones en el portafolio global óptimo (es decir, z = Φ wT). Cuando hay restricción para vender en corto se adicionan dos restricciones al problema: una para la no negatividad de los ponderadores de cada una de las acciones (zi ≥ 0, para i = 1,...,n), y otra para la no negatividad del ponderador del activo sin riesgo zF (esto se obtiene cuando (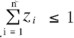 ). En este caso, la elección del portafolio de acciones no siempre es independiente de las preferencias, es decir, no siempre se cumple la propiedad de la separación6.
). En este caso, la elección del portafolio de acciones no siempre es independiente de las preferencias, es decir, no siempre se cumple la propiedad de la separación6.
En síntesis, la inclusión del activo sin riesgo en el portafolio logra mejorar –de acuerdo con el axioma de la media y la varianza– el conjunto eficiente de Markowitz y, por tanto, el óptimo del inversionista. El portafolio de acciones es independiente de las preferencias si no se imponen restricciones adicionales en el problema [ 25] , como la de vender en corto.
La maximización de una función de utilidad esperada incluyendo un activo sin riesgo
Asumiendo que la función de utilidad esperada corresponde a la ecuación [ 17] , el problema [ 32’] queda expresado como:
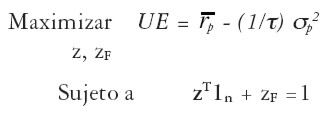 |
Esta maximización es equivalente a resolver el problema de minimización de su valor negativo:
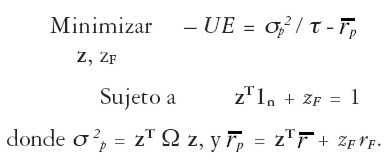 |
El problema sin restricción a la venta en corto puede resolverse mediante el método de Lagrange:
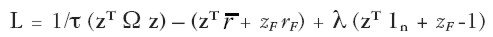 |
Las condiciones de primer orden son:
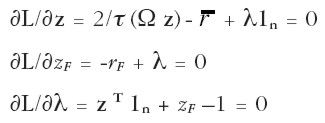 |
De la segunda ecuación se desprende que λ = rF. Sustituyendo ésta en las primeras n ecuaciones del anterior sistema, y despejando Ωz se tiene:
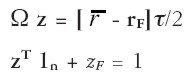 |
Este sistema tiene n+1 incógnitas (los ponderadores) y n+1 ecuaciones. Finalmente, este sistema puede expresar en términos matriciales como:
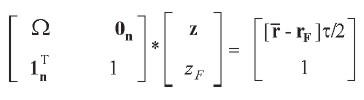 |
En consecuencia, el portafolio global óptimo [ z, zΦ] T se obtiene resolviendo:
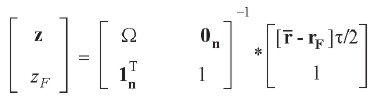 | [33] |
FRONTERA E-T Y PORTAFOLIO ÓPTIMO CON CINCO ACCIONES COLOMBIANAS
Aquí se construye la frontera E-M y la frontera E-T con cinco acciones colombianas, a saber: Cementos Argos, Bavaria, Cementos Paz del Río, Banco de Bogotá y Compañía Nacional de Chocolates. A partir de estas acciones se construye un portafolio óptimo para un inversionista conservador y otro portafolio para un inversionista emprendedor, asumiendo la posibilidad de vender en corto y que no hay costos de comisión. El mismo ejercicio se realiza asumiendo restricción a la venta en corto.
Tomando los precios históricos promedios mensuales ponderados de enero 1999 a diciembre 2002 publicados por la Superintendencia de Valores (www.supervalores.gov.co), estimamos el retorno medio para cada una de las cinco acciones y la matriz de varianzas y covarianzas de los retornos. Para el cálculo de rendimientos se emplea el retorno logarítmico, el cual es consistente con el sistema de capitalización continua:
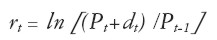 |
donde dt representa el dividendo en el mes t, Pt y Pt-1 representan el precio en el mes t y t-1 respectivamente. Los datos obtenidos se resumen en el vector de rendimientos medios diarios y la matriz de varianzas y covarianzas de retornos diarios:
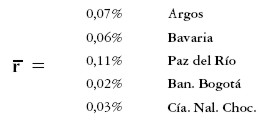 |
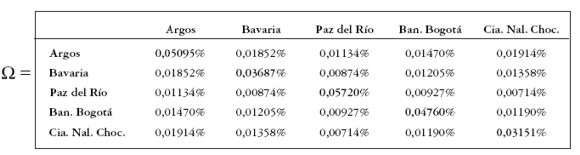 |
Se empleará como tasa de retorno sin riesgo el 7% continuo anual, equivalente a un rendimiento continuo diario de 0,019%.
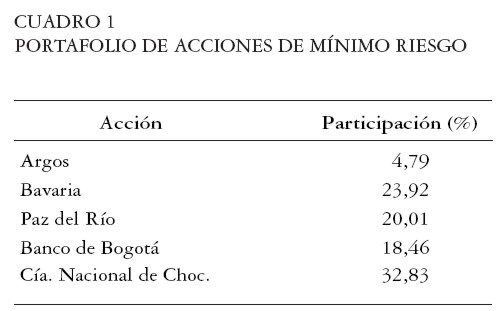
Portafolio de acciones de mínimo riesgo sin restricción a vender en corto
Al reemplazar el anterior vector de retornos diarios medios y la matriz de varianzas y covarianzas en la ecuación [ 14] , podemos obtener el portafolio de acciones de mínimo riesgo. Al resolver [ 14] se obtiene el portafolio del Cuadro 1, el cual tiene un retorno esperado diario de 0,054% continuo, con una volatilidad diaria de 1,347%. Esta volatilidad es la mínima posible para cualquier portafolio compuesto exclusivamente por estas cinco acciones. Para construir la frontera E-M debemos resolver el sistema de ecuaciones [ 11] dando valores al retorno requerido del portafolio 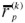 por encima de 0,054% continuo diario.
por encima de 0,054% continuo diario.
 |
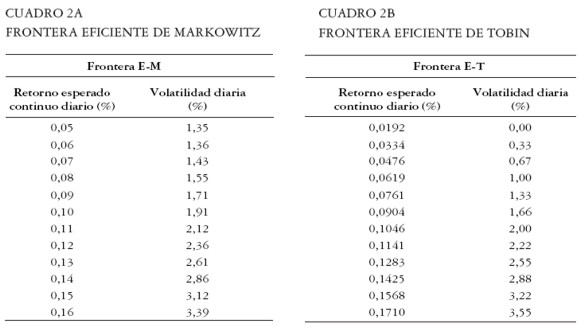
Frontera E-M y Frontera E-T sin restricciones a la venta en corto
La frontera E-M se construye a partir de la solución de la ecuación [ 11] para diferentes niveles de retornos requeridos de portafolio. De igual modo, se construye la frontera E-T a partir de la ecuación [ 29] . Algunos puntos de la frontera E-M y de la frontera E-T se presentan en los Cuadros 2a y 2b.
 |
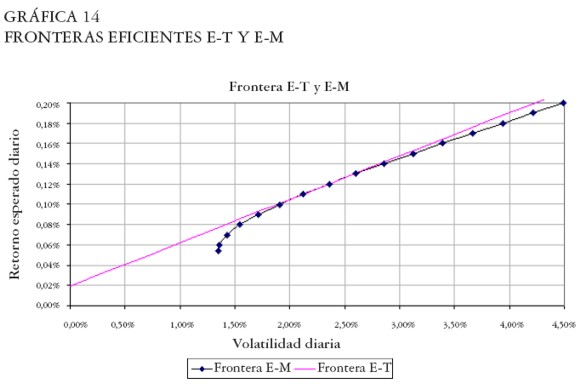 |
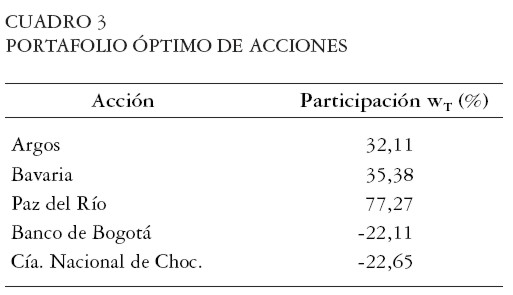
Al reemplazar el vector de retornos medios y la matriz de varianzas y covarianzas de las cinco acciones en la ecuación [ 28] , obtenemos el portafolio óptimo de acciones. El retorno esperado y la volatilidad diaria de este portafolio es de 0,1141% y 2,217% respectivamente. Éste es el portafolio tangente a la frontera E-M (Gráfica 14) el cual indica la venta en corto de las acciones del Banco de Bogotá y de la Compañía Nacional de Chocolates. Ver Cuadro 3.
 |
Maximización de la utilidad esperada de un inversionista conservador y otro emprendedor, sin restricción a vender en corto
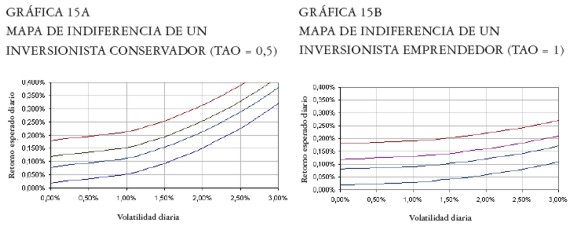
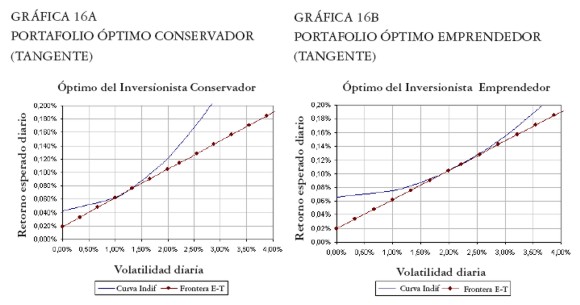
Ahora suponemos dos inversionistas con aversión al riesgo y preferencias del tipo UE = 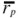 - (1 / τ) σ2 p, con τ = ½ para un inversionista conservador y τ = 1 para un inversionista emprendedor. Las Gráficas 15a y 15b muestran los mapas de indiferencia en el espacio Media-Volatilidad, para estos inversionistas. Aunque ambos inversionistas tienen aversión al riesgo, el inversionista conservador (τ = ½ ) es más precavido que el inversionista emprendedor (τ = 1), razón por la cual su mapa de indiferencia es de mayor pendiente.
- (1 / τ) σ2 p, con τ = ½ para un inversionista conservador y τ = 1 para un inversionista emprendedor. Las Gráficas 15a y 15b muestran los mapas de indiferencia en el espacio Media-Volatilidad, para estos inversionistas. Aunque ambos inversionistas tienen aversión al riesgo, el inversionista conservador (τ = ½ ) es más precavido que el inversionista emprendedor (τ = 1), razón por la cual su mapa de indiferencia es de mayor pendiente.
 |
Resolviendo el sistema de ecuaciones [ 33] se obtienen los siguientes portafolios globales óptimos para cada inversionista:
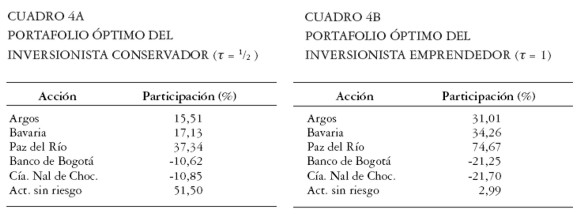 |
Se observa que el portafolio global del inversionista conservador tiene una participación en acciones de sólo 49,5% y el restante 51,5% en el activo libre de riesgo. El retorno esperado de este portafolio es de 0,065% continuo diario, con una volatilidad de 1,075% diaria. En contraste, el portafolio del inversionista emprendedor contiene 97% de su composición en acciones, y sólo 3% en el activo sin riesgo. El portafolio del inversionista emprendedor tiene mayor retorno esperado, de 0,11% continuo diario, pero también una mayor volatilidad, de 2,15% diaria. Ambos portafolios indican la venta en corto de las acciones Banco de Bogotá y Compañía Nacional de Chocolates. La acción con mayor participación es Cementos Paz del Río.
Las Gráficas 16a y 16b presentan los dos óptimos. Como se puede apreciar, el portafolio óptimo conservador tiene una combinación de riesgo-rendimiento menor a la del portafolio óptimo emprendedor.
 |
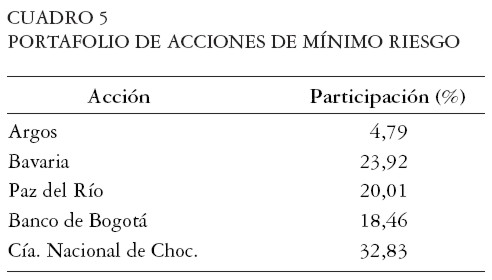
Portafolio de acciones de mínimo riesgo con restricción a vender en corto
Ahora se repite el ejercicio anterior pero con restricciones a la venta en corto7 . El portafolio obtenido de acciones de mínimo riesgo con restricción a vender en corto fue:
 |
Portafolio de acciones tangente
Al resolver la ecuación [ 31] se obtuvo el portafolio de acciones tangente, el cual se presenta en el Cuadro 6.
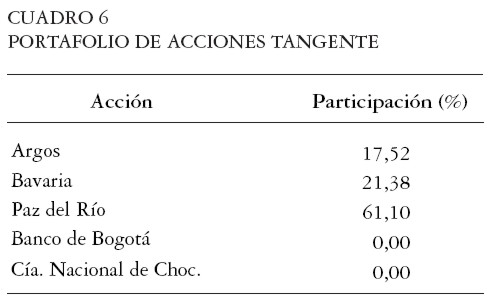 |
Este portafolio de acciones no siempre es óptimo puesto que al imponer restricciones a la venta en corto, el Teorema de la Separación no siempre se cumple. Adelante se muestra que para el inversionista emprendedor el portafolio de acciones sí depende de las preferencias y difiere del portafolio tangente del Cuadro 6.
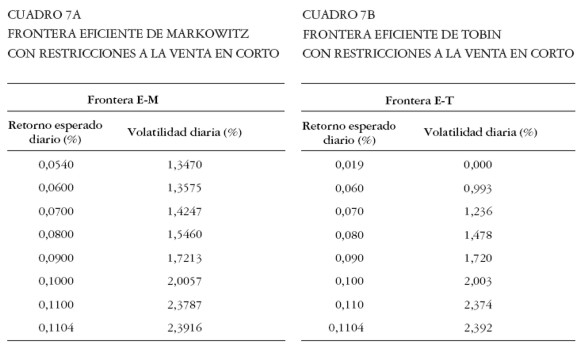
Fronteras E-M y E-T con restricciones a la venta en corto
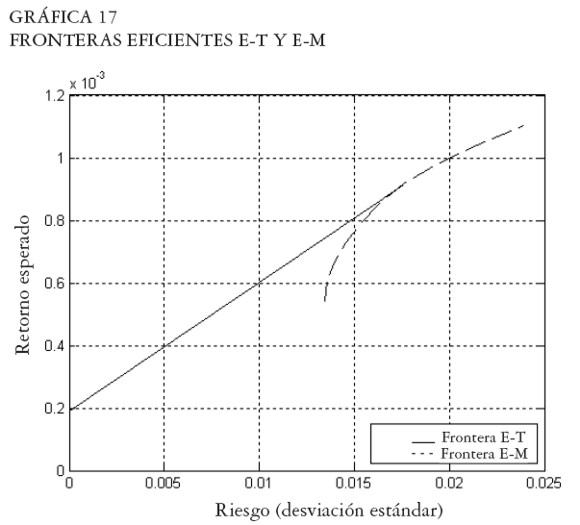
Al resolver los problema [ 15] y [ 31] se encontraron las frontera E-M y E-T con restricción a la venta en corto. Algunos puntos de esta frontera se presentan en los Cuadros 7a y 7b. La Gráfica 17 muestra la frontera eficiente de Markowitz y la frontera eficiente de Tobin, ambas están acotadas superior e inferiormente como resultado de restringir la venta en corto. A la derecha del punto tangente la frontera E-T coincide con la frontera E-M puesto que no es posible el apalancamiento a través de la venta en corto del activo sin riesgo.
 |
Maximización de la utilidad esperada de un inversionista conservador y otro emprendedor, con restricción a vender en corto
Ahora buscamos los portafolios óptimos de los dos inversionistas: el conservador y el emprendedor. Resolviendo el sistema de ecuaciones [ 33] se obtienen los siguientes portafolios globales óptimos para cada inversionista. Ver Cuadros 8a y 8b.
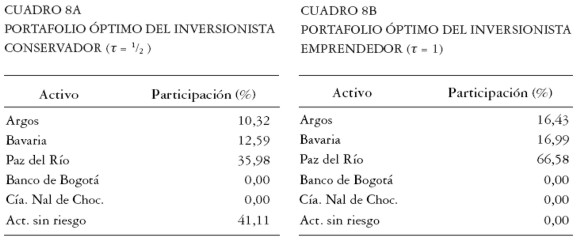 |
 |
El portafolio global del inversionista conservador tiene una participación en acciones de 58,89% y el restante 41,11% en el activo libre de riesgo. El retorno esperado de este portafolio es de 0,062% continuo diario, con una volatilidad de 1,032% diaria. De otro lado, el portafolio del inversionista emprendedor está constituido exclusivamente por acciones, con un retorno esperado de 0,094% continuo diario y una volatilidad de 1,824% diaria. El portafolio óptimo de acciones del inversionista emprendedor no coincide con el portafolio tangente del Cuadro 6, es decir, no se cumple el Teorema de la Separación porque se restringe la venta en corto.
CONSIDERACIONES FINALES
La teoría del portafolio es un buen modelo de diversificación basado en la correlación de los rendimientos de los activos, antes que en el número de activos. Sin embargo, sólo considera los dos primeros momentos de la distribución de los retornos: la media y la varianza. Esta simplificación no supone inconvenientes cuando los retornos de los activos presentan distribución normal, pero infortunadamente en la práctica esto no ocurre. Una característica común en las distribuciones de retornos es la presencia de leptocurtosis, es decir, que hay una concentración considerable de datos alrededor de la media, y colas más pesadas que las de una distribución normal. Al considerar únicamente los dos primeros momentos de la distribución se está omitiendo el comportamiento leptocúrtico de la distribución del retorno. De otro lado, el modelo de Markowitz es estático, es decir, ofrece un portafolio eficiente en un punto dado del tiempo. Bajo condiciones de alta volatilidad, un portafolio eficiente puede dejar de serlo en cuestión de segundos por el simple cambio en los precios, lo cual hace variar las composiciones del portafolio. Finalmente, es importante resaltar que éste es un modelo de equilibrio particular y no de equilibrio general, es decir, este modelo no ofrece una valoración de equilibrio de mercado, sino más bien un método de inversión diversificada. El modelo de Valoración de Activos de Capital (CAPM) es la versión de equilibrio de mercado de la teoría del portafolio, puesto que se pregunta: (i) cómo se comporta un mercado en el cual todos los agentes son diversificadores del tipo Markowitz, (ii) existe un equilibrio, y (iii) de existir un equilibrio cuál es. La principal conclusión de este modelo es que el rendimiento de equilibrio de un activo no depende de su volatilidad si no del riesgo sistemático o riesgo de mercado, el cual se mide con un indicador denominado beta.
NOTAS AL PIE
1 Esta medida refleja solamente la relación lineal entre dos variables.
2 Término que se explica en el siguiente apartado.
3 Esto es cierto para portafolios constituidos exclusivamente con acciones. Cuando se introduce un activo sin riesgo y no hay restricción a vender en corto, esta tangencia no implica la máxima utilidad esperada. Esto se explica por el Teorema de la Separación [ Tobin 1958] .
4 En el contexto de un modelo de equilibrio de mercado, esta recta se conoce como la Línea del Mercado de Capitales [ Sharpe 1964] . No se emplea este nombre porque la teoría del portafolio no es un modelo de equilibrio.
5 Aquí se hace una prueba intuitiva de este teorema. Para una prueba formal ver Lintner [ 1965] .
6 Ver demostración en Sharpe [ 1970, anexo B] .
7 Aquí se emplea el programa MATLAB para la optimización.
REFERENCIAS BIBLIOGRÁFICAS
1. Francis, J. y Archer, S. 1971. Portfolio Analysis, Ed. Prentice Hall. [ Links ]
2. Lintner, J. 1965. "The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets", Review of Economic and Statistics, n. 47, 13-37. [ Links ]
3. Luenberger, D. 1998. Investments Science, Oxford. [ Links ]
4. Markowitz, H. 1952. "Portfolio selection", Journal of Finance, v. 7, marzo, 77-91. [ Links ]
5. Markowitz, H. 1959. Portfolio Selection: Efficient Diversification of Investment, Ed. New York Wiley, edición revisada 1991. [ Links ]
6. Márquez, D. 1981. Carteras de inversión: fundamentos teóricos y modelos de selección óptima, Ed. Limusa. México. [ Links ]
7. Medina, C. y Echeverry, J. 1993. "La selección de portafolios y la frontera eficiente: el caso de la bolsa de Medellín", Lecturas de Economía, n. 39, julio-diciembre, Medellín. [ Links ]
8. Medina, L. 2000. Selección de portafolio: teoría y caso práctico con las principales acciones de cada sector, monografía, Universidad Nacional de Colombia, Bogotá. [ Links ]
9. Messuti, J., Álvarez, V. y Graffi, H. 1992. Selección de inversiones: introducción a la teoría de la cartera, Ediciones Macchi, Buenos Aires. [ Links ]
10. Neumann, J. y Morgenstern, O. 1944. Theory of Games and Economic Behavior, Princeton University Press. [ Links ]
11. Sharpe, W. 1964. "Capital asset prices: a theory of market equilibrium under conditions of risk", Journal of Finance, n. 19, 425-442. [ Links ]
12. Sharpe, W. 1970. Portfolio Theory and Capital Markets, McGraw Hill. Nueva York. [ Links ]
13. Tobin, J. 1958. "Liquidity preference as behavior toward risk", Review of Economics Studies, n. 25, febrero, 68-85. [ Links ]














