Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.23 no.40 Bogotá Jan./June 2004
ALCANCE DE LA MERCANCÍA PATRÓN DE SRAFFA. DOS NUEVAS EXTENSIONES
Edith Alicia Klimovsky*
* Profesora del Departamento de Economía de la Universidad Autónoma Metropolitana, Azcapotzalco, y del Doctorado en Ciencias Económicas de la Universidad Autónoma Metropolitana. La autora agradece las observaciones de Carlo Benetti y Christian Bidard. Enviar los comentarios al correo: ekb@correo.azc.uam.mx. Artículo recibido el 12 de abril de 2004 y aprobado el 11 de junio del mismo año.
Resumen
Basándonos en la mercancía patrón de Sraffa mostramos, en primer lugar, que es posible explicar la variación de los precios cuando cambia la distribución no sólo cuando existe una sola técnica para cada mercancía, como lo hace Sraffa, sino también cuando hay una pluralidad de métodos de producción. En segundo lugar, demostramos que la noción de excedente relevante para la comprensión de las ganancias es el excedente de trabajo, de modo que la proposición ricardiana según la cual las ganancias dependen de este excedente, se verifica aun sin necesidad de suponer la teoría del valor-trabajo.
Palabras clave: teoría clásica, mercancía patrón, excedente, precios, tasa de ganancia. JEL: B12, D30, D46, E11.
Abstract
Based on Sraffa’s standar commodity, we show that it is possible to explain price variation as distribution changes, not just when there is a single technique for each market, as put forward by Sraffa, but also when there is more than one production method. We also show that the concept of relevant surplus for understanding profit lies in surplus of work, so that the Ricardian proposition (according to which profit depends on such surplus) can be verified without the need for supposing value-work theory.
Key words: classical theory, standar commodity, surplus, prices, profit rate. JEL: B12, D30, D46, E11.
Résumé
En partant de la marchandise modèle de Sraffa nous démontrons, tout d´abord, qu´il est possible d´expliquer la variation des prix quand la distribution change, non seulement quand il n´existe qu´une seule technique pour chaque marchandise, comme le fait Sraffa, mais également quand il existe une diversité des modes de production. Nous démontrons ensuite que la notion d´excédent, importante pour la compréhension des bénéfices, correspond à l´excédent de travail, de telle façon que la proposition ricardienne selon laquelle les bénéfices dépendent de cet excédent, se vérifie sans même avoir besoin d´envisager la théorie de la valeur-travail.
Mots clés : théorie classique, merchandise étanol, excédent, prix, taux de bénéfice. JEL : B12, D30, D46, E11.
Proporciones particulares, tales como las proporciones patrón, pueden dar transparencia a un sistema, y hacer visible lo que está oculto
[ Sraffa 1960, § 31]
INTRODUCCIÓN
En la tradición clásica, la tasa de ganancia es la variable central para el análisis del funcionamiento del capitalismo. Dicha tasa es un cociente en términos de valor que se determina, para una técnica y un salario dados, simultáneamente con los precios. Este enfoque plantea dos cuestiones básicas. La primera se refiere al análisis de la variación de los precios consecutiva a cambios en la técnica y en la distribución. La segunda concierne a la interpretación de la tasa de ganancia a fin de encontrarle un sentido más profundo que el de simple incógnita de un sistema de ecuaciones simultáneas. En esta perspectiva, una contribución fundamental de Sraffa es la mercancía patrón. Con esta construcción auxiliar, Sraffa inaugura un método analítico muy fértil en la teoría clásica: todo sistema económico tiene asociadas proporciones particulares que le dan transparencia, pues revelan sus propiedades esenciales, haciendo visible lo que está oculto. Este aporte no ha recibido el reconocimiento que merece, e incluso ha resultado “casi incomprensible para un teórico moderno” [ Hahn 1982, 358].
En Producción de mercancías, Sraffa construye la mercancía patrón para dar cuenta de las variaciones de los precios que resultan de las modificaciones de la distribución cuando existe un único método para la producción de cada mercancía. Una propiedad importante de la mercancía patrón es dar un fundamento material, derivado del sistema físico de producción, a la tasa máxima de ganancia que se determina como una relación física. En este artículo nos proponemos mostrar que el alcance de esta mercancía va mucho más allá de lo que Sraffa señaló.
El origen de toda esta problemática se encuentra en la obra de Ricardo. Por una parte, Ricardo muestra que los precios varían, tanto debido a las modificaciones en la distribución para una técnica dada, como por el cambio de la técnica misma. A su vez, este último puede ser o no el resultado de variaciones en la distribución. Preocupado por aclarar los efectos sobre la ganancia del cambio en los precios consecutivo a variaciones del salario y de la técnica, Ricardo busca sin éxito una “unidad de medida invariable”. Sraffa retoma el problema dejado abierto por Ricardo, y demuestra que gracias a la mercancía patrón se puede comprender cómo varían los precios cuando se modifica la distribución en la hipótesis de un único método de producción para cada mercancía. Nuestro primer objetivo es debilitar esta hipótesis de Sraffa y, basándonos en la construcción sraffiana, mostrar que es posible explicar la variación de los precios cuando cambian las técnicas de producción como consecuencia de variaciones en la distribución (sección I).
Ricardo aborda la cuestión de la determinación de la tasa de ganancia en el Ensayo de 1815 y en los Principios. El concepto de mercancía patrón le permite a Sraffa interpretar la teoría del Ensayo como una determinación física de la tasa de ganancia en el caso particular en que el trigo es el único producto que interviene en su producción y que participa en la de todas las demás mercancías. En los Principios, Ricardo afirma que “en todos los países y todos los tiempos, las utilidades dependen de la cantidad de mano de obra necesaria para proveer a los obreros de los artículos necesarios” [ 1821, cap. VI, p. 98; y cap. I, sec. 7, p. 36]. En su “Introducción” a las Obras y Correspondencia de David Ricardo, Sraffa señala que Ricardo establece esta proposición suponiendo que se verifica la teoría del valor-trabajo. Se llega así a una cuestión central de la teoría clásica de los precios y la distribución, habitualmente presentada como el enfoque del excedente1. Encontramos en Ricardo dos nociones de excedente relacionadas con la tasa de ganancia: un excedente físico (trigo) en el Ensayo y un excedente de trabajo en los Principios. ¿Cuál de estas nociones es relevante para la tasa de ganancia? ¿Qué alcance tiene la afirmación ricardiana de los Principios? Utilizando la mercancía patrón de Sraffa, nuestro segundo objetivo es mostrar que la noción de excedente de trabajo es la más pertinente y que su relación con la tasa de ganancia no supone la hipótesis restrictiva del valor-trabajo, ampliando así el alcance de la proposición de Ricardo (sección II).
COMPRENSIÓN DEL MOVIMIENTO DE LOS PRECIOS
La solución de Sraffa para una técnica dada
En el marco de la formalización sraffiana de la teoría clásica, los precios dependen de los métodos de producción utilizados y del nivel de la variable exógena, siendo independientes de las proporciones en que las mercancías son producidas. Cuando varía el salario para una técnica dada, si la relación trabajo/precio de los medios de producción no es la misma en todas las ramas, las mercancías deben modificar su precio respecto al precio de sus medios de producción para poder pagar la nueva tasa general de ganancia. Por consiguiente, dada la técnica, los cambios en la distribución alteran por lo general todos los precios, incluso el de la unidad de medida. Por lo tanto, no queda claro si la variación de las relaciones de cambio se debe a la modificación del precio de las mercancías o a la del precio de la unidad de medida. En este sentido, el movimiento de los precios consecutivo a una modificación de la distribución resulta incomprensible. Para resolver este problema cuando se dispone de un único método para la producción de cada mercancía, Sraffa construye una mercancía, bautizada mercancía patrón, cuyas condiciones de producción son tales que puede pagar la tasa de ganancia uniforme sin necesidad de variar su precio respecto al precio de sus medios de producción ante cambios en el salario. Sraffa reconoce que, en este caso, “tal mercancía no sería menos susceptible que cualquier otra de aumentar o descender en precio respecto de otras mercancías individuales; pero sabríamos con certeza que tal fluctuación tendría su origen exclusivamente en las peculiaridades de la producción de la mercancía que estaba siendo comparada con ella, y no en las de su propia producción.” [ Y concluye] “si pudiéramos descubrir tal mercancía, nos encontraríamos en posesión de un patrón capaz de aislar los movimientos de precios de cualquier otro producto, de modo que pudieran ser observados como en un vacío” [ Sraffa 1960/1966, 37-38]. Así, la mercancía patrón constituye una unidad de medida invariable de los precios frente a cambios en la distribución para una técnica dada.
Ahora bien, la relación entre el precio de una mercancía y el precio de sus medios de producción será la misma para todo estado de la distribución sólo si el producto y los medios de producción, y por ende también el producto neto, son proporcionales. En este caso se puede hablar de una relación producto neto a medios de producción de esta mercancía que será constante para todos los niveles posibles de la variable de distribución exógena. Para identificar cuál es esta relación para la mercancía patrón basta considerar un estado particular de la distribución, correspondiente al salario nulo, en que la relación precio del producto neto a precio de los medios de producción es igual a la tasa máxima de ganancia R para todas las mercancías y, por ende, también para la mercancía patrón. Por consiguiente, la mercancía patrón es una mercancía compuesta tal que la relación entre la cantidad de cada una de las mercancías que la componen que figura en el producto neto y la cantidad que figura en los medios de producción (es decir, la tasa de excedente físico) es igual a R. Dicho en otros términos, todas las mercancías que componen la mercancía patrón tienen la misma tasa de excedente físico, que es igual a la tasa máxima de ganancia del sistema.
Sobre la base de la indicación anterior, Sraffa construye el sistema que produce la mercancía patrón para la técnica dada. Dicho sistema, llamado sistema patrón, se obtiene cambiando las proporciones del sistema efectivo de modo que la estructura del producto sea igual a la estructura de los medios de producción totales. El vector q’ de multiplicadores que transforman el sistema efectivo en el sistema patrón es la solución del sistema de ecuaciones siguiente:
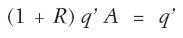 |
Donde A > 0 es la matriz de coeficientes técnicos. Dado que el sistema patrón está definido para una técnica dada, a cada conjunto de métodos de producción le corresponde un sistema patrón diferente. En consecuencia, la mercancía patrón se modifica cuando varía la técnica. Así pues, no es posible explicar cómo un cambio técnico para un nivel dado de la variable de distribución exógena afecta los precios. Este límite de la mercancía patrón es indiscutible.
Como el sistema patrón y el sistema efectivo sólo difieren en las proporciones, ambos tienen la misma solución. En el sistema patrón, la tasa máxima de ganancia es igual a la tasa de excedente físico de la mercancía patrón. Por consiguiente, una propiedad importante del sistema patrón, que Sraffa menciona sin subrayarla, es que permite determinar la tasa máxima de ganancia de la economía como una relación física, o sea, con independencia de los precios.
Extensión para una multiplicidad de técnicas dadas
Cuando existen métodos alternativos para la producción de las mercancías, los cambios en la distribución pueden implicar modificaciones en los métodos de producción utilizados. Sraffa examina esta cuestión en la tercera parte de su libro (cap. XII). En este caso, las variaciones en el nivel de la variable de distribución exógena afectan no sólo los precios sino también el sistema productivo, modificándose entonces la mercancía patrón. ¿Es inteligible la evolución del precio de las mercancías más allá de los intervalos de la variable de distribución exógena para los cuales la técnica no cambia? Sraffa no se plantea siquiera la pregunta, lo cual es sorprendente dada la importancia que acuerda a la mercancía patrón como unidad de medida en las otras partes de su libro, y que ahora se ve restringida. Por lo general se admite la imposibilidad de explicar cómo varían los precios cuando los cambios en la distribución alteran los métodos productivos: precios expresados en términos de unidades de medida distintas no pueden ser comparados.
Nos proponemos mostrar que, contrariamente a esta respuesta negativa, es posible desarrollar la lógica de Sraffa y aclarar, para un estado del conocimiento técnico, como varían los precios cuando los métodos de producción cambian como resultado de una variación en la distribución. El argumento se basa en la demostración de Sraffa [ 1960/1966, cap. XII] en el sentido de que el cambio en la técnica de producción de una mercancía sólo se puede realizar en el punto en que coexisten el antiguo y el nuevo método de producción, y en el cual los dos sistemas productivos tienen la misma tasa de ganancia, el mismo salario y los mismos precios relativos. Salvo en este tipo de puntos, prevalece un solo sistema productivo al cual está asociada una única mercancía patrón. Esta mercancía cambia cuando la modificación en la distribución altera el sistema de producción. El movimiento de los precios puede descomponerse en dos variaciones consecutivas, a ambos lados del punto de coexistencia en que ambos sistemas tienen los mismos precios relativos, midiéndose en cada sistema la evolución de los precios en términos de la mercancía patrón correspondiente. La variación total del precio de cada mercancía es el producto de las variaciones calculadas a partir del punto de coexistencia.
Ilustramos esta idea por medio de un ejemplo numérico de una economía, extremadamente simple, que produce dos mercancías: existe un único método de producción para el trigo mientras que el hierro puede ser producido mediante dos métodos diferentes. Dos sistemas económicos son, por lo tanto, posibles. El sistema I es:
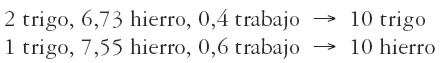 |
Los métodos de producción del sistema II son:
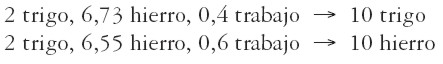 |
Ambos sistemas son igualmente beneficiosos para una tasa de ganancia del 10%. El sistema I es más redituable para tasas de ganancia superiores al 10%, y el II para tasas inferiores.
Tomemos como punto de partida una tasa de ganancia del 15% y supongamos que baja al 5%. Esta disminución va a acarrear una variación en los métodos de producción (cuando la tasa de ganancia es del 15%, se utiliza el sistema I, mientras que para la tasa del 5% opera el sistema II) y un cambio en los precios relativos: el precio relativo hierro/trigo aumenta en 3,48%. Este aumento se descompone en una subida del 1,79% cuando la tasa de ganancia pasa del 15% al 10%, y luego en un alza del 1,66% cuando cae del 10% al 5%. ¿Cómo se explican estos cambios en el precio relativo hierro/trigo? ¿Se deben a la modificación de los precios de ambas mercancías? ¿Y a qué tipo de variaciones obedecen? El esclarecimiento de esta cuestión requiere precisar cómo se han modificado los precios de cada una de ellas ante esta variación de la tasa de ganancia.
Dado que los métodos de producción utilizados cambian cuando la tasa de ganancia pasa del 15% al 5%, disponemos de dos mercancías patrón: una que permite calcular cómo evolucionan los precios del trigo y del hierro cuando la tasa de ganancia cae del 15% al 10%, y otra cuando baja del 10% al 5%. Ahora bien, como para la tasa del 10% el precio relativo hierro/trigo es el mismo cualquiera que sea la mercancía patrón utilizada como unidad de medida, podemos determinar cómo varían los precios del trigo y del hierro considerando como eje dicho estado de la distribución, y conjugar luego las variaciones respecto del mismo. Entre la tasa de ganancia del 15% y del 10%, el precio del trigo medido en mercancía patrón del sistema I baja en 1,54% y el del hierro aumenta en 0,22%. Entre la tasa de ganancia del 10% y del 5%, el precio del trigo medido en mercancía patrón del sistema II disminuye en 1,26% y el del hierro sube en 0,38%. Podemos concluir que el aumento de 3,48% del precio relativo hierro/trigo, cuando la tasa de ganancia se reduce del 15% al 5%, es el resultado de una disminución del 2,78% del precio del trigo y de un aumento de 0,60% del precio del hierro 2. Este resultado es válido para un estado dado del conocimiento técnico, pues es sensible a la secuencia de las técnicas utilizadas cuando varía la distribución3.
GANANCIA Y EXCEDENTE
Precios y excedentes
En la formalización sraffiana de la teoría clásica, el sistema de precios se escribe:
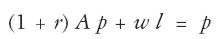 | [1] |
Donde l > O indica cómo se distribuye el trabajo homogéneo entre las ramas. Si llamamos u’ al vector (fila) unidad, se tiene entonces,
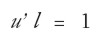 | [2] |
El salario w representa la masa salarial de la economía4. Este sistema tiene un grado de libertad. La determinación endógena de la tasa de ganancia r implica la fijación exógena del salario para lo cual se agrega la ecuación:
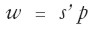 | [3] |
Interpretamos el vector (fila) s’ como la canasta de bienes que resulta de la negociación entre trabajadores y capitalistas, que desemboca en un doble acuerdo social relativo a los dos aspectos distintos del salario: su nivel y la composición de la canasta en términos de la cual se miden los salarios. El vector s’ representa, por lo tanto, el poder de compra de la masa salarial y no el consumo de los obreros.
De la ecuación [ 1] se infiere que los precios son la solución del siguiente sistema:
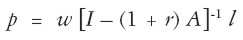 |
Incorporando la ecuación anterior en [ 3] se obtiene una ecuación cuya única incógnita es la tasa de ganancia.
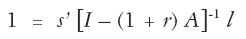 | [4] |
La tasa de ganancia depende de las condiciones de producción directas e indirectas, representadas por el vector [ I – A]-1l, de los bienes que componen el vector s’.
En el sistema de precios se distinguen tres nociones de excedente. La primera es el producto neto que es un dato puramente técnico, e indica las cantidades de bienes producidos que no son utilizadas como medios de producción. Dicho vector es:
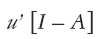 |
La otras dos nociones dependen de la distribución. La segunda es el vector que llamamos excedente físico, y que se obtiene descontando del producto neto los bienes que constituyen la masa salarial, es decir:
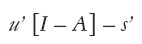 |
La tercera es el excedente de trabajo que indica la cantidad del trabajo total empleado –igual a la unidad en virtud de [ 2]– que no se utiliza en la producción de la canasta salarial s’. Se trata de un agregado, definido por la diferencia:
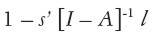 |
Las nociones de excedente físico y de excedente de trabajo están íntimamente relacionadas, siendo una la condición de la otra. Por una parte, si los salarios absorben la totalidad del producto neto, no existe excedente físico y el excedente de trabajo desaparece. Por la otra, sólo puede haber un excedente físico si hay excedente de trabajo. Por consiguiente, ambas nociones se implican mutuamente y son lógicamente equivalentes.
Relevancia del excedente de trabajo
De la ecuación [ 4] se infiere que se tendrá r > O sólo si:
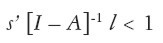 | [5] |
Entonces, el excedente de trabajo constituye la condición para la existencia de una tasa de ganancia positiva. Dado que A > O, s’ > O y l > O, f(r) = s’ [ I – (1 + r) A]-1 l es una función creciente de la tasa de ganancia, cuya derivada segunda también es positiva. Por lo tanto, como se puede apreciar en la Gráfica 1, cuanto mayor sea el excedente de trabajo mayor será la tasa de ganancia. Dada la equivalencia lógica entre excedente de trabajo y excedente físico, la ecuación [ 5] significa también que la tasa de ganancia será positiva sólo si existe un excedente físico.
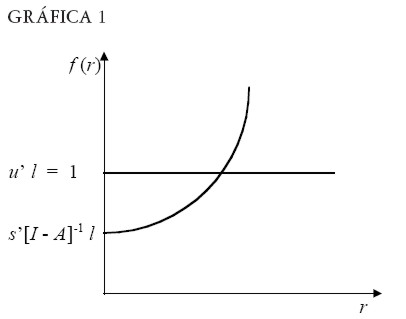 |
Aunque el excedente físico y/o el excedente de trabajo son la condición para que las ganancias sean positivas, su relación con la tasa de ganancia es compleja. Para una misma técnica y un estado dado de la distribución, ambos dependen de la medida del salario. Una diferencia importante es que el excedente físico cambia cuando varían las proporciones entre las ramas, mientras que el excedente de trabajo es independiente de dichas proporciones. Recordemos que, dados la técnica y el salario, la tasa de ganancia y los precios son independientes de las proporciones. En consecuencia, según las proporciones, a una misma tasa de ganancia le corresponden excedentes físicos y masas de ganancia diferentes, pero siempre el mismo excedente de trabajo.
Lo anterior nos lleva a preguntarnos si es posible determinar la tasa de ganancia sobre la base del excedente de trabajo, y no del excedente físico, en cuyo caso para un salario post factum,5 se tendría:
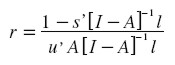 | [6] |
La respuesta es negativa porque, en la sociedad capitalista, los bienes por lo general no se intercambian en proporción a las cantidades de trabajo empleadas en su producción. Esto es así debido a la norma capitalista de distribución del excedente, a saber la uniformidad de la tasa de ganancia. En virtud de esta norma, la tasa general de ganancia está definida en términos de precios, y es igual a:
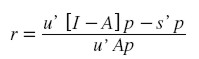 | [7] |
De esta forma, la ganancia se identifica con la evaluación en precios del excedente físico y no con el excedente de trabajo. Se llega así al siguiente resultado paradójico: el excedente de trabajo es, como vimos, la noción de excedente relevante para la tasa general de ganancia, pero en la definición de esta última aparece la evaluación en precios del excedente físico cuya dimensión, a diferencia de la del excedente de trabajo, no guarda ninguna relación con el nivel de esta tasa.
Si la composición en valor del capital es uniforme, las ecuaciones [ 6] y [ 7] son idénticas, y los precios relativos coinciden con los valores-trabajo relativos. Es en este marco que Ricardo inscribe su proposición. Se trata de establecer una relación entre ganancia y excedente de trabajo fuera de esta hipótesis restrictiva.
Nos proponemos mostrar que esto es posible utilizando las propiedades del sistema patrón cuando el salario está medido en términos de la mercancía patrón. En tal caso, la tasa de ganancia tiene una expresión puramente física y es, por lo tanto, independiente de la evaluación de las mercancías, ya sea en precios o en valores-trabajo. Así pues, en el sistema patrón, y estando el salario medido en mercancía patrón, la tasa de ganancia es una relación entre el excedente de trabajo y el trabajo incorporado en el capital invertido –nos referimos aquí a una tasa de excedente en trabajo, pero también podríamos definir la tasa de ganancia como una tasa de excedente en mercancías–. En suma, en el sistema patrón, a diferencia de lo que ocurre en el sistema efectivo, la ganancia puede identificarse tanto con el excedente físico, evaluado en precios, como con el excedente de trabajo.
Volvamos ahora al sistema efectivo. Este último y el sistema patrón sólo difieren en las proporciones en que las mercancías son producidas y, para un salario dado, medido en mercancía patrón, ambos tienen la misma tasa de ganancia, el mismo vector de precios y el mismo excedente de trabajo, pero excedentes físicos diferentes. De lo anterior resulta que, si el salario está expresado en mercancía patrón, la tasa de ganancia tiene una relación unívoca perfectamente definida con el excedente de trabajo del sistema efectivo, cualesquiera que sean las proporciones. En consecuencia, cuando el salario está medido en mercancía patrón, la proposición ricardiana de los Principios sigue siendo válida: aun sin suponer la teoría del valor-trabajo, la tasa de ganancia depende del excedente de trabajo. En cambio, la relación entre ganancias y excedente físico no es significativa.
NOTAS AL PIE
1 Ver, por ejemplo, Garegnani [ 1987].
2 El índice 1,0348 resulta del cociente entre los índices 1,0060 y 0,9722, donde el primero es igual al producto de los índices 1,0022 y 1,0038, y el segundo igual al producto de los índices 0,9846 y 0,9874.
3 Agradecemos a Christian Bidard por esta observación.
4 Para la homogeneización del trabajo, ver Klimovsky [ 1998].
5 El argumento es similar para un salario adelantado. La única diferencia consiste en la adición de la cantidad de trabajo total empleada en la producción de la canasta salarial al capital adelantado que figura en el denominador de la ecuación [ 6]. Análogamente, es necesario agregar el valor de la masa salarial al capital que figura en el denominador de la ecuación [ 7].
REFERENCIAS BIBLIOGRÁFICAS
1. Garegnani, P. (1987). Surplus Approach to Value and Distribution. En J. Eatwell et al. (Eds.), The New Palgrave: A Dictionary of Economics (t. IV, pp. 560-574). London: Macmillan Press. [ Links ]
2. Hahn, F. (1982). The Neo-Ricardiens. Cambridge Journal of Economics. 6, 353-374. [ Links ]
3. klimovsky, E. A. (1998). Trabajo homogéneo y bienes-salario en la teoría ricardiana. En M. Teubal (Ed.), Teoría, estructura y procesos económicos. Ensayos en honor al Dr. Julio H. G. Olivera (pp. 109-125). Buenos Aires: Eudeba. [ Links ]
4. Ricardo, D. (1815). Ensayo sobre la influencia del bajo precio del grano sobre los beneficios del capital. En P. Sraffa (Ed.), (1950). Obras y correspondencia de David Ricardo (pp. 3-27). México: FCE. 1960, vol. IV. [ Links ]
5. Ricardo, D. (1821). Principios de economía política y de tributación. En P. Sraffa (Ed.), (1950). Obras y correspondencia de David Ricardo. México: FCE. 1959, vol. I. [ Links ]
6. Sraffa, P. (1950). Introducción. En P. Sraffa (Ed.), Obras y correspondencia de David Ricardo (pp. XI-XLVIII). México: FCE. 1959, vol. I. [ Links ]
7. Sraffa, P. (1960/1966). Producción de mercancías por medio de mercancías. Barcelona: Oikos Tau. [ Links ]














