Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.23 no.40 Bogotá Jan./June 2004
MODELOS DE CRECIMIENTO. UNA INTERPRETACIÓN KEYNESIANA
Luis Lorente*
* Profesor Titular y Emérito de la Universidad Nacional de Colombia. Miembro correspondiente de la Academia Colombiana de Ciencias Económicas. Director de CEGA. Enviar los comentarios al correo: llorentes@unal.edu.co. Artículo recibido el 7 de mayo de 2004 y aprobado el 11 de junio del mismo año.
Resumen
Los modelos estándar de la teoría del crecimiento privilegian el papel del ahorro como explicación central del proceso de acumulación. La tradición keynesiana afirma que el ahorro es un simple residuo de las decisiones de inversión y que la acumulación deriva de la demanda efectiva. Esta no es la capacidad de compra de los consumidores, sino el agregado de las decisiones de producción de los empresarios. Los modelos estándar de crecimiento pueden ser reinterpretados como componentes de un modelo keynesiano donde el crecimiento está determinado por la demanda efectiva.
Palabras clave: teoría del crecimiento, modelo neoclásico de crecimiento, modelo keynesiano de crecimiento, demanda efectiva, agregación, distribución. JEL: E12, E13, E25, O41.
Abstract
The standard models of growth theory stress the role of saving as the main explanation for the accumulation process. The Keynesian tradition states that saving is a simple residue from investment decisions and that accumulation derives from effective demand. This does not represent consumers’ buying capacity but rather the sum of managers’ production decisions. Standard growth models can be reinterpreted as components of a Keynesian model where growth is determined by effective demand.
Key words: growth theory, neoclassical growth model, Keynesian growth model, effective demand, aggregation, distribution. JEL: E12, E13, E25, O41.
Résumé
Les modèles standard de la théorie de la croissance privilégient le rôle de l´épargne comme explication centrale du processus d´accumulation. La tradition keynésienne affirme que l´épargne n´est qu´un simple résidu des décisions d´investissement et que l´accumulation provient de la demande réelle. Celle-ci n´est pas la capacité d´achat des consommateurs, sinon l´agrégat des décisions de productions des entrepreneurs. Les modèles standard de croissance peuvent être réinterprétés comme des composantes d´un modèle keynésien où la croissance est déterminée par la demande réelle.
Mots clés : théorie de la croissance, modèle néo-classique de croissance, modèle keynésien de croissance, demande réelle, agrégation, distribution. JEL: E12, E13, E25, O41.
INTRODUCCIÓN
Las teorías del crecimiento parten de dos modelos básicos, el de Harrod-Domar y el de Solow, que dieron lugar a dos tradiciones diferentes. El primer modelo pertenece a una tradición aparentemente keynesiana, planteada en términos de variables macro y basada en relaciones de distribución del ingreso. El segundo es el prototipo de los modelos de teoría neoclásica, aparentemente basado en funciones de producción y con una fundamentación micro, plenamente desarrollada en la variante dinámica que suele denominarse modelo de Ramsey.
Examinaremos a continuación ambos modelos, excluyendo de momento sus variantes dinámicas, para mostrar que los dos admiten una interpretación diferente de la convencional y mucho más próxima al enfoque keynesiano de un crecimiento generado por variables de demanda y, en particular, por la demanda efectiva en el sentido original del término.
Usualmente se identifica demanda efectiva con capacidad de compra del consumidor. El sentido dado por Keynes a este término es muy diferente: para él representa el resultado de las decisiones de producción de los empresarios, entre las cuales destaca la inversión como motor del crecimiento1. Esas decisiones determinan el nivel de empleo así como los pedidos de bienes de capital e intermedios y, por consiguiente, el ingreso generado en la economía. Una parte de dicho ingreso se contabiliza como ahorro y, en una economía cerrada, debe ser precisamente igual al monto agregado de la inversión. No es un asunto de ex ante y ex post, sino una relación inevitable del circuito económico: la inversión decidida no es consumo y, por lo tanto, tiene que estar respaldada por instrumentos financieros que representan ahorro. Podemos medirla como elemento activo o de la producción y llamarla inversión, o bien como elemento pasivo y contabilizar los instrumentos o formas de ahorro en que se concreta una parte del ingreso generado, pero las dos sumas no pueden diferir en el agregado porque son sólo dos aspectos de una misma realidad.
Las expectativas de los empresarios se validan si los productos obtenidos son adquiridos por el consumidor o por las empresas que los usan como bien intermedio o de capital. Para un análisis de largo plazo, podemos aceptar este balance entre la producción de bienes y el uso que la economía les da, sea como inversión o como consumo.
De igual manera, cualquiera que sea el origen de los recursos monetarios usados por los empresarios para poner en marcha sus actividades, el mercado se encargará de igualar su monto con el del ahorro correspondiente. No importa si su origen es una emisión monetaria pura que se añade al circuito convencional de compras y ventas: de todas formas, el mercado crea la contraparte en instrumentos de deuda que quedan en mano de los empresarios o que son transferidos por éstos a los hogares en el mercado de capitales.
La financiación es parte esencial de este esquema, tanto como las expectativas de los empresarios, pues sin aquélla no es posible poner en práctica las decisiones de producción. En el agregado, dado que las deudas de un agente privado son las acreencias de otro, la mayor parte de esas financiaciones se compensan mutuamente y el resultado neto es la cuenta monetaria contra el banco emisor. De ahí la importancia del dinero para apoyar las decisiones que implican un aumento de la producción agregada. Sin embargo, no es el dinero la causa de la inversión, sino un simple instrumento de la misma.
Bajo esta visión del circuito económico, hay dos regímenes diferentes.
Cuando existen capacidad instalada ociosa, inventarios y fuerza de trabajo desempleada, la demanda efectiva puede crecer con rapidez, sin verse limitada por el nivel previo de producción. La emisión podría servir para dinamizar la producción sin que necesariamente aumenten los precios, pero que esto suceda o no depende de las expectativas de los empresarios y no simplemente de la creación de nuevos medios de pago, que el mercado podría rechazar o convertir en inflación. Viceversa, en presencia de expectativas favorables al crecimiento, la expansión de la actividad podría verse restringida por falta de dinero (que limita a su vez la disponibilidad de recursos financieros). Sin embargo, la oferta ilimitada de dinero no genera expectativas ni decisiones de inversión.
El otro régimen es el del pleno empleo, cuando sólo es posible invertir lo que ya forma parte de la producción corriente porque no hay margen alguno para producir bienes de inversión sin restringir al mismo tiempo la de bienes de consumo. En este caso, la emisión no puede tener efecto alguno diferente de incrementar los precios.
Expectativas y dinero juegan un papel asimétrico en el mecanismo del crecimiento, característica esencial para construir modelos estrictamente keynesianos de corto plazo. En este trabajo filtraremos estas asimetrías introduciendo un supuesto simplificador: que los empresarios cuentan con información completa (sus expectativas de venta se realizan) y que la política monetaria es perfectamente acomodaticia (en el presente contexto, si el dinero es exactamente el necesario para que todo el sistema financiero funcione tal como desean los empresarios, su papel es neutral y podemos trabajar en términos de “economía real”).
Estos dos supuestos permiten utilizar los modelos de Harrod-Domar y de Solow sin cambio formal, aunque el significado de sus relaciones funcionales deba ser reinterpretado de acuerdo con el esquema keynesiano expuesto.
En el análisis que sigue utilizaremos otro supuesto adicional: que el factor trabajo es una restricción (pleno empleo de la fuerza de trabajo), mientras que el factor capital cuenta con un margen de capacidad instalada ociosa y de inventarios suficiente para sostener el ritmo de inversión deseado por las empresas. Este supuesto es cercano a la idea neoricardiana de “producción de mercancías por medio de mercancías”, donde no puede existir una escasez permanente de bienes producidos, sino sólo de trabajo o de recursos naturales. Dicha hipótesis parece natural para un análisis del largo plazo, donde hay tiempo suficiente para atender cualquier demanda de bienes de capital o intermedios que sea compatible con la restricción de venta de los bienes finales producidos y con las expectativas de expansión de los productores.
Bajo tales premisas, veremos a continuación que el modelo de Harrod-Domar puede representar un caso de crecimiento restringido por el pleno empleo de la fuerza de trabajo, donde la función técnica de producción determina cuál es la cantidad de capital necesaria y, por consiguiente, la inversión deseada2. El ahorro aparece como simple consecuencia de esa decisión de invertir.
La reinterpretación del modelo de Solow parte de dos observaciones clave: su éxito econométrico cuando se aplica con datos de cuentas nacionales y la imposibilidad de construir una función de producción tipo Cobb-Douglas mediante agregación de funciones de producción micro. La segunda observación destruye la pretendida fundamentación micro del modelo apenas se sale del supuesto de un agente representativo que produce un solo bien, que es a la vez de consumo y de capital. Esto es lo que sucede, precisamente, cuando el modelo se aplica a datos de cuentas nacionales, que agregan multitud de productos y tecnologías diferentes en uso simultáneo.
Sin embargo, es posible hallar una justificación macro de la relación entre producto y factores descrita por una función Cobb-Douglas, que no depende de las tecnologías en uso.
Dicha justificación depende de dos condiciones: la primera es que la participación del trabajo en el producto total sea aproximadamente constante, y la segunda, que el modelo permita representar una forma muy común de crecer, que consiste en añadir unidades de producción idénticas a las que ya están en operación (más fábricas construidas con igual diseño tecnológico). La primera es un hecho empírico, observable en muchos países durante períodos prolongados, aunque no es una condición universal ni teóricamente necesaria. De hecho, requiere una explicación endógena que complica el modelo y que no exploraremos aquí. La segunda no excluye que existan otras formas de crecer, basadas en innovaciones o en economías de escala, sino solamente que esa forma simple de crecimiento sea compatible con el modelo.
Con la interpretación propuesta, la función Cobb-Douglas del modelo se convierte en una restricción originada en la distribución del producto, que es una condición estrictamente macro o, si se quiere, de origen institucional. Cuando se añade el supuesto de pleno empleo de la fuerza de trabajo, esta restricción distributiva señala cuál es la cantidad de capital compatible con el empleo efectivamente usado y determina, de esta manera, la inversión que deberán hacer los empresarios, es decir, el monto de la inversión “deseada”. De nuevo, el ahorro aparece como residuo del circuito: dado el volumen de producción compatible con la condición distributiva, el ahorro coincidirá con la inversión realizada.
En resumen, con la interpretación sugerida, ambos modelos pueden servir como piezas para armar modelos keynesianos de crecimiento de largo plazo. Desde luego, el planteamiento completo de éstos exigiría añadir elementos monetarios y, además, reemplazar la condición de pleno empleo de la fuerza de trabajo, que aquí se utiliza para determinar el monto de “inversión deseada”, por otros supuestos más flexibles y realistas.
EL AHORRO EN LOS MODELOS CONVENCIONALES DEL CRECIMIENTO
El modelo de Solow representa una tradición de crecimiento por acumulación de ahorros, muy diferente de la teoría keynesiana de la inversión como elemento causal, la cual produce un ahorro como simple residuo del circuito económico.
La desviación del enfoque keynesiano comienza, en realidad, con la función de consumo agregado planteada por el mismo Keynes:
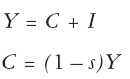 |
de donde se deduce inmediatamente:
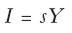 |
En un modelo keynesiano o kaleckiano, I incluye tanto el ahorro previo como la inversión autónoma, pero si descartamos esta última, como viene a ocurrir en los modelos de síntesis neoclásica, en los cuales aparece la definición del ahorro como S = Y - C, obtenemos la relación:
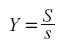 |
que expresa el “multiplicador” implícito en los modelos de síntesis neoclásica y en el de Solow.
El supuesto implícito en el análisis convencional es que sólo es posible invertir la parte de la producción previa que no se destinó al consumo, fracción que se identifica con el ahorro. La dicotomía entre producir para invertir o para consumir expresa en el fondo el supuesto de pleno empleo de todos los factores. En contraste, el concepto keynesiano de inversión autónoma expresa la idea de que parte del producto corriente debe atribuirse a la decisión de invertir, sin la cual no habría tal producto sino otro menor. En este caso, queda implícito que por lo menos uno de los factores no está restringido por la condición de pleno empleo, por lo cual es posible incrementar la producción en bienes dirigidos a la inversión.
Cada vez que adoptamos una propensión al ahorro s como parámetro dado, es decir, como una constante fijada de antemano, estamos introduciendo la misma interpretación del proceso económico implícita en el modelo de Solow, es decir, que el ahorro es lo que genera la inversión y explica la acumulación.
La misma confusión está presente en la discusión del crecimiento que encontramos en la señora Robinson y en Harrod. Su planteamiento parte de definir dos tasas de ahorro, para discutir luego qué sucedería si ambas difieren entre sí. Una es el ahorro que permitiría aprovechar el aumento del trabajo disponible y el cambio técnico, la cual determina cuál es la tasa de crecimiento natural. La otra es el ahorro que la economía en conjunto está dispuesta a realizar, que define cuál es la tasa de crecimiento garantizado. En esencia, el problema surge de otorgar un papel preponderante al ahorro y descartar la inversión autónoma, la presencia de capacidad instalada ociosa y el papel del dinero, tres temas clave del enfoque keynesiano para discutir el problema del desempleo.
Tomemos como ejemplo el conocido modelo de Harrod-Domar. Hay dos versiones matemáticamente equivalentes de este modelo: la primera parte de una relación técnica entre capital y producto que supone constante, mientras que la segunda invierte la lectura de esta misma relación y la interpreta como un multiplicador del aumento de capital deseado correspondiente al aumento planeado en la producción. Inmediatamente entra en acción el acelerador para inducir una nueva inversión que será convertida por el multiplicador en nuevos incrementos de la producción, con lo cual vuelve a aparecer la relación constante entre capital y producto que es el punto de partida en la otra variante del modelo.
Los supuestos clave de este modelo son los de pleno empleo de los factores disponibles (explícito para el capital en la primera variante e implícito en la segunda, y explícito en ambas variantes para la fuerza de trabajo o empleo), y el supuesto de ausencia de inversión autónoma, es decir, la identidad entre ahorro previo e inversión.
Un resultado central es que existe un nivel único del ahorro compatible con el crecimiento de la población, dado por la ecuación:
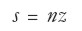 |
donde s es la propensión al ahorro, n la tasa de crecimiento de la población L y z es la relación capital/producto (z = K/Y), dada por razones técnicas y fija por consiguiente.
La ecuación anterior se interpreta como resultado problemático porque, en principio, la propensión al ahorro podría ser, en la práctica, diferente a la exigida por la anterior ecuación y ningún mecanismo de esta economía permitiría restablecer el equilibrio. Precisamente el problema de “filo de la navaja” estriba en que, ante una diferencia entre la tasa de ahorro efectiva y la compatible con el crecimiento de la población, la economía tiende a profundizar el desequilibrio macro en lugar de regresar a la trayectoria de crecimiento de “la edad de oro”.
Una de las dos soluciones clásicas fue la de Kahn, que describe una “edad de oro bastarda”, donde n representa la tasa de crecimiento del empleo, pero ésta es inferior a la tasa de crecimiento de la población, con lo cual existe un desempleo creciente.
La otra fue la de Kaldor, que consiste en reconocer que existen propensiones al ahorro diferentes según el nivel de ingreso, alta para los que reciben rentas de capital y baja para los trabajadores. De esta forma, la concentración del ingreso durante el desarrollo podría aumentar la tasa de crecimiento de la economía. En el fondo, esta salida sólo establece una relación entre crecimiento y distribución del ingreso, quizá más clara en los modelos de Kalecki, pero no resuelve el problema porque mantiene la identidad entre ahorro previo e inversión.
Más tarde aparecieron versiones del modelo (varios de los usados por el Fondo Monetario Internacional para fines de programación macro) que incorporan “ahorro externo” como elemento capaz de complementar el ahorro interno y asegurar un despegue de la acumulación y el desarrollo. Aunque muy usados en el pasado –y aún en el presente–, no existe evidencia de que sus supuestos se cumplieran en la práctica [ Easterly 1999]. En definitiva, su falla debe interpretarse como una muestra de que el ahorro no es la causa de la inversión ni de la acumulación, por lo que el “ahorro externo” puede desplazar ahorro interno, en lugar de sumarse a él, o simplemente perderse porque las expectativas de los empresarios no permiten que ni el uno ni el otro se conviertan en inversión efectiva real.
INTERPRETACIÓN KEYNESIANA DEL MODELO DE HARROD-DOMAR
Una formulación estrictamente keynesiana del crecimiento debe incluir en forma explícita el papel del dinero como puente entre el ahorro y la inversión y como fuente de financiamiento para la inversión autónoma.
Aquí nos limitaremos a exponer una variante del modelo de Harrod-Domar que elimina la relación causal del ahorro hacia la inversión, que es un primer paso hacia la formulación de un modelo verdaderamente keynesiano donde el ahorro debe aparecer como simple residuo en la operación del circuito económico.
En un modelo de Harrod-Domar sin cambio técnico la función de producción es lineal y está dada por dos relaciones:
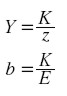 |
donde z y b son dos constantes (coeficientes técnicos que describen la tecnología) y donde E es el empleo, que está sujeto a la condición:
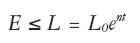 |
La economía descrita acumula capital así:
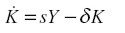 |
Mientras E < L, el valor de la propensión media al ahorro s puede ser cualquiera y su nivel define la tasa de crecimiento, pero cuando se alcanza el pleno empleo, s tiene que ajustarse al nivel que sea compatible con esta condición y con las demás ecuaciones del modelo.
La operación en la primera fase, la de población “sobrante”, podría representar el caso de una economía urbana que se expande en medio de un entorno agrícola donde existe un excedente de población subocupada. A medida que la economía urbana genera nuevos puestos de trabajo, atrae migrantes hacia la ciudad que completan la oferta necesaria de mano de obra y no existe problema alguno de empleo. La formulación aquí usada sigue identificando ahorro con inversión, pero el nivel de s podría estar dado por razones ajenas a la decisión de los consumidores, y limitado únicamente por la capacidad de la estructura productiva para incorporar nuevo capital (al estilo de Kaldor). Sin embargo, un análisis completo de este posible mecanismo exige introducir el dinero como medio para poner en marcha una capacidad instalada ociosa, asunto que no exploraremos aquí. Baste por ahora reconocer que, dentro de un intervalo razonable de valores, el nivel de s es arbitrario mientras no se alcance la segunda fase de operación, cuando la disponibilidad de mano de obra comienza a actuar como limitante del crecimiento.
Lo que se busca mostrar a continuación es que, durante esa segunda fase con pleno empleo de la fuerza de trabajo, el parámetro s debe interpretarse como una consecuencia de la capacidad para invertir de la economía, es decir, como un residuo de la decisión de invertir, y no como la causa de ésta.
Una vez agotado el excedente de mano de obra, la condición de pleno empleo implica: K = bL = bLoent y Lo son constantes, K crece exponencialmente a tasa n.
Tenemos:
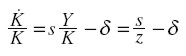 |
y, de acuerdo con la respuesta anterior, sabemos que:
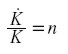 |
Igualando los miembros de la derecha de ambas expresiones, obtenemos:
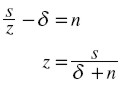 |
que nos determina el valor de s compatible con esta tecnología, ya que z, n y δ son constantes dadas. Obsérvese que esta fórmula es idéntica a la que determina el nivel de crecimiento balanceado o estacionario en el modelo de Solow, aunque han cambiado las interpretaciones de los símbolos y, por ende, el sentido de la causalidad.
Las razones para invertir pueden ser cualesquiera: el caso es que las decisiones de inversión quedan limitadas por una restricción técnica que es la necesidad de emplear un número determinado de trabajadores por unidad de capital, unida a la disponibilidad limitada de trabajo.
Dada esa inversión técnicamente determinada, el ahorro aparece como simple consecuencia: sin más inversión, no existe más producto ni puede haber mayor ahorro; viceversa, tampoco puede existir un ahorro inferior a la inversión realizada.
Esta es, precisamente, la causalidad keynesiana que exige que el ahorro sea un simple residuo de las decisiones de inversión, en lugar de cumplir el papel neoclásico de causa y motor de la inversión.
En este modelo básico es fácil introducir un cambio técnico exógeno, al estilo del que se utiliza en el modelo de Solow.
Suponiendo que el efecto del cambio técnico es un aumento exponencial de la productividad, podemos explorar los efectos de un cambio en la productividad del capital, que permite obtener más producto por unidad de capital, de manera que:
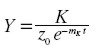 |
y también analizar los efectos de un aumento en la productividad del trabajo, que requiere cada vez menos trabajo por unidad de capital, así que:
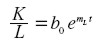 |
donde mK es la tasa de cambio de la productividad del capital y mL la correspondiente al trabajo.
Lo mismo que sucede con el modelo de Solow, veremos inmediatamente que el cambio técnico sólo puede ocurrir en la productividad del trabajo y no en la del capital.
En efecto, tenemos: 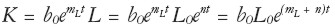 que es exponencial con tasa n + mL.
que es exponencial con tasa n + mL.
Por consiguiente:
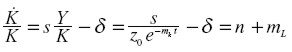 |
de donde se deduce:
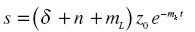 |
Es obvio que el valor de mL puede ser cualquiera (desde luego, pequeño y mayor que cero). En cambio, deberemos tener mK = O porque cualquier valor positivo nos haría disminuir s hasta cero en forma exponencial.
De nuevo encontramos un resultado formalmente igual al del modelo de Solow: sólo es admisible un cambio técnico “neutral de Harrod”, es decir, que eleve la productividad del trabajo, y la solución de crecimiento balanceado satisface la relación:
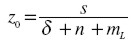 |
aunque aquí debemos interpretarla “al revés”, con el parámetro s como resultado en vez de dato exógenamente fijado.
El resultado obtenido acerca del tipo de cambio técnico viable se explica fácilmente desde la perspectiva del circuito económico: el aumento en la productividad del trabajo lleva asociado un aumento en el consumo real de los trabajadores, lo cual permite realizar la venta de la producción adicional. En cambio, el aumento en la productividad del capital conduciría a producir una cantidad finita de bienes finales con un capital que tiende a cero en el largo plazo.
Moraleja: el salario nominal debe crecer en promedio a la tasa de inflación más la tasa de aumento de productividad, so pena de frenar el ritmo de crecimiento por falta de mercado para sus productos. No existe razón similar para aumentar la tasa de ganancia del capital, ni podemos esperar un efecto positivo para el crecimiento porque haya un aumento en la tasa de beneficio.
UNA REINTERPRETACIÓN DEL MODELO DE SOLOW
Acabamos de ver que el modelo de Harrod-Domar admite una interpretación estrictamente keynesiana donde la inversión está determinada por el pleno empleo de la fuerza de trabajo y por restricciones técnicas, y donde el ahorro aparece como un simple residuo del proceso de crecimiento. Al mismo tiempo, vimos que existe un paralelo formal entre los resultados obtenidos y las ecuaciones del modelo de Solow, es decir, una semejanza en las fórmulas que describen el estado estacionario, pero con una diferencia radical en la interpretación económica de las variables involucradas.
Dado que el modelo de Solow es más flexible que el de Harrod-Domar y que suele dar mejor ajuste econométrico con series tomadas de cuentas nacionales, resulta atractivo buscar una reinterpretación no neoclásica de dicho modelo. Como veremos a continuación, esto es posible y depende de dos observaciones:
1. No es admisible el supuesto fundamento microeconómico del modelo de Solow porque no es posible construir una función de producción agregada; en su lugar, sólo existe un fundamento macro, el cual depende de que la participación de los factores en el producto permanezca aproximadamente constante, es decir, de un fenómeno de distribucón del ingreso, el cual da como resultado que aparezca una función Cobb-Douglas que relaciona producto, capital y trabajo.
2. Al reincorporar las relaciones entre capital y trabajo en el modelo como una consecuencia de la relación de distribución del ingreso, la inversión puede ser explicada por otras razones y el ahorro aparece como el residuo que garantiza un balance contable en el agregado.
Repaso del modelo de Solow
El planteamiento convencional del modelo de Solow contiene todos los elementos típicos de un modelo neoclásico: competencia perfecta y pleno uso de los factores, función de producción que representa la frontera tecnológica para cada combinación posible de los factores, y un proceso de acumulación que depende del ahorro (equivalente a la fracción no consumida del producto corriente). Se supone que el dinero es neutral y, de hecho, todo el modelo se plantea en términos reales. El único aspecto no neoclásico consiste en suponer que la tasa de ahorro es una constante dada (inconsistencia que elimina la variante dinámica conocida como modelo de Ramsey-Cass-Koopmans).
Consecuente con el supuesto de competencia perfecta, están presentes muchas unidades de producción que operan con el tamaño óptimo y la tecnología más adecuada (si ofrecen un mismo producto, tienen que producirlo en condiciones idénticas, ya que no hay restricciones de acceso a capital o tecnología para ningún agente y, por ende, cualquier posible ventaja de economías de escala tiene que haber sido incorporada por todos y cada uno de ellos). Una consecuencia inmediata de este supuesto es que el crecimiento debe producirse exclusivamente por adición de nuevas unidades de producción iguales a las ya existentes, por lo cual la función de producción agregada debe ser homogénea de primer grado.
Adicionalmente existe un cambio técnico exógeno que modifica la productividad de los factores, pero que también es igual para todos los agentes. Dicho cambio tiene que ser exógeno porque no es posible representar la inversión en conocimiento abstracto, ni en diseños que podrían ser utilizados por cualquiera sin pagar nuevamente su costo de desarrollo. Esto es consecuencia de que la función de producción sea homogénea de primer grado, por lo cual la remuneración de los dos factores, capital y trabajo, agota el producto (teorema de Euler) y no deja remanente alguno para remunerar la generación de conocimiento3.
Expresado de otra manera, si Y = F(A, K, L), donde A representa un conocimiento que tiene costo generar, pero que luego puede usarse indefinidamente sin costo adicional, entonces F(λA, λK, λL) > λF(A, K, L) . De acuerdo con este resultado, A no puede aparecer como un factor de producción adicional porque no sería posible remunerarlo, así que debe incluirse en el modelo como un cambio exógeno de la productividad, en cuyo aumento ningún empresario está dispuesto a invertir.
Formalmente, el modelo se plantea para un solo producto que es al mismo tiempo bien de consumo y bien de capital (aunque luego se utiliza con datos de cuentas nacionales que representan una mezcla de productos y de procesos de producción heterogéneos).
Las ecuaciones de equilibrio son:
1. Pleno empleo de la población, que crece a una tasa exógena, L = Loent.
2. Pleno uso de la capacidad instalada, determinada por la función de producción agregada: Y = F(K, AL), donde A representa un aumento exógeno de productividad del trabajo a tasa exponencial, A = Aoegt.
3. Ahorro como una fracción constante del producto, que se traduce automáticamente en inversión bruta, sY = I.
La inversión así definida es el motor de la acumulación, de acuerdo con la ecuación diferencial: 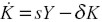 , donde δ representa una pérdida periódica de capital por desgaste (no existe un concepto de obsolescencia, a pesar del cambio técnico, porque éste es exógeno y se aplica por igual a todas las unidades de producción).
, donde δ representa una pérdida periódica de capital por desgaste (no existe un concepto de obsolescencia, a pesar del cambio técnico, porque éste es exógeno y se aplica por igual a todas las unidades de producción).
Obsérvese que, en la segunda condición de equilibrio, el cambio técnico representado por A aumenta directamente la productividad del trabajo (cambio técnico neutral de Harrod). Escribir Y = AF(K, L) con Acreciendo exponencialmente implicaría que la relación capital/producto se acercara exponencialmente a cero, mientras que escribir Y = F(AK, L) con A implicaría un aumento de la remuneración del capital, ∂F / ∂K, a un ritmo exponencial. Ambas consecuencias serían inaceptables en el largo plazo. En cambio, usar AL significa que el salario real del trabajador crecerá exponencialmente, a la par con su productividad; el producto podrá ser consumido sin problema alguno y los demás parámetros y relaciones entre variables permanecerán acotados en el largo plazo.
Como la función de producción es homogénea de primer grado, podemos definir las variables reducidas: y = Y / AL y k = K / AL, con lo cual la función de producción es y = f(k) y la ecuación diferencial del modelo se convierte en:
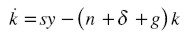 |
El análisis de esta ecuación muestra que existe un estado estacionario, definido por 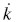 = O, que es estable, es decir, que si la economía comienza con un capital k inferior al determinado por esa condición, crece hasta alcanzarlo y, viceversa, si comienza con una dotación superior de capital, la reduce hasta regresar al nivel estacionario de capital per cápita.
= O, que es estable, es decir, que si la economía comienza con un capital k inferior al determinado por esa condición, crece hasta alcanzarlo y, viceversa, si comienza con una dotación superior de capital, la reduce hasta regresar al nivel estacionario de capital per cápita.
Podemos encontrar de inmediato una relación interesante:
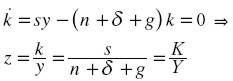 |
Esto significa que la relación capital/producto es constante apenas se alcanza el estado estacionario de k. Y cuando el capital reducido, k, permanece constante, el capital K y el producto Y crecen a la misma tasa, que es la de crecimiento de AL, es decir, g + n .
Los problemas de la función de producción agregada
A diferencia de las muchas otras formas de dar fundamento micro a modelos macro –teorías micro de Kalecki, Sraffa, poskeynesianos, austríacos, evolucionistas, etc.–, la neoclásica utiliza como premisa la existencia de funciones de producción y de consumo agregadas. La pregunta clave para este enfoque es si, efectivamente, es posible construir funciones agregadas de producción y de consumo que tengan fundamento en funciones micro de características similares.
En el caso de las funciones de consumo, las condiciones son tolerables:
1. Que los individuos tengan propensiones marginales al consumo constantes.
2. Que dichas propensiones sean aproximadamente iguales para todos.
3. Que la distribución del ingreso permanezca constante.
La mayoría de países cumplen la tercera y las otras dos pueden aceptarse como resultado de un proceso de imitación o emulación social.
El único problema grave aparece en modelos de largo plazo, ya que las dos primeras son incompatibles con la innovación de productos y la diversificación de los consumos.
En el caso de las funciones de producción, las condiciones para construir la función agregada son tan exigentes que equivalen a suponer una única empresa representativa.
Hay bastantes trabajos al respecto, de Leontief [ 1947] , Nataf [ 1948] , Sato [ 1975] y otros más, pero los resultados más interesantes son los de Franklin Fisher, publicados en varios artículos desde 1969 hasta el presente [ Fisher 1969; Felipe y Fisher 2003] .
Fisher toma en cuenta que la función de producción no es una descripción de una técnica, sino el resultado de escoger la mejor técnica disponible para cada combinación de los factores. Así, el problema consiste en agregar el óptimo de funciones micro y obtener un óptimo de producción agregada. Las condiciones que encuentra para agregar funciones micro del tipo Cobb-Douglas se resumen así:
1. Tiene que haber rendimientos constantes a escala.
2. Las funciones micro deben ser todas iguales, salvo por un coeficiente constante de eficiencia del capital (por ejemplo, F(bK, L) con bdistinto para cada empresa).
3. Si hay trabajo diferenciado, se necesitan salarios relativos que aseguren que todas las empresas contratan trabajadores de cada especialidad en proporciones iguales.
4. Si hay más de un producto, todas las unidades micro tienen que producir la misma canasta de bienes en iguales proporciones.
En la práctica, estas cuatro condiciones equivalen a suponer empresas idénticas, es decir, un agente representativo, con todas las dificultades que esto trae.
La idea de agente representativo aparece ya en Marshall y fue discutida desde 1920 –Clapham en un artículo con el sugerente título “Of empty economic boxes” [ 1922] – hasta 1939 –Mason y comienzos de la economía industrial–. Los trabajos de Clark [ 1961] sobre competencia dinámica cierran esta discusión a fines de los años cincuenta, durante la cual destacaron las críticas de Schumpeter, Sraffa, Young y Mason. Los argumentos en contra del uso de agentes representativos tienen que ver con el análisis de la competencia en mercados realistas y se resumen en tres puntos:
1. La objeción sistémica: el aumento de costos de unas empresas puede deberse al crecimiento de otras distintas que usan los mismos insumos (interacción entre agentes heterogéneos con objetivos en conflicto, que invalida el análisis de equilibrio parcial y que compromete la definición de funciones objetivo agregadas).
2. Existe innovación de productos y de procesos, cuya representación exige cambiar la función de producción, ya que no se pueden representar como un movimiento a lo largo de una función única.
3. Hay diferenciación de productos y otras estrategias de competencia, por lo cual empresas heterogéneas pueden presentar reacciones de precio divergentes durante el ciclo de negocios.
Como consecuencia de estos análisis, la economía industrial abandona el agente representativo y estudia estructuras de mercados con agentes heterogéneos desde los años sesenta [ Schohl 1999] . Por esa razón, resulta paradójico que, precisamente en 1960, Grunfeld y Griliches propongan el uso del agente representativo en modelos macro y que éste sea adoptado sin discusión metodológica previa.
Grunfeld y Griliches [ 1960] parten de trabajos previos de Theil, quien muestra que la agregación perfecta sólo puede diseñarse si se conoce la totalidad de parámetros micro, pero estos autores aducen que los errores de agregación se compensan mutuamente y el resultado debe ser una función media o agregada aproximadamente correcta. Sin embargo, este argumento equivale a decir que las diferencias o idiosincrasias de las empresas micro no tienen importancia para definir el agregado, lo cual destruye la fundamentación micro en su esencia misma.
En definitiva: el uso de un agente representativo para justificar funciones de producción agregadas no es sólo asunto de conveniencia práctica y simplicidad de los modelos, sino que es una consecuencia ineludible de la imposibilidad de agregar agentes heterogéneos.
Las consecuencias de su uso son las mismas anotadas en la crítica a Marshall:
1. No se reconoce la especificidad del fenómeno macro como propiedad emergente de un agregado de individuos heterogéneos que interactúan (elemento importante en la teoría de Keynes, quien decide trabajar directamente con los agregados e intenta representar propiedades emergentes como resultado de esa interacción, es decir, propiedades que no están presentes en los individuos por separado).
2. Los modelos de crecimiento que los usan excluyen la innovación y sólo representan los fenómenos de tipo acumulativo (exclusión del desarrollo tecnológico schumpeteriano, sustituido por un cambio técnico exógeno). Como consecuencia, el residuo de Solow o Productividad Total de Factores no puede ser explicado en forma endógena.
La función Cobb-Douglas
Vista la heterogeneidad de producciones micro en cualquier economía real, que en muchos casos no admiten representación individual mediante funciones tipo Cobb-Douglas, es apenas obligado preguntarse a qué se debe el éxito empírico de esa función agregada en el ajuste de modelos de Solow sobre datos de cuentas nacionales.
La respuesta es que el ajuste de la función Cobb-Douglas agregada no depende de una fundamentación micro, sino de dos condiciones macro:
1. Que sea posible crecer añadiendo unidades iguales a las existentes (homogeneidad de primer grado).
2. Que la participación de los factores en el producto nacional sea aproximadamente estable.
Ninguna de las dos expresa una necesidad económica ni tecnológica ineludible, aunque la primera podría justificarse por argumentos de conveniencia: una forma de crecer consiste en añadir nuevas unidades de producción micro exactamente iguales a las que ya existen y sería deseable que cualquier modelo de crecimiento admitiera ese caso particular. Ahora bien, el crecimiento proporcional de K, L y Y es precisamente la condición de homogeneidad de primer grado.
En realidad, la homogeneidad de primer grado sólo es imprescindible si se desea mantener el supuesto de competencia perfecta, como sucede en la formulación convencional del modelo de Solow. En efecto, para que haya muchas empresas compitiendo sin restricciones de acceso a capital ni a tecnología, se necesita que todas ellas tengan el tamaño óptimo para la tecnología óptima dada por la función de producción micro. En otras palabras, que sean todas iguales entre sí, lo cual deja la adición de nuevas unidades idénticas como única vía para crecer.
En cuanto a la segunda condición refleja una regularidad empírica, presente por largos períodos en muchos países pero que, a su vez, exige una explicación. Una posibilidad está en incorporar al modelo un mecanismo de ejército de reserva como el planteado por Goodwin [ 1967] : cuando los salarios aumentan, se adopta tecnología más intensiva en capital y la demanda de trabajo desciende, con lo cual los salarios regresan al nivel previo; podríamos añadir que si los salarios bajan, deja de formarse capital humano y su escasez eleva nuevamente la remuneración del trabajo, así que aparece un nivel relativamente estable de participaciones de los factores en el producto. Sin embargo, esta explicación se basa en argumentos de distribución del ingreso que nada tienen que ver con la tecnología en sí misma, ni pueden servir como soporte para justificar una u otra función neoclásica de producción.
Veamos entonces por qué las dos condiciones “macro” antes mencionadas privilegian la función de Cobb-Douglas.
Comencemos por una identidad de cuentas nacionales:
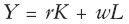 |
Esta relación sugiere otra en tasas de crecimiento, así:
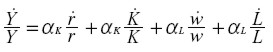 |
donde definimos:
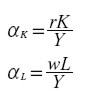 |
Desde luego, las participaciones αK y αL así definidas son funciones variables en el tiempo, que pueden depender incluso de K y de L; solamente sabemos que suman la unidad, porque así lo exige la identidad de partida.
Hasta aquí, no hemos introducido ningún supuesto acerca de funciones de producción, ya que partimos de una identidad contable que simplemente afirma que el producto se divide entre remuneración al capital y remuneración al trabajo.
Hagamos intervenir ahora la segunda condición antes mencionada, la de que las participaciones de los factores sean constantes. En tal caso, la ecuación diferencial planteada admite una integración sencilla:
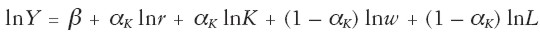 |
donde β es una constante de integración, con lo cual:
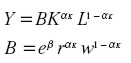 |
El resultado es una relación funcional del tipo Cobb Douglas en K y en L, aunque con un factor B que es variable en el tiempo. Si este factor dependiera además de K o de L o de ambas variables, la aparente homogeneidad de primer grado en K y L podría fallar.
Aquí es donde interviene la primera condición antes mencionada. Si la función Y = F(K, L) es homogénea de primer grado en K y L, por el teorema de Euler sabemos que:
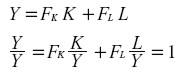 |
y por comparación con la identidad contable, y también de acuerdo con las definiciones de αK y de αL, podemos identificar r = FK; w = FL, sin que ello implique supuesto alguno de competencia perfecta.
Pero:
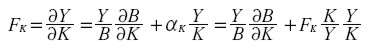 |
de donde se deduce que:
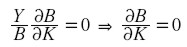 |
y por igual razón,B es también independiente de L.
La homogeneidad de primer grado nos lleva, pues, a concluir que el coeficiente B es una función del tiempo independiente de los niveles de K y de L, deducción compatible con el resultado empírico de que B suele ser una función exponencial del tiempo con tasa de crecimiento aproximadamente constante, es decir, del tipo:
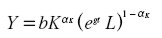 |
Solución explícita del modelo de Solow
Continuemos ahora con el desarrollo convencional del modelo de Solow. Cuando utilizamos una función Cobb-Douglas, Y = bK α(AL) 1 - α, la función reducida equivalente adopta una forma exponencial y = f(k) = bK α. Sustituyendo esta expresión en la ecuación diferencial del modelo de Solow obtenemos:
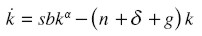 |
que es una ecuación no lineal del tipo Bernoulli, linealizable mediante el cambio de variable z = k 1 - α. Este cambio de variable equivale a expresar la ecuación en términos de la relación capital/producto, z = K / Y = k / y .
En efecto, la ecuación se transforma así:
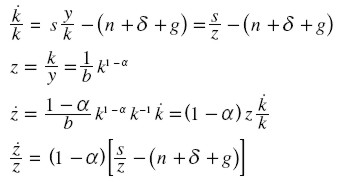 |
expresión que podemos escribir:
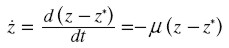 |
donde introducimos las constantes:
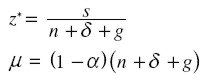 |
La integración es inmediata y proporciona una solución explícita del modelo de Solow:
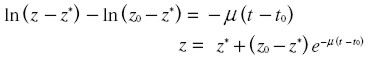 |
donde zo es el valor inicial de z para el instante inicial to. Normalmente, zo < z*, por lo cual la aproximación al estado estacionario tendrá lugar “desde abajo”, es decir, acumulando capital hasta alcanzar la relación capital/producto, z* del estado estacionario. Ocasionalmente, la economía podría tener un capital inicial excesivo, zo > z*, y la aproximación ocurriría entonces “desde arriba”, es decir, desacumulando capital.
El ahorro como consecuencia del pleno empleo
Supongamos ahora que F(K, L) no representa una función de producción dada por la tecnología conocida, sino que expresa una relación de distribución, es decir, que refleja la condición de que la participación de los factores en el producto permanezca constante.
En tal caso, la inversión estará determinada por la condición de pleno empleo de la población L y por la condición de distribución del ingreso antes mencionada.
En otros términos, f(k) permite calcular el aumento de K necesario para que la relación K / AL resultante sea compatible con la participación constante del capital en la distribución del ingreso agregado.
El resultado del modelo admite la siguiente interpretación: “existe una estrategia de inversión que conduce a un estado estacionario de crecimiento, la cual consiste en invertir una proporción s constante del producto corriente”.
Es importante señalar que el “producto corriente” incluye como parte del mismo la inversión realizada, es decir, que incorpora cualquier nivel de inversión que los empresarios hayan decidido y que la capacidad instalada haya hecho técnicamente viable. De esta manera, la inversión no está limitada por una producción anterior ni, por consiguiente, por un ahorro previo; al contrario, el ahorro corriente contabiliza de otra manera la misma inversión corriente y es también igual a sY porque, como dice Keynes, “nacen iguales”. La inversión es el elemento activo que necesitamos explicar, mientras que el ahorro aparece como simple residuo del proceso de crecimiento.
La ecuación:
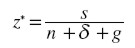 |
debe leerse en esta forma: “existe una relación capital/producto z* de crecimiento estacionario que se alcanza manteniendo en todo instante una inversión corriente proporcional al producto corriente sY ”.
MODELOS DE CRECIMIENTO ESTRICTAMENTE KEYNESIANOS
Hemos visto que es posible reinterpretar los modelos de crecimiento convencionales, tanto el lineal de Harrod-Domar como el más flexible de Solow, de manera que la inversión juegue el papel activo y el ahorro aparezca como simple consecuencia del circuito económico en el proceso de crecimiento.
Todo esto se percibe con mayor claridad en el ejemplo del modelo Harrod-Domar, que establece una relación técnica lineal y definida explícitamente desde un comienzo entre K y AL. En esa formulación del modelo de crecimiento es claro que la condición de pleno empleo determina la inversión necesaria para alcanzarlo, y que el ahorro compatible aparece como un residuo.
Pero como la evidencia empírica indica que, en muchos casos, lo que permanece constante es la distribución del producto entre factores, condición equivalente a considerar la función Cobb-Douglas como una restricción que refleja la distribución del producto agregado, esta función debe determinar implícitamente la relación K / AL necesaria en cada instante del crecimiento. Alcanzar el K compatible con cada nivel de AL determina aquí la inversión y el ahorro vuelve a aparecer por residuo.
Sería posible establecer otras condiciones técnicas o de distribución que regulen la inversión necesaria para alcanzar trayectorias de crecimiento de largo plazo, es decir, plantear modelos diferentes de los dos usados como ejemplo en este artículo e igualmente compatibles con la idea keynesiana del ahorro como residuo.
Sin embargo, para alcanzar un modelo verdaderamente keynesiano, faltaría incluir el dinero o la financiación de la inversión en forma explícita, de manera que sea posible justificar una inversión autónoma claramente independiente de cualquier ahorro previo. La clave para que esto sea viable técnicamente es que exista una capacidad instalada ociosa que dicha financiación pueda poner en marcha.
NOTAS AL PIE
1 Este resumen sigue de cerca los planteamientos de Barrére [ 1985] , Chick [ 1983] y Graziani [ 1990] . El lector puede hallar un paralelo crítico de teorías del dinero en Deleplace y Nell [ 1996] .
2 Es importante advertir la diferencia entre la función técnica de producción, que establece una relación entre capital y trabajo para una tecnología fija, y el concepto neoclásico de función de producción que describe la mejor tecnología disponible para cada combinación de trabajo y capital que podamos imaginar. En el caso del modelo Harrod-Domar, la función técnica de producción es un coeficiente técnico fijo que determina una relación capital/producto única y constante, sin posibilidad alguna de modificar las proporciones relativas de esos dos factores.
3 Ver la discusión de este punto en Romer [1990].
REFERENCIAS BIBLIOGRÁFICAS
1. Barrére, A. (1985). Les fondements de l’économie monétaire de production. En A. Barrére (Ed.), Keynes aujourd´hui: théories et politiques (Cap. 1). Paris: Economica. [ Links ]
2. Chick, V. (1983). Macroeconomics after Keynes: a reconsideration of the General Theory. MIT Press. [ Links ]
3. Clapham, J. H. (1922). Of empty economic boxes. Economic Journal. 32, 305-314. [ Links ]
4. Clark, J. M. (1961). Competition as a dynamic process. NBER, Washington DC. [ Links ]
5. Deleplace, G. y Nell, E. J. (1996). Afterword: Why and How to Replace the Microeconomic Theory of Money. En Deleplace y Nell (Eds.), Money in motion: the post keynesian and circulation approaches. (pp. 725-749) London: Macmillan Press. [ Links ]
6. Easterly, W. (1999). The ghost of financing gap: how the Harrod-Domar model still haunts development economics. Journal of Development Economics. 60 (2), 423-438. [ Links ]
7. Felipe, J. y Fisher, F. M. (2003). Aggregation in production functions: what applied economists should know. Metroeconomica. 54 (2-3), 208-262. [ Links ]
8. Fisher, F. M. (1969). The existence of aggregate production functions. Econometrica. 37(4), 553-577. [ Links ]
9. Fisher, F. M. (1993). Aggregation, aggregate production functions and related topics. MIT Press. [ Links ]
10 .Graziani, A. (1990). La théorie du circuit monétaire. Economies et Sociétés: Monnaie et Production. 7, 7-36. Traducido en Coyuntura Colombiana. CEGA, sept. 1997, 55, 67-96. [ Links ]
11. Goodwin, R. M. (1967). A growth cycle. En C. H. Feinstein (Ed.), Capitalism and Economic Growth (pp. 54-58). Cambridge Univ. Press. Reproducido y ampliado en G.K. Hunt, J.G. Schwartz (Eds.), A critique of economic theory. Penguin, 1972, pp. 442-449. [ Links ]
12. Grunfeld, Y. y Griliches, Z. (1960). Is aggregation necessarily bad? Review of Economics and Statistics. 42(1), 1-13. [ Links ]
13. Leontief, W. W. (1947). Introduction to a theory of the internal structure of functional relationships. Econometrica. 15(4), 361-373. [ Links ]
14. Mason, E. S. (1939). Price and production policies of large-scale enterprise. American Economic Review. 29(1), 61-74. [ Links ]
15. Nataf, A. (1948). Sur la possibilité de construction de certains macromodèles. Econometrica. 16(3), 232-244. [ Links ]
16. Romer, P. M. (1990). Endogenous technological change. Journal of Political Economy. 98(5), parte 2, S71-S102. [ Links ]
17. Sato, K. (1975). Production functions and aggregation. North-Holland. [ Links ]
18. Schohl, F. (1999). The paradoxical fate of the representative firm. Journal of History of Economic Thought. 21 (1), 65-80. [ Links ]
19. Shaik, A. (1974). Laws of production and laws of algebra: the Humbug production function. Review of Economics and Statistics. 56(61), 115-120. [ Links ]
20. Sraffa, P. (1930). Increasing returns and the representative firm: a criticism. Economic Journal, Marzo, S89-S93. [ Links ]
21. Young, A. (1928). Increasing returns and economic progress. Economic Journal, 38, 527-542. [ Links ]














