IMPACTO DE LAS CATÁSTROFES EN EL VALOR DE LAS ACCIONES. EL CASO LATINOAMERICANO

Alfonso Pedraza Martínez*

* Profesor de la Facultad de Administración de la Universidad de los Andes. Este artículo es una síntesis del trabajo de grado para optar por el título de Magíster de la Universidad Nacional de Colombia. El autor agradece los comentarios de los profesores Leonardo Duarte y Andrés Villaquirán. También agradece a la sala virtual de la Facultad de Administración de la U. Andes por su colaboración en la búsqueda de la información. Enviar los comentarios al correo: apedraza@uniandes.edu.co. Artículo recibido el 27 de abril de 2004 y aprobado el 11 de junio del mismo año.

Resumen

La presente investigación aplicó la metodología de Knight y Pretty [ 1996] a catástrofes de seis empresas latinoamericanas para establecer cuál es el impacto de una catástrofe en el valor de las acciones de tales firmas. En comparación con los resultados de Knight y Pretty [ 1996] , en Latinoamérica la caída en el valor de las empresas en la bolsa tiene una pendiente menor que en USA y Europa, sin embargo, el impacto es más duradero.

Palabras claves: decisión bajo incertidumbre y riesgo, valoración de activos financieros, mercados financieros latinoamericanos. JEL: D81, G12, G15.

Abstract

This research applied Knight and Pretty’s methodology [ 1996] to catastrophes in six Latin-american companies for establishing how the impact of a catastrophe affects the value of such firms’ shares. Compared to Knight and Pretty’s results [ 1996] , the fall in value of stock-exchange rated companies in Latin-america follows a less inclined slope than in the USA or Europe; however, such impact is much more long-lasting.

Key words: decision-making in conditions of uncertainty and risk, valuing financial assets, Latin-American financial markets. JEL: D81, G12, G15.

Résumé

Cette recherche a appliqué la méthodologie de Knight et Pretty [ 1996] aux catastrophes de six entreprises latino-américaines afin d´établir quel est l´impact d´une catastrophe sur la valeur des actions de ces entreprises. En comparaison avec les résultats de Knight et Pretty [ 1996] , en Amérique latine la chute de la valeur des entreprises en bourse a une courbe moindre qu´aux Etats-Unis et en Europe, cependant, l´impact est plus durable.

Mots clés : décision sous risque et incertitude, évaluation des actifs financiers, marchés financiers latino-américains. JEL: D81, G12, G15.

INTRODUCCIÓN

En el mundo actual los hechos catastróficos que afectan a las empresas han cobrado vigencia como problemas de estudio económico tanto desde el punto de vista físico, al comprometer instalaciones, equipos de cómputo y recurso humano, como desde el punto de vista financiero, al afectar el valor de sus acciones en la Bolsa.

En 1996, Knight y Pretty publicaron la investigación titulada “The Impact of Catastrophes on Shareholder Value”, basada en el estudio de la variación de los retornos anormales diarios en 15 casos de catástrofes de empresas de Estados Unidos y Europa. Los autores obtuvieron los retornos anormales como la diferencia entre el retorno esperado y el retorno real para cada día. A su vez, el retorno esperado fue calculado mediante el modelo CAPM de valoración de activos.

En el presente artículo se utilizó la metodología de Knight y Pretty en seis empresas latinoamericanas para determinar el impacto de una catástrofe en el valor de las acciones de las firmas de los países de esta región.

El artículo se desarrolla en el siguiente orden: (i) exposición del modelo CAPM, (ii) presentación del modelo econométrico utilizado, (iii) reseña de las seis catástrofes estudiadas, (iv) presentación de los resultados de la investigación en relación con los retornos diarios esperados y el volumen transado para las seis compañías, y (v) presentación de las conclusiones.

EL MODELO CAPM

Se sigue el modelo de Knight y Pretty [ 1996] para determinar el impacto de las catástrofes en el valor de las empresas. Se entiende como catástrofe cualquier fenómeno inesperado ocasionado por causas naturales o humanas que implique la pérdida de vidas humanas o desastres ecológicos, con suficiente relevancia para figurar en medios de comunicación internacionales. Como ya se mencionó, estos autores construyeron su modelo a partir del modelo CAPM¹ que fue concebido como una herramienta teórica para el análisis microeconómico de inversiones en condiciones de riesgo [ Sharpe 1964, 425] . El CAPM permite predecir los retornos de los activos financieros a partir de su relación con los retornos del mercado financiero, en el cual se transan a través de una medida de riesgo conocida como Beta.

Un antecedente importante del modelo CAPM es el teorema de la utilidad esperada, formulado en 1944 por von Neumann y Morgenstern, el cual postula que la utilidad de un evento incierto es el valor esperado de la utilidad de sus pagos². Basado en los resultados de von Neumann y Morgenstern, Markowitz [ 1952] estableció que para conformar un portafolio financiero eficiente no basta con maximizar su valor esperado a la tasa de descuento apropiada, sino que se debe minimizar el riesgo implícito del portafolio medido a través de la varianza³.

Markowitz [ 1952, 79] mostró que los retornos entre activos pueden estar correlacionados, y que por esto la diversificación no puede eliminar toda la varianza. Por consiguiente, hay que medir ese riesgo y tenerlo en cuenta cuando se construye un portafolio. Markowitz también demostró que es posible aumentar el valor esperado del portafolio y reducir su varianza. Los supuestos principales de Markowitz son: expectativas de probabilidades estáticas y conocimiento de las probabilidades de los eventos por parte de los inversionistas.

Sharpe [ 1964] presentó los fundamentos teóricos del modelo CAPM complementados por Lintner [ 1965] quien encontró que el riesgo total de un activo dado es la suma de la varianza de su retorno en el período transado con la covarianza combinada de sus retornos con todos los demás activos del mercado. Bodie et al. [ 2002] presentan un buen resumen de los supuestos y resultados del modelo. Ver Anexo 1.

El modelo CAPM está construido sobre la base de que la prima de riesgo apropiada para un activo debe ser determinada por su contribución al riesgo del portafolio total. El riesgo del portafolio es lo que le importa a los inversionistas; lo que gobierna las primas de riesgo que ellos demandan.

Sin embargo, Banz [ 1981] encontró que el tamaño de la firma en el mercado mejoraba la explicación de los retornos promedio dada por Beta. Así, los retornos promedio sobre los activos pequeños eran mucho mayores que sus betas estimados, y los retornos esperados sobre los activos grandes eran muy pequeños. Aunque otros investigadores presentaron trabajos con hallazgos similares, fue en la década de los noventa cuando se produjo la crítica más importante al CAPM.

Fama y French [ 1992] llegaron a dos conclusiones negativas acerca de la aplicación empírica del CAPM: (i) la relación entre Beta y los retornos mensuales promedio de los activos financieros para el período 1941-1990 era débil en el mercado de Estados Unidos, (ii) Beta no fue suficiente para explicar los retornos promedio. El tamaño (capitalización del mercado) capturaba las diferencias entre los retornos promedio del período 1941-1990 que eran perdidas por Beta. El resultado principal fue que entre 1963 y 1990 el valor de la firma en el mercado y el valor en libros capturaban la variación en los retornos promedio mejor que Beta [ Fama y French 1992, 450] .

Según estos autores, era posible que las aparentes fallas empíricas del modelo CAPM se debieran a malas aproximaciones al portafolio de mercado. En otras palabras, el mercado verdadero es eficiente en varianza media, pero las aproximaciones usadas en las pruebas empíricas no lo son.

El verdadero portafolio de mercado permitiría superar las anomalías en las pruebas existentes y revelar si Beta es suficiente para explicar los retornos esperados [ Fama y French 1996, 1957] .

Kothari et al. [ 1995] concluyeron que al utilizar retornos anuales en la estimación de Beta los resultados eran robustos a favor del modelo CAPM para el mismo período estudiado por Fama y French. Además, mostraron que los resultados de estos últimos tenían un sesgo, debido a la base de datos de información financiera utilizada, que mejoraba los resultados de la regresión. Sin embargo, encontraron evidencia que el efecto tamaño (ME) también mejoraba las predicciones del modelo.

El modelo CAPM también ha sido aplicado en mercados emergentes como el colombiano. Burbano [ 1997] obtuvo valores de Beta para 26 empresas inscritas en las bolsas de Bogotá y Medellín, y encontró diversos comportamientos, desde aquellas firmas que parecen no verse afectadas por el comportamiento global del mercado (Simesa con Beta igual a 0,25), hasta las que presentan una estrecha relación con el mismo (Bancoquia con Beta igual a 1,0). Al analizar los R-cuadrado, Burbano [ 1997, 32] encontró que para algunas empresas en Colombia el riesgo –o variabilidad total– estaba explicada, en un alto porcentaje, por su relación con los vaivenes propios del mercado del país.

Según Estrada [ 2001] el problema de la aplicación del modelo CAPM en mercados emergentes radica en el supuesto de integración de mercados, el cual implica que los activos con el mismo nivel de riesgo deben tener el mismo retorno esperado sin importar en dónde son transados. En mercados segmentados, las barreras al arbitraje pueden permitir que activos con las mismas características de riesgo, pero transados en diferentes ubicaciones, tengan retornos diferentes.

Estrada [ 2001] propuso una medida de riesgo igual a la relación entre la desviación semiestándar de los retornos del activo respecto al mercado local y la desviación semiestándar del retorno respecto al mercado mundial que ya había sido sugerida por Markowitz [ 1952] , y utilizada por otros autores con buenos resultados.

Un factor adicional de riesgo en los mercados emergentes es el riesgo país. Esta variable está asociada al riesgo político que emana del poder discrecional de las autoridades gubernamentales. Estos poderes son más significativos en tanto el marco institucional sea menos formal y menos confiable. Sabal [ 2001, 3] muestra que, dada la debilidad que caracteriza las instituciones, el riesgo político es especialmente relevante en los países emergentes.

Aunque el debate sobre el uso del modelo CAPM sigue abierto, y está en pleno desarrollo en mercados emergentes, existe evidencia de que Beta es una buena medida de riesgo, aun en mercados como el latinoamericano. Por esta razón, se tomó la decisión de aplicar el modelo de Knight y Pretty (K&P), basado en el CAPM, para medir el impacto de las catástrofes en el valor de las acciones en el caso latinoamericano.

EL MODELO K&P

A continuación se presenta el modelo original de Knight y Pretty [ 1996] , junto con una crítica a la manera como estos autores miden los retornos anormales acumulativos (CAR)⁴.

El modelo de Knigth y Pretty (K&P)

Para aislar el efecto de la catástrofe en el valor de las acciones es necesario apartarlo de otros eventos que pueden impactarlas simultáneamente. En el trabajo de K&P esto se hace con la estimación de los retornos anormales para un período inmediatamente siguiente a la catástrofe y luego acumularlos durante un año, lo que resulta en un conjunto de retornos del portafolio del día cero, conocido como retornos acumulativos anormales (CAR). La segunda fase excluye cualquier efecto específico de una Compañía que no esté relacionado con la catástrofe.

Formalmente, el retorno anormal sobre la acción i en el día t se define como:

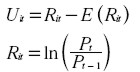Donde: R_it = el retorno sobre la acción i en el día t, E = operador de valor esperado, P_t = precio de la acción en el día t.

El retorno esperado es modelado mediante el CAPM como E(R_it ) = a_i + b_i R_mi, donde R_mi es el retorno sobre el portafolio del mercado en el día t.

Los parámetros del modelo, a_i y b_i , representan el intercepto y la pendiente, estimados en un modelo de regresión de mercado de la forma R_it = α_i + β_i R_mt + ε_it.

El proceso de ajuste del riesgo se basa en el modelo CAPM. El parámetro de riesgo sistemático, Beta, es calculado para cada Compañía, y es igual a la pendiente en una regresión de series de tiempo del retorno sobre el stock i (R_it). En este sentido, los resultados se suponen aislados de las influencias externas del mercado.

Los retornos anormales para cada firma son acumulados (CAR) sobre la ventana de eventos –serie de precios– de la manera siguiente:

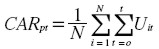Donde CAR_pt = retorno anormal acumulativo sobre el portafolio p en el día t, relativo al día de la catástrofe (t = O), U_it = retorno anormal de la acción i, N = número de catástrofes corporativas en el portafolio p.

Además, se calcula el impacto sobre el volumen de las transacciones. Esta medida se define en relación con el volumen promedio de las transacciones de la acción. Formalmente, UTV_it = TV_it / ATV_i , donde TV_it = volumen transado de la acción i en el día t, ATV_i = volumen promedio de transacciones de 12 meses de la acción i, sobre los meses -6 a O y 1 a 7.

UTV_it se calcula en todas las acciones para el primer mes siguiente al evento. Se asume que mientras que una catástrofe corporativa puede afectar el comportamiento del precio stock a lo largo del año posterior al evento, cualquier impacto sobre la actividad de transacciones será evidente sólo en el primer mes posterior al evento.

Crítica al modelo K&P

El modelo Knight y Pretty [ 1996] utiliza los retornos anormales acumulativos (CAR) como la medida de la pérdida de valor de las acciones debido al evento catastrófico. Sin embargo, al utilizar la fórmula: 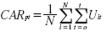, sumaron los retornos anormales diarios de cada acción, pero no realizaron una comparación con el día anterior al evento.

El Cuadro 1 presenta un ejemplo de impacto de una catástrofe en una acción dada. En la columna Ut(%) se ve la caída de los retornos de la acción. La caída en los retornos anormales del modelo Knight y Pretty para este evento se aprecian en la tercera columna (CAR K&P %). Sin embargo, la recuperación de la catástrofe se debería medir tomando como referencia el día cero, así, la cuarta columna contiene los valores normalizados de los datos a partir del día cero. Y la caída real de los retornos, en términos porcentuales, se aprecia en la última columna del Cuadro.

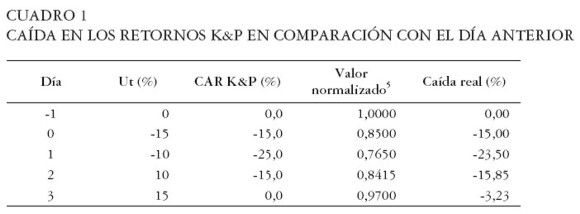Como se observa en el Cuadro 1, existe una diferencia de -3,23% el día 3 después de la catástrofe cuando se contrasta la caída de los retornos con el día cero en vez de sumar los retornos diarios de las acciones (metodología de K&P). En vista de lo anterior, en la presente investigación se utilizó el método de normalización y comparación con el día anterior a la catástrofe (día cero) para determinar el impacto en el valor de las acciones. Más adelante se presentan las diferencias encontradas con los cálculos del método de Knight y Pretty.

SELECCIÓN DE CASOS

La selección de las catástrofes de empresas latinoamericanas inscritas en bolsas de valores, que cumplieran los criterios de la definición, se realizó mediante los pasos descritos a continuación:

1. Encontrar las empresas latinoamericanas inscritas en NYSE y las más transadas en los mercados locales de Argentina, Brasil, Chile, Colombia, México, Panamá, Perú, Puerto Rico y Venezuela⁶.

2. Definir palabras clave relacionadas con catástrofes, como por ejemplo catástrofe, desastre, terremoto, inundación, huracán, incendio, derrame, explosión, bomba, muerte, asesinato, secuestro.

3. Buscar en bases de datos electrónicas de periódicos y revistas internacionales. Se utilizó el buscador www.lexis-nexis.com que tiene acceso a archivos de más de 15 mil periódicos y revistas de todo el mundo.

4. Comparar las fechas de las catástrofes con las fechas de inscripción en bolsa de las empresas y, entonces, escoger sólo los eventos sucedidos después de la inscripción.

5. Obtener las series de tiempo de las acciones de las empresas, de los índices de los mercados bursátiles y de las tasas de cambio de las monedas locales respecto al dólar⁷. Las series de precios de las acciones y de los índices se obtuvieron de Morgan Stanley, Yahoo Finance: www.yahoo.com y Bloomberg. Las tasas de cambio estaban disponibles en www.oanda.com.

Después de una preselección de 12 catástrofes, y cumplido todo el proceso descrito, se seleccionaron las catástrofes relacionadas en el Cuadro 2.

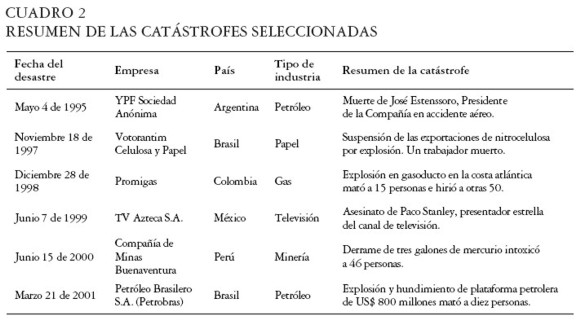YPF

País: Argentina. Fecha: 4 de mayo de 1995. Tipo de catástrofe: accidente aéreo. Descripción: muerte del Presidente de la Compañía. Medios: The New York Times, The Associated Press, Financial Times, The British Broadcasting Corporation, Argentine News Agency, The Gazette (Canadá).

El Presidente de YPF, la mayor Compañía petrolera argentina, José Estenssoro, estaba entre las siete personas que murieron cuando un Jet privado se estrelló en la cordillera de los Andes. Entre las víctimas también estaba Juan Pedrals, Gerente General de la Empresa Nacional de Petróleos de Chile.

José Estenssoro, Presidente ejecutivo de YPF S.A. de Argentina, era ampliamente respetado en América Latina por haber transformado la Compañía, que era una empresa monopolista estatal fuertemente subsidiada cuando él asumió el control en 1990, en un modelo de eficiencia.

La noticia afectó a los inversionistas. En la Bolsa de New York, donde YPF se transa en forma de ADR, YPF cayó US$ 1, a US$ 20,25 (un 4,71%).

Las directivas de YPF hicieron una reunión de emergencia para superar la situación. Al momento del accidente la Compañía no contaba con un gerente con la habilidad y liderazgo de Estenssoro para realizar el reemplazo.

Votorantim

País: Brasil. Fecha: 18 de noviembre de 1997. Tipo de catástrofe: explosión. Descripción: una explosión mató a un obrero, hirió a cuatro más y obligó a parar las exportaciones de Nitrocelulosa de la Compañía. Medios: Gazeta Mercantil, Agence France Presse.

Nitro Química, del grupo Votorantim, alegó motivos de fuerza mayor para suspender sus exportaciones de nitrocelulosa debido a una explosión en su fábrica en el barrio São Miguel Paulista de São Paulo. Nitro Química era el tercer exportador de nitrocelulosa⁸ del mundo, y estaba redireccionando su operación hacia el mercado doméstico.

La explosión ocurrió en uno de los dos digestores de celulosa que contienen ácido nítrico. Con la explosión volaron partes y piezas de los digestores, una de las cuales hirió a un empleado en la cabeza, y le causó la muerte por traumatismo craneal. Otros cuatro resultaron heridos. “Hemos comunicado a nuestros principales clientes internacionales que no estaremos disponibles para realizar nuestros envíos hasta que reparemos nuestra unidad de nitrocelulosa”; dijo Mario Bavaresco Jr., Director Superintendente de Nitro Química.

Promigas

País: Colombia. Fecha: 28 de diciembre de 1998. Tipo de catástrofe: explosión. Descripción: una explosión de gasoducto mató a 15 personas e hirió a otras 50. Medios: Reuters, Turkish Daily News, El Universal (Venezuela).

En el norte de Colombia, 15 personas murieron y otras 50 resultaron heridas cuando una tubería de gas natural explotó accidentalmente. La explosión redujo 35 casas a escombros. Los socorristas señalaron que más víctimas podrían estar atrapadas debajo de las ruinas en el poblado de Piedra de Arroyo, en el Departamento del Atlántico, según información de Reuters.

Por su parte, el jefe regional de la policía, coronel Humberto Santos, declaró que la mayoría de los muertos, entre ellos dos niños, presentaba graves quemaduras en sus cuerpos. Santos descartó las insinuaciones sobre un atentado terrorista como causa de la explosión, y dijo que fue un accidente.

El gasoducto de 57 centímetros de diámetro corre debajo del centro del pueblo, de aproximadamente cinco mil habitantes. La tubería formaba parte de la cadena de gas nacional operada por Promigas, una unidad de la estadounidense Enron Corp. y el principal distribuidor de gas en la costa caribeña de Colombia.

TV Azteca

País: México, Fecha: 7 de junio de 1999. Tipo de catástrofe: asesinato. Descripción: asesinato de Paco Stanley. Medios: The New York Times, CNN, Agence France Presse, EFE News Service, Toronto Star Newspapers, The Independent (Londres), The Guardian (Londres), The Observer.

El importante presentador de la Televisión Mexicana, Francisco “Paco” Stanley de 56 años, conocido como el Johnny Carson de la televisión mexicana, fue asesinado con arma de fuego por un hombre que le disparó más de 26 veces, cuando se desplazaba en su automóvil por una autopista de Ciudad de México con otras tres personas que resultaron heridas. Según las autoridades el asesinato fue premeditado; no obedeció a intento de secuestro ni de robo.

Stanley dirigió programas musicales y comedias incluyendo Siempre en Domingo, Alegrías del Mediodía, La Carabina de Ambrosio y El Club del Hogar, todos para el canal Televisa, donde trabajó por décadas. En el último año, Stanley se había cambiado a TV Azteca, donde presentaba dos programas de concurso.

Compañía de Minas Buenaventura

País: Perú. Fecha: 15 de junio de 2000. Tipo de catástrofe: derrame de mercurio. Descripción: un derrame de tres galones de mercurio en la mina Yanacocha intoxicó a 46 personas. Medios: Financial Times, Denver Post.

En la mina Yanacocha, a 600 kilómetros de Lima, fueron derramados tres galones de mercurio de un camión en Choropampa, a 53 millas de la mina, que era propiedad de Newmont Mining Corporation y de la Compañía de Minas Buenaventura. Una vez detectado el derrame, los oficiales de la mina notificaron al contratista peruano RANSA, el cual comenzó la labor de limpieza y atención a la gente de la región.

El Ministerio de Salud de Perú puso a disposición un equipo para diagnosticar y tratar a las personas con síntomas de envenenamiento. En Choropampa vivían cerca de 3.500 personas. Al final, fueron identificadas 46 personas del área con síntomas de envenenamiento con mercurio.

Según Ronald Cambre, Chairman y CEO de Newmont, este accidente fue catastrófico. Newmont era el mayor productor de oro de Norte América, y el segundo en importancia en el mundo. “Nuestra preocupación principal es la salud y la seguridad de la gente de Choropampa. Aunque el derrame no fue nuestra responsabilidad, tenemos una estrategia agresiva para implementar controles de salud y monitoreo ambiental”; dijo R. Cambre.

Petrobras

País: Brasil. Fecha: 21 de marzo de 2001. Tipo de catástrofe: explosión y derrame de Petróleo. Descripción: explosión en plataforma petrolera mata a 10 personas y causa gran derrame de petróleo. Medios: New York Times, Reuters News Service, Herald Sun (Melbourne, Australia), Financial Times, The Washington Post, The Gazzete (Australia), Gazeta Mercantil (Brasil), The Independent (Londres).

La plataforma petrolera de Petrobras, situada a 78 millas de la costa brasilera, se hundió después de cinco días de grandes esfuerzos por mantenerla a flote y recuperar los cadáveres de los 10 trabajadores que se encontraban a bordo en el momento de la explosión. Henri Philippe Reichstul, Presidente de la Compañía, dijo que era inevitable que al menos 400.000 galones de combustible se esparcieran por el océano Atlántico. La plataforma, instalada a un costo superior a los US$ 800 millones, producía 84.000 barriles de crudo y 1,3 millones de metros cúbicos de gas natural por día. La plataforma estaba asegurada por US$ 500 millones.

RESULTADOS

Los modelos se construyeron con base en los índices que se muestran en el Cuadro 3:

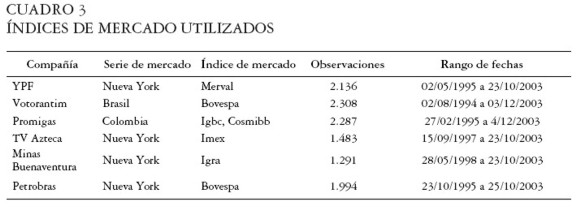Como se describió anteriormente, el retorno anormal sobre la acción i en el día t se definió como: U_it = R_it - E(R_it ), donde el retorno esperado fue modelado como E(R_it ) = a_i + b_i R_mt y los parámetros del modelo, a_i y b_i fueron estimados en un modelo de regresión lineal de mercado: R_it = α_i + β_i R_mt + ε_it.

Retorno diario esperado de las acciones

Una vez realizados los cálculos, se obtuvieron los resultados resumidos en el Cuadro 4.

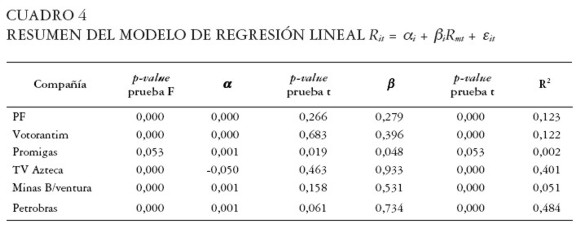La prueba F del Cuadro 4 indica que en todos los casos, excepto en Promigas, existe una relación lineal entre las variables independiente y dependiente.

La constante no dio resultados significativos en ninguno de los casos, así que los resultados posteriores se basan en regresiones del tipo R_it = β_i R_mt + ε_it, lo que implica una intersección con el origen. Este hecho es consistente con los resultados del modelo CAPM, enunciados arriba, y obliga a ajustar el modelo mediante la eliminación de la constante. Los resultados del modelo ajustado se muestran en el Cuadro 5.

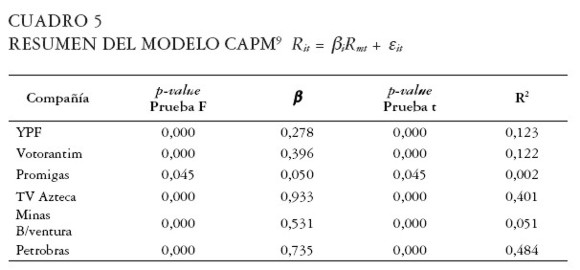La Compañía cuyos retornos tienen mayor relación con los retornos del mercado es TV Azteca, con un coeficiente Beta de 0,933, seguida por Petrobras con 0,735. El coeficiente de determinación indica que en los casos de TV Azteca y Petrobras, más del 40% de la variación en los retornos de las acciones es explicado por la variación en los retornos de los mercados, en YPF y Votorantim más del 12%, en el caso de Minas Buenaventura el 5,1% de la variación es explicada por el mercado.

Aunque en el caso de Promigas no se rechazó la hipótesis de relación lineal entre las variables dependiente e independiente, el coeficiente de determinación muestra una relación lineal muy pequeña entre ambas variables. Además, el coeficiente Beta está muy cerca a cero, lo que indica una relación muy baja de los retornos de la acción con los retornos del mercado⁹.

El coeficiente de determinación permitió establecer que para los casos de Petrobras y TV Azteca una proporción mayor del 40% de la variación en los retornos de la acción es explicada por el modelo. En el caso de Minas Buenaventura, el 5,1% de los casos son explicados por el modelo mientras que para YPF y Votorantim más cerca del 5% y 2,5% de la variación en los retornos de la acción es explicada por el modelo. En el caso de Promigas sólo el 0,2% de la variación en el retorno de la acción es explicado por el modelo utilizado.

Movimiento de las acciones en el mercado bursátil

Para buscar una explicación de los resultados obtenidos, se presenta el Cuadro 6 con el resumen del movimiento de las acciones de las diferentes Compañías en el mercado bursátil. Se muestra la media, la desviación estándar y una medida de relación estandarizada del volumen diario transado.

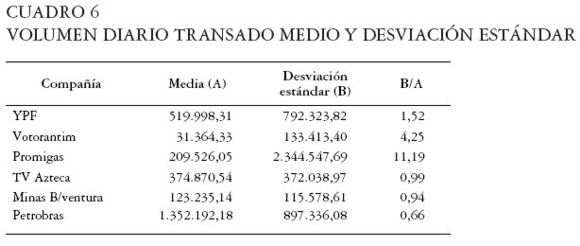Se observan diferencias grandes tanto en el volumen transado como en la desviación estándar entre Compañías. En los casos de TV Azteca, Minas Buenaventura y Petrobras, el cociente entre la desviación estándar y la media del volumen transado es menor que uno; son las empresas que operaron con mayor regularidad en el mercado durante el período de estudio. El caso de Promigas es especial (B/A = 11,19), al ser una empresa que casi no opera en el mercado, con pocos inversionistas, con días de altísimo volumen transado y saltos en el precio, que invalidan los resultados obtenidos a través del modelo CAPM.

Impacto de las catástrofes en el valor de las acciones

Aunque se presentan los resultados de Promigas, no se incluyen en el análisis del portafolio conformado por las empresas del estudio debido a que los problemas encontrados en la estimación del modelo CAPM invalidan los resultados del modelo utilizado para esta compañía en particular. Ver Anexo 1.

Los resultados del modelo para determinar el impacto de las catástrofes en el valor de las acciones se presentan a continuación.

Impacto promedio

La máxima disminución en el valor de las acciones respecto al día cero durante la primera semana de transacciones luego de la catástrofe fue (el cuarto día) de -4,38%. La máxima disminución en los retornos respecto al día cero durante el primer año de transacciones fue de -17,61% el día 103 después de la catástrofe. Ver Gráfica 1.

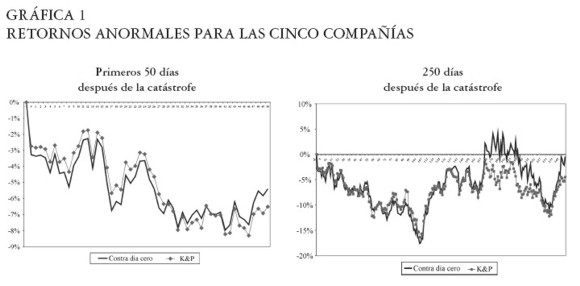Al realizar el cálculo de los retornos anormales con el método de comparación con el día cero ocurre una recuperación el día 169 después de la catástrofe (con un retorno anormal de 2,22%) mientras que con el método de K&P no se logró alcanzar un retorno igual o mayor que el del día anterior a la catástrofe.

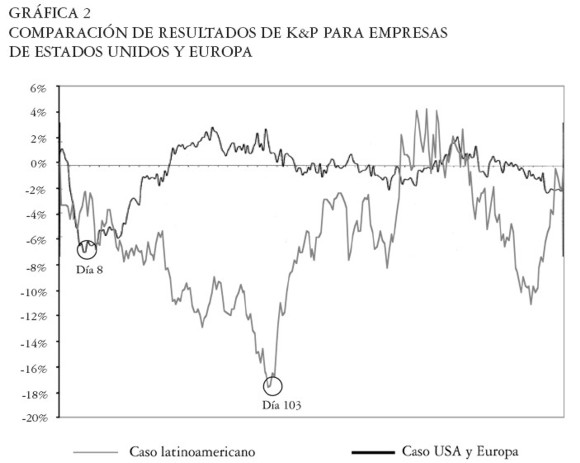
En comparación con los resultados de la investigación de K&P para empresas de Estados Unidos y Europa, en la cual la recuperación ocurrió 50 días después de la catástrofe luego de una caída inicial cercana al 8%, la caída en el valor de las acciones en el caso latinoamericano fue cerca de la mitad pero la recuperación tomó tres veces más tiempo. Ver Gráfica 2. Este hecho podría estar relacionado con la estructura de los mercados financieros de los países latinoamericanos y con la actividad de las empresas estudiadas en dichos mercados.

Compañías recuperadas vs no recuperadas

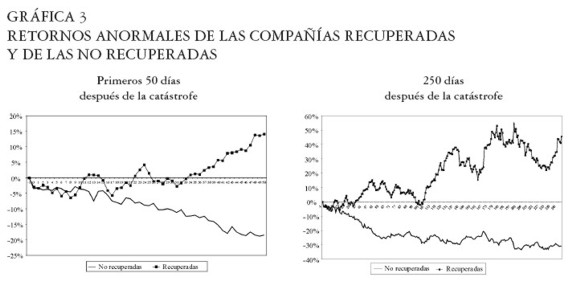
Las Compañías que se lograron recuperar de las catástrofes durante el primer año, en términos de retornos anormales¹⁰, fueron TV Azteca y Petrobras. En contraste, YPF, Votorantim y Minas Buenaventura no alcanzaron valores superiores al del día anterior a la catástrofe sufrida, incluso un año después del suceso. Ver Gráfica 3.

Impacto por empresa

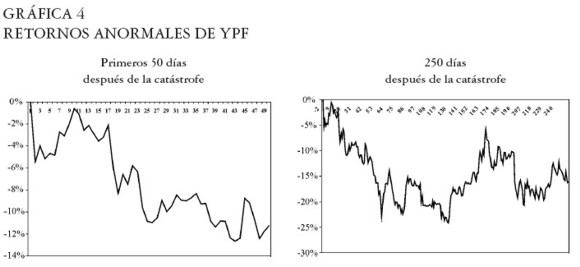
YPF

Máxima caída en los retornos anormales: -24,19% el día 129 después de la catástrofe. Ver Gráfica 4.

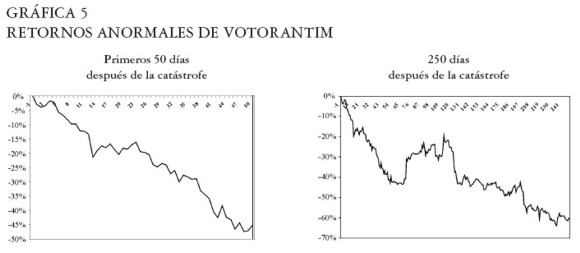
Votorantim

Máxima caída en los retornos anormales: -63,89% el día 236 después de la catástrofe. Ver Gráfica 5.

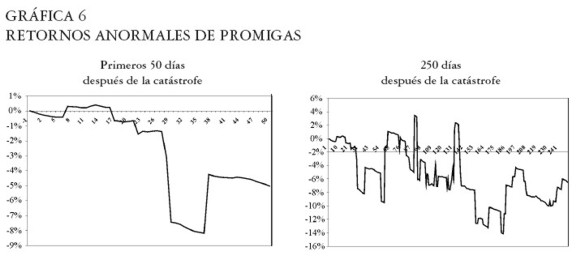
Promigas

Máxima caída en los retornos anormales: -14,14% el día 182 después de la catástrofe. Ver Gráfica 6.

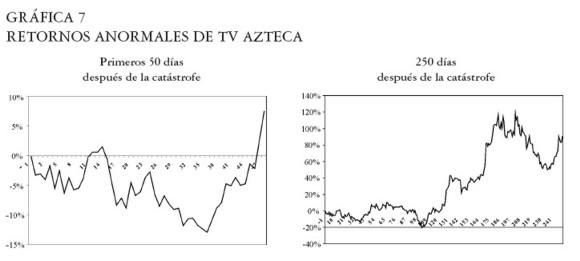
TV Azteca

Máxima caída en los retornos: -20,0% el día 102 después de la catástrofe. Ver Gráfica 7.

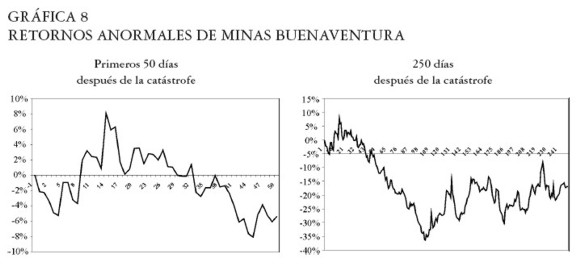
Minas Buenaventura

Máxima caída en los retornos anormales: -36,4% el día 103 después de la catástrofe. Ver Gráfica 8.

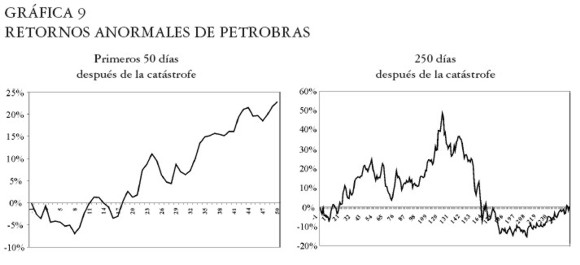
Petrobras

Máxima caída en los retornos anormales: -7,0% el octavo día después de la catástrofe. Ver Gráfica 9.

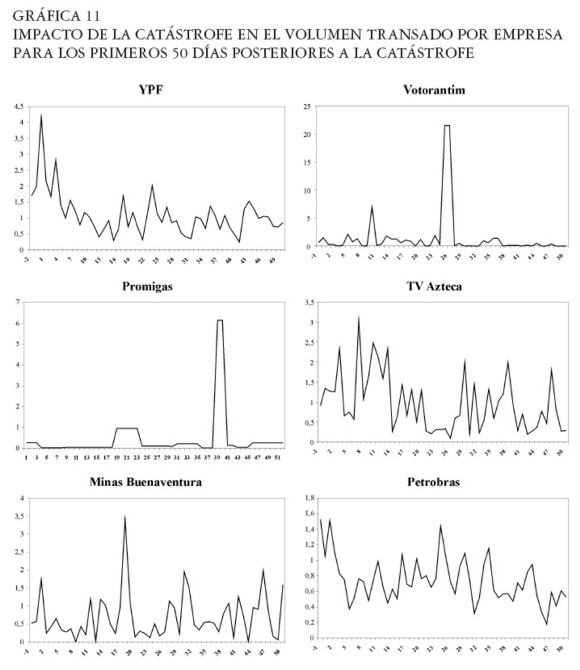
Impacto de las catástrofes en el volumen transado

La valoración del impacto en el volumen transado se realizó con la fórmula propuesta por K&P, UTV_it = TV_it / ATV_i, calculada para los primeros 50 días posteriores al evento.

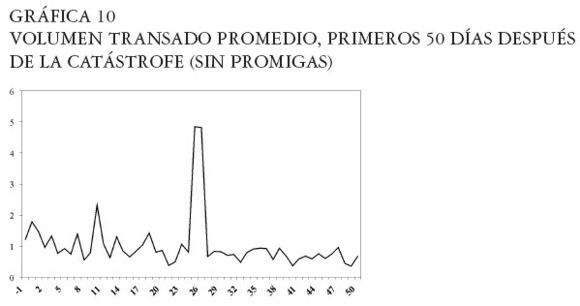
Impacto en el volumen transado promedio

En la Gráfica 10 se observa el volumen transado promedio de las cinco Compañías para un período de 50 días después de la respectiva catástrofe. Para verificar las hipótesis de igualdad en la media y homogeneidad en la varianza durante los primeros 50 días después de la catástrofe, se dividió el promedio de volumen transado de las seis Compañías en dos grupos compuestos por los días: [ -1, 25] y [ 26, 50] , en relación con el evento catastrófico, se utilizó la pruebas t para muestras independientes para probar las diferencias en la media y la homogeneidad de varianza de Levene¹¹. Los resultados se presentan en el Cuadro 10.

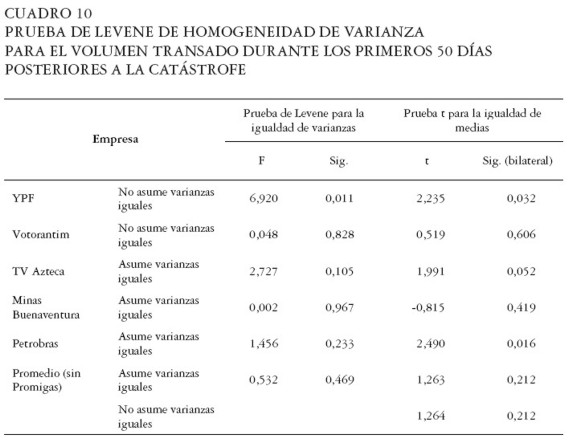Según los resultados de la prueba t, la media del volumen transado del promedio de los casos no sufrió una variación significativa durante los primeros días después de las catástrofes. Sin embargo, la prueba t permitió rechazar la hipótesis nula de igualdad en las medias en los casos de YPF y Petrobras, mientras que en los casos de Votorantim, TV Azteca y Minas Buenaventura no se encontró evidencia empírica suficiente para efectuar el rechazo.

La prueba de Levene únicamente permitió rechazar la hipótesis nula de homogeneidad en la varianza en el caso de YPF. En los demás casos, el p-value asociado con la estadística F ANOVA estándar fortalece el argumento y permite afirmar que no se presentaron cambios significativos en el volumen transado de las acciones del portafolio.

Impacto en el volumen transado por Empresa

En la Gráfica 11 se observa que sólo YPF y Petrobras sufrieron variaciones en el volumen transado como consecuencia de las catástrofes. Por otra parte, la no variación en la media del volumen transado para el portafolio de acciones del estudio difiere del hallazgo de K&P en cuya investigación sí se presentó una variación del volumen transado del portafolio catastrófico. Este hecho podría tener relación con la estructura de los mercados latinoamericanos y con la frecuencia y el volumen de transacciones de las empresas en bolsa.

CONCLUSIONES

Conocer la evolución de los retornos anormales de las acciones a partir del momento de la catástrofe podría servir a los gerentes e inversionistas para tomar medidas precautelativas al enfrentar eventos de esta naturaleza. La importancia de medir el impacto de las catástrofes en el valor de las acciones de las empresas involucradas está en la información adicional que reciben los gerentes para ajustar sus estrategias y contingencias, así como en la información que reciben los inversionistas interesados en conformar portafolios que incluyan empresas que, por la naturaleza de su operación o por las características del medio en que se desenvuelven, se vean expuestas a perturbaciones catastróficas que puedan afectar su valor en bolsa.

Sin embargo, el impacto total de las catástrofes en el valor de las empresas en el caso latinoamericano está mediado por su frecuencia y volumen de transacciones  en el mercado accionario. En empresas con bajo volumen de transacción es de suponer que gran parte del impacto será recibido por los socios mayoritarios, y no se verá reflejado de la misma forma en el mercado accionario. En el caso de empresas transadas con regularidad en el mercado, el valor del impacto podría interpretarse como el retorno anormal de la acción del día anterior a la catástrofe menos el mayor valor negativo del retorno anormal de la acción dentro de un intervalo de tiempo después del suceso. En la presente investigación, siguiendo la metodología de K&P, el intervalo tomado para la medición fue un año.

Al aplicar el modelo de K&P al caso latinoamericano surgieron algunos problemas para validar los supuestos de regresión lineal implícitos en el uso del modelo CAPM como herramienta de pronóstico de los retornos diarios esperados. Este hecho llevó a excluir el caso de Promigas del análisis de resultados, debido a que la relación lineal entre los retornos de las acciones de la empresa y los retornos del mercado colombiano no fue significativa en el período de estudio. Sin embargo, el modelo dio buenos resultados en los casos de Petrobras y TV Azteca, principalmente. En estos dos casos se cumplieron todos los supuestos de regresión y los coeficientes de determinación fueron superiores a 0,4. Es posible que este hecho tenga relación con el volumen de acciones transado por estas dos Compañías.

Hechas estas consideraciones, se puede afirmar que en el caso latinoamericano la caída en el valor de las empresas en el mercado bursátil tiene una pendiente negativa menor que en el caso de Estados Unidos y Europa, pero dicho impacto es más duradero. Mientras que en el caso latinoamericano la caída inicial promedio es de 4,36% en el octavo día, en los casos estudiados por K&P es cercano al 8%. La recuperación promedio en los casos investigados por K&P sucedió alrededor del día 50 después del evento catastrófico, mientras que en el caso latinoamericano ocurrió hasta el día 169 luego de la catástrofe. Esto indica que en comparación con los mercados de Estados Unidos y Europa, los latinoamericanos reaccionan más lentamente frente a hechos que puedan afectar el precio de los activos transados.

En cuanto al impacto de las catástrofes en el volumen de acciones transado, en el caso latinoamericano sólo en uno de los seis casos (Petrobras) se encontró evidencia empírica para afirmar que hubo un aumento en el volumen de transacciones producto de los eventos catastróficos. Este resultado difiere del obtenido de K&P para casos de empresas de Estados Unidos y Europa. Este hecho podría estar relacionado con la dinámica de los mercados de las acciones de las firmas latinoamericanas, que tienen menor liquidez y reaccionan lentamente en comparación con los mercados de Estados Unidos y Europa.

NOTAS AL PIE

1 CAPM corresponde a la sigla en inglés: Capital Asset Pricing Model.

2 La utilidad es aditivamente separable en los resultados y lineal en las probabilidades; ver Varian [ 1992, 205] .

3 Este razonamiento es válido para consumidores con aversión al riesgo, es decir, con funciones de utilidad cóncavas. El grado de aversión al riesgo se puede medir por medio de la segunda derivada de la función de utilidad esperada, que se normaliza dividiendo por la primera, esta medida es conocida como la medida de Arrow-Pratt de la aversión (absoluta) al riesgo.

4 CAR corresponde a la sigla en inglés de Cumulative Abnormal Return.

5 Este valor se calculó asignando el valor de la unidad al día anterior a la catástrofe, y hallando los valores para los días siguientes como el producto del valor normalizado del día inmediatamente anterior (t-1) y el valor de Ut para el día del cálculo (t).

6 Se identificaron 115 empresas de estos nueve países. Además, se realizó una búsqueda en empresas de los mercados financieros de Costa Rica, Nicaragua, Paraguay, Uruguay y Bolivia, sin encontrar resultados útiles para la investigación.

7 Las tasas de cambio de Argentina, Brasil, México y Perú fueron utilizadas en el análisis de YPF, TV Azteca, Minas Buenaventura y Petrobras, cuyas series históricas de precios fueron obtenidas de NYSE y se relacionaron con los índices bursátiles de cada país (que están en moneda local) para eliminar el efecto de riesgo país.

8 La nitrocelulosa se utiliza para producir tintas y barnices.

9 Las pruebas de los supuestos de regresión se presentan en el Anexo 1.

10 Se debe tener en cuenta que todos estos resultados están en términos de retornos anormales, es decir, del precio con respecto al índice del mercado, y no del precio de la acción de cada Compañía. Por ejemplo, si una Compañía cayó en 20% durante el primer año pero el mercado cayó 50% se presenta como una recuperación.

11 La prueba de homogeneidad de varianza de Levene consiste en efectuar un análisis de la varianza sobre las diferencias en valor absoluto entre las observaciones y la mediana manteniendo el diseño original.

12 Prueba no paramétrica de Kolmogrov-Smirnov para la hipótesis de normalidad de los residuos realizada con el 10% de la muestra elegido en forma aleatoria en cada caso. La hipótesis nula de normalidad se rechaza para p-values menores que 0,05.

13 Para una distribución normal se espera una curtosis –de los residuos de las regresiones– cercana a tres [ Pyndick y Rubinfeld 2001, 48] .

14 Para una distribución normal se espera un coeficiente de asimetría de los residuos de las regresiones cercano a cero [ Pyndick y Rubinfeld 2001, 48] .

15 Se probó la hipótesis de homogeneidad en varianza, se rechazó para p-values menores que 0,05.

16 Cuando los valores sucesivos de 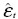están cerca entre sí, el estadístico DW será bajo, indicando la presencia de correlación serial positiva. La estadística caerá en el rango de 0 a 4, con un valor cercano a 2 indicando que no hay correlación serial de primer orden; ver Pyndick y Rubinfeld [ 2001, 171] y Suriñach et al. [ 1995, 29] .

17 En el caso de Promigas no fue posible realizar el ajuste por el método de los cuadrados ponderados debido al alto número de valores estimados del error iguales a cero, debido al bajo volumen de transacciones de la acción en el mercado colombiano.

PRUEBAS DE LOS SUPUESTOS DE REGRESIÓN

De acuerdo con Pyndick y Rubinfeld [ 2001, 60] , las características del modelo de retornos diarios estimado hacen necesaria la validación de los supuestos de regresión lineal, que son:

1. La relación entre las variables dependiente e independiente es lineal.

2. El error tiene un valor esperado cero, E(ε) = O

3. El término de error tiene una varianza constante para todas las observaciones, E(ε ²) = σ ².

4. Las variables aleatorias ε_i son estadísticamente independientes. Por tanto, E(ε _i ε_j ) = O, para i diferente de j.

5. El término del error está distribuido en forma normal.

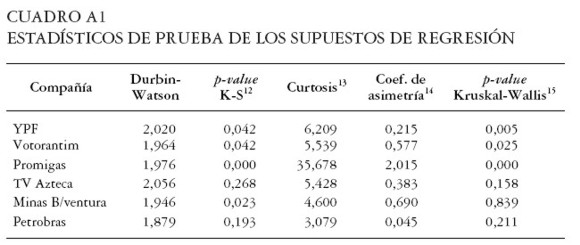
En el Cuadro A1 se presenta un resumen de los estadísticos de prueba de regresión para el modelo de retornos diarios esperados de las acciones, que se desarrolla a continuación.

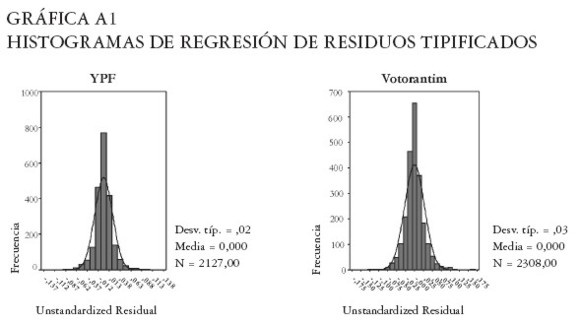
Normalidad de los residuos de regresión

Como se observa en la Gráfica A1, en todos los casos la media de los residuales es igual a cero, por lo tanto, se cumple el supuesto de regresión lineal.

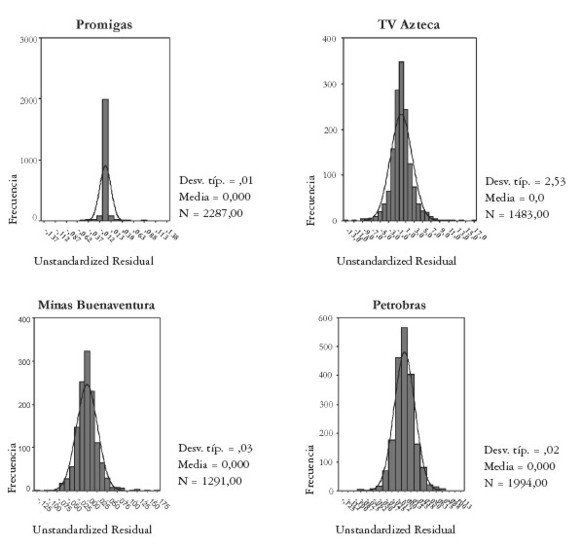El resultado de la prueba de normalidad de Kolmogorov-Smirnov rechazó la hipótesis nula de normalidad de los residuos en los casos de YPF, Votorantim, Promigas y Minas Buenaventura. Una posible explicación de este hecho puede estar en la gran concentración de datos alrededor de la media para estas cuatro series, lo que las convierte en distribuciones leptocúrticas. Por su parte, no se rechazó la hipótesis de normalidad de los residuos en los casos de TV Azteca y Petrobras.

Correlación serial

En cuanto a la prueba de Durbin-Watson¹⁶ para la correlación serial, basada en los residuos de regresión de mínimos cuadrados ordinarios, todos los valores se situaron alrededor de 2, razón por la cual, se puede rechazar la hipótesis nula de correlación serial para los residuos de las seis series analizadas.

Homogeneidad en varianza de los residuos

La prueba de homogeneidad en la varianza se realizó utilizando la prueba no paramétrica de Kruskal-Wallis, dado que no supone una distribución normal para los residuales de las regresiones del modelo [ SPSS 2000, 8-18] . El procedimiento consistió en dividir cada serie por grupos, donde cada grupo equivale a un año de transacciones, y luego, definir rangos ordenados para el total de la muestra en cada uno de los casos.

La hipótesis nula de homogeneidad en la varianza de los residuales se rechazó para YPF, Votorantim y Promigas. Debido a este hecho, aunque los estimadores de mínimos cuadrados obtenidos son insesgados y consistentes no son eficientes, es decir, las varianzas de los parámetros estimados no son las mínimas. Además, las varianzas estimadas de los parámetros son estimadores sesgados de la varianza verdadera de los parámetros estimados [ Pyndick y Rubinfeld 2001, 152] . Cabe destacar que al excluir los datos de 2003 en la serie de YPF no se rechazó la hipótesis nula, al obtener un p-value de 0,924.

Por otra parte, no se rechazó la hipótesis de homogeneidad en la varianza de los residuos para los casos de TV Azteca, Minas Buenaventura y Petrobras, lo que valida el supuesto de regresión.

Para solucionar el problema de heteroscedasticidad encontrado en las regresiones de YPF, Votorantim y Promigas¹⁷, se utilizó el método de mínimos cuadrados ponderados, predividiendo todas las observaciones por la raíz cuadrada del valor estimado del error al cuadrado en el modelo propuesto por White [ 1980] para corregir la heteroscedasticidad. Este método corrige la heteroscedasticidad sin causar mayores alteraciones en los coeficientes. Así, el nuevo Beta obtenido para Votorantim fue 0,398.

En el caso de YPF se optó por excluir de la muestra las observaciones del año 2003, debido a que se cuenta con suficiente información de los años anteriores para estimar el valor de Beta sin incurrir en problemas de heteroscedasticidad. El nuevo valor de Beta obtenido para YPF fue 0,284, con un coeficiente de determinación de 0,129. Los resultados obtenidos se resumen en el Cuadro A2.

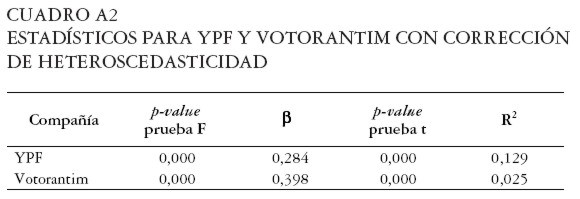Al realizar las pruebas de homogeneidad en varianza, el coeficiente de determinación de Votorantim disminuyó drásticamente pero el valor de Beta estimado no sufrió una modificación semejante. En cuanto a YPF, se corrigió el problema de heteroscedasticidad con un ajuste del coeficiente de determinación de 0,006.

El Cuadro A3 presenta un resumen de la validación de los supuestos de regresión para las seis catástrofes incluidas en la investigación. En los casos de TV Azteca y Petrobras se cumplieron todos los supuestos.

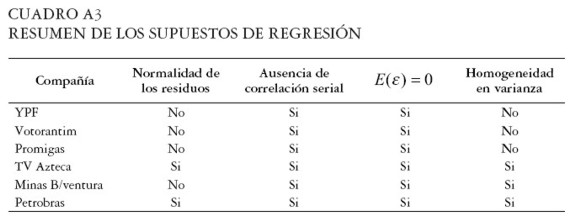REFERENCIAS BIBLIOGRÁFICAS

1. Banz, Rolf. (1981). The Relationship Between Return and Market Value of Common Stocks. Journal of Financial Economics. 9, 3-18.        [ Links ]

2. Bodie, Z., Kane, A. y Marcus, A. (2002). Investments. McGraw Hill.        [ Links ]

3. Burbano, Antonio. (1997). El Modelo CAPM en Colombia. Monografía 47. Monografías Serie Finanzas. Bogotá: Universidad de los Andes.        [ Links ]

4. Estrada, Javier. (2001). The Cost of Equity in Emerging Markets: A Downside Risk Approach. Emerging Markets Quarterly. Spring, 63-72.        [ Links ]

5. Fama, Eugene y French, Kenneth. (1992). The Cross-Section on Expected Stock Returns. The Journal of Finance. 47(2), 427-465.        [ Links ]

6. Fama, Eugene y French, Kenneth. (1996). The CAPM is Wanted, Dead or Alive. The Journal of Finance. 51(5), 1947-1958.        [ Links ]

7. Knight, Rory y Pretty, Deborah. (1996). The Impact of Catastrophes on Shareholder Value. Templeton College, England: University of Oxford.        [ Links ]

8. Kothari, S., Sahnken, J. y Sloan, R. (1995). Another Look at the Cross-section of Expected Stock Returns. The Journal of Finance. 50(1), 185-224.        [ Links ]

9. Lintner, John. (1965). Security Prices, Risk, and Maximal Gains From Diversification. The Journal of Finance. 20(4), 587-615.        [ Links ]

10. Markowitz, Harry. (1952). Portfolio Selection. The Journal of Finance. 7(1), 77-91.        [ Links ]

11. Pyndick, Robert y Rubinfeld, Daniel. (2001). Econometría, modelos y pronósticos. McGraw Hill.        [ Links ]

12. Sabal, Jaime. (2001). La tasa de descuento en países emergentes. Documento de trabajo. IESA.        [ Links ]

13. Sharpe, William F. (1964). Capital Asset Prices: A theory of Market Equilibrium under Conditions of Risk. The Journal of Finance. 19(3), 425-442.        [ Links ]

14. SPSS Inc. Statistical Analysis Using SPSS 10.0. Año 2000.        [ Links ]

15. Varian, Hal. (1992). Análisis Microeconómico. 3ª edición. Antoni Bosh.        [ Links ]

16. White, H. (1980). A Heteroskedastic-Consistent Covariance Matrix Estimator and a direct test for Heteroskedasticity. Econometrica. 48, 817-838.        [ Links ]

17. Sitios web consultados: www.lexis-nexis.com, www.oanda.com, www.yahoo.com.        [ Links ]