EL FORMALISMO AXIOMÁTICO EN ECONOMÍA

AXIOMATIC FORMALISM IN ECONOMICS

Camilo Andrés Franco de los Ríos*

* Economista de la Universidad de los Andes. El autor agradece los comentarios de los profesores Hernando Matallana, Álvaro Moreno, Luis Jorge Ferro y Tomás Rodríguez. Enviar los comentarios al correo: camilofranco@terra.com.co. Artículo recibido el 23 de mayo de 2005, aprobada su publicación el 1 de noviembre.

Resumen
A través de la reflexión crítica sobre la tensión existente entre el desarrollo del cuerpo del conocimiento económico a imagen de la matemática, se descubre una doble ruptura epistemológica en el desarrollo de la teoría económica. La primera, ocurrida a mediados del siglo XIX, reconoce en la matemática el lenguaje natural para la economía. La segunda, situada en el período de entre-guerras, identifica la incorporación del formalismo científico al cuerpo del conocimiento económico walrasiano.

Palabras claves: microeconomía, axiomática, dinero. JEL: B13, B40.

Abstract
Critical reflection concerning the tension existing between developing the body of economic knowledge in the image of mathematics led to discovering a double epistemological rupture in developing economic theory. The first, in the mid nineteenth century, recognised mathematics as being the natural language of economics. The second (situated in the inter-war period) identified incorporating scientific formalism into the body of knowledge pertaining to Walrasian economics’.

Key words: microeconomics, axiomatic formalism, money. JEL: B13, B40.

Résumé
Par la réflexion critique sur la tension existant dans le développement du corps de connaissance économique à l´image des mathématiques, nous découvrons une double rupture épistémologique dans le développement de la théorie économique. La première, qui survient au milieu du XIXe siècle, reconnaît dans les mathématiques le langage naturel de l´économie. La deuxième, qui se situe dans la période de l´entre-deux guerres, identifie l´incorporation du formalisme scientifique du corpus des connaissances économiques walrasiennes.

Mots clés: micro-économie, axiomatisation, argent. JEL: B13, B40.

Las representaciones o descripciones no son nunca independientes de normas. Y la elección de esas normas se basa en actitudes que necesitan de la evaluación crítica mediante argumentos porque no pueden ser deducidas lógicamente ni probadas empíricamente (J. Habermas 1993).

En este artículo se presenta una reflexión crítica sobre la relación entre la matemática y la economía. Al explorar el desarrollo de estas disciplinas se pueden analizar los criterios utilizados al interior de cada una para establecer el carácter científico de la teoría y sus argumentos. Se propone entonces identificar la tensión existente entre el desarrollo del cuerpo de conocimiento económico y los parámetros de rigor que proporciona la imagen del conocimiento matemático para el caso particular de la ciencia económica neoclásica, pero que también es pertinente para la discusión teórica general.

La premisa metodológica de este trabajo concibe las relaciones sociales de magnitud como el objeto de estudio de la ciencia económica, siendo específicamente el carácter cuantitativo de estas relaciones lo que justifica la aplicación del método matemático como su forma de expresión. Y en tanto esta forma de expresión es lo que permite ostentar un procedimiento cierto, extendiendo su metodología para representar el contenido teórico válido, encontramos que la economía se debe desempeñar simultáneamente en dos mundos diferentes: el económico y el matemático. Entonces, debemos centrar el núcleo del problema en la traducción del lenguaje económico al matemático y del matemático al económico.

En síntesis, se trata de considerar bajo una mirada histórica, y a partir de una revisión de los estudios de economía y matemáticas, la elección de un criterio de validación del conocimiento que se presenta como un criterio de forma, mas no de contenido. Ello en la medida en que es el propio formalismo lógico el que se establece como criterio normativo para la ciencia económica, en particular para el caso de la teoría neoclásica, tal como ocurre con la demostración de la existencia de una solución para el sistema walrasiano de ecuaciones del equilibrio general.

En consecuencia, se sugiere que la aproximación axiomática de David Hilbert (1917) valida el problema abstracto planteado por Walras (1874), estableciéndose así una lectura de la realidad económica según una sola lógica –monismo epistemológico– en función de una definición determinista de los conceptos económicos básicos, validada científicamente mediante el método mismo de exposición, y no como resultado de la confrontación de interpretaciones que sugieren diferentes lógicas económicas, como un momento propio del proceso científico-económico.

Ahora bien, para la época en que se establece el sistema walrasiano de ecuaciones del equilibrio general, el cual expresa condiciones de igualdad entre oferta y demanda para todos los bienes y servicios existentes en cada uno de los mercados, se afirma que existe una solución significativa para el mismo, desde el punto de vista económico, y que dicha solución es única. Esto, debido a la creencia generalizada de que la solución al sistema depende de la condición de igualdad entre el número de ecuaciones y el número de incógnitas, las cuales se refieren a los precios relativos expresados en términos de un bien numerario. Pero bajo esta condición se puede cumplir, tanto que el sistema no tenga solución, como que exista más de una.

Por ende, demostrar su solución y con ella probar la existencia del equilibrio era una tarea pendiente dentro de la disciplina económica. No fue sino hasta la década de 1930 que se dieron los primeros y más notables avances hacia una demostración matemática de la existencia de una solución para dicho sistema de ecuaciones. Para este momento ya se contaba con el trabajo analítico de G. Cassel (1932), que exponía de manera simplificada el modelo de Walras, sin hacer referencia a este, haciéndolo más accesible para la comunidad matemática interesada. Como eje de su teoría de distribución, Cassel argumenta en contra del uso de los conceptos de utilidad marginal y valor, utilizando las categorías de utilidad, precios y demanda como conceptos primitivos, donde su existencia es elemental, y su proceso de formación no necesita ser especificado.

Es cuando Karl Schlesinger entra en escena al exponer las ecuaciones en cuestión en el coloquio matemático de Viena, tomando parte del trabajo On the Production Equations of Economic Theory of Value publicado en 1933-4, el cual utiliza el modelo presentado por Cassel en 1918, que una vez traducido en 1932 puede ser difundido a través del mundo anglosajón. Este coloquio organizado por Karl Menger (hijo del reconocido economista Carl Menger, uno de los autores primigenios de la denominada revolución marginalista), y al cual asistían regularmente destacados matemáticos y científicos como Kurt Gödel, Nöbeling, Alt, Beer y Tarski, fue fundamental para que en los años treinta se definiera el desarrollo de la ciencia económica neoclásica a partir de la teoría del equilibrio general.

A continuación se propone hacer explícito un giro epistemológico observable en el desarrollo de la teoría económica neoclásica planteada, en un principio, como ciencia social por los autores primigenios de esta corriente de pensamiento, hacia un marco de definiciones que la llevan a ser concebida como ciencia matemática, de carácter duro o exacto. Con el deseo de alcanzar el estatuto de una ciencia dura, utiliza los criterios de rigor en el razonamiento que exige el formalismo lógico-deductivo, según la imagen del conocimiento matemático que maneja en su interior, como aval para el desarrollo cierto de su cuerpo de conocimiento.

LA AXIOMATIZACIÓN DE LA CIENCIA ECONÓMICA

El lenguaje matemático, en cuanto método analítico necesario para deducir o demostrar una verdad-teorema de acuerdo con el formalismo hilbertiano, requiere de dos pasos esenciales para su fructífera aplicación en la economía. Primero, todos los supuestos necesarios para representar matemáticamente un fenómeno económico deben ser enumerados completa y precisamente. Segundo, las conclusiones sólo son válidas una vez demostrada su deducción directa de los supuestos explícitamente formulados (Wald 1951).

Recordando el ambiente agitado que se vivía en el Coloquio de Viena, A. Wald y K. Schlesinger entran en contacto bajo el auspicio de Oskar Morgenstern, de manera que Wald recibe la tarea de demostrar rigurosamente la existencia de una única solución para el sistema de ecuaciones del equilibrio general competitivo. Presenta entonces un modelo de producción (1933-4) y un modelo de intercambio (1934-5), donde demuestra la existencia de un único equilibrio para cada caso. Ante la gran importancia de su trabajo y el carácter limitado de su publicación, Wald fue persuadido para escribir un tercer artículo, en 1936, exponiendo sus resultados, el cual fue traducido al inglés y publicado en Econometrica en 1951 como tributo a la vida de un autor que produjo un giro decisivo en cuanto a método y objetivo, para las ciencias sociales. Es con base en este artículo, que podemos analizar su respuesta a la pregunta planteada por Schlesinger acerca de una solución económicamente significativa –en la medida en que todas las incógnitas sean no negativas– para el sistema de ecuaciones heredado de Walras y simplificado por Cassel.

El modelo que Schlesinger expone, contiene una gran innovación con respecto al modelo casseliano, pues los precios de los factores ya no son determinados exógenamente según el principio de escasez, sino que pueden ser tanto escasos como libres (condición introducida mediante la incógnita u_i). Se supone la existencia de bienes producidos y de factores no producidos u originarios los cuales se utilizan en la producción de los primeros. También se asumen proporciones fijas entre los factores y el producto final. Es así como se producen n bienes finales con una tecnología especificada por coeficientes técnicos constantes a_ij, donde i es la cantidad del factor utilizado en la producción de una unidad del bien j, mientras que denota las unidades disponibles de factores de producción en un periodo dado, oferta que se supone totalmente inelástica. Se asume que en el proceso de producción se utilizan m unidades de y se producen n unidades de un bien S_j (cantidades representadas por s_j) en un determinado periodo de tiempo. Se define s_j como el precio del bien j y p_i como el precio del factor i, tal que el sistema debe determinar los valores de p_i , s_j y s_j a partir de los datos con que se le alimenta, a decir, , a_ji. Se caracterizan las funciones de demanda f_j (s₁,...,s_n), las cuales son dadas y son independientes de la distribución del ingreso, y finalmente ui es incógnita, tal que para todo i, u_i ³ 0 (en caso de ser un bien libre, u_i > 0):

= a_i1s₁ + a_i2s₂ + ... + a_ins_n + u_i (i = 1,..., m)

u_ip_i = 0 (i = 1,..., m)

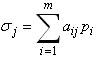j = 1,..., n

[1]

j = 1,..., n

Abraham Wald demuestra que el sistema de ecuaciones [1] posee un único conjunto solución con elementos no negativos para las 2m + 2n incógnitas. La condición de existencia necesita de los siguientes seis supuestos (tengamos en cuenta que se necesita un supuesto más para asegurar la unicidad de los precios de los factores):

1. > 0 (i = 1,..., m), de manera que se asegura la existencia de una cantidad positiva para cada uno de los factores de producción R_i (donde r_i representa la cantidad de los factores R_i utilizada en el proceso de producción).

2. a_ij ³ 0 (i = 1,..., m; j = 1,..., n), implica la necesidad de una cantidad no negativa de R_i para la producción de una unidad de S_j.

3. Para cada j existe al menos una i tal que a_ij > 0, de forma que al menos uno de los factores de producción sea necesario en la producción de un bien S_j.

4. La función f_j (s₁,...,s_n) es no negativa y continua para todas las n-tuplas de números no negativos s₁,..., s_n, donde s_j ¹ 0. Se estipula aquí una relación continua entre los precios y las cantidades demandadas, para simplificar el tratamiento matemático del problema.

5. En cuanto a esta condición, su forma matemática expresa que la cantidad demandada por un bien S_j es cero solamente cuando el precio por una unidad se vuelve infinitamente grande. Esto implica que la demanda s_j por S_j es positiva para cualquier precio (positivo y finito). Se asume que, en general, la demanda a cualquier precio finito es positiva.

Hasta este punto, el sistema axiomático se presenta como un sistema formal abierto. En la medida en que la estructura lógica del sistema lo requiere, la solución para [1] ha de exigir una mayor restricción sobre el comportamiento de los individuos. Wald introduce entonces una última hipótesis, considerando en un nivel agregado lo que hasta su momento se utilizaba para describir el comportamiento individual de un agente económico (Ingrao e Israel 1990). Es en el momento en que Wald reconoce la necesidad de otorgarle un significado económico apropiado a su formulación matemática, que en vez de introducir el sexto supuesto en un nivel agregado, decide presentarlo como una caracterización del comportamiento individual. De esta manera, Wald (1951) argumenta que del sexto axioma se sigue que el mismo comportamiento se ha de sostener para todo individuo W. Al hacerlo, es evidente que una vez el método matemático ha encontrado sus resultados, la interpretación económica debe entrar a justificar su razón de existencia, y proporcionar un contenido que obedece más a una lógica puramente matemática, que a una económica.

6. Este supuesto establece una mayor restricción sobre el tipo de las funciones de demanda f_j (s₁,...,s_n). Sea W cierto individuo de la economía con una demanda de s^w_j unidades por S_j a los precios s_j, para j = 1, 2,..., n. El número s_j de las unidades producidas (en equilibrio) del bien S_j es entonces la suma de las cantidades s^w_j para todo individuo W. De esta manera se puede suponer (o demostrar a partir del teorema de la teoría del valor que dice que la utilidad marginal de un bien S_j para el individuo W depende solamente de la cantidad del bien que posea)¹ que si a los precios s'₁,...,s'_n el individuo W demanda s^w₁ + Ds^w₁,..., s^w_n + Ds^w_n, mientras que a los precios demanda , donde al menos uno de los números:

Ds^w_j < 0 y si 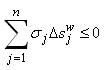, entonces .

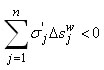Esta es la forma tradicional de lo que hoy se conoce como el axioma de preferencias reveladas, nombre que se le debe esencialmente al análisis de economía moderna desarrollado por Samuelson en 1938. Weintraub (1983) nos advierte sobre lo fuerte que resulta este supuesto, sobre todo por su importancia para los teoremas sobre la estabilidad de los precios de equilibrio; aunque la presente investigación se limite exclusivamente al problema de la existencia de dichos precios.

Las contribuciones de A. Wald sobre el trabajo desarrollado en economía matemática, acerca de la existencia de una solución para el sistema de ecuaciones walrasiano, tienen gran importancia metodológica, además de lo que se refiere al contenido de sus teoremas. La aplicación del método axiomático, en la medida en que brinda un procedimiento que permite la completa exposición de los supuestos que sustentan la teoría del equilibrio general, lleva implícita una interpretación económica de los axiomas, la cual es posterior a su formulación matemática. Es una cuestión de justificación a posteriori: el método matemático viene primero que el económico (Ingrao e Israel 1990).

Observamos que se deben establecer ciertos supuestos sobre los datos que se han de introducir en las ecuaciones una vez han sido formuladas, de manera que se asegure la existencia de una solución. Este punto ilustra el peligro de que un modelo económico adquiera vida propia según el mundo ideal o formal de la teoría matemática, según los estándares de rigor proyectados por la imagen del conocimiento matemático sobre la disciplina económica. Si los datos no cumplen con los requerimientos estipulados, la existencia de dicha solución se pone en peligro, como el mismo A. Wald (1951) advierte al final de su artículo.

La objeción más fuerte que se presenta para la aplicación del método axiomático se refiere a la dicotomía entre la teoría y su interpretación, tal que la falta de contenido económico de su estructura axiomática sesga la lectura que la teoría puede proporcionar sobre los datos que alimentan a sus categorías económicas, dado que los supuestos se eligen de acuerdo con lo que se quiere demostrar –el método axiomático se convierte en un método de carácter puramente teoremático–, y su interpretación ocurre una vez han sido formulados, de manera que lo matemático se presenta como el campo de trabajo para la economía, mas no como una expresión alterna o de apoyo para el análisis del problema económico. Esto lleva a reconocer una tensión epistemológica y teórica en la ciencia económica, de manera que no es sino hasta que la teoría se desarrolle mediante este método puramente racional que se podrá determinar la relación entre sus interpretaciones prácticas o conceptuales, y aquello que se propone modelar. En consecuencia, identificamos un vacío en el desarrollo de la economía neoclásica debido a la imagen formal del conocimiento matemático que incorpora como su referente directo de rigor científico, pues el método axiomático es por principio preintuitivo y esencialmente abstracto.

LA GEOMETRÍA: FIGURA DEL CONOCIMIENTO

La historia de la matemática revela una larga búsqueda del hombre por conseguir un conocimiento válido y permanente. Desde los griegos antiguos se ha pensado que el razonamiento es un proceso sujeto a esquemas, gobernado –al menos en parte– por leyes totalmente formulables. Encontramos que Aristóteles codifica los silogismos y Euclides la geometría, dos ejemplos que convergen en la investigación por descubrir las bases del pensamiento lógico-deductivo. Este es un problema ligado con la verdad, pues se busca explicitar el punto de partida sobre el que se ha de sostener una demostración.

Tal es el caso de Los Elementos de Euclides (año 300 a.c. aprox.), obra maestra que utiliza como base, para su construcción geométrica, definiciones a partir de las cuales puede generar postulados autoevidentes y llegar a formular axiomas o nociones comunes de los cuales se logran deducir teoremas. Es importante señalar que la coherencia de la teoría depende entonces de la evidente configuración de los objetos concretos tomados a través de sus postulados. Los parámetros de rigor introducidos aquí plantean, pues, la deducción de proposiciones válidas a partir de postulados intuitivamente ciertos, es decir, respaldados por una imagen figurada del mundo que se propone medir y estudiar.

Dos milenios después de formulada la certidumbre a la manera de Euclides, sus seguidores todavía trataban de demostrar el quinto postulado a partir de los cuatro primeros, con el propósito de no tener que darlo por supuesto. Uno de ellos, Girolamo Saccheri (1667-1733)², se propuso demostrar que al negar el quinto postulado se debía llegar a una teoría contradictoria. Lográndolo, el nombre de Euclides quedaría reivindicado ante su elección de dicho postulado, y su concepción geométrica quedaría validada como la única posible. Saccheri no logra llegar a una contradicción en términos lógicos (descubre resultados “repugnantes para la naturaleza de una línea recta”), pero sí crea una de acuerdo con prejuicios sobre lo que es para él –como para muchos otros geómetras del momento– la única geometría verdadera y apta para representar la imagen intuitiva del mundo real³.

Esta figura del conocimiento presuponía como algo dado, tanto el concepto de espacio como los primeros conceptos básicos para las construcciones en el espacio. En la medida en que daba solamente definiciones nominales y sus especificaciones esenciales sólo tomaban forma en lo que ahora conocemos como axiomas, la relación entre esas presuposiciones permanecía incomprendida, sin saber en qué medida era necesaria, ni aun si era posible (en relación con lo que se proponía modelar). Este vacío iría cociendo a través del tiempo, dentro de la comunidad matemática, las condiciones justas para descubrir una nueva interpretación de lo verdadero, mediante la concepción de teorías esencialmente abstractas o coherentes en sí mismas. Es entonces a partir del quinto postulado de la formulación de la geometría euclidiana, el conocido postulado de las paralelas⁴, que se van a desarrollar los posteriores descubrimientos para nuevas construcciones geométricas.

Se necesitó esperar más de cuatro décadas para que los geómetras se familiarizaran y reconocieran un nuevo mundo de posibilidades lógicas, abandonando la figura intuitiva de toda construcción imaginable. Para 1823 ya se había publicado la obra titulada Los principios de la geometría de Lobachevski, además del trabajo de János Bolyai donde claramente se hacía referencia a la primera geometría no euclidiana⁵. Es hasta 1867 que la tradición matemática y filosófica empieza a abrirse a las posibilidades generadas por la nueva concepción no euclidiana de la geometría. Los cuatro primeros postulados de Euclides se mantenían fijos (componiendo lo que se conoce como ‘geometría absoluta’ mientras que el quinto se podía sustituir sin llegar a contradicción alguna. Sobre una esfera de curvatura constante positiva se podía realizar una geometría no euclidiana como la de Riemann (1854), mientras que sobre una superficie de curvatura constante negativa (pseudoesfera) se podía realizar la de Bolyai-Lobachevski.

Como consecuencia de los trabajos desarrollados sobre las diferentes geometrías existentes a partir de los parámetros de rigor planteados por Euclides, pero que al mismo tiempo se fundaban sobre un sistema axiomático distinto al euclidiano⁶, la geometría euclidiana dejaba de funcionar como única figura del mundo real. Para los geómetras no euclidianos, el problema consistía en concebir distintas clases de ‘puntos’ y ‘líneas’ igualmente válidas que no contradijeran el principio de una realidad coherente en sí misma, es decir, posible en relación con su estructura lógica.

Luego de considerar los postulados de Euclides como ciertos, por más de dos mil años, el descubrimiento de geometrías distintas entre sí e igualmente válidas (como la geometría no euclidiana de Riemann o la de Bolyai-Lobachevski), que a finales del siglo XIX alertó a la comunidad matemática sobre aquello que se consideraba como conocimiento cierto, llevó a serios cuestionamientos acerca de lo que es o lo que representa una demostración. Esto desembocaría en una revolución al interior de la matemática, que a su vez provocaría nuevas investigaciones sobre su fundación, dentro de las cuales la propuesta formalista de Hilbert representaría un papel clave. En tal propuesta el método axiomático era la herramienta lógico-deductiva que hacía posible atacar los problemas que por principio estaban vedados al puro pensamiento de contenidos: la cuestión acerca de si es posible demostrar que un enunciado sea verdadero, por razones puramente lógicas (Ackermann y Hilbert 1975).

HILBERT Y LA AXIOMÁTICA ABSTRACTA

En 1899, con la obra Fundamentos de geometría, David Hilbert (matemático y meta-matemático alemán) abre el camino hacia la axiomatización de diferentes ramas de la matemática, de manera que en el mismo siglo XIX construye formalizaciones más estrictas que las de Euclides (desde 1899 la geometría euclidiana está expuesta a la manera de Hilbert, aunque con un mayor número de axiomas a los estrictamente necesarios), posibilitando a la vez la formulación de geometrías no-euclidianas.

Bajo el enfoque estructural, un sistema autosuficiente se puede construir de dos maneras: con base en elementos muy simples definidos axiomáticamente, y cuya combinación puede terminar siendo bastante complicada, o describiendo axiomáticamente el sistema en su conjunto, y lo que se supone debe ser la manera de funcionar, sin especificar sus elementos. El método axiomático-deductivo descansa en la especificación de unos pocos y sencillos axiomas, los cuales definen implícitamente los términos y las relaciones básicas (preintuitivas). Así se construyen sistemas cerrados o ideales sin importar cómo se consigue el sistema en su conjunto.

El objetivo de este método es deducir teoremas a partir de su estructura interna. Esta forma lógica necesita demostrar su coherencia absoluta para asegurar la existencia del objeto axiomático, en esencia abstracto, ya que no tiene referente concreto que afirme su viabilidad (como ocurre con el método euclidiano). Desde que se establece este método como el referente de rigor para validar el conocimiento matemático, la atención no se centra en el contenido de los enunciados, sino en su encadenamiento (cadenas de signos de acuerdo con ciertas reglas de aplicación estricta).

Una figura es una construcción para la intuición, muestra de que un enunciado es imaginable. Una figura no es un enunciado, y en un sistema formal escrito con signos que le son propios, no hay sino enunciados. Esto explica la formulación de un llamado al abandono de la intuición (H. C. Kennedy citado en Campos 1994, 341).

Según la escuela de Bourbaki, los axiomas se constituyen en los bloques fundamentales para sostener el edificio matemático, tal que las deducciones que se hacen a partir de ellos son posibles gracias a las relaciones descritas como resultado de los axiomas de la geometría. “Esta es la idea principal: son los axiomas los que hacen posible la descripción” (Campos 1994, 429). Cuando las definiciones toman el papel fundamental en el sistema euclidiano de rigor matemático-deductivo, el objeto de estudio existe en razón de una referencia a lo concreto, lo cual es intuible. Mediante los axiomas del formalismo hilbertiano, vacíos de todo contenido, se abandonan las referencias a la intuición para concentrarse en la estructura lógica de la teoría. La coherencia del sistema axiomático es la que garantiza la existencia de las deducciones, mientras que el objeto primitivo, elemental para la construcción de cada axioma, existe por sí mismo.

La clave para entender el método axiomático está en el hecho de que de los axiomas, a la manera de Hilbert, no se desprende falsedad ni verdad. En este momento lo que entendemos por dichos conceptos cambia⁷. Si los axiomas y sus consecuencias no se contradicen entre sí, entonces, son verdaderos, y las cosas definidas por ellos, existen. Al parecer, lo único válido es suponer lo que explícitamente puede expresar el sistema axiomático mediante la combinación de términos elementales, pero una vez preseleccionados estos términos –que permiten interpretar el mensaje teórico determinando los conceptos y el campo de conocimiento propio de una sola teoría– la formalización obliga a asumir cualquier significado pasivo que los mismos términos puedan adquirir. Ello, mediante la manipulación de reglas combinatorias que inevitablemente trascienden su simbología vacía (volveremos sobre este punto en la siguiente sección).

De esta forma, se adopta un criterio de certidumbre lógica: el de consistencia interna, donde la teoría se encuentra en un espacio dentro del cual se excluye todo juicio de valor, de manera que lo verdadero o lo falso –de vuelta al sentido común– se encuentra sólo en la aplicación de sus últimas consecuencias o teoremas sobre el campo de conocimiento interpretable⁸. Esta lógica permite deducir verdades ‘vacías’ a partir de axiomas falsos. La teoría se compone, entonces, de unos términos básicos y vacíos de contenido que se relacionan entre sí, formando nuevos conceptos, según lo permita la lógica interna del sistema axiomático. La verdad de las deducciones ya no se basa en una referencia a lo concreto, o en una realidad externa que la afirme, sino en que sea posible (conforme a la coherencia entre los supuestos y las conclusiones) con base en una estructura ideal.

Citando a Campos (1994, 479): “la axiomática se desprende de la geometría y se convierte en una disciplina sui generis, llamada por Hilbert la teoría de la demostración y, posteriormente, metamatemática”. Este método gana entonces una nueva dimensión en cuanto se proclama análogo al método científico, en cuanto a que una teoría es considerada legítima sólo si logra su correspondiente traducción formal a un lenguaje puramente matemático, como el mismo Hilbert dice,

Cuando los hombres de ciencia se decidan por el método axiomático, deberán hacer un examen profundo de los axiomas desde un punto de vista de su mutua independencia al interior del sistema y de la no contradicción del mismo [...] pues todo lo que puede ser objeto de pensamiento científico cae, en cuanto esté maduro para la construcción de una teoría, bajo el método axiomático y, por ende, bajo la teoría matemática (Hilbert 1917 citado en Campos 1994, 494).

Una vez formulada la tarea para la axiomatización del conocimiento científico, lo más importante en el momento de su aplicación es la aparición de nuevos límites, que para la matemática pura no necesariamente existen, dado el carácter concreto del objeto científico de estudio. Sus limitaciones inherentes radican en cómo se elige definir sus elementos básicos o partes elementales, pues todo resultado depende de ello. Dicha elección no tiene reglas rigurosas, por lo que un juicio al respecto es una cuestión de sentido común.

Recapitulando, cualquier teoría axiomática debe pasar la prueba de que al remover toda interpretación, su estructura matemática se ha de sostener por sí sola. Es en este sentido que G. Debreu se permite la construcción de la Teoría del valor (1959) en economía, sustituyendo la ambigüedad de un concepto económico por un objeto matemático al cual se le han de aplicar solamente reglas definidas de razonamiento (Hildenbrand 1983). Se trata de la cancelación, expulsión y omisión de la intuición como eje fundamental en el proceso formativo de toda construcción teórica válida, según la imagen del conocimiento, proporcionada por la matemática al interior del cuerpo de conocimiento walrasiano del equilibrio general.

GÖDEL Y LOS SISTEMAS FORMALES

La concepción filosófica de la ciencia que enmarca la axiomatización a la manera de Euclides nos dice que los primeros principios son enunciados absolutamente evidentes en lo que concierne a la realidad física –por tanto no pueden ser contradictorios–. No obstante, al encontrarnos con un esquema axiomático-abstracto de la realidad, y dado el modo como son escogidos los axiomas, es necesario demostrar que el sistema resultante no puede engendrar contradicción alguna, so pena de negar su posible existencia. Sin embargo, como Neuman advierte:

Ningún sistema formalizable puede demostrar, con sus propios medios, que esté exento de contradicción interna: no se trata de una posición filosófica o de una actitud intelectual plausible, sino del resultado de una prueba matemática rigurosa de un género extremadamente complejo (Neumann en ‘Tribute to Dr. Gödel’, en Campos 1994, 533).

Ante la crisis de las matemáticas de finales del siglo XIX, surge el programa formalista de Hilbert con dos objetivos centrales: construir un sistema formal completo que reúna las principales teorías de la matemática clásica en una sola, y probar su consistencia. De esta manera se podría construir una fundación sólida para las matemáticas, libre de toda antinomia, reuniendo bajo una misma estructura el conocimiento acumulado hasta el momento.

Este programa, la completa formalización de la matemática clásica, debía expresar sus conceptos mediante signos gráficos, organizados por hileras, de forma que el razonamiento se llevara a cabo por la sola manipulación combinatoria de estas. La demostración se reducía a una deducción formal conforme a reglas mecánicas. Por otro lado, el pedido por una demostración sobre la consistencia interna del sistema parecía difícil de imaginar, pues no es claro cómo justificar los métodos de razonamiento con base en ellos mismos. A pesar de esto, Hilbert conservaba la esperanza de encontrar una demostración de coherencia basada únicamente en modos finitistas (una porción de los métodos matemáticos), la cual fuera suficiente para demostrar la solidez del todo.

La voz disonante apareció en 1931 con el artículo, Sobre proposiciones formalmente indecidibles de Principia Matemática y sistemas afines, cuando K. Gödel mostró la imposibilidad de llevar a cabo el Programa Finitista de Hilbert. En primera instancia, Gödel demuestra que, absolutamente, ningún sistema axiomático que cumpla ciertas condiciones de aceptabilidad es completo, pues para cada uno de ellos se puede construir una proposición indecidible. Dicha incompletitud no tiene remedio por más axiomas que se añadan. En segunda instancia, demuestra la imposibilidad de probar al interior del mismo sistema su consistencia. Para cada uno de los sistemas formales de la matemática clásica se puede efectivamente construir una sentencia indecidible: tal que j como Øj sean deducibles. Por lo tanto, es imposible probar la consistencia de un sistema formal de la matemática clásica dentro del mismo⁹. “Gödel probó que el cálculo lógico es suficiente pero que las teorías interesantes formuladas con su ayuda son incompletas” (Gödel 1981, 113).

La prueba de Gödel supone implantar la paradoja de Epiménides (aquel cretense que afirmaba que todos los cretenses son mentirosos) en el corazón mismo de los “Principia Matemática”¹⁰ de Russell y Whitehead (pero sin caer en la paradoja), haciéndolos mucho menos interesantes para la posterior investigación matemática. Según se entiende, la razón de existencia de proposiciones indecidibles dentro de sistemas formales que contengan a la aritmética, radica en que una completa descripción epistemológica de un lenguaje dado no puede ser dada en ese mismo lenguaje. Ello, por cuanto el concepto de verdad de las sentencias de dicho lenguaje no puede ser definido dentro del mismo.

La intuición de esta demostración se puede entender como una construcción de auto-referencia al interior de un sistema formal dado (Campos 1994, 549-553, Hofstadter 2001, caps. XII, XIV, XV):

S: el sistema es consistente
G: G no es deducible

Como S es un sistema consistente, donde toda proposición debe ser deducible, G debe ser demostrable.

S
S Þ G

Pero si G, entonces G, es decir, G no es deducible:

G
G Þ ØG
G Þ ØG

Una manera de expresar la coherencia del sistema es negando G. Esto se ve en la cadena lógica que seguimos: dado que se supone G, y llegamos a una contradicción (G Ù ØG), se debe negar G:

ØG

Si S, entonces tanto G como G son deducibles. Por lo tanto se debe negar S:

S
S Þ G
G Þ ØG
ØS
S Ù ØS

La consistencia del sistema es, por consiguiente, indecidible. En consecuencia, el Programa Finitista de Hilbert muere, pero sobrevive la Axiomática Abstracta como método para demostrar que un enunciado sea verdadero por razones puramente lógicas¹¹. Enmarcando este resultado en una larga investigación dentro de la matemática acerca de lo que es una demostración, se tiene que la deducción lógica, como demostración matemática, no es nada más que una prueba dentro de un sistema fijo de proposiciones (Hofstadter 2001). No obstante, pareciera que el concepto de existencia no pudiera relativizarse sin destruir por completo su sentido.

[...] el sistema formal, por tanto, ya no es prototipo de verdad absoluta, ya no hay verdades absolutas garantizadas lógicamente, la matemática ya no da tales garantías, la razón humana ya no puede asegurar con base en la matemática que se conozcan tal tipo de verdades, como lo pretendía el racionalismo (Nagel y Newman, en Campos 1994, 552).

Como resultado, una demostración es una figura donde cada premisa es un axioma, o se obtiene mediante el uso de una deducción anterior. Para una proposición indecidible en un sistema axiomático dado, dicha proposición se puede añadir al sistema extendido de axiomas siempre y cuando ésta sea consistente con aquel sistema, de manera que la verdad o consistencia se asegura ahora con respecto a la estructura en la que se han fijado los axiomas. Es de anotar, como se evidencia, que al encontrarnos en el reino de la lógica ya no hablamos de una única verdad, sino de un sinnúmero de verdades, de manera que se nos presentan dos formas de solucionar la incompletitud del ejemplo gödeliano: agregar G o agregar ØG (caso que nos recuerda la repugnancia saccheriana de acuerdo con lo que nuestra intuición nos dice que debe ser un sistema formal completo).

EL PAPEL DE LA INTUICIÓN

Debemos introducir el concepto de aceptabilidad para tomar en consideración las diferencias de criterio al aceptar un sistema formal en vez de otro, en la medida en que dicho concepto hace referencia directa a la interpretación de un sistema formal dado con respecto a su objeto de estudio (Curry 1970). La compatibilidad es lo primordial al considerar la aceptabilidad, siendo aquélla relativa a la elección de las categorías económicas o términos básicos que han de conformar el cuerpo de conocimiento de la teoría en su concepción axiomática. De modo complementario, se puede examinar su pertinencia científica, en cuanto al contenido que se permite representar.

Recordemos que una demostración matemática requiere, para afirmar su existencia –aunque de manera relativa– una estructura libre de antinomias. Elige los términos básicos que tomarán la forma de símbolos vacíos para su manipulación lógica. Una concepción tal posibilita el tratamiento matemático de problemas económicos aislados de su dinámica habitual, de manera que la teoría se libera de interpretaciones en la medida en que se mantiene en un plano puramente formal. Esto le permite, a la construcción matemática, ostentar una descripción completa sobre el mundo económico, ya que sus deducciones se presentan necesarias en cuanto sus hipótesis lo exigen, pero sus hipótesis se eligen para deducir lo que de antemano se quiere demostrar. De este modo, cuando se aplica la axiomática en el sentido hilbertiano al cuerpo de conocimiento económico, éste lo adopta teoremáticamente y debe justificar, a posteriori, la pertinencia de las deducciones como resultado inevitable de su cuerpo axiomático. Sus propiedades semánticas cobran, entonces, una relevancia preponderante sobre sus demás funciones técnicas ordinarias (Mongin 2003). Ante la conversión de conceptos económicos elementales en objetos matemáticos fijos, la interpretación del mensaje teórico obedece a un eminente monismo metodológico, reduciendo, de este modo, las posibilidades de interpretación del objeto científico de estudio.

Se identifica una tensión entre las dos dimensiones del análisis, por un lado, la matemática y, por otro, la económica, las cuales hacen parte de un mismo proceso para obtener la aceptabilidad científica de una propuesta teórica. Esto, por cuanto un sistema cerrado de proposiciones no es más que una ilusión matemática, que en el momento de abrirse al mundo de las interpretaciones, debe ser sometido a un juicio sobre la pertinencia de su contenido. Esto requiere de una mirada crítica, tanto retrospectiva sobre el contexto bajo el cual se desarrolla el conocimiento (reconociendo una interacción innegable entre la experiencia y el pensamiento abstracto), como introspectiva acerca de la elección de las categorías esenciales para representar el objeto de estudio que estas significan, lo cual termina por fijar el desarrollo y capacidad de análisis de la teoría. En este momento cabe diferenciar entre el formalismo hilbertiano y un formalismo intuitivo, el cual, como su nombre lo indica, incorpora consideraciones intuitivas o de contenido en la formación de la teoría.

Ante la duda sembrada por Gödel acerca de los sistemas formales, al afirmar que no podemos estar seguros de que todas las consideraciones sobre el contenido de las proposiciones incluidas en dichos sistemas sean representables (Gödel 1981), el formalismo intuitivo se presenta como un método complementario que puede llevar a descubrimientos más fecundos sobre las posibilidades de análisis de una teoría particular, además de que puede llegar a resumir diferentes pruebas en una sola.

Pueden existir axiomas tan abundantes en sus consecuencias verificables que proporcionen tanta luz a un amplio campo y que ofrezcan métodos tan poderosos para resolver problemas (e incluso, en la medida de lo posible, para resolverlos constructivamente) que, sin que importe que sean o no intrínsecamente necesarios, deberían ser aceptados en el mismo sentido en que lo es cualquier teoría física bien establecida (Gödel 1981, 350).

Surge aquí un interrogante central sobre el tratamiento axiomático de las ciencias sociales, en la medida en que el nexo aplicado entre la teoría y su interpretación es fundamental y necesario para el completo desarrollo de su conocimiento. En efecto, en el momento en que la economía abandona todo recurso a la intuición con el objeto de lograr una ciencia exacta, ajena a toda sustancia económica, entra en el mundo de los sistemas formales axiomáticos fundado en la nueva imagen del conocimiento matemático propuesto por Hilbert y seguido por Bourbaki; una imagen formal y en apariencia libre de determinaciones normativas pero que por su misma naturaleza abstracta se puede convertir en criterio de ‘juicio objetivo’ del campo de conocimiento económico. Esto sentencia el siguiente postulado: en cuanto quiere obtenerlo todo de sí misma, la teoría se hace inevitablemente ideológica.

El problema parece encontrarse en el uso que se le pueda dar al método axiomático, pues como lo advertimos en la crisis de los fundamentos de las matemáticas, el inmutable rigor matemático no se debe dar demasiado por supuesto. Como afirma P. Mongin (2003), la axiomatización puede hacer explícito el proceso formal de deducción a partir de premisas científicas, o puede desvincular totalmente a los sistemas formales de toda referencia con la realidad económica, profundizando en la separación de sus signos (sintaxis) y su sentido (semántica). Esta axiomatización puede llevar a juzgar la conveniencia de una teoría conforme a consideraciones ajenas a su sustancia específica, relegando a un segundo plano los esfuerzos de ingenio intelectual, más fecundos en intuición, que la sola analogía a las teorías metamatemáticas acerca de lo que es una demostración. La autonomía de los sistemas formales puede llegar al punto extremo de constituirse en “objetos de estudio independientes con vida propia” (ibid., 135). La axiomatización de la economía obtiene así una etiqueta de advertencia.

A gran distancia de su origen empírico, o después de muchas reproducciones “abstractas”, un tema matemático está en peligro de degeneración [...] siempre que alcance este punto, me parece que el único remedio es el retorno rejuvenecedor a la fuente: la reintroducción de ideas más o menos directamente empíricas [...] condición necesaria para conservar el frescor y vitalidad de la materia (Neumann 1969, 452-3).

La aceptabilidad es una elección propia de la materia de estudio, donde la revisión constante de su cuerpo teórico obliga a reconsiderar la imagen de rigor utilizada para validar su conocimiento. En general, no hay sistema lógico que sea aceptable a priori para el propósito de concebir una determinada realidad económica, en particular con respecto al modelo walrasiano de equilibrio general, al instalarse como paradigma inamovible de la economía moderna. Considerando lógicas alternas podríamos dar cuenta de la fe existente en la lógica clásica como una cuestión de hábito y, de igual forma, de la aceptabilidad de sistemas lógicos como una cuestión que surge en el preciso momento en que se marca una distancia prudencial con respecto al lenguaje matemático propio de un sistema formal.

FORMA Y CONTENIDO

Examinemos por un momento la significación de la ‘forma’ cuando se quiere interpretar su contenido. En la medida en que la formación sintáctica del mensaje teórico puede ser verificada, los procedimientos cognoscitivos necesarios para reconocer sus atributos se mantienen identificables. Dicho procedimiento es mecánico. En segunda instancia, la simbología que le da forma al mensaje contiene atributos cuya identificación puede ser no finalizable. Esto es lo que ocurre cuando se quiere determinar la teoremidad o no teoremidad de todas las proposiciones dentro de un sistema formal que permita representar todos sus predicados recursivos primitivos, es decir, todo enunciado cuya verdad o falsedad pueda ser decidida por medios mecanizables. Los aspectos semánticos de la ‘forma’ requieren entonces de un procedimiento de identificación diferente al que comúnmente se usa para verificar que una cadena de razonamiento está bien formada.

Si se sostiene que el criterio formalista, en su concepción hilbertiana (axiomática abstracta), es suficiente para estructurar la ciencia económica, estamos desconociendo los atributos semánticos en la construcción de la completa significación del mensaje teórico. De este modo, la formalización que exige una dicotomía entre forma y contenido omite consideraciones propias del método científico que su simbología no permite representar. Al convertirse en totalitaria en sus bases internas, la disciplina rechaza las alternativas. Este parece ser el caso para el estado actual de la economía neoclásica, pues ante su proceso de matematización se crea la ilusión sobre la existencia de una verdad absoluta, cuando en realidad el método matemático es una técnica, un método específico para la práctica. Este velo ideal, un velo de símbolos, enmascara el mundo de la práctica, el mundo histórico y político.

En consecuencia, se tiene una forma de pensamiento y conducta que es inmune a cualquier orden que no sea el de la racionalidad establecida. Se preserva un estado de hechos aparente que llega a estar incorporado en el aparato técnico y lingüístico que lo reproduce mecánicamente. Es entonces que se hace un llamado por la transformación de una verdad lógica a una verdad histórica, de manera que el contenido histórico, propio del pensamiento dialéctico, estructure el proceso de traducción necesario para volver de un único pensamiento lógico matemático a uno esencialmente social. Lo importante, aquí, es concebir un criterio propiamente económico para el cual la estructura de su teoría fundacional esté en función de su contenido, y no al revés, como ocurre en el desarrollo de la economía del equilibrio general.

El largo camino hacia el pensamiento científico necesita efectivamente de la inferencia y la deducción lógica; la primera marca el camino para el desarrollo de la segunda. Podemos acordar que todavía falta un paso mucho más alto de abstracción o matematización para configurar los conceptos del pensamiento con la dinámica habitual, en tanto el desarrollo de nuevas herramientas matemáticas lo permita. De manera complementaria y necesaria, se debe construir un proceso de socialización de la economía. El mensaje económico, que intentamos aprehender de la realidad, necesita un proceso de dos tiempos: una traducción formal y una traducción social. Esto obedece a otra lógica, una lógica económica por excelencia. Si volvemos la mirada a la fuente, a lo más o menos empírico, contemplamos la importancia del dinero en la génesis de la experiencia económica en cuanto vínculo social (Marx 1968) como medio de pago (Keynes 1943 y 1971, Hahn 1983).

Recordemos que la teoría económica neoclásica, en su alto grado de matematización en que se encuentra, contempla el dinero –medio de pago– como categoría dispensable para un sistema que se encuentra en equilibrio general perpetuo, donde el dinero –medio de cambio– no interfiere sobre el proceso de formación de un sistema de precios, tal que en aras de eficiencia necesita estar completamente controlado, y precisa de confianza perfecta en cuanto a las expectativas futuras sobre la economía. Es la restricción presupuestal y racional sobre el comportamiento del individuo la que reemplaza el rol que el dinero desempeña en el proceso efectivo de formación de precios, donde las condiciones estáticas del análisis axiomático llevan a fijarlos por anticipado.

La hipótesis neoclásica que conduce a una concepción económica de este tipo se basa en que los bienes físicos se pueden mover libremente en el mercado, sin necesidad de la especificación de un proceso de formación de precios para las mercancías o de su correspondiente tecnología de intercambio. En este análisis todo bien es completamente líquido, hasta el punto de no necesitar del crédito para especificar el comportamiento económico en el mercado (Shubik 1975). El pedido científico por la restricción de liquidez, que todo individuo enfrenta en la realidad, queda pues ignorado, ya que en el momento de introducirla, el modelo de equilibrio no es apto para el cometido (Radner 1968).

De esta manera, el modelo del equilibrio general walrasiano, el más desarrollado en términos formales en tanto cuerpo de teoría económica, no encuentra lugar para la existencia del dinero. Dado que la única manera en que la institución del dinero puede ser neutral es que la teoría no cuente con una explicación científica de la misma (Hahn 1984, 12), surge la necesidad de considerar construcciones teóricas alternas (Hahn 1983, Davidson 2003).

Las economías con oro o papel moneda o relaciones especiales de crédito tienen una relación con las economías no monetarias similar a la de las geometrías no euclidianas con la geometría euclidiana. Tienen diferentes reglas o axiomas que cambian o aumentan las posibilidades del sistema (Shubik 1992, 14).

El vacío conceptual presente en la formulación de los fundamentos de una teoría monetaria en el marco del equilibrio general, da cuenta del modo en que la teoría neoclásica representa una economía monetaria a la manera de una economía no esencial, en el sentido que ninguna variable monetaria es necesaria para la descripción o determinación del equilibrio económico. Se presenta pues una tensión inherente al marco teórico de la ciencia económica neoclásica, entre un sistema económico no esencial, que no da razón de la existencia de la institución de la moneda, y uno de carácter monetario que carece de la debida fundación epistemológica, necesaria si se quieren trabajar de manera completa, bajo un marco analítico apropiado, los problemas económicos monetarios que plantea una economía de mercado.

CONCLUSIONES

El concepto de rigor matemático absoluto no es inmutable, y su variabilidad nos lleva a considerar aspectos diferentes a la sola abstracción matemática para asegurar la validez general de una teoría o la existencia de una solución en especial. Se observa que lo que la comunidad económica ha considerado como científicamente válido a lo largo del siglo XX corresponde a una metodología científico-axiomática que escapa a consideraciones fundacionales sobre el proceso constitutivo de su cuerpo teórico. Este método legitimador, que sólo es una forma determinada de hacer matemática, funciona como la imagen de rigor científico para el cuerpo de conocimiento neoclásico.

Al desconocer sus límites, la economía instala el método matemático dentro de su mismo cuerpo de conocimiento para obtener proposiciones-teoremas (según una justificación sintáctica), y luego, en un salto mortal entre niveles de comprensión, la (única) verdad económica, tal que el contenido económico está en función de la estructura formal de la teoría. Quien da este paso decisivo, no sin antes advertir los peligros, es Abraham Wald (1951), quien lo incorpora y desarrolla en la teoría walrasiana del equilibrio general al elegir su estructura axiomática teoremáticamente, a expensas del contenido económico, el cual queda relegado a describir la teoría mediante su posterior justificación.

Reconociendo el trabajo de Gödel, los sistemas formales pueden expresar el conocimiento que sus axiomas le permitan deducir mediante reglas mecánicas, mas no garantizan que puedan representar su contenido mediante una división verificable entre teoremas y no teoremas. El análisis de contenidos se hace indispensable. Se desenmascara una falacia metodológica, por cuanto un sistema formal no garantiza la deducción de todas las verdades que pretende formular. Su incompletitud es el reflejo de querer definir (implícitamente) todos los términos del sistema económico mediante un número finito de axiomas. Rechazamos, entonces, la dicotomía entre la teoría y sus interpretaciones, ya que dicha dicotomía guía a la disciplina científica ciegamente a un monismo metodológico, interpretando sus conceptos de acuerdo con los valores de verdad que la manipulación lógico-deductiva exige.

Esta investigación concibe un criterio de aceptabilidad que examina la compatibilidad de la herramienta analítica con respecto al problema científico que se propone desarrollar y evalúa la pertinencia de sus resultados. La reflexión crítica que esto supone, proyecta una mirada retrospectiva sobre el proceso constitutivo de la teoría, y otra de tipo introspectivo hacia el cuerpo de conocimiento existente. Así nos encontramos con la tensión inherente a la teoría económica (en su versión clásica y neoclásica), identificada de manera precisa por autores como Hahn (1983), Radner (1968) y Shubik (1975), la cual proviene de la aporía de un paradigma que sugiere la visión de una economía en la cual el dinero no es esencial, pero que debe incorporarlo a una teoría del valor de manera obligatoria ante la necesidad de dar razón del fenómeno monetario, sin contar con la fundación epistemológica apropiada.

En el plano lógico-formal se sugiere la construcción del dinero como categoría económica fundacional, cuya introducción necesita de un nuevo axioma que obliga a la resignificación del cuerpo de la teoría económica existente. Este nuevo axioma, al no poder ser deducido, y contener un concepto nuevo para la teoría del equilibrio, asegura su independencia con respecto al cuerpo axiomático existente (una sentencia es independiente del restante conjunto de axiomas si y sólo si su negación es consistente con ellos). En el plano de la intuición, el científico se puede remontar a la experiencia histórica como punto de partida de la reflexión teórica. Innes (2004), Keynes (1943 y 1971) y Hahn (1983) coinciden por razones diversas, en la necesidad de introducir el dinero como medio de pago para la resolución de esta tensión.

La utilización de la forma matemática debe ser instrumental para la economía, pero no una norma metodológica, como lo sugiere el método axiomático, de manera que sirva como herramienta analítica para el desarrollo de su contenido específico (el económico). Esto implica reconocer en la forma matemática un lenguaje paralelo, el cual necesita de un proceso de traducción que ligue una teoría concebida por la matemática con su respectiva dimensión económica. El estado moderno de la ciencia económica exige la comprensión de la matemática tanto como de la economía. La primera obedece a un proceso de matematización. La segunda, a un proceso de socialización, en razón de la relación innegable entre el conocimiento abstracto y su correspondiente desarrollo histórico. Esto sugiere una consideración diferente acerca de lo que se entiende por ‘certeza’, ya que ésta no se consigue mediante la manipulación de los símbolos, sino que se va formando a través del cultivo del conocimiento, mediante los conceptos mismos.

NOTAS AL PIE

1. La utilidad marginal debe ser además una función estrictamente decreciente y monotónica (Wald 1951).

2. En su obra titulada “Euclides vindicado de toda imperfección, o, conato geométrico mediante el cual se establecen los verdaderos primeros principios de toda la geometría”.

3. Demostró más de 15 teoremas, que ahora hacen parte de la geometría de Bolyai-Lobachevski.

4. La definición 23 de los Elementos define a las rectas paralelas como las que estando en el mismo plano y siendo prolongadas indefinidamente en ambos sentidos, no se encuentran una a otra en ninguno de ellos (Euclides 1991, 196). De este modo todas las perpendiculares trazadas de una paralela a otra son iguales, lo cual se vendría a demostrar que no necesariamente se cumple. A partir de esta definición Euclides (ibid., 197-198) dice: “Postúlese que si una recta al incidir sobre dos rectas hace los ángulos internos del mismo lado menores que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán en el lado en el que están los (ángulos) menores que dos rectos”. En otras palabras, Aleksandrov (2003, tomo 3, 124) explica que “por un punto exterior a una recta se puede trazar una y sólo una paralela a dicha recta (en referencia a rectas infinitas)”.

5. Coincidencialmente, el descubrimiento de la geometría no euclidiana fue por obra simultánea de un húngaro de 21 años, Bolyai, y un ruso de 30, Lobachevski.

6. Siguiendo la escuela de Bourbaki, los postulados se pueden ver como axiomas en la medida en que es a partir de estos que se ha de desarrollar toda posible deducción. La diferencia radica en que para Euclides, los postulados hacen referencia a objetos concretos, mientras que el método axiomático desvincula a estos postulados de todo contenido intuible o figurado.

7. “Los axiomas de la geometría son convenciones, para las cuales la noción común de ‘verdad’ no tiene sentido. La ‘verdad matemática’, de este modo, reside únicamente en la deducción lógica a partir de premisas puestas arbitrariamente a la manera de axiomas” (Poincaré 1902; citado por Campos 1994, 475).

8. En lo que toca a la economía neoclásica, bajo su aproximación axiomática, se trata aquí de la dicotomía que Debreu reconoce en el prefacio de la Teoría del valor, 1959 (obra canónica en el desarrollo de la teoría del equilibrio general), entre la teoría y sus interpretaciones, tal que su estructura matemática se vea favorecida.

9. “... consistencia en el sentido formal (o hilbertiano), es decir, la consistencia es considerada como una propiedad puramente combinatoria de ciertos sistemas de signos y de sus reglas de juego” (Gödel 1981, 99).

10. Obra que pretendía deducir toda la matemática clásica a partir tan sólo de reglas lógicas.

11. “Programa finitista de Hilbert” y “axiomática abstracta” son tomados de Weintraub (2002, cap. 3).

REFERENCIAS BIBLIOGRÁFICAS

1. Ackermann, W. y Hilbert, D. Elementos de lógica teórica, Madrid: Editorial Tecnos, 1975 [1962].        [ Links ]

2. Aleksandrov, A. D., Kolmogorov, A. N. y Laurentiev, N. A. La matemática: su contenido, métodos y significado, tomo 3, Madrid: Alianza Universidad, 2003.        [ Links ]

3. Campos, Alberto. Axiomática y geometría: desde Euclides hasta Hilbert y Bourbaki, Universidad Nacional de Colombia, Bogotá: Unibiblos, 1994.        [ Links ]

4. Cassel, G. The Theory of Social Economy, New York: Harcourt, Brave and Co, 1932 [1918].        [ Links ]

5. Curry, H. Outlines of a Formalist Philosophy of Mathematics, Amsterdam, London: North-Holland Publishing Company, 1970.        [ Links ]

6. Davidson, Paul. “Is ‘mathematical science’ an oxymoron when used to describe economics?”, Journal of Post Keynesian Economics, 25(4): 527-546, 2003.

7. Debreu, Gerard. Theory of Value. An axiomatic approach to of economic equilibrium, Cowles Foundation, New York: Yale University, 1959.        [ Links ]

8. Debreu, Gerard. “Theoretic models: mathematical form and economic content”, Econometrica, 54(6): 1259-1270, 1986.

9. Debreu, Gerard. “The mathematization of economic theory”, American Economic Review, 81(1): 1-7, 1991.

10. Euclides. Elementos. Libro I. Editorial Gredos. Madrid, 1991.        [ Links ]

11. Gödel, Kurt. Obras completas, Madrid: Alianza Editorial, 1981.        [ Links ]

12. Habermas, J. Ciencia y técnica como “ideología”, México: Tecnos, 1993.

13. Hahn, Frank. Money and Inflation, Cambridge, Mass.: The MIT Press, 1983.        [ Links ]

14. Hahn, Frank. Equilibrium and Macroeconomics, Cambridge, Mass.: The MIT Press, 1984.        [ Links ]

15. Hilbert, David. Fundamentos de geometría, 1917 [1899].        [ Links ]

16. Hildenbrand, W. Mathematical economics: Twenty papers of Gerard Debreu, Cambridge University Press, 1983.        [ Links ]

17. Hofstadter, D. Gödel, Escher, Bach. Un eterno y grácil bucle, traducción de M. Usabiaga y A. Rousseau. Barcelona: Tusquets Editores, 2001.        [ Links ]

18. Ingrao, B. and Israel, G. The Invisible Hand. Economic Equilibrium in the History of Science, The MIT Press, 1990.        [ Links ]

19. Innes, M. “What is Money?”, The Banking Law Journal, May. On line: www.warrenmosler.com/docs/docs/innes_final.htm, 2004 [1913].

20. Keynes, J. M. Teoría general de la ocupación, el interés y el dinero, México D. F.: Fondo de Cultura Económica, 1943 [1936].        [ Links ]

21. Keynes, J. M. A Treatise on Money, London: Macmillan, 1971.        [ Links ]

22. Neumann, John von. “El matemático. Selección por James Newman”, El mundo de las matemáticas, v. 5, traducido por Simon and Schuster, Inc. NY: Edición Grijalbo, 1969 [1956].

23. Marx, Karl. Manuscritos económico-filosóficos de 1844, México: Edición Grijalbo, 1968.        [ Links ]

24. Mongin, Philippe. “L’axiomatisation et las théories économiques”, Revue économique, 54(1): 99-138, 2003.

25. Morgenstern, Oskar. “Abraham Wald, 1902-1950”, Econometrica, 19(4), 1951.

26. Radner, Roy. “Competitive equilibrium under uncertainty”, Econometrica, 36(1): 31-58, 1968.

27. Shubik, Martín. “The general equilibrium model is incomplete and not adequate for the reconciliation of micro and macroeconomic theory”, KYKLOS, 28(3): 545-573, 1975.

28. Shubik, Martín. Economía política: un enfoque desde el punto de vista de la teoría del juego, traducido por Roberto R. Reyes. México: Fondo de Cultura Económica, 1992.        [ Links ]

29. Wald, Abraham. “On some system of equations of mathematical economics”, Econometrica, 19(4): 368-403, 1951 [1936].

30. Walras, Leon. Elements of Pure Economics, Irwin, Homewood, 1954.        [ Links ]

31. Weintraub, E. Roy. “On the existence of a competitive equilibrium: 1930-1954”, Journal of Economic Literature, XXI: 1-39, 1983.

32. Weintraub, E. Roy. “Whose Hilbert?”, in B. Herrnstein and E. Weintraub, How Economics Became a Mathematical Science (pp. 72-100), Durham and London: Duke University Press, 2002.