TEORÍAS SOBRE COBERTURA CON CONTRATOS DE FUTURO

Vicent Aragó Manzana *

Doctor en Ciencias Económicas y Empresariales, actualmente se desempeña como Profesor Titular del Departamento de Finanzas y Contabilidad de la Universidad Jaurne I (Castelló, España). E-mail: arago@cotin.uji.es. Dirección de correspondencia: Cam pus Riu Sec. 12071. Castelló, España.

Este artículo fue recibido el 24 de abril de 2008 y su publicación aprobada el 2 de septiembre de 2008.

Resumen

En este trabajo se presenta una revisión de las principales teorías sobre cobertura con contratos de futuro y de los distintos métodos de estimación utilizados para determinar el ratio de cobertura óptimo. La aproximación a la cobertura más utilizada en la literatura especializada es la basada en el modelo de la teoría de carteras. No obstante, debido a sus hipótesis relacionadas con la función de utilidad del inversor y con las propiedades de la función de distribución de los rendimientos, XI han surgido nuevas propuestas (por ejemplo, las construidas a partir del coeficiente de Gini y el concepto de Lower Partial Moments), que intentan reducir dichas restricciones.

Palabras clave: contratos de futuros, ratio de cobertura óptimo, Coeficiente de Gini, Lower Partial Moments, Modelos GARCH, Cointegración, Ratio de cobertura de mínima varianza. JEL: G10, G11, C30.

Abstract

This paper presents a reviewof themain theories on hedgingwith futures contracts, and the various estimation methods used to estimate the optimum hedge ratio. The most widely used approach to hedging in the extensive literature in this field of research is unquestionably that based on the theoretical model from portfolio theory. However, because of the hypotheses on which this model is based, related to the investor utility function and to the properties of the distribution function of returns, new approaches have arisen that attempt to overcome these restrictions; specifically, the approach based on the Gini coefficient, and on the concept of Lower Partial Moments, which is also dealt with in this paper.

Key words: futures, Optimum Hedge Ratio, Gini coefficient, Lower Partial Moments, GARCH models, cointegration, Minimum Hedge Ratio. JEL: G10, G11, C30.

Résumé

Dans ce travail on propose une révision des théories principales sur la couverture par les contrats à terme et des méthodes d´estimation différentes utilisées pour déterminer le ratio optimale de couverture. L´approche par la couverture la plus utilisée dans la littérature spécialisée est basée sur le modèle de la théorie de portefeuille. Cependant, à cause de ses hypothèses relatives à la fonction d´utilité de l´investisseur et aux propriétés de fonction de distribution des rendements, ont surgi des nouvelles alternatives (par exemple, celles construites à partir du coefficient de Gini et du concept de Lower Partial Moments), lesquelles essaient de surpasser ces limites.

Mot clés: contrats d´avenir, ratio optimale de couverture, coefficient de Gini, Lower Partial Moments, Modèles GARCH, cointégration, ratio de couverture de variabilité minimale. JEL : G10, G11, C30.

Una de las principales razones esgrimidas en la literatura financiera para explicar la existencia de contratos de futuros es la posibilidad que éstos ofrecen para realizar coberturas. Una adecuada gestión del riesgo de una cartera de inversión. requiere que se considere tanto el riesgo especifico co mo el de mercado. La diversificación es una forma adecuada de eliminar el primero de ellos, sin embargo, la forma que tradicionalmente se ha seguido para gestionar el riesgo de mercado es costosa e inconsistente con una estrategia de inversión determinada (Monis. 1989). Estas limitaciones son algunos de los motivos que han influido en las diferentes instituciones y profesionales para buscar nuevas formas o instrumentos que permitan una gestión más eficiente de éste.

Desde su aparición. los contratos de futuro sobre índices bursátiles se han convertido en una herramienta muy utilizada, ya que han abierto nuevas formas de gestionar el riesgo de mercado a través de la cobertura. A diferencia de los métodos tradicionales de gestión del riesgo, la cobertura es una forma relativamente más barata y consistente con una estrategia de inversión específica, lo que facilita llevarla a cabo con independencia de la composición de la cartera y sin necesidad de realizar ninguna modificación de ésta.

Alcanzar la posición de riesgo adecuada dada la riqueza de un inversor, no consiste solamente en la elección de un tipo de activo con unas caracte rísticas de riesgo, sino también en conseguir un equilibrio apropiado entre activos arriesgados y sin riesgo. Operar con futuros es una forma de conseguir este equilibrio y una dimensión adecuada del riesgo.

Partiendo de una posición larga al contado formada por una cartera de acciones, la venta de un contrato de futuros sobre índices es funcionalmen te equivalente a vender las acciones de la cartera de inversión e invertir lo obtenido en instrumentos de renta fija (activos sin riesgo). En sentido contrario, comprar un contrato de futuros es funcionalmente equivalente a financiar parte de la adquisición de la cartera a préstamo, es decir, vender deuda e invertir lo obtenido en la cartera de acciones.

Las diferentes aproximaciones a la cobertura difieren básicamente respecto a los objetivos que se buscan con ella. Aunque, tradicionalmente, se ha considerado como función principal de la anterior la disminución o gestión del riesgo, no es menos cierto que existen estrategias de coberturas cuyo objetivo se centra en la maxirnizución del beneficio a través de la realización de coberturas selectivas o especulación en la base (Working, 1953). Existen tres modelos de cobertura que proporcionan reglas de decisión diferentes en relación con la posición a tomar en el mercado de futuros dada la de contado: esto es el valor del ratio de cobertura.

a) Tradicional o "Naive". El objetivo de esta aproximación es disminuir el riesgo. Consiste en tomar una posición en el mercado de futuros de la misma magnitud, pero de signo contrario a la mantenida en el activo arriesgado que se intenta cubrir (1:1). De acuerdo con este modelo no se considera la existencia del riesgo de base derivado del hecho que los cambios de precio en los mercados de contado y futuro no son de la misma magnitud, por lo que esta aproximación no elimina el riesgo en su totalidad. No obstante, la toma de una posición de estas características disminuirá el riesgo de la cartera cubierta respecto a la de contado, ya que el arbitraje (Schwartz y Laastsch, 1991) yla convergencia de la base en al fecha de vencimiento (Figlewski, 1985) posibilitan un acotamiento en la magnitud del riesgo de base.

b) Maximización del beneficio. Esta aproximación a la cobertura nace a partir del trabajo de Working (l953). Se considera que el objetivo de la cobertura no es únicamente la disminución del riesgo, sino también la mejora del beneficio que puede obtenerse realizando coberturas de caácter selectivo. Por coberturas de carácter selectivo se entienden aquellas que son realizadas cuando se espera que la evolución de los precios relativos de contado y futuro, en definitiva la evolución de la base, sea favorable al inversor. Working¹ (1953) analiza la relación existente entre el tamaño de la base para un determinado periodo y su subsiguiente cambio, y encuentra que bases positivas (definida como diferencia entre futuro y contado) elevadas tienden a venir seguidas por cambios de carácter negativo y al contrario. Si la base es lo suficientemente grande para esperar cambios de ésta de carácter negativo, deberá realizarse la cobertura tomando una posición corta en futuros de igual magnitud a la mantenida al contado.

En definitiva el aspecto que determinará que un inversor decida realizar una cobertura selectiva, será el tamaño de la base y las expectativas referentes a su evolución futura. No obstante, la consideración de que la base es lo suficientemente elevada² para esperar una evolución favorable, y por tanto, tomar posiciones en el mercado de futuros, dependerá en última instancia de las preferencias del inversor recogidas en su función de utilidad y de su grado de aversión al riesgo. Muchos autores coinciden en señalar que aunque tradicionalmente se la ha considerado como una aproximación a la cobertura, no es más que una manera de especular sobre la evolución de la base y no propiamente una política de cobertura, entendida como una forma de gestionar el riesgo.

c) Teoría de selección de carteras. Esta teoría recoge de forma explícita los rasgos fundamentales de comportamiento racional del inversor, que consiste en buscar la distribución de su riqueza entre las diferentes oportunidades de inversión y conseguir una composición de su cartera que haga máximo el rendimiento dado un nivel de riesgo, o minimice el riesgo para un nivel de rendimiento dado. Se basa en un análisis media-varianza (M-V), en el cual se asume implícitamente que el rendimiento de los precios es normal o que la función de utilidad de los inversores es cuadrática.

Dentro de este modelo de cobertura cabe distinguir dos grandes aproxima ciones que se diferencian según la actitud del inversor frente al riesgo. En la primera, se asume que el grado de aversión al riesgo del agente que decide cubrirse es máximo y el objetivo que se persigue es minimizar el riesgo de la posición cubierta; mientras que en la segunda el objetivo perseguido es la maximización de una función objetivo en la que se consideran conjunta mente el riesgo y el rendimiento.

El objetivo que se persigue en este trabajo es presentar un resumen de las diferentes aproximaciones teóricas a la cobertura con contratos de futuros. Debido a la gran cantidad de trabajos, tanto teóricos como de aplicaciones empíricas, publicados en revistas de reconocido prestigio, se considera que el esfuerzo realizado es valioso, no sólo como forma de presentar las diferentes aproximaciones al tema objeto de estudio, sino como guía y punto de partida para todos aquellos interesados en esta área de conocimiento.

Dado que los distintos modelos de cobertura sustentados en el modelo teórico del análisis de selección de carteras engloban como casos particulares a las dos primeras aproximaciones señaladas (naive y maxirnización del beneficio), el trabajo se centrará en esta última. También se presentarán, analizarán y discutirán las distintas formas de estimar el ratio de cobertura óptimo. Bajo estas consideraciones el trabajo se ha estructurado de la siguiente forma: en la primera sección se estudia la aproximación a la cobertura considerando como su objetivo la minimización del riesgo: el segundo apartado se dedica al análisis de la cobertura considerando como objetivo la maximización de una función objetivo³ y en el tercer segmento se analizan los diferentes métodos de estimación propuestos para determinar el RCMV

MIIININIlZACIÓN DEL RIESGO

En este apartado se considera que el objetivo del inversor al realizar la cobertura es minimizar el riesgo de la cartera cubierta. Aunque de forma tradicional para medir el riesgo se ha utilizado la varianza, no es menos cierto que existen distintas formas de medirlo. Por ello, seguidamente se presen tan distintas medidas del riesgo y cómo su consideración puede afectar la determinación del ratio de cobertura.

Así, en primer lugar, se utilizará la varianza del rendimiento como medida de riesgo. También se analizará la utilización del coeficiente medio de Gini-extendido. Ésta es una medida de dispersión que presenta la ventaja que no debe realizarse ningún supuesto sobre la función de distribución de los rendimientios, corno ocurre en el caso anterior, y adicionalmente proporciona soluciones que son eficientes bajo la óptica de dominio estocástico. Por último, también se propone otra medida de dispersión en la cual sólo se consideran las desviaciones del rendimiento de carácter negativo, con objeto de recoger sólo la variabilidad o riesgo de las pérdidas frente al de las ganancias⁴ y poder determinar la posición en futuros que minimice el riesgo de pérdidas en lugar del riesgo total.

Esta última medida es interesante, ya que diversos estudios (Mao, 1970) muestran que los inversores o gestores de carteras, asocian el riesgo a la variabilidad de resultados negativos o pérdidas (downside risk) y no tanto a la de sus ganancias (upside potential). Esta asimetría entre resultados positivos y negativos respecto a un valor objetivo, pone de manifiesto que la varianza no es una medida que recoja el riesgo, al menos tal y como es percibido por los inversores.

Riesgo medido por el estadístico de la varianza: ratio de cobertura de mínima varianza (RCMV)

Jonhson (1960) Y Stein (1961) son los primeros autores en utilizar la teoría de selección de carteras nara estimar ratios de cobertura de mínima varían y su aplicación empírica al caso de mercaderías. Ederington (1979), basandose en los trabajos anteriores, utiliza esta misma aproximación para mercados financieros. El objetivo que se persigue bajo este criterio es minimizar el riesgo de la posición cubierta, medido por la varianza del rendimiento. Se supone un inversor averso al riesgo, de forma que no considera los efectos de la cobertura sobre el rendimiento de su cartera.

Jonhson define la cobertura, dada una posición en el mercado de contado (x_i ) como: "La posición que se tomará en el mercado que se utiliza como cobertura (x_j ), de forma que el riesgo de precio de mantener las dos posiciones entre T y T + 1 sea el mínimo posible. El riesgo de precio puede ser considerado como la varianza de la distribución de probabilidad para el cambio de precios entre T y T + 1 de quién posee el bien al contado en T y donde el precio entre T y T + 1 se considera una variable aleatoria⁵".

De acuerdo con esta aproximación, tal y como se recoge en la ecuación (1) el objetivo perseguido es el de minimizar (Min) la varianza (Var) del rendimiento de la cartera cubierta durante el periodo t (R_{p, t} ), donde R_{s, t} y R_{f, t} son los rendimientos de contado y futuro durante el periodo t, respectivamente, y h_{t -1} el ratio de cobertura.

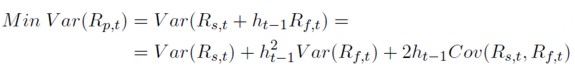[1]

El valor del ratio que minimiza la varianza de la cartera cubierta. se obten drá de las condiciones de primer orden y resolviendo para h_{t -1} (ecuación 2). Tal y como señala Ederington (1979) esta expresión corresponde con la pendiente de la recta de regresión por MCO entre los cambios de precios (o rendimientos) al contado respecto a los de futuro, como se aprecia en la ecuación (3)⁶.

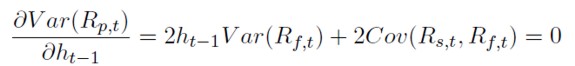[2]

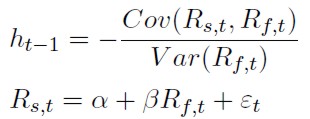[3]

La expresión del RCMV ha sido utilizada en multitud de trabajos; sin embargo, al utilizar esta aproximación se están asumiendo una serie de hipótesis muy restrictivas. La primera, es que el objetivo del inversor se centra exclusivamente en disminuir el riesgo de su cartera, no prestando ninguna atención sobre los efectos en la rentabilidad.⁷ En segundo lugar, que los residuos del modelo de regresión estimados no presentan problemas (auto correlación, heteroscedasticidad, etcétera). Finalmente y derivado del hecho de que este criterio se basa en las premisas de la teoría de selección de carteras, se asume que el rendimiento de los mercados se distribuye corno una normal o que la función de utilidad de los inversores es cuadrática.

Con objeto de relajar esta última restricción han surgido trabajos que pro ponen utilizar corno medida del riesgo de la cartera cubierta el Coeficiente Medio de Gini Extendido (MGE); realizan un análisis Media-Coeficiente de Gini que presenta la ventaja sobre el análisis tradicional (M-V) que es consistente con las reglas de dominio estocástico con independencia de los supuestos sobre la distribución de los rendimientos o la función de utilidad del inversor.

Otra vía utilizada en trabajos en los cuales se considera que el objetivo de la cobertura es la disminución del riesgo, ha sido estimar ratios de cobertura que minimicen, únicamente, el riesgo de pérdidas (downside risk) del inversor, y no el riesgo o variabilidad tanto de las pérdidas corno de las ganancias, como mide el estadístico de la varianza. Este tipo de cobertura se realiza utilizando momentos parciales más bajos (Lower Partial Moments, de aquí en adelante LPM).

A continuación se exponen estas formas de implementar la cobertura con siderando medidas alternativas a la varianza como forma de medir el riesgo de la posición cubierta. En primer lugar se recoge la aproximación Coeficiente Media de Gini Extendido, para utilizar luego el concepto de LPM.

Riesgo medido utilizando el coeficiente de Gini-extendido

Cheung et al. (1990) proponen la aproximación de dominio estocástico a la cobertura con instrumentos derivados. Estos autores utilizan la diferencia media de Gini (Γ)⁸ como una medida del riesgo. La ventaja de esta medida de dispersión respecto a la varianza, es que no es necesario realizar ningún supuesto restrictivo sobre la función de distribución de! inversor. Estos autores utilizan, lo que denominan un análisis Media-Gini (MG), que tiene el atributo de ser consistente con las reglas de dominio estocástico.

Hodgson y Okunev (1992) Y Kolb y Okunev (1992), amplían el análisis inicial de Cheung et al. utilizando el coeficiente Media Gini Extendido (MGE) como medida de dispersión, lo que les permitirá ampliar el estudio considerando agentes con diferentes grados de aversión al riesgo.

Yitzhaki (1983) define el coeficiente MGE de acuerdo con la ecuación (4), donde: G(R) es la función de distribución del proyecto de inversión R y V es el parámetro que mide la aversión al riesgo.

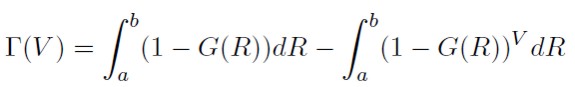[4]

El coeficiente MGE representa una familia de coeficientes de dispersión, donde las diferencias entre éstos se producen de acuerdo con diferentes va lores del parámetro V. Cuanto mayor es el valor de V más averso al riesgo es un inversor y mayor es la prima de riesgo exigida. Los inversores neutrales al riesgo se caracterizan por valores de V = 1, los aversos al riesgo por 1 < V < ∞, mientras que los inversores arriesgados se caracterizan por valores de V comprendidos entre 0 ≤ V ≤ 1. Es importante señalar que la aproximación MG es un caso particular de la MGE para V = 2.

Yitzhaki (1983) demuestra que para que un proyecto de inversión sea estocásticarnente superior (o domine estocásticamente) a otro, de acuerdo con las reglas de primer y segundo orden, es necesario que se cumplan las desigualdades 5 y 6, donde: µ_i y Γ_{i (v)}, son la media y la diferencia media de Gini extendida de los dos proyectos de inversión que se comparan.

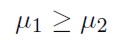[5]

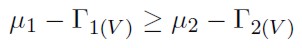[6]

Al combinar las anteriores expresiones Yitzhaki (1983), define el siguiente criterio de eficiencia: un proyecto de inversión es eficiente de acuerdo con la aproximación MGE sobre otro si se cumplen lass anteriores desigualdades, de esta forma se podrá asegurar que el primer proyecto domina estocásticamente al primer proyecto, conforme las reglas de segundo orden.

Es importante destacar que al utilizar la media y la diferencia media de Gini como los estadísticos que describen la función de distribución de los proyectos de inversión estudiados, no habrá necesidad de realizar ningún supuesto sobre la función de distribución de los rendimientos, como ocurre en el análisis media-varianza. Por otra parte, este tipo de análisis proporciona condiciones necesarias para que se produzca un dominio estocástico, con independencia de la función de distribución de probabilidad del rendimiento de los proyectos analizados.

Tal y como se puede apreciar en la Gráfica 1, algunos proyectos que son eficientes desde el punto de vista de la aproximación M - V, no lo son desde la aproximación de dominio estocástico.

El cálculo del coeficiente extendido de Gini se realiza como se indica en la expresión (7) (Shalit y Yitzhaki 1984), a partir de la covarianza (Cov) entre el rendimiento de la cartera cubierta (R_p) y el complemento de la función de distribución (C F D) elevado al valor del parámetro que mide la aversión al riesgo del inversor (V) menos uno ((1 - F(R_p))^{V -1}):

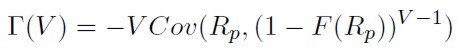[7]

Si se sustituye el valor del rendimiento de la cartera cubierta y se diferencia respecto al ratio de cobertura h_t-1, se obtendrá la expresión 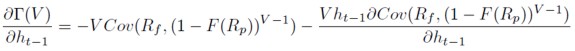(8):

[8]

Finalmente, igualando a cero y despejando el valor del ratio, se obtiene:

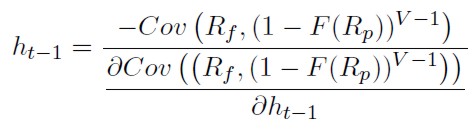[9]

El problema de esta última expresión, es que el denominador es difícil de calcular, por lo tanto para estimar el ratio de cobertura (h_t-1) se utiliza un proceso de iteración. Siguiendo los trabajos de Hodgson y Okunev (1992) y Kolb y Okunev (1992, 1993), este proceso comenzará dándole un valoral ratio de cobertura (X_f), con el cual se podrá estimar el rendimiento de la posición cubierta. Adicionalmente, ordenando los rendimientos de la cartera observados de menor a mayor, se podrá estimar el complemento de la función de distribución de éste (CFD)⁹ elevado a V -1, de acuerdo con la expresión 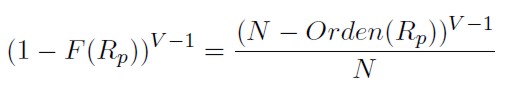(10):

[10]

Donde: N es el número de observaciones y (R_p) representa el orden de los rendimientos de la cartera cubierta organizados de menor a mayor.

Una vez calculados los valores de R_p y de CFD, se puede estimar el Coeficiente Extendido de Gini (Γ(V)), de acuerdo con la expresión (7). Este proceso se repetirá, para diferentes valores del X_f, hasta minimizar el valor de Γ(V).

Se destaca como demuestra Shalit (1995) que si la distribución conjunta de los rendimientos del contrato de futuro y del subyacente se comporta como una normal el ratio de cobertura que se obtendrá según esta aproximación coincidirá con el RCMV.

Riesgomedido utilizando el concepto demomentos parcialesmás bajos (Lower Partial Moments - LPM)

Tradicionalmente, en la mayor parte de la literatura financiera se mide el riesgo utilizando la varianza o la desviación típica, de forma que se consideran tanto las desviaciones de carácter negativo como las positivas de una variable aleatoria. No obstante, parece lógico pensar, que tanto los inversores individuales como los institucionales que acuden al mercado con la finalidad de realizar una cobertura, están más interesados en la posibilidad de reducir o cubrir sus posibles pérdidas y la variabilidad de éstas, que en las de sus posibles ganancias. Desde este punto de vista, lo que el inversor buscará será una disminución del riesgo, medido por la posibilidad de reducción de pérdidas o resultados negativos, más que de la varianza del rendimiento en donde se recogen ambos lados de la distribución. Esta aproximación cobra sentido bajo la evidencia que presentan los rendimientos de activos financieros, referente a la existencia de problemas de asimetría y de ausencia de un comportamiento según una distribución normal.

Bawa (1975, 1978), propone para medir el downside risk, lo que se conoce como momentos parciales mas bajos¹⁰ ya que sólo la parte a la izquierda de un valor objetivo de la distribución de una variable es utilizada para su cálculo. Consiste en ajustar la función de distribución por debajo de un umbral u objetivo determinado.

Sea R_pi el rendimiento de la cartera cubierta. El enésimo momento parcial de una variable aleatoria R_pi vendrá representado en la ecuación (11). Para el cálculo de la expresión anterior no se considerarán los valores que exceden a "c" y sólo se tendrán en cuenta los que se sitúan por debajo.

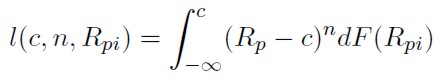[11]

Donde F (R_p ) representa la función de distribución de R_p° y "c" el rendimiento objetivo. Las principales propiedades de esta medida son:

1. Para unos valores dados de "c” y "n” los LPM están completamente determinados por la función de distribución, lo que significa que si R_p1 y R_p2 tienen la misma distribución, se cumplirá:

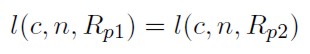[12]

2. LPM incrementa al aumentar c. Dados c₁ > c₂,

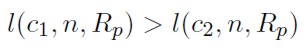[13]

3. Si la distribución de R_pi es simétrica en "c” y n = 2, el LPM corresponderá al estadístico de semivarianza, valor propuesto por Markowitz como medida de riesgo alternativa a la varianza:

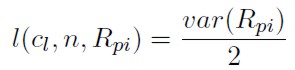[14]

Analizadas las propiedades de este tipo de momentos, el siguiente paso será determinar el ratio de cobertura que minimiza el LPM de orden enésimo (la expresión de este momento se recoge en 15) y no la varianza del rendimiento de la cartera cubierta:

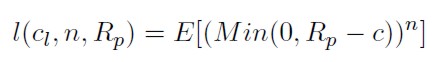[15]

Donde E(*) representa el operador esperanza. La derivada de la ecuación anterior no proporciona una solución analítica del ratio de cobertura, por lo que su estimación deberá realizarse utilizando algún método o aproximación numérica. A continuación y siguiendo el trabajo de Eftekhari (1998), se especifica un método numérico para la estimación del ratio de cobertura que minimiza la expresión anterior, para el caso particular de momentos de segundo orden (n = 2). En primer lugar, se determinará el rendimiento de la cartera cubierta (R_c,t = R_s,t-h * R_f,t) para un valor inicial pequeño del ratio de cobertura (por ejemplo, h = -1,5) para cada periodo de la muestra utilizada; en la cual el subíndice "t” representa el valor de cada variable en cada periodo.

Obtenido el rendimiento de la cartera para cada periodo estudiado, el valor del LPM de orden 2 se calcula de acuerdo con la expresión 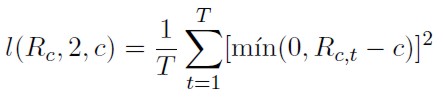(16).

[16]

Finalmente, se estimará nuevamente la expresión anterior sumando una cantidad adicional (por ejemplo 0, 001) al valor del ratio de cobertura utilizado inicialmente. Este proceso se repetirá hasta alcanzar un valor del ratio de cobertura lo suficientemente elevado (por ejemplo h = 1,5). El valor del ratio de cobertura buscado será el que proporcione un valor más pequeño de la expresión anterior.

Lien y Tse (1998) demuestran que el ratio obtenido utilizando esta medida de riesgo será el mismo del RCMV si la distribución conjunta de los rendimientos de contado y futuro sigue una normal.

MAXIMIZAR FUNCIÓN OBJETIVO

En este apartado se analiza la aproximación a la cobertura, basada en la teoría de selección de carteras, en la cual el objetivo que se persigue es maximizar la función de utilidad, o en su caso una función objetivo en la que se considera conjuntamente el efecto de la cobertura sobre el rendimiento y riesgo de la cartera cubierta.

En primer lugar se diferenciarán dos conceptos, el RCMV y ratio de cobertura óptimo, que a menudo son utilizados indistintamente con el mismo significado. En segundo lugar, se determinan las condiciones que deben cumplirse para que la expresión del RCMV coincida con la que maximiza la función de utilidad esperada de un agente.

RCMV y ratio de cobertura óptimo

Aunque en muchos trabajos los conceptos de RCMV y ratio de cobertura óptimo son utilizados de forma indistinta, es importante diferenciar el significado de ambos conceptos para evitar posibles confusiones.

Ratio de cobertura óptimo podría definirse como el número de contratos de futuro que deberá mantener un inversor para maximizar una determinada función objetivo, mientras que RCMV es el número de contratos de futuros que minimiza el riesgo (medido por la varianza) del rendimiento de la posición cubierta. Tradicionalmente, en la mayoría de trabajos esta función objetivo corresponde a una determinada especificación de la función de utilidad esperada. Por otra parte, Howard y D´Antonio (1984) consideran como función objetivo el cociente entre el exceso de rendimiento de la cartera cubierta con respecto a un activo libre de riesgo y la desviación estándar del rendimiento de esta misma cartera (índice de Sharpe).

El hecho sobre el que se trata de llamar la atención, es que aunque a priori existen diferencias entre ambos conceptos, si se acepta que el mercado de futuros es eficiente, la expresión que determina el RCMV y la de ratio de cobertura que maximiza la función de utilidad esperada del inversor, coincidirán. Este aspecto es analizado con mayor detenimiento en el siguiente sub-apartado. Esto es importante porque permite determinar una expresión del ratio de cobertura que será independiente de las preferencias individuales del inversor.

Aspectos que provocan que RCMV y el ratio de cobertura óptimo coincidan

En este apartado se considerará, que el objetivo que se intenta alcanzar con la cobertura es maximizar la utilidad esperada del valor final de la riqueza del agente (W_t). Bajo esta consideración, los trabajos de Beninga et al. (1983, 1984), Heaney y Poitras (1991) y Lence (1995), especifican los supuestos bajo los que el ratio de cobertura óptimo es independiente de la forma de la función de utilidad del agente averso al riesgo. Estas condiciones son las que determinan que el RCMV se corresponda con el ratio óptimo (el que maximiza una función de utilidad esperada específica), y las que se han utilizado para justificar la utilización de la aproximación de mínima-varianza para determinar el ratio de cobertura.

Beninga et al. (1983, 1984), demuestran analíticamente cuáles son las condiciones suficientes que deben cumplirse para que el RCMV sea también un ratio de cobertura óptimo e independiente de la función de utilidad de un agente. Las resume como:

1. Insesgadez del precio del contrato de futuros o lo que igual, que el precio del contrato de futuros siga un martingala.

2. Correlación nula entre el precio de futuros (F_t) y el término de perturbación de error (e_t) del modelo de regresión:¹¹

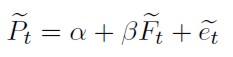[17]

Heaney y Poitras (1991), asumiendo normalidad en la distribución conjunta de los precios contado y futuro, determinan el ratio de cobertura óptimo considerando dos supuestos. En primer lugar, que no existe posibilidad de prestar ni pedir prestado a un tipo libre de riesgo; en segundo lugar relajando la anterior esta posibilidad, lo que se acerca a un escenario más realista. De esta forma, comparan las expresiones analíticas obtenidas con la propuesta por Ederington (Cov(R_s,t,R_f,t) / var(R_f,t)).

Las conclusiones del trabajo de Heaney y Poitras son:

• Bajo la consideración del primer supuesto, el ratio de cobertura óptimo estará constituido por dos componentes, uno que corresponderá a la expresión del RCMV propuesta por Ederington¹², sumado a un término adicional que dependerá de características estadísticas de las series (rendimiento y varianza del rendimiento del contrato de futuros) y de la función de utilidad que se considere del inversor (propensión al riesgo).
• Si se relaja el supuesto de no poder pedir y/o prestar a un tipo libre de riesgo, el ratio de cobertura óptimo sólo depende de parámetros de la función de distribución conjunta¹³. Los autores destacan, como indican Beninga et al. (1982, 1983) e independientemente del supuesto considerado, que si el precio del contrato de futuros sigue una martingala, el ratio de cobertura óptimo corresponderá al RCMV.

A continuación se recogen las expresiones que se obtienen bajo ambos supuestos.

Posición de contado fija (no es posible prestar ni pedir prestado)

Se asume un mundo de dos periodos en el que una parte de la riqueza inicial (W_t-1) de un inversor se encuentra invertida en un activo con riesgo y que existe un mercado de futuros sobre ese mismo activo que el inversor utiliza para cubrirse. Se considera que no existen costes de transacción y la toma de posiciones en el mercado de futuros no supone ningún desembolso adicional. El problema al que se enfrenta el inversor es maximizar en "t” el valor de su cartera:

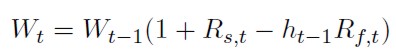[18]

Donde W_t y W_t-1 son el valor de la cartera en t y t - 1, respectivamente; h_t-1 representa el cociente entre el valor invertido en futuros sobre el total de riqueza inicial; y R_s,t y R_f,t son respectivamente, el rendimiento obtenido al contado y futuro.

Dada esta restricción, el problema de optimización al que se enfrenta el inversor puede ser generalizado a cualquier función de utilidad definida:

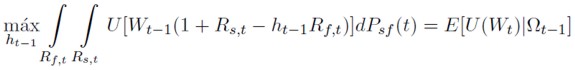[19]

Siendo Ω_t-1 es el conjunto de información disponible en t - 1.

La condición de primer orden vendrá dada por:

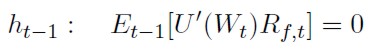[20]

Donde E_t-1 representa el operador esperanza condicionado al conjunto de información disponible en t - 1(Ω_t-1).

Considerando que U´(W_t ) y el rendimiento esperado del contrato de futuros (R_f,t) son variables aleatorias, y la definición de covarianza¹⁴, la ecuación (20) podrá expresarse como:

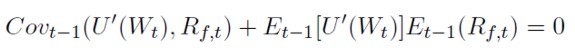[21]

Bajo la hipótesis de que la función de distribución conjunta de R_s,t y R_f,t es normal condicionada al conjunto de información disponible en t-1(Ω_t-1), es posible aplicar el Lema de Rubinstein¹⁵(1976). La aplicación de este Lema, junto con la consideración de las restricciones presupuestarias, permite llegar hasta 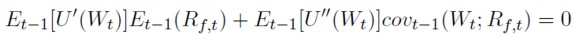(22):

[22]

Sustituyendo W_t por su expresión recogida en (18), se obtiene:

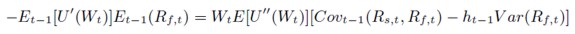[23]

Despejando h_t-1, se llega a la expresión 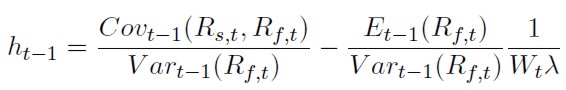(24):

[24]

Donde: λ = U"(W_t) / U´(W_t) es el coeficiente de aversión al riesgo de Pratt-Arrow.

Se aprecia que el ratio de cobertura óptimo, depende de las preferencias del inversor modeladas a través de su función de utilidad. Sin embargo, bajo el supuesto que el rendimiento esperado condicionado al conjunto de información del contrato de futuros es cero (E_t(R_f ) = 0), o lo que es igual, el precio del futuro sigue una martingala (E_t-1(F_t) = F_t-1), las expresiones del ratio de cobertura óptimo y del RCMV coincidirán, pudiéndose expresar de acuerdo con 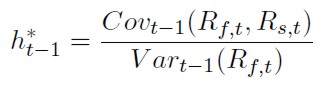(25):

[25]

Posibilidad de prestar y/o pedir prestado

Se asumirá un mundo de dos periodos en el que una parte de la riqueza inicial (W_t-1) de un inversor se encuentra invertida en un activo con riesgo y que existe un mercado de futuros sobre ese mismo activo que el inversor utiliza para cubrirse. Se considerará que no existen costes de transacción y la toma de posiciones en el mercado de futuros no supone ningún desembolso adicional. En este caso, existe la posibilidad de prestar y/o pedir prestado a una tasa libre de riesgo, lo que provoca que la posición de contado sea un aspecto más que debe determinarse en el proceso de maximización. El problema al que se enfrenta el inversor es maximizar en t el valor de su cartera:

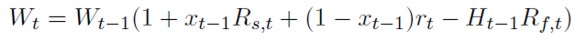[26]

Donde: W_t y W_t-1 son el valor de la cartera en t y t - 1, respectivamente; x_t-1 es la parte de la riqueza invertida en el activo con riesgo; H_t-1 representa el cociente entre el valor invertido en futuros sobre el total de riqueza inicial; r_t es el tipo de interés libre de riesgo; y R_s,t y R_f,t son respectivamente, el rendimiento obtenido al contado y futuro.

Dada esta restricción, el problema de optimización al que se enfrenta el inversor puede ser generalizado a cualquier función de utilidad definida como:

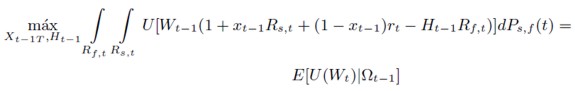[27]

Donde, Ω_t-1 es el conjunto de información disponible en t - 1.

Las condiciones de primer orden vendrán dadas por (28) y (29):

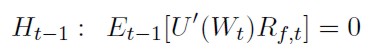[28]

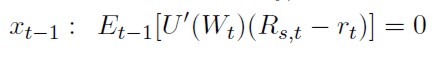[29]

Considerando que U´(W_t), el rendimiento esperado del contrato de futuros (R_f,t) y el exceso de rendimiento de contado sobre el tipo de interés sin riesgo (E(R_s,t - r_t)) son variables aleatorias, así como la definición de covarianza, se podrán expresar las condiciones de primer orden como (30) y (31):

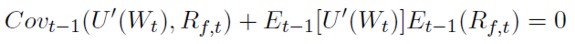[30]

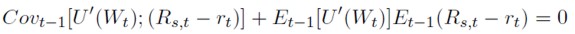[31]

Bajo la hipótesis de que la función de distribución conjunta de R_s,t y R_f,t es normal condicionada al conjunto de información disponible en "t - 1” (Ω_t-1), es posible aplicar el Lema de Rubinstein (1976). La aplicación de este Lema, junto con la consideración de las restricciones presupuestarias, conduce a las siguientes expresiones:

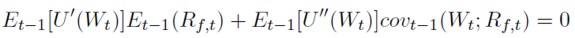[32]

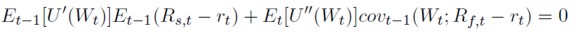[33]

Expresando las ecuaciones matricialmente y resolviendo se obtiene:

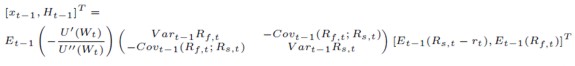[34]

Si el ratio de cobertura óptimo (h*_t-1) se define como el cociente entre H_t-1 y x_t-1, se obtiene la expresión

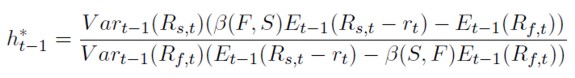[35]

Donde

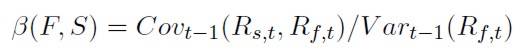
y

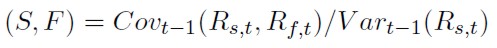
Se aprecia que el ratio de cobertura óptimo, bajo el supuesto que se puede prestar y pedir prestado a un tipo de interés libre de riesgo, es independiente de como sea haya modelado la función de utilidad y de W_t. Adicionalmente, si se supone que el rendimiento esperado condicionado al conjunto de información del contrato de futuros es cero (E_t(R_f ) = 0) o que el precio del futuro sigue una martingala (E_t(F_t+1) = F_t), las expresiones del ratio de cobertura óptimo y del RCMV coincidirán. El ratio de cobertura óptimo vendrá representado por la expresión:

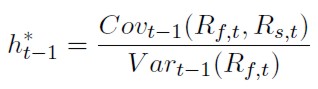[36]

A modo de conclusión, se quiere reseñar que independientemente de los dos supuestos anteriormente considerados, bajo la hipótesis que el mercado de futuros es eficiente, el RCMV es también el que maximiza la función de utilidad esperada del inversor con independencia de la expresión que se utilice para modelar las preferencias de éste. Este aspecto, junto al hecho de que la aproximación de mínima varianza haya sido, sin lugar a dudas, la más utilizada en estudios de carácter empírico sobre cobertura, ha motivado a recoger en el siguiente apartado, tratando de guardar un orden cronológico, los métodos de estimación más utilizados para estimar el RCMV.

MÉTODOS DE ESTIMACIÓN RCMV

El método que tradicionalmente se ha utilizado para estimar el RCMV, debido básicamente a su simplicidad de cálculo, es el propuesto por Ederington (1979), el cual consiste en estimar la pendiente de una recta de regresión por Mínimos Cuadrados Ordinarios (MCO). El RCMV concuerda con la pendiente de la recta de regresión entre la diferencia de precios al contado respecto a la del futuro que se utiliza como cobertura (cov(R_s,t ,R_f,t)/ var(R_f,t)).

No obstante, este método de cálculo del RCMV no ha estado exento de controversia (Miffre, 2004; Harris y Shen, 2003). En las líneas que siguen se realiza un análisis, de marcado carácter teórico, de las controversias y diferentes métodos que se han propuesto para llevar a cabo la estimación del RCMV. En primer lugar, se recogerá la controversia existente hacia mediados de los años ochenta referente a que tipo de variables utilizar (niveles, diferencias o rendimientos). A finales de esta década surgen trabajos en los que se propone utilizar la metodología desarrollada por Box-Jenkins para solucionar los problemas de autocorrelación que se obtienen con MCO. A principios de los noventa, se considera la existencia de relaciones de cointegración entre las series de contado y futuro con objeto de recoger los desequilibrios de la senda de largo plazo e integrar las relaciones de equilibrio a largo plazo y la dinámica de corto plazo. Con esta finalidad se incorpora en el modelo de regresión el Término de Corrección de Error (TCE). Finalmente, se cierra este apartado analizando los modelos de heterocedasticidad condicional autorregresiva (ARCH y GARCH), los cuales posibilitan considerar momentos de segundo orden condicionales no constantes y superar las limitaciones que supone tomar en cuenta funciones de distribución constantes en el tiempo.

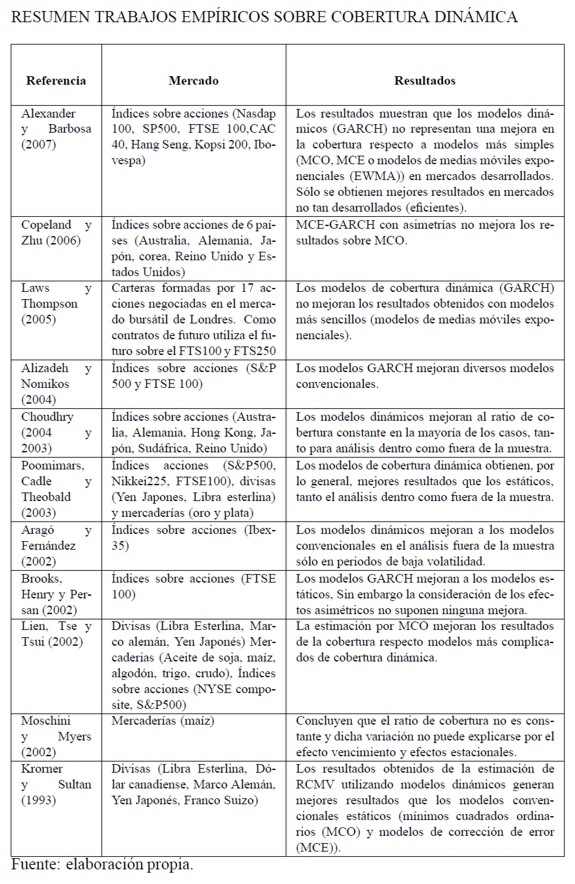
En el Anexo 1¹⁶ se presenta una tabla resumen de distintos trabajos de carácter empírico en la cual se compara, básicamente, si los modelos dinámicos suponen una mejora con respecto a los modelos estáticos. El análisis de las diferencias obtenidas con los modelos dinámicos es interesante y no está exenta de controversia como se podrá comprobar en el anexo. Se debe tener en mente que los modelos dinámicos supondrán la consideración de modelos de estimación mucho más complejos que los estáticos, por lo que es interesante preguntarse si dicho esfuerzo tiene una recompensa en términos de un aumento en la efectividad.

Puede darse el caso, como así se manifiesta en alguno de los trabajos recogidos, que los modelos GARCH permitan una mejor modelización de las series temporales de contado y futuro consideradas, pero también puede ocurrir que las mejoras obtenidas en la cobertura sean simplemente marginales o incluso que no se produzcan, más si se tienen en cuenta los costes de transacción en los que se incurre en una estrategia dinámica al de tener que ajustar el ratio de cobertura frente a la llegada de información al mercado. Dicho de otra forma, puede que la cobertura dinámica no sea efectiva desde un punto de vista económico.

Mínimos Cuadrados Ordinarios: variables en rendimientos versus diferencias

A raíz del trabajo de Brown (1985), surge a nivel teórico una fuerte controversia¹⁷ con respecto a qué tipo de variables utilizar para estimar el valor del RCMV por MCO. No se pone en tela de juicio el método de estimación, sino las implicaciones y diferencias que pueden existir en la utilización de las variables expresadas en niveles, diferencias o rendimientos.

Witt et al. (1987) analizan las diferencias que la utilización de variables en niveles, diferencias y rendimientos producen sobre el RCMV, no obteniendo evidencia que demuestre una mejora en la efectividad de la cobertura significativa en ningún caso. Destacan que la utilización de una u otra dependerá del tipo de cobertura que se realice. Muy relacionado con este tipo de análisis está el trabajo de Myers y Thompson (1989), quienes al igual que Witt et al. (1987) consideran que dependiendo de los objetivos que se buscan con la cobertura se deberá utilizar una regla de cobertura diferente. Sin embargo, discrepan en que esos objetivos no son el aspecto que determina cómo deben ser estimados los parámetros de la regla seguida. Estos autores argumentan que la estimación por MCO sólo es adecuada bajo ciertas hipótesis muy restrictivas sobre el modelo de equilibrio de precios de contado y futuro. Proponen incorporar en el modelo de regresión todo el conjunto de información disponible hasta ese momento. Esto lo hacen incluyendo, adicionalmente a los precios de futuro como variable explicativa de los precios de contado, un vector en el cual se incorporen un conjunto de variables que puedan ser importantes en la obtención de la estimación del ratio de cobertura¹⁸.

Metodología Box-Jenkins: modelos arima

Es común en la mayoría de trabajos¹⁹ que utilizan la regresión por MCO para estimar el RCMV, encontrar problemas de autocorrelación en la serie de residuos estimados. Si se da esta situación, los parámetros estimados serán insesgados y consistentes, pero ineficientes. Adicionalmente, también se obtendrán infraestimaciones de sus errores estándar, lo que afectará a los contrastes que se realicen sobre ellos e invalidará los métodos de inferencia.

Para solucionar este aspecto Herbst et al. (1989, (1992) sugieren utilizar la metodología propuesta por Box-Jenkins, consistente en tres etapas. En la primera se busca la correcta especificación de la serie temporal de datos que se estudia. En la segunda, se estima el modelo propuesto y en la tercera se analiza si el modelo utilizado se ajusta adecuadamente a los datos, de forma que si no lo hace, se repite el proceso desde la primera etapa hasta encontrar un modelo adecuado. Siguiendo esta metodología, se intenta determinar el modelo auto-regresivo integrado de medias móviles (ARIMA(p, d, q)) que más se ajusta a la serie temporal de datos disponible.

El modelo matemático utilizado en los anteriores trabajos es:

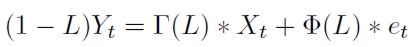[37]

Donde: L es el operador de retados; Γ(L) una función de transferencia; Φ(L) estructura del término de error (e_t).

Las estimaciones obtenidas de esta forma, permiten obtener parámetros más eficientes. Sin embargo, la pendiente de la recta de regresión no corresponderá en este caso al cociente entre las covarianzas de ambos rendimientos y la varianza.

Relaciones de cointegración: término de corrección de error

Son muchos los trabajos en los que se evidencia la existencia de relaciones de cointegración entre las series de precios del mercado de contado y futuro, tanto para mercados financieros como para mercaderías²⁰, lo que se traducirá en la existencia de una tendencia estocástica común. La existencia de relaciones de cointregación es una característica que ha sido incluida en la especificación del modelo econométrico utilizado para estimar el RCMV.

Ghosh (1993) propone la utilización de la teoría de la cointegración introducida por Granger (1981) y desarrollada por Engle y Granger (1987), ya que de esta forma se podrán integrar las relaciones de equilibrio a largo plazo y la dinámica de corto plazo. Según el autor la no consideración de estas relaciones dará lugar a infraestimaciones del RCMV debido a una mala especificación del modelo de regresión utilizado.

Bajo el supuesto de que los precios del mercado de contado y futuro están cointegrados y que el vector de cointegración toma el valor (1,-1), la desviación con respecto al equilibrio de largo plazo recogida en el término de corrección de error, corresponderá al valor de la base (B_t = S_t - F_t). Normalmente, en trabajos de carácter empírico se acepta la existencia de relaciones de cointegración entre contado y futuro para contratos de futuro cercanos a vencimiento²¹.

De esta forma, los desequilibrios a largo plazo pueden considerarse como una medida del valor de la base para un determinado período. Trabajos como los de Viswanath (1993), Lence et al. (1996), Park y Switzer (1995a, 1995b) y Lien y Luo (1994) incluyen la base como variable explicativa en el modelo econométrico de regresión y obtienen resultados superiores en relación con modelos en los cuales ésta no es incluida.

Lien (1996) expone de forma analítica los resultados obtenidos de forma empírica por Ghosh (infraestimación del RCMV al no considerar las relaciones de cointegración). Concluye que cuanto mayor es la respuesta de las series frente a los desequilibrios de largo plazo, menor será la efectividad alcanzada con el modelo que no considera las relaciones de cointegración con respecto al que lo hace.

A continuación se recoge el modelo propuesto por este autor bajo la hipótesis de que las perturbaciones de los mercados son homocedásticas²². La evolución dinámica de los rendimientos de ambos mercados se representa a través del siguiente modelo de corrección de error²³:

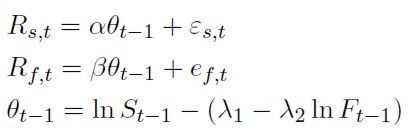[38]

Donde: R_s,t y R_f,t son los rendimientos del activo de contado y futuro, respectivamente, calculados como la diferencia de primer orden de los logaritmos neperianos de dos precios consecutivos; θ_t-1 son las desviaciones con respecto a la senda de equilibrio a largo plazo, y S_t y F_t son los precios de contado y futuro.

La expresión del ratio de cobertura de mínima varianza, viene representado por el cociente entre la covarianza condicional de los rendimientos contadofuturo en relación con la varianza condicional del rendimiento del futuro.

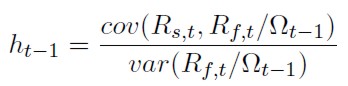[39]

Se suponen dos tipos de agentes con diferentes conjuntos de información. Uno que considerará la dinámica del sistema de acuerdo con las expresiones anteriores (incorpora los desequilibrios de largo plazo) y otro que no tendrá en cuenta este aspecto (llamado inversor "miope”). En concreto:

Sean Ω_t y Ω*_t los conjuntos de información del agente informado y miope en "t”, respectivamente.

Para el caso del agente miope las expresiones que se obtienen para la cov(R_s,t ,R_f,t) y var(R_f,t) condicionados a su conjunto de información ( Ω*_{t- 1} ) se recogen en la siguiente expresión:

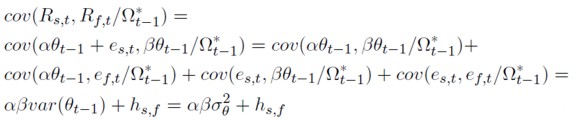[40]

Donde: h_s,f recoge la covarianza del rendimiento (no esperado) entre contado y futuro; h_i es la varianza de la variable "i” ∀i = s, f; y σ²_θ es la varianza del TCE.

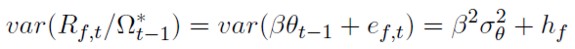[41]

Sustituyendo en la expresión del RCMV se obtendrá:

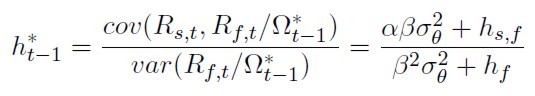[42]

Por otra parte, la expresión del RCMV del agente que considera un modelo correctamente especificado y que incorpora dentro de su conjunto de información θ_t-1, será:

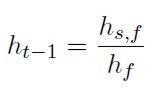[43]

La expresión (44) recoge el valor de la diferencia entre el ratio de cobertura del agente miope y el informado.

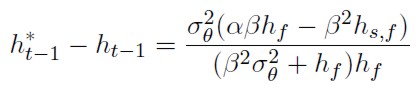[44]

Si realmente las series están cointegradas, la reacción de ambos mercados frente a desequilibrios a largo plazo será de sentido contrario, aspecto que provocará que bien α o β (parámetros asociados al TCE), tome valores negativos. Este aspecto, determina que siempre el resultado de la expresión anterior sea menor que cero, poniendo de manifiesto que no considerar las relaciones de cointegración entre ambas series de precio, conducirá a la realización de coberturas no óptimas, ya que la posición que se adoptará en el mercado de futuros será inferior a la derivada del modelo de regresión correctamente especificado.

Modelos con corrección de error GARCH Bivariantes

El objetivo que se perseguía en todos los métodos propuestos con anterioridad, era especificar correctamente el modelo de regresión con el cual poder obtener estimaciones eficientes de los parámetros. Sin embargo, otra forma alternativa para determinar el RCMV es a partir de la estimación de los momentos de segundo orden de la función de distribución conjunta de los precios de contado y futuro. Anteriormente se consideraba que la función de distribución de ambas series de precio era constante y por lo tanto también el RCMV. No obstante, diversos trabajos empíricos realizados con series temporales de carácter financiero, coinciden en señalar la existencia de problemas de heterocedasticidad, lo que provocará que la función de distribución condicional difiera de la incondicional y deje de tener sentido estimar RCMV constantes²⁴. Con objeto de estimar momentos de segundo orden no constantes que varíen ante la llegada de información al mercado, se han utilizado modelos de Heterocedasticidad Condicional Autoregresiva Generalizados (GARCH). Estos modelos permiten ajustar la dinámica de la matriz de covarianzas, y adicionalmente, recoger dos evidencias que se producen en los precios de activos financieros: leptocurtosis de la función de distribución no condicionada y agrupamiento de la volatilidad derivado de una dependencia de las varianzas condicionales.

Se plantea de esta forma coberturas dinámicas, en las que la matriz de covarianzas se ajusta a la llegada de nueva información y, por lo tanto, la posición a tomar en el mercado de futuros. La expresión del RCMV coincidirá con la tradicional, a excepción que ahora se utilizan momentos de segundo orden condicionales. Es básicamente a partir de la década de los noventa cuando los modelos de volatilidad condicional²⁵ son utilizados para especificar un RCMV condicionado al conjunto de información disponible por el inversor.

Una expresión general de los momentos condicionales de primer y segundo orden podría ser la recogida en la expresión:

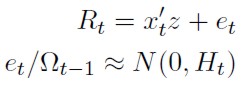[45]

Donde: R_t = (R_s,t ,R_f,t)´ representa un vector (2 × 1) formado por los rendimientos de contado y futuro; xt´ representa la matriz (2 × k) de variables exógenas en el que se puede incluir, además de otras, el término de corrección de error –y por tanto considerar la existencia de relaciones de cointegración–; z la matriz de parámetros (k × 2) y Ω_t-1 conjunto de información disponible en "t-1”. En este caso se ha supuesto que las perturbaciones se distribuyen como una normal, aunque podría establecerse cualquier otro tipo de distribución (por ejemplo t-Student).

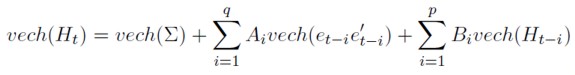[46]

Esta es la llamada representación vectorial de un modelo GARCH multivariante. Uno de los principales problemas²⁶ que presenta esta especificación, es el número de parámetros a estimar. Para el caso general, su número será igual al producto (n(n + 1)/2) * (1 + (n(n + 1)/2) * (p + q). Aún considerando el caso de dos variables (n = 2) y GARCH(p = 1, q = 1), el número sigue siendo muy elevado, concretamente igual a 21. A continuación, se recoge la expresión de la matriz de covarianzas para este último caso.

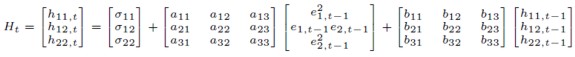[47]

Con el fin de solventar estos problemas han surgido especificaciones en las que se reduce el número de parámetros a estimar. En concreto, las más utilizadas para el caso que nos ocupa han sido: diagonal (Bollerslev, Engle y Wooldridge 1988), correlación constante entre los rendimientos contadofuturo (Bollerslev 1990) y BEKK (Baba, Engle, Kraft y Kroner 1990). Adicionalmente, en la modelización de las varianzas condicionales puede considerarse el llamado efecto "apalancamiento” (Black 1976 y Christie 1982), con objeto de recoger y modelar la asimétrica respuesta de la volatilidad frente a innovaciones positivas en la rentabilidad (buenas noticias) o negativas (malas noticias). Existen diversos modelos que mejoran las limitaciones del modelo original (GARCH) e incorporan este efecto asimétrico al modelar las varianzas condicionales; una completa relación de éstos, se encuentra en los trabajos de Engle y Ng (1993) y Hentschel (1995).

Un ejercicio interesante puede ser la extensión del modelo de Lien (1996) considerando que los mercados de contado y futuro presentan perturbaciones heterocedásticas. Este aspecto permitirá analizar cómo afecta la variación de la volatilidad a la diferencia de RCMV estimada con el modelo de regresión correcta e incorrectamente especificado.

Esto puede ser analizado sustituyendo en la expresión obtenida de la diferencia de ratios de cobertura los momentos incondicionales de segundo orden por momentos condicionales²⁷. Posteriormente, se han calculado las siguientes diferenciales:

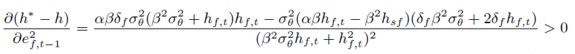[48]

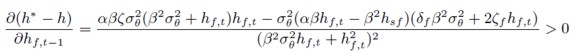[49]

El desarrollo de ambas expresiones permite observar que son mayores que cero, lo que implica que cuanto mayor sea la volatilidad del mercado de futuros, menor será el error cometido al no considerar el término de corrección de error si se compara con el modelo que si lo incorpora.

CONCLUSIONES

En este trabajo se han recogido distintas teorías sobre la cobertura con contratos de futuro y diversos métodos de estimación del ratio de cobertura óptimo. Debido a que la aproximación más utilizada es la de teoría de carteras e incluye como casos particulares a diversas de las teorías analizadas, se ha prestado especial atención a dicha aproximación como forma de determinar la posición a tomar en el mercado de futuros.

Dentro de esta teoría se ha considerado que el coberturista puede buscar, básicamente, dos objetivos: en primer lugar minimizar el riesgo de la posición cubierta, utilizando diferentes expresiones para medirlo; y por otra parte, la maximización de una función objetivo que depende tanto del riesgo como del rendimiento de la posición cubierta.

También se han recogido y analizado los métodos que tradicionalmente se han utilizado para estimar el RCMV, debido a que es sin duda la aproximación a la cobertura más utilizada en trabajos empíricos para diferentes mercados de futuro. Así mismo, se ha hecho hincapié en las condiciones que deben cumplirse para que este último maximice la función de utilidad del inversor; dicho de otra manera, que coincida con el ratio de cobertura óptimo.

Es importante enunciar un concepto que es básico y al que no se le ha prestado la respectiva atención. El RCMV se define como: cov(R_s,t ,R_f,t)/ var(R_f,t). Este cociente corresponde a la pendiente de la recta de regresión entre los precios de contado y de futuro en caso de que se utilicen MCO. Muchas de las críticas que se ha realizado a la estimación del RCMV por MCO señalan que los residuos obtenidos de esta forma, no tienen buenas propiedades estadísticas (autocorrelación, heteroscedasticidad, no estacionariedad, etcétera), lo que generará estimaciones ineficientes del parámetro de la pendiente de la recta de regresión (Johnston 1989).

Para mejorar la eficiencia de las estimaciones se han propuesto diferentes métodos; sin embargo, la utilización de éstos conduce a que la pendiente de la recta de regresión ya no corresponda a la formula del RCMV como ocurre en el caso de MCO (Sutcliffe 1997). Por ello, se propone la utilización de modelos GARCH Bivariantes en los que se considera la existencia de relaciones de cointegración. Este tipo de modelos además de incluir a los anteriores, bajo ciertas restricciones como casos particulares, no pierde de vista que el objetivo es determinar el cociente entre la covarianza y varianza. Adicionalmente, permite modelar la matriz de covarianzas condicionada al conjunto de información disponible, lo que permite obtener estimaciones no constantes del RCMV que varían ante la llegada de nueva información al mercado. Sin embargo, no se debe dejar de considerar el resultado obtenido en diversos trabajos de carácter empírico y que el esfuerzo que requiere la estimación de estos modelos dinámicos suponga una mejora, en la efectividad de la cobertura.

NOTAS AL PIE

1 El estudio de coberturas selectivas lo realiza para el mercado de trigo en U.S.A.

2 Por otra parte, la existencia de arbitraje provocará que la base se mantenga dentro de unas bandas. Siempre que éstas se sobrepasen la actuación conjunta de arbitrajistas provocará que disminuyan.

3 Levy y Markowitzs (1979) determinan las condiciones para que los resultados que se obtengan al maximizar una función que dependa positivamente del rendimiento, y negativamente de un parámetro que mida la aversión al riesgo del inversor y de la varianza (tomada como medida de riesgo). sean parecidos a los que se obtendrían al maximizar la verdadera función de utilidad del inversor. Este hecho, determina que en muchos tra bajos sobre cobertura se hable de funciones objetivo, en las que se considera el binomio rentabilidad-riesgo y no la función de utilidad (Heifner 1972, Peck 1975, Anderson y Dunthine 1980, 1981. Howard y D'Antonio 1984, 1987. Chang y Shanker 1986).

4 En términos anglosajones a la primera se la llama "downside risk" y la segunda "upside risk"

5 La letra cursiva es una traducción del artículo de Jonhson (1960)

6 La misma expresión del RCMV se hubiese obtenido si se hubiese fijado como objetivo minimizar la varianza del valor final de la riqueza (Wt) del inversor:

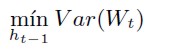
siendo

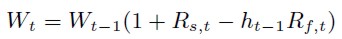
7 En el siguiente sub-apartado se recoge la aproximación a la cobertura en la que se tienen en cuenta sus efectos sobre ambos conceptos.

8 La diferencia media de Gini (Γ) es un estadístico que se utiliza como medida de la dispersión de una variable aleatoria y fue introducido por Yitzhaki (1982, 1983) en el campo de los estudios financieros.

9 Para una crítica al método de estimación de la función de distribución ver Lien y Luo (1993 b).

10 Esta expresión es la traducción del término Lower Partial Moments (LPM).

11 Por su parte Lence (1995), muestra teóricamente que la correlación nula es necesaria, pero no suficiente; mientras que la independencia es suficiente, pero no necesaria para obtener ratios de cobertura independientes de la función de utilidad del agente inversor. Para obtener ratios de cobertura independientes de las preferencias del inversor, deberá cumplirse que: exista una relación lineal entre los precios de contado y futuro como la recogida en la anterior expresión y que el precio de futuros (F_T ) sea condicionalmente independiente de e_t. Una variable (y) es condicionalmente independiente de otra (x) sii cov(y, f(x)) = 0 para toda función f(·).

12 Anderson y Danthine (1981) lo llaman componente de cobertura pura y al otro término especulativo puro.

13 Al mismo resultado llega Myers (1991).

14 Dadas dos variables aleatorias "x” e "y”, se cumplirá que: Cov(x, y) = E(xy) - E(y)E(x).

15 Si dos variables aleatorias "x” e "y” se distribuyen como una normal, y sea g(·) una función diferenciable, se tendrá que: Cov(g(x), y) = E(g"(x))cov(x, y).

16 Se agradecen los comentarios de uno de los evaluadores, quien destacaba la idoneidad de presentar esta tabla.

17 Ejemplos de trabajos donde se plantea esta problemática son los de Brown (1985, 1986), Khal (1986), Witt et al. (1987), Hill y Schneeweis (1981), Bond et al. (1987), Myers y Thompson (1989).

18 El modelo de estimación que proponen se recoge en al siguiente ecuación:

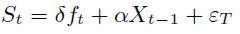
Donde: δ es el parámetro que determinará el RCMV; ε es la perturbación y X_t-1 representa un vector donde deben incluirse las variables que recojan el conjunto de información relevante para la estimación del RCMV por parte del inversor. Adicionalmente, si existe evidencia que ambas series presentan una raíz unitaria, la anterior ecuación deberá ser expresada en primeras diferencias.

19 Hill y Schneeweis (1981), Brown (1985), Herbst et al. (1989, 1992), entre otros.

20 Véase: Lai y Lai (1991), Fonterbery y Zapata (1993), Crowder y Hamed (1993) para mercaderías, y Wahab y Lashagari (1993), Ghosh (1993), Ghosh y Gilmore (1997), Pizzi, Economopoulos y O´Neill (1998) para activos financieros.

21 Evidencia en contra de este resultado se encuentra, por ejemplo en: Baillie y Myers (1991) y Schroder y Goodwin (1991).

22 En el siguiente apartado esta hipótesis se relaja y se considera la existencia de problemas de heterocedasticidad.

23 El análisis podría haberse realizado incluyendo un vector de variables explicativas para cada mercado sin que esto afectase a las conclusiones finales. No obstante, y con objeto de facilitar la exposición no se considerará este aspecto.

24 Otra forma de estimar ratios de cobertura no constante se ha realizado utilizando modelos de coeficientes de regresión no constante. Este método es utilizado por Garmmatikos y Saunders (1983) para recoger la posibilidad que la pendiente de la recta de regresión por MCO que determina el valor del RCMV no sea constante. Tal como señalan estos autores imponer a priori la constancia del coeficiente de regresión, cuando en realidad éste no lo es, provocará sesgos en la estimación del ratio de cobertura óptimo y por lo tanto en la efectividad de la cobertura.

25 Un resumen detallado de diferentes modelos de volatilidad condicional se encuentra en, por ejemplo: Bollerslev et al. (1992), Bera y Higgins (1993), Bollerslev et al. (1994) o Engle y Kroner (1995).

26 Otro tendría que ver con las condiciones que deben cumplir los parámetros de la matriz para que sea definida positiva.

27 En concreto, si se supone que e_t ≈ N (0, H_t) condicionada al conjunto de información de ambos tipos de agentes en t - 1 (se debe recordar que: Ω , Ω*, para el agente informado y "miope”, respectivamente), y una modelización para los momentos de segundo orden:

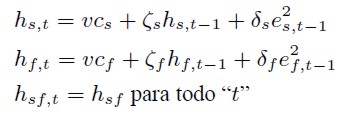
Suponer covarianzas constantes simplifica la expresión del numerador de las ecuaciones (48) y (49). Las conclusiones se mantienen si éstas se modelan como no constantes.

ANEXOS

Anexo 1

REFERENCIAS BIBLIOGRÁFICAS

1. Alexander, C. y Barbosa, A. (2007). Effectiveness of minimum-variance hedging. Journal of Portfolio Management, Winter, 33(2), 46-59.        [ Links ]

2. Alizadeh, A. y Nomikos, N. (2004). A Markov regime switching approach for hedging stock indexes. Journal of Futures Markets, 24, 649-674.        [ Links ]

3. Anderson, R. y Danthine, J. P. (1980). Hedging and joint production: theory and illustrations. Journal of Finance, 35, 487-501.        [ Links ]

4. Anderson, R. y Danthine, J. P. (1981). Cross hedging. Journal of Political Economy, 89, 1182-1196.        [ Links ]

5. Aragó, V. y Fernández, M. A. (2002). Cobertura con contratos de futuro. Revista de Economía Aplicada, 10, 39-62.        [ Links ]

6. Baba, Y., Engle, R. F., Kraft, D. F. y Kroner, K. F. (1990). Multivariate simultaneous generalized ARCH. Mimeo, Department of Economics, San Diego: University of California.        [ Links ]

7. Baillie, R. T. y Myers, R. J. (1991). Bivariate GARCH estimation of the optimal commodity futures hedge. Journal of Applied Econometrics, 6, 109-124.        [ Links ]

8. Bawa, V. S. (1975). Optimal rules for ordering uncertain prospects. Journal of Financial Economics, 2, 95-121.        [ Links ]

9. Bawa, V. S. (1978). Safety first, stochastic dominance and optimal portfolio choice. Journal of Financial and Quantitative Analysis, 13, 255-271.        [ Links ]

10. Beninga, S., Eldor, R. y Zilcha, I. (1983). Optimal hedging in the futures market under price uncertainty. Economics Letters, 13, 141-145.        [ Links ]

11. Beninga, S., Eldor, R. y Zilcha, I. (1984). The optimal hedge ratio in unbiased futures markets. Journal of Futures Markets, 4, 155-159.        [ Links ]

12. Bera, A. y Higgins, M. (1993). ARCH models: Properties, estimation and testing. Journal of Economics Surveys, 7, 305-366.        [ Links ]

13. Black, F. (1976). Studies of stock market volatility changes. Proceedings Of The American Statistical Association Business and Economic Statistic Section, 177-181.        [ Links ]

14. Bollerslev, T. (1990). Modelling the coherence in short-run nominal exchange rates: a multivariate generalized ARCH approach. Review of Economics and Statistics, 72, 498-505.        [ Links ]

15. Bollerslev, T., Engle, R. F. y Wooldridge, J.M. (1988). A capital asset pricing model with time-varying covariances. Journal of Political Economy, 96, 116-131.        [ Links ]

16. Bollerslev, T., Engle, R. F. y Nelson, D. B. (1994). ARCH Models. En R. F. Engle y D. L. McFadden (ed.), Handbook of Econometrics. Oxford: Elsevier Science.        [ Links ]

17. Bollerslev, T., Chou, R. y Kroner, K. (1992). ARCH modelling in finance. Journal of Econometrics, 52, 5-59        [ Links ]

18. Bond, G. E., Thompson, S. R. y Lee, B. M. S. (1987). Application of a simplified hedging rule. Journal of Futures Markets, 7, 65-72.        [ Links ]

19. Brown, S. (1985). A reformulation of the portfolio model of hedging. American Journal of Agricultural Economics, 67, 1010-1012.        [ Links ]

20. Brown, S. (1986). A reformulation of the portfolio model of hedging: Reply. American Journal of Agricultural Economics, 68, 508-512.        [ Links ]

21. Brooks, C., Henry, O. C. y Persand, G. (2002). The effect of asymmetries on optimal hedge ratios. Journal of Business, 75, 333-352.        [ Links ]

22. Chang, J. S. y Shanker, L. (1986). Hedging effectiveness of currency options and currency futures. Journal of Futures Markets, 6, 298-305.        [ Links ]

23. Chen, K. C., Sears, R. S. y Tzang, D. N. (1987). Oil prices and energy futures. Journal of Futures Markets, 7, 501-518.        [ Links ]

24. Cheung, C. S., Kwan, C. C. y Yip, P.C. (1990). The hedging effectiveness of options and futures: A mean-gini approach. Journal of Futures Markets, 10, 61-73.        [ Links ]

25. Christie, A. (1982). The stocastic behavior of common stock variances: value, leverage, and interest rate effects. Journal of Financial Economics, 10, 407-432.        [ Links ]

26. Choudhry, T. (2003). Short-run derivations and optimal hedge ratio: evidence from stock futures. Journal of Multinational Financial Management, 13, 171-192.        [ Links ]

27. Choudhry, T. (2004). The hedging effectiveness of constant and time-varying hedge ratios using three Pacific Basin stock futures. International Review of Economics and Finance, 13, 371-385.        [ Links ]

28. Copeland, L. y Zhu, Y. (2006). Hedging effectiveness in the index futures market. Cardiff Economics Working Paper E2006/10. Cardiff, UK: Cardiff Business School.        [ Links ]

29. Crowder, W. J. y Hamed, A. (1993). A cointegration test for oil futures market efficiency. Journal of Futures Markets, 13, 933-941.        [ Links ]

30. Ederington, L. (1979). The hedging performance of the new futuresmarkets. Journal of Finance, 34, 157-170.        [ Links ]

31. Eftekhari, B. (1998). Lower partial moment hedge ratios. Applied Financial Economics, 8, 645-652.        [ Links ]

32. Engle, R. F. y Granger, C. W. (1987). Cointegration and error correction: Representation, Estimation, and Testing. Econometrica, 55, 251-276.        [ Links ]

33. Engle, R. F. y Kroner, K. F. (1995). Multivariate simultaneous generalized ARCH. Econometric Theory, 11, 122-150.        [ Links ]

34. Engle, R. F. y Ng, V. K. (1993). Measuring and testing the impact of news on volatility. Journal of Finance, 5, 1749-1778.        [ Links ]

35. Figlewski, S. (1984). Hedging performance and basis risk in stock index futures. Journal of Finance, 39, 657-669.        [ Links ]

36. Figlewski, S. (1985). Hedging with stock index futures: Theory and application in a new futures market. Journal of Futures Markets, 5, 183-199.        [ Links ]

37. Fortenbery, T. R. y Zapata, H. O. (1993). An examination of cointegration relations between futures and local grain markets. Journal of Futures Markets, 13, 921-932.        [ Links ]

38. Ghosh, A. (1993). Hedging with stock index futures: Estimation and forecasting with error correction model. Journal of Futures Markets, 13, 743-752.        [ Links ]

39. Ghosh, A. y Gilmore, C. G. (1997). The rolling spot futures contract: An error correction model analysis. Journal of Futures Markets, 17, 117-128.        [ Links ]

40. Grammatikos, T. y Saunders, A. (1983). Stabilitity and the hedging performance of foreing currency futures. Journal of Futures Markets, 3, 295-305.        [ Links ]

41. Granger, C. (1981). Some properties of time series data and their use in econometric model specification. Journal of Econometrics, 16, 121-130.        [ Links ]

42. Harris, R. y Shen, J. (2003). Robust estimation of the optimal hedge ratio. Journal of Futures Markets, 23, 799-816.        [ Links ]

43. Heaney, J. y Poitras, G. (1991). Estimation of the optimal hedge ratio, expected utility, and ordinary least squares regression. Journal of Futures Markets, 11, 603-612.        [ Links ]

44. Heifner, R. G. (1972). Optimal hedging levels and hedging effectiveness in cattle feeding. Agricultural Economics Research, 2, 25-36.        [ Links ]

45. Hentschel, L. (1995). All in the family nesting symmetric and asymmetric GARCH models. Journal of Financial Economics, 39, 71-104.        [ Links ]

46. Herbst, A., Kare, D. y Caples, S. (1989). Hedging effectiveness and minimum risk hedge ratios in the presence of autocorrelation: Foreing currency futures. Journal of Futures Markets, 9, 185-197.        [ Links ]

47. Herbst, A., Swanson, P.E. y Caples, S.C. (1992). Determination of Hedging strategies using foreign currency futures contracts markets. Journal of Futures Markets, 1, 93-104.        [ Links ]

48. Hill, J. y Schneeweis, T. (1981). A note on hedging effectiveness of foreign futures markets. Journal of Futures Markets, 1, 659-664.        [ Links ]

49. Hill, J. y Schneeweis, T. (1982). The hedging effectiveness of foreign currency futures. Journal of Financial Research, 1, 95-104.        [ Links ]

50. Hill, J. y Schneeweis, T. (1986). International risk reduction with financial and foreign currency futures. En F.J.Fabozzi (ed.), Advances in Futures and Optinos Research (pp. 113-135), vol 1, part B. Greenwich, Connecticut: JAI Press.         [ Links ]

51. Hodgson, A. y Okunev, J. (1992). An alternative approach for determining hedge ratios for futures contracts. Journal of Business Finance & Accounting, 19, 211-224.        [ Links ]

52. Howard, Ch. y D´Antonio, L. (1984). A risk return measure of hedging effectiveness. Journal of Financial and Quantitative Analisys, 19, 101-112.        [ Links ]

53. Howard, Ch. y D´Antonio, L. (1987). A risk return measure of hedging effectiveness: A reply. Journal of Financial and Quantitative Analisys, 22, 377-381.        [ Links ]

54. Johnson, L. (1960). The theory of hedging and speculation in commodity futures. Review of Economic Studies, 27, 139-151.        [ Links ]

55. Johnston, J. (1989). Métodos de econometria. Barcelona: Vicens-Vives.        [ Links ]

56. Junkus, J. y Lee, Ch. (1985). Use of three stock index futures in hedging decisions. Journal of Futures Markets, 5, 201-222.        [ Links ]

57. Kahl, K. (1986). A reformulation of the portfolio model of hedging: Comment. American Journal of Agricultural Economics, 68(4), 1010:1012.        [ Links ]

58. Kolb, R. y Okunev, J. (1992). An empirical evaluation of the extended mean-gini coefficient for futures hedging. Journal of Futures Markets, 12, 177-186.        [ Links ]

59. Kolb, R. y Okunev, J. (1993). Utility maximizing hedge ratios in the extended mean-gini framework. Journal of Futures Markets, 13, 597-609.        [ Links ]

60. Kroner, K. F. y Sultan J. (1993). Time-varying distributions and dynamic hedging with foreign currency futures. Journal of Financial and Quantitative Analysis, 28, 535-551.        [ Links ]

61. Lai, K. S. y Lai, M. (1991). A cointegration test for market efficiency. Journal of Futures Markets, 11, 567-575.        [ Links ]

62. Laws, J. y Thompson, J. (2005). Hedging effectiveness of stock index futures. European Journal of Operational Research, 163, 177-191.        [ Links ]

63. Lence, S. H. (1995). On the optimal hedge under unbiased futures price. Economics Letters, 47, 385-388.        [ Links ]

64. Lence, S. H., Hayenga, M. L. y Patterson, M.D. (1996). Storage profitability and hedge ratio estimation. Journal of Futures Markets, 16, 655-676.        [ Links ]

65. Levy, H. yMarkowitz, H.M. (1979). Approximating expected utility by a function of mean and variance. American Economic Review, 3, 308-317.        [ Links ]

66. Lien, D. (1996). The effect of cointegration relationship on futures hedging: A note. Journal of Futures Markets, 16, 773-780.        [ Links ]

67. Lien, D. y Luo, X. (1994). Multiperiod hedging in the presence of conditional heteroskedasticity. Journal of Futures Markets, 14, 927-955.        [ Links ]

68. Lien, D. y Tse, Y. K. (1998). Hedging time-varying downside risk. Journal of Futures Markets, 18, 705-722.        [ Links ]

69. Lien, D., Tse, Y. K. y Tsui, A. K. C. (2002). Evaluating the hedging performance of the constant-correlation GARCH model. Applied Financial Economics, 12, 791-798.        [ Links ]

70. Mao, J. C. T. (1970). Models Of Capital Budgeting, E-V Vs. E-S. Journal of Financial and Quantitative Analysis, 5, 657-676.        [ Links ]

71. Miffre, J. (2004). Conditional OLS minimum variance hedge ratios. Journal of Futures Markets, 24, 945-964.        [ Links ]

72. Morris, Ch. (1989). Managing stock market risk with stock index futures. Economic Review, 6, 3-16.        [ Links ]

73. Moschini, G. y Myers, R. (2002). Testing for constant optimal hedging ratio to model specification. Journal of Empirical Finance, 9, 589-603.        [ Links ]

74. Myers, R. (1991). Estimating time varying optimal hedge ratios on futures markets. Journal of Futures Markets, 11, 39-53.        [ Links ]

75. Myers, R. J. y. Thompson, S. R (1989). Generalized optimal hedge ratio estimation. American Agricultural Economics association, 71, 858-868.        [ Links ]

76. Park, T. y Switzer, L. (1995a). Bivariate GARCH estimation of the optimal hedge ratios for stock index futures: A note.Journal of Futures Markets, 15, 61-67.        [ Links ]

77. Park, T. y Switzer, L. (1995b). Time-varying distributions and the optimal hedge ratios for stock index futures. Applied Financial Economics, 5, 131-137.        [ Links ]

78. Peck, A. (1975). Hedging and income stability: Concepts, Implications, and an example. American Economic Review, 57, 410-419.        [ Links ]

79. Pizzi, M. A., Economopoulos, A. J. y O´Neill, H. M. (1998). An examination of the relationship between stock index cash and futures markets: A cointegraion approach. Journal of Futures Markets, 18, 297-305.        [ Links ]

80. Poomirnars, P., Cadle, J. y Theobald, M. (2003). Futures hedging using dynamic models of the variance/covariance structure. Journal of Futures Markets, 23, 241-260.        [ Links ]

81. Schroeder, T. C. y Goodwin, B. K. (1991). Price discovery and cointegration for live hogs. Journal of Futures Markets, 11, 685-696.        [ Links ]

82. Schwartz, T. V. y Laastsch, F. E. (1991). Dynamic efficiency and price leadership in stock index cash and futures markets. Journal of Futures Markets, 6, 669-683.        [ Links ]

83. Shalit, H. (1995). Mean-Gini hedging in futures markets. Journal of Futures Markets, 15, 617-635.        [ Links ]

84. Shalit, H. y Yitzhaki, S. (1984). Mean-gini, portfolio theory, and the pricing of risky assets. Journal of Finance, 39, 1449-1468.        [ Links ]

85. Stein, J.L. (1961). The simultaneous determinations of spot and futures prices. American Economic Review, 5, 1012-1025.        [ Links ]

86. Sutcliffe, Ch. (1997). Stock index Futures. Londres: International Thompson Business Press.        [ Links ]

87. Wahab, M. y Lashgari, M. (1993). Price dynamics and error correction in stock index and stock index futures markets. Journal of Futures Markets, 13, 711-742.        [ Links ]

88. Viswanath, P. V. (1993). Efficient use of information, convergence adjustments, and regression estimates of hedges ratios. Journal of Futures Markets, 13, 43-53.        [ Links ]

89. Witt, H., Schroeder, T. y Hayenga, M. (1987). Comparison of analytical approaches for estimating hedge ratios for agricultural commodities. Journal of Futures Markets, 7, 135-146.        [ Links ]

90. Working, H. (1953). Futures traiding and hedging. American Economic Review, 43, 314-343.        [ Links ]

91. Yitzhaki, S. (1982). Stochastic dominance, mean variance and gini"s mean difference. American Economic Review, 72, 178-185.        [ Links ]

92. Yitzhaki, S (1983). On an extension of the gini inequality index. International Economic Review, 24, 617-628.        [ Links ]