Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.29 no.52 Bogotá Jan./June 2010
ANÁLISIS DE LA DISTRIBUCIÓN DE LAS TASAS DE RETORNO ACCIONARIAS HACIENDO USO DE LA DISTRIBUCIÓN G Y H DE TUKEY
Andrés Mauricio Mendoza Piñeros*
José Alfredo Jiménez Moscoso**
* Estadístico y Magíster en Economía, investigador del Centro de Investigaciones para el Desarrollo de la Universidad Nacional de Colombia (Bogotá, Colombia). E-mail: ammendozap@unal.edu.co. Dirección de correspondencia: Calle 44 No 45-67, Unidad Camilo Torres, Bloque B4 - CID (Bogotá, Colombia).
** Magíster en Banca y Finanzas y en Ciencias Estadística. Profesor asociado del Departamento de Matemáticas de la Universidad Nacional de Colombia (Bogotá, Colombia). E-mail: josajimenezm@unal.edu.co. Dirección de correspondencia: Cra 30 No 45-03, Facultad de Ciencias, Universidad Nacional de Colombia (Bogotá, Colombia).
Los autores agradecen los valiosos comentarios de los árbitros anónimos de la Revista Cuadernos de Economía.
Este artículo fue recibido el 28 de noviembre de 2008 y su publicación aprobada el 12 de diciembre de 2009.
Resumen
En el artículo se presentan algunas propiedades y limitaciones de la familia de distribuciones g y h de Tukey. Se desarrolla la función de densidad cuando los parámetros g y h no son constantes, lo cual es un gran avance considerando la recurrencia de este aspecto en las aplicaciones sobre el comportamiento de las distribuciones de los activos financieros. Estos desarrollos teóricos permiten hacer un análisis más detallado en el sector accionario cuando se desea conocer y describir el comportamiento de la distribución de las tasas de retorno. Palabras clave: distribuciones g y h de Tukey, cuantiles, sesgo y alargamiento de las colas. JEL: G12, C46, C16, G17.
Abstract
This paper presents some properties and limitations of the Tukey´s g and h family of distributions. It develops the density function when the parameters g and h are not constant, which is a major breakthrough considering the recurrence of this in the applications of the behaviour of distributions of financial assets. These theoretical developments allow a more detailed analysis in the stock sector when one wants to know and describe the behaviour of the distribution of rates of return.
Key words: Tukey´s g and h family of distributions, quantiles, skewness and elongation of the tails. JEL: G12, C46, C16, G17.
Résumé
Dans cet article on présente les propriétés et les limitations de la famille de distributions g et h de Tukey, on développe la fonction de densité lorsque les paramètres g et h ne sont pas constants. Ceci est une contribution considérable en vue des applications au comportement des distributions des actifs financiers. Ces développements théoriques permettent de faire une analyse plus détaillée du secteur des actions lorsqu´on souhaite connaître et décrire le comportement de la distribution des taux de rendement.
Mot clés: distributions g et h de Tukey, quantiles, biais et prolongement des queues. JEL: G12, C46, C16, G17.
A nivel teórico y práctico, el modelo de Movimiento Browniano Geométrico (MBG) y el Modelo de Black and Scholes (MBS) son muy utilizados en el mercado de acciones para conocer el comportamiento de un activo y medir las expectativas de la volatilidad del mercado. Particularmente, en el MBG los logaritmos de los cocintes de precios sucesivos son independientes y siguen una distribución normal. Por su parte, los retornos futuros dependen de los valores presentes (propiedad de Markov).
La forma de la distribución de los cambios de la tasa de retorno es un factor importante en la determinación del menor riesgo de inversión en acciones, además tiene gran importancia desde un punto de vista académico, puesto que ésta provee información descriptiva concerniente a la naturaleza del proceso generado por cambios de la tasa de retorno1. Asimismo, es de gran utilidad para el trabajo empírico en esta área.
Por las razones antes expuestas, el objetivo de este artículo es conocer la distribución del retorno de las acciones haciendo uso de la distribución g y h de Tukey, siendo ésta una herramienta eficiente en el modelamiento de fenómenos financieros, al recoger la asimetría y la curtosis.
El artículo está organizado de la siguiente manera: en la primera sección se presenta la distribución g y h de Tukey y se hace una breve revisión de sus propiedades. En el apartado siguiente, se muestra la metodología de estimación de parámetros. En la tercera parte se expone un caso aplicado a un activo particular, en el cual la función de densidad tiene parámetros no constantes y se evidencia un ajuste significativo sobre la distribución empírica de los datos. Finalmente, se presentan las conclusiones.
PRELIMINARES
La distribución g y h ya ha sido utilizada en finanzas por autores como: Badrinath y Chatterjee (1988), Mills (1995), y Badrinath y Chatterjee (1991), con el fin de modelar el retorno en un índice accionario y el retorno en acciones en varios mercados. En Dutta y Babbel (2002) y Dutta y Babbel (2005) se emplea la distribución para modelar tasas de interés y opciones en tasas de interés, mientras que en Dutta y Perry (2007) la g y la h son usadas para estimar riesgo operativo. Sin embargo, en estos artículos no se presenta de manera explícita la función de densidad.
A continuación se presenta su definición básica y sus propiedades como lo hizo Tukey (1977).
Familia de distribuciones g y h de Tukey
Sea Z una variable aleatoria con distribución normal estándar y sean g y h dos constantes (parámetros). La variable aleatoria Y dada por:
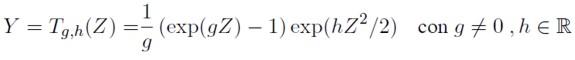 | [1] |
tiene distribución g y h de Tukey.
Los parámetros g y h miden respectivamente el sesgo y alargamiento de las colas de la distribución g y h de Tukey.
Cuando h = 0 la distribución g y h de Tukey se reduce a:
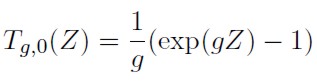 | [2] |
Ésta tiene una distribución g de Tukey, también conocida como familia de distribuciones lognormales, porque presentan un alargamiento de las colas distinto a la distribución normal estándar y son sesgadas con respecto a esta última.
De forma similar, cuando g → 0 la distribución g y h de Tukey esta dada por:
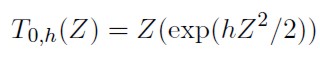 | [3] |
la cual tiene una distribución h de Tukey. Este tipo de distribuciones, tienen la característica de ser simétricas, pero con colas más pesadas que la distribución normal estándar a medida que h crece.
En la práctica, los parámetros g y h son no constantes, por ello, en este artículo se plantea la transformación dada en (1) como sigue:
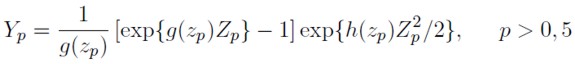 | [4] |
Siendo p el p-ésimo percentil de la distribución.
Por otra parte
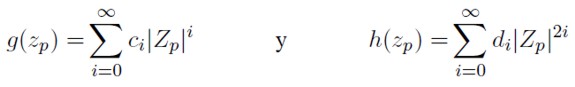 | [5] |
es decir g(zp ) y h(zp ) son polinomios de |Zp| y ambos determinan funciones pares.
Con el fin de determinar la distribución de una variable aleatoria X, se introducen parámetros de localización (A) y escala (B), y se estiman cuatro parámetros atendiendo la siguiente relación:
 | [6] |
Función de densidad
La función de densidad se evalúo considerando que los parámetros que controlan el sesgo y el alargamiento de las colas de la distribución son constantes (g y h), Jiménez M. (2004).
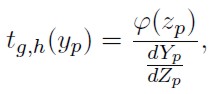 | [7] |
Siendo φ(x ) la función de densidad normal estándar. A partir de 7 en Jiménez M. (2004) se establece que la función de densidad tg,h(yp ) de una variable aleatoria Y con distribución g y h de Tukey, está dada por:
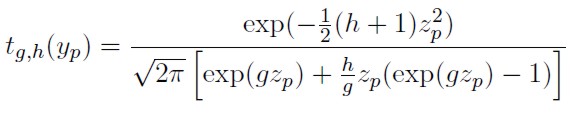 | [8] |
yp y zp denotan el p-ésimo cuantil de la transformación Y = T g,h (Z ) y de la distribución normal estándar, respectivamente.
Siguiendo la misma metodología se obtiene que la función de densidad de la expresión (4), viene dada por
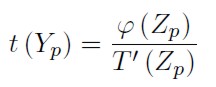 | [9] |
donde
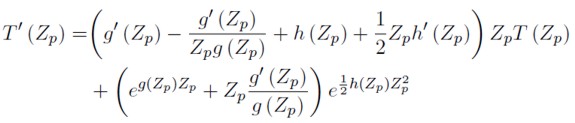
Adicionalmente, en Jiménez M. (2004) a partir de la ecuación (8), se deriva la función de densidad para las distribuciones g de Tukey y h de Tukey.
La función de densidad para la variable aleatoria X, dada en la expresión (6) viene dada en Jiménez M. (2004) como una función de la distribución g y h de Tukey:
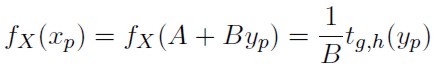 | [10] |
ESTIMACIÓN DE LOS PARÁMETROS DE LA FAMILIA DE DISTRIBUCIONES g Y h DE TUKEY
Método de cuantiles introducido por Hoaglin (1985)
En Hoaglin (1985), se presenta la estimación de los parámetros de la familia de distribuciones g y h de Tukey.
Usando las siguientes ecuaciones, con Zp = −Z1−p y p < 0,5:
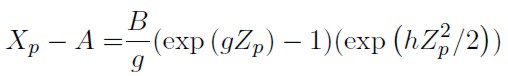 | [11] |
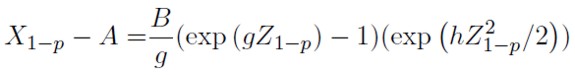 | [12] |
Para la estimación de los parámetros, se tienen en cuenta las siguientes propiedades, las cuales fueron recopiladas en Dutta y Babbel (2002):
1. X es una transformación estrictamente creciente de Z. Es decir, la transformación de una normal estándar a una g y h es uno a uno.
2. El parámetro de localización de la distribución g y h de Tukey, es estimado por la mediana de los datos; es decir, A = X0.5.
3. La estimación del parámetro que controla el sesgo de la distribución (g ), se estima generalmente, por la mediana de los gp dados por la siguiente expresión:
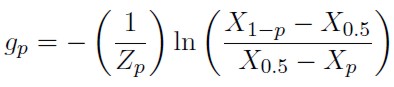
4. Cuando, g ≠ 0, el parámetro que controla el alargamiento de las colas (h), se estima mediante
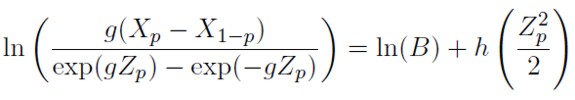
El valor de h se obtiene haciendo uso de una regresión lineal; en la cual, el coeficiente de la regresión estima el valor de h. El valor de B se obtiene tomando la función exponencial del intercepto de la regresión. Dado que la distribución no es simétrica g ≠ 0, se pueden obtener dos estimaciones más para h y por ende, dos estimaciones diferentes del alargamiento para las dos colas de la distribución:
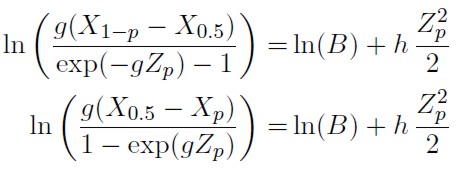
La estimación del parámetro h debe considerar las tres estimaciones.
5. Cuando, g → 0, h se estima teniendo en cuenta la siguiente regresión lineal:
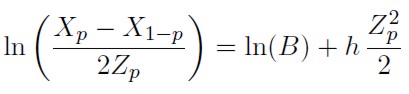 | [13] |
6. En la práctica, el comportamiento de los parámetros g y h puede tener patrones más complejos que los estipulados anteriormente; por ello, una forma de estimarlos es tratarlos como polinomios de Z2 p
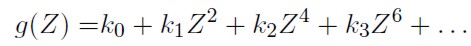 | [14] |
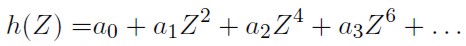 | [15] |
La característica de estos patrones y el grado del polinomio, pueden ser determinados graficando gp y hp contra Z2 p, respectivamente.
Modificación del método de cuantiles de Hoaglin (1985)
En esta sección se presenta una nueva propuesta para estimar los parámetros de la distribución g y h de Tukey, partiendo del método propuesto por Hoaglin (1985) y Jiménez M. (2004).
La estimación de los parámetros de la distribución g y h de Tukey, se lleva a cabo teniendo en cuenta que el sesgo puede inducir a patrones de alargamiento de las colas en los datos. Por tanto es importante investigar la naturaleza del alargamiento de las colas luego de que el sesgo haya sido considerado. La nueva estimación es análoga a la propuesta en Hoaglin (1985), pero asumiendo que p > 0,5 y considerando:
1. Cuando g ≠ 0, el parámetro que controla el alargamiento de las colas (h), se estima mediante
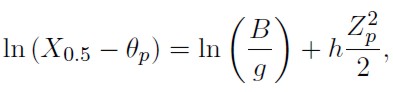 | [16] |
Con θp < X0,5, para todo p > 0,5 y
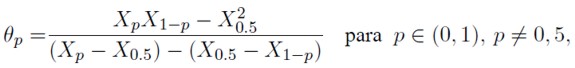 | [17] |
nótese que θp = θ1−p. El valor de h se obtiene haciendo uso de una regresión lineal; donde el coeficiente de la regresión estima el valor de h y el valor de B se cacula multiplicando el valor de g por la función exponencial del intercepto de la regresión. En Jiménez M. y Martínez C. (2006) se propone que si θp = 0 entonces h tiende a cero (distribuciones g de Tukey).
2. Cuando, g → 0 (distribuciones h de Tukey), h se estima teniendo en cuenta la siguiente regresión lineal:
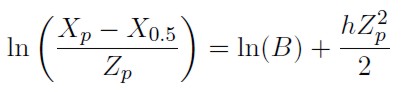 | [18] |
3. Un caso particular de las distribuciones g y h de Tukey, son las distribuciones g de Tukey, donde g ≠ 0 y h = 0. Para esta familia de distribuciones, el parámetro g se calcula como se indicó anteriormente y la estimación del parámetro de escala se obtiene al promediar los percentiles de la variable X dados por las ecuaciones 11 y 12:
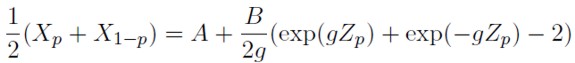 | [19] |
Ahora, expresando exp(gZp ) y exp(−gZp ), en series de potencias:
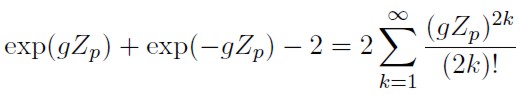
y se expresa 2k! en términos de la función Gamma obteniéndose que (2k)! = Γ(2k + 1) = (2k)Γ(2k), por tanto la expresión (19) queda determinada por:
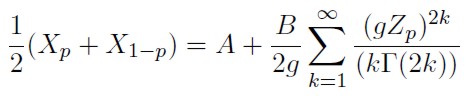 | [20] |
Para valores de |g| ≤ 0,5, la ecuación (20) toma la siguiente forma
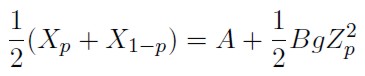 | [21] |
Para la implementación práctica se hace uso de las siguientes relaciones:
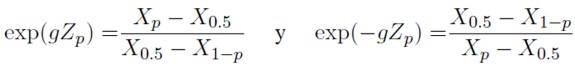
B se estima utilizando una regresión lineal sin intercepto, con base en la siguiente ecuación:
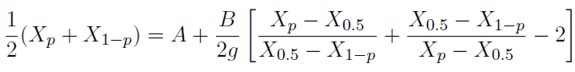 | [22] |
4. Adicionalmente, el comportamiento de los parámetros g y h son estimados mediante las expresiones dadas en (5).
¿Por qué estimar los parámetros de la distribución g y h de Tukey utilizando el método de cuantiles de Hoaglin?
En la estimación de los parámetros de la distribución g y h (con parámetros constantes), métodos alternativos pueden ser usados: máxima verosimilitud o de momentos (Majumder y Ali, 2008). Estos métodos limitan el uso de la riqueza estructural de la distribución g y h de Tukey y aunque el método de máxima verosimilitud genera estimaciones con menor nivel de error, el costo computacional del cálculo de los parámetros de la g y h es muy alto.
El método basado en cuantiles usa la estructura de la distribución g y h de Tukey, utilizando el comportamiento de las colas de la distribución empírica de los datos y no la información del centro de esta distribución como lo realiza el método de Momentos o Máxima Verosimilitud (Hoaglin, 1985).
La metodología empleada en este artículo, para estimar los parámetros no constantes (polinomios de Z) de la distribución g y h que se ajusten a los datos, es la propuesta por Hoaglin (1985) –método basado en cuantiles. Varios autores argumentan que un método de estimación de parámetros mediante máxima verosimilitud asigna pesos iguales a todos los datos usados en el ajuste, mientras que el método basado en cuantiles puede poner más peso en las colas de la distribución. No obstante, las diferencias entre los métodos de estimación dependen del tamaño de muestra, en el caso particular de las series financieras, es suficientemente grande y por lo tanto, la pérdida de eficiencia es mínima (He y Raghunathan, 2006).
APLICACIÓN
Muestra
En este apartado, se utiliza la distribución g y h de Tukey como herramienta para describir la distribución de las tasas de retorno de las acciones de la compañía Boeing2. Se tomaron los precios diarios de las acciones ajustados por los dividendos, entre enero 3 de 2000 y noviembre 7 de 2005, para un total de 1.471 precios históricos. El precio del activo está dado en dólares para los días bursátiles del año.
Histograma de frecuencias y coeficientes de asimetría y curtosis
En el Cuadro 1 se presentan las estadísticas descriptivas de los datos:
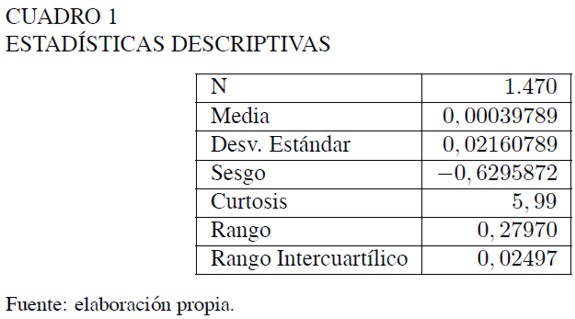
A partir de los gráficos de secuencia (comportamiento de la variable a través del tiempo), presentados para la tasa de rendimiento y la tasa de retorno, se evidencia que tanto el comportamiento como los valores que toma cada una de las variables son los mismos. Por tanto, se analizará la tasa de retorno ya que es la variable que utiliza Fama (1965) en sus estudios y con base en su comportamiento se estima el retorno promedio y la volatilidad de un activo. La característica de leptocurtosis se nota claramente en la Gráfica 1.
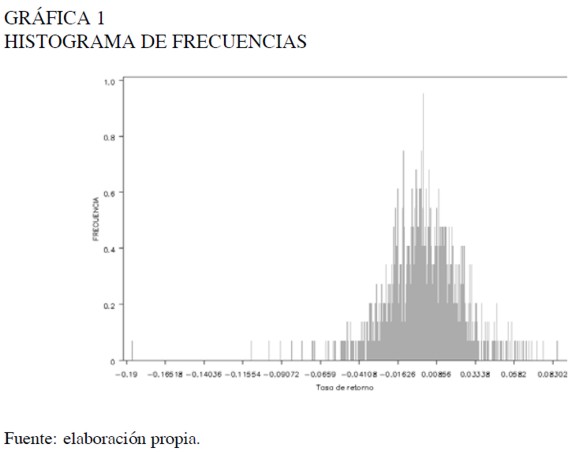
El histograma de frecuencias (Gráfica 1) y los coeficientes de asimetría y curtosis indican que la distribución de la variable de estudio tiene un leve grado de sesgo a la izquierda y es leptocúrtica. En este gráfico se observa un comportamiento irregular en las colas de la distribución, lo cual Fama denominó colas pesadas o "Heavy tails". Adicionalmente, las pruebas de normalidad indican que la variable de estudio no sigue una distribución normal, con un nivel de significancia de 1%.
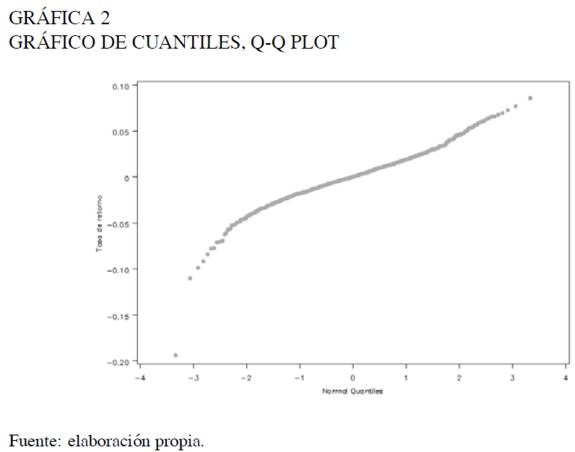
Descripción del comportamiento del sesgo y alargamiento de las colas
A continuación se realiza un análisis descriptivo del comportamiento de la forma de la distribución de la tasa de retorno, utilizando medidas de sesgo y alargamiento de las colas descritas en Hoaglin, Mosteller y Tukey (1985), las cuales permiten observar y evaluar el grado de sesgo y alargamiento de las colas de una manera más detallada y no tan global como los coeficientes de asimetría y curtosis (gráficas 3 y 4).
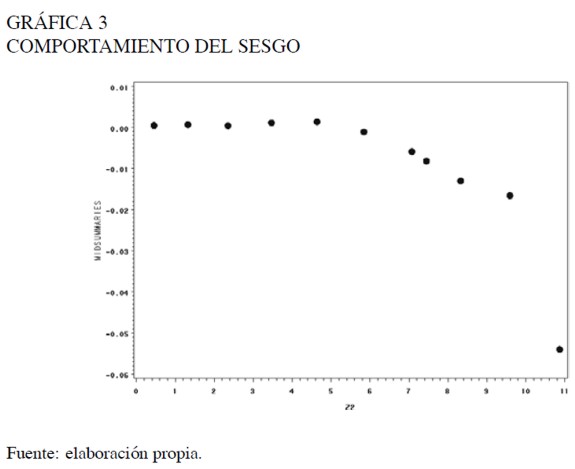
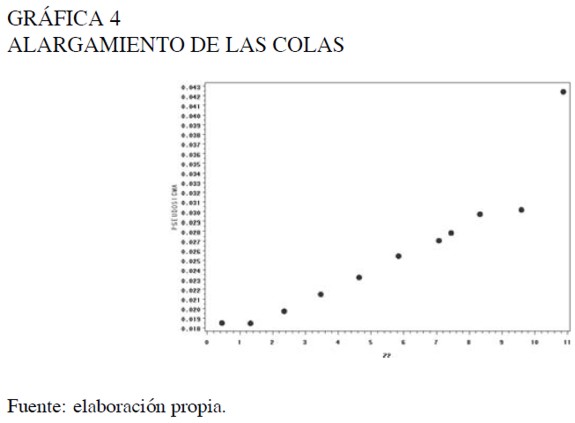
En la Gráfica 3 se observa que la distribución es sesgada a izquierda al igual que lo indicaba el coeficiente de asimetría. En las gráficas 3 y 4 se evidencia un comportamiento constante alrededor de cero en el centro de la distribución, lo que indica que esta parte de la distribución tiene un comportamiento simétrico alrededor de la mediana. La asimetría de la distribución se agudiza en las colas de la distribución, notando que para el periodo de estudio se encontraron tasas de rendimiento con pérdidas inferiores a −10%, en tanto que la mayor tasa de ganancia estaba alrededor de 8%.
Como en las gráficas 3 y 4 no se observa un patrón constante, se evidencia que la forma de la distribución varía a través de los percentiles. Por tanto, se utilizará un análisis de regresión para determinar el comportamiento del sesgo y el alargamiento de las colas, utilizando como variables explicativas un polinomio construido con los valores absolutos de los percentiles de la distribución normal estándar (|Zp|).
Comportamiento del sesgo de la distribución
A partir del análisis descriptivo del sesgo y al observar que las estimaciones de g(zp ) varían a través de los percentiles, se estima el grado de sesgo considerando que g(zp ) es explicado por un polinomio de |Zp|. Para ello se hace uso de un análisis de regresión (Gráfica 5).
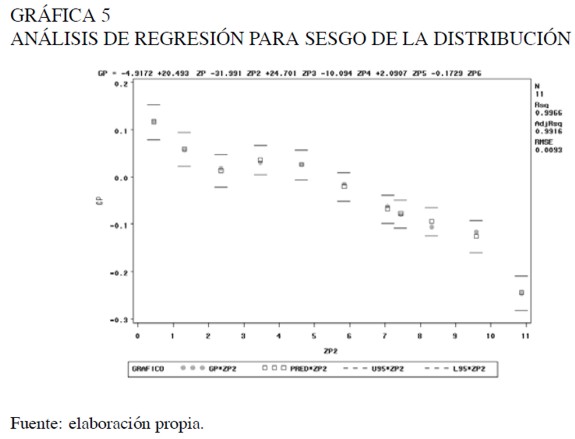
El ajuste del modelo es bastante bueno. El coeficiente de determinación es cercano a 1, la estadística F indica una significancia global del modelo y los valores predichos para el grado de sesgo son bastante cercanos a los niveles de sesgo observados para los datos. En este análisis de regresión todos los parámetros son significativos al 1%.
Un gran avance en este artículo es la descripción del comportamiento del sesgo en términos de un polinomio de los percentiles de la distribución normal estándar Zp; debido a que en la literatura sólo se evalúan polinomios de Z2 p . En el caso aquí analizado, se evidenciaron mejores resultados al considerar la relación entre el nivel de sesgo con Zp que con Z2 p .
Comportamiento del alargamiento de las colas de la distribución
Con base en el comportamiento no constante del alargamiento de las colas en el análisis descriptivo y bajo la estimación de g(zp ) en el análisis de regresión para el sesgo, se implementó un análisis de regresión tomando como variables respuesta las descritas en los métodos de estimación, y las variables explicativas correspondientes a un polinomio de Z2 p . Este análisis se realizó de igual manera para las dos colas de la distribución, teniendo en cuenta otra variable respuesta para cada cola.
En el análisis de regresión para el alargamiento de las colas sin desagregar el análisis para cada cola, se evidenció un ajuste acertado (Gráfica 6). La tabla de análisis de varianza presenta una significancia global aceptable. El coeficiente de determinación es cercano a la unidad, indicando que la explicación del modelo es próxima a 100%. La mayoría de los parámetros son significativos a un nivel de significancia de 1%, excepto el coeficiente asociado a Z2 p el cual es significativo al 11%. La exclusión de esta última variable implicaba predicciones menos acertadas que si era incluída.
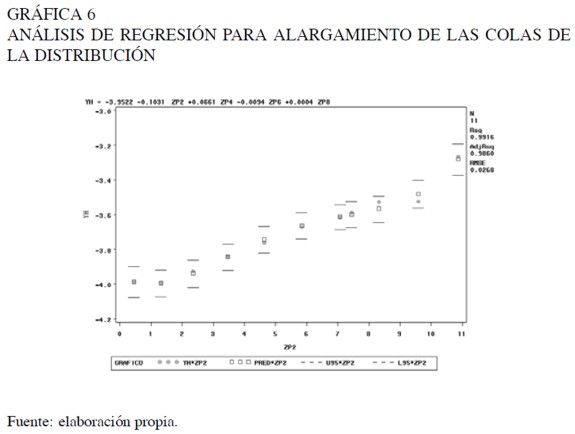
Al observar el comportamiento del alargamiento de las colas individualmente (gráficas 7a y 7b), se aprecia que los modelos de regresión son similares en significancia, tanto global como marginal, y los coeficientes estimados son muy cercanos al análisis de regresión en el cual se contempla toda la distribución.
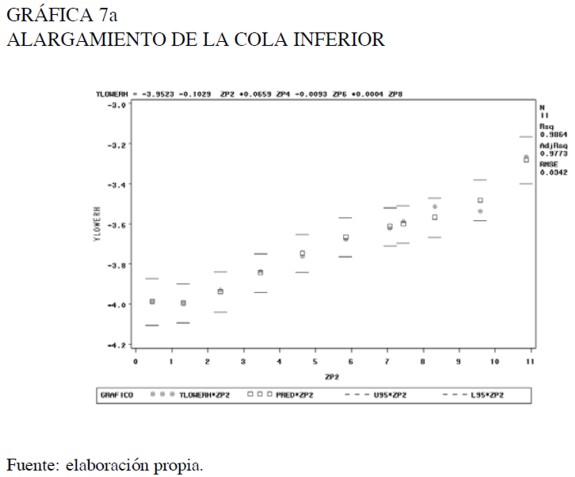
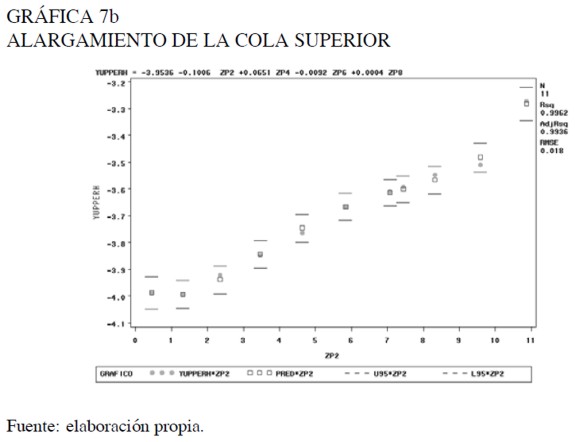
Se evidencia que el comportamiento del alargamiento de las colas no difiere significativamente de una cola a otra. Además, analizar este comportamiento para cada cola de la distribución presenta problemas de sobreestimación, tal como lo indican algunos autores entre ellos Dutta y Babbel (2002), Mills (1995), y Badrinath y Chatterjee (1988). El parámetro de localización es estimado por la mediana de los registros históricos, esta medida tuvo el valor de 0. El parámetro de escala es estimado por la exponencial del intercepto de la regresión aplicada, para determinar el comportamiento del alargamiento de las colas de la distribución, este valor fue 0,019212.
Percentiles estimados
El análisis de la distribución descrito en este artículo utiliza percentiles de la forma p = 2−k con k = 1, 2, 3, . . ., teniendo en cuenta una progresión geométrica que va desde el percentil 0, 5 hasta el 0, 999511719 para la cola superior, y de manera simétrica para cola inferior. En el Cuadro 2 se muestra la estimación de estos percentiles.
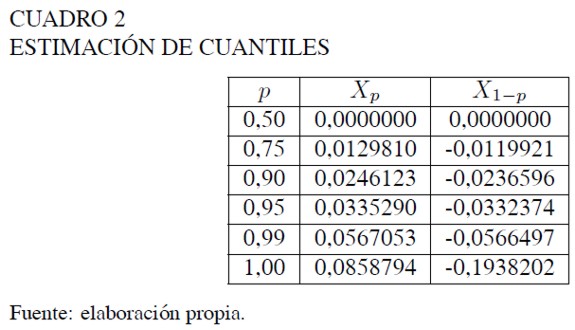
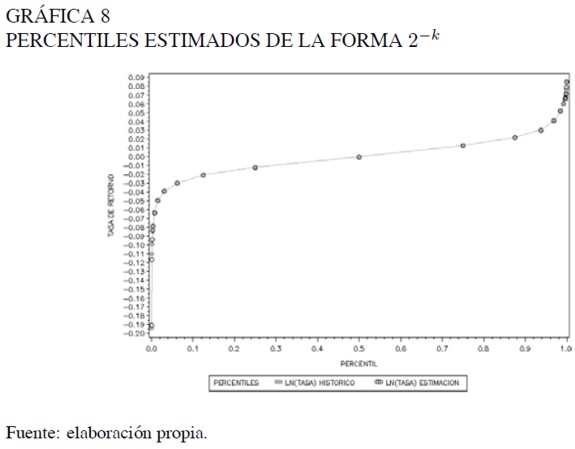
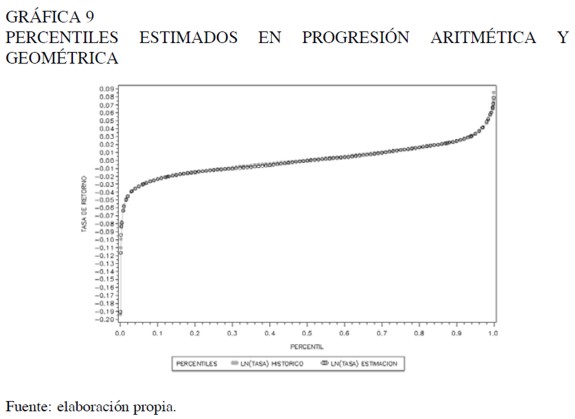
Para estos percentiles se analizó la bondad de ajuste de la distribución g y h de Tukey para la tasa de retorno. Los gráficos 8 y 9 muestran que la estimación de estos percentiles comparada con los datos históricos del activo para el periodo de estudio, es bastante acertada.
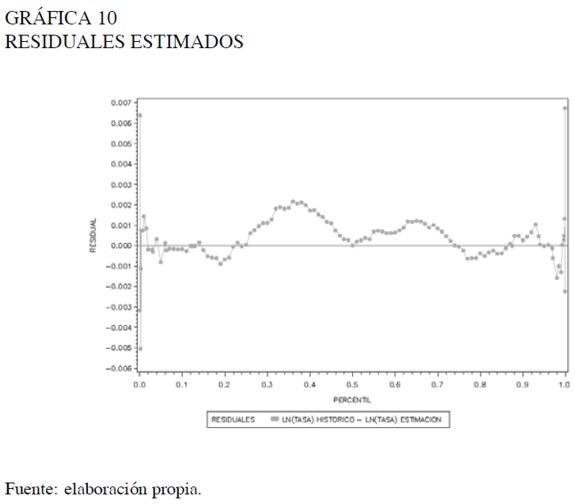
En la bondad de ajuste del análisis de la distribución también se estudiaron los residuales estimados. La Gráfica 10 muestra el comportamiento de los residuales del modelo estimado (asumiendo g y h como polinomios de |Zp|), evidenciando que los residuales de los percentiles del centro de la distribución están entre −0, 001 y 0, 002, en tanto que los de las colas de la distribución oscilan entre −0,005 y 0,0065. Es claro que las diferencias entre los valores históricos y estimados son pequeñas, a lo más se tiene una diferencia cercana a 0,5 unidades porcentuales con respecto al valor histórico registrado para la tasa de retorno.
Función de densidad de la tasa de retorno
Una vez determinado el comportamiento del sesgo y alargamiento de las colas de la distribución, y los parámetros de localización (mediana) y escala, se puede describir la distribución de la variable de estudio. Lo anterior fue utilizado en la bondad de ajuste de la distribución g y h de Tukey estimada y estableciéndose que ésta describe adecuadamente los registros históricos del activo. La Gráfica 11 corresponde a la distribución que representa la función de densidad de la distribución g y h de Tukey para la variable tasa de retorno.
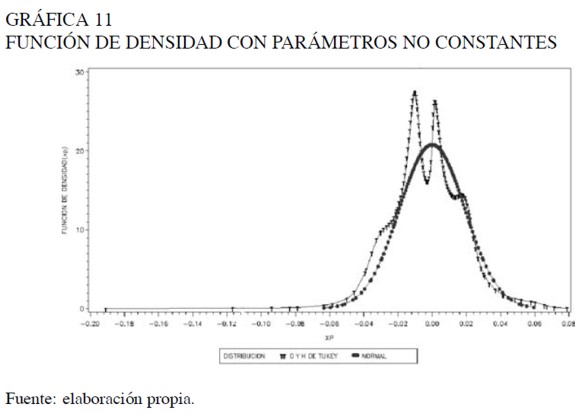
Se evidenció que los parámetros que determinan la forma de la distribución de la tasa de retorno, no son constantes y varían a través de los percentiles. Por tanto, se debe desarrollar la función de densidad para la distribución g y h de Tukey en presencia de esta situación.
La estimación de los parámetros y la variable Yp para la tasa de retorno de la compañía Boeing, está dada por:
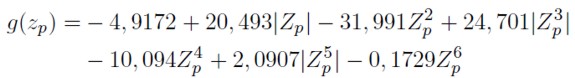 | [23] |
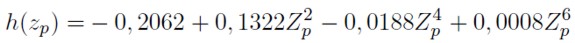 | [24] |
Aquí se usa el hecho que |Z2n p | = Z2n p , teniendo en cuenta que g(zp ) y h(zp ), notados en las ecuaciones (23) y (24), representan el parámetro del sesgo y alargamiento de las colas como función de los percentiles de la distribución normal estándar.
Luego la expresión (6) queda de la iguiente manera:
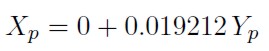 | [25] |
Siendo Yp dada por la expresión (4). Como se nota en la Gráfica 11, la función de densidad tiene un comportamiento similar al histograma de los datos históricos de la variable de estudio presentado en la Gráfica 1.
CONCLUSIONES
En este artículo se mostró que la distribución g y h de Tukey es una herramienta útil en la descripción del comportamiento de las tasas de retorno de un activo.
En la aplicación se aprecia que la tasa de retorno no sigue la distribución normal y por tanto, su distribución no dependen únicamente de la volatilidad y del valor promedio de la tasa de retorno en un periodo, sino también de la forma de la distribución: sesgo y alargamiento de las colas.
Adicionalmente, se encontró que el comportamiento del sesgo y alargamiento de las colas de la distribución de la tasa de retorno de la compañía Boeing, varía a través de los percentiles, lo cual indica que la volatilidad de esta tasa no es constante.
Los desarrollos teóricos realizados en este artículo, permiten hacer uso de la familia de distribuciones g y h de Tukey en un amplio campo de acción, tanto en el cálculo de probabilidades a partir de la función de distribución como en la descripción gráfica y analítica de la función de densidad, aún cuando los parámetros de sesgo y alargamiento de las colas no son constantes.
La estimación de parámetros constantes de la distribución g y h de Tukey puede realizarse por distintos métodos, pero para utilizarlos es necesario considerar los supuestos y restricciones de los modelos econométricos. Para el caso en que los parámetros sean no constantes la modelación puede realizarse mediante la metodología de Hoaglin o la propuesta en este artículo dependiendo del comportamiento de la tasa de retorno.
NOTAS AL PIE
1 En este artículo, la tasa de retorno durante el período t se consigue suponiendo un proceso de capitalización continua, es decir:

Siendo Pt el precio en el tiempo t.
2 Los datos históricos de este activo fueron tomados de http://finance.yahoo.com.
ANEXO 1.
RESULTADOS DE LAS SIMULACIONES
Tablas de análisis de varianza y efectos marginales
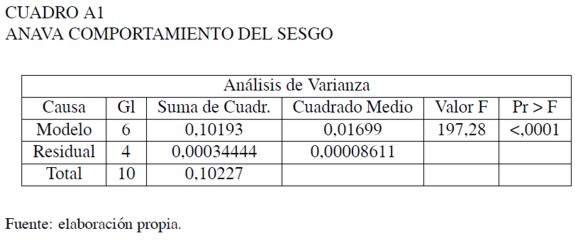
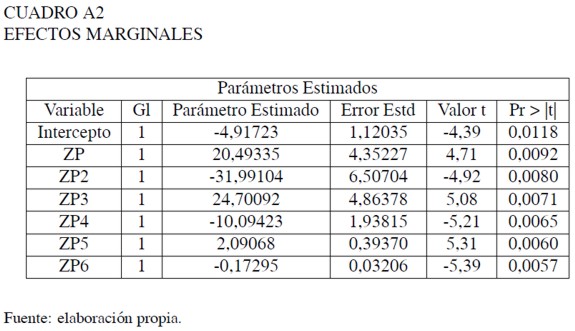
Estimación del alargamiento de las colas de la distribución
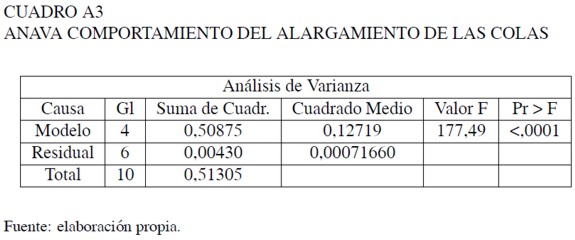
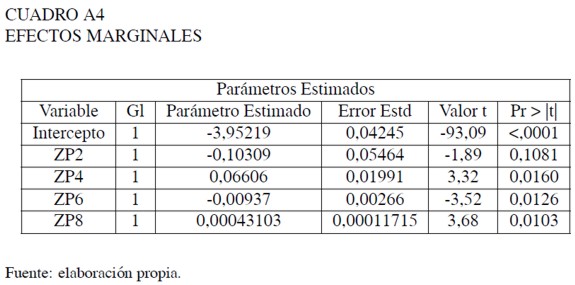
Estimación del alargamiento de la cola inferior de la distribución
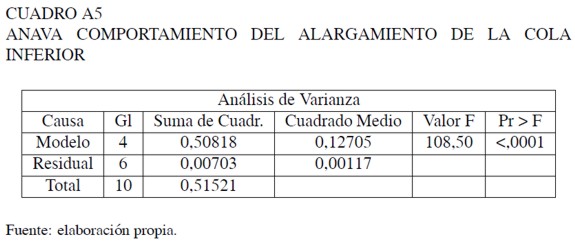
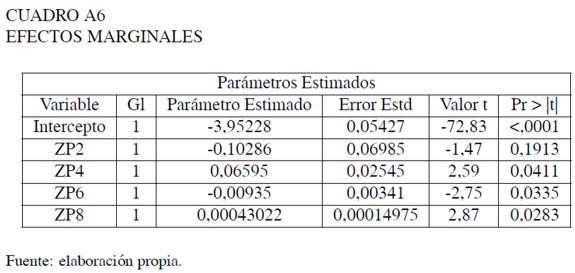
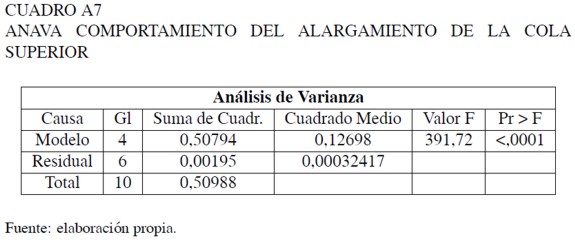
Estimación del alargamiento de la cola superior de la distribución
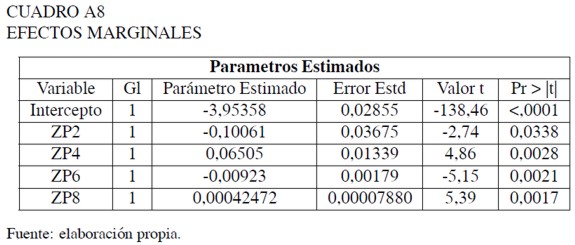
REFERENCIAS BIBLIOGRÁFICAS
[1] Badrinath, S. y Chatterjee, S. (1988). On measuring skewness and elongation in common stock return distributions: The case of the market index. The Journal of Business, 61(4), 451-472. [ Links ]
[2] Badrinath, S. y Chatterjee, S. (1991). A data analytic look at skeness and elongation in common stock return distributions. Journal of Business & Economic Statistics, 9(2), 223-233. [ Links ]
[3] Dutta, K. K. y Babbel, D. F. (2002). On measuring skewness and kurtosis in short rate distributions: The case of the us dollar london inter bank offer rates. Center for Financial Institutions Working Papers 02-25. Philadelphia: University of Pennsylvania. [ Links ]
[4] Dutta, K. K. y Babbel, D. F. (2005). Extracting probabilistic information from the prices of interest rate options: Tests of distributional assumptions. The Journal of Business, 78(3), 841-870. [ Links ]
[5] Dutta, K. K. y Perry, J. (2007). A tale of tails: An empirical analysis of loss distribution models for estimating operational risk capital. Working Paper No. 06-13. Boston: Federal Reserve Bank of Boston. [ Links ]
[6] Fama, E. F. (1965). The behavior of stock market prices. The behavior of stock market prices, 38, 34-105. [ Links ]
[7] He, Y. y Raghunathan, T. E. (2006). Tukeys gh distribution for multiple imputation. The American Statistician, 60(3), 251-256. [ Links ]
[8] Hoaglin, D.C. (1985). Summarizing shape numerically: the g-and-h distributions. En: Hoaglin, D.C., Mosteller, F., Tukey, J.W. (Eds.), Exploring Data Tables, Trends, and Shapes (461-513). New York: John Wiley & Sons. [ Links ]
[9] Hoaglin, D. C., Mosteller, F. y Tukey, J. W. (1985). Exploring Data Tables, Trends, and Shapes. New York: JohnWiley & Sons. [ Links ]
[10] Jiménez M., J. A. (2004). Aproximaciones de las funciones de riesgo del tiempo de sobrevivencia mediante la distribución g-h de Tukey. Trabajo de grado no publicado (Especialización en Actuaría). Universidad Nacional de Colombia, Facultad de Ciencias, Departamento de Matemáticas. [ Links ]
[11] Jiménez M., J. A. y Martínez C., J. (2006). Una estimación del parámetro de la distribución g de Tukey. Revista Colombiana de Estadística, 29(1), 1-16. [ Links ]
[12] Majumder, M. M. A. y Ali, M. M. (2008). A comparison of methods of estimation of parameters of tukeys gh family of distributions. Pakistan Journal of Statistics, 24(2), 135-144. [ Links ]
[13] Mills, T.C. (1995). Modelling skewness and kurtosis in the London stock exchange ft-se index return distributions. The Statistician, 44(3), 323-332. [ Links ]
[14] Tukey, J.W. (1977). Modern techniques in data analysis, NSF-sponsored regional research conference at Southeastern Massachusetts University. North Dartmouth, MA. [ Links ]












