Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.29 no.53 Bogotá July/Dec. 2010
¿CUÁL ES EL CRECIMIENTO DE LARGO PLAZO DE LA ECONOMÍA CHILENA? UNA RESPUESTA FORMAL PARA UNA ANTIGUA PREGUNTA
Byron Idrovo*
* Magister en Economía y Estadística. Trabaja actualmente en la Gerencia de Estudios de la Cámara Chilena de la Construcción (Santiago de Chile, Chile). E-mail: bidrovo@cchc.cl. Dirección de correspondencia: Marchant Pereira 10, piso 3 (Santiago de Chile, Chile).
El autor agradece los valiosos comentarios de dos árbitros anónimos y los aportes de la Gerencia de Estudios de la Cámara Chilena de la Construcción.
Este artículo fue recibido el 4 de febrero de 2009, la versión ajustada fue recibida el 2 de junio de 2010 y su publicación aprobada el 23 de julio de 2010.
Resumen
El objetivo del presente estudio es estimar la tasa de crecimiento de la economía en un contexto de plena utilización de los recursos productivos. Se emplean para el análisis modelos univariados de series de tiempo, incluyendo una tendencia determinística (con quiebres de medias), y un modelo de estado-espacio que considera una tendencia estocástica y un componente cíclico, estimado por Filtro de Kalman. El componente cíclico es calculado con y sin cambios de régimen (Markov-switching models), de acuerdo con la idea de Friedman (1993) –plucking model. Los resultados indican que la tasa de crecimiento potencial de la economía chilena sería superior al 4% anual, acompañada de ciclos económicos asimétricos.
Palabras clave: ciclos, crecimiento de tendencia, filtro de Kalman, Chile. JEL: C22, E32, N36, O54.
Abstract
The objective of the present study is to estimate the economy growth rate in the context of full use of the productive resources. Time series univariete models, including a deterministic tendency (with mean breaks), and a space-state model that considers a stochastic tendency and a cyclic component, estimated by Kalman´s filter were used. The cyclic component is calculated with and without regime chages (Markov-switching models), according to Friedman´s idea –plucking model. The results indicate that the Chilean economy potential growth rate would be greater than 4% annually, accompanied by economic asymmetric cycles.
Key words: economy, cycles, growth tendency, Kalman´s filter, Chile. JEL: C22, E32, N36, O54.
Résumé
L´objectif de ce travail est d´estimer le taux de croissance de l´économie dans un contexte de pleine utilisation des ressources productives. On utilice pour cette analyse des modèles univariés de séries temporelles avec une tendance déterministe (avec moyenne variable) et un modèle d´état – espace comprenant une tendance stochastique et une composante cyclique, estimé à partir du filtre de Kalman. La composante cyclique est calculée avec et sans changements de régime (Markov-switching models), conformément à l´idée de Friedman (1993) –plucking model. Les résultats indiquent que le taux de croissance potentiel de l´économie chilienne serait supérieur à 4% par an, accompagnée par des cycles économiques asymétriques.
Mots clés : économie, cycles, croissance tendancielle, filtre de Kalman, Chili. JEL : C22, E32, N36, O54.
El PIB potencial es la cantidad óptima de bienes y servicios que es capaz de producir la economía de un país en un horizonte de largo plazo. La optimalidad tiene que ver con la capacidad productiva del país en un contexto de plena utilización de los recursos disponibles (capital, trabajo, energía, tiempo, entre otros), cuya conjunción define un punto de la frontera de posibilidad de producción.
En este sentido, el PIB potencial (o capacidad productiva de pleno empleo) es una medida de referencia importante para identificar el estado del ciclo por el que transita la economía, permitiendo anticipar oportunamente sus efectos macroeconómicos. Por ejemplo, cuando el PIB efectivo supera notablemente al potencial durante un tiempo prolongado, se dice que la economía se encuentra en un régimen expansivo lo que eventualmente se traduce en un mayor crecimiento de los precios, como respuesta a las presiones de demanda con respecto a una oferta limitada (o producción potencial) de bienes y servicios. Sucede lo contrario cuando la actividad actúa por debajo de su frontera de posibilidades de producción, produciéndose un estado recesivo en la economía, en este contexto, se contrae la demanda con respecto a la oferta y los precios tienden a disminuir. Esto último también es nocivo para la economía, ya que las expectativas de que los precios continúen a la baja inducen a que los agentes económicos posterguen inversión y consumo (a la espera de que los precios continúen contrayéndose), lo que eventualmente reciente aún más la economía.
He ahí la importancia de estimar sistemáticamente la brecha de capacidad productiva (diferencia entre el PIB efectivo y potencial). Ésta constituye una medida de alerta temprana para las autoridades monetarias y fiscales en el manejo de sus instrumentos de política (fine tuning), con el fin de mantener la actividad efectiva en torno a su nivel de tendencia de largo plazo y promover las medidas necesarias para incrementar la productividad, alcanzando tasas de crecimiento potencial más elevadas. En suma, calcular el crecimiento potencial de la economía siempre es relevante y lo es aún más en Chile, donde el encarecimiento de la matriz energética enfrió el aparato productivo del país, debido a los altos precios internacionales de los combustibles y el déficit del gas natural proveniente de Argentina, lo que a su vez, afectó a la baja el crecimiento potencial de la economía.
Por otra parte, la medición del PIB potencial abre una discusión referente a si la serie de tiempo es estacionaria en tendencia o en diferencias. La estacionariedad en tendencia supone que las marcadas oscilaciones (o más bien desvíos) del PIB efectivo con respecto a su tendencia son transitorias, por lo que el nivel de actividad de largo plazo estaría gobernado por un proceso tendencial cuya tasa de crecimiento corresponde a la variación anual del PIB potencial (o más bien "tasa natural" de crecimiento de la economía). Por su parte, la estacionariedad en diferencia supone la presencia de una o más raíces unitarias en el nivel del PIB. En este caso, es posible asumir que el PIB potencial es gobernado por una tendencia estocástica que sigue una caminata aleatoria.
Fuentes, Gredig y Larraín (2008) estiman la tasa de crecimiento potencial de la economía chilena con base en tres métodos distintos de medición: una función de producción desarrollada enMenashe y Yahkin (2004); modelos de espacio de estado, estimados con filtro de Kalman (Kalman, 1960); y estimaciones de un modelo estructural de vectores autorregresivos (SVAR). Los resultados obtenidos con las diferentes mediciones fueron similares. Por lo que los autores concluyen que la tasa de crecimiento potencial promedio de la economía chilena varió entre 5,2% y 5,8% entre 1998 y 2007.
Otros autores como Gallego y Johnson (2001) y Contreras y García (2002), cuyos resultados no distan significativamente de los hallazgos de Fuentes, Gredig y Larraín (2008), basan sus estimaciones del crecimiento potencial en modelos derivados de funciones de producción.
Así mismo, el Informe de Política Monetaria (IPoM) publicado por el Banco Central en mayo de 2008, señala que el significativo aumento del costo de la energía se reflejó en una menor productividad total de factores, lo que redujo transitoriamente el nivel de producto tendencial.
En efecto, el crecimiento de largo plazo de la actividad habría disminuido de 5% hasta ubicarse en un rango de 4,5% a 5% en 2008. Sin embargo, el presente documento argumenta formalmente que la tasa potencial estaría marginalmente por debajo de dicho rango y con un moderado ajuste de la actividad cuando ésta se desvía de su trayectoria de largo plazo. Los resultados indican que la tasa de crecimiento potencial de la economía chilena sería superior a 4% anual, acompañada de ciclos económicos asimétricos.
Lo anterior se concluye de la utilización de modelos univariados de series de tiempo –incluyendo una tendencia determinística (con quiebres de medias) y un modelo de estado–, que consideran una tendencia estocástica y un componente cíclico, estimado por Filtro de Kalman. El componente cíclico es calculado con y sin cambios de régimen, basado en los modelos de cadenas de Markov (Markov-switching models).
A diferencia del modelo de espacio-estado planteado por Fuentes, Gredig y Larraín (2008) –en el que el componente cíclico del PIB se iguala a un término de error de media cero y varianza constante–, el presente artículo considera un proceso subyacente AR(2) del componente cíclico del índice mensual de actividad económica (Imacec).
Basado en la idea de Friedman (1993) plucking model1, el componente cíclico de la actividad económica considera la presencia de cambios de régimen (o ciclos asimétricos). Este tipo de modelo fue desarrollado en Estados Unidos con el propósito de identificar si las fluctuaciones del PIB real de dicho país se caracterizaban por ser mayoritariamente transitorias o permanentes2.
Inicialmente, Clark (1987) estima un modelo de componentes inobservados, imputando restricciones de simetría en los ciclos económicos e innovaciones permanentes y transitorias no correlacionadas. Entre sus resultados, se destaca el hecho de que los movimientos observados del producto estadounidense son primordialmente transitorios. Por su parte, Kim y Nelson (1999a) identificaron el efecto suavizador en el componente permanente del PIB real de Estados Unidos, causado por las rigideces planteadas en el modelo de Clark (1987).
Así, estos autores desarrollaron un modelo similar al de Clark, pero considerando la existencia de ciclos asimétricos, mediante la aplicación de procesos de cambio de régimen en el intercepto del componente transitorio (Markov-switching models). Entre los principales hallazgos de Kim y Nelson (1999a) se encuentra que los períodos de recesión de Estados Unidos son transitorios y asimétricos.
De otra parte, Sinclair (2010) sostiene que los modelos que suponen simetría en los ciclos económicos tienden a sobresaltar los movimientos permanentes de la economía, habida cuenta de la dominancia que ejercen los períodos expansivos en el comportamiento del PIB. En este contexto, el presente trabajo estima el crecimiento tendencial de la economía chilena, relajando el supuesto de simetría de los ciclos económicos;para luego comparar este resultado con la medida de tendencia determinística y estocástica –considerando la restricción de ciclos homogéneos.
El presente estudio está organizado de la siguiente forma: la primera sección corresponden al marco teórico; la segunda parte muestra la estimación de la tasa de crecimiento potencial de la economía suponiendo que ésta oscila entorno a una tendencia determinística con quiebres de media; el tercer apartado replica el análisis de la sección anterior, pero considerando que el proceso generador de datos sigue una tendencia estocástica; en el cuarto segmento se concluye.
MARCO TEÓRICO
En esta sección se presentan los modelos estadísticos utilizados para el cálculo de la tasa de crecimiento de largo plazo de la economía chilena. Los modelos están basados en series cronológicas univariadas, asumiendo tendencia determinística y estocástica, respectivamente.
Modelo con tendencia determinística
Por naturaleza una tendencia determinística no tiene asociada una distribución de probabilidad, es decir, cada evento de una sucesión de observaciones ocurre con certeza. En este contexto, una serie yt cuya trayectoria intertemporal muestra una clara pendiente (positiva o negativa), podría ser modelada a través de una tendencia lineal (t). Así, se espera que dicha tendencia capture el comportamiento de "largo plazo" de yt –en otras palabras, se dice que yt es estacionaria en tendencia. Formalmente, tiene la siguiente especificación log-lineal:
Siendo α y β los parámetros a estimar que corresponden al intercepto y a la tasa compuesta de crecimiento de la variable yt; εt es un término de error integrado de orden cero. En efecto, la dinámica de largo plazo de yt estaría colapsada en β.
Lo anterior, también puede ser analizado desde una perspectiva de la econometría inglesa –particularmente, se hace referencia al análisis de cointegración de series de tiempo. Dos series no estacionarias Γt = {yt, t} se dicen cointegradas, si existe una relación de equilibrio estable a largo plazo entre tales series. En otras palabras, se dice que los errores de la ecuación [1] son estacionarios (o integrados de orden cero), implicando en que eventualmente el lado izquierdo de dicha ecuación sea igual al término de lado derecho. Así, la matriz de una única fila Θ = (1, - β) es el vector de cointegración, por lo que Γ´t Θ = 0 es estacionario. No obstante, puede que en el corto plazo (período a período) yt se aleje de t, pero a lo largo del tiempo el comportamiento de las variables en Γt volverá a mostrar una relación de equilibrio estable, es decir Γt Θ convergerá a cero. La relevancia estadística de la cointegración está en las buenas propiedades de los estimadores OLS de la regresión. Es más, los estimadores OLS resultan ser superconsistentes –ya que convergen al verdadero valor de α y β a una tasa 1/ T , en lugar de la tasa 1/ √ T como ocurre generalmente.
Finalmente, otra de las ventajas de la relación cointegradora es que a través de un modelo de corrección de errores (MCE), permite separar la dinámica de corto plazo del comportamiento de largo plazo –es decir, el MCE captura los desajustes que ocurren período a período con respecto a la relación de equilibrio de largo plazo.
Modelo con tendencia estocástica: un enfoque de variable inobservada
Esta alternativa metodológica, relaja el supuesto de que la serie sea estacionaria en tendencia. Al respecto, Nelson y Plosser (1982) proponen un modelo en que la actividad económica sigue una caminata aleatoria con deriva y no una tendencia determinística, por lo que la no estacionariedad de la serie yt podría ser removida tomando primeras diferencias. Su análisis más reciente sugiere que la mayor parte de la volatilidad de los shocks en la economía de Estados Unidos podría ser asignada al componente de tendencia no estacionario, con pequeños shocks sobre el componente cíclico.
Por otra parte, dado que los promedios anuales ocultan ciertos patrones de comportamiento de la actividad económica evidentes en datos de mayor frecuencia (trimestral o mensual), Clark (1987) aplica una versión de componentes inobservados con frecuencia mensual para el cálculo de la tendencia, a la vez que evalúa la relativa importancia de la tendencia estocástica y el componente cíclico en la actividad económica.
Para distinguir entre modelos con tendencia determinística y estocástica se consideró el siguiente sistema de series de tiempo, propuesto por Clark (1987) y Kim y Nelson (1999b):
Siendo yt el indicador de actividad; ηt el componente de tendencia estocástica de la economía que sigue un proceso de caminata aleatoria con deriva gt –que a su vez supone que esta variable es dominada por un proceso de caminata aleatoria sin constante; y xt es el componente cíclico de la actividad económica, que se asume como estacionario.
El cálculo del crecimiento potencial está basado en la derivación del filtro de Kalman para la estimación de variables inobservadas en modelos representados de la forma estado-espacio (State-Space models). Este es un método estadístico de estimación recursiva (por máxima verosimilitud) de una colección de ecuaciones matemáticas. La idea esencial de este tipo de modelos descansa en la hipótesis de que existe un estado subyacente de actividad, el cual es retroalimentado con información observable período a período (o más bien con señales del estado de la economía). Así, esta metodología relaja el supuesto de que la actividad económica de largo plazo estaría gobernada por un proceso de tendencia determinística –que asume una tasa constante de variación anual del producto potencial.
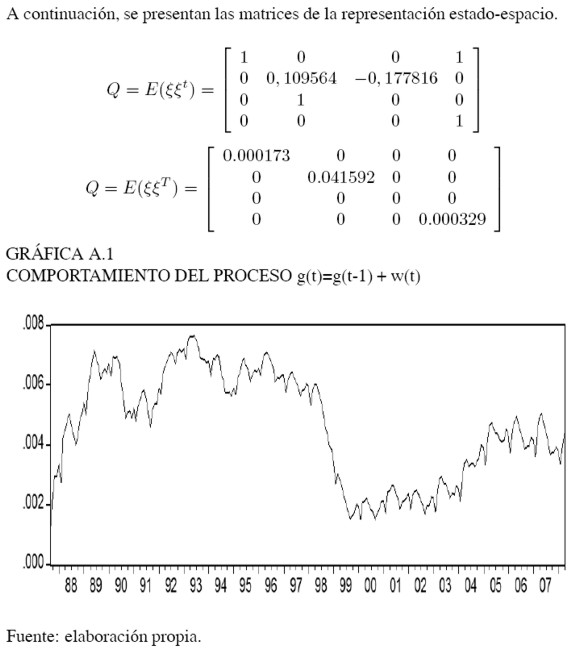
A continuación se expone la representación estado-espacio del anterior sistema de ecuaciones:
Las dos últimas ecuaciones corresponden a la ecuación de estado y medida, respectivamente. Este sistema matricial es estimado mediante máxima verosimilitud3.
ESTIMACIÓN DEL MODELO
La actividad económica oscila en torno a una tendencia determinística4
Las estimaciones basadas en el IMACEC (variable de actividad económica de mayor frecuencia con relación al PIB), revelaron que los shocks que enfrenta el nivel del indicador económico con respecto a su evolución tendencial son en su mayoría transitorios, pero con cambios estructurales que afectan de manera permanente al nivel del IMACEC (esto es lo que en la literatura estadística de series cronológicas se conoce como cointegration with break). Esto implica que el nivel del IMACEC presenta un comportamiento creciente y estable en el tiempo. De lo anterior, se obtuvo que el crecimiento potencial de la economía –medido como la variación mensual anualizada de la tendencia subyacente del IMACEC– se encuentre en torno a 4% anual, valor que difiere del rango medio estimado por el Banco Central (4,5%) y publicado en su IPoM de mayo de 2008.
La tasa de crecimiento potencial está basada en un modelo semilogarítmico desarrollado a partir de la siguiente fórmula de interés compuesto para el cálculo del valor futuro de un activo, que en este caso es el indicador de actividad IMACEC.
Una versión modificada de la expresión anterior, es utilizada comúnmente en la especificación de modelos empíricos de crecimiento
En la cual μt es el término de error del modelo. El efecto neto, que puede ser positivo o negativo, de los factores omitidos es capturado por dicho término de error.
Empleando logaritmo para linealizar se tiene:
O lo que es lo mismo
Esta ecuación es un modelo semilogarítmico (o más bien log-lineal), el cual se utiliza, por regla general, para el cálculo de tendencias de crecimiento de largo plazo Greene (2003). En este caso lnIMAACEC0 corresponde al intercepto de la relación lineal (α), el cual se asume constante en el tiempo; y ln(1+r) corresponde a la pendiente (β) que representa la tasa compuesta de crecimiento autónoma proporcional por cada período.
Con base en lo anterior, la tasa de crecimiento anual es:
Siendo rA la tasa anual de crecimiento (o tasa de crecimiento potencial).
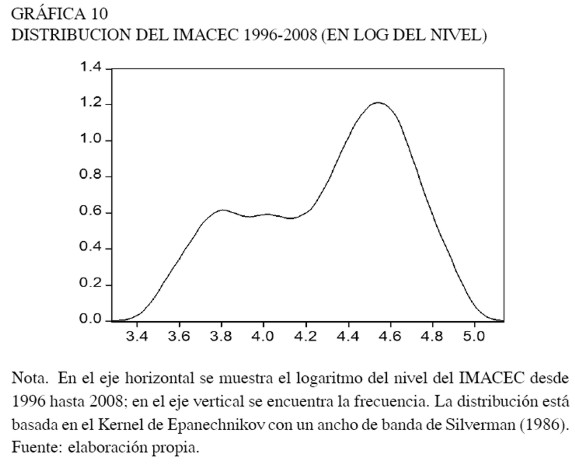
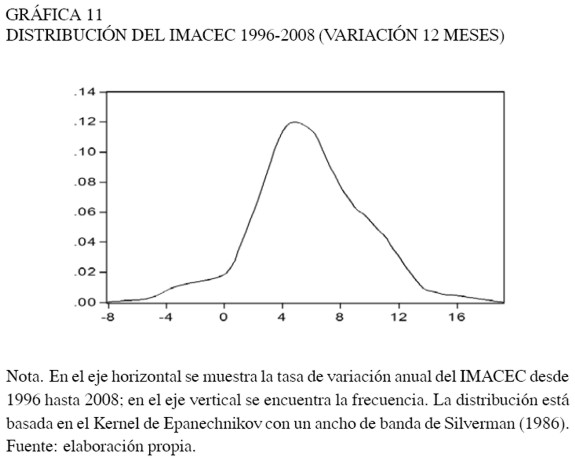
Sin embargo, la actividad no está exenta de sufrir de vez en cuando cambios permanentes de nivel –de otro modo su trayectoria sería puramente tendencial. En este caso, estimar el modelo descrito en la ecuación (7) sería contraproducente, ya que la distribución incondicional del IMACEC presenta más de una moda, indicando la presencia de al menos dos estados o regímenes de la economía5 (ver Gráficas 1 y 2). Por lo tanto, al no controlar por los cambios estructurales de nivel y/o tendencia en la especificación de la ecuación (7), tanto las propiedades estadísticas de los estimadores como los estadísticos de prueba serían pocos o nada concluyentes para garantizar la existencia de una tasa natural de crecimiento de la economía.
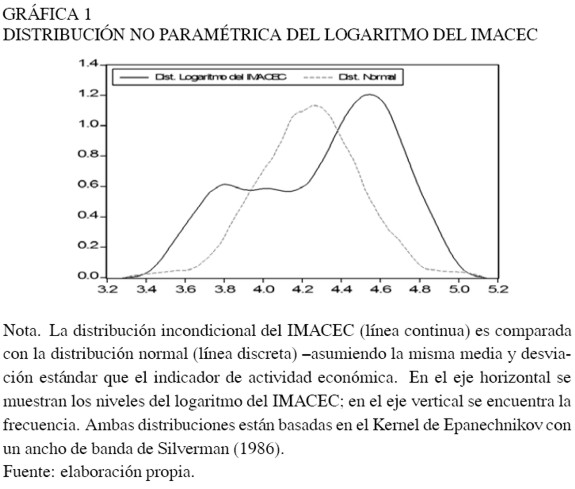
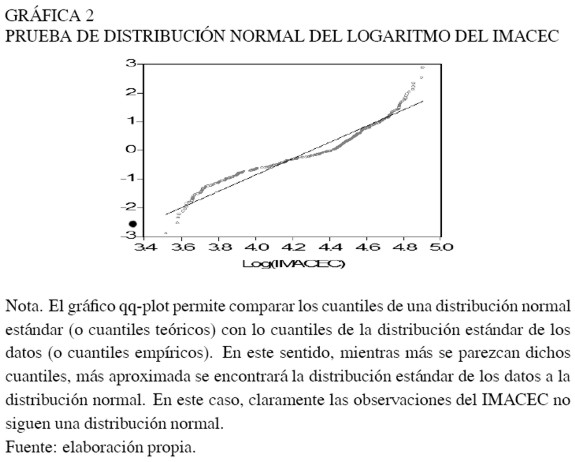
Por ello, se realizaron otros test que permiten identificar si el nivel del IMACEC exterioriza sólo cambios de nivel, sólo de tendencia o ambos (nivel y tendencia). En efecto, los resultados de los test (Dickey y Fuller – aumentado–, 1979; Phillips y Perron, 1988; Zivot y Andrews, 1992) fueron concluyentes en que el nivel de la serie de actividad económica oscila alrededor de una tendencia, pero con cambios de nivel en el tiempo (Zivot y Andrews). Es más, el test F secuencial de Perrón (1990) arrojó tres cambios estructurales de nivel repartidos entre los años 1989, 1991 y 1995. Esto último respalda la posibilidad de que la evolución del IMACEC experimente una "tasa natural" de crecimiento.
El siguiente modelo permite ajustar el IMACEC a una variable de tendencia, controlando por los tres cambios estructurales de su nivel. Este modelo describe la relación de largo plazo entre el IMACEC y su tendencia.
Siendo α la constante; β la tasa compuesta de crecimiento de largo plazo de la economía; y {θk }3 k=1 los coeficientes que acompañan a las variables ficticias (dkt) que capturan los quiebres de nivel en una serie de tiempo.
La estimación de los parámetros para el cálculo de la tendencia del IMACEC se muestra en el Cuadro 1. La Gráfica 3 compara la evolución del indicador económico con su nivel de tendencia estimada.
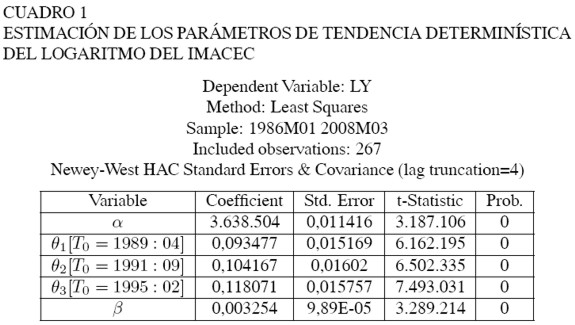
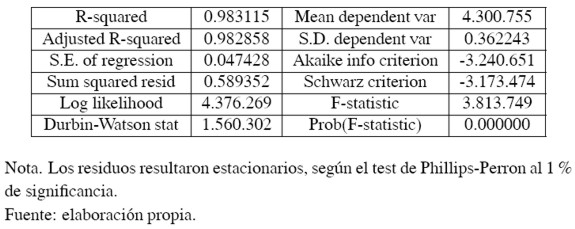
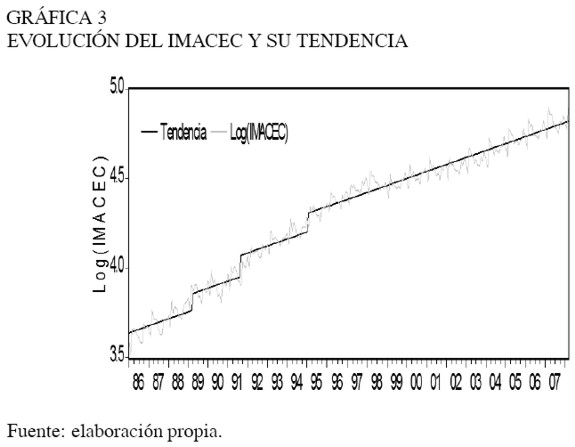
A partir de las estimaciones con información disponible a marzo de 2008, se tiene que el crecimiento potencial de la economía estaría cerca de 0,33% mensual, lo que en términos anualizados sería 4% en promedio6. Al respecto cabe destacar que, a diferencia del PIB efectivo7 de Cuentas Nacionales, la producción potencial es una medida subyacente (no observable) de actividad, ya que sus fundamentos (la estabilidad de precios, una baja tasa de desempleo –tasa natural de paro–, y la ausencia de capacidad instalada ociosa en el aparato productivo) no siempre se observan a lo largo del tiempo. De esta forma, su cálculo debe ser sistemático y sólo constituye una aproximación basada en la información pública más reciente.
Por otra parte, una de las ventajas de analizar series tendenciales es que permiten separar el componente de largo plazo del componente de corto plazo (o dinámica de ajuste hacia la relación de largo plazo). Este último componente se obtiene de estimar la siguiente relación lineal, que incluye el término de error de la relación de largo plazo definida en la ecuación (11). La interpretación de dicho término es el error de corrección de los desvíos del nivel del IMACEC con respecto a su tendencia de largo plazo.
Siendo λ el componente de corrección de los desvíos del IMACEC con respecto a su tendencia de largo plazo, es decir, en el corto plazo λ es distinto de cero, pero en el largo plazo λ tiende a 1, a la vez que el componente de error de la relación de largo plazo tiende a cero, garantizando el calce del IMACEC con su tendencia (nivel potencial del IMACEC).
En el Cuadro 2 se presenta la estimación de la dinámica de corto plazo (descrita en un modelo de corrección de errores), de la que se desprende lo siguiente: cuando el nivel de actividad se desvía de su tendencia, ésta tarda en promedio cerca de siete meses en retomar su trayectoria de largo plazo8.
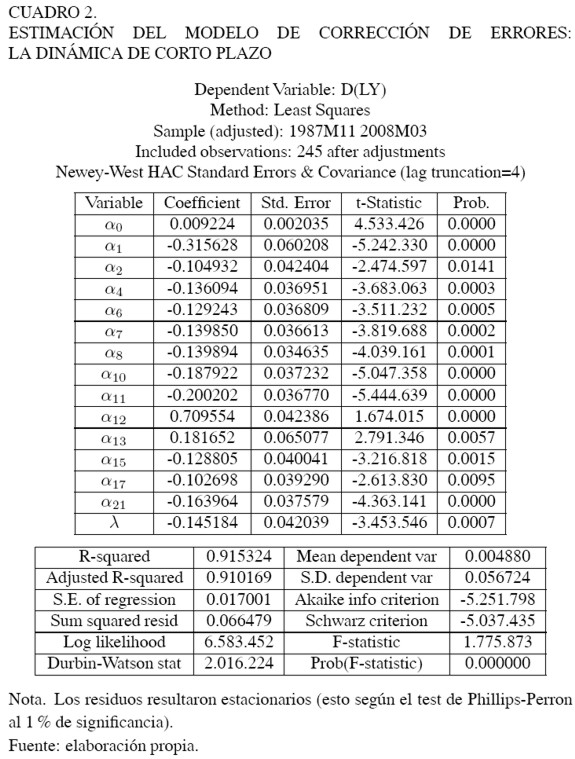
Los residuos ajustados del modelo de corrección de errores –que describe la dinámica de corto plazo del IMACEC respecto a su tendencia– siguen una distribución unimodal que además es normal (ver Gráficos 4 y 5).
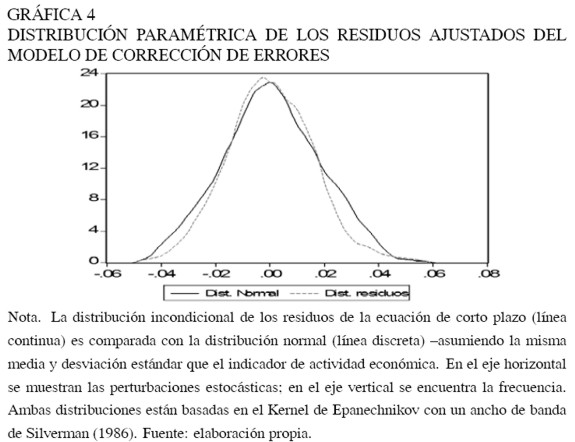
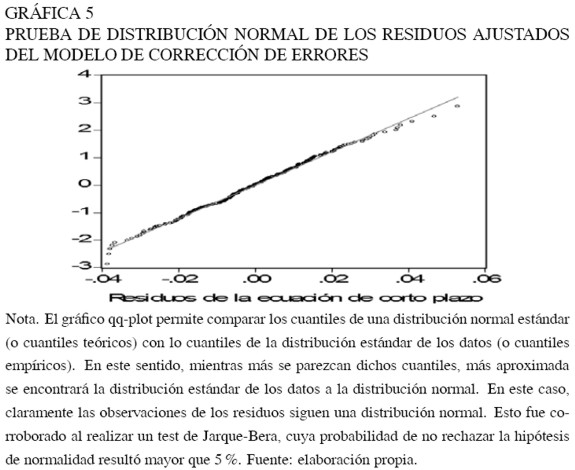
Finalmente, dado que la distribución de los residuos de la ecuación de corto plazo es unimodal y no presenta mayor masa de probabilidad en sus colas (o valores extremos), se puede afirmar, una vez más, que la serie del IMACEC es estacionario en tendencia, es decir, la actividad económica presenta una tendencia en su evolución de largo plazo, que se expande a una tasa de 4% anual. No obstante, en el corto plazo los niveles del IMACEC muestran desviaciones con respecto a su relación de largo plazo, tardando "en promedio" cerca de siete meses –desde que se produjo el desvío– en converger a la tendencia.
La actividad económica oscila en torno a una tendencia estocástica9
Esta sección relaja el supuesto de que el IMACEC oscila en torno a una tendencia determinística. Por lo tanto, la evolución de largo plazo de la actividad económica posee una distribución de probabilidad, es decir, período a período el nivel de tendencia de la actividad económica ocurre con una cierta probabilidad. Así, a partir del modelo planteado en la segunda sección y estimado por filtro de Kalman, se obtuvieron los siguientes resultados que se presentan en el Cuadro 3.

Todos los parámetros resultaron significativos, lo que avala parcialmente la estructura del modelo de series de tiempo planteado en la sección 2. El proceso autorregresivo AR(2) del componente cíclico del IMACEC es débilmente estacionario, puesto que los coeficientes φ1 y φ2 cumplen con las siguientes condiciones de estacionariedad.
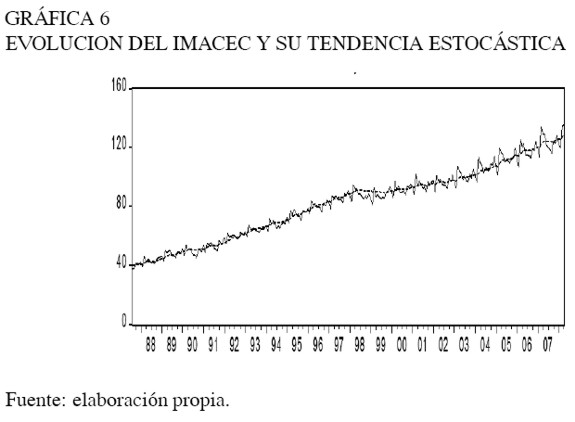
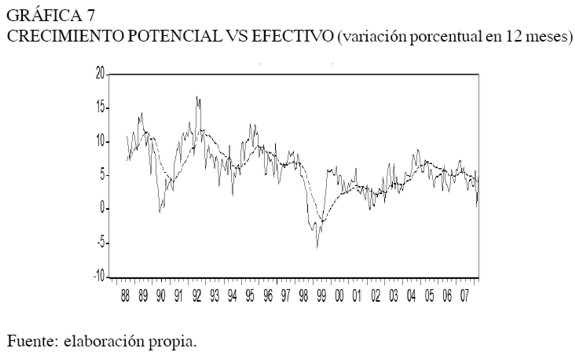
No obstante, las estimaciones indican una relativa persistencia del ciclo económico, lo que podría explicarse por las rigideces del mercado laboral que impiden la inmediata reasignación de los factores productivos en el proceso de producción. La serie de tendencia estocástica y su tasa de variación anual para la economía chilena se muestran en la Gráfica 6, junto con la evolución del indicador de actividad con frecuencia mensual (Gráfica 7). En efecto, el crecimiento potencial de la economía fue 4,3% en 200810.
Por otra parte, Perron (1990) sugiere que las pruebas de raíz unitaria son sesgadas a no rechazar la hipótesis nula (tiene raíz unitaria) cuando el proceso generador de datos es estacionario con medias switching. De esta manera, se podría suponer que el nivel del IMACEC está sujeto a cambios de régimen (Johnson, 2001). Es más, cuando la suma de los coeficientes de un proceso AR es perceptiblemente más baja que 1, ignorar los cambios de régimen daría lugar a la presencia de componentes estacionarios altamente persistentes. Kim y Nelson (1999a) y Sinclair (2010) consideran esta posibilidad al relajar el supuesto de simetría en el componente cíclico de la actividad económica –de acuerdo con la idea de Friedman (1993) plucking model. En este contexto, otro método alternativo para la estimación del crecimiento potencial de la economía es considerar que cuando la distribución de frecuencia de una serie de tiempo es multimodal (como es el caso del IMACEC), dicha serie puede ser modelada asumiendo distintos estados que la gobiernan (proceso Markoviano), con una matriz de transición que describe la probabilidad de mantenerse o transitar hacia un nuevo estado (Hamilton, 1994a).
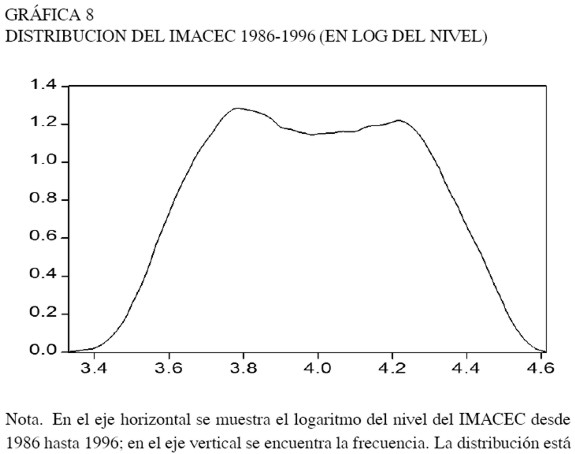
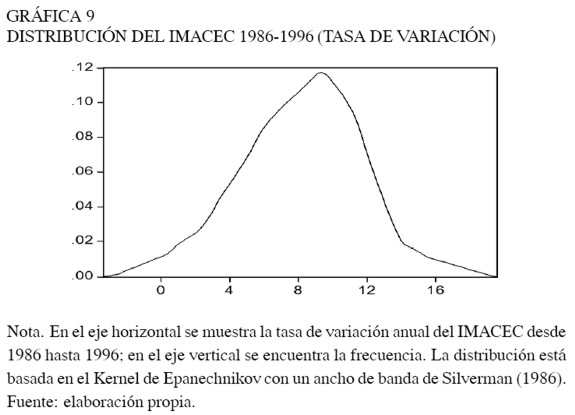
Las gráficas 8, 9, 10 y 11 presentan las distribuciones de frecuencia tanto para el nivel del IMACEC como para su tasa de variación anual y permiten identificar una primera evidencia de que las medias del indicador pueden variar a lo largo del tiempo. Por lo tanto, obviar la presencia de cambios de régimen al menos en medias, podría conducir a la sobrestimación de la persistencia de los ciclos económicos.

Basado en la crítica anterior, se especificó el modelo propuesto en la sección 2, pero considerando la presencia de cambios de régimen en el proceso AR(2) del componente cíclico (Kim y Nelson, 1999a y Sinclair, 2010). En otras palabras, aquí se consideran movimientos asimétricos del ciclo económico:
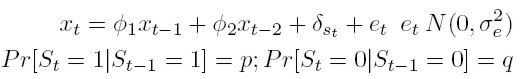 | [13] |
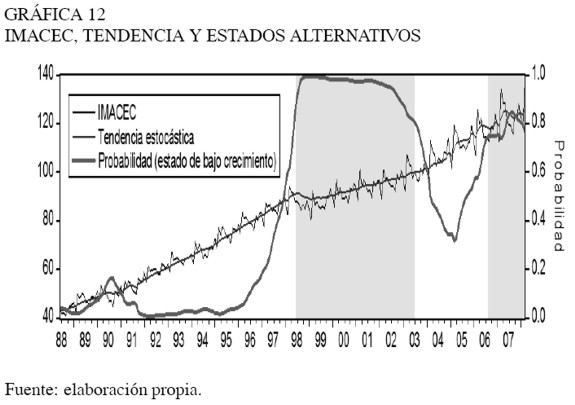
En la Gráfica 12 se evidencia la evolución de la actividad económica efectiva (medida por el nivel del IMACEC) junto con la estimación de su nivel potencial y la probabilidad de que la actividad económica se encuentre la mayor parte del tiempo bajo su nivel de pleno empleo. De igual forma, es posible identificar que los ciclos de la economía chilena son asimétricos.
La Gráfica 13 permite identificar la relación entre la tasa de crecimiento en doce meses del IMACEC y la tasa anual obtenida de la tendencia estocásticas.
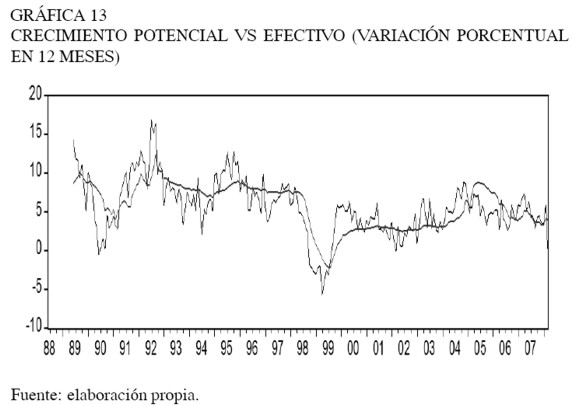
De la Gráfica 13 se desprenden varios períodos del ciclo económico. El primero corresponde al período pre-crisis asiática (o boom económico), en el que la tasa de crecimiento de la actividad potencial fue 8% anual –con una baja probabilidad de que el nivel del IMACEC transitara persistentemente bajo su nivel potencial. El segundo período considera el cambio estructural de la economía causado por la crisis asiática, en el que la variación anual del producto potencial habría disminuido drásticamente, para luego en el período post-crisis, mantenerse en torno a 3% anual –escenario que habría durado cerca de cuatro años, acompañado de probabilidades relativamente altas de que el producto permaneciera bajo su nivel potencial. Por otra parte, desde la segunda mitad de 2004 hasta la primera de 2006, el nivel de crecimiento de largo plazo fue 5% anual –con la expectativa que desde los primeros meses de 2004 se iniciaría la ansiada recuperación económica. Finalmente, a partir del segundo semestre de 2006 se avizora un escenario menos favorable para la economía chilena, con probabilidades superiores al 50% de estar bajo su nivel potencial.
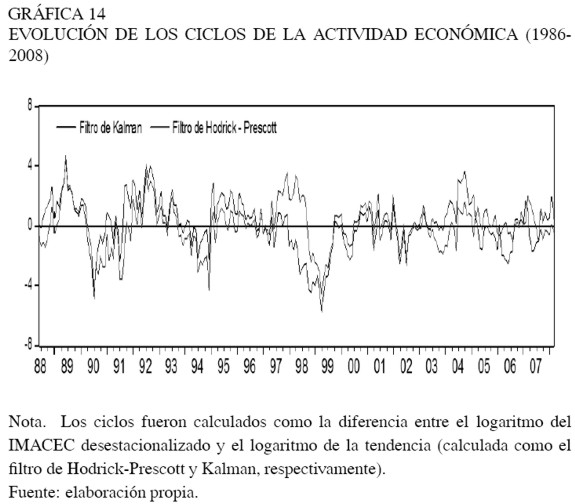
Esta metodología aplicada para la estimación del comportamiento tendencial del IMACEC arroja una tasa de crecimiento de largo plazo en torno a 4,1% anual, y con escasas posibilidades de aumentar en el mediano plazo. Finalmente, los filtros Hodrick-Prescott y Kalman (con cambios de régimen) indican que la actividad estaría muy próxima a su nivel potencial (Gráfica 14), lo que significa que las brechas de capacidad productiva, prácticamente, se habrían disipado.
COMENTARIO FINAL
Calcular el crecimiento potencial de la economía siempre es relevante y lo es aún más en Chile, donde el encarecimiento de la matriz energética enfrió el aparato productivo del país, debido a los altos precios internacionales de los combustibles y el déficit del gas natural proveniente de Argentina, lo que a su vez, afectó a la baja el crecimiento potencial de la economía. En este escenario se estimó la tasa de crecimiento de la economía chilena en un contexto de plena utilización de los recursos productivos. Se emplearon para el análisis modelos univariados de series de tiempo –incluyendo una tendencia determinística (con quiebres de medias) y un modelo de estadoespacio que considera una tendencia estocástica y un componente cíclico, estimado por Filtro de Kalman. El componente cíclico fue estimado con y sin cambios de régimen (Markov-switching models), de acuerdo con la idea de Friedman (1993) –plucking model. Los resultados indicaron que la tasa de crecimiento potencial de la economía chilena es superior al 4% anual, acompañada de ciclos económicos asimétricos.
Por último, cabe mencionar que el procedimiento utilizado en este documento es una de varias alternativas de cálculo de la actividad subyacente de pleno empleo de los recursos productivos, ya que en la literatura no hay consenso con respecto al método de medición del crecimiento tendencial de la economía. Sin embargo, los modelos de estado-espacio utilizados en el presente artículo son previsiblemente más apropiados para estimar el producto potencial, ya que éste es una variable no observada.
NOTAS AL PIE
1 De acuerdo con el modelo Plucking de Friedman (1993), el componente transitorio es afectado fundamentalmente por un shock discreto, determinado por una variable no observada.
2 Otra técnica más tradicional para estimar el crecimiento tendencial de la economía es la descomposición del residuo de Solow en el que se estima una función de producción neoclásica de tipo Cobb-Douglas (los argumentos de dicha función son el stock de capital en cada momento del tiempo, la fuerza de trabajo, y la productividad total de los factores); otra alternativa es utilizar modelos RBC (Kydland y Prescott, 1982), que en un marco de equilibrio general, relajan el supuesto de que la formación de capital se imponga exógenamente, en cuyo escenario tanto la decisión de trabajar como la de acumulación de capital se determinan de forma conjunta y con base en las relaciones económicas fundamentales.
3 Para profundizar en la estimación por máxima verosimilitud, ver Kim y Nelson (1999b).
4 Esta sección está construida siguiendo el trabajo realizado por Chumacero y Quiroz (1996) que estiman la tasa natural de crecimiento de la economía chilena 1985-1996. En este trabajo se utiliza la misma metodología para actualizar la tasa de crecimiento tendencial entre 1986 y 2008. No obstante, en los siguientes apartados se exploran otras técnicas para el cálculo del crecimiento de largo plazo.
5 Hamilton (1994) muestra que la existencia de más de una moda en la distribución de una serie de tiempo, implica la presencia de raíz unitaria.
6 La anualización de la tasa de crecimiento mensual se obtiene de la siguiente fórmula: 4% = [(1+0, 33 %)12 − 1](100)
7 Es la suma total de bienes y servicios que es capaz de producir la economía de un país y que para efectos de medición y/o comparación se traduce en términos monetarios.
8 Este resultado se obtiene del inverso del valor absoluto de 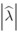
9 Esta sección está construida siguiendo los trabajos de Harvey (1989) y Hamilton (1994a).
10 La estimación de la tasa de crecimiento tendencial actualizada a 2009 no difiere significativamente de la observada en 2008. No obstante, el nivel de crecimiento potencial de la economía en 2009 considera el efecto de la reciente crisis financiera internacional en la producción interna de Chile.
REFERENCIAS BIBLIOGRÁFICAS
[1] Banco Central de Chile. (2008). Informe de Política Monetaria, mayo. Santiago de Chile: Banco Central de Chile. Recuperado de http://www.bcentral.cl/publicaciones/politicas/pdf/ipm052008.pdf. [ Links ]
[2] Clark-Peter, K. (1987). The Cyclical Component of U.S. Economic Activity. Quartely Journal of Economics, 102(4), 797-814. [ Links ]
[3] Contreras, G. y García, P. (2002). Estimating Gaps and Trends for the Chilean Economy. Economic Growth: Sources, Trends and Cycles. Santiago de Chile: Banco Central de Chile. Recuperado de http://www.bcentral.cl/estudios/bancacentral/pdf/v6/523_554contreras_garcia.pdf. [ Links ]
[4] Chumacero, R. y Quiroz, J. (1996). La Tasa Natural de Crecimiento de la Economía Chilena: 1985-1996. Cuadernos de Economía, 33(100), 453-472. [ Links ]
[5] Dickey, D.A. y W.A. Fuller. (1979). Distribution of the Estimators for Autoregressive Time Series With a Unit Root. Journal of the American Statistical Association, 74(366), 427-431. [ Links ]
[6] Friedman, M. (1993). The Plucking Model´ of Business Fluctuations Revisited. Economic Inquiry, 31(2), 171-177. [ Links ]
[7] Fuentes, R., Gredig, F. y Larraín, M. (2008). La Brecha de Producto en Chile: Medición y Evaluación. Economía Chilena, 11(2), 7-30. [ Links ]
[8] Gallego, F. y Johnson, C. (2001). Teorías yMétodos de Medición del Producto de Tendencia: Una Aplicación al Caso de Chile. Economía Chilena, 4(2), 27-58. [ Links ]
[9] Greene,W.H. (2003). Econometric Analysis (Fifth Edition). New Jersey: Prentice Hall. [ Links ]
[10] Hamilton, J.D. (1994). Time Series Analysis. Princeton, NJ: Princeton University Press. [ Links ]
[11] Harvey, A. C. (1989). Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge: Cambridge University Press. [ Links ]
[12] Johnson, C. (2001). Un Modelo de Switching para el Crecimiento en Chile. Cuadernos de Economía, 38(115), 291-319. [ Links ]
[13] Kalman, R.E. (1960). A New Approach to Linear Filtering and Prediction Problems. Journal of Basic Engineering, 82(D), 35-45. [ Links ]
[14] Kim, C.J. y Nelson, C.R. (1999a). Friedman´s Plucking Model of Business Fluctuations: Tests and Estimates of Permanent and Transitory Components. Journal of Money, Credit, and Banking, 31(3), 317-334. [ Links ]
[15] Kim, C.J. y Nelson, C.R. (1999b). State Space Models with Regime Switching: Classical and Gibbs-Sampling Approaches with Applications. Cambridge, Massachusetts: The MIT Press. [ Links ]
[16] Kydland, F. and Prescott, E. (1982). Time to build and aggregate fluctuations. Econometrica, 50(6), 1345-1370. [ Links ]
[17] Menashe, Y. y Yakhin, Y. (2004). Mind the Gap: Structural and Nonstructural Approaches to Estimating Israel´s Output Gap. Israel Economic Review, 2(2), 79-106. [ Links ]
[18] Nelson, C.R. y Plosser, C.I. (1982). Trends and random walks in macroeconomic time series: Some evidence and implications. Journal of Monetary Economics, 10(2), 139-162. [ Links ]
[19] Perron, P. (1990). Testing for a Unit Root in a Time Series with a Changing Mean. Journal of Business and Economic Statistics, 8(2), 153-162. [ Links ]
[20] Phillips-Peter, C.B. y Perron, P. (1988). Testing for a Unit Root in Time Seriesc Regression. Biometrika, 75(2), 335-346. [ Links ]
[21] Silverman, B.W. (1986). Density Estimation for Statistics and Data Analysis. Londres: Chapman y Hall. Disponible en: http://gemini.econ.umd.edu/jrust/econ623/lectures/silverman_density_estimation.pdf. [ Links ]
[22] Sinclair-Tara, M. (2010). Asymmetry in the Business Cycle: Friedman´s Plucking Model with Correlated Innovations. Studies in Nonlinear Dynamics & Econometrics, 14(1), article 3. [ Links ]
[23] Zivot, E. y Andrews-Donald, W.K. (1992). Further Evidence on the Great Crash, the Oil-Price Shock and the Unit-Root Hypothesis. Journal of Business and Economic Statistics, 10(3), 251-270. [ Links ]













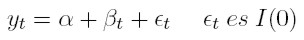 [1]
[1] 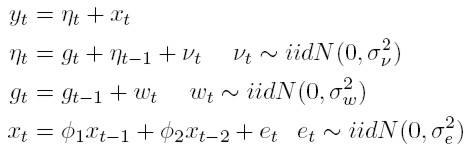 [2]
[2] 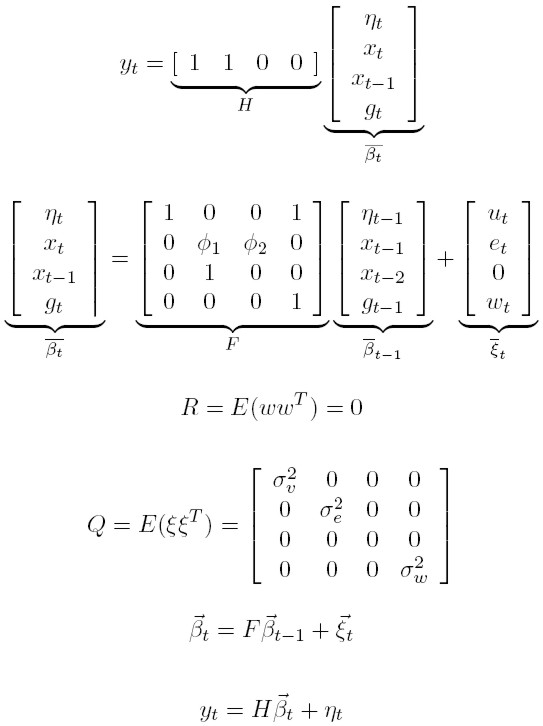 [3]
[3] 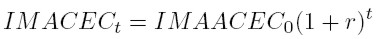 [4]
[4] 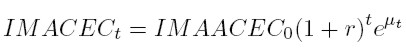 [5]
[5] 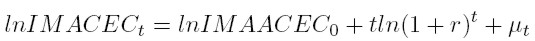 [6]
[6] 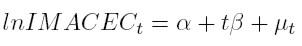 [7]
[7] 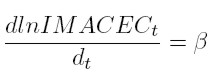 [8]
[8] 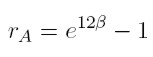 [9]
[9] 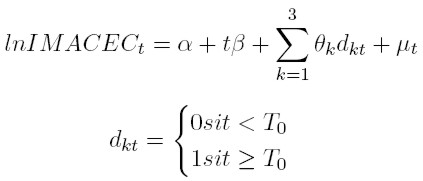 [10]
[10] 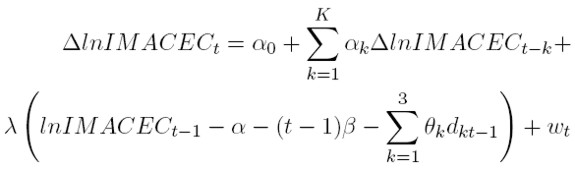 [11]
[11] 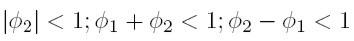 [12]
[12] 
