Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.29 no.53 Bogotá July/Dec. 2010
CAOS EN EL MERCADO DE COMMODITIES
Christian Espinosa Méndez*
* Doctor en Finanzas, se desempeña actualmente como Director Académico del Magíster en Finanzas de la Facultad de Economía y Empresa, de la Universidad Diego Portales (Santiago de Chile, Chile). Dirección de correspondencia: Manuel Rodríguez 253, Facultad de Economía y Empresa, Universidad Diego Portales (Santiago de Chile, Chile). E-mail: christian.espinosa@udp.cl.
Resumen
Este artículo aplica seis técnicas y herramientas (análisis gráfico, gráfico de recurrencia, entropía de espacio temporal, coeficiente de Hurst, exponente de Lyapunov y dimensión de correlación), a las series de retornos del cobre, oro, petróleo, plata, zinc, aluminio, plomo y níquel, con el fin de corroborar la existencia de un comportamiento caótico en el mercado de commodities. Se encuentra evidencia de que los mercados financieros se comportan de forma caótica en contra de la hipótesis de aleatoriedad. Se contrasta, igualmente, no-normalidad, no-aleatoriedad y no-linealidad. Los resultados encontrados contradicen algunos de los supuestos básicos de la teoría financiera moderna.
Palabras clave: gráfico de recurrencia, coeficiente de Hurst, exponente de Lyapunov, dimensión de correlación, test BDS, metales, caos, commodities. JEL: C12, C14, G10, G14, G15.
Abstract
This article employs six techniques and tools such as chart analysis, chart recurrence, space temporary entropy, Hurst coefficient, Lyapunov exponent and dimension correlation on the copper, gold, oil, silver, zinc, aluminium, nickel, and lead return series to corroborate the existence of a chaotic behaviour in the market for commodities. Evidence that the financial markets behave in a chaotic way versus the randomness hypothesis is found. In addition, the study contrasts non-normally, non-randomness and nonlinearity. These results contradict some of the basic assumptions of modern financial theory.
Key words: recurrence chart, Hurst coefficient, Lyapunov exponent, dimension correlation, BDS test, metals, chaos, commodities. JEL: C12, C14, G10, G14, G15.
Résumé
Cet article applique six techniques et outils (analyse graphique, graphique de récurrence, entropie d´espace temporelle, coefficient de Hurst, exposant de Lyapunov et dimension de corrélation), aux séries de retours du cuivre, de l´or, du pétrole, de l´argent, du zinc, de l´aluminium, du plomb et du nickel, pour corroborer l´existence d´un comportement chaotique sur le marché de commodities. On trouve que les marchés financiers se comportent d´une forme chaotique contre l´hypothèse d´aléatoriété. On remarque, également, la présence de non-normalité, non-aléatoriété et non- linéarité. Les résultats contredisent certains des hypothèses de base de la théorie financière moderne.
Mots clés : graphique de récurrence, coefficient de Hurst, exposant de Lyapunov, dimension de corrélation, test BDS, métaux, chaos, commodities. JEL : C12, C14, G10, G14, G15.
Este artículo fue recibido el 10 de julio de 2009, la versión ajustada fue recibida el 15 de marzo de 2010 y su publicación aprobada el 15 de agosto de 2010.
En 2006 y 2007 el mercado de commodities experimentó uno de los crecimientos más vertiginosos de las últimas décadas. Los precios del petróleo, cobre y oro, sólo por nombrar algunos productos, llegaron a niveles insospechados. Con respecto a esto, los argumentos del alza en el nivel de precios de estos commodities se atribuyeron a factores de demanda (principalmente de China, India y Rusia), a factores de oferta (restricciones en los niveles de inventarios) y a otros que de algún modo hacen que la producción no satisfaga la demanda creciente (alza en los costos de producción, rezagos en la inversión para exploración de nuevos yacimientos, debilitamiento del dólar, factores climatológicos y de estabilidad geopolítica, son los más habituales). A lo anterior, debe sumarse que muchas inversiones se concentraron en estos mercados, buscando aprovechar las alzas en los precios, lo cual ha aumentado la volatilidad y el atractivo para que especuladores y arbitrajistas ingresen a estos mercados.
Si bien son ciertos los análisis precedentes, también lo es el hecho que explican sólo en parte el alza en los precios de los commodities y, por consiguiente, las proyecciones de largo plazo habitualmente no son correctas.
Dado esto, es importante identificar cuál es la dinámica que sigue el comportamiento de estos activos; de esta manera, modelar su evolución y conocer a muy corto plazo cuál será su estado futuro.
Ahora, si se observa un commodity como un activo financiero deseable para invertir se requiere saber por qué motivo cambia de precio. En el siglo XX, se distinguen tres corrientes de pensamiento que han tratado de dar una explicación al cambio de los precios de activos financieros. Estas son; el análisis fundamental1, el análisis técnico2 y la llamada "teoría financiera moderna"3. Mucho se ha escrito a favor y en contra de cada una de estas posturas; sin embargo, ninguna dice certeramente cuál es el proceso subyacente que explica el cambio en los precios de estos activos. A los enfoques mencionados hay que agregar nuevos hallazgos, tales como: mercados fractales, dependencias de largo plazo y la existencia de un comportamiento caótico que presentan las series financieras.
En particular, la contrastación de comportamiento caótico en economía se inició en la década de 1980, aplicada a variables macroeconómicas como el PIB y los agregados monetarios (Le Barón, 1994); desde entonces se han realizado diversos estudios en la búsqueda de comportamiento caótico en series financieras y económicas (Los, 2000; y Los y Yu, 2008), entre otros).
En este contexto, lo habitual es encontrar investigaciones que utilizan técnicas y herramientas tales como el coeficiente de Hurst, exponente de Lyapunov y la dimensión de correlación para la contrastación de comportamiento caótico en dichas series. Por ejemplo, Kyaw, Los y Zong (2004), utilizando wavelet multiresolution analysis (MRA) para las series diarias de los índices bursátiles y tasas de cambio latinoamericanos, encontraron un coeficiente de Hurst igual o mayor a 0,5 en todos los países, excepto en Colombia, lo que corrobora la existencia de dependencias de largo plazo que contienen estas series. Similares resultados encontraron Los y Yu (2008) para el mercado accionario de China; Sadique y Silvapulle (2001) en los retornos accionarios de Korea, Malasia, Singapur y Nueva Zelandia; y Corazza y Malliaris (2002) en cinco mercados monetarios.
Por su parte, Rajaratnam y Weston (2004) encontraron un exponente de Lyapunov de 0,132 para la serie del tipo de cambio entre Nueva Zelanda y Estados Unidos, para el período comprendido entre 1985 y 2004, lo que comprueba la existencia de un comportamiento caótico.
En un trabajo reciente Parisi, Espinosa, y Parisi (2007) encuentran un comportamiento caótico en las Bolsas de Comercio de Argentina, Brasil, Canadá, Chile, Estados Unidos, Perú y México. Aplicando distintas técnicas y métodos como análisis gráfico, análisis de recurrencia, entropía de espacio temporal, coeficiente de Hurst, exponente de Lyapunov y dimensión de correlación, encuentran resultados que sugieren que los mercados bursátiles americanos se comportan de forma caótica, en contra de la hipótesis de mercados eficientes o de aleatoriedad.
Tomando este trabajo como referencia, la presente investigación corrobora la existencia de un comportamiento caótico en ocho series de commodities (cobre, oro, petróleo, plata, zinc, aluminio, plomo y níquel). La implicación de contrastar un comportamiento caótico en estos mercados consiste en que, a diferencia de la hipótesis de mercados eficientes, la información (o nueva información) que se agrega a la serie de precios de commodities (cambios en la oferta y demanda del commodity, anuncio de aumento o disminución de inventarios, modificación en la estructura de costos de producción, etcétera), no es externa sino que endógena. Esto indicaría que el desafío ya no consiste en dar una explicación estadística, o de otro tipo, a variables estocásticas para que ayuden a mejorar el pronóstico de la evolución futura de dichas series, sino que se centraría en descubrir la dinámica subyacente de cada uno de estos mercados. Desde el punto de vista práctico, justifica la búsqueda de técnicas predictivas que incorporen los nuevos hallazgos a la hora de invertir en estos mercados, al menos a muy corto plazo. En síntesis, el principal aporte de la teoría de caos es que otorga una explicación teórica de la existencia de sistemas dinámicos con comportamientos irregulares, sin la necesidad de recurrir a variables estocásticas.
El determinar si hay alguna dinámica caótica en la evolución de los precios de commodities es el objetivo de este trabajo, para ello se ha estructurado en cuatro secciones. En el primer apartado se especifican los datos y se corrobora no-normalidad. En la segunda parte se desarrollan siete pruebas para verificar la existencia de un comportamiento caótico en las series en estudio. En el tercer segmento se aplican test estadísticos para contrastar no-aleatoriedad y no-linealidad. Finalmente, se formulan las principales conclusiones.
DATOS Y NO NORMALIDAD
Los datos corresponden al precio de cierre diario de los commodities COBRE, ORO, PETROLEO, PLATA, ZINC, ALUMINIO, PLOMO y NIQUEL. La elección del número de datos se ajustó a los requerimientos de los diversos cálculos estimados y a la disponibilidad de los mismos. Las fuentes de información fueron Economática para los precios del aluminio, zinc, plomo y níquel; Cochilco para precios del cobre, oro y plata; y el Banco Central de Chile para precios del petróleo WTI.
El Cuadro 1 presenta los cuatro primeros momentos de la distribución de los retornos diarios de los precios de commodities en estudio.
Se observa que el retorno promedio diario del níquel es el más alto para el período de la muestra con un 0, 118%, lo que implica un retorno anualizado de 28, 32%. A su vez, la desviación estándar promedio diaria alcanza 2, 32%, por lo que la tasa anualizada representa 35, 99%. Según la teoría financiera moderna retornos más altos presentarán riesgos, medidos como la desviación estándar, mayores. Así se debiera esperar desviaciones menores para el resto de los commodities. No obstante, para el petróleo la desviación estándar promedio diaria alcanza 2, 77%, por lo que la tasa anualizada representa un 42, 93%, con un retorno promedio diario asociado del 0, 031%, es decir, un retorno anualizado de 7, 44%. En otras plabras, mayores retornos no implican, necesariamente, mayores riesgos.
Ahora, si se considera el cobre se observa que el retorno medio diario es el menor de la muestra con 0, 023%, lo que implica un retorno anualizado de 5, 52%, y la desviación estándar promedio diaria alcanza a 1, 578%, por lo que la tasa anualizada representa un 24, 45%. El oro, por su parte, presenta un retorno medio diario de 0, 042%, lo que implica un retorno anualizado de 10, 08%, y una desviación estándar promedio diaria de 0, 920%, por lo que la tasa anualizada es 14, 25%4.
El coeficiente skewness acepta la hipótesis nula de que el coeficiente de asimetría tiene un valor de 0. Por su parte, el coeficiente de kurtosis genera un estadístico z mayor a 1, 96, en valor absoluto, para todos los retornos de commodities, lo que rechaza la hipótesis nula de que el coeficiente de kurtosis tenga un valor de 3. Esta característica es observada habitualmente en retornos de activos financieros (leptokurtosis).
Por último, los resultados del test de Jarque-Bera muestran, claramente, que la probabilidad de que los retornos de commodities provengan de una distribución normal es casi nula. Así, la no normalidad y la elevada kurtosis suelen ser indicios de que la serie ha sido generada por un proceso no lineal.
DETECCIÓN DE COMPORTAMIENTO CAÓTICO
A continuación se aplica una serie de herramientas proporcionadas por la teoría de caos, para entender la dinámica de la evolución de los rendimientos de commodities y corroborar la existencia de un comportamiento caótico en dichas series.
Análisis gráfico
Siguiendo a Peters (1994) se buscan indicios de una serie con comportamiento caótico mediante el análisis gráfico. En la Gráfica 1 se observa la evolución diaria del precio del cobre en cuatro horizontes de tiempo. No resultan diferencias importantes entre éstas.
El hecho de que estas series tengan la misma apariencia en distintas escalas de tiempo es un indicio de que se está ante un fractal; sin embargo, no es garantía definitiva de que sea un proceso caótico. Similar evidencia se encuentra para el resto de las series en estudio.
Gráfico de recurrencia
Otra manera de analizar series temporales desde una perspectiva gráfica es construir Gráficos de recurrencia. En este contexto, una señal de determinismo se evidencia entre más estructurado sea el gráfico de recurrencia y una señal de aleatoriedad se presenta cuando sea más uniforme y no tenga un patrón identificable5.
En la Gráfica 2 se muestran los gráficos de recurrencia para una serie aleatoria generada en una planilla Excel que toma valores entre 1 y 5.000 y el gráfico de recurrencia para el atractor extraño de Lorenz –una con comportamiento caótico y la otra no–, para establecer la diferencia gráfica.

En el gráfico de recurrencia correspondiente al atractor de Lorenz (más estructurado) se observa una señal de determinismo en contraste con la serie aleatoria (más uniforme). Así mismo, en el primero, se detectan líneas horizontales que denotan la existencia de órbitas periódicas inestables, lo cual también es consistente con series que presentan un comportamiento caótico.
Para la construcción de los gráficos de recurrencia se utilizó el programa Visual Recurrence Analysis (VRA)6 que utiliza la técnica Información Mutua (AMI) para determinar el tiempo de retardo y el método de Falsos Vecinos Cercanos (FNN) para la dimensión de inmersión7. Los resultados de los cálculos de AMI y FNN se muestran en el Cuadro 2.
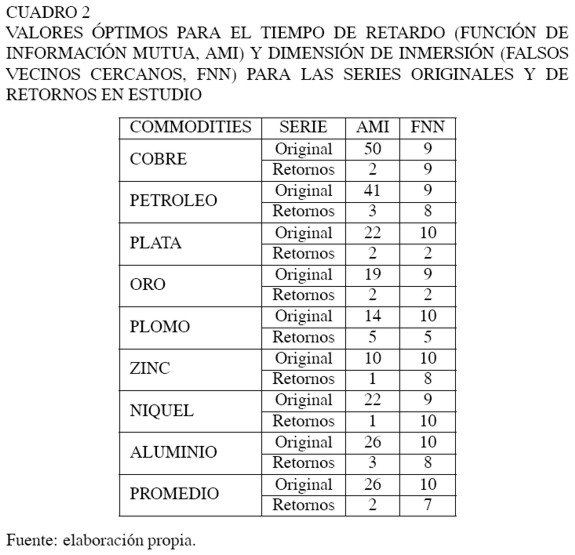
Los gráficos de recurrencia de las series originales de los commodities en estudio se asemejan a los de una serie aleatoria que no tiene un patrón definido, a diferencia de los gráficos de recurrencias aplicados a los retornos que se asemejan más a datos con comportamiento caótico como el del atractor de Lorenz. Véase la Gráfica 3 para un ejemplo de los gráficos de recurrencia de los commodities petróleo y níquel.
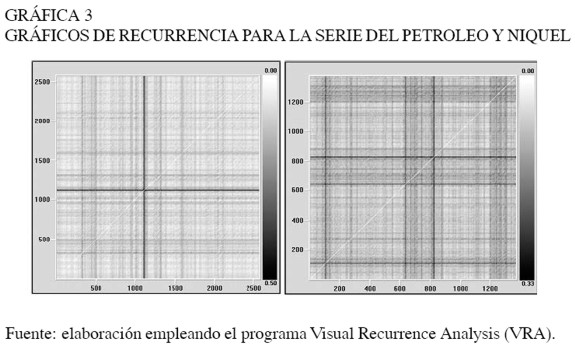
Entropía de espacio temporal
Siguiendo la búsqueda de comportamiento caótico se aplicó la herramienta Entropía de Espacio Temporal (STE). La STE compara la distribución de colores sobre un gráfico completo de recurrencia con la distribución de colores sobre cada línea diagonal del gráfico.
En síntesis, se comparan las distancias entre todos los pares de vectores en el espacio reconstruido con las distancias entre las diversas órbitas que se desarrollan durante el tiempo. El resultado se normaliza y se presenta como porcentaje. Así, porcentajes cercanos a 100 indicarán aleatoriedad en la serie, cercanos a 0 representarán series periódicas y entre 0 y 100 indicarán series con comportamiento caótico. Los resultados se muestran en el Cuadro 3.
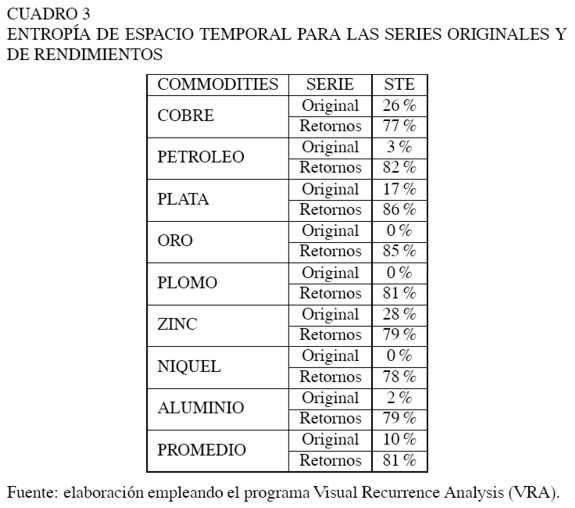
De acuerdo con el Cuadro 3, se puede identificar un comportamiento caótico en las series de commodities, 81% para las series de retornos y 10% para las series originales. Los resultados de las series de retornos es un indicio claro, pero no definitorio, de estar en presencia de series con comportamiento caótico.
Dependencias de largo plazo
El análisis del rango reescalado o análisis R/S, propuesto por Hurst (1951) y posteriormente afinados por Mandelbrot y Wallis (1969) y Mandelbrot (1972) es utilizado para contrastar la dependencia a largo plazo en una serie temporal. En síntesis, el estadístico R/S mide el rango de las desviaciones de las sumas parciales de una serie temporal con respecto a su media, reescalado por la desviación típica de la serie. Una consecuencia importante del análisis del rango reescalado es que permite determinar el exponente de Hurst.
Mandelbrot y Wallis (1969) afirman que el rango reescalado de las subseries está asintóticamente relacionado con su longitud y plantean formalmente:
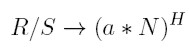 | [1] |
En el que α es una constante, N es el número de observaciones, H es el exponente o coeficiente de Hurst, R/S es el estadístico R/S(N) que depende del tamaño de la serie y que se define como el rango de variación de la serie partido por su desviación típica.
Así, cuando R/S(N) es observado sobre varios valores de N y aplicando una regresión de mínimos cuadrados ordinarios, se obtiene:
Siendo H el coeficiente de Hurst. Mandelbrot (1972) demuestra que H puede variar entre 0 y 1. Así, si se encuentra entre 0, 5 y 1 indicaría persistencia en la serie, si se encuentra entre 0 y 0, 5 indica no-persistencia y un valor igual a 0, 5 indicaría que el comportamiento de la serie es completamente aleatorio8.
Los resultados que se resumen en el Cuadro 4 muestran un coeficiente de Hurst mayor a 0, 5 en todas las series, excepto para el petróleo, lo que es un apoyo robusto a la existencia de dependencias de largo plazo en las series de commodities.
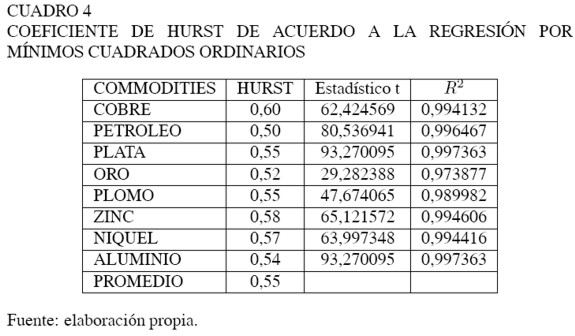
Las acciones de la Organización de Países Exportadores de Petróleo (OPEP) puede ocasionar que la serie de petróleo pierda memoria. Así, un "efecto reset"9 puede estar operando cada vez que la OPEP toma una decisión en cuanto a la oferta. Este síntoma podría ser explicado a través de un análisis multifractal, cuestión que es dejada para un próximo estudio. Para el resto de las series se confirma una memoria de largo plazo contenida en las series bajo estudio.
Exponente de Lyapunov
El Exponente de Lyapunov (λ) sirve para medir, en un sistema dinámico, la sensibilidad a las condiciones iniciales. Ello se hace mediante una función exponencial, en la cual el exponente determina la tasa de divergencia de órbitas adyacentes que parten de puntos próximos (Nieto del Alba, 1998).
Existen diferentes algoritmos10 para calcular el máximo exponente de Lyapunov. No obstante, la mayoría de estos métodos no son aplicables para series de tiempo pequeñas y son relativamente difíciles de implementar. Rosenstein, Collins y De Luca (1993) desarrollaron un método que, después de reconstruir la dinámica del atractor, permite que el algoritmo desarrollado localice el punto Yn, más cercano a cada punto de la trayectoria Yn. Además, impone la restricción que los puntos vecinos más cercanos deben tener una separación espacial mayor que el período medio de las series de tiempo. Esto permite considerar que cada par de vecinos corresponden a condiciones iniciales muy cercanas pero de diferentes trayectorias. Así, el máximo exponente de Lyapunov es aproximadamente la velocidad media de separación de los puntos vecinos más cercanos.
Los resultados del exponente de Lyapunov11, que se encuentran resumidos en el Cuadro 5, indican que λ > 0, para todas las series originales y las de retornos de commodities en estudio, lo que representa un indicio de la existencia de un comportamiento caótico en los retornos de commodities.
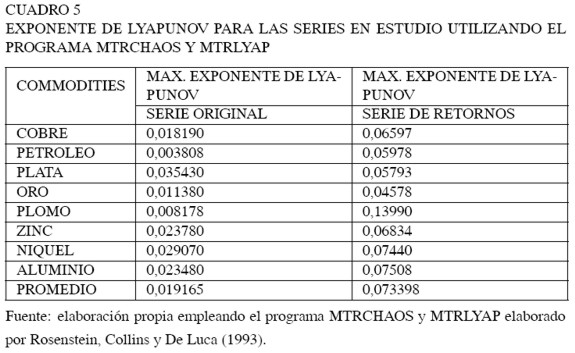
Dimensión de correlación
La dimensión de correlación (Dc) de un sistema dinámico es una medida de su complejidad y permite discriminar entre un sistema determinista y uno aleatorio (Grassberger y Procaccia, 1983). Así, si (Dc) es igual a uno indicará una serie con comportamiento de oscilaciones periódicas; si (Dc) es igual a dos una con oscilaciones cuasi periódicas; y si (Dc) es mayor a dos una serie con comportamiento caótico. Al igual que para el cálculo del exponente de Lyapunov se utiliza el programa MTRCHAOS y MTRLYAP elaborado por Rosenstein, Collins y De Luca (1993) para el cómputo de la dimensión de correlación. El Cuadro 6 muestra los resultados.
Se encuentra una dimensión de correlación promedio de 2, 161 y mayor a dos en todas las series de retornos analizadas. Lo anterior, es un indicio más sobre la existencia de un comportamiento caótico en las series de commodities.
TEST ESTADÍSTICOS
Los resultados de las herramientas descritas en el apartado anterior apoyan la hipótesis de fractal contra la de aleatoriedad. Sin embargo, es necesario aplicar test estadísticos que confirmen estos hallazgos. En particular, se aplica el test de Rachas para carácter aleatorio (o test de Wald-Wolfowitz) y el test BDS propuesto por Brock, Dechert y Scheinkmann (1987).
El test no paramétrico de Wald-Wolfowitz plantea en su hipótesis nula que la serie es aleatoria. Los resultados que se muestran en el Cuadro 7 confirman que las series de retornos de commodities en estudio no son aleatorias y el tipo de esquema resultante indica que la dinámica del sistema subyacente a la serie temporal es de carácter cíclico.
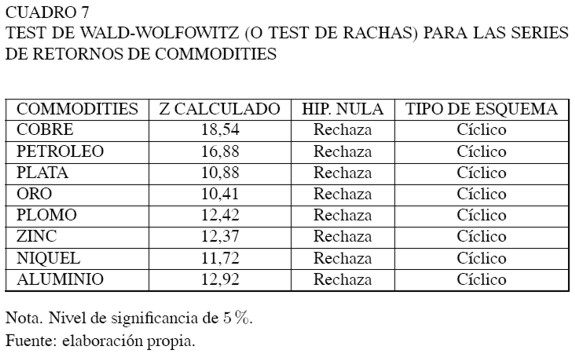
La hipótesis nula del test BDS (H0) es que la serie es independiente e idénticamente distribuida (i.i.d.). Por lo tanto, si eventualmente existiese algún tipo de dependencia entre las observaciones debería ser producida por algún mecanismo no lineal de generación de datos. Los autores demuestran que el estadístico del test se distribuye asintóticamente como una Normal Estándar (con media cero y varianza unitaria).
Para la realización del test se construyen m-historias en función de los datos existentes X m t ≡ {Xt,Xt−τ, Xt−2τ , . . . , Xt−(m−1)τ }, siendo m la dimensión de inmersión y τ el tiempo de retardo. Luego, se escoge una distancia ε > 0 y se determina si dos m-historias están cercanas (con una distancia inferior a ε)12.
Si la serie es i.i.d., entonces la probabilidad de que la distancia sea menor o igual a será constante. Esta probabilidad se logra utilizando la medida de integral de correlación desarrollada por Grassberger y Procaccia (1983), que corresponde al límite de la fracción de pares de historias que están cercanas cuando aumenta el tamaño de la muestra.
Es importante señalar que la eficiencia del test BDS al aplicarlo en muestras pequeñas es mejor para dimensiones menores (m), no obstante, los resultados mejorarán al ampliar el tamaño muestral independiente de la dimensión y la distancia consideradas. Además el test tiene potencia para detectar dependencia no lineal determinista y estocástica (Hsieh, 1991).
Con el objetivo de obtener consistencia en los resultados, en este trabajo se consideraron 8 dimensiones (3 ≤ m ≤ 10) y 4 distancias (ε) diferentes (0, 5σ, 1σ, 1, 5σ, 2σ). Los resultados del test BDS, que se muestran en el Cuadro 8 8a, permiten identificar estructuras no lineales en la series de retornos de commodities bajo estudio, para todas las dimensiones y distancias utilizadas.
Paralelamente, y de acuerdo con el método propuesto por Brock (1986), se aplicó el test BDS a las series de residuos de modelos estimados a partir de las series de retornos de commodities, ajustados con el mejor retardo de un proceso autorregresivo. Dichos resultados (Cuadro 9 9a), respaldan los obtenidos sobre las series de retornos originales.
En síntesis, se evidencia un comportamiento no-aleatorio y no-lineal en las series de retornos de commodities, así como en las series de residuos de los modelos estimados.
CONCLUSIONES
Empleando análisis gráfico, gráfico de recurrencia, entropía de espacio temporal, coeficiente de Hurst, exponente de Lyapunov y dimensión de correlación sobre las series de retornos del cobre, oro, petróleo, plata, zinc, aluminio, plomo y níquel se corrobora la existencia de un comportamiento caótico en el mercado de commodities y se contrasta no-normalidad, noaleatoriedad y no-linealidad.
Los hallazgos de esta investigación se suman a los ya encontrados en diversos mercados y activos financieros y avalan la hipótesis de caoticidad en series financieras en contra de la hipótesis de aleatoriedad.
En particular se comprueba que los retornos de commodities no son bien representados por una distribución normal, no son lineales, exhiben dependencias de largo plazo y presentan un comportamiento caótico. Lo anterior, contradice algunos de los supuestos básicos de la teoría financiera moderna y aboga por la necesidad de buscar nuevos modelos que incorporen estas cualidades y que representen más fielmente la evolución de los precios de dichos activos.
La implicación teórica de estos hallazgos radica en el hecho que, a diferencia de la hipótesis de mercados eficientes, la información (o nueva información) que se agrega a la serie de precios de commodities (cambios en la oferta y demanda del commodity, anuncio de aumento o disminución de inventarios, modificación en la estructura de costos de producción, entre otros) no es externa sino que endógena. Por lo tanto, el desafío ya no consiste en dar una explicación estadística, o de otro tipo, a variables estocástica que ayudan a mejorar el pronóstico de la evolución futura de dichas series, sino que radica en descubrir la dinámica de cada uno de estos mercados. Desde el punto de vista práctico, justifica la búsqueda de técnicas predictivas a la hora de invertir en commodities, al menos en el corto plazo.
NOTAS AL PIE
1 Este tipo de análisis manifiesta que el precio de las acciones tiene un valor intrínseco que depende de las condiciones presentes y futuras de la empresa. Así, puede ser representado por el valor presente de todos los beneficios futuros de la compañía.
2 Plantea que lo más importante es analizar los movimientos de todos los inversionistas, los cuales están reflejados en la evolución histórica de los precios. Lo anterior es posible mediante la aplicación de osciladores técnicos o bien, a través de la observación de las gráficas (chartistas).
3 La teoría financiera moderna surge con la tesis doctoral de Louis Bachelier (1900) llamada "La teoría de la especulación". En ella se utilizó el concepto de movimiento browniano para describir el comportamiento de los precios en los mercados y se obtuvo la primera formulación teórica de las caminatas aleatorias (Mansilla, 2003). Los supuestos básicos de dicha tesis incluían que los cambios en los precios eran independientes y que éstos podían ser bien representados por una distribución Gaussiana.
4 Esta evidencia también es encontrada para cada commodity al observar su retorno y desviación histórica.
5 Véase Espinosa (2007) para más detalles.
6 VRA es un programa elaborado por Eugene Kononov basándose en la definición de gráfico de recurrencia de Eckmann, Kamphorst y Ruelle (1987) y en el RQA de Zbilut y Webber (1992).
7 Para una descripción de estas técnicas véase Kennel, Brown y Abarbanel (1992).
8 Cabe señalar que Lo (1991) plantea que, si bien es cierto que el análisis R/S puede detectar dependencia de largo plazo en series temporales, dicho análisis presenta sensibilidad a la dependencia de corto plazo. Para soslayar esta deficiencia plantea una modificación al rango reescalado que denomina rango reescalado modificado (RRM). Sin embargo, se ha encontrado evidencia que el análisis de Lo (1991) sobrerrechaza la hipótesis de memoria larga (Teverovsky, Taqqu y Willinger, 1999).
9 Básicamente, el "efecto reset" consiste en que en determinadas series, luego de un "shock externo" (como una decisión de recorte del suministro mundial de petróleo, por ejemplo), desaparezcan las dependencias que contenía antes del evento (Espinosa, 2007).
10 Wolf, Swift, Swinney y Vastano (1985), Sato, Sano y Sawada (1987) y Casdagli (1989), entre otros.
11 Se utiliza el programa MTRCHAOS y MTRLYAP elaborado por Rosenstein, Collins y De Luca (1993), el cual permite calcular el máximo exponente de Lyapunov y los parámetros necesarios para estimar dicho exponente.
12 Dos m-historias son cercanas si la mayor diferencia, en valor absoluto, entre los elementos que las componen es inferior a ε.
REFERENCIAS BIBLIOGRÁFICAS
[1] Bachelier, L. (1900). Théorie de la spéculation. Annales Scientifiques de l´Ecole Normale Supérieure, tomo 17, 21-86. [ Links ]
[2] Brock,W.A. (1986). Distinguishing random and deterministic systems: Abridged version. Journal of Economic Theory, 40, 168-195. [ Links ]
[3] Brock,W.,W. Dechert y J. Scheinkman (1987). A Test for Independence Based on the Correlation Dimension. Wisconsin: University of Wisconsin at Madison, Department of Economics. [ Links ]
[4] Corazza, M. y Malliaris, A.G. (2002). Multi-Fractality in Foreign Currency Markets. Multinational Finance Journal, 6(2), 65-98. [ Links ]
[5] Eckmann, J.P., S.O. Kamphorst y D. Ruelle (1987). Recurrence Plots of Dynamical Systems. Europhysics Letters, 4(9), 973-977. [ Links ]
[6] Espinosa, C. (2007). Comportamiento caótico en los mercados bursátiles latinoamericanos utilizando Visual Recurrence Análisis. Revista Análisis Económico, 55, 159-183. [ Links ]
[7] Espinosa, C. (2007). Memoria de largo plazo y Efecto Reset en retornos accionarios latinoamericanos. Estudios de Administración, 14(1), 47-70. [ Links ]
[8] Grassberger, P. & Procaccia I. (1983). Measuring the Strangeness of Strange Attractors. Physica, 9, 189-208. [ Links ]
[9] Hsieh, D. A. (1991). Chaos and nonlinear dynamics: Application to financial markets. Journal of Finance, 46, 1839-1877. [ Links ]
[10] Hurst, H.E. (1951). Long-term Storage Capacity of Reservoirs. Transactions of the American Society of Civil Engineers, 116, 770-799. [ Links ]
[11] Kennel, M.B., Brown, R. y Abarbanel, H.D.I. (1992). Determining embedding dimension for phase space reconstruction using a geometrical construction. Physica, 45, 403-3411. [ Links ]
[12] Kyaw, N.A., Los, C.A. y Zong, S. (2004). Persistence characteristics of Latin American financial markets. Journal of Multinational Financial Management, 16(3), 269-290. [ Links ]
[13] Le Barón, B. (1994). Chaos and nonlinear forecastability in Economics and Finance. Philosophical Transactions of Royal Society of London, 348, 397-404. [ Links ]
[14] Lo, A.W. (1991). Long-term memory in stock market prices. Econometrica. 59, 1279-1313. [ Links ]
[15] Los, C. (2000). Visualization of Chaos for Finance Majors. Adelaide: Adelaide University. [ Links ]
[16] Los, C. y Yu, B. (2008). Persistence Characteristics of the Chinese Stock Markets. International Review of Financial Analysis, 17(1), 64-82. [ Links ]
[17] Mandelbrot, B. (1972). A statistical methodology for non-periodic cycles: From the covariance to R/S analysis. Annals of Economic and Social Measurement, 1, 259-290. [ Links ]
[18] Mandelbrot, B. y Wallis, J.R. (1969), Robustness of the rescaled range R/S in the measurement of noncyclic long-run statistical dependence. Water Resources Research, 5, 967-988. [ Links ]
[19] Mansilla R. (2003). Introducción a la Econofísica. Madrid: Equipo Sirius S.A. [ Links ]
[20] Nieto del Alba, U. (1998). Historia del tiempo en economía. Madrid: Editorial McGraw Hill. [ Links ]
[21] Parisi, F., Espinosa, C. y Parisi, A. (2007). Pruebas de ComportamientoCaótico en Índices Bursátiles Americanos. El Trimestre Económico, 74(4), 901-27. [ Links ]
[22] Peters, E. (1994). Fractal Market analysis: Applying chaos theory to investment and economics. San Francisco: JohnWiley & Sons Inc. [ Links ]
[23] Rajaratnam, P. y Weston, R. (2004). A Chaotic analysis of the New Zeland exchange rate. Wellington: New Zealand Association of Economists (Inc.). [ Links ]
[24] Rosenstein M.T., Collins J.J. y De Luca C.J. (1993). A practical method for calculating largest Lyapunov exponents from small data sets. Physica, 65, 117-134. [ Links ]
[25] Sadique, S. y Silvapulle, P. (2001). Long-term memory in stock market returns: international evidence. International Journal of Finance & Economics 6(1), 59-67. [ Links ]
[26] Sato S., Sano M., y Sawada Y. (1987). Practical methods of measuring the generalized dimension and the largest Lyapunov exponent in high dimensional chaotic systems. Progress of Theoretical Physics, 77(1), 1-5. [ Links ]
[27] Teverovsky V., Taqqu M. y Willinger W. (1999). A critical look at Lo´s modified R/S statistic. Journal of statistic planning and inference, 80, 211-227. [ Links ]
[28] Wolf A., Swift J.B., Swinney H.L y Vastano J.A. (1985). Determining Lyapunov exponents from a time series. Physica, 16, 285-317. [ Links ]
[29] Zbilut, J.P. y C.L. Webber Jr. (1992). Embeddings and delays as derived from quantification of recurrence plots. Physics Letters A, 171, 199-203. [ Links ]













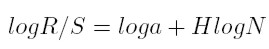 [2]
[2] 
