Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772On-line version ISSN 2248-4337
Cuad. Econ. vol.30 no.55 Bogotá July/Dec. 2011
IDENTIFICACIÓN DE EPISODIOS DE DEPENDENCIA NO LINEAL EN EL PESO MEXICANO
Semei Coronado Ramírez*
Leonardo Gatica Arreola**
*Doctor en Negocios y Estudios Económicos. Se desempeña actualmente como profesor del Centro Universitario de Ciencias Económico Administrativas (CUCEA) del Departamento de Métodos Cuantitativos de la Universidad de Guadalajara. E-mail: crs514@cucea.udg.mx, semeic@gmail.com. Dirección de correspondencia: Periférico Norte 799, Módulo M-201, Núcleo Los Belenes, Zapopan. C.P. 45000. (Jalisco, México).
**Doctor en Economía. Se desempeña actualmente como profesor del Centro Universitario de Ciencias Económico Administrativas (CUCEA) del Departamento de Métodos Cuantitativos de la Universidad de Guadalajara. E-mail: leonardo.gatica@cucea.udg.mx, leonardo.gatic@gmail.com. Dirección de correspondencia: Periférico Norte 799, Módulo K-302, Núcleo Los Belenes, Zapopan. C.P. 45000. (Jalisco, México).
Este artículo fue recibido el 14 de mayo de 2010, la versión ajustada fue recibida el 20 de octubre de 2010 y su publicación aprobada el 22 de noviembre de 2010.
Resumen
El siguiente documento identifica episodios de dependencia no-lineal en el tipo de cambio mexicano (peso mexicano/dólar norteamericano), entre enero de 1995 y septiembre de 2010. Para ello se utiliza la metodología Hinich Portmanteau, la cual emplea una prueba de alta frecuencia para detectar episodios de dependencia no lineal, por medio de funciones ventana. Se proporciona una explicación de los sucesos económicos y políticos que pudieron haber provocado que el tipo de cambio tuviera un comportamiento no lineal. La detección de episodios no lineales puede ayudar a explicar la dificultad para pronosticar este tipo de series.
Palabras clave: tipo de cambio, no linealidad, bicorrelación, estadístico Hinich Portmanteau, México. JEL: C22, G17, 054, O11.
Abstract
This document identifies non linear dependence events in the Mexican exchange rate (Mexican peso/U.S. Dollar.), between January 1995 and September 2010. For this purpose the Hinich Portmanteau test, which uses a high frequency test to detect nonlinear episodes through small window functions, is used. An explanation of events that could lead the nonlinear behavior and the non linear dependency of the exchange rate series is provided. The detection of such non-linear episodes may help to explain the difficulty in forecasting this type of series.
Key words: Mexican exchange rate, non-linear, bicorrelation, Hinich Portmanteau test, Mexico. JEL: C22, G17, 054, O11.
Rèsumè
Ce document identifie des épisodes de dépendance non-linéaire dans le taux de change mexicain (peso Mexicain / dollar), entre janvier 1995 et septembre 2010. Pour cela on utilise la méthodologie de Hinich-Portmanteau, qui fait usage d’un test de haute fréquence pour détecter des épisodes de dépendance non-linéaire à partir de fonctions fenêtre. On offre ainsi une explication aux événements économiques et politiques qui ont pu avoir provoqué la non-linéarité du comportement du taux de change. La détection d’épisodes non-linéaires peut aider à expliquer les difficultés dans la prédiction de ce type de séries.
Mots clés : taux de change, non-linéarité, bicorrélation, Hinich Portmanteau, Mexique. JEL: C22, G17, 054, O11.
La volatilidad de diferentes series del mercado financiero o económico se ha modelado a través de diferentes métodos. Desde la propuesta hecha por Engel (1982),quien desarrolla el modelo Autoregresivo con Heterocedasticidad Condicional (ARCH) bajo el supuesto de media cero y varianza no constante sobre el pasado, se ha desarrollado un importante número de investigaciones que parten de esta metodología. Otro trabajo pionero en el análisis de la volatilidad son los modelos Autoregresivos Generalizados con Heterocedasticidad Condicional (GARCH) de Bollerslev (1986) y su objetivo es determinar que no hay errores en la varianza. Sin embargo, estos métodos de análisis no logran modelar correctamente el comportamiento de los eventos de dependencia no lineal, que por lo general presentan estas series, y por el cual la volatilidad de este tipo de series no es ajena al supuesto de no linealidad.
Existen algunos estudios que abordan el problema de no linealidad en una serie y que pueden capturar la existencia de un comportamiento de dependencia no lineal, como es el caso del estadístico de Bicorrelación Hinich Portmanteau. éste ha sido empleado para analizar diferentes tipos de series, principalmente financieras y económicas. Por ejemplo, ha sido utilizado para presentar evidencia de no linealidad en el retorno de las acciones del NYSE (Hinich y Patterson, 1985), y en el índice bursátil asiático –se estudió el comportamiento no lineal para cinco países asiáticos– (Lim, Azali e Hinich, 2006).
El método también se ha empleado para estudiar los efectos de eventos políticos y de política económica en series bursátiles como el índice de rendimiento del Kuala Lumpur (KLCI) (Lim e Hinich, 2005). Otro ejemplo es el trabajo de Hinich y Serletis (2007), quienes han aplicado la prueba para detectar episodios no lineales en el tipo de cambio del dólar canadiense.
El objetivo de este documento es identificar los eventos de dependencia no lineal del tipo de cambio mexicano, así como los posibles eventos políticos y/o económicos que pudieran haber causado este comportamiento, a partir de la adopción de un régimen de tipo de cambio flexible en 1995. Los trabajos tomados como referencia son el de Bonilla, Romero-Meza e Hinich (2007) –en el cual se detecta episodios no lineales para varios tipos de cambio latinoamericanos, incluido el mexicano, y se deja abierta la línea de investigación para analizar eventos políticos y/o económicos que pudieran haberlos ocasionado– y el de Romero, Bonilla e Hinich (2007) que analiza el mercado accionario de Chile, detectando fechas de posibles eventos causantes de la no linealidad de la serie.
En el presente trabajo se utiliza el estadístico Hinich Portmanteau, que detecta periodos no lineales, por medio de funciones ventanas. Para cada ventana la hipótesis nula es que la serie es lineal, en otras palabras, se considera H0: la serie es ruido blanco.
Se encuentran veintidós ventanas significativas que rechazan H0 y se describen circunstancias políticas y/o económicas que pudieron causar la no linealidad. Dado que existen eventos de dependencia no lineal en la serie, ésta no puede analizarse por cualquier modelo Autoregresivo con Heterocedasticidad Condicional (ARCH) o Autoregresivo Generalizado con Heterocedasticidad Condicional (GARCH), aún cuando algunos logran capturar ciertos tipos de asimetrías en la series1. Lo anterior se debe a que estos modelos no cuentan con estructuras estadísticas capaces de detectar dependencia no lineal, lo cual podría causar errores en los pronósticos.
El documento se divide en cuatro secciones. En la primera se hace una revisión de la literatura. En la segunda parte se describen de los datos. En la tercera se presenta la metodología y se analizan los resultados. En el apartado final, se formulan las conclusiones.
REVISIÓN DE LA LITERATURA
Hace apenas dos décadas el tipo de cambio en México era controlado o intervenido por el gobierno o el banco central. El sistema financiero y económico sufrió un colapso en diciembre de 1994 y a partir de 1995 se instrumentaron políticas fiscales y monetarias que han permitido restablecer la confianza en el sistema financiero mexicano. Dos de las más importantes son la liberalización del tipo de cambio y la independencia del banco central (Bazdresch y Werner, 2002).
Como en el caso de cualquier tipo de cambio, existe un importante número de trabajos que buscan analizar y predecir la volatilidad del tipo de cambio mexicano. Por ejemplo, Benavides (2004) lo ha analizado para predecir la volatilidad del precio futuro con respecto al dólar americano, utilizando modelos univariantes y multivariantes ARCH y GARCH, así como un modelo multivariante ARCH BEKK, nombrado así después del trabajo de Baba, Engle, Kraft y Kroner (BEKK).
Este último modelo sirve para estimar la varianza y la covarianza condicionales. Su utilidad también radica en que puede relacionar la volatilidad con diferentes activos financieros. Aún así, todos los modelos mencionados siguen el supuesto de una distribución normal y, por tanto, no pueden capturar comportamientos no lineales del tipo de cambio.
Bazdresch y Werner (2002), reconocen implícitamente que existe un comportamiento no lineal y asimétrico en el tipo de cambio, al señalar que a partir de la adopción del régimen de libre flotación, el tipo de cambio se ha caracterizado por periodos de tranquilidad que cambian repentinamente a episodios de gran volatilidad. En este mismo trabajo, los autores emplean un método lineal para tratar de capturar esta dinámica. Para explicar estos comportamientos, Bazdresch y Werner desarrollan un modelo monetario de determinación del tipo de cambio con equilibrios múltiples. En éste los cambios en las expectativas del mercado sobre el riesgo cambiario dan origen a dos equilibrios, uno con pequeñas depreciaciones y baja volatilidad, y otro en el cual se presentan grandes depreciaciones y alta volatilidad. Para la estimación del modelo utilizan un método de coeficientes indeterminados, proponiendo una solución con parámetros desconocidos que sustituyen en la solución, para determinar los valores apropiados de los parámetros. Este proceso puede explicar más de 40% del sesgo implícito en los mercados de forwards del peso.
Por su parte, Ramírez y Martínez (2005) contrastan la eficiencia del mercado de futuros del dólar en México aplicando el principio de expectativas racionales por medio de una ecuación de regresión y análisis de cointegración. Los autores analizan el tipo de cambio spot y futuro, concluyendo que las dos series rechazan la hipótesis nula de existencia de raíz unitaria de Dickey-Fuller2 y que son no estacionarias.
Por su parte, Fullerton, Hattori y Calderón (2001) modelan el tipo de cambio por corrección de errores utilizando la balanza de pagos y la política monetaria. Los resultados estimados para todas las especificaciones de la prueba son débiles. De hecho, la mayoría de los coeficientes son estadísticamente insignificantes y con signos opuestos. Concluyen que la serie sigue una caminata aleatoria3.
Otros estudios que han analizado la volatilidad del tipo de cambio mexicano son el de Huerta y Hernández (1995), Kakkar (2001) y Arranz e Iglesias (2005). En este último caso, se avanza en el uso de modelos de volatilidad estocástica que han demostrado ser más adecuados que los de la familia ARCH, en el análisis de este tipo de series. Sin embargo, al igual que los métodos empleados en todos los trabajos anteriormente referidos, se parte del supuesto de normalidad y de distribuciones independientes e idénticas (i.i.d.). Si existen episodios de dependencia no lineal en una serie, este tipo de modelos son incapaces de capturar este comportamiento.
Existe, no obstante, una literatura creciente en la identificación del comportamiento no lineal. A partir del trabajo seminal de Hinich y Patterson (1985), se desarrollaron las herramientas estadísticas para identificar la presencia de procesos no lineales en series financieras (Brooks, 1996). Desde entonces el número de trabajos que se han enfocado en identificar episodios de comportamiento no lineal en series económicas y financieras ha ido en aumento. Varios trabajos reportan comportamiento no lineal en el mercado accionario norteamericano y que identifican episodios de no linealidad en el mercado financiero norteamericano – Hsieh (1989, 1991); Kohers, Pandey y Kohers (1997); Patterson y Ashley (2000) y Skaradzinski (2003). Evidencia similar ha sido encontrada por Antoniou, Ergul y Holmes (1997); Ammermann (1999); Ahmed, Rosser, Barkley y Uppal (1999); Ammermann y Patterson (2003); Lim, Hinich y Liew (2005), y Lim y Hinich (2005) para el caso de mercados asiáticos, y por Panunzi y Ricci (1993), Abhyankar, Copeland y Wong (1997), Brooks (1996), Brooks y Hinich (1998, 2001), Afonso y Teixeira (1998), Opong, Mulholland, Fox y Farahmand (1999), Kosfeld y Robé (2001), Fernández y Sosvilla (2003) y Panagiotidis (2005) en el caso de los mercados europeos. Para el caso latinoamericano la literatura es más escasa, sin embargo, existen trabajos como el de Bonilla, Romero-Meza y Hinich (2006) y Romero et al. (2007), los cuales encuentran evidencia de comportamiento no lineal.
Por otra parte, existen documentos discutiendo los problemas de los modelos GARCH para analizar los tipos de cambio latinoamericanos (Bonilla et al., 2007). Brooks y Hinich (1998) probaron la validez de la especificación de una estructura GARCH para los errores de series financieras, en el caso de los tipos de cambio. Sus resultados demuestran que existe una estructura estadística que no puede ser capturada por los modelos GARCH y cualquier tipo de modelo derivado de estos. La metodología de estos trabajos en su gran mayoría recurre a análisis de alta frecuencia de las series, la cual será utilizada en este documento.
LOS DATOS
Los datos para este análisis fueron obtenidos del Banco de México, considerando la serie del tipo de cambio nominal peso mexicano-dólar U.S. al cierre de venta diario, entre el 3 de enero de 1995 y el 13 de septiembre de 2010. Los datos se transformaron en términos de la relación TCt = ln (tct –tct–1), siendo tct la tasa de tipo de cambio al cierre en el tiempo t y tct –1 el tipo de cambio al cierre previo. El número de observaciones son 3.949. La Gráfica 1 muestra el comportamiento del tipo de cambio (peso mexicano-dólar U.S.) en su transformación logarítmica.
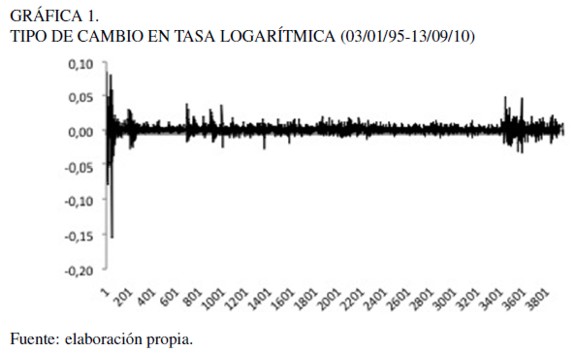
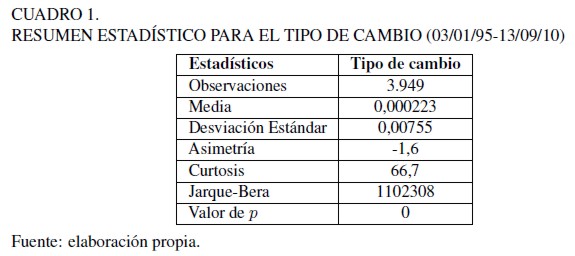
El Cuadro 1 muestra el resumen de las estadísticas descriptivas para la serie. Se observa que la asimetría es positiva, lo cual indica que los datos están por encima del valor de la media. La curtosis al ser positiva tiene forma leptocúrtica, esto no quiere decir que la distribución tenga menos varianza, por el contrario, es más probable que ofrezca más valores extremos que una distribución normal.Finalmente, con el estadístico Jarque-Bera se rechaza la hipótesis nula con un 95 porciento de confianza, lo cual indica que la serie no tiene una distribución normal.
METODOLOGÍA Y RESULTADOS
Métodos de análisis
En este análisis se sigue a Hinich y Patterson (2001) y se emplea el estadístico Hinich Portmanteau para detectar episodios transcendentes de dependencia no lineal en la serie. Este modelo separa las observaciones en pequeños marcos (ventanas) de igual longitud no traslapadas, aplicando los estadísticos C y H a cada una de las ventanas para analizar la autocorrelación y la bicorrelación bajo el supuesto H0: las observaciones son ruido blanco.
Considérese que x(t) denota la serie de tiempo, siendo t un entero. Si T es la longitud de cada ventana, entonces la k – sima ventana se describe como {y(t k ), y(tk + 1), … , y(tk + n – 1)}. La siguiente ventana no traslapada será entonces {y (tk + 1), y(tk +1 + 1), … , y(tk +1 + n – 1)}, siendo tk –1 = tk + n. Para cada ventana, H 0 : x(tk ) es un proceso estacionario ruido puro4 con bicorrelaciones cero, para cada una de ellas y H1: x(tk) el proceso en cada ventana es aleatorio con correlaciones diferentes a cero Cxx(r) = E[x(t) (t + r)] o bicorrelaciones no cero Cxxx(r, s) = E[x(t) x (t + r) x (t + s)], en el dominio principal 0 < r < s < L, donde L es el número de rezagos definido en cada ventana.
Las observaciones han sido estandarizadas 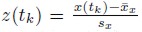 – restando la media de cada ventana
– restando la media de cada ventana 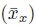 y divididas entre la desviación estándar de la ventana (sx)).
y divididas entre la desviación estándar de la ventana (sx)).
La correlación muestral es definida de la siguiente forma:
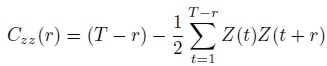 | [1] |
El estadístico para detectar dependencia serial en las series para cada ventana, se denota por C y es el siguiente:
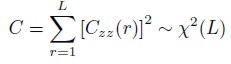 | [2] |
La bicorrelación (r, s) está definida como:
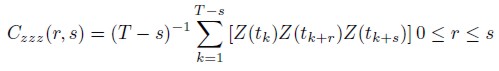 | [3] |
El estadístico para detectar la no linealidad en la serie en el modelo Hinich Port-manteau se denota por H5:
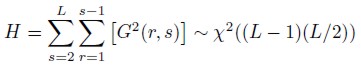 | [4] |
Y
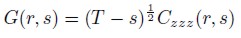 | [5] |
Los estadísticos C y H, tienden a una distribución X2 con (L – 1)(L/2) grados de libertad, T si el número de rezagos L = T c con 0 < c < 0, 5, siendo c un parámetro libre, bajo la hipótesis nula H 0: el proceso es ruido blanco. Entonces, U = F(H) tiene una distribución uniforme (0, 1), donde F es una distribución X 2 con (L – 1)(L/2) grados de libertad. El programa opera sobre la variación transformada U = F(H).
Basándose en simulaciones de Montecarlo se recomienda utilizar un valor c = 0, 4 con el fin de maximizar la robustez del estadístico y garantizar una validación aproximada de la teoría asintótica. El método es una simplificación y generalización del método usado para procesos de señales.
Una ventana es significativa para cualquiera de los estadísticos C o H, si se rechaza H 0 al nivel de significancia del umbral. Para cada una de las dos pruebas (autocorrelación y bicorrelación), 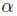 para cada ventana es:
para cada ventana es: 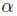 ventana = 1 – [(1 –
ventana = 1 – [(1 – 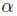 c)(1 –
c)(1 – 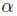 H )] (Ammerman, 1999). En este estudio se utiliza un umbral de 0, 1%. En este caso la probabilidad de rechazar H0, cuando realmente es verdadera es de una en cada cien a ese nivel de significancia, el cual minimiza la probabilidad de obtener dependencias cuando no existen (Lim et al., 2005).
H )] (Ammerman, 1999). En este estudio se utiliza un umbral de 0, 1%. En este caso la probabilidad de rechazar H0, cuando realmente es verdadera es de una en cada cien a ese nivel de significancia, el cual minimiza la probabilidad de obtener dependencias cuando no existen (Lim et al., 2005).
Esto sucede si se aplica la prueba de bicorrelación a cualquier modelo GARCH, realizando una adecuación en los datos. Se hace un ajuste a las observaciones, transformándolas en un conjunto binario
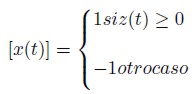 | [11] |
Si Z(t) es modelado por un proceso de tipo GARCH, las innovaciones son i.i.d, lo cual genera un proceso ruido blanco. Esta transformación hace que el modelo GARCH sea puro ruido y no puro ruido blanco. Así que si se rechaza H0 para ambos estadísticos C o H, entonces las estructuras estadísticas que tiene la serie no pueden ser capturadas por un modelo GARCH o algún tipo derivado de este. Este rechazo se puede deber a que las innovaciones tienen dependencia serial, lo cual viola el supuesto principal de i.i.d de los modelos GARCH y sus derivados (Lim et al., 2005).
Resultados
El Cuadro 2 presenta los estadísticos C y H6, realizando la transformación binaria a la serie completa. Los resultados muestran que se rechaza H0 para ambos estadísticos. Esto viola el supuesto de innovaciones i.i.d., que plantean los modelos GARCH. Eso implica que los modelos GARCH no pueden capturar estructuras estadísticas que están presentes en el proceso subyacente y los parámetros son desconocidos en la serie del tipo de cambio.
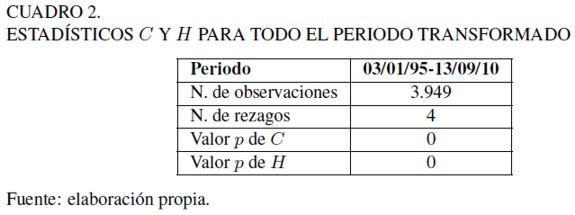
A continuación, se investiga sobre la dependencia no lineal en el proceso subyacente, realizando pequeñas submuestras que son los marcos o ventanas. La serie ha sido dividida en un conjunto de 131 ventanas no traslapadas de longitud 30 de 30 observaciones, debido a que un mes tiene aproximadamente 30 días7.
Se estableció un umbral de 0, 1% para los valores de los estadísticos C y H8.Esta es la probabilidad de obtener un 0, 1 por ciento de ventanas significativas no traslapadas. Se encontraron veintidós ventanas que presentan evidencia de episodios de dependencia no lineal. Los resultados se muestran en el Cuadro 3.
Estos resultados rechazan H0: de puro ruido, para los dos estadísticos C y H en la serie del tipo de cambio en México (peso-dólar US), lo que viola el supuesto estricto de los modelos GARCH que capturan los cambios de la volatilidad a través del tiempo. La implicación de este resultado es que los datos no pueden ser modelados por un proceso GARCH de ningún tipo ya que no pueden modelar estructuras estadísticas de dependencia no lineal.
El Cuadro 3 presenta las fechas de las veintidós ventas en las que se observa evidencia de comportamiento no lineal causado por algún evento político, financiero o económico. En cuanto a 1995, la primera ventana significativa se encuentra entre los meses de enero y febrero y corresponde aún al pánico posterior a la devaluación de diciembre del año anterior. En los siguientes meses no se observan episodios no lineales que evidencien algún tipo de intervención o comportamiento financiero que los pudiera disparar. Es hasta la segunda mitad del año cuando se vuelven a presentar ventanas significativas, las cuales se explican por el aumento en las reservas del Banco de México debido a una inyección de capital del exterior – tanto de manera directa al banco, como a través de la Secretaría de Hacienda y Crédito Público (SHCP). En este periodo el Banco de México llegó a acumular reservas por valor de 6,168 millones de dólares.
Un número importante de ventanas se vuelve a presentar a mediados de 1997 y corresponden a las elecciones intermedias, en las que por primera vez el partido oficial perdió la mayoría absoluta en la Cámara de Diputados. Igualmente el partido de izquierda gana las primeras elecciones para designar el gobierno del Distrito Federal. La pérdida de la mayoría absoluta en el Congreso provocó una inadecuación de las normas internas de este órgano y la complicación e incertidumbre en el proceso de negociación y definición de la ley de ingresos y el proyecto de egresos, lo cual sin duda tuvo un impacto al inicio del siguiente año.
Es muy probable que este clima de incertidumbre sobre la política fiscal haya resultado en los episodios que se observan en el primer trimestre de 1998. Junto con este proceso, en ese mismo trimestre el Banco de México anunció su programa de política monetaria para contrarrestar la meta anual de inflación de 12% al cierre del año. Además, la SHCP dio a conocer el calendario y los montos de colocación de valores públicos, para dar certidumbre a los participantes en el mercado financiero nacional. Posiblemente estos dos hechos de política económica tuvieran un impacto reflejado en los episodios de dependencia no lineal para ese periodo.
Para las ventanas de 1999, el proceso de negociación del presupuesto en el ambiente causado por la pérdida de la mayoría absoluta puede ser el responsables de los eventos no lineales observados al inicio y al final del año, así como a comienzo de 2000. Vale la pena señalar que durante este último año, únicamente se detectó un periodo de dependencia en el mes de enero, a pesar de tratarse del año electoral en el que el Partido Revolucionario Institucional (PRI) perdió las elecciones después de 70 años de hegemonía.
Las siguientes ventanas significativas se encontraron en el segundo trimestre del 2001. Durante este lapso existían expectativas inflacionarias a la baja y la tasa de interés nominal se redujo, igualmente, se suspendió la opción de venta de divisas al Banco de México por parte de la SHCP.
Las ventanas detectadas en el 2005 corresponden a distorsiones en algunos de los precios de artículos básicos y las adecuaciones consecuentes en el corto plazo para alcanzar la meta inflacionaria. En este lapso, hay un cierre de las fronteras a las importaciones de carne de los Estados Unidos, debido a la enfermedad de las vacas locas y la fiebre aviar, además de una caída importante en la producción de tomate por factores climáticos; en consecuencia, las exportaciones hacia los Estados Unidos se reducen. En este contexto, existen varios aumentos del corto9 por parte del Banco de México y se presenta incertidumbre en la arena política. Durante esos meses el candidato de izquierda que contendría en las elecciones del año siguiente, toma la delantera en las encuestas y su popularidad es creciente dentro de un clima de hostigamiento en su contra, encabezado por el Presidente de la República en turno, hecho que no hizo más que fortalecerlo.
Las ventanas significativas en 2006 corresponden a los meses de junio y julio. En ese momento había en México un gran revuelo en la arena político-electoral debido a las elecciones presidenciales. Este proceso fue conflictivo y muy competido y sin duda la incertidumbre sobre quién sería el nuevo presidente y las expectativas de los posibles escenarios afectó el comportamiento del mercado cambiario mexicano.
Una vez que el proceso electoral y de sucesión presidencial finalizó, se observan dos periodos de no linealidad en el segundo semestre de 2007. Estos eventos probablemente están ligados a los incrementos en los precios de los productos básicos (frutas, hortalizas, maíz10 y tortilla). En este contexto, el Banco de México enfrenta mayores incentivos para continuar con su política de aumento del corto para lograr alcanzar las metas inflacionarias. Posteriormente a los eventos detectados en el 2007, se presenta un amplio periodo donde no existe evidencia de episodios de dependencia no lineal. Este periodo de estabilidad refleja una política cambiaria neutral y posiblemente la certidumbre que el triunfo del candidato de la derecha y el debilitamiento de la izquierda, pero sobre todo la estabilidad que en la arena política que se generó después de un año de las elecciones presidenciales, provocó mayor confianza en los merados financieros y en las expectativas de los agentes que se reflejan en la ausencia de episodios no lineales.
Es en los primeros meses de 2010 que se identificó un importante número de ventanas que evidencian comportamiento no lineal. Esto puede ser causado por una reforma fiscal deficiente y el aumento de las tasas impositivas, lo cual afecta los mercados financieros. Este proceso fallido de reforma fiscal, afectó de manera importante y negativa, la percepción de los agentes sobre la posibilidad de la construcción de una política fiscal adecuada, debido a la recuperación de la mayoría en el Congreso por parte del PRI y a las negociaciones de carácter político electoral que determinan los acuerdos sobre la política económica.
CONCLUSIONES
En este trabajo se aplicó el estadístico Hinich Portmanteau para detectar episodios de dependencia no lineales en la serie del tipo de cambio mexicano y, siguiendo la idea Bonilla et al. (2007) y Romero et al. (2007), se mencionaron los posibles eventos políticos y/o económicos que pueden explicar este comportamiento.
Se encontraron 16, 79% de ventanas significativas, lo cual implica que la serie tiene un comportamiento que los modelos de las familias ARCH/GARCH no pueden capturar como lo han demostrado Brooks y Hinich (1998). Ya que en esos periodo el tipo de cambio mexicano presenta estructuras de dependencia no lineal que se contraponen a los supuestos de normalidad y de i.i.d. Los modelos que parten de estos supuestos no pueden modelar correctamente el comportamiento de la serie.
Los resultados del análisis también implican que, dada la evidencia del comportamiento de dependencia no lineal que tiene el tipo de cambio en una economía en desarrollo como la mexicana, el mercado cambiario no se comporta de forma eficiente. Este resultado es consistente con otros análisis realizados para economías en desarrollo.
Este estudio intenta aportar una alternativa para conocer las estructuras estadísticas de las series de tiempo, específicamente la del tipo de cambio, y con base en sus resultados poder discutir el uso adecuado de cierto tipo de modelos para su análisis y pronóstico. En particular, los resultados encontrados en este trabajo hacen evidente la cautela con la que se debe proceder en el uso de modelos de las familias ARCH, GARCH o de modelos con volatilidad estocástica para estudiar el tipo de cambio en el caso de México. Este argumento puede extenderse para el estudio de otras series, ya que en muchas ocasiones la toma de decisiones de política se basa en análisis que utilizan este tipo de modelos, lo cual podría dar resultados erróneos si no se consideran los problemas que estas técnicas tienen para capturar estructuras de dependencia no lineal que pueden estar presentes en las series.
Una de las posibles líneas de investigación que se desprende de los resultados aquí presentados es la posibilidad de investigar la correlación del tipo de cambio con otras variables, contrastarla con alguno de los filtros aplicados a los ciclos económicos para conocer mejor su comportamiento y así determinar si siguen existiendo episodios no lineales.
NOTAS AL PIE
1 Existen también modelos de alta frecuencia que son superiores en la detección de asimetrías a los modelos del tipo GARCH. Un ejemplo de estos es el estadístico REVERSE (Ver Hinich y Rothman, 1998).
2 Estadístico para detectar raíces unitarias en los procesos autoregresivos (AR).
3 Para que siga una caminata aleatoria una serie, se debe partir del supuesto de que sigue una distribución normal.
4 Una serie de tiempo que es un proceso estacionario, puede ser puro ruido o puro ruido blanco. En contraste una serie ruido blanco es cuando su función de autocovarianza es cero para todos los rezagos. Eso no implica que las innovaciones sean independientes, al menos que la serie sea Gaussiana.
5 Para ver la demostración matemática y sus propiedades ver Hinich (1996).
6 Los estadísticos C y H fueron computados con el programa T23 disponible en http://hinich.webhost.utexas.edu/.
7 La longitud de las ventanas deberá ser lo suficientemente larga para aplicar los estadísticos C y H, pero también suficientemente corta para poder capturar episodios no lineales dentro de cada una (Brooks y Hinich, 1998).
8 El programa que se utilizó es el T23 disponible en http://hinich.webhost.utexas.edu/.
9 Política que utiliza el Banco de México para controlar la inflación. Es el dinero que deja de proveer el Banco de México a los bancos en sus operaciones dirias para que al cierre se sobregiren e impulsen a la alza la tasa de interés y así incentivar el ahorro y frenar el consumo.
10 En este caso, causado por el aumento en la producción de etanol.
REFERENCIAS BIBLIOGRÁFICAS
[1] Abhyankar, A., Copeland, L. y Wong, W. (1997). Uncovering non-linear structure in real-time stock-market indexes the S&P 500, the DAX, the Nikkei 225 and the FTSE-100. Journal of Business and Economic Statistics, 15(1), 1-14. [ Links ]
[2] Afonso, A. y Teixeira, J. (1998). Non-linear tests of weakly efficient markets evidence from Portugal. Estudios de Economia, 19, 169-87. [ Links ]
[3] Ahmed, E., Rosser, J., Barkley, J. y Uppal, J. (1999). Evidence of non-linear speculative bubble in pacific-rim stock markets. Quarterly Review of Economics and Finance, 39(1), 21-36. [ Links ]
[4] Ammerman, P. (1999). Nonlinearity and overseas capital markets: evidence from the Taiwan stock exchange. (Tesis inédita de doctorado). Virginia Polytechnic Institute, USA. [ Links ]
[5] Ammermann, P. y Patterson, D. (2003). The cross-sectional and cross-temporal universality of non-linear serial dependencies evidence from world stock indices and the Taiwan stock exchange. Pacific-Basin Finance Journal, 11(2), 175-95. [ Links ]
[6] Antoniou, A., Ergul, N. y Holmes, P. (1997). Market efficiency, thin trading and non-linear behavior evidence from an emerging market. European Financial Management, 3(2), 175-90. [ Links ]
[7] Arranz, M. y Iglesias. M. (2005). Análisis de los tipos de cambio en la economía mexicana y comparación con otros países: Un enfoque de volatilidad estocástica. Investigación Económica, 64(253), 159-169. [ Links ]
[8] Bazdresch, S. yWerner, A. (2002). El comportamiento del tipo de cambio en México y el régimen de libre flotación: 1996-2001. (Documento de Investigación 2002-09). México D.F.: Banco de México. Recuperado de http://www.banxico.org.mx/dyn/documents/%7B551708AA-9D83-687A-03C1-50DEA76A1F12 %7D.pdf. [ Links ]
[9] Benavides, G. (2004). Predictive accuracy of futures optiones implied volatility: the case of exchange rate futures Mexican peso-US dollar. (Documento de trabajo).México D.F.: Banco de México. Recuperado de http://papers.ssrn.com/sol3/papers. cfm?abstract_id=600742 [ Links ]
[10] Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31(3), 307-327. [ Links ]
[11] Bonilla, C., Romero-Meza, R. y Hinich, J.M. (2007). GARCH inadequacy for modeling exchange rates: empirical evidence from Latin America. Applied Economics, 39(19), 2529-2533. [ Links ]
[12] Bonilla, C., Romero-Meza, R. y Hinich, M. (2006). Episodic nonlinearity in Latin American stock market indices. Applied Economics Letters, 13(3), 195-199. [ Links ]
[13] Brooks, C. (1996). Testing for non-linearity in daily sterling exchange rates. Applied Financial Economics, 6(4), 307-17. [ Links ]
[14] Brooks, C. y Hinich, M. (1998). Episodic nonstationary in exchange rates. Applied Economics Letters, 5(11), 719-722. [ Links ]
[15] Brooks, C. y Hinich, M. (2001). Bicorrelations and cross-bicorrelations as nonlinearity tests and tools for exchange rate forecasting. Journal of Forecasting, 20(3),181-96. [ Links ]
[16] Engel, R. (1982). Autoregressive conditional heteroskedasticity with estimates of variance of United Kingdom inflation. Econometrica, 50(4), 987-1007. [ Links ]
[17] Fernández S.J. y Sosvilla, S. (2003) Modeling the linkages between US and Latin American Stock Markets. Applied Economics, 35(12), 1423-1434. [ Links ]
[18] Fullerton, T., Hattori, M. y Calderón C. (2001). Error correction exchange rate modeling: evidence for Mexico. Journal of Economics y Finance, 25, 358-368. [ Links ]
[19] Hinich, J.M. (1996). Testing for dependence in the input to a linear time series model. Nonparametric Statistics, 6(2-3), 205-221. [ Links ]
[20] Hinich, J.M., y Patterson, M.D. (1985). Evidence of nonlinearity in daily stock returns. Journal of Business and Economic Statistics, 3(1), 69-77. [ Links ]
[21] Hinich, M. y Rothman, P. (1998). Frequency-domain test of time reversibility. Macroeconomic Dynamics, 2(1), 72-88. [ Links ]
[22] Hinich, J.M. y Patterson, M.D. (2001). The episodic behavior of dependencies in high frequency stock returns. Mimeo. Recuperado de http://web.austin.utexas.edu/hinich/files/Statistics/Episodic-stocks.pdf [ Links ]
[23] Hinich, J.M. y Serletis, A. (2007). Episodic nonlinear event detection in the Canadian exchange rate. Journal of the American Statistical Association, 102(477), 68-74. [ Links ]
[24] Hsieh, D. (1989). Testing for non-linear dependence in daily foreign exchange rates.Journal of Business, 62(3), 339-368. [ Links ]
[25] Hsieh, D. (1991). Chaos and non-linear dynamics application to financial markets. Journal of Finance, 46(5), 1839-1877. [ Links ]
[26] Huerta, A. y Hernández, F. (1995). Comportamiento del tipo de cambio real y desempeño económico en México. Economía Mexicana Nueva Época, 4(2), 239-263. [ Links ]
[27] Kakkar, V. (2001). Long run real exchange rates: evidence from Mexico. Economics Letters, 72(1), 79-82. [ Links ]
[28] Kohers, T., Pandey, V. y Kohers, G. (1997). Using non-linear dynamics to test for market efficiency among the major U.S. stock exchanges. Quarterly Review of Economics and Finance, 37(2), 523-45. [ Links ]
[29] Kosfeld, R. y Robé, S. (2001). Testing for nonlinearities in German bank stock returns. Empirical Economics, 26(3), 581-97. [ Links ]
[30] Lim, K. y Hinich, M. (2005). Cross-temporal universality of non-linear serial dependencies evidence from Asian stock indices. Economics Bulletin, 7(1), 1-6. [ Links ]
[31] Lim, K., Azali, M. y Hinich, J.M. (2006). Model identification of ARCH/GARCH using non-linearity test an application on Asean-5 foreign exchange markets. Mimeo. Recuperado de http://hinich.webhost.utexas.edu/files/Economics/Bispec-exchange.pdf [ Links ]
[32] Lim, K., Hinich, J.M. y Liew, V. (2005). Statistical inadequacy of GARCH models for Asian stock markets: evidence and implications. Journal of Merging Market Finance, 4(3), 264-279. [ Links ]
[33] Opong, K., Mulholland, G. Fox, A. y Farahmand, K. (1999). The Behavior of some UK equity indices an application of Hurst and BDS tests. Journal of Empirical Finance, 6(3), 267-82. [ Links ]
[34] Panagiotidis, T. (2005). Market capitalization and efficiency. Does it matter? evidence from the Athens stock exchange. Applied Financial Economics, 15(10), 707-713. [ Links ]
[35] Panunzi, F. y Ricci N. (1993). Testing non linearities in Italian stock exchange. Rivista Internazionale di Scienze Economiche e Commerciali, 40, 559-574. [ Links ]
[36] Patterson, D. y Ashley, R. (2000). A non-linear time series workshop: A toolkit for detecting and identifying non-linear time series dependence. Norwell: Kluwer Academic Publishers. [ Links ]
[37] Ramírez, R.A. y Martínez, D.A. (2005). Eficiencia en el mercado de futuros del dólar en México. Agricultura, Sociedad y Desarrollo, 2(1), 47-50. [ Links ]
[38] Romero, M.R., Bonilla, C. y Hinich, J.M. (2007). Nonlinear event detection in the Chilean stock market. Applied Economics Letters, 14(13), 987-991. [ Links ]
[39] Skaradzinski, D. (2003). The non-linear behavior of stock prices the impact of firm size, seasonality, and trading frequency. (Tesis inédita de Doctorado). Virginia Polytechnic Institute and State University, USA. [ Links ]














