Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.31 no.56 Bogotá Jan./June 2012
MULTIVARIATE VOLATILITY MODELS: AN APPLICATION TO IBOVESPA AND DOW JONES INDUSTRIAL
Jorge Alberto Achcar 1
Edilberto Cepeda-Cuervo 2
Milton Barossi-Filho 3
1 Ph.D. in statistics, currently works as professor of the Social Medicine Department of the Universidade de Sâo Paulo (Brazil). E-mail: achcar@fmrp.usp.br. Mailing address: Avenida Bandeirantes, 3900 centro 14049-900, Ribeirao Preto, Sâo Paulo (Brazil).
2 Ph.D. in Mathematics, currently works as professor of the Statistics Department of the Universidad Nacional de Colombia. E-mail: ecepeda@unal.edu.co. Mailing address: Cra 30 No 45-03, Ciudad Universitaria, Departamento de estadística (Bogotá, Colombia).
3 Ph.D. in Economics and associate professor at the Department of Economics, University of Sâo Paulo (Brazil). E-Mail: mbarossi@usp.br. Mailing address: Av. dos Bandeirantes, 3900 Monte Alegre 14049-400, Ribeirâo Preto, Sâo Paulo (Brazil).
This article was received on february 11 2009, the adjusted versión was remitted on april 26 2011 and its publication was approved on may 10 2011.
Abstract
In this paper, we present a brief description of multivariate GARCH models. Usually, their parameter estimates are obtained using maximum likelihood methods. Considering new methodological processes to model the volatilities of time series, we need to use another inference approach to get estimates for the parameters of the models, since we can have great difficulties to obtain the maximum likelihood estimates due to the complexity of the likelihood function. In this way, we obtain the inferences for the volatilities of time series under a Bayesian approach, especially using popular simulation algorithms as the Markov Chain Monte Carlo (MCMC) methods. As an application to illustrate the proposed methodology, we analyze log-returns of IBOVESPA and Dow Jones Industrial in a weekly basis from 04/27/1993 to 11/03/2008.
Key words: multivariate GARCH, stochastic volatility models, financial time series, bayesian methodology, MCMC methods. JEL: G17, G19, C11, C32, C53.
Resumen
En este artículo se presenta una breve descripción de modelos GARCH multivariados y se realizan inferencias de la volatilidad de series de tiempo usando un enfoque Bayesiano, utilizando algoritmos de simulación de Monte Carlo (MCMC). Como una aplicación para ilustrar la metodología propuesta, se analizan los logretornos de IBOVESPA y Dow Jones Industrial en una base semanal de 04/27/1993 para 11/03/2008.
Palabras clave: GARCH multivariados, modelos de volatilidad estocástica, series de tiempo financieras, metodología bayesiana, simulación de Monte Carlo. JEL: G17, G19, C11, C32, C53.
Rèsumè
Dans cet article on présente une brève description des modèles GARCH multivariés et on fait d'analyse d'inférence sur la volatilité des séries temporelles en utilisant une approche bayésienne et des algorithmes de simulation de Monte Carlo (MCMC). Comme application pour illustrer la méthodologie proposée, on étudie des log-rendements d'IBOVESPA et du Dow Jones Industriel sur une base hebdomadaire entre 27/04/1993 et 03/11/2008.
Key words: GARCH multivarié, modèles de volatilité stochastique, séries temporelles financières, méthodes bayésiennes, simulation de Monte Carlo. JEL: G17, G19, C11, C32, C53.
The ARCH models (autoregressive conditional heteroscedasticity), introduced by Engle (1982), and the GARCH (generalized autoregressive conditional heteroscedasticity) models, proposed by Bollerslev (1986), are generally applied to model the volatility of the financial time series (Taylor, 1982; Tauchen and Pitts, 1983; Bollerslev, 1990; Bollerslev, Chou, and Kroner, 1992; Engle, 2001). However, a stylized fact of the financial volatility is that bad news tend to have a larger impact on the volatility than good news, and these models do not have taken into account this fact. Thus, to incorporate this effect some variants of GARCH models were proposed in the literature. Among these variants of GARCH models, we consider the class of EGARCH models, proposed by Nelson (1991).
In statistical literature, important results have been introduced to extend the univariate GARCH model to multivariate GARCH (MGARCH) models. The first MGARCH model for the conditional covariance matrices was the so-called VEC model of Bollerslev, Engle, and Wooldridge (1988). The multivariate ARCH model was proposed by Engle, Granger, and Kraft (1984). Bauwens, Laurent and Rombouts (2006) are another important reference that discusses MGARCH models.
Another class of statistical models, the so-called stochastic volatility models (SV), has been a satisfactory alternative to analyze financial time series, when compared with GARCH models. SV models are more flexible than model financial time series, given that they assume two processes for the noise. One process for the observation and another for the latent volatility. Comparative studies between SV models and models type GARCH are well known in the literature (see for example, Taylor, 1994; Ghysels, Harvey and Renault, 1996; Shephard, 1996; Kim, Nelson and Startz, 1998). Bayesian Methods using Markov Chain Monte Carlo (MCMC) are applied to the analysis of financial time series assuming SV models (see for example, Meyer and Yu, 2000), given the great difficulties in the classical statistical approach with the complexity of the likelihood function.
From the economic and financial points of view, GARCH models were a very popular tool for forecasting time series' behavior. The extensive literature concerning this methodology clearly influenced academic research on this issue. However, it does not take so much time in order to realize how poor these models fit economic and financial time series behaviors. Then a new class of volatility models was introduced, i.e. stochastic volatility models.
Upon the results provided by them, we have concentrated our attention on stochastic volatility models estimated by Bayesian methods.
Specific attention was given in this paper to multivariate stochastic volatility models as proposed by Meyer and Yu (2000) and Yu and Meyer (2006). Our concern is the relationship between two stock markets indexes, IBOVESPA, Brazilian Stock Exchange Mark, and DJI, New York Stock Exchange Index. Thus relationship is quite important because it has been a benchmark for investors all over the world mainly concerning returns on investments alternatives on assets in development and emerging markets.
Theoretically, there are some economic and financial features that are expected to prevail after analyzing IBOVESPA and DJI returns time series. First, expected returns' volatility in emerging markets is higher than development markets returns' volatility. Second, time series long memory behavior is supposed to last more in emerging markets and an additional source of volatility due to a causal relationship can be verified from the development to emerging markets. Finally an asymmetric behavior concerning stock market returns reinforces the hypothesis there is a leverage effect that frequently affects the magnitudes of profits and losses on investing in stocks in emerging markets.
Indeed, the results we have achieved, due to the methodology employed in this paper, confirm all the features raised by the standard literature on this issue. An exception on this matter concerns the leverage effect, which was not an explicit objective of this paper. In fact, combining multivariate stochastic volatility models and Bayesian methods for estimating those is a successful strategy on demonstrating the main economic and financial features rose above.
This article is divided into 5 sections. In section 2 we define the MARCH models, as in Zivot and Wang (2006). This section includes two subsections entitled Exponentially Weighted Covariance Estimate and Diagonal VEC model. In section 3, the bivariate stochastic volatility models or GSV, are defined. In section 4, logreturns of IBOVESPA and DJI in a weekly basis form 04/27/1993 to 11/03/2008 are analyzed.
MULTIVARIATE GARCH MODELS
Exponentially Weighted Covariance Estimate
In the multivariate context, cross-correlations of the levels and the volatility series are also of interest. Cross-correlation in the levels can be modeled using vector autocorrelation (VAR). Let yt be a k × 1 vector of multivariate time series,
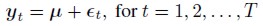 | [1] |
Where μ is a k × 1 mean vector, and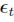 is a k × 1 vector of white noise with zero mean. The sample covariance matrix is given by
is a k × 1 vector of white noise with zero mean. The sample covariance matrix is given by
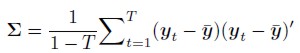 | [2] |
Where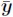 is the k× 1 vector of the sample mean. Allowing for time varying covariance and an ad hoc approach, we use exponentially decreasing weights as follows:
is the k× 1 vector of the sample mean. Allowing for time varying covariance and an ad hoc approach, we use exponentially decreasing weights as follows:
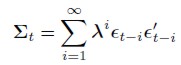 | [3] |
Where 0 < λ < 1 so that smaller weights are set on lagged observations over the past history. Since
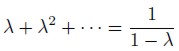 | [4] |
the weights are usually scaled so that they sum up to one; that is,
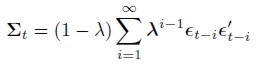 | [5] |
Equation (5) can be rewritten to obtain the following recursive form for exponentially weighted covariance matrix:
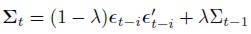 | [6] |
This will be referred to as the EWMA model of time varying covariance. From equation (6), given λ and an initial estimate Σ1, the time varying exponential weighted covariance matrices can be computed.
If we assume that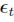 in (6) follows a multivariate normal distribution with zero mean, and ∑t = Cov(
in (6) follows a multivariate normal distribution with zero mean, and ∑t = Cov(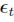 ) is treated as the covariance of
) is treated as the covariance of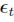 conditional on the past history, the likelihood function of the observed time series can be written as:
conditional on the past history, the likelihood function of the observed time series can be written as:
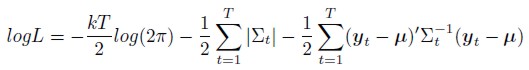 | [7] |
Since ∑t can be recursively calculated as in (6), the log likelihood function can also be evaluated. Thus the mean vector μ and λ can be treated as known in the model and estimated using quasi-maximum likelihood estimation method, given the initial value of ∑1.
Diagonal VEC model
The EWMA model is generalized as follows:
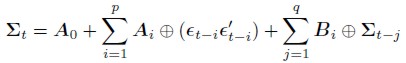 | [8] |
Where the symbol ⊕ stands for Handamard product, i.e., element by element multiplication, and every coefficient Ai and Bj has dimension k × k. This model was first proposed by Bollerslev, Engle, and Wooldridge (1988), and is called diagonal VEC, or DVEC (p,q) model. In order to understand the intuitive approach behind DVEC model, let us take the bivariate DVEC (p, q) model into account, given by:
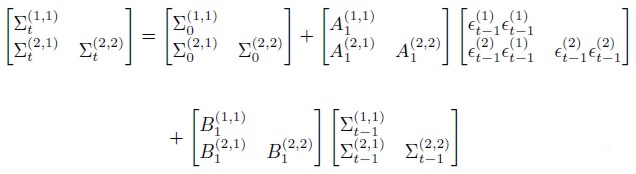 | [9] |
Where only the lower triangular part of the system is admitted, with Xij denoting the (ij)-th element of the matrix X, and (i) the i-th element of
(i) the i-th element of . The last matrix can be rewritten as follows:
. The last matrix can be rewritten as follows:
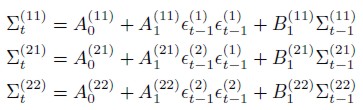 | [10] |
So the(ij)-th element of the the time varying covariance matrix depends only on its own lagged element and the corresponding cross-product of errors. As result the volatility of each series follows a GARCH process as the covariance process can also be treated as a GARCH model in terms of the cross moment errors.
BIVARIATE STOCHASTIC VOLATILITY MODELS (BSV)
Different classes of the multivariate volatility models are introduced in the literature (see for example Yu and Meyer, 2006). In the present paper we consider six bivariate models. In order to describe these models, we start by taking N > 1 fixed integer numbers that resemble the size of the data set. Let Z(t) = (Z1(t),Z2(t))´, t = 1, 2, 3 ..., N be the series recording the result of the same event performed in two different locations at the same time. (In here , for v a vector or a matrix we use v´ to indicate the transpose of v.) Consider a vector of latent variables h(t) = (h1(t), h2(t)), t = 1, 2, 3 ... ,N where hi(t) are defined by the following autoregressive model AR(1):
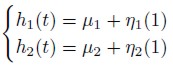 | [11] |
and for t = 2,3 ..., N
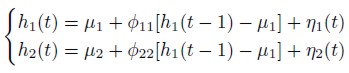 |
Where 0 < ø11, ø22 < 1 and also η(t) = η1(t), η2(t)) has a bivariate normal distribution with mean vector 0 = (0, 0) and variance-covariance matrix given by the 2 diagonal matrix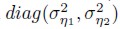
Consider H´(t), t = 1, 2, 3... ,N a 2 × 2 diagonal matrix with individual terms given by exp(h1(t)/2), exp(h2(t)/2), i.e., H´(t) = diag(exp(h1(t)/2),exp(h2(t)/2). Let Y´(t) = (Y1(t), Y2(t))´, t = 1, 2, 3 ... ,N be modeled by:
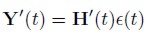 | [12] |
Where (t) = (
(t) = ( 1(t),
1(t), 2(t))´ is the vector of error components having a bivariate Normal distribution with mean vector 0 and variance-covariance matrix ∑
2(t))´ is the vector of error components having a bivariate Normal distribution with mean vector 0 and variance-covariance matrix ∑ given by:
given by:
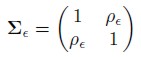 | [13] |
With ρ ≥ 0. Hence. Y(t). t = 1, 2,...,N is such that Y1(t) = exp(h1(t)/2)
≥ 0. Hence. Y(t). t = 1, 2,...,N is such that Y1(t) = exp(h1(t)/2) 1(t) and Y2(t) = exp(h2(t)/2)
1(t) and Y2(t) = exp(h2(t)/2) 2(t). t = 1, 2,... ,N are the logarithms of the returns of Z1(t) and Z2(t) centered around their averages.
2(t). t = 1, 2,... ,N are the logarithms of the returns of Z1(t) and Z2(t) centered around their averages.
Remark. By definition, we observe that E[Y( t)] = 0 and the variance-covariance matrix for Y(t) is given by,
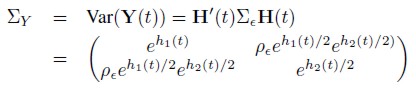 | [14] |
for t = 1, 2, ... ,N. Furthermore, Y(t) = (Y1(t), Y2(t))´, t = 1, 2, ... ,N has a bivariate Normal distribution with density
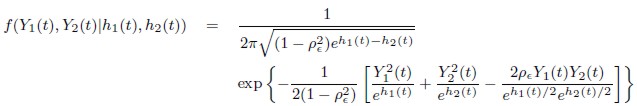 | [15] |
Also observe from (11) and the definition of η(t) that the latent variables h(t) = (h1(t), h2(t)) have normal distributions. In fact the density function of hi(1) is a normal distribution N(μi, σ2 ηi) and given hi(t - 1), hi(t) has a density function N(μi + øii[ hi(t - 1) μi], σ2 ηi) for i = 1, 2 and t = 2, ... ,N.
Stochastic volatility models are introduced in this paper and discussed as follows.
Model I
In this model we assumed that the error coordinates i(t), i = 1, 2 are independent, i.e., ρ
i(t), i = 1, 2 are independent, i.e., ρ = 0. Hence, Y(t), t = 1, 2, ... ,N will have Normal distribution with mean vector 0 and with variance-covariance matrix as a diagonal matrix given by ∑
= 0. Hence, Y(t), t = 1, 2, ... ,N will have Normal distribution with mean vector 0 and with variance-covariance matrix as a diagonal matrix given by ∑ 0 = diag(eh1(t), eh2(t)).
0 = diag(eh1(t), eh2(t)).
Model II
In this version of the model the covariance ρ between
between 1(t) and
1(t) and 2(t) is taken to be an unknown constant quantity that ought to be estimated. Hence, Y(t), t = 1, 2, ... ,N will have a Normal distribution with mean vector 0 and variancecovariance matrix given by (3).
2(t) is taken to be an unknown constant quantity that ought to be estimated. Hence, Y(t), t = 1, 2, ... ,N will have a Normal distribution with mean vector 0 and variancecovariance matrix given by (3).
Model III
In a third version of the model we keep the assumption of Model II, except for the way latent variable h2(t), t = 1, 2, ... ,N, is defined. We assume the presence of the Granger causality when modeling h2(t) and the latent variable h2(t) is now given by
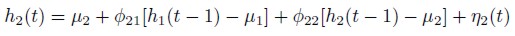 | [16] |
Where t = 2, 3, ... ,N and 0 <ø21, ø22 < 1. Remark. From (16), if ø21 ≠= 0, then the second return Granger causes the volatility of the second return.
Model IV
In this version of the model we take the assumptions of Model II except that an additional hypothesis on correlation between 1(t) and
1(t) and 2(t) is inserted. In this way, we assume that
2(t) is inserted. In this way, we assume that (t) = (
(t) = ( 1(t),
1(t), 2(t))´ has a bivariate normal distribution with mean vector 0 and variance-covariance matrix ∑
2(t))´ has a bivariate normal distribution with mean vector 0 and variance-covariance matrix ∑ (t) a 2 × 2 matrix, for t = 1, 2, ... ,N, by ∑
(t) a 2 × 2 matrix, for t = 1, 2, ... ,N, by ∑ given by
given by
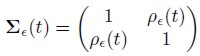 | [17] |
Where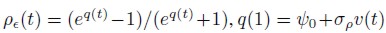 and for t = 1, 2, ... ,N, we have
and for t = 1, 2, ... ,N, we have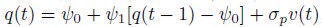 , with v(t), t = 1, 2, ...,N, independent and identically distributed quantities with common normal distribution N(0,1) (see for example Yu and Meyer, 2005). We further assume that q(1) has a Normal distribution
, with v(t), t = 1, 2, ...,N, independent and identically distributed quantities with common normal distribution N(0,1) (see for example Yu and Meyer, 2005). We further assume that q(1) has a Normal distribution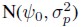 and for t = 2, 3, ... ,N, we also assume that given q(t-1), the quantity q(t) has a normal distribution
and for t = 2, 3, ... ,N, we also assume that given q(t-1), the quantity q(t) has a normal distribution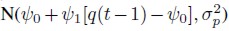 .
.
Remark. In this stochastic volatility model with dynamic correlation between the error components, correlation changes, and volatility as well. Also, we need to have - 1 < ρ (t) < 1 in order to have a well defined variance-covariance matrix ∑
(t) < 1 in order to have a well defined variance-covariance matrix ∑ (t).
(t).
Model V
In Model V we take into account the same hypotheses of Model IV, except for h2(t). For this latent variable we assume the same hypotheses as in Model III. Therefore, we consider the presence of the Granger causality for the latent variable h2(t), i.e., h2(t) is given by (16).
Model VI
In this model we admit a similar setting as that of model I, but error coordinates i(t), i = 1, 2, have a bivariate Student t distribution with v degrees of freedom, t = 1, 2, ... ,N. Therefore, the vector
i(t), i = 1, 2, have a bivariate Student t distribution with v degrees of freedom, t = 1, 2, ... ,N. Therefore, the vector (t) has a density t(0,∑
(t) has a density t(0,∑ 0, v), where v represents degrees of freedom and its density function is given by:
0, v), where v represents degrees of freedom and its density function is given by:
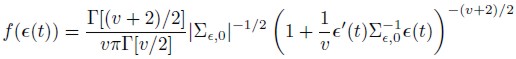 | [18] |
Where Γ(x) denotes a Gamma function.
Remark. Using a heavy tail Student distribution, we allow for the presence of extra Kurtosis for the distribution of returns. It is also interesting to observe that other versions for the BSV models can be considered.
BAYESIAN ANALYSIS
In this section we present a Bayesian framework for the models discussed above, divided into three categories. Those in the so-called Class I, are the models that have the error vector (t) = (
(t) = ( 1(t),
1(t), 2(t))´ normally distributed with mean vector 0 and a constant correlation for the error components model, i.e., the correlation is either zero or a constant not depending on t. The models falling into this class are models I, II, and III. In class II, we include models where
2(t))´ normally distributed with mean vector 0 and a constant correlation for the error components model, i.e., the correlation is either zero or a constant not depending on t. The models falling into this class are models I, II, and III. In class II, we include models where (t) is normally distributed with mean vector 0, but the correlation between
(t) is normally distributed with mean vector 0, but the correlation between 1(t) and
1(t) and 2(t) depends on time, i.e., models IV and V. Finally, in Class III we have model VI.
2(t) depends on time, i.e., models IV and V. Finally, in Class III we have model VI.
Bayesian inference is based on the simulated samples from the joint posterior distribution obtained using the Gibbs sampling algorithm.
Class I
If model I is considered then the vector of parameters to be estimated is θ1 = (ø11, ø22, σ2η1, σ2η·2, μ1, μ2). We assume that øii, σ2ηi , and μi have as prior distributions a Beta, an Inverse Gamma, and a Normal distribution, respectively, i = 1, 2, i.e., øii, ø2ηi, and μi have Beta(aii, bii), IG(ci, di), and N(ei, fi) prior distributions respectively, where the hyperparameters aii, bii, ci, di, ei, and fi are known, i = 1, 2. (In here, we are considering the Beta(a, b) and IG(c, d) as the Beta and Inverse Gamma distributions with means a/(a + b) and d/(c - 1), and variances ab/[( a + b)2(a + b + 1)] and d2/[( c - 1)2(c - 2)], c > 2, respectively).
When model II is admitted the vector of parameters is θ¸II = (θI, ρ ). In this case, we assume that ρ
). In this case, we assume that ρ has an uniform prior distribution U(-1,1). And the same set of prior distributions for θI as in the model I, with possibly different values for the hyperparameters.
has an uniform prior distribution U(-1,1). And the same set of prior distributions for θI as in the model I, with possibly different values for the hyperparameters.
In models I and II, the joint density functions of the latent variables h(t) = (h1(t), h2(t)), given the vector of parameters θ¸, is given by
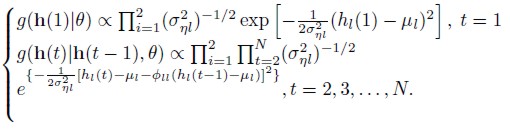 | [19] |
Let θ¸ = θII and take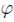 = (θ, h), with h = (h(1), h(2), ... , h(N)). Hence, the joint distributions of θ¸ and h for Y = (Y(1),... Y(N)) in Model II is given by:
= (θ, h), with h = (h(1), h(2), ... , h(N)). Hence, the joint distributions of θ¸ and h for Y = (Y(1),... Y(N)) in Model II is given by:
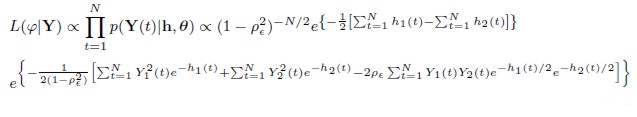 | [20] |
When θ¸ = θ I , we set ρ = 0 in (20).
= 0 in (20).
Therefore, for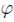 = (θ¸I , h) or
= (θ¸I , h) or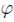 = (θII,h), the joint posterior distribution of the vector of parameters and h is given by
= (θII,h), the joint posterior distribution of the vector of parameters and h is given by
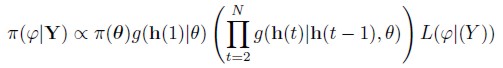 | [21] |
Where π(θ) is the prior distribution of the vector of parameters with θ = θI , θII , L(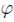 |Y) is the likelihood function of the model given by (20), and g(h(1)|θ),g(h(t)|h(t - 1), θ), t = 2, 3, ... ,N, are given by the set of recursive functions (19).
|Y) is the likelihood function of the model given by (20), and g(h(1)|θ),g(h(t)|h(t - 1), θ), t = 2, 3, ... ,N, are given by the set of recursive functions (19).
Assuming Granger causality for h2(t) and constant correlation for the errors component in model III, the vector of parameters is θIII = (θII ,ø21). The same set of prior distributions for θII is taken with possibly different hyperparameters.
Additionally, for the variable ø21 we choose a Beta distribution Beta( a21, b21 ).
The likelihood function of model III is given by 20. The joint posterior distribution of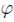 = (θ, h) has also the same expression as in model I and II, i.e., the expression given by (21) but taking θ = θIII and replacing the density function g(h(t)|h(t-1), θ), t = 2, 3, ..., N, by
= (θ, h) has also the same expression as in model I and II, i.e., the expression given by (21) but taking θ = θIII and replacing the density function g(h(t)|h(t-1), θ), t = 2, 3, ..., N, by
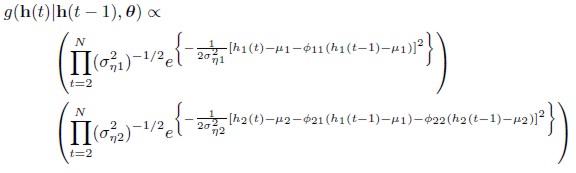 | [22] |
Class II
Stochastic volatility models with dynamic correlation for the error components are fit into this class of models. When Model IV is considered the vector of parameters is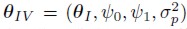 . The prior distribution for θI is taken to be the same as in Class I. The prior distribution for
. The prior distribution for θI is taken to be the same as in Class I. The prior distribution for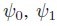 and σ2p p is a Normal distribution N(0, f3), Beta distribution Beta(f, g) and Inverse Gamma distribution IG(c3, d3), respectively, where the hyperparameters c3, d3, f3, f, g are known.
and σ2p p is a Normal distribution N(0, f3), Beta distribution Beta(f, g) and Inverse Gamma distribution IG(c3, d3), respectively, where the hyperparameters c3, d3, f3, f, g are known.
Hence, the joint likelihood function for θ = θIV of this class of models is given by
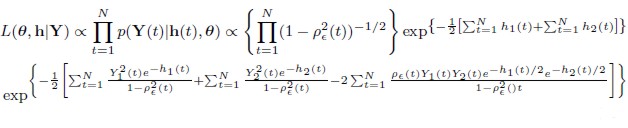 | [23] |
The joint posterior distribution of = (θ h, q), where θ = θIV and q = q(1, q(2),..., q(N)), is given by
= (θ h, q), where θ = θIV and q = q(1, q(2),..., q(N)), is given by
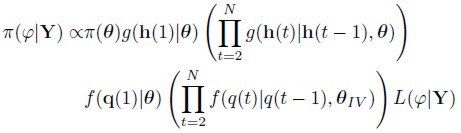 | [24] |
Where Φ(θ) is the joint prior distribution for θ g(h(1)|θ) and g(h(t)|h(t-1), θ) are defined by (22), f(q(1)|θ) and f(q(t)|q(t - 1), θ) are the Normal density functions of q(1), and the conditional Normal density function of q(t) given q(t -1) and L( ,Y) is the likelihood function defined in 23.
,Y) is the likelihood function defined in 23.
Admitting a stochastic volatility model with dynamic correlation for the error components and Granger causality for h2(t), t = 2, 3, ... ,N, in model V, the vector of parameters here is θV = (θIV , ø21). We take the same prior distribution for θIV except for the parameters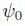 and
and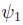 , which now have Gamma distributions with appropriate hyperparameters. We still set a Beta(a21, b21) prior distribution for ø21.
, which now have Gamma distributions with appropriate hyperparameters. We still set a Beta(a21, b21) prior distribution for ø21.
The likelihood function for this model is also given by 20. The posterior distribution is similar to 21, the difference is that g(h(t)|h(t - 1), θ), t = 2, 3, ... ,N is given by (19) with θ replaced by θV .
Class III
In this class of models, we assume that the error components have a bivariate Student t distribution with v > 2 degrees of freedom. The latent variables h(t) = (h1(t), h2(t)), t = 1, 2, ... ,N are defined as in model I.
The likelihood function could be obtained directly from 18 or representing the bivariate Student t distribution as a mixture of a bivariate Normal distribution and a Gamma distribution (see for example Bernardo and Smith, 1995).
Following the latter approach, first we have that the distribution for (t) is given by,
(t) is given by,
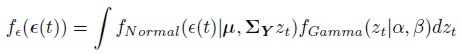 | [25] |
Where fNormal( (t)|μ, ∑) denotes bivariate Normal density with mean vector μ and variance-covariance matrix ∑ and fGamma(z)|α,β is a Gamma density with mean α/β and variance α/β2.
(t)|μ, ∑) denotes bivariate Normal density with mean vector μ and variance-covariance matrix ∑ and fGamma(z)|α,β is a Gamma density with mean α/β and variance α/β2.
Therefore, take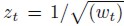 , where wt has as Gamma distribution, Gamma (λw, λw), and is such that E(wt) = 1 and Var(wt) = λw-1 . Hence, the conditional distribution of Y (t) given ∑Y and wt is a bivariate Normal distribution with mean vector 0 and variance-covariance matrix
, where wt has as Gamma distribution, Gamma (λw, λw), and is such that E(wt) = 1 and Var(wt) = λw-1 . Hence, the conditional distribution of Y (t) given ∑Y and wt is a bivariate Normal distribution with mean vector 0 and variance-covariance matrix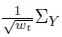 , where ∑Y is given by 14.
, where ∑Y is given by 14.
The vector of parameters for Model VI is θVI = (θII ,λw) and for w = (w1,w2,... ,wN,), the likelihood function of the model is given, for = (θIV , h,w), by
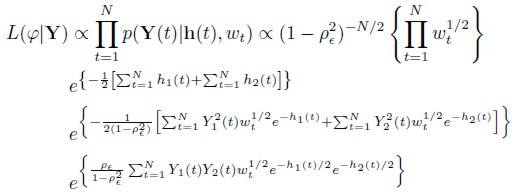 | [26] |
The prior distributions of θII are the same as used in Class I models (with possibly different hyperparameters) and we set a prior Gamma distribution Gamma(fϒ, gϒ) for λw. We also have that fϒ and gϒ) are known hyperparameters.
ANALYSIS OF IBOVESPA AND DOWJONES INDUSTRIAL TIME SERIES
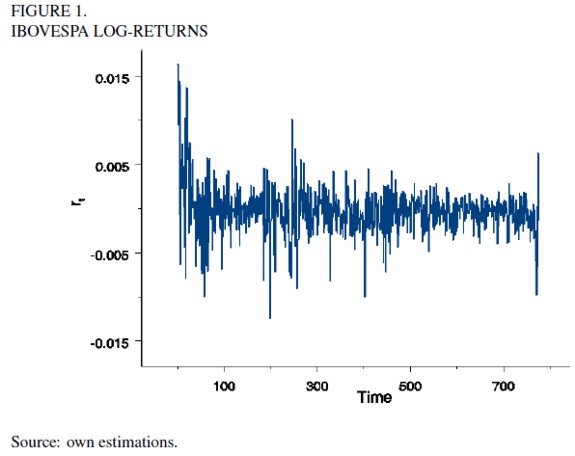
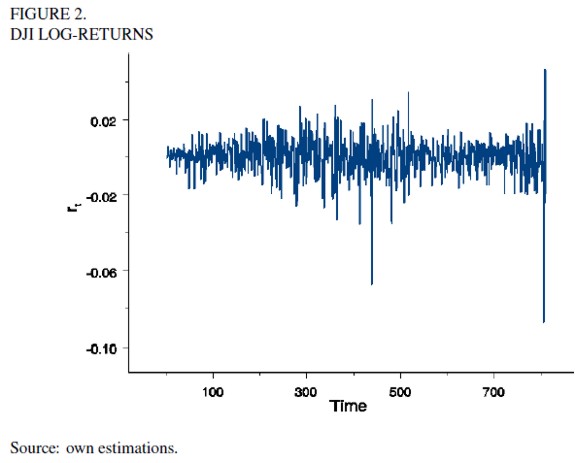
In this section, we analyze the log-returns of IBOVESPA and DJI in a weekly basis from 04/27/1993 to 11/03/2008. Figures 1 and 2 show the indicators' behaviors and show a large volatility for the last month of 2008 in both cases. For the average price of shares in the New York stock market, higher spikes in the middle of the interval correspond to the 2000 stock market crash. For DJI, it is easy to show that second order moments' autocorrelation and cross-correlation are significant at least up to the first lag, indicating the covariance matrix of DJI and IBOVESPA may be varying and is serially correlated.
Using multivariate GARCH model
First, we assume a multivariate GARCH model as introduced in section 2, to analyze the two time series. When estimating the parameters of the model given by 5, we found that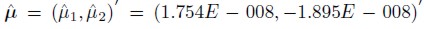 , and
, and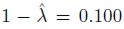 . In the same way, the parameter estimates of model 6 are
. In the same way, the parameter estimates of model 6 are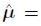
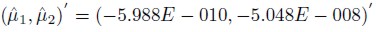 and
and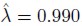 .
.
Table 1 shows the estimates of EWMA models . In this table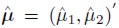 A(i, j) corresponds to the (i, j)-th element of A0, ARCH(i, j, k) corresponds to the (j, k)-th element of Ai, and GARCH(i, j, k) corresponds to the (i, k)-th element of Bj . In this model
A(i, j) corresponds to the (i, j)-th element of A0, ARCH(i, j, k) corresponds to the (j, k)-th element of Ai, and GARCH(i, j, k) corresponds to the (i, k)-th element of Bj . In this model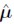 and its correspondent standard deviation are given by
and its correspondent standard deviation are given by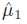 = 8.468E - 009(0.00082189) and
= 8.468E - 009(0.00082189) and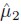 = - 3.614E -007(0.00215481), respectively.
= - 3.614E -007(0.00215481), respectively.
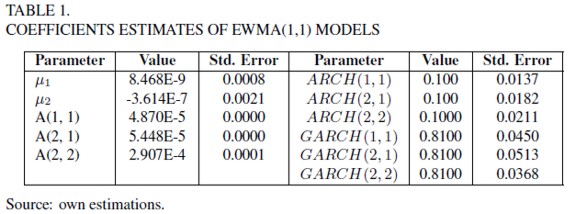
For model discrimination, we can use different existing Bayesian criteria. A special and popular criterion is given by DIC (Deviance Information Criterion) and smaller values of it indicate better models (Spiegelhalter, Thomas, Best, and Lund, 2002)). The values of DIC can also be negative. For this model the DIC value is given by DIC = -6655.965.
Using BSM models
In order to analyze IBOVESPA and DJI time series, we estimate six BSV models as discussed in section 3. Models' estimations are carried out through WinBUGS, which (Spiegelhalter, Thomas, Best and Lund, 1999) simulates samples for the posterior distribution in each case. From its output we also obtain Monte Carlo individual estimates for DIC. The following set of prior distribution are assumed:
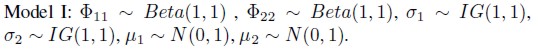
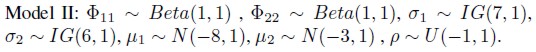
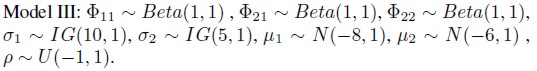
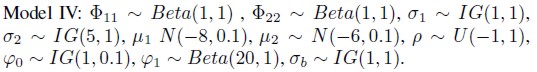
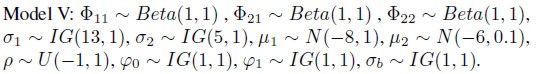
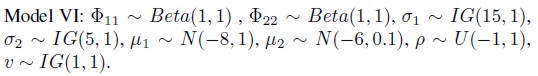
It is important to observe all obtained information used before for choosing prior hyperparameters is taken into account for individually estimating the six models. So, a sort of empirical Bayesian methodology is applied and this procedure is quite relevant for convergence of Gibbs sampling algorithm.
A burn-in period of size 5000 is implemented in order to eliminate the effect of initial values for the iterative procedure used to simulate the Gibbs samples. After burn-in initial values, we choose every 10th sample for each parameter with a total of 1000 Gibbs samples admitted to obtain the posterior summaries of interest. The convergence of the Gibbs sampling algorithm is monitored by time series plots for the simulated Gibbs samples for each parameter.
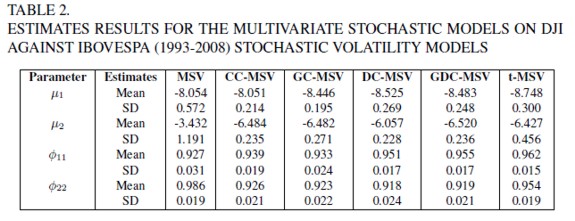
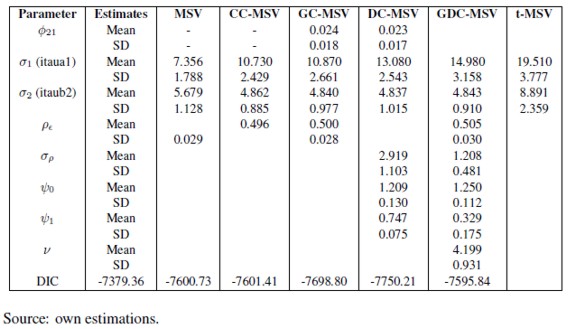
In table 2, we have the posterior summaries of interest for the six BSV models. DIC estimates are automatically obtained from theWinBugs software and they are based on the 1,000 simulated Gibbs samples, with values: DICI = -7379.36, DICII = -7600.73, DICIII = -7601.41, DICIV = -7698.80, DICV = -7750.21, and DICV I = -7595.840, indicating Model V is better fit by the data.
ECONOMIC ANALYSIS OF THE RESULTS
Financial time series behavior has been an issue extensively discussed in Economics. Since Engle (1982), the academic research on this specific topic has been concerned with stochastic volatility models, especially its ARCH and GARCH versions. Apart from Engle's methodology, our concern in this paper is about bivariate stochastic volatility models estimation applying MCMC Bayesian methods.
Since the American departure from the Dollar-Gold parity at the beginning of the seventies, stock market's volatility has raised concerns demanding more from the academic researchers. Moreover, the sequence of recent financial crashes awakes even more the necessity of understanding the meaning of volatility on driving stocks returns. Recently, the American mortgage crisis showed how sensitive stock markets are to expectations that directly affect stocks volatility. In fact, US stock rices dropped 35,5% on average from the first week of August until the last week of November last year.
Most of these facts raise the question on what primarily determines the stock prices behavior. From the economic point of view, market expectation is a major determinant, but the knowledge about some additional stylized facts helps us to shed some additional light on this matter. Clearly, the bad news involving the credit insolvency of a couple of American banks performed a remarkable role, however market mood turned into a bear only after Lehman Brother bankruptcy was declared.
In fact this is the effective role of the expectations on the markets, but from that episode on investors started reacting by selling most of their assets in order to raise funds for clearing other economic losses. From a ex post point of view it is possible to conclude that other facts have also played an special role on blowing stock market's volatility all over the world. Undoubtedly, stock market returns are subject to excess volatility, what characterizes a leptokurtic stock return distribution. So, the probabilities of bad and good outcomes were totally distorted from the Normal distribution perspective.
Second, a shock on volatility persists more than normally expected. This is a time series phenomenon accurately described by the first order correlation coefficient of the model's volatility equation. Brazilian stock market, in particular, is a benchmark on persistence, since our best estimates for this coefficient are close to one. Another remarkable stylized fact concerns the existence of cross-correlation towards assets and markets around the world. Such evidence is sufficient to confirm how deep last year's financial crash has impacted assets' prices and markets.
However, we also know these episodes do not last forever. Contrarily, stock market returns revert to their normal pace after a while, but this lapse is enough to burn down significant amounts of wealth invested in these markets. In summary those are more than sufficient reasons for carefully analyzing combined stock market portfolio returns volatility.
In order to investigate the stochastic behavior of stock returns volatility, we estimated bivariate stochastic volatility models involving two market indexes time series: US Dow Jones Industrial (DJI henceforth) and Brazilian IBOVESPA. Created in 1896 by the editor of The Wall Street Journal, DJI is the second oldest American stock market index and is straightforwardly obtained, because it is based on a simple average formula for calculating price returns of the 30 biggest and most important American corporations. In fact, DJI is not a trade mark of the New York Stock Exchange, but of The Wall Street Journal, then choosing what corporation will enter or will not is not an issue for NYSE (New York Stock Exchange). Furthermore, there is no forward determined criterion for making this choice, but being an American corporation and a market leader in the industry it is included are two of them.
Brazilian IBOVESPA (Sâo Paulo Stock Exchange Index) is the most important stock market indicator in South America measuring stocks total returns performance. By definition, it is the constant value of a theoretical portfolio established on January 02, 1968 and based on a hypothetical investment value. No additional capital inversion was made since then, admitting only adjustments to take account for corporations' pay outs. Clearly, IBOVESPA embodies not only stock prices changes, but also the impact of dividends. In this sense, IBOVESPA is an index that accounts for stocks' total return. Differently from DJI, IBOVESPA is calculated and published by Sâo Paulo Stock Exchange, so there is a clear criterion for choosing what stocks should be in the theoretical portfolio.
In order to proceed on this sort of analysis, we take the weekly log-returns of US DJI and Brazilian IBOVESPA from April 27, 1993 to November 03, 2008, a sample that includes two of the major recent crashes (September 11, 2001 and the recent mortgage crisis in USA) in NYSE and consequently BOVESPA. Moreover, Brazilian stock market has been hit by other episodes mainly after successive international crisis during the nineties. Characteristically, the stock market in Brazil is more volatile than that in the USA, and this justifies private interests on obtaining returns usually higher than those offered by other markets.
Granger causality effect investigation is carried out and based on weekly data because most of the relevant movements on returns are restricted to a near past. This is a very specific feature due to financial time series, and said feature invalidates any trial to extend returns co-movements beyond longer frequency data. Furthermore, though data are taken in weekly basis, Granger causality is a long term concept. In this sense we investigate persistence on this causal behavior between volatility in IBOVESPA and DJI due to co-movements on weekly returns that are projected onto the future time series data generating process. Truly weekly behavior is persistent over time upon influencing investments decisions.
Then, we estimated six multivariate stochastic volatility models named as basic multivariate Stochastic volatility (MSV), constant correlation SV (CC-MSV), Granger causality SV (GC-MSV), dynamic SV (DC-MSV), Granger causality and dynamic SV (GCC-MSV), and a fat tail SV (t-MSV), and interesting results came up. The first model accounts for errors independence and normality assumption concerning the random terms and we label it by MSV. On the sequence, we assume a non-zero covariance between the two equations errors terms, and covariance is a number to be estimated and labeled it by CC-MSV. Third, the presence of Granger causality from DJI to IBOVESPA is taken into account when modeling the latent variable in model three. In this sense, the volatility of the second return is Granger caused by the volatility of the first return, raising a theoretical and testable implication concerning the causality direction between the returns volatility in US and in Brazil.
A dynamic correlation approach is introduced in the fourth model, which accounts for the possibility of a dynamic behavior for cross-correlation among assets and markets. According to Yu and Meyer (2006), this model is labeled as DC-MSV. Following the two previous models, Granger causality and dynamic correlation are both introduced in the fifth model. Such a procedure is admitted in order to capture returns volatility direction of causality and cross-correlation dynamics and is named GCC-MSV. Finally, a heavy tail Student's t distribution is introduced in the original MSV model in order to check for the presence of extra kurtosis in the returns distributions. Form the financial point of view t-MSV models are less likely to provide a good fit, once kurtosis is already a fact for stochastic volatility models, then an excess kurtosis should be a little odd, but not impossible. Excess kurtosis means stock brokers automatically and dynamically adjust their portfolio over time, which clearly sounds as an unlikely procedure.
Estimates of the six models are contained in Table 3. One result strikes most; the introduction of a correlation between the two volatility equations errors provides always a better fit. Definitely, models DC-MSV and GCC-MSV are superior, once their evaluation is based on the DIC criterion. Even CC-MSV is a good fit when compared to MSV and t-MSV models. A second fact calling attention is the Granger causality significance measured mainly by GCC-MSV and GC-MSV models.
Persistence on volatility is a result that strikes us most, though it may rise some questioning concerning structural breaks. Since returns on IBOVESPA and DJI are calculated on weekly basis and persistence on volatility on financial time series is a disputable fact, structural break is a long run feature. Clearly, some persistence on volatility is due to the time series correlation, a phenomenon captured by the coefficients ρ and σρ, estimated for GC-MSV and GDC-MSV models.
and σρ, estimated for GC-MSV and GDC-MSV models.
As expected an excess kurtosis model does not fit quite well. Moreover, excess volatility for the Brazilian stock market would be a difficult task to justify, once the volatility behavior in this market is already excessive (This can be seen by the estimated coefficients for σu1 and σu2) compared to other stock markets.
Concerning the theoretical risk-return relationship, the estimated coefficients for means and volatilities confirm what should be expected. Once we empirically verify μ1 < μ2, and σu1 < σu2, agreeing with the portfolio theory, so the volatility pricing procedure is theoretically based upon.
About volatility persistence, the evidences do not support the hypothesis that Brazilian volatility persists more than American volatility. Except for MSV's estimates of ø22, the other model's estimates for the same parameter support the hypothesis that American volatility persistence is greater than Brazilian one. Probably on introducing the September 11 event in the sample and suppressing part of the information on US mortgage crisis last year stressed the volatility behavior in US compared to Brazil. However, though volatility persistence is a fact in the literature, comparison of this persistence among countries is not an undisputable fact and differences can frequently arise. Furthermore, a significant part of this persistence can already be captured by ø21.
Remarkably interesting are the signal and magnitude of the ø21 estimate. This is a measure for the impact of a shock on the DJI's volatility over the IBOVESPA volatility, which appears to be not as sensitive as we would expect at a first glance. However, since the estimate of the coefficient is equal to 0.023 it means a 100% increase in American stock market volatility will have an average impact of 116.4% over Brazilian stock market volatility. Such interpretation of the result is amazing, mainly for institutional investors.
Finally, the dynamics of the volatility spill-over effects are described by the estimates of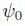 and
and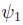 in GCC-MSV model4. Clearly, there is a high correlation starting point (
in GCC-MSV model4. Clearly, there is a high correlation starting point (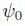 ), which is mitigated by a less than one
), which is mitigated by a less than one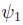 coefficient, suggesting the feasibility of mean reverted spilling-over volatility shocks. Furthermore, as the integration among international markets becomes tighter, spill-over effects are more likely to mutually affect stock markets.
coefficient, suggesting the feasibility of mean reverted spilling-over volatility shocks. Furthermore, as the integration among international markets becomes tighter, spill-over effects are more likely to mutually affect stock markets.
Nowadays, negotiations involving Brazilian corporations' stocks in NYSE are almost a complete reality, at least for Petrobrás5 and Vale's6 shares. The dynamic behavior of cross-correlation among Brazilian and American stock markets raises a very important issue, because once we assume stock markets integration is a irreversible fact, then the room for capital controls is none or at least extremely narrow. Pursuing this sort of economic policy as Brazil just did is an invitation for corporation's migration to NYSE. It seems Brazilian economic policy is starting to deviate from a previous capital markets development commitment.
FOOTNOTES
4 All the analysis is based on the estimates provided by this model, because DIC criterion allows us to choose it as the best model.
5 Petrobrás is the Brazilian state owner enterprize, which is a leader at national level on oil industry.
6 Vale is the newest denomination for Vale do Río Doce Corporation, which is a private enterprize in mining industry.
BIBLIOGRAPHY
[1] Bauwens, L., Laurent, S. and Rombouts, J.V.K. (2006). Multivariate GARCH models: A survey. Journal of Applied Econometrics, 21, 79-109. [ Links ]
[2] Bollerslev, T. (1986). Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307-327. [ Links ]
[3] Bollerslev, T. (1990). Modelling the Coherence in Short-Run Nominall Exchange Rates: A Multivariate Generalized Arch Model. The Review of Economics and Statistics, 72(3), 498-505. [ Links ]
[4] Bollerslev, T., Engle, R.F. and Wooldridge, J.M. (1988). A Capital Asset Pricing Model with Time-Varying Covariances. Journal of Political Economy, 96, 116-131. [ Links ]
[5] Bollerslev, T.; Chou, R. Y. and Kroner, K.F. (1992). ARCH modeling in finance; a review of the theory and empirical evidence. Journal of Econometrics, 52, 5-59. [ Links ]
[6] Engle, R. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of UK Inflation. Econometrica, 50, 987-1007. [ Links ]
[7] Engle, R. (2001). GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics. The Journal of Economic Perspectives, 15(4), 157-168. [ Links ]
[8] Engle, R.F., Granger, C.W.J. and Kraft, D.F. (1984). Combining competing forecast of inflation using a bivariate ARCH model. Journal of Economic Dynamics and Control, 8, 151-165. [ Links ]
[9] Ghysels, E., Harvey, A.C., Renault, E. (1996). Stochastic Volatility. In G.S. Rao and C.R. Maddala (Eds.). Statistical Methods in Finance (pp. 119-191). Amsterdam: North-Holland. [ Links ]
[10] Kim, C.-J., Nelson, C.R. and Startz, R. (1998). Testing for mean reversion in heteroskedastic data based on Gibbs sampling augmented randomization. Journal of Empirical Finance, 5, 131-154. [ Links ]
[11] Meyer, R. and Yu, J. (2000). BUGS for a Bayesian analysis of stochastic volatility models. The Econometrics Journal, 3(2), 198-215. [ Links ]
[12] Nelson, B.D. (1991). Conditional Heterocedasticity in Asset Returns: A New Approach, Econometrica, 59(2), 347-370. [ Links ]
[13] Shephard, N. (1996). Statistical aspects of ARCH and stochastic volatility. In D.R. Cox, O.E. Barndorff-Nielson, D.V. Hinckley and N. Shephard (eds.). In time Series Models in Econometrics, Finance and Other Fields (pp. 1-67). London: Chapman & Hall. [ Links ]
[14] Spiegelhalter, D.J., Thomas, A., Best, N.G. and Lund, D. (1999). WinBUGS User Manual. Cambridge, United Kingdon: MRC Biostatistics Unit. [ Links ]
[15] Spiegelhalter, D.J., Best, N.G., Carlin, B.P. and Van der Linde, A. (2002). Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64(4), 583-639. [ Links ]
[16] Tauchen, G. and Pitts, M. (1983). The price variability-volume relationship on speculative markets. Econometrica, 51(2), 485-505. [ Links ]
[17] Taylor, S.J. (1982). Financial returns modelled by the product of two stochastic processes, a study of daily sugar prices. 1961-79. In Anderson, O.D. (eds.). Time Series Analysis: Theory and practice (pp. 203-226). Amsterdam: North-Holland. [ Links ]
[18] Taylor, S.J. (1994). Modelling stochastic volatility: a review and comparative study. Mathematical finance, 4, 183-204. [ Links ]
[19] Yu, J. and Meyer, R. (2006). Multivariate Stochastic Volatility Models: Bayesian Estimation and Model Comparison. Econometric Reviews, 25, 361-384. [ Links ]
[20] Zivot, E. and Wang, J. (2006). Time series with S-PLUS (Second Edition). New York: Springer. [ Links ]













