Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.31 no.spe57 Bogotá June/Dec. 2012
SINCRONIZACIÓN DE LOS CICLOS ECONÓMICOS: EL CASO DE COLOMBIA, ECUADOR Y VENEZUELA
Andrés Salamanca Lugo 1
1 Economista y Magister en Matemática Aplicada. E-mail: asalamancal@unal.edu.co. Dirección de correspondencia: Dirección: Calle 138 N. 108-12 Int. 22 Apto. 101 (Bogotá D.C., Colombia). El autor agradece a Enrique López, por el valioso tiempo que dedicó a discutir diversos aspectos de las versiones preliminares de este trabajo; a Martha Misas, por su apoyo y guía en la comprensión del modelo econométrico empleado; a los participantes de los Seminarios de Economía del Banco de la República (Banca Central de Colombia) y Fedesarrollo (Centro de Investigación Económica y Social), por sus valiosos comentarios; y las acertadas consideraciones realizadas por los evaluadores anónimos.
Este artículo fue recibido el 14 de febrero de 2011, la versión ajustada fue remitida el 25 de abril de 2011 y su publicación aprobada el 15 de junio de 2011.
Resumen
En este documento se investiga acerca de la existencia y la identificación de un ciclo económico común entre Colombia, Ecuador y Venezuela. Se busca una evidencia de la sincronización de los ciclos económicos de estos países, a través de diferentes medidas no paramétricas, en conformidad con los ciclos y mediante la construcción de un ciclo común de referencia. De acuerdo con esto, se ajusta un modelo de Markov-Switching autoregresivomultivariado (MS-VAR) que confirma la existencia de dicho ciclo. Finalmente, la cronología del ciclo común es reconstruida a partir de las probabilidades suavizadas del modelo y es contrastada con el ciclo común de referencia.
Palabras clave: ciclos económicos, sincronización, Markov-switching. JEL: C32, E32, F43, N16, E37.Abstract
This paper deals with the existence and identification of a common growth cycle between Colombia, Ecuador, and Venezuela. Evidence of synchronization between cycles of these countries through different non-parametric measures of conformity of the cycles and through a reference cycle is found. A Markov-Switching Vector Autoregressive model (MS-VAR) is then used to identify the common cycle and the results confirm the existence of such a cycle. Finally, the common cycle is dated on the basis of smoothed probabilities and compared with a reference cycle.
Keywords: economic cycles, synchronization, Markov-switching. JEL: C32, E32, F43, N16, E37.
Rèsumè
Cet article examine l'existence et l'identification d'un cycle économique commun entre la Colombie, l'Equateur et le Venezuela. Il recherche la preuve de la synchronisation des cycles économiques de ces pays, par le biais de diverses mesures non-paramétriques, en conformité avec les cycles et au moyen de la construction d'un cycle commun de référence. En conséquence, l'étude utilise un modèle de Markov-Switching autorégressifmultivarié (MS-VAR), lequel confirme l'existence du dit cycle. Enfin, la chronologie du cycle commun est reconstruite à partir des probabilités lissées du modèle et est comparée avec le cycle commun de référence.
Mots-clés: cycles économiques, synchronisation, Markov-switching. JEL: C32, E32, F43, N16, E37.
El análisis de la sincronización y/o desacoplamiento (decoupling) de los ciclos económicos entre diferentes países se ha convertido en un tema de especial importancia, tanto en el ámbito académico como en ámbito de la política económica. La existencia de choques externos que fluyen a través de una fuente común hacia las diferentes economías ha sido una importante razón para que muchos estudios se hayan concentrado en los efectos de la sincronización de los países. En el contexto de una integración internacional, conceptos como ciclo común y comovimientos han hecho pensar que países con fuertes nexos, en términos de la correlación y concordancia de sus ciclos económicos, son más propensos a afrontar menos costos de integración que aquellos cuyos ciclos son asincrónicos. No obstante, la existencia de fuertes vínculos entre la cadencia en el crecimiento de las economías puede llevar a pensar que una gran proporción de la varianza en las tasas de crecimiento se puede trasmitir a cada economía individual. De este modo, el costo de la sincronización de la economía puede llegar a ser más alto que las ganancias de la integración.
Numerosos estudios han mostrado que los ciclos de las economías europeas han venido ganando sincronía en los últimos años -véase por ejemplo Krolzig y Toro, 2004; Artis, Krolzig y Toro, 2002; Massmann y Mitchell, 2004, y Böwer y Guillemineau, 2006-. En el contexto de la Unión Europea, el análisis de la sincronización de los ciclos económicos entre países ha pasado a ser un importante asunto de estudio, más en términos de política económica que en términos académicos. Obviamente, la sincronización de los ciclos nacionales en este tipo de integraciones es una condición necesaria para el éxito de la política monetaria en los programas de estabilización macroeconómica supranacional. De igual forma, otros estudios han concentrado su atención en formas de integración que son más de tipo económico que regional; por ejemplo, trabajos como los de Schirwitz y Wälde (2004) y Tomljanovich y Ying (2005) analizan el grado de sincronización entre los países que componen el G-7; Darvas, Rose y Szapáry (2005) estudian los efectos de la divergencia fiscal sobre la sincronización de los ciclos de los países de la Organización Económica para la Cooperación y el Desarrollo (OECD); e Inklaar, Jong-A-Pin y De Haan (2005) analizan el comercio como un determinante de la sincronización de los países miembros de la OECD 2. Queda claro que gran parte de la literatura que analiza la sincronización de los ciclos económicos ha centrado su atención en el estudio de las economías desarrolladas; pocos esfuerzos se han dedicado al estudio de este fenómeno en el contexto de las economías en desarrollo.
De acuerdo con estos argumentos, este documento investiga la existencia e identificación de un ciclo económico común entre Colombia, Ecuador y Venezuela. Se ajusta un modelo de Markov-Switching autoregresivo multivariado (MS-VAR) con el fin de confirmar, a través de una inferencia óptima, la existencia de dicho ciclo. Finalmente, la cronología del ciclo común es reconstruida a partir de las probabilidades suavizadas del modelo y es contrastada con un ciclo común de referencia, elaborado mediante una metodología no-paramétrica.
ANÁLISIS DE LA SINCRONIZACIÓN DE LOS CICLOS ECONÓMICOS
El progresivo proceso de globalización y la integración de los mercados mundiales se han convertido en objetos de análisis que, durante los últimos años, han ganado un terreno importante en la comprensión de las fluctuaciones cíclicas de las economías. En particular, el desarrollo de la Unión Económica y Monetaria (EMU) de la Unión Europea ha despertado un especial interés en el estudio de las características comunes de los ciclos económicos de las naciones que componen esta forma de integración. La existencia de una fuente común, a través de la cual los choques externos fluyen hacia las economías particulares, se ha convertido en un tema de especial atención por parte de los policy-makers. Es natural pensar que la sincronización de los ciclos es una condición necesaria (aunque no suficiente) para el éxito de las políticas y los programas de estabilización macroeconómica a nivel supranacional. No obstante, la existencia de fuertes vínculos entre los ritmos de crecimiento de las economías puede llevar a pensar que una gran proporción de la varianza en las tasas de crecimiento se puede trasmitir a cada economía individual. De este modo, el costo de la sincronización de las economías puede llegar a ser más alto que las ganancias de la integración.
Así como los gobiernos, el sector privado también busca orientar sus acciones, no solo con base en la información de las condiciones de la economía nacional, sino también a la espera de que los efectos de las fluctuaciones de la actividad económica en otras naciones se trasmitan a la economía local. De este modo, la integración de los mercados ha propiciado que los cambios en la política comercial, monetaria y/o fiscal, e incluso el estado de las economías en otras naciones del mundo puedan influenciar significativamente la efectividad de los programas macroeconómicos nacionales.
Como se señaló en la introducción de este trabajo, existen un sinnúmero de investigaciones que han encontrado una evidencia de la sincronización en los ciclos económicos de diferentes grupos de economías, como por ejemplo las que componen la Unión Europea, el G-7 y los países miembros de la OECD, entre otros. Así mismo, otros trabajos se han concentrado en los determinantes de tal sincronización. No obstante, existen muy pocas investigaciones que se hayan orientado al análisis del ciclo económico común de Latinoamérica, si es que tal fenómeno existe. Por ejemplo, Engel e Issler (1993) encontraron, a través de un análisis de correlaciones, que estas resultan significativas solo para grupos de países; Arnaudo y Jacobo (1997) muestran que las fluctuaciones económicas son muy variables y poco uniformes; y Hecq (2002), por su parte, encuentramediante un análisis de ciclos comunes, en un modelo de vectores de cointegración, que los comovimientos de los ciclos son un fenómeno entre grupos de países, más no es general. Por otro lado, estas investigaciones abordan el problema sin considerar las no-linealidades inherentes a los ciclos económicos. Existe, sin embargo, una excepción al respecto: el trabajo de Mejía-Reyes (2000) estudia las características de los ciclos económicos de ocho economías latinoamericanas a través de múltiples modelos de Markov-Switching autoregresivos univariados (MS-AR); además, busca la evidencia de un ciclo común de tales economías mediante un análisis multivariado de Markov-Switching. Los resultados encontrados muestran que no existe un ciclo común entre las economías estudiadas. En conclusión, los resultados hacen evidente que, en general, no es posible hablar de un ciclo común latinoamericano.
Otras fuentes de interés en el estudio de los ciclos comunes han sido los determinantes de la sincronización de las economías. En el contexto de las naciones europeas, estudios como los de Böwer y Guillemineau (2006) y García-Herrero y Ruiz(2008) muestran que, en general, los determinantes de la sincronización pueden variar en el tiempo; sin embargo, el comercio bilateral y los vínculos financieros entre las naciones se constituyen como las principales fuentes de sincronización de los ciclos económicos.
Por otro lado, estudios más amplios, que incorporan muchas más economías del mundo, han encontrado evidencia similar al respecto. Por ejemplo, Baxter y Kouparitsas (2004), mediante un análisis de cotas extremas -Extreme-Bounds Analysis (EBA)- encuentran que, para un conjunto de cien economías, el comercio bilateral es un determinante robusto de los comovimientos de los ciclos entre países; Kose, Prasad y Terrones (2003), con una muestra de 76 naciones (21 países industrializados y 55 países en desarrollo), hallan la evidencia de que la integración comercial y financiera de los mercados incrementa los efectos indirectos de las fluctuaciones macroeconómicas; por último, el estudio de Calderón, Chong y Stein (2003), con información anual para 147 naciones, muestra que: i) los países con mayor comercio bilateral exhiben una mayor sincronización de sus ciclos económicos, y que ii) dicho impacto es mayor para los países industriales que para los países en desarrollo 3.
A pesar de la evidencia aportada por estos y otros estudios, a la fecha sigue siendo una cuestión no resuelta si la integración económica promueve o no la sincronización de los ciclos económicos. Por ejemplo, Eichengreen (1992), mediante un extenso análisis de los costos y beneficios de la unificación monetaria europea, argumenta que la integración no necesariamente habrá de reflejarse en una mayor homogeneidad entre los ritmos de crecimiento de los paísesmiembros de la EMU. Considera que la consecución de la EMU llevará a una mayor especialización regional, la cual se reflejará en mayores choques de tipo región-específicos. En la misma línea, Krugman (1993) predice que, mientras la integración del mercado continúe, Europa tendrá que afrontar el surgimiento de choques región-específicos; sin embargo, y a diferencia de Eichengreen (1992), argumenta que la naturaleza de dichos choques es predominantemente permanente. Además, autores como Ruiz- Porras (2010) sustentan que la globalización y la falta de sincronización de los ciclos económicos entre las economías han contribuido a prolongar los problemas asociados a la crisis global. Por un lado, la diversidad de conclusiones a las cuales llegan los estudios acerca de la sincronización de los ciclos económicos, particularmente en el caso de las economías latinoamericanas, ponen de manifiesto la necesidad de ahondar en el estudio riguroso y detallado de este fenómeno. Por otro lado, la mayoría de los estudios no consideran la existencia de no-linealidades inherentes en el ciclo económico, lo cual puede conducir a sobreestimar o subestimar los resultados de dichos estudios.
En las secciones siguientes, buscaremos evidencias de sincronización en los ciclos económicos de Colombia, Ecuador y Venezuela, empleando para ello dos diferentes metodologías: en un primer caso, se construye un ciclo común de referencia, al igual que un índice de conformidad en los comovimientos de la tasa de crecimiento real de las tres naciones; en un segundo caso, se utiliza la generalización para modelos multivariados de Markov-Switching, propuesta por Krolzig (1997), con el fin de identificar a través de un análisis de inferencia óptima el ciclo común entre estos países.
Evidencia de sincronización bajo técnicas no-paramétricas
Detección de los puntos de quiebre
En esta sección se empleará la definición de ciclo propuesta por Burns y Mitchell (1946), expresada en términos de los puntos de quiebre (turning points) de una serie. Definir los periodos de expansión y contracción de la actividad económica requiere, entonces, identificar el conjunto de puntos de quiebre que definen los picos (peaks) y valles (troughs) de la serie de crecimiento real del PIB. En este trabajo se emplea el algoritmo propuesto por Harding y Pagan (H-P) (1999). En cada caso se aplican dos reglas fundamentales que constituyen el punto central de la técnica. En primer lugar, se determina un máximo (o mínimo) local si es el punto más alto (o bajo) entre los dos trimestres predecesores y antecesores a su posición, es decir, se define que ha ocurrido un pico en el tiempo 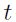 si
si 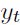 es el
es el 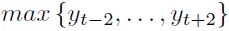 , y un valle si
, y un valle si 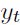 es el
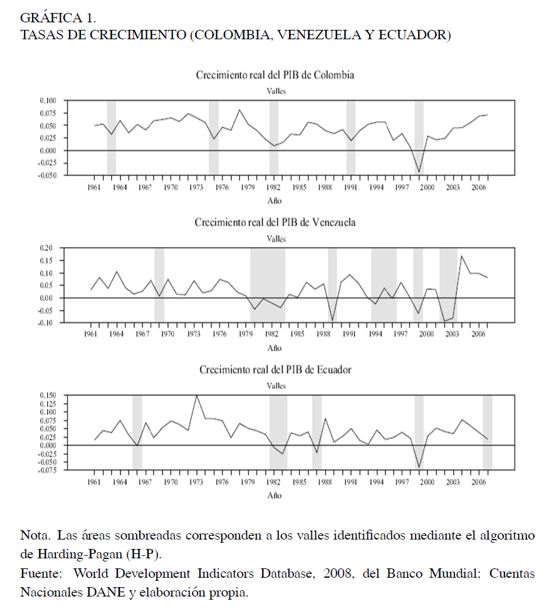
es el 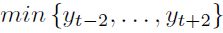 . En segundo lugar, siempre se debe completar un ciclo, es decir, un pico siempre es seguido de un valle y viceversa. Una vez se ha depurado la serie, se imponen los puntos de quiebre a la serie original. El resultado final se construye a partir del refinamiento de tales puntos sobre el conjunto de observaciones sin suavizar 4. A partir de las series anuales (1961-2007) del crecimiento real de las tres economías consideradas, se implementó el algoritmo H-P 5. Los valles detectados para la serie de crecimiento real del PIB de cada país, mediante esta metodología, se presentan en la Gráfica 1.
. En segundo lugar, siempre se debe completar un ciclo, es decir, un pico siempre es seguido de un valle y viceversa. Una vez se ha depurado la serie, se imponen los puntos de quiebre a la serie original. El resultado final se construye a partir del refinamiento de tales puntos sobre el conjunto de observaciones sin suavizar 4. A partir de las series anuales (1961-2007) del crecimiento real de las tres economías consideradas, se implementó el algoritmo H-P 5. Los valles detectados para la serie de crecimiento real del PIB de cada país, mediante esta metodología, se presentan en la Gráfica 1.
A simple vista, se observa que el comportamiento dinámico del producto real de cada país difiere significativamente. En particular, la volatilidad de cada serie es característica de cada economía, así como los niveles medios de crecimiento. Es fácil caracterizar al menos dos periodos comunes de recesión: los primeros años de la década de los ochenta y los últimos años de la década de los noventa. Los años que van de 1980 a 1983 se caracterizaron por:
1. El alza de las tasas de interés decidida por la reserva Federal de los Estados Unidos en 1979.
2. Los efectos negativos de la segunda recesión económica mundial (1980- 1982), originada en los últimos años de la Guerra Fría. 3. las graves consecuencias que sobre la balanza de pagos de las economías latinoamericanas tuvo la crisis de la deuda.
Por su parte, la década de los noventa se identificó por los efectos de la crisis financiera mexicana (1994) y las consecuencias posteriores de la crisis asiática en 1997, que exacerbó la crisis financiera rusa en 1998 (conocida también como crisis del rublo).
Estos resultados ilustran la gran vulnerabilidad de estas economías ante choques externos, debida en gran medida a su especial dependencia comercial y financiera de la economía estadounidense. Si bien la coincidencia de ciertos hechos estilizados de los ciclos de estas economías aporta una idea de un movimiento conjunto, esto por sí solo no constituye evidencia suficiente de sincronización, ya que los ritmos de crecimiento de cada nación son muy particulares. En este sentido, introduciremos algunas medidas que permitan de forma objetiva evaluar la concordancia de los comovimientos en la cadencia de los ciclos económicos de estos países.
Una alternativa para mediar la concordancia de los ciclos económicos fue propuesta por Harding y Pagan (1999). Ellos proponen una medida no-paramétrica de comovimiento que emplea una variable indicadora binaria de las recesiones y los auges. El grado de concordancia está definido como la fracción de veces que el ciclo referencia 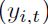 y el ciclo específico
y el ciclo específico 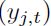 están en el mismo estado:
están en el mismo estado:
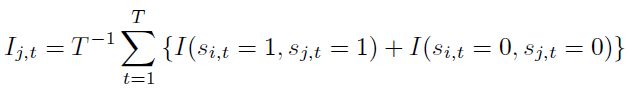 | [1] |
Donde I(.) es una función indicadora, la variable 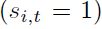 si
si 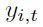 ha sido identificada como un pico, y
ha sido identificada como un pico, y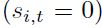 si ha sido clasificada como un valle. En otras palabras, este índice mide el grado de conformidad entre los ciclos específicos de dos países. Este índice es, de alguna manera, una medida más flexible que el coeficiente de correlación, ya que requiere de algún método para distinguir entre las recesiones y los auges.
si ha sido clasificada como un valle. En otras palabras, este índice mide el grado de conformidad entre los ciclos específicos de dos países. Este índice es, de alguna manera, una medida más flexible que el coeficiente de correlación, ya que requiere de algún método para distinguir entre las recesiones y los auges.
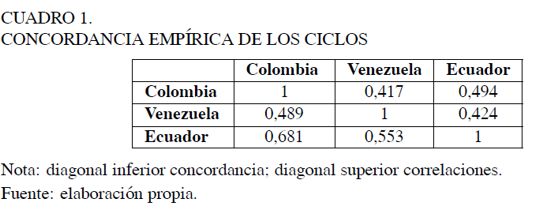
A partir de las series anuales (1961-2007) del crecimiento real de las tres economías,se construyeron los índices de concordancia para cada combinación de países. Si observamos los índices de concordancia reportados en el Cuadro 1, podemos constatar que existe un alto grado de conformidad entre los ciclos de estas tres naciones, es decir, los comovimientos de los ciclos entre pares de naciones son muy sincronizados. En particular, el 48,9% de las veces, Colombia y Venezuela se encuentran simultáneamente en una misma fase, ya sea recesión, auge o crecimiento moderado 6. Podemos observar también que las correlaciones indican una fuerte asociación lineal entre ambas tasas de crecimiento para todos los pares de combinaciones.
Por último, se construye un índice de conformidad conjunta que permita, a través de un ciclo de referencia, describir el estado común de las cuatro economías. De acuerdo con el índice de concordancia propuesto por Harding y Pagan, la conformidad de dos ciclos es el porcentaje de veces que el ciclo de dos economías se encuentra en el mismo estado. Basado en la idea general de esta medida, es posible construir un índice que refleje el porcentaje de países que se encuentran en una misma fase del ciclo (i.e., recesión) en cada instante del tiempo. Según este criterio, un estado del ciclo común es un promedio ponderado de la cantidad de países que están en esa misma fase. Formalmente, el índice de referencia está definido como:
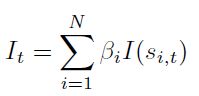 | [2] |
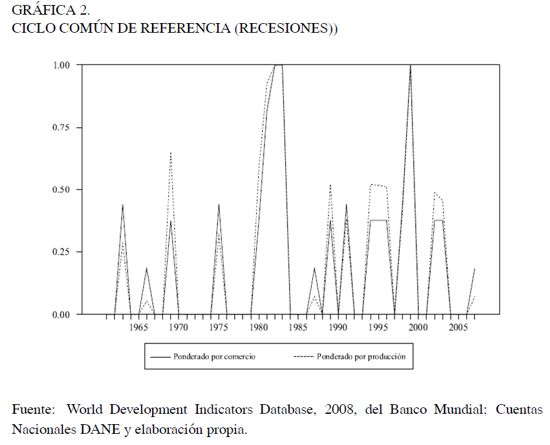
Donde N es el número de países considerados y βi corresponde al ponderador del país i. Esta medida, sin embargo, requiere que tanto los estados como los ponderadores sean especificados por alguna metodología particular. En esta aplicación, se emplean los puntos de quiebre utilizados en el cálculo del índice de concordancia y los ponderadores se construyen de dos formas diferentes: (i) como la participación de cada nación (exportaciones + importaciones) en el comercio total entre estas naciones; y (ii) como la participación del PIB de cada país en el producto agregado de estos 7. La Gráfica 2 muestra los ciclos de referencia construidos a través del ponderador fijo por comercio y mediante el ponderador móvil por producción.
La descripción de este ciclo de referencia confirma algunas de las conclusiones encontradas en el análisis previo de la evolución económica de cada país, el cual mostró que entre 1981-1983 y 1998-1999 se registraron los dos movimientos recesivos de mayor intensidad, que impactaron a las tres economías simultáneamente.
Otro hecho de relevancia son los efectos de la crisis del petróleo en 1975. Observemos que si empleamos el ponderador por producción, la sincronización relativa durante ese año aumenta considerablemente, lo cual se debe a que Colombia ha ostentado siempre una mayor participación en la producción total entre estos países. Esto muestra que los resultados obtenidos de este tipo de análisis están fuertemente influenciados por la ponderación de cada país en el ciclo de referencia. Si se observa con detenimiento la Gráfica 1, podemos darnos cuenta que, a excepción de Colombia, ninguna de las naciones latinoamericanas consideradas sufrió los efectos inmediatos directos o indirectos de la contracción de la oferta de petróleo y el aumento de su precio en 1975; por tanto, el ponderador por comercio parece ser más sensato al respecto
.En conclusión, bajo está metodología hemos encontrado una evidencia de comovimientos entre los ciclos económicos de las economías estudiadas, no obstante, la coincidencia de los puntos de quiebre entre los diferentes ciclos de cada nación pone de manifiesto el interrogante acerca de la suficiencia de esta medida para la existencia de un ciclo común. Con el fin de obtener una inferencia óptima acerca de los estados comunes de estas economías, se emplea la extensión propuesta por Krolzig (1997) para modelos multivariados de Markov-Switching, en la cual la sincronización es tratada en el sentido de un estado markoviano común.
Evidencia de sincronización en el modelo MS-VAR
Como ya se argumentó, la trasmisión de los choques a través de las economías y las características (de corto y largo plazo) comunes de las series son elementos de análisis muy importantes en el estudio de los ciclos económicos; sin embargo, son pocos los trabajos que se enfocan en investigar estos componentes mediante el uso de modelos de series de tiempo no-lineales. En contraste, muchos estudios empíricos consideran el ciclo económico como un fenómeno de cada país. En esta sección se busca una evidencia de la sincronización mediante la extensión propuesta por Krolzig (1997) para modelos multivariados de Markov-Switching, en la cual la sincronización es tratada en el sentido de un estado markoviano común.
La estructura del modelo es la siguiente: las economías pueden encontrarse en dos o tres estados diferentes 8; en cada uno de ellos, la tasa de crecimiento del PIB de cada país sigue un proceso autoregresivo en el que la media del proceso depende del estado en el cual la economía se ubique y las transiciones entre ellos están gobernadas por una cadena de Markov estacionaria. La simplicidad del proceso, así como la interpretación de los estados en términos de periodos de alto (auge) o bajo (recesión) crecimiento se convierten en el atractivo de este modelo.
Sea 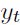 un vector compuesto por la tasa anual del crecimiento real del producto de cada país. El estado o régimen del proceso estocástico que gobierna a
un vector compuesto por la tasa anual del crecimiento real del producto de cada país. El estado o régimen del proceso estocástico que gobierna a 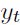 está indexado por una variable aleatoria
está indexado por una variable aleatoria 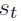 que toma el valor uno
que toma el valor uno 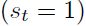 si el proceso está en el régimen uno, y así sucesivamente para el número total de estados. Si hay M diferentes regímenes, las transiciones entre estos están gobernadas por una cadena de Markov ergódica de orden 1, cuyas probabilidades de transición están dadas por:
si el proceso está en el régimen uno, y así sucesivamente para el número total de estados. Si hay M diferentes regímenes, las transiciones entre estos están gobernadas por una cadena de Markov ergódica de orden 1, cuyas probabilidades de transición están dadas por:
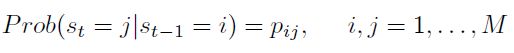 | [3] |
La probabilidad de transición 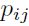 indica la probabilidad de que se transite al estado j, dado que se está en el estado i. Observe que:
indica la probabilidad de que se transite al estado j, dado que se está en el estado i. Observe que:
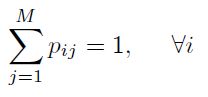
Estas probabilidades de transición definen una matriz de transición:

Entonces, el proceso estocástico de 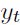 en cada estado es:
en cada estado es:
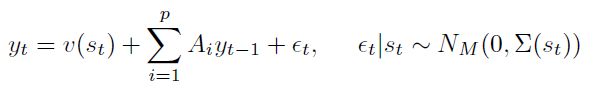 | [4] |
El término 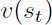 es un vector que contiene el intercepto de cada proceso de
es un vector que contiene el intercepto de cada proceso de 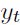 en el estado
en el estado 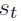 . En particular, si en el periodo t el estado dos ocurre, entonces
. En particular, si en el periodo t el estado dos ocurre, entonces 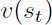 adopta el valor de
adopta el valor de 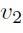 en el periodo t.
en el periodo t.
Sean 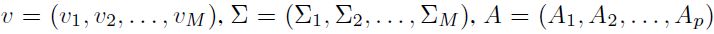 . Entonces, el vector de parámetros poblacionales a estimar es
. Entonces, el vector de parámetros poblacionales a estimar es 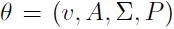 . La estimación del vector θ se lleva a cabo mediante la maximización de la función de verosimilitud a través del algoritmo EM (Krolzig, 1997). Si bien este modelo no corresponde como tal a una definición del ciclo económico común, por lo menos permite mejorar la inferencia del proceso markoviano si el ciclo común es una característica que comparten las variables. La contemporaneidad en los cambios de régimen analizada con las técnicas no paramétricas, sugiere la existencia de comovimientos comunes que deben ser estudiados bajo una metodología que considere el sistema como un todo.
. La estimación del vector θ se lleva a cabo mediante la maximización de la función de verosimilitud a través del algoritmo EM (Krolzig, 1997). Si bien este modelo no corresponde como tal a una definición del ciclo económico común, por lo menos permite mejorar la inferencia del proceso markoviano si el ciclo común es una característica que comparten las variables. La contemporaneidad en los cambios de régimen analizada con las técnicas no paramétricas, sugiere la existencia de comovimientos comunes que deben ser estudiados bajo una metodología que considere el sistema como un todo.
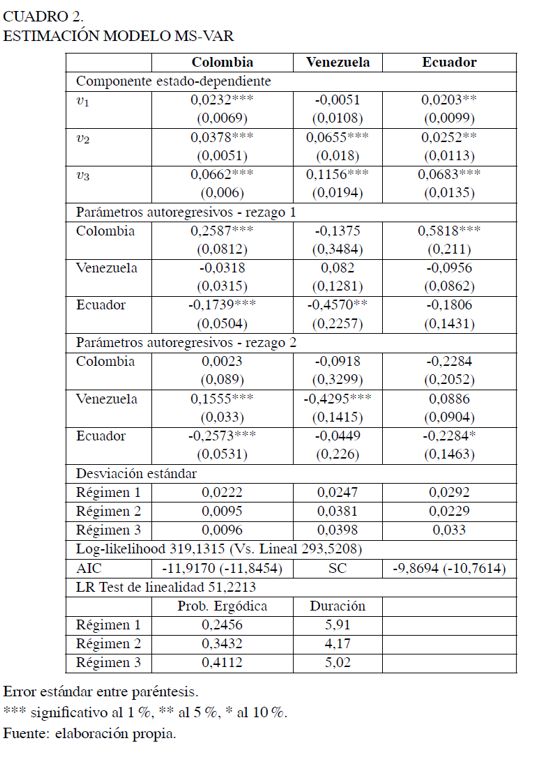
Se ajustó un modelo MS-VAR de tres estados al crecimiento anual del producto real de Colombia, Ecuador y Venezuela 9. Para realizar el ajuste y la especificación del mejor modelo, se consideró un conjunto de rezagos p = 0, . . . , 4; el valor óptimo de p se determinó mediante los criterios de información Akaike (AIC) y Schwarz (SC), así como a través de la correlación serial (simple y parcial) de los residuales predictivos y suavizados, y se realizaron pruebas de heteroscedasticidad estado-dependiente y linealidad, siguiendo las líneas propuestas por Krolzig (1997). Se encontró que la mejor especificación corresponde al modelo:
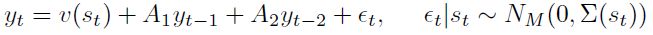 | [5] |
Como el modelo de tres estados permite un cambio en el (I)ntercepto del VAR(2) y posee (H)eteroscedasticidad estado-dependiente, entonces lo denominamos MSIH(3) - VAR(2). El Cuadro 2 contiene los resultados de la estimación del modelo por máxima verosimilitud 10.
Inicialmente se estimó el modelo asumiendo que la varianza del término de perturbación es estado-dependiente, hipótesis que fue soportada por el test de verosimilitud (Likelihood Ratio Test) reportado en el Cuadro 2 11.
El estadístico LR obtenido (p - valor) para el modelo MSIH fue χ2(12) = 39.081(0, 0000), según el test 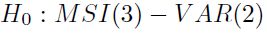 vs.
vs. 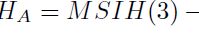
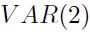 .
.
No-linealidades en el ciclo común
De acuerdo con Hansen (1992), probar la no-linealidad, explicada por cambios de régimen (modelo de Markov-Switching) contra la hipótesis nula de linealidad, es un proyecto complicado, pues, por un lado, bajo la hipótesis nula existen parámetros no identificados (e.g. las probabilidades de transición), y, por otro lado, los puntajes (scores) asociados con los parámetros de interés bajo la hipótesis alternativa pueden ser iguales a cero bajo la hipótesis nula. Hansen (1992) propone un test formal para probar la hipótesis nula de linealidad a través de un estadístico LR estandarizado. Desafortunadamente, la distribución asintótica del estadístico LR estandarizado depende de la muestra y de los parámetros, de modo que generar una tabla de dicha distribución no es posible. La generación de la distribución asintótica requiere de la simulación del estadístico LR para un grid de valores de las probabilidades de transición y parámetros estado-dependientes. No obstante, como es señalado en Krolzig (1997), es posible emplear la distribución asintótica clásica del estadístico χ2, aunque el test es conservador, de bajo poder y tamaño. Por otro lado, Davies (1977) derivó una cota superior para el nivel de significancia del estadístico LR bajo parámetros no identificados, la cual puede ser aplicada para probar la hipótesis nula de linealidad.
De acuerdo con el estadístico χ2(18) = 51, 22 reportado en el Cuadro 2, la hipótesis nula de linealidad es rechazada, tanto para la distribución asintótica clásica (p - valor = 0, 000) como para la cota superior de Davies (p - valor = 0, 002), mostrando evidencia estadística a favor del modelo MS.
Medias condicionales y no-condicionales
Como el VAR posee componentes autoregresivos, los interceptos no pueden ser interpretados como las medias condicionales de cada estado; sin embargo, dado que el proceso es estacionario 12, es posible calcular la media del proceso 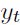 en cada régimen a través de la expresión
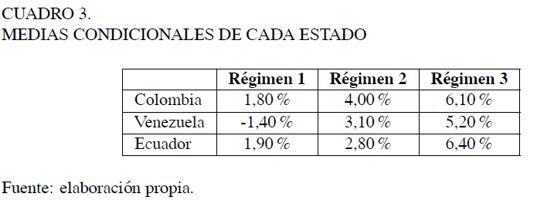
en cada régimen a través de la expresión 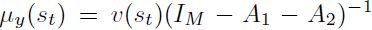 . El Cuadro 3 contiene las medias condicionales de cada variable.
. El Cuadro 3 contiene las medias condicionales de cada variable.
Dados estos resultados, cada régimen puede ser interpretado como crecimiento bajo (o contracción), moderado y alto (o expansión), respectivamente. Por otro lado, la media no condicionada está dada por 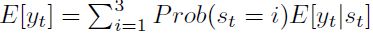 y es igual a 4,3% para Colombia, 2,9% para Venezuela y 4,0% para Ecuador.
y es igual a 4,3% para Colombia, 2,9% para Venezuela y 4,0% para Ecuador.
Transiciones y persistencia
Las diferencias en la persistencia de cada régimen se pueden observar al detallar las magnitudes de la duración media en cada estado y la probabilidad no-condicionada de permanecer en él. Por ejemplo, la duración aproximada de los periodos de crecimiento bajo es 5,9 años; los periodos de crecimiento moderado duran en promedio 4,2 años y, por último, el estado de crecimiento elevado se prolonga por 5 años. Es interesante notar que las fases del ciclo común poseen una duración esperada mucho mayor que la duración media de las fases individuales de cada economía. Este hecho ilustra que el estado común de las economías no puede ser visto como la suma de las características de los ciclos individuales. El hecho de que las fases de contracción sean tan prolongadas se debe, principalmente, a que la parte más profunda de la fase depresiva de cada economía no coincide en el mismo año. De este modo, mientras unas economías se ubican en fases de contracción no tan profundas, las otras economías se hallan en la parte más baja de su ciclo y, por tanto, el estado común de crecimiento bajo perdura hasta que todas las economías se ubican en una senda expansiva de la actividad económica.
Por otro lado, la matriz de probabilidades de transición (Cuadro 4) nos permite observar la asimetría del ciclo económico común en términos de la duración de sus fases y los cambios de estado. Por un lado, una vez las economías se encuentra en la fase contraccionista, la probabilidad de permanecer en ella es muy alta 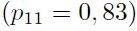 , y, por otro lado, salir de tal estado implica pasar siempre a una fase de expansión directamente
, y, por otro lado, salir de tal estado implica pasar siempre a una fase de expansión directamente 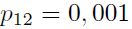 y
y 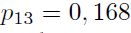 . Así mismo, se puede observar que transitar a una fase de crecimiento bajo requiere pasar necesariamente por un estado de crecimiento moderado
. Así mismo, se puede observar que transitar a una fase de crecimiento bajo requiere pasar necesariamente por un estado de crecimiento moderado 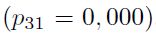 . Los dos resultados anteriores evidencian una gran asimetría en las fases de expansión y contracción del ciclo económico común. Por último, cabe resaltar que, una vez la economía se sitúa en un estado particular, la probabilidad de permanecer en él es considerablemente alta.
. Los dos resultados anteriores evidencian una gran asimetría en las fases de expansión y contracción del ciclo económico común. Por último, cabe resaltar que, una vez la economía se sitúa en un estado particular, la probabilidad de permanecer en él es considerablemente alta.
Cronología del ciclo
Es posible reconstruir la cronología del ciclo a través de la inferencia óptima acerca del estado de la economía y a partir de la información contenida en la muestra y el valor estimado de los parámetros del modelo. Sea 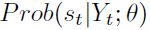 la inferencia acerca del valor de
la inferencia acerca del valor de 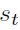 , basada en la información de la muestra hasta el tiempo t y el conocimiento de los parámetros poblacionales θ. A este tipo de inferencia sobre el estado de la economía en cada instante del tiempo se le conoce como probabilidades filtradas, y su estimador óptimo es obtenido mediante un algoritmo recursivo basado en la regla de Bayes13.
, basada en la información de la muestra hasta el tiempo t y el conocimiento de los parámetros poblacionales θ. A este tipo de inferencia sobre el estado de la economía en cada instante del tiempo se le conoce como probabilidades filtradas, y su estimador óptimo es obtenido mediante un algoritmo recursivo basado en la regla de Bayes13.
Generalizando la anterior notación, es posible obtener la inferencia acerca del estadode la economía en cada instante del tiempo; esta vez, no solo considerando la información disponible hasta el instante t, sino incorporando la información contenida en toda la muestra. Sea 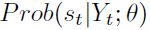 la inferencia acerca del valor de st, basada en la información completa de la muestra y en el conocimiento de los parámetros poblacionales θ. A este tipo de inferencia acerca del estado de la economía en cada instante del tiempo se le denomina probabilidades suavizadas, y su estimador óptimo es obtenido mediante el algoritmo de Kim (véase Hamilton,1994).
la inferencia acerca del valor de st, basada en la información completa de la muestra y en el conocimiento de los parámetros poblacionales θ. A este tipo de inferencia acerca del estado de la economía en cada instante del tiempo se le denomina probabilidades suavizadas, y su estimador óptimo es obtenido mediante el algoritmo de Kim (véase Hamilton,1994).
Una diferencia importante entre las probabilidades suavizadas y las probabilidades filtradas es que las primeras sobreestiman el poder predictivo del modelo, lo cual se debe a que se emplea mayor información que la requerida por el modelo para determinar la tasa de crecimiento en una fecha determinada; sin embargo, esto per se no constituye un inconveniente, ya que determinar una fase particular del ciclo con información posterior a su ocurrencia tiene en cuenta el hecho de que existen características del ciclo que pueden cambiar en el tiempo, pero que aún no han ocurrido. De esta forma, grandes discrepancias entre las probabilidades filtradas y suavizadas pueden deberse a particularidades del ciclo que han cambiado a través del tiempo.
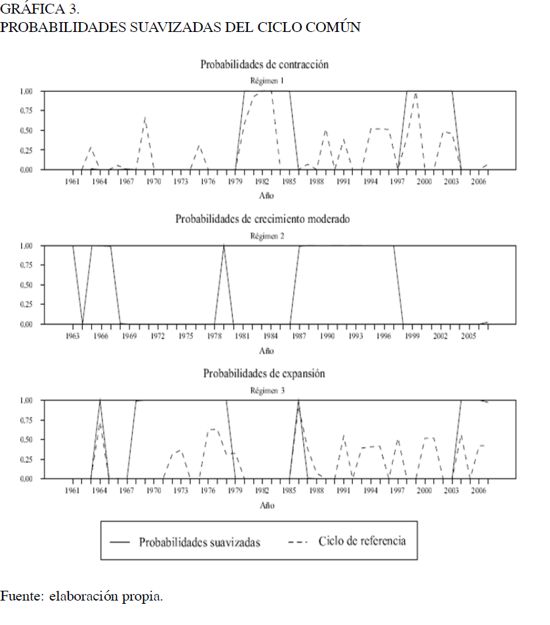
A diferencia del ciclo común de referencia, la clasificación a través del modelo de Markov-Switching es independiente de cualquier tipo de ponderación sobre cada país. Por lo anterior, cualquier transformación escalar creciente del crecimiento de algún país resultará en la misma clasificación de los regímenes. Adicionalmente, la datación del ciclo mediante las probabilidades filtradas y/o suavizadas constituye un ejercicio de inferencia óptima libre de subjetividades, escalas o información previa relacionada con las fechas en las cuales la economía se ubica en cada régimen. La Gráfica 3 ilustra las probabilidades suavizadas de cada régimen, así como la datación llevada a cabo mediante el ciclo de referencia.
Como se puede observar, tanto la metodología no-paramétrica como el modelo MS - VAR coinciden en datar las fechas de principios de los ochenta y finales de los noventa como recesiones. De igual forma, se aprecia que algunos de los movimientos expansivos fuertes identificados en las tres economías son caracterizados por las probabilidades suavizadas. Aunque los movimientos más fuertes en las fluctuaciones comunes de las economías son capturados por ambas técnicas, existen, sin embargo, grandes diferencias en la datación de ambas metodologías. Estas diferencias significativas se deben principalmente a que la determinación de los puntos de quiebre a través del algoritmo de Harding-Pagan es una técnica de detección local, es decir, solo considera la información de la muestra alrededor de cada punto de quiebre, mientras que la inferencia que se extrae a través del modelo no-lineal se hace teniendo en cuenta toda la información disponible de la muestra, al menos en el caso de las probabilidades suavizadas.
La clasificación de los regímenes y las fechas de ocurrencia de cada estado se realiza asignando a cada observación 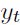 un estado particular. La regla aplicada en este caso consiste en asignar la observación en el tiempo t al régimen m ∈ {1, 2, 3} con la máxima probabilidad suavizada, es decir:
un estado particular. La regla aplicada en este caso consiste en asignar la observación en el tiempo t al régimen m ∈ {1, 2, 3} con la máxima probabilidad suavizada, es decir:
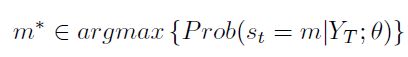 | [6] |
Cuando a través de las probabilidades suavizadas se observa que algún conjunto de observaciones adyacentes pueden ser clasificadas en algún régimen particular, entonces es posible computar la probabilidad conjunta de que esas observaciones se encuentren en uno u otro régimen simultáneamente. El Cuadro 5 contiene la clasificación de varios conjuntos de observaciones en cada régimen, de acuerdo con la máxima probabilidad conjunta de que dichas fechas pertenezcan al mismo estado en forma coincidente.
Contribución del ciclo común
Es posible calcular la contribución del ciclo común al ciclo individual de cada país, descomponiendo el vector de series de tiempo en un componente gaussiano y otro no gaussiano que refleje los efectos de la cadena de Markov sobre el sistema. Reescribiendo la ecuación (4) como:
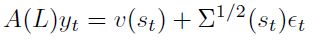 | [7] |
Donde 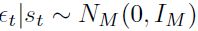 y
y 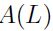 es el polinomio de rezago y postmultiplicando a ambos lados de (7) por
es el polinomio de rezago y postmultiplicando a ambos lados de (7) por 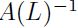 , se tiene:
, se tiene:
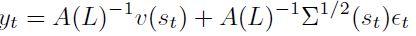 | [8] |
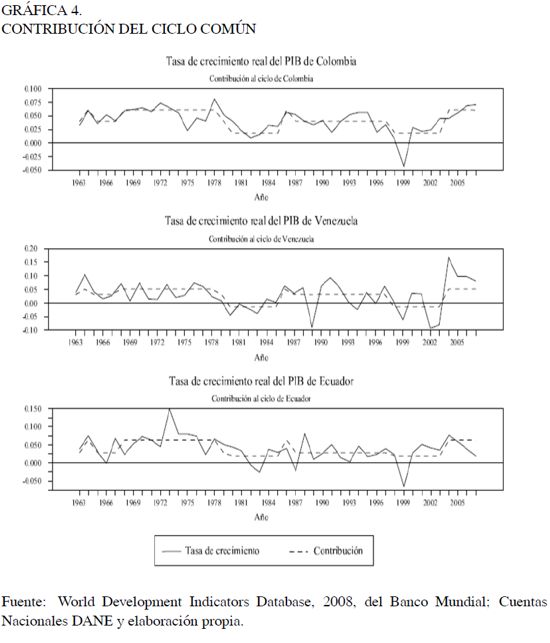
Donde el segundo término tiene media cero. La Gráfica 4 muestra una evidente sincronización que es más visible durante las fases de contracción de las tres economías. Se observa también que son más sincronizadas Colombia y Venezuela, lo cual se debe a que el comercio bilateral entre este par de naciones es mayor que con Ecuador.
CONCLUSIONES
La caracterización del ciclo común entre Colombia, Venezuela y Ecuador reveló una fuerte evidencia estadística, que permite corroborar la existencia de un estado markoviano común en el cual las fluctuaciones de cada economía están caracterizadas por comovimientos similares de la actividad productiva en cada país. El ciclo común está determinado por fases de contracción, crecimiento moderado y expansión. Los tres estados del ciclo evidenciaron una fuerte persistencia con una duración media de 5 años cada uno. El análisis de la matriz de probabilidades de transición mostró que salir de las fases contraccionistas implica pasar directamente a una fase de crecimiento elevado; de igual forma, transitar a una fase de crecimiento bajo requiere pasar por una fase de crecimiento moderado. Estos resultados evidencian una gran asimetría en las fases de contracción y expansión del ciclo económico común.
NOTAS AL PIE
2 Véase también el trabajo de Chauvet y Yu (2006).
3 Véase también el trabajo de Imbs (2004).
4 Los valles son refinados definiendo su amplitud, así como las fechas adyacentes a cada valle, que corresponden a tasas de crecimiento similarmente bajas (o incluso negativas); de este modo un valle puede abarcar más de un año.
5 Es importante anotar que este algoritmo fue desarrollado para ser utilizado en series de frecuencia trimestral, aunque en esta aplicación se emplea indistintamente. Se realizaron, sin embargo, diversos ejercicios, modificando la amplitud de la ventana móvil. La única amplitud que mostró un buen desempeño en los resultados fue una ventana de orden  .
.
6 En cada caso, los valles se interpretan como recesiones, los picos como auges y las observacionesque no corresponden ni a picos ni a valles, como crecimiento moderado.
7 Para realizar el cálculo del ponderador por comercio, se empleó el comercio total en el año 2000 entre los países considerados para construir un ponderador fijo; por otro lado, para realizar el computo del ponderador por producción, se construyó un conjunto de ponderadores móviles en el cual, en cada año, el peso de cada país corresponde a su participación dentro del PIB agregado de ese año.
8 Por simplicidad de la descripción se consideran únicamente dos o tres estados de la economía; sin embargo, pueden ser considerados más regímenes, aunque su interpretación económica puede volverse más difícil.
9 En ejercicios adicionales se realizaron estimaciones con modelos de dos estados, no obstante estas especificaciones resultaron poco satisfactorias al reproducir algunos hechos estilizados identificados en el ejercicio no-paramétrico.
10 Todas las estimaciones reportadas en este documento fueron llevadas a cabo a través de la clase MSVAR de Ox. Véase Krolzig (1998).
11 Comprobar la significancia estadística de la no-linealidad, explicada por el modelo de Markov-Switching contra la hipótesis nula de linealidad, es un asunto complicado, debido a la existencia de parámetros no identificados bajo la hipótesis nula (Unidentified Nuisance Parameters), como lo muestra Hansen (1992); sin embargo, esto no es de especial interés en el test LR para comprobar la hipótesis de homoscedasticidad, ya que, tanto bajo la hipótesis nula como bajo la alternativa, el número de estados permanece invariante.
12 Nótese que, para un valor de S fijo, el proceso 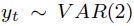 es estable, pues las raíces del polinomio característico
es estable, pues las raíces del polinomio característico 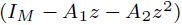 se encuentran fuera del círculo unitario complejo, es decir,
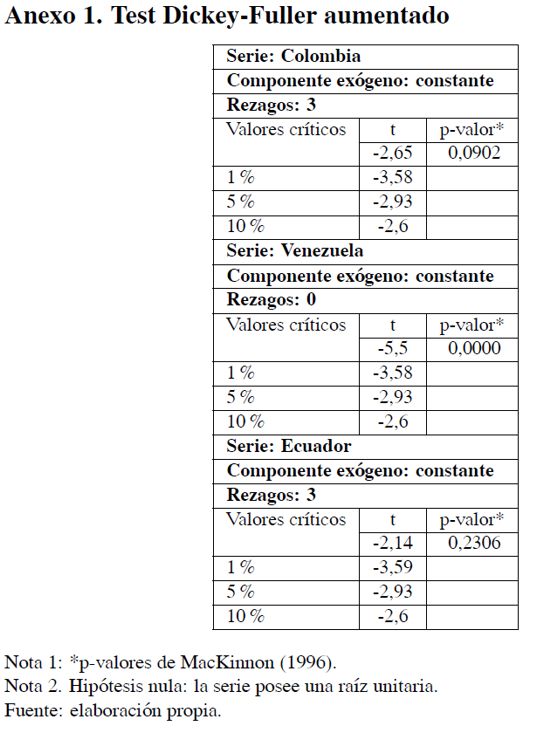
se encuentran fuera del círculo unitario complejo, es decir, 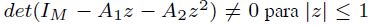 . De este modo, el proceso es estacionario. Véase el Anexo para consultar las pruebas de estacionariedad individual de las series.
. De este modo, el proceso es estacionario. Véase el Anexo para consultar las pruebas de estacionariedad individual de las series.
13 Una explicación más extensa de este algoritmo puede ser encontrada en Hamilton (1994).
REFERENCIAS BIBLIOGRÁFICAS
1. Arnaudo, A. y Jacobo, A. (1997). Macroeconomic Homogeneity within Mercosur: An Overview. Estudios Económicos, 12(1), 37-51. [ Links ]
2. Artis, M., Krolzig, H. M., y Toro, J. (2002). The European Business Cycle, Economic (Working Paper Series E2002/19). Andalucía: Centro de Estudios Andaluces. [ Links ]
3. Baxter, M. y Kouparitsas, M. (2004). Determinants of Business Cycle Comovement: A Robust Analysis (Working Paper 2004-14). Federal Reserve Bank of Chicago. [ Links ]
4. Burns, A. y Mitchell, W. (1946). Measuring Business Cycles. New York: National Bureau of Economic Research. [ Links ]
5. Böwer, U. y Guillemineau, C. (2006). Determinants of Business Cycle Synchronization Across Euro Area Countries (Working Paper Series 587). Frankfurt: European Central Bank. [ Links ]
6. Calderón, C., Chong, A., y Stein, E. (2003). Trade Intensity and Business Cycle Synchronization: Are Developing Countries any Different? (Working Paper 478). Washington, D.C.: Inter-American Development Bank, Research Department. [ Links ]
7. Chauvet, M. y Yu, C. (2006). International Business Cycles: G7 and OECD Countries. Economic Review, Q1, 43-54. [ Links ]
8. Darvas, Z., Rose, A., y Szapáry, G. (2005). Fiscal Divergence and Business Cycle Synchronization: Irresponsibility is idiosyncratic (Working Paper Series 2005/3). Budapest: Magyar Nemzeti Bank. [ Links ]
9. Davies, R. (1977). Hypothesis Testing When a Nuisance Parameter is Present Only Under the Alternative. Biometrika, 64, 247-254. [ Links ]
10. Eichengreen, B. (1992). Should the Maastricht Treaty Be Saved? (Princeton Studies in International Finance 74). Princeton, N.J.: Princeton University. [ Links ]
11. Engel, R. e Issler, J. (1993). Common Trends and Common Cycles in Latin America. Revista Brasileira de Economia, 47, 149-176. [ Links ]
12. García-Herrero, A. y Ruiz, J. (2008). Do Trade and Financial Linkages Foster Business Cycle Synchronization in a Small Economy? (Documentos de Trabajo 0810). Madrid: Banco de España. [ Links ]
13. Hamilton, J. (1994). Time Series Analysis. Princeton, N.J.: Princeton University. [ Links ]
14. Hansen, B. (1992). The Likelihood Ratio Test Under Nonstandard Conditions: Testing the Markov-Switching Model of GNP. Journal of Applied Econometrics, 7(S), S61-S82. [ Links ]
15. Harding, D. y Pagan, A. (1999). Dissecting the Cycle (Working Paper 13/99). Melbourne: University of Melbourne. [ Links ]
16. Hecq, A. (2002). Common Cycles and Common Trends in Latin America. Medium Econometrische Toepassingen, 10, 20-25. [ Links ]
17. Imbs, J. (2004). Finance, Specialization and Synchronization. Review of Economics and Statistics, 86(3), 723-734. [ Links ]
18. Inklaar, R., Jong-A-Pin R., y De Haan, J. (2005). Trade and Business Cycle Synchronization in OECD Countries: A Re-examination, Cesifo (Working Paper Series 1546). Institute for Economic Research at The University of Munich, Center for Economic Studies. [ Links ]
19. Kose, M., Prasad, E. y Terrones, M. (2003). How Does Globalization Affect the Synchronization of Business Cycles? (Discussion Paper Series 702). Institute for the Study of Labor (IZA). [ Links ]
20. Krolzig, H. M. (1997). Markov-Switching Vector Autoregressions. (Lectures Notes in Economics and Mathematical Systems, 454). New York: Springer. [ Links ]
21. Krolzig, H. M. (1998). Econometric Modeling of Markov-Switching Vector Autoregressions Using MSVAR for Ox. (Discussion Paper). Oxford: Department of Economics, University of Oxford. [ Links ]
22. Krolzig, H. M. y Toro, J. (2004). Classical and Modern Business Cycle Measurement: The European Case. Spanish Economic Review, 7(1), 1-21. [ Links ]
23. Krugman, P. (1993). Integration, specialization and regional growth: Notes on 1992, EMU and stabilization. En Francesco Giavazzi y Francisco Torres (Eds.), The Transition to Economic and Monetary Union in Europe. Cambridge and New York: Cambridge University Press. [ Links ]
24. MacKinnon, J. G. (1996). Numerical Distribution Functions for Unit Root and Cointegration Tests. Journal of Applied Econometrics, 11, 601-618. [ Links ]
25. Massmann, M. y Mitchell, J. (2004). Reconsidering the Evidence: Are Eurozone Business Cycles Converging? Journal of Business Cycle Measurement and Analysis, 3(1), 275-307. [ Links ]
26. Mejía-Reyes, P. (2000). Asymmetries and Common Cycles in Latin America: Evidence from Markov-Switching Models. Economía Mexicana, 9(1), 189-225. [ Links ]
27. Ruiz-Porras, A. (2010). Globalización, ciclos económicos y crisis global, 2007- 2010. Expresión Económica, 24, 43-61. [ Links ]
28. Schirwitz, B. y Wälde, K. (2004). Synchronization of Business Cycles in G7 and EU14 Countries. Bruselas: European Commission, Directorate General Economic and Financial Affairs, Economic Studies and Research. [ Links ]
29. Tomljanovich, M. y Ying, F. (2005). We're All Connected: Business Cycle Synchronization in G-7 Countries. Recuperado de http://academics.hamilton.edu/economics/home/marc_t.pdf. [ Links ]