Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.32 no.spe61 Bogotá Dec. 2013
POVERTY TRAPS, ECONOMIC INEQUALITY AN INCENTIVES FOR DELINQUENCY
Edgar Villa1
Andrés Salazar2
1 Corresponding author, email: edgar.villa@unisabana.edu.co. Escuela Internacional de Ciencias Económicas y Administrativas. Universidad de La Sabana.
2 MSc. in Economics from Tilburg University (The Netherlands). Dirección de correspondencia Carrera 56A No. 130A - 86, casa 33, Bogotá, Colombia. Corresponding author, email: asalazar@ dnp.gov.co. Departamento Nacional de Planeación.
Abstract
This paper explores theoretical linkages between poverty traps, economic inequality and delinquency in a perfect competition overlapping generations model characterized by dual legal production sectors and one illegal sector. The model posits an absence of credit for human capital accumulation, which generates barriers to skilled educational attainment. We find that the existence of a poverty trap under conditions of sufficient initial economic inequality and costly indivisible human capital investment generates persistent delinquency in the long run. We examine steady state changes caused by shocks that increase skilled wages or reduce land assets available to the unskilled, finding that these shocks produce outbursts of delinquency that die out later if the shocks are temporary but increases permanently otherwise. We also find that an increase on relative poverty has an ambiguous effect on long run delinquency rates while an increased focus on law enforcement policies, intended to increase deterrence and incapacitation, reduces delinquency in the long run and increases wealth inequality.
Keywords: poverty traps, inequality, delinquency, human capital.
JEL: I30, J31, K42, O11, O17.
Resumen
Este artículo explora la conexión teórica entre trampas de pobreza, desigualdad económica y delincuencia en un modelo de generaciones traslapadas de dos sectores productivos legales y uno ilegal con ausencia de crédito para la acumulación de capital humano que generan barreras a trabajadores para obtener educación. Se encuentra que la existencia de una trampa de pobreza bajo una suficiente desigualdad económica inicial e indivisibilidad costosa de la inversión en capital humano genera delincuencia persistente en el largo plazo. Se estudian choques que incrementan el salario de trabajadores educados o que reducen activos para los trabajadores no educados, los cuales, si son temporales, generan aumentos en delincuencia en el corto plazo que luego tienden a diluirse en el tiempo; de lo contrario, producen mayor persistencia en la delincuencia. Se halla que el aumento en la proporción de pobreza relativa en la economía tiene un efecto ambiguo sobre el nivel de delincuencia en el largo plazo. Finalmente, se encuentra que políticas que aumentan la seguridad de los individuos en la economía disminuyen la delincuencia en el largo plazo pero se acompañan de un aumento en la desigualdad en riqueza.
Palabras clave: trampas de pobreza, desigualdad, delincuencia, capital humano.
JEL: I30, J31, K42, O11, O17.
Résumé
Cet article explore la connexion théorique entre les pièges de la pauvreté, l'inégalité économique et la délinquance dans un modèle de générations chevauchant deux secteurs productifs légaux et un illégal avec une absence de crédit pour l'accumulation de capital humain qui dressent des barrières aux travailleurs pour obtenir une éducation. On trouve que l'existence d'un piège de pauvreté avec une inégalité économique initiale suffisante et une indivisibilité coûteuse de l'investissement en capital humain entraîne une délinquance persistante à long terme. Nous étudions des chocs qui augmentent le salaire de travailleurs éduqués ou qui réduisent des actifs pour les travailleurs non éduqués, qui, s'ils sont provisoires génèrent une augmentation de la délinquance à court terme et qui ensuite ont tendance à se diluer dans le temps ; par contre ils produisent une plus grande persistance de la délinquance. On trouve que l'augmentation de la proportion de pauvreté relative dans l'économie possède un effet ambigu sur le niveau de délinquance à long terme. Enfin, on constate que des politiques qui améliorent la sécurité des individus dans l'économie diminuent la délinquance à long terme mais sont accompagnées par une augmentation des inégalités en richesse.
Mots-clés : pièges de la pauvreté, inégalité, délinquance, capital humain.
JEL : I30, J31, K42, O11, O17.
Este artículo fue recibido el 21 de diciembre de 2012, ajustado el 1o de mayo de 2013 y su publicación aprobada el 17 de julio de 2013.
A person in imminent danger [who] cannot be helped in any other way... may legitimately supply his own wants out of another's property (Thomas Aquinas, ed. Gilby, 1975)
INTRODUCTION3
The study of the economics of crime initiated by Becker (1968) emphasized that studies of incentives to crime should assume that individuals are rational in the sense that their decisions on whether or not to engage in illegal activities are based on expected benefits and costs in the environment in which they live. According to this view the best policy to counteract crime would be to decrease the net expected benefits of illegal activities by increasing marginally the severity of sentences for more serious crimes alongside the probability of apprehension and conviction an individual faces when opting to engage in these activities. However, social approaches seek to understand the incentives individuals face in their environments that limit their access to legal opportunities and indirectly enhance incentives to engage in illegal activities. As Bourguignon (1999) has argued "The economic motivation behind crime is essentially the appropriation of the property of somebody else or the pursuit of illegal activity at the risk of being caught and punished. Therefore, it is natural to expect that crime offenders be found among those who have relatively more to gain from these activities and relatively little to lose in case of being caught. These presumably belong to the neediest groups in society (the poor), their number being larger and their motivation being stronger the more unequal the distribution of resources in society". Importantly, this view does not go against the Beckerian view of crime economics but actually tends to complement it since it seeks a deeper understanding of the fundamental way social forces constrain the economic incentives that influence rational decision makers when confronted with choosing between legal and illegal activities. Importantly, legal opportunities also have to do with investment in education, since - as the literature on the economics of education has found - there is evidence that human capital accumulation can weaken incentives for delinquency (Lochner, 2004, 2010; Lochner-Moretti, 2001). In particular, this literature argues that educational attainment is causally related to higher returns in the labor market as well as positive externalities at the social level, suggesting that policies that enhance educational opportunities for poorer segments of the population have a positive externality that lowers incentives to delinquency.
As is well known, poverty has been persistent in the history of human economic development. As Aquinas suggests in the text cited at the start of this paper poverty has long been associated with delinquency since ancient times, and even the Church considered it to be legitimate if individuals had extremely limited economic opportunities. From a modern economic point of view in which property rights have been privileged, it is unlikely for any type of delinquency to be considered justified, even in the face of poverty, since this would go against economic prosperity deteriorating investment returns. In this view higher delinquency rates should cause economic downturns. But delinquency is an economic choice for individuals, and presumably a lack of legal economic opportunities might generate higher incentives for delinquency. Hence, delinquency may be subject to simultaneous causality. If this is the case, social policies to subsidize education might end up alleviating poverty which in turn might contribute to lowering incentives to delinquency. However, poverty on its own may not cause delinquency because if everybody is poor the incentives for delinquency may not be strong enough, due to the low net benefits that would be expected within such an environment. In this sense, inequality seems to be a crucial social force that would have to be present and to interact with high poverty levels in order for incentives to delinquency to be generated.
The social view, which takes inequality and poverty into account, suggests a carrot- type policy that would enhance legal opportunities, thereby inducing individuals not to make delinquent choices. As argued above, since the pioneering work of Becker (1968) the literature on the economics of crime has stated that in order to lower delinquency it is necessary to extend and increase law enforcement policies to directly deter individuals from choosing delinquent activities, or to incapacitate them. This view suggests a stick-type policy that punishes individuals who opt for delinquency. Both approaches suggest that it is important to understand the social and economic incentives that lead an individual to choose delinquency and how these incentives interact with poverty, educational investment, economic inequality and legal punishments.
This paper builds an overlapping generations model under perfect competition similar to the one developed by Galor-Zeira (1993) in order to study the theoretical linkages between poverty traps, economic inequality, human capital attainment and incentives for delinquency. The model involves a dual economy in which delinquents emerge from environments with high levels of inequality and poverty, as well as limitations to the acquisition of human capital; optimally they choose to prey on legal workers. We find that for given levels of law enforcement measures delinquency is persistent in the long run if a poverty trap exists and the economy starts out with sufficient wealth inequality and a large fraction of unskilled workers, lowering unskilled wages. We then study comparative dynamics, shifting the model's parameters temporarily or permanently. We find that an increase in the legal skilled wage, due to a technological innovation, generates higher inequality and therefore delinquency in the long run. Moreover, we find that a higher proportion of poor households does not necessarily generate more delinquency since this depends crucially on the elasticity of unskilled wages when more unskilled legal workers enter the legal sector in the economy. Moreover, we find that policies that increase the effectiveness of law enforcement can generate higher levels of inequality in the long run, given the existence of a poverty trap that paradoxically contributes to increasing incentives for delinquency.
This paper is organized into five parts including the introduction. The second part consists of a literature review that examines the links between delinquency, ecoPoverty nomic inequality, poverty and investment in education. The third part constructs the formal model, which explores the theoretical linkages between poverty traps, educational investment, economic inequality and incentives to delinquency. The fourth part explores comparative dynamics with respect to parameter changes. The fifth part presents our conclusions.
LITERATURE REVIEW
Building on Becker's (1968) and Ehrilich's (1973) contributions, the economics of crime literature, has focused on the effect of deterrence and incapacitation on criminal behavior. This tradition understands delinquency as a result of individual rational choice where the benefits of illegal activities outweigh the costs (punishment in case of apprehension and conviction) relative to the current set of legal opportunities. As a consequence, deterrence theory research has predominantly been concerned with the isolated effects of the severity and certainty of sanctions for illegal behavior. This has tended to produce arguments in favor of extending and increasing law enforcement policies in order to reduce incentives for delinquency. Several recent papers have sought to confirm this policy approach. In particular, Drago, Galbiati and Vertova (2009) using a quasi experiment for Italy find empirical evidence that supports the view that incapacitating convicted delinquents by imprisoning them lowers their subsequent recidivism, generating a net social benefit. Moreover, Owens (2009) finds empirical evidence that higher sentences decrease recidivism for delinquents while Di Tella and Schargrodsky (2004) found evidence,also through a quasi experiment this time for the city of Buenos Aires after a terrorist attack, that an increase in police enforcement lowers (inelastically) local motor vehicle theft (around one street block from the point where police enforcement increased). Thus, these articles and others provide empirical support for the Beckerian view that greater sentences and increased probability of apprehension deter potential delinquents. This view would suggest that extreme sentences suchas the death penalty would deter potential offenders, as argued by Ehrlich (1975) for the United States. Nonetheless, Donohue and Wolfers (2005) re-examined the empirical evidence for the United States and found no empirical evidence supporting the idea that the death penalty actually deters potential criminals.
Some economic and social literature argues that delinquency is unlikely to be eliminated completely merely through law enforcement policies à la Becker since delinquency is an individual choice taken in the presence of barriers to entering legal sectors that yield economic opportunities (Eide, 1997). Specifically, both poverty and economic inequality are social conditions that may induce illegal behaviors due the lack of other legal ways to acquire income and build assets. There is evidence of this non-Beckerian view that inequality and poverty can create incentives to delinquency for given levels of police and judicial enforcement. For example, Bourguignon (1999), Kelly (2000), Fajnzylber, Lederman and Loayza (2002) and Soares (2004) have found empirical evidence that positively associates property crimes with inequality using cross-country data. Moreover, Machin and Meghir (2004) found for Great Britain that an increase in poverty (measured as the reduction of unskilled wage levels) was associated with a rise in property crime.
Moreover, the accumulation of human capital can play a role in reducing incentives to delinquency. Indeed, the literature on the economics of education has found evidence that human capital accumulation can discourage illegal activities. For example, Freeman (1996) showed that encouraging educational attainment costitutes a preventive policy for crime and found an inverse relationship between the two variables. Tauchen et al. (1994) found a negative relationship between the act of studying or working and the probability of committing criminal acts. Lochner and Moretti (2001) also showed that there is an inverse relationship between school attainment and crime rates. Specifically they found that young people who finish high school are less likely to get involved in delinquent activities. Moreover, Lochner (2004, 2010) has argued that educational attainment has a positive externality in reducing crime since it increases the opportunity cost of engaging in illegal activities. All this evidence seems to suggest that the social environment in which individuals live can create incentives for delinquency for given levels of law enforcement.
According to Kelly (2000) the link between inequality and delinquency has been examined using three main theories of crime: the economic theory of crime, social disorganization theory, and strain theory. In the literature on the economic theory of crime, it has been argued that economic differences have been a necessary condition in maintaining incentives to commit felonies; thus, property crimes may partly be the consequence of excessive economic inequality, as argued by Bourguignon (1999) and Fender (1999). Others have considered the effect of inequality on crime. For example, Ehrlich (1973) used the fraction of the population in an area earning less than half the median income as a proxy for inequality, and showed that the decision to participate in criminal activities involving material gains is positively associated with income inequality. Witte and Tauchen (1994) examined the impact of earnings on criminal participation and Kelly (2000, p. 537), using the FBI Uniform Crime Reports for the United States, concluded that "the impact of inequality on violent crime is large, even after controlling for the effects of poverty, race, and family composition". Social disorganization theory emphasizes the existence of several factors such as poverty, family stability, residential mobility and ethnic heterogeneity, which encourage some members of communities to engage in illegal activities and weaken social control of this behavior (Shaw & McKay, 1942). This theory conjectures that income inequality causes delinquency in an indirect way, due to the fact that inequality is related to poverty and that this factor is more likely to induce individuals to commit illegal acts. Finally, strain theory, based on Merton's (1938) work, developed the idea of anomie - a lack of social norms or the failure of a social structure to provide the mechanisms and pathways necessary if people are to achieve their goals, generating deviant behaviors such as crime. According to this theory individual alienation can arise from income inequality and is also related to other measures of deprivation such as poverty and unemployment. This idea is connected with the argument that criminality is based on an individual process consisting of an assessment of economic incentives and social norms.
A more modern view, similar to strain theory, has been developed by authors such as Bowles (2006) and Polterovich (2008) which studies institutional changes in a dynamic evolutionary framework where inequality and poverty traps emerge along with inefficient endogenous institutional arrangements. Moreover, neighborhood effects emerging from social preferences may induce criminal behavior in equilibrium, as shown in Durlauf (1996, 2001). Other theoretical contributions show that parasitic enterprises can feed on productive businesses, as in Mehlum, Moene and Torvik (2003, 2006) where the fraction of parasitic enterprises is determined endogenously, depending on the institutional arrangements according to which an economy operates, namely, the legal and illegal opportunities faced by individuals. According to this literature poverty traps are a dreadful equilibrium in a multiple equilibrium environment in which they are sustained over time by inefficient or perverse institutions. An approach that seeks to explain the persistence of poverty traps by combining evolutionary game theory and multiple equilibria, in which agents imitate the behaviors of others in order to explain the persistence of poverty traps, is found in Accinelli and Sanchez Carrera (2011) and Sanchez Carrera (2012).
CONCEPTUAL FRAMEWORK
It is a common belief that criminals and/or delinquents just happen to be bad people who like (prefer) preying on the innocent. As Cook, Ludwig and McCracy (2011) argue "[i]n the simplistic version, the population consists of good guys and bad guys. The bad guys commit crimes and the good guys do not. The crime rate is proportional to the number of bad guys who are at large. Crime control then is a matter of locking up as many bad guys as possible". This prevalent idea suggests heterogeneity in the moral or ethical costs felt by a given population that could yield some type of non pecuniary incentives that persuade some individuals to refrain from commiting violent crimes like forcible rape, murder and aggravated assault, while others would feel no such compunction. In this view bad guys would not respond directly to economic incentives since they are born bad and do not know any better. Cook et al. (2011) argue "[w]hat is missing from the 'good guys, bad guys' account of crime is that crime is a choice and as such is influenced by incentives as well as character. Indeed, the theory of crime developed by economists (economics of crime) begins where the character analysis leaves off, and focuses on how incentives influence crime related choices for someone of given character (or, as economists would say, preferences)". In this sense the model that we develop takes seriously Cook and Ludwig's argument that "...the incentives to engage in crime relate to the perceived payoff to crime, the opportunity cost of time spent doing crime, and the risks associated with crime -including inherent risks (gang warfare, victim retaliation) and the risk of punishment. Those incentives depend on individual circumstances and are subject to change with changes in criminal and licit opportunities".
The model
Consider a small open economy that produces a homogenous good that can be used for consumption and investment. The good can be produced by two technologies, one uses skilled labor and capital and the other unskilled labor and land. These define a two-legal-sector economy that demands labor from potential workers. However, some potential workers might choose to become delinquents and enter an illegal sector with the explicit purpose of acquiring consumption goods by preying on workers from the legal sector. Formally, production in the legal skilled labor sector is described by 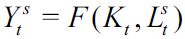 where
where 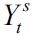 is output, Kt is capital and
is output, Kt is capital and 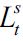 is skilled labor, while F is a concave production function with constant returns to scale. It is assumed that investment in human and in physical capital is made one period in advance and that there are no adjustment costs to investment and no depreciation of capital. Legal firms can borrow from world markets at interest rate r > 0 . Given the absence of adjustment costs for investment and the fact that the number of skilled workers is known one period in advance, the amount of capital in the skilled labor sector is adjusted each period so that
is skilled labor, while F is a concave production function with constant returns to scale. It is assumed that investment in human and in physical capital is made one period in advance and that there are no adjustment costs to investment and no depreciation of capital. Legal firms can borrow from world markets at interest rate r > 0 . Given the absence of adjustment costs for investment and the fact that the number of skilled workers is known one period in advance, the amount of capital in the skilled labor sector is adjusted each period so that 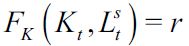 . Hence there is a constant capital-labor ratio in this sector, which determines the wage of skilled labor ws which is, in addition, constant. This wage ws depends on r and on technology only.
. Hence there is a constant capital-labor ratio in this sector, which determines the wage of skilled labor ws which is, in addition, constant. This wage ws depends on r and on technology only.
Production in the legal unskilled labor sector is described by 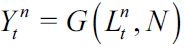 where
where 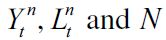 are output, unskilled labor and land respectively. Let the aggregate amount of land be fixed at
are output, unskilled labor and land respectively. Let the aggregate amount of land be fixed at 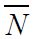 , so that demand of unskilled labor is
, so that demand of unskilled labor is
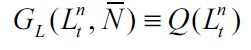 |
where Q is a function that describes the diminishing marginal productivity of unskilled labor. We assume that all markets are perfectly competitive and expectations are fully rational. The illegal sector is an abstraction of an organized sector that is dedicated exclusively to preying on workers. It abstracts from the different types of illegal pecuniary activities that arise in the real world, such as larceny, theft in general, burglary, kidnapping, economic extortion, armed robbery etc., but can be understood as having the same end in sight, namely material incentives to prey on workers.4, 5 The organization of the "firms" that operate in this sector is conceptualized in the following manner: members of the organization acquire income from illegal activities and then share it equally with all the other members. This is a strong assumption that simplifies the organization that in the real world would presumably be hierarchical and divide the income acquired unequally. The acquisition of income by delinquents in the illegal sector is described by the following "pseudo production function" which is assumed to be linear in terms of input labor, where delinquents and workers are matched randomly:
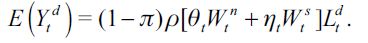 | [1] |
The term 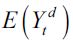 denotes the expected income acquired through delinquency, θt and ηt are respectively the probabilities of encountering both unskilled and skilled workers in period t
denotes the expected income acquired through delinquency, θt and ηt are respectively the probabilities of encountering both unskilled and skilled workers in period t  , is the labor used in the delinquent sector,
, is the labor used in the delinquent sector, represents the fraction of the wealth that a delinquent is able to acquire from his or her victims in any given encounter, while
represents the fraction of the wealth that a delinquent is able to acquire from his or her victims in any given encounter, while 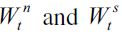 denote the overall wealth levels of unskilled and skilled workers respectively. Since the model involves two kinds of individuals, namely legal workers and delinquents, it must be the case that θt + ηt = 1 - λt where λt is the probability in period t of encountering a delinquent in any given random match. We assume that encounters between delinquents do not generate any net gain for either party. With probability
denote the overall wealth levels of unskilled and skilled workers respectively. Since the model involves two kinds of individuals, namely legal workers and delinquents, it must be the case that θt + ηt = 1 - λt where λt is the probability in period t of encountering a delinquent in any given random match. We assume that encounters between delinquents do not generate any net gain for either party. With probability 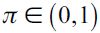 the delinquent is apprehended and convicted by law enforcement authorities, in which case no wealth is maintained by the delinquent6, while with probability (1-π) a delinquent can obtain a net amount
the delinquent is apprehended and convicted by law enforcement authorities, in which case no wealth is maintained by the delinquent6, while with probability (1-π) a delinquent can obtain a net amount 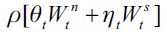 of expected income under random matching. We call π the punishment probability.
of expected income under random matching. We call π the punishment probability.
We can define an average expected "implicit wage" acquired by a delinquent in this economy as 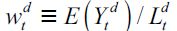 given the assumption of income sharing among members of the illegal sector. We can therefore rearrange (1) to represent
given the assumption of income sharing among members of the illegal sector. We can therefore rearrange (1) to represent 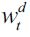 as
as
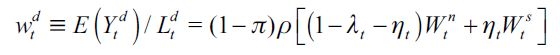 | [2] |
Note that 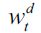 is a decreasing function in λt which means that a higher probability of encountering a delinquent lowers the material incentives for all delinquents in this sector. Hence, the illegal sector becomes less attractive when more delinquents enter it.
is a decreasing function in λt which means that a higher probability of encountering a delinquent lowers the material incentives for all delinquents in this sector. Hence, the illegal sector becomes less attractive when more delinquents enter it.
Individuals in this economy live two periods (young and adult) in overlapping generations. In each generation there is a continuum of individuals of size L. Each individual has just one child (there is no population growth), can work as unskilled in the first period of their life or invest in human capital when young and work as a skilled worker when adult, or choose a delinquent path when young. For the sake of simplicity we shall assume that all individuals consume as adults and only work during one period of their lives. Unskilled workers and delinquents work when young, while skilled workers do so when adult. Delinquents enjoy their loot when adult assuming they have not been apprehended by law enforcement authorities when young. Moreover, we assume that decisions are irreversible, which implies that a delinquent cannot go back to the legal unskilled sector when they become adults.7 Individuals who choose to educate themselves invest h>0 when young and are able to work in the skilled labor sector when adult, given that we assume away unemployment.
All individuals consume when adult, work one period of their life, care in the same way about their children and lose utility if they choose to live a delinquent life. This is modelled with a log utility specification in the following way
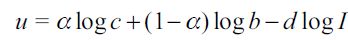 |
where 0<α<1 captures the weight of consumption of an individual, c is consumption in the second period, b is the bequest left to his or her child, I is a psychic or moral cost8 of committing delinquent acts, d = {0,1} is a binary variable such that d = 1 means that an individual chooses to be a delinquent and zero otherwise. Hence, there are only three occupations that individuals can choose: unskilled worker (n), skilled worker (s) and delinquent (d).
All individuals are born with the same potential abilities and preferences and will bear the same psychic or moral cost from engaging in illegal activities.9 They differ only in the amounts they inherit from their parents in terms of wealth xt where Dt (xt) is the cumulative distribution function of wealth xt in period t with support [0,∞) . This distribution satisfies 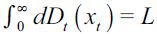 . As argued above we assume the existence of financial markets that allow individuals to save and earn interest on their savings at interest rate r>0 , established exogenously by world markets. The financial markets lend these funds to firms that pay interest rate r. However, we assume an extreme imperfection in the credit market for individual borrowers wishing to invest in education, namely that no access to credit is allowed to finance investment in human capital.10 Hence, individuals born in period t, who choose to invest in human capital can do so only if they have enough wealth to pay for the investment h.11
. As argued above we assume the existence of financial markets that allow individuals to save and earn interest on their savings at interest rate r>0 , established exogenously by world markets. The financial markets lend these funds to firms that pay interest rate r. However, we assume an extreme imperfection in the credit market for individual borrowers wishing to invest in education, namely that no access to credit is allowed to finance investment in human capital.10 Hence, individuals born in period t, who choose to invest in human capital can do so only if they have enough wealth to pay for the investment h.11
Optimal Bequests
Recall that λt denotes the probability in period t that a legal worker will encounter a delinquent. If the encounter occurs, the delinquent steals fraction ρWt from a worker with overall wealth Wt; otherwise the encounter does not occur and the worker loses nothing. Therefore an individual born in period t with wealth Wt chooses bt in order to maximize expected utility
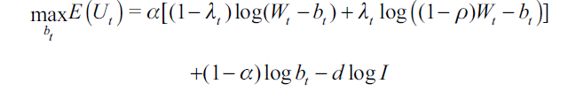 | [3] |
We assume that stealing directly affects the consumption of the victim through wealth that is lost, since it is equal to Wt−bt if the individual is not matched with a delinquent and (1−ρ)Wt−bt if matched with one. The first order condition of the optimization problem boils down to
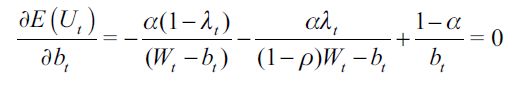 | [4] |
The resulting equation is a quadratic function for bt with the following solution
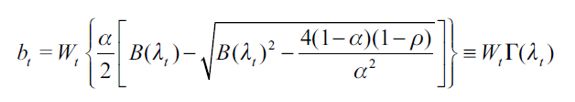 | [5] |
where 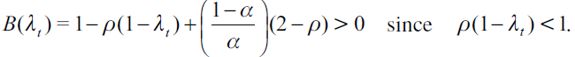 . Importantly, the optimal bequest is a linear function of Wt and we take the negative root as the solution of the problem12, showing in the appendix that Γ'(λ)<0 and 0< Γ(λ)<1 for all λ∈[0,1] which guarantees that the optimal bequest is always positive. Interestingly the economic interpretation of Γ'(λ)<0 0 is quite intuitive since it means that the more likely an individual is to be robbed the less likely it is that she will be able to bequeath to her child and therefore the more likely it is that she will use her wealth to pay for consumption. This shows how the likelihood of being a victim of delinquency affects inheritances negatively.
. Importantly, the optimal bequest is a linear function of Wt and we take the negative root as the solution of the problem12, showing in the appendix that Γ'(λ)<0 and 0< Γ(λ)<1 for all λ∈[0,1] which guarantees that the optimal bequest is always positive. Interestingly the economic interpretation of Γ'(λ)<0 0 is quite intuitive since it means that the more likely an individual is to be robbed the less likely it is that she will be able to bequeath to her child and therefore the more likely it is that she will use her wealth to pay for consumption. This shows how the likelihood of being a victim of delinquency affects inheritances negatively.
Replacing 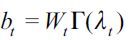 in the expected utility function that is maximized in (3) yields the expected life time indirect utility function
in the expected utility function that is maximized in (3) yields the expected life time indirect utility function
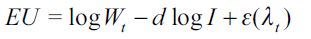 | [6] |
where 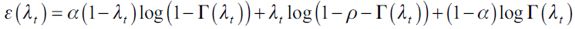 . Note that
. Note that 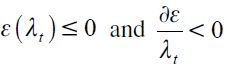 . Function (6) proves important to determine the different choices that individuals make.
. Function (6) proves important to determine the different choices that individuals make.
Occupation Choices
We now turn to describing individual optimal decisions. There are three occupations that individuals can choose: unskilled worker (n), skilled worker (s) and delinquency (d). Overall wealth consists of inherited wealth denoted by x and income earned during the lifetime of an individual. Therefore, the overall wealth levels of unskilled and skilled workers are respectively 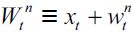 and
and 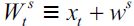 for period t. Consider an individual who inherits
for period t. Consider an individual who inherits 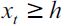 , decides to work as a skilled worker (d=0) and invest in human capital. This person's lifetime indirect expected utility and bequest are respectively
, decides to work as a skilled worker (d=0) and invest in human capital. This person's lifetime indirect expected utility and bequest are respectively
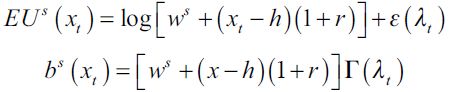 |
Consider now an individual who inherits an amount 0< xt< h of wealth in her first period of life and decides to work as an unskilled worker (d= 0) and not to invest in human capital; her lifetime indirect expected utility and bequest are:
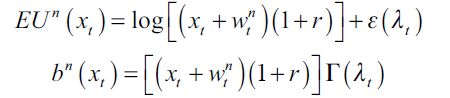 |
Alternatively, consider an individual who inherits an amount 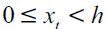 of wealth in his first period of life and decides to become a delinquent (d = 1) loses utility log I for certain and has the lifetime expected utility and bequest:
of wealth in his first period of life and decides to become a delinquent (d = 1) loses utility log I for certain and has the lifetime expected utility and bequest:
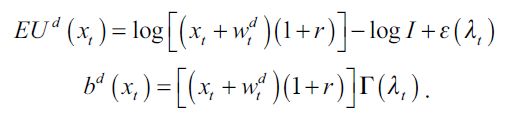 |
Since occupational choices are irreversible once taken, delinquents who choose this path when young cannot subsequently become skilled workers because they forgo the opportunity of investing in education during their first period of life.
Consequently, no educated delinquents can arise in the model. Moreover, if the wage differential between skilled and unskilled is sufficiently wide, taking into account investment costs h, all legal workers would prefer to work as skilled labor. To appreciate this, note that 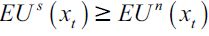 is true if and only if
is true if and only if
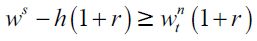 | [7] |
for every t. We assume that (7) holds true for every value of 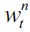 . Otherwise there would be no incentive to invest in human capital. Nonetheless, the possibility of gaining access to education depends on inherited wealth, since individuals with inherited wealth xt strictly less than h, cannot educate themselves given that any possibility of financing this investment with future earnings has been assumed away.
. Otherwise there would be no incentive to invest in human capital. Nonetheless, the possibility of gaining access to education depends on inherited wealth, since individuals with inherited wealth xt strictly less than h, cannot educate themselves given that any possibility of financing this investment with future earnings has been assumed away.
Individuals with inherited wealth less than h have to decide between working as unskilled labor or becoming delinquents. Individuals prefer to work as legal unskilled workers rather than become delinquents as long as 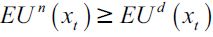 , that is as long as13
, that is as long as13
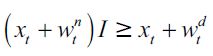 | [8] |
Note from (2) that 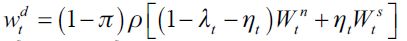 and by constructi
and by constructi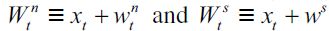 . Replacing these in (8) yields a threshold wealth level as a function of λt and
. Replacing these in (8) yields a threshold wealth level as a function of λt and 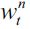 expressed as
expressed as
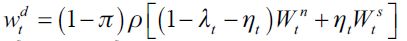 | [9] |
From now on we assume that I≥2, implying that the denominator in (9) is positive while if I is large enough under a small wage gap the numerator can be negative, which explains the max operator.
Determining the Legal Unskilled Wage and Short-Run Equilibrium
We turn now to determining the unskilled equilibrium wage 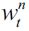 at time t. The supply of unskilled labor depends on the wealth distribution of the economy, as individuals with wealth between
at time t. The supply of unskilled labor depends on the wealth distribution of the economy, as individuals with wealth between 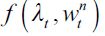 and h choose to be unskilled workers, given that we shall assume throughout that
and h choose to be unskilled workers, given that we shall assume throughout that 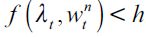 . Therefore, since each individual uses one unit of labor for each period, the supply function of unskilled labor in period t is given by
. Therefore, since each individual uses one unit of labor for each period, the supply function of unskilled labor in period t is given by
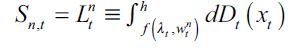 | [10] |
Competitive markets in the unskilled sector equate aggregate demand and supply of unskilled labor i.e. 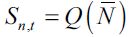 to determine the unskilled wage
to determine the unskilled wage 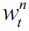 in each period. Given that the aggregate demand is fixed in any given period for a given value of
in each period. Given that the aggregate demand is fixed in any given period for a given value of 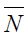 this unskilled equilibrium wage depends negatively on the fraction of unskilled workers in the economy i.e.
this unskilled equilibrium wage depends negatively on the fraction of unskilled workers in the economy i.e. 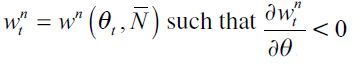 such that wtnt0 . Importantly it increases with the level of land in the economy, i.e.
such that wtnt0 . Importantly it increases with the level of land in the economy, i.e. 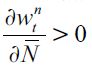 given that this would shift demand to the right, and for the same supply of workers, the unskilled wage must increase. For future reference define
given that this would shift demand to the right, and for the same supply of workers, the unskilled wage must increase. For future reference define 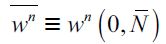 as the highest feasible unskilled wage when no individual would supply unskilled labor and
as the highest feasible unskilled wage when no individual would supply unskilled labor and 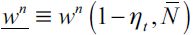 as the lowest yet positive unskilled wage when all labor of individuals with less than h is allocated to the legal unskilled sector.
as the lowest yet positive unskilled wage when all labor of individuals with less than h is allocated to the legal unskilled sector.
Figure 1 illustrates both the demand and supply of unskilled labor such that at their intersection the unskilled wage is determined. Notice that at 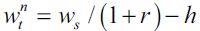 individuals are indifferent between investing in human capital and working as unskilled labor, hence the supply curve is upward sloping but becomes flat at this wage. Nonetheless, the curve can contain vertical segments.
individuals are indifferent between investing in human capital and working as unskilled labor, hence the supply curve is upward sloping but becomes flat at this wage. Nonetheless, the curve can contain vertical segments.
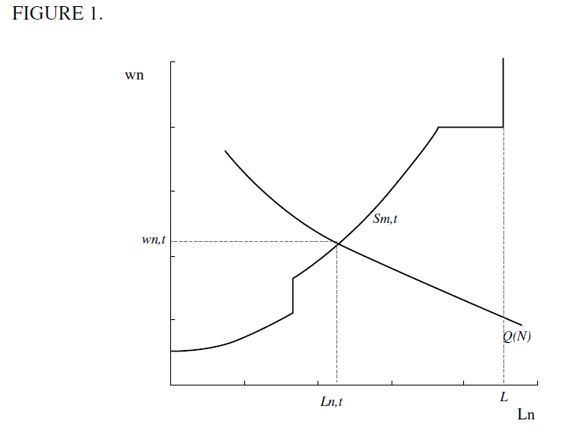
The amount an individual inherits in his or her first period of life, therefore, fully determines their decisions about whether to invest in human capital, work as unskilled labor or become delinquents and how much to consume and bequeath. Hence, the distribution Dt determines economic performance in period t, consisting of: the amount of skilled labor 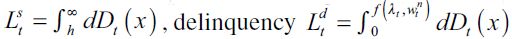 , and unskilled labor
, and unskilled labor 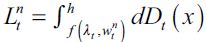 .
.
Rational expectations require consistency of expectations and chosen occupations such that the following equations should be satisfied
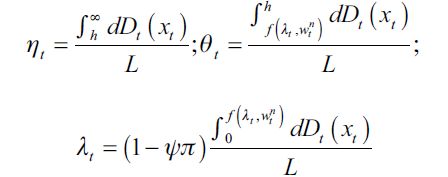 | [11] |
where the fraction 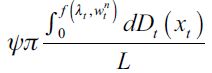 represents the fraction of delinquents that are apprehended and effectively convicted in period t under random matching. Here we assume that not all apprehended delinquents can be convicted since it is not always feasible to have enough "evidence" to incriminate suspected felons. We assume that only a fraction
represents the fraction of delinquents that are apprehended and effectively convicted in period t under random matching. Here we assume that not all apprehended delinquents can be convicted since it is not always feasible to have enough "evidence" to incriminate suspected felons. We assume that only a fraction 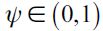 of apprehended delinquents are effectively found guilty beyond reasonable doubt of the crime of which they are accused. This rationalizes that law enforcement authorities can only incapacitate effectively at most ψ of the fraction of apprehended delinquents in a given period by actually putting them in prison.14 This motivates the following definition.
of apprehended delinquents are effectively found guilty beyond reasonable doubt of the crime of which they are accused. This rationalizes that law enforcement authorities can only incapacitate effectively at most ψ of the fraction of apprehended delinquents in a given period by actually putting them in prison.14 This motivates the following definition.
Definition 1 A short-run rational expectations equilibrium (SREE) of the economy described above consists of a distribution of fractions vt=[λt, θt, ηt] for period t where λt, θt, ηt=1 such that in period t individuals choose occupations that maximize expected utility, firms have zero profits, markets balance and conditions (11) are met.
The following theorem provides sufficient conditions to secure the existence and uniqueness of a SREE with a positive fraction of delinquents in the economy.
Theorem 1 If the economy described above satisfies (7) for all 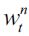 and the distribution of wealth Dt generates an unskilled wage equilibrium such that
and the distribution of wealth Dt generates an unskilled wage equilibrium such that 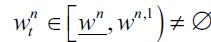 then it has a unique SREE with
then it has a unique SREE with 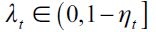 for any given t. Otherwise λt = 0 .
for any given t. Otherwise λt = 0 .
Proof: See the appendix.
Note that a positive fraction of delinquents in equilibrium arises in the SREE if the distribution of wealth Dt generates an unskilled wage equilibrium such that 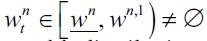 i.e. if there is a high enough wealth inequality such that the wealth distribution entails a sufficiently low unskilled wage in equilibrium. This amounts to saying that if there is a sufficient number of poor unskilled workers delinquency arises in equilibrium. On the other hand, if the wealth distribution is such that the unskilled wage is above wn,1 then delinquency does not arise in equilibrium. This implies that the more poverty there is in the economy the more there would be delinquency, given a high wealth inequality and low enough unskilled wages. Hence, a clear link between poverty, wealth inequality and delinquency in the short run.
i.e. if there is a high enough wealth inequality such that the wealth distribution entails a sufficiently low unskilled wage in equilibrium. This amounts to saying that if there is a sufficient number of poor unskilled workers delinquency arises in equilibrium. On the other hand, if the wealth distribution is such that the unskilled wage is above wn,1 then delinquency does not arise in equilibrium. This implies that the more poverty there is in the economy the more there would be delinquency, given a high wealth inequality and low enough unskilled wages. Hence, a clear link between poverty, wealth inequality and delinquency in the short run.
The Dynamics of Wealth Accumulation and the Poverty Trap
The distribution of wealth not only determines equilibrium in period t, but also the distribution of inheritance during the next period through the following dynamic equation:
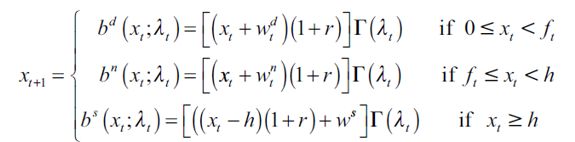 | [12] |
where for simplicity we denote 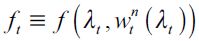 . As seen above, individuals who have x greater or equal to h choose to become skilled workers, those with x less than ft choose delinquency while individuals who inherit between ft and h choose to become unskilled workers. Using
. As seen above, individuals who have x greater or equal to h choose to become skilled workers, those with x less than ft choose delinquency while individuals who inherit between ft and h choose to become unskilled workers. Using 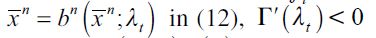 and assuming from here onwards a sufficient condition
and assuming from here onwards a sufficient condition 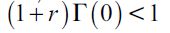 then we get wealth level
then we get wealth level 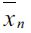 well defined given by
well defined given by
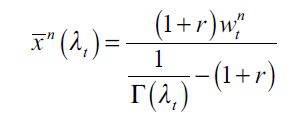 | [13] |
which is positive and where 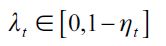 is a SREE fraction of non apprehended delinquents. Using
is a SREE fraction of non apprehended delinquents. Using 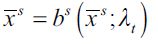 in (12) and again under
in (12) and again under 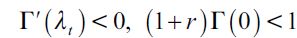 produces wealth level
produces wealth level 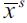 given by
given by
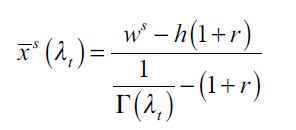 | [14] |
Under assumption (7), 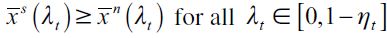 .
.
Note that wealth level 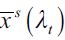 decreases in λt given that Γ'(λ)<0 while
decreases in λt given that Γ'(λ)<0 while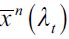 can increase or decrease, as
can increase or decrease, as 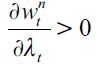 while Γ'(λ)<0. From (13) it may be seen that a change in λt has two effects on
while Γ'(λ)<0. From (13) it may be seen that a change in λt has two effects on 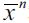 one determining the fraction of wealth that can be inherited Γ(λt) and another affecting the unskilled wage equilibrium
one determining the fraction of wealth that can be inherited Γ(λt) and another affecting the unskilled wage equilibrium 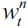 . We assume that the second effect is the one that dominates in the following sense: if the elasticity of unskilled wages with respect to λ is large enough such that
. We assume that the second effect is the one that dominates in the following sense: if the elasticity of unskilled wages with respect to λ is large enough such that
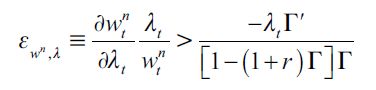 | [15] |
then we have 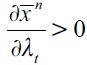 15 The right side threshold
15 The right side threshold 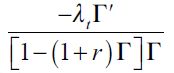 is non negative under
is non negative under 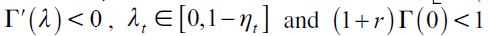 . Assumption (15) simply states that Γ' is not as sensitive to changes in λ relative to the sensitivity of the unskilled wage equilibrium
. Assumption (15) simply states that Γ' is not as sensitive to changes in λ relative to the sensitivity of the unskilled wage equilibrium 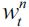 in λ. In other words, as λ increases θ decreases making the unskilled wage rise and more than offsetting the fall in Γ We assume from here onwards that condition (15) is always satisfied.
in λ. In other words, as λ increases θ decreases making the unskilled wage rise and more than offsetting the fall in Γ We assume from here onwards that condition (15) is always satisfied.
Figure 2 illustrates a typical configuration of the short-run dynamics of wealth accumulation in the economy given by (12). The points at which the curve intersects with the 45 degree line corresponds to 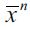 and
and 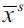 , giving a SREE value λt . Individuals with wealth levels less than h (including unskilled workers and delinquents) would move in the short run towards
, giving a SREE value λt . Individuals with wealth levels less than h (including unskilled workers and delinquents) would move in the short run towards 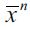 while those with wealth levels greater than h move towards
while those with wealth levels greater than h move towards 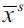 . Neverthetheless, these wealth levels depend explicitly on λt and the dynamics of wealth accumulation should not be considered to be the long run steady state wealth levels since it would be necessary to determine the value
. Neverthetheless, these wealth levels depend explicitly on λt and the dynamics of wealth accumulation should not be considered to be the long run steady state wealth levels since it would be necessary to determine the value 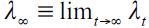 within the dynamic system, to which λt converges in the long run.
within the dynamic system, to which λt converges in the long run.
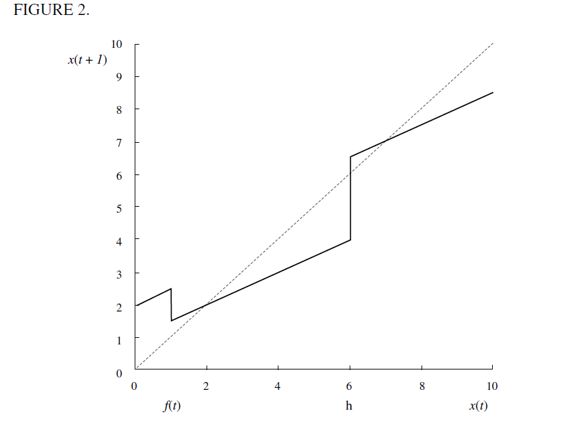
Let us examine the long-run behavior of the dynamic equation (12). From (9) one can see that the cutoff point ft and loot 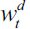 decrease with λt while
decrease with λt while 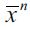 increases under assumption (15). Hence, in Figure 2 where
increases under assumption (15). Hence, in Figure 2 where 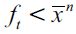 is satisfied in period t, as the dynamics step in ft+1 rises as a non-negligible fraction of non-apprehended delinquents migrate from the illegal sector towards the legal unskilled sector, decreasing λt+1 . The wealth level
is satisfied in period t, as the dynamics step in ft+1 rises as a non-negligible fraction of non-apprehended delinquents migrate from the illegal sector towards the legal unskilled sector, decreasing λt+1 . The wealth level 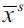 necessarily increases as λt decreases, while
necessarily increases as λt decreases, while 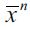 falls under assumption (15). Thus, as the economy in Figure 2 develops over time, delinquency decreases, while the wealth gap
falls under assumption (15). Thus, as the economy in Figure 2 develops over time, delinquency decreases, while the wealth gap 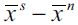 grows. This generates two cases for consideration: i) a vanishing fraction of delinquents such that λ∞ = 0 and ii) persistent delinquency λ∞> 0. If λ∞ = 0 then long run behavior conforms to the Galor-Zeira model abstracting from credit markets for households. However, we argue below that in the long run it is possible to have λ∞> 0 under certain conditions. In any case this convergence process requires a consideration of a steady state in which
grows. This generates two cases for consideration: i) a vanishing fraction of delinquents such that λ∞ = 0 and ii) persistent delinquency λ∞> 0. If λ∞ = 0 then long run behavior conforms to the Galor-Zeira model abstracting from credit markets for households. However, we argue below that in the long run it is possible to have λ∞> 0 under certain conditions. In any case this convergence process requires a consideration of a steady state in which 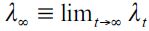 . Consequently, a steady state in the dynamics of wealth accumulation such that λ∞> 0 requires the migrationoutflow to be equal to the migration inflow to the delinquent sector. This leads to the following definition.
. Consequently, a steady state in the dynamics of wealth accumulation such that λ∞> 0 requires the migrationoutflow to be equal to the migration inflow to the delinquent sector. This leads to the following definition.
Definition 2 A long-run rational expectations equilibrium (LREE) consists of a SREE in which 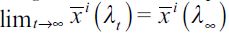 for i = n,s, and the long-run wealth threshold f∞ satisfies
for i = n,s, and the long-run wealth threshold f∞ satisfies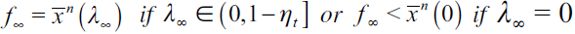 .
.
To obtain an intuition for this definition consider Figure 2 and let us focus on the dynamics of the bequest functions bd (xt;λt) and bn (xt;λt) as time evolves. Since the process starts off such that 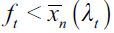 then some fraction of the offspring of (non apprehended) delinquent households cross f (namely those with wealth levels arbitrarily close to ft) and enter the legal unskilled sector inducing a decrease in λt+1.16 This in turn increases the threshold ft+1, the loot
then some fraction of the offspring of (non apprehended) delinquent households cross f (namely those with wealth levels arbitrarily close to ft) and enter the legal unskilled sector inducing a decrease in λt+1.16 This in turn increases the threshold ft+1, the loot 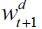 and decreases
and decreases  under assumption (15). The net effect is that λ should eventually decrease weakly so long as
under assumption (15). The net effect is that λ should eventually decrease weakly so long as 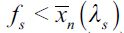 for some s>t. This process continues up to the point in which equality
for some s>t. This process continues up to the point in which equality 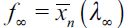 occurs consistent with persistent delinquency
occurs consistent with persistent delinquency 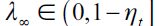 . Nonetheless,it is possible that delinquency will vanish before this equality is reached i.e.
. Nonetheless,it is possible that delinquency will vanish before this equality is reached i.e. 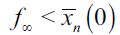 , consistent with λ∞= 0 . A similar logic occurs for the case in which the dynamic process starts off with
, consistent with λ∞= 0 . A similar logic occurs for the case in which the dynamic process starts off with 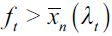 . In this case delinquency increases as more households are induced by the dynamics around
. In this case delinquency increases as more households are induced by the dynamics around 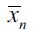 to enter the delinquent sector, increasing
to enter the delinquent sector, increasing 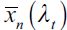 under assumption (15) and decreasing ft, so that eventually condition
under assumption (15) and decreasing ft, so that eventually condition 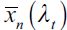 is satisfied in the long run.
is satisfied in the long run.
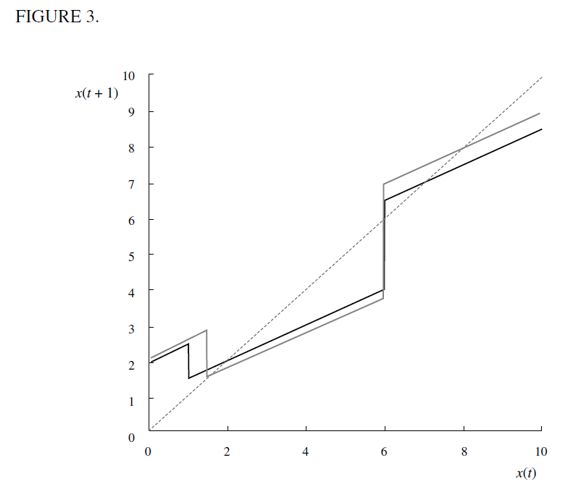
Figure 3 illustrates the limiting behavior of the dynamic system where the thin line is consistent with the case 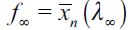 for persistent delinquency
for persistent delinquency 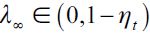 .
.
Note that 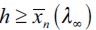 arises in the long run since we have assumed h >ft for all t and this entails a poverty trap which induces persistent inequality and eventually delinquency λ∞ > 0 in the long run. To see this, note that apprehended and convicted delinquent households that have only
arises in the long run since we have assumed h >ft for all t and this entails a poverty trap which induces persistent inequality and eventually delinquency λ∞ > 0 in the long run. To see this, note that apprehended and convicted delinquent households that have only 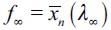 (or ε less wealth) in the long run will not be able to increase their wealth in
(or ε less wealth) in the long run will not be able to increase their wealth in 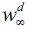 , forcing them to leave a bequest smaller than
, forcing them to leave a bequest smaller than 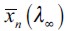 for their offspring, given that they still have to consume when adults. Hence, these offspring would necessarily choose to become delinquents over and again, consistent with having persistent delinquency in the economy. On the other hand, non apprehended delinquents that have only
for their offspring, given that they still have to consume when adults. Hence, these offspring would necessarily choose to become delinquents over and again, consistent with having persistent delinquency in the economy. On the other hand, non apprehended delinquents that have only 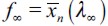 (or ε less of wealth) would be able to secure loot
(or ε less of wealth) would be able to secure loot 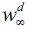 allowing them to bequest a wealth level greater than
allowing them to bequest a wealth level greater than 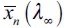 . Hence, their offspring would choose to become legal workers during the next period. Nevertheless, because of the existence of a poverty trap these households would eventually end up withf
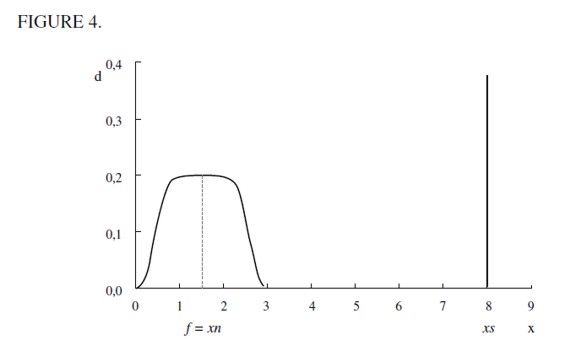
. Hence, their offspring would choose to become legal workers during the next period. Nevertheless, because of the existence of a poverty trap these households would eventually end up withf 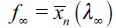 in the long run and could therefore end up having offspring who would choose to become delinquents. It is this outflow and inflow of individuals from and to the illegal sector that would have to be balanced in the long run consistent with a LREE such that λ∞> 0 remains constant. Figure 4 illustrates a bimodal pdf wealth distribution d∞ consistent with this dynamic process and corresponds to the thin line of Figure 3.
in the long run and could therefore end up having offspring who would choose to become delinquents. It is this outflow and inflow of individuals from and to the illegal sector that would have to be balanced in the long run consistent with a LREE such that λ∞> 0 remains constant. Figure 4 illustrates a bimodal pdf wealth distribution d∞ consistent with this dynamic process and corresponds to the thin line of Figure 3.
Moreover, to get persistent delinquency in the long run requires additionally that 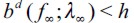 . To see why, consider what would happen if
. To see why, consider what would happen if 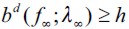 . In this case the offspring of non-apprehended delinquent households with wealth level f∞ would inherit enough to educate themselves, leapfrogging the poverty trap and eventually entering the skilled sector. Hence, in the long run λ∞ = 0 . For persistent delinquency to develop
. In this case the offspring of non-apprehended delinquent households with wealth level f∞ would inherit enough to educate themselves, leapfrogging the poverty trap and eventually entering the skilled sector. Hence, in the long run λ∞ = 0 . For persistent delinquency to develop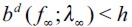 is required. It remains to be shown that under certain conditions there exists a LREE with persistent delinquency.
is required. It remains to be shown that under certain conditions there exists a LREE with persistent delinquency.
Theorem 2 If the economy described above satisfies 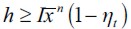 as well as assumptions (15), (7) for all
as well as assumptions (15), (7) for all 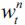 such that the initial wealth distribution D0 generates
such that the initial wealth distribution D0 generates 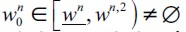 then there exists a unique LREE of the economy described above such that
then there exists a unique LREE of the economy described above such that 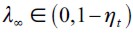
Proof: See the appendix.
Some remarks are in order.
1) Assumption 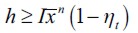 allows for the existence of the poverty trap which in turn makes it more likely that persistent delinquency will arise in the long run. This is because h is sufficiently large relative to
allows for the existence of the poverty trap which in turn makes it more likely that persistent delinquency will arise in the long run. This is because h is sufficiently large relative to 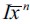 , implying that the bn function intersects the 45 degree line. Moreover, this assumption importantly includes
, implying that the bn function intersects the 45 degree line. Moreover, this assumption importantly includes 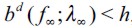 , meaning that delinquent households cannot leapfrog over the poverty trap.
, meaning that delinquent households cannot leapfrog over the poverty trap.
2) Condition 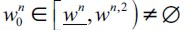 requires that initial wealth distribution should generate an unskilled equilibrium wage low enough for incentives for delinquency to arise. Moreover, the threshold value
requires that initial wealth distribution should generate an unskilled equilibrium wage low enough for incentives for delinquency to arise. Moreover, the threshold value 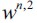 satisfies
satisfies 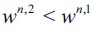 showing that for persistent delinquency to arise there needs to be a sufficient mass of poor unskilled workers to ensure the unskilled wage equilibrium is low enough (lower than wn,2). This implies that poverty coupled with wealth inequality is a sufficient condition for delinquency in the short run but not for persistent delinquency in the long run unless a poverty trap exists.
showing that for persistent delinquency to arise there needs to be a sufficient mass of poor unskilled workers to ensure the unskilled wage equilibrium is low enough (lower than wn,2). This implies that poverty coupled with wealth inequality is a sufficient condition for delinquency in the short run but not for persistent delinquency in the long run unless a poverty trap exists.
Consider Figure 3 again and let us focus on the thin line that represents the steady state wealth distribution compatible with 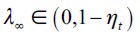 such that
such that 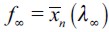 . Outflow migration from the illegal delinquent sector to the legal unskilled one should be just the same as inflow migration from the former to the latter. Hence, we have a continuous flow of households leaving the illegal sector for some time only to return to it eventually because of the poverty trap. It is therefore perfectly possible to have dynastic households that pass in and out of delinquency many times. This circular flow is maintained because of the condition
. Outflow migration from the illegal delinquent sector to the legal unskilled one should be just the same as inflow migration from the former to the latter. Hence, we have a continuous flow of households leaving the illegal sector for some time only to return to it eventually because of the poverty trap. It is therefore perfectly possible to have dynastic households that pass in and out of delinquency many times. This circular flow is maintained because of the condition 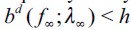 that does not allow delinquent households to leapfrog the poverty trap. This intuition is also illustrated in Figure 4 where in the long run the wealth distribution around the poverty trap is not a single point but a region.
that does not allow delinquent households to leapfrog the poverty trap. This intuition is also illustrated in Figure 4 where in the long run the wealth distribution around the poverty trap is not a single point but a region.
ECONOMIC DEVELOPMENT AND COMPARATIVE DYNAMICS
As in the original Galor-Zeira model (1993) a sufficiently unequal initial wealth distribution, such that the initial unskilled wage is low enough, i.e. 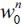 satisfies
satisfies 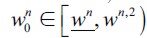 implies that an economy would end up in economic underdevelopment meaning either that there is club-convergence in wealth or that the economy's wealth distribution converges to a bimodal distribution as in Figure 4. In this case there is the possibility of persistent delinquency due to the poverty trap around
implies that an economy would end up in economic underdevelopment meaning either that there is club-convergence in wealth or that the economy's wealth distribution converges to a bimodal distribution as in Figure 4. In this case there is the possibility of persistent delinquency due to the poverty trap around 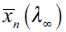 where λ∞> 0 . On the other hand, if an economy starts out with less unequal initial wealth distribution, such that the initial unskilled wage
where λ∞> 0 . On the other hand, if an economy starts out with less unequal initial wealth distribution, such that the initial unskilled wage 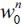 is sufficiently high, i.e.
is sufficiently high, i.e. 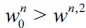 , then the economy would end up achieving economic development characterized by convergence such that all wealth converges to
, then the economy would end up achieving economic development characterized by convergence such that all wealth converges to 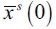 in the long run, where λ∞ = 0. Hence, the model predicts empirically that economies that start out with high inequality in wealth distribution end up as underdeveloped economies and suffer high crime rates relative to the paths of developed economies. This theoretical prediction has some support empirically in a number of studies for cross-country data, such as Fajnzylber, Lederman and Loayza (2001, 2002), Soares (2004), Soares and Naritomi (2010). Importantly, the theoretical model developed here rationalizes these empirical findings.
in the long run, where λ∞ = 0. Hence, the model predicts empirically that economies that start out with high inequality in wealth distribution end up as underdeveloped economies and suffer high crime rates relative to the paths of developed economies. This theoretical prediction has some support empirically in a number of studies for cross-country data, such as Fajnzylber, Lederman and Loayza (2001, 2002), Soares (2004), Soares and Naritomi (2010). Importantly, the theoretical model developed here rationalizes these empirical findings.
We now turn to the LREE steady state of an underdeveloped economy with persistent delinquency λ∞> 0 in which some parameters are shifted temporarily or permanently. These include a technological shock to productivity in the skilled sector (ws), a change in the amount of land in the unskilled sector ( 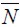 ), a change in the punishment probability ( π ), a decrease in human capital investment (h), a continuous technological innovation in the unskilled legal sector through improvements in F and finally a change in the proportion of relative poverty in the model θ∞ leaving η∞ unaltered.
), a change in the punishment probability ( π ), a decrease in human capital investment (h), a continuous technological innovation in the unskilled legal sector through improvements in F and finally a change in the proportion of relative poverty in the model θ∞ leaving η∞ unaltered.
Let us consider a temporary one-time exogenous technological shock that increases ws. Let us trace the effects within the model. In this case the initial threshold value f increases above 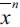 , since as equation (9) shows this threshold value is an increasing function of ws, making the illegal sector attractive for individuals with wealth less than f, because the "implicit" illegal wage wd is shifted upward as it is also an increasing function in ws. All this implies that there is an increase in λ∞ Hence, as λ∞ increases,the
, since as equation (9) shows this threshold value is an increasing function of ws, making the illegal sector attractive for individuals with wealth less than f, because the "implicit" illegal wage wd is shifted upward as it is also an increasing function in ws. All this implies that there is an increase in λ∞ Hence, as λ∞ increases,the 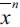 wealth level also increases under assumption (15) while the resulting influx of delinquents reduces the initial rise in f and therefore the dynamics yield
wealth level also increases under assumption (15) while the resulting influx of delinquents reduces the initial rise in f and therefore the dynamics yield 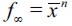 in the long run, returning to preshock wealth levels. Hence, a temporary increase in ws produces a peak of delinquency that eventually dies out later on. If the shock is permanent the logic is the same but there is a permanent increase in λ∞ responding to a permanent increase in the incentives to enter the illegal sector. In this case, the long-run wealth level
in the long run, returning to preshock wealth levels. Hence, a temporary increase in ws produces a peak of delinquency that eventually dies out later on. If the shock is permanent the logic is the same but there is a permanent increase in λ∞ responding to a permanent increase in the incentives to enter the illegal sector. In this case, the long-run wealth level 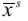 decreases permanently while
decreases permanently while 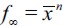 increases permanently. Therefore, the model predicts that societies with higher wage gaps (more income inequality) tend to have more crime.
increases permanently. Therefore, the model predicts that societies with higher wage gaps (more income inequality) tend to have more crime.
Consider now a temporary decrease in the level of aggregate land  .17 In this case there is an inward shift of labor demand in the unskilled labor sector, reducing the equilibrium unskilled wage
.17 In this case there is an inward shift of labor demand in the unskilled labor sector, reducing the equilibrium unskilled wage 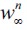 . This in turn reduces θ∞ while increasing λ∞ proportionally, since there is no leapfrogging over the poverty trap in a LREE steady P state that would affect η∞. From (13) and (14) it may be seen that
. This in turn reduces θ∞ while increasing λ∞ proportionally, since there is no leapfrogging over the poverty trap in a LREE steady P state that would affect η∞. From (13) and (14) it may be seen that 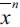 increases under assumption (15) while
increases under assumption (15) while 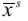 has to decrease due to
has to decrease due to 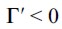 . Also, the threshold value f in equation (9) decreases with an increase in λ∞ since
. Also, the threshold value f in equation (9) decreases with an increase in λ∞ since
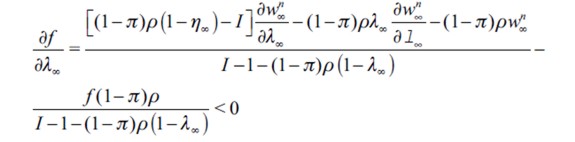
given that 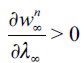 and I ≥ 2 as well as the parameter restrictions imposed on the model. Hence, situation
and I ≥ 2 as well as the parameter restrictions imposed on the model. Hence, situation 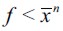 arises, resulting in an incentive for subsequent generations to leave the delinquent sector, after which the dynamics step in, reestablishing
arises, resulting in an incentive for subsequent generations to leave the delinquent sector, after which the dynamics step in, reestablishing 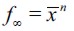 at the original pre-shock levels. Hence, a temporary negative shock in
at the original pre-shock levels. Hence, a temporary negative shock in 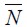 also generates a peak of delinquency that dies down later on. If the shock is made permanent there is a higher long run delinquent fraction λ∞consistent with a lower fraction θ∞ of skilled workers in the economy. This in turn implies that the condition
also generates a peak of delinquency that dies down later on. If the shock is made permanent there is a higher long run delinquent fraction λ∞consistent with a lower fraction θ∞ of skilled workers in the economy. This in turn implies that the condition 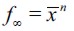 would be reestablished eventually at a lower level, as
would be reestablished eventually at a lower level, as 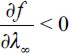 while
while 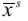 also decreases permanently. The model rationalizes the positive effect on crime that emerges under forced displacement which has occurred all too often in the recent past in underdeveloped countries, including in Colombia.
also decreases permanently. The model rationalizes the positive effect on crime that emerges under forced displacement which has occurred all too often in the recent past in underdeveloped countries, including in Colombia.
Consider now a permanent increase in the punishment probability π due, say, to technological innovations in the apprehension and/or conviction of delinquents. In this case there is an initial decrease in the expected loot 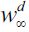 as well as in threshold value f∞ because it is clear from (9) that f∞ is a decreasing function of π since situation
as well as in threshold value f∞ because it is clear from (9) that f∞ is a decreasing function of π since situation 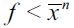 arises there is an incentive for delinquents to leave the illegal sector towards the unskilled labor sector generating a decrease in λ∞ and a proportional increase in the fraction of unskilled labor θ∞ which in turn decreases the unskilled wage equilibrium
arises there is an incentive for delinquents to leave the illegal sector towards the unskilled labor sector generating a decrease in λ∞ and a proportional increase in the fraction of unskilled labor θ∞ which in turn decreases the unskilled wage equilibrium 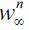 . Therefore,
. Therefore, 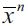 subsequently decreases under assumption (15) while
subsequently decreases under assumption (15) while 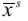 increases due to the lower level of λ∞ given that
increases due to the lower level of λ∞ given that 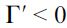 . Condition
. Condition 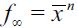 is reestablished in the long run at a lower level than before the change in π. Hence, a permanent increase in π decreases crime levels permanently because λ∞ decreases permanently too. However, this generates a permanent increase in wealth inequality since
is reestablished in the long run at a lower level than before the change in π. Hence, a permanent increase in π decreases crime levels permanently because λ∞ decreases permanently too. However, this generates a permanent increase in wealth inequality since 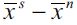 increases. Hence, a permanent increase in π is associated with an increase in wealth inequality due to the existence of the poverty trap.
increases. Hence, a permanent increase in π is associated with an increase in wealth inequality due to the existence of the poverty trap.
Consider a decrease in the human capital investment cost (h) due, say, to the introduction of public education (adjusted by quality) that allows human capital investment to be subsidized through taxation τ levied on the skilled workers of the economy such that equation (7) still holds in the following sense
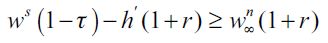 | [16] |
where 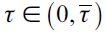 is the tax on skilled workers,
is the tax on skilled workers, 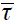 denotes the highest tax compatible with having equation (16) satisfied as an equality, so that choosing to study is still optimal for households that can afford it, and
denotes the highest tax compatible with having equation (16) satisfied as an equality, so that choosing to study is still optimal for households that can afford it, and 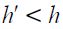 . There are three cases to consider. First, if
. There are three cases to consider. First, if 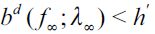 then nothing is altered in the model; second, if
then nothing is altered in the model; second, if 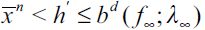 then non-apprehended delinquent households that have bequests greater than h' would have offspring who are able to leave the poverty trap and migrate towards skilled labor in future generations; finally, if
then non-apprehended delinquent households that have bequests greater than h' would have offspring who are able to leave the poverty trap and migrate towards skilled labor in future generations; finally, if 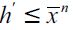 then eventually the poverty trap disappears since all households can choose to invest in human capital and abandon the delinquent sector while the economy becomes in the long run a developed economy.
then eventually the poverty trap disappears since all households can choose to invest in human capital and abandon the delinquent sector while the economy becomes in the long run a developed economy.
Let us consider now a continuous improvement through time in the technology used by unskilled labor, G. In this case the poverty trap eventually ceases to exist and the economy converges to 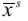 (0) . This implies that in the medium run there would be club-convergence as in Figure 4, but in the long run there would be absolute convergence towards
(0) . This implies that in the medium run there would be club-convergence as in Figure 4, but in the long run there would be absolute convergence towards 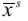 (0) . This process would be similar to the one described in Galor (1996).
(0) . This process would be similar to the one described in Galor (1996).
It is generally recognized in the field of development economics that the concept of poverty has absolute and relative dimensions. While the concept of relative poverty has to do with the fraction of the population that is in the lower tail of the income/wealth distribution, the concept of absolute poverty involves a minimum standard of living, usually associated with an income-defined poverty line. Our model does not include poverty in this latter sense as it is only concerned with relative poverty. We are interested in studying an underdeveloped economy with persistent delinquency in the long run where the fraction of households in the lower tail of the wealth distribution curve increases, and then tracing its effects. Suppose that an underdeveloped economy is in its LREE steady state with persistent delinquency and that a non-negligible fraction of the offspring of skilled workers becomes impoverished permanently by an exogenous shock, say because their inherited wealth has been destroyed.18 Assume that their wealth level is now just above 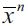 . This is equivalent to having a change in the long-run wealth distribution, D∞ , such that a decrease in η∞ is compensated by a proportional increase in θ∞ , where
. This is equivalent to having a change in the long-run wealth distribution, D∞ , such that a decrease in η∞ is compensated by a proportional increase in θ∞ , where 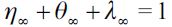 stays unaltered. Given that there is no population growth in the model this is equivalent to comparing one society with a relatively equal distribution with another that has a more unequal wealth distribution. To simplify matters as much as possible, consider a decrease in η∞ that is compensated by a proportional increase only in fraction θ∞, since the impoverished offspring end up with wealth greater than or equal to
stays unaltered. Given that there is no population growth in the model this is equivalent to comparing one society with a relatively equal distribution with another that has a more unequal wealth distribution. To simplify matters as much as possible, consider a decrease in η∞ that is compensated by a proportional increase only in fraction θ∞, since the impoverished offspring end up with wealth greater than or equal to 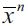 , which does not directly affect fraction λ∞ In this case the unskilled wage
, which does not directly affect fraction λ∞ In this case the unskilled wage 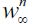 necessarily decreases because the fraction of unskilled workers θ∞ grows. This makes threshold value f decrease, since it may be seen from (9) that only the numerator decreases, as we explain below, given that by construction λ∞ remains unaltered. The numerator N of equation (9) in the long run can be rewritten in the following way
necessarily decreases because the fraction of unskilled workers θ∞ grows. This makes threshold value f decrease, since it may be seen from (9) that only the numerator decreases, as we explain below, given that by construction λ∞ remains unaltered. The numerator N of equation (9) in the long run can be rewritten in the following way
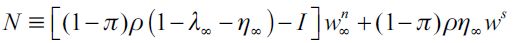 | [17] |
which we can then derive with respect to η∞ to get
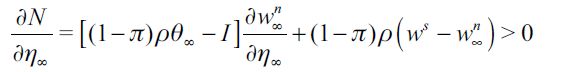
as 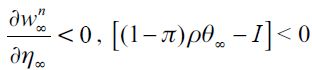 given that we have
given that we have 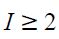 and
and 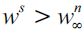 . Hence, the threshold value f necessarily decreases with the distribution change that reduces η∞ such that θ∞ is proportionally increased, leaving λ∞ unaltered. Moreover, the long-run wealth level
. Hence, the threshold value f necessarily decreases with the distribution change that reduces η∞ such that θ∞ is proportionally increased, leaving λ∞ unaltered. Moreover, the long-run wealth level 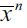 also decreases, since λ∞ is unaltered and
also decreases, since λ∞ is unaltered and 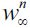 decreases. Hence, the net effect is unpredictable and ambiguous since it is not clear if the threshold value f is greater or smaller than the long-run wealth
decreases. Hence, the net effect is unpredictable and ambiguous since it is not clear if the threshold value f is greater or smaller than the long-run wealth 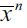 after the distribution change. Hence we have to consider two cases:
after the distribution change. Hence we have to consider two cases:
1) Consider first that 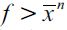 arises. Then to reestablish the long run equilibrium condition i.e.
arises. Then to reestablish the long run equilibrium condition i.e. 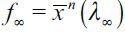 , fraction λ∞ necessarily has to increase due to the existence of greater incentives to enter the illegal sector. This causes
, fraction λ∞ necessarily has to increase due to the existence of greater incentives to enter the illegal sector. This causes 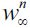 to increase along with
to increase along with 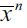 , under assumption (15) while threshold value f decreases. Hence, the distribution change makes the model work such that it increases λ∞ at the expense of decreasing θ∞ to reestablish the steady state condition. This allows us to conclude that in this case a higher proportion of poverty generates higher delinquency levels.
, under assumption (15) while threshold value f decreases. Hence, the distribution change makes the model work such that it increases λ∞ at the expense of decreasing θ∞ to reestablish the steady state condition. This allows us to conclude that in this case a higher proportion of poverty generates higher delinquency levels.
2) Consider now that situation 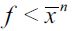 arises in which case fraction λ∞ would necessarily decrease at the expense of increasing θ∞, given that there is no leapfrogging of the poverty trap. This in turn would make the equilibrium wage
arises in which case fraction λ∞ would necessarily decrease at the expense of increasing θ∞, given that there is no leapfrogging of the poverty trap. This in turn would make the equilibrium wage 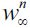 decrease, making the long run wealth level
decrease, making the long run wealth level 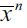 decrease as well, under assumption (15) . Furthermore, threshold value f increases so that eventually the long run equilibrium condition
decrease as well, under assumption (15) . Furthermore, threshold value f increases so that eventually the long run equilibrium condition 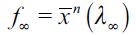 is reestablished. Hence, the distribution change decreases λ∞ at the expense of increasing θ∞ in order to reestablish the steady state, which allows us to conclude that in this case a higher proportion of poverty generates lower levels of delinquency.
is reestablished. Hence, the distribution change decreases λ∞ at the expense of increasing θ∞ in order to reestablish the steady state, which allows us to conclude that in this case a higher proportion of poverty generates lower levels of delinquency.
We conclude that when there is no leapfrogging over the poverty trap a greater proportion of (relative) poverty in the economy does not lead necessarily to greater delinquency levels, precisely because the unskilled equilibrium wage is flexible and changes the incentives to delinquency accordingly. Moreover, this unpredictable outcome also occurs if we think of an increase in the proportion of skilled workers η∞, which is equivalent to an increase in the accumulation of human capital. This is because an increase in η∞ such that 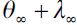 is also decreased would lead to similarly two cases as the ones just considered which would suggest that greater numbers of skilled workers in the economy (i.e. more educated households or human capital accumulation) may lead to more delinquency but will not necessarily do so.
is also decreased would lead to similarly two cases as the ones just considered which would suggest that greater numbers of skilled workers in the economy (i.e. more educated households or human capital accumulation) may lead to more delinquency but will not necessarily do so.
CONCLUSIONS
Delinquency seems to be quite persistent in developing economies which present high income inequality. To understand the relation between delinquency and inequality we studied a perfect competition overlapping generations model, similar to the one devised by Galor-Zeira (1993), which under conditions of sufficient initial inequality and costly indivisible human capital investments, generates persistent delinquency in the long run. The model takes seriously the idea that delinquents choose a criminal life rationally when faced with a lack of legal opportunities to enter a skilled sector that requires certain levels of education. It builds on a dual legal production sector economy in which delinquents from the poorest households self-select themselves to participate in the illegal sector of the economy, preying on legal workers. We characterize the optimal bequest of dynastic households in three occupational activities (delinquency, unskilled and skilled workers) that emerge in the economy and which govern and are determined by wealth distribution and its evolution. We illustrate conditions under which a delinquency fraction exists in the short run and we define a steady state of the dynamic system compatible with the possibility of persistent delinquency in the long run. We find that for given levels of law enforcement, deterrence and incapacitation delinquency is persistent in the long run for an underdeveloped economy if the initial unskilled equilibrium wage is low enough because initially high numbers of unskilled workers coupled with high wealth inequality provides opportunities for delinquency.
We studied the comparative dynamics of an underdeveloped economy with persistent delinquency, finding that temporary technological shocks that increase skilled wages or reduce land assets for unskilled workers increase incentives for delinquency producing a peak of delinquency that dies out later. If these shocks are made permanent then delinquency increases permanently in the long run. We found that a greater proportion of relative poverty in the economy has an ambiguous effect on incentives for delinquency due to the flexibility of the unskilled wage equilibrium that changes the incentives to enter the illegal sector. Permanent increases in law enforcement deterrence and incapacitation reduce delinquency at the cost of increasing wealth inequality in the long run, due to the presence of the poverty trap. Moreover, a continuous increase in the technology used by unskilled labor eventually makes the poverty trap disappear as well as eliminating the incentives for delinquency which makes the economy converge to a high wealth level in the long run.
Further research could focus on heterogeneity in the moral-psychic cost of engaging in illegal activities as well as unemployment in the legal skilled sector, tracing their effects on the incentives for delinquency. Moreover, the model could be further adapted to include illegal goods, like drugs, studying their effect on the incentives for delinquency. Finally, the model could endogenize the probability of punishment in order to rationalize the positive empirical correlation that exists between crime rates and law enforcement allocations.
FOOTNOTES
3 We are grateful for the comments of the participants of Seminars held at the Pontificia Universidad Javeriana, the Universidad Autónoma de Bucaramanga and the Universidad de los Andes where this paper was presented and at the Banco de la República and the Departamento Nacional de Planeación. Naturally all remaining errors are ours.
4 This differs for illegal activities like illegal drugs which are goods that are considered to be illegal but are produced in the same way as legal goods. We abstract from this issue to make the model as tractable as possible.
5 We consider delinquency as the illegal activity with the explicit objective of acquiring income. Nonetheless, not all types of crimes could be considered delinquent acts. For example, homicides from serial killers are violent crimes that are not motivated by any pecuniary motive, which in this view would not be considered to be a delinquent act but would be considered a violent crime act.
6 We assume that once a robbery occurs with probability π law enforcement authorities are able to apprehend and convict the delinquent and give back the wealth seized to the victim at no cost to them.
7 This assumption of irreversibility is strong but Witte and Tauchen (1994) find evidence of a negative relation between studying and/or working with the probability of engaging in criminal activities. They argue that this behavior comes from individuals being tied to legal activities as a result of their contact with either an educational or labor institution and not necessarily due to a higher education attainment that brings higher wages.
8 This psychic or moral cost can represent guilt or shame of committing criminal acts and should correspond to the monetary equivalent.
9 We assume that I is the same for everyone in the economy. This simplifies the moral heterogeneity in the population, making the model as tractable as possible.
10 This might be rationalized by assuming that individuals who invest a certain amount in their education by acquiring credit can leave the economy at zero cost without paying back the loan.
11 This is a working assumption that can be relaxed with less stringent market imperfections, in line with Galor-Zeira (1993), without affecting our principal results.
12 This is because of the economic intuitiveness of the solution Γ'(λ)<0, explained below.
13 We have assumed in this calculation that an individual considers himself as negligible when becoming a delinquent in the sense that he does not think he will vary the fraction of delinquents in the economy. This is due to the continuum of individuals in the population which implies that the term ε(λt) can safely be eliminated on both sides of the inequality.
14 Importantly, individuals that are put in prison in period t do not circulate in the economy in that period therefore they are modeled here "as if " they disappeared or vanished in the distribution of wealth for (only) period t. They could still have children in prison so the population growth is zero at all times.
15 This seems counterintuitive but one has to recognize that this only comes from having 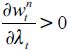 which is quite intuitive as it means that when there are more delinquents in the illegal sector then the unskilled wage in the legal sector should increase because fewer legal unskilled workers are available.
which is quite intuitive as it means that when there are more delinquents in the illegal sector then the unskilled wage in the legal sector should increase because fewer legal unskilled workers are available.
16 This is because as dynastic delinquent households accumulate wealth they eventually cross threshold fs for some period s > t in a process that is only delayed for a finite number of periods by eventual law enforcement detentions.
17 Instead of thinking of this as land destruction a more reasonable scenario would be forced displacement of poor households from rural areas towards urban areas because of violence, which has occurred for example in Colombia.
18 One can think of skilled workers that went bankrupt for some exogenous reason and ended up wealth just above 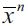 .
.
19 Recall the Liebniz rule: 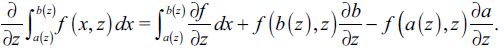
APPENDIX
Proposition 1 Under the assumptions of the model 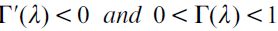 for all
for all 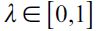
Proof. First we show that 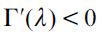 for all
for all 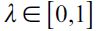 . From (5) differentiating with respect to λ we get
. From (5) differentiating with respect to λ we get
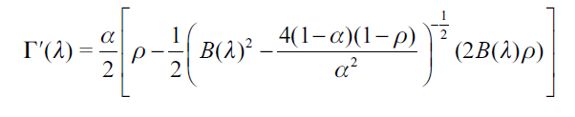
since 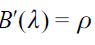 . It is sufficient to show that
. It is sufficient to show that
which is satisfied since
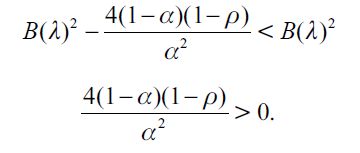
We have used the fact that 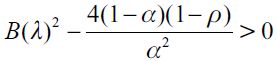 for all
for all 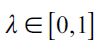 . To see why this is the case, define
. To see why this is the case, define
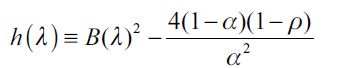
and note that 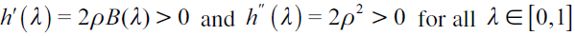 . Hence the function is strictly convex, increasing, and does not attain a minimum in the interval
. Hence the function is strictly convex, increasing, and does not attain a minimum in the interval 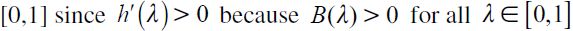 .
.
Second, we show 0<()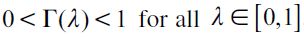 . First let us show that
. First let us show that 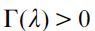 for all
for all 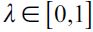 . From (5) it is sufficient to show that is positive for all
. From (5) it is sufficient to show that is positive for all 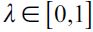 Note
Note
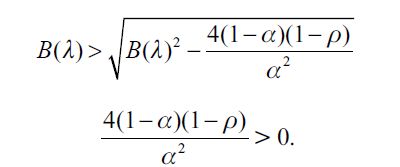
Finally to show that 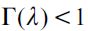 for all
for all 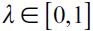 .it is sufficient to show
.it is sufficient to show 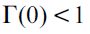 since we have shown
since we have shown 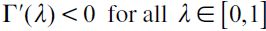 . Notice that for the negative root
. Notice that for the negative root
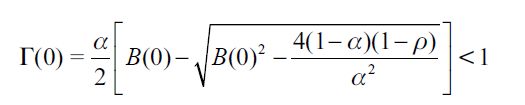
if the following holds
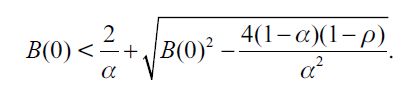
Since we know that 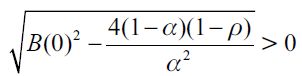 and it is added to
and it is added to 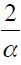 , we just need to show that
, we just need to show that 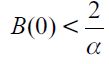 , which comes down to showing that
, which comes down to showing that
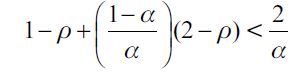
which is satisfied since 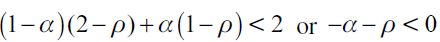 .
.
Theorem 1 If the economy described above satisfies (7) for all 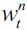 and the distribution of wealth Dt generates an unskilled wage equilibrium such that
and the distribution of wealth Dt generates an unskilled wage equilibrium such that 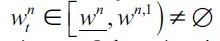 then it has a unique SREE with
then it has a unique SREE with 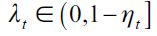 for any given t. Otherwise λt = 0 .
for any given t. Otherwise λt = 0 .
Proof. Firms have zero profits in equilibrium given the assumption of constant returns to scale in both legal sectors. Individuals maximize the expected utility and optimally choose bequests and occupations in period t given the threshold values h and 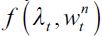 . To establish the existence of a SREE it is necessary to establish the existence of
. To establish the existence of a SREE it is necessary to establish the existence of 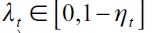 that satisfies (11), recognizing that the cutoff wealth level
that satisfies (11), recognizing that the cutoff wealth level 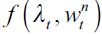 is a function of λt for given ηt from (9). Since by definition
is a function of λt for given ηt from (9). Since by definition 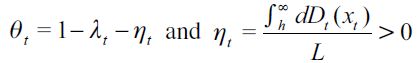 is given for any t it follows that an increase in λt results in a proportional decrease in θt one for one. Since the unskilled wage equilibrium satisfies
is given for any t it follows that an increase in λt results in a proportional decrease in θt one for one. Since the unskilled wage equilibrium satisfies 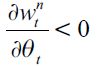 it must be the case that
it must be the case that 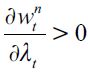 .
.
Consequently, define the following continuous function in λt
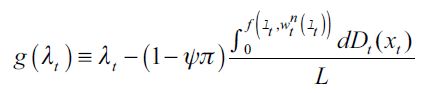
in support [0,1â ηt ]. Note that evaluating at zero yields
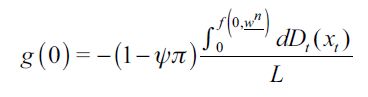
which is zero if 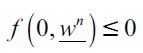 or equivalently if
or equivalently if 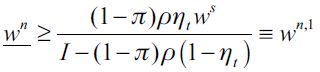 , where
, where 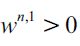 given that I ≥2 . Now
given that I ≥2 . Now 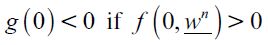 arises or equivalently
arises or equivalently 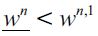 is satisfied. Furthermore under (7),
is satisfied. Furthermore under (7), 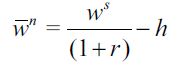 such that
such that
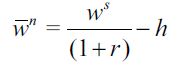
which holds since the fraction of skilled workers and delinquents that are not captured by law enforcement authorities cannot exceed one. The continuity of g(·) establishes that there exists a λt that satisfies
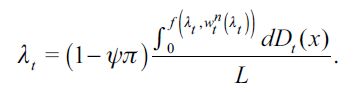
Moreover note that according to Leibniz rule19
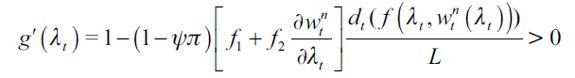
since 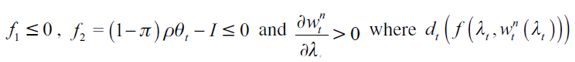 is the density function of Dt evaluated at
is the density function of Dt evaluated at 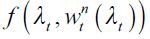 which is always positive. Hence, the SREE is unique for each t.
which is always positive. Hence, the SREE is unique for each t.
Theorem 2 If the economy described above satisfies 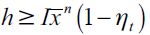 as well as assumptions (15), (7) for all
as well as assumptions (15), (7) for all 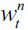 such that the initial wealth distribution D0 generates
such that the initial wealth distribution D0 generates 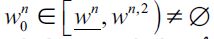 then there exists a unique LREE of the economy described above such that
then there exists a unique LREE of the economy described above such that 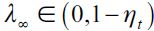
Proof. Consider a SREE and note that assumptions 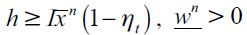 and
and 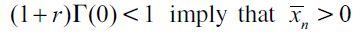 intersects the 45 degree line and is bounded away from infinity generating a poverty trap, since otherwise the bn function would not intersect the 45 degree line. Assumption (7) guarantees that
intersects the 45 degree line and is bounded away from infinity generating a poverty trap, since otherwise the bn function would not intersect the 45 degree line. Assumption (7) guarantees that 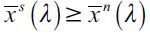 . Define the following function in the domain [0,1â ηt ]
. Define the following function in the domain [0,1â ηt ]
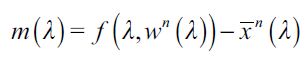
which is a continuous function of λ given that both 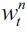 and
and 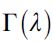 are continuous in λ. Note that
are continuous in λ. Note that 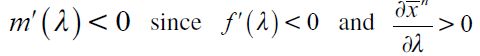 under assumption (15). Moreover,
under assumption (15). Moreover, 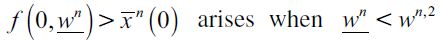 where
where 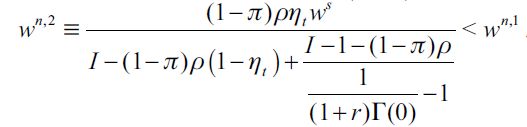 . Hence
. Hence 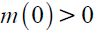 and
and 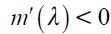 , which generates persistent delinquency, since
, which generates persistent delinquency, since  must involve a positive value such that
must involve a positive value such that 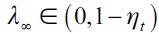 . On the other hand if,
. On the other hand if, 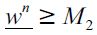 it follows that
it follows that 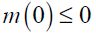 and the long run steady state is compatible with
and the long run steady state is compatible with 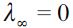 . We still need to check that bd
. We still need to check that bd 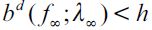 holds. Assumption
holds. Assumption 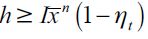 implies that
implies that 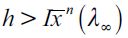 which can be rewritten as
which can be rewritten as
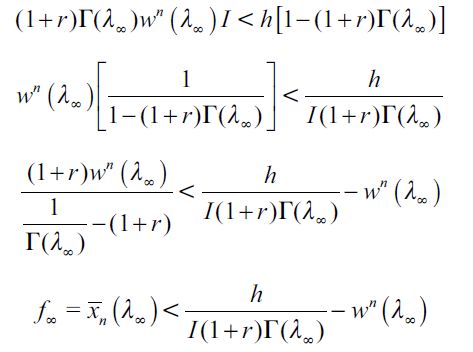
since in LREE with 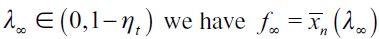 . Moreover
. Moreover
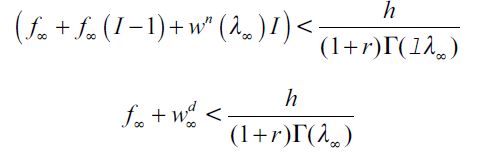
since from (2) 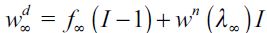 . Note that this last expression rearranged corresponds to
. Note that this last expression rearranged corresponds to 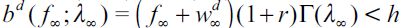 . Hence,
. Hence, 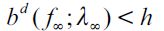 is satisfied.
is satisfied.
REFERENCES
[1] Accinelli, E., & Sanchez J. C. (2011). The evolutionary game of poverty traps. The Manchester School. Blackwell Publishing Ltda and The University of Manchester, 80(4), 381-400. [ Links ]
[2] Bowles, S. (2006). Institutional poverty traps. In S. Bowles, S. Durlauf & K. Hoff (Eds.), Poverty traps (pp. 116-138). Princeton University Press. [ Links ]
[3] Becker, G. (1968). Crime and punishment: An economic approach. Journal of Political Economy, 76(2), 169-217. [ Links ]
[4] Bourguignon, F. (1999). Crime as a social cost of poverty and inequality: A review focusing on developing countries. Revista Desarrollo y Sociedad, 44, 61-99. [ Links ]
[5] Cook, P., Ludwig J., & McCrary, J. (2011). Controlling crime: Strategies and tradeoffs. Chicago: University of Chicago Press. [ Links ]
[6] Di Tella, R., & Schardrodsky, E. (2004). Do police reduce crime? Estimates using the allocation of police forces after a terrorist attack. The American Economic Review, 94(1), 115-133. [ Links ]
[7] Donohue, J., & Wolfers, J. (2005). Uses and abuses of empirical evidence in the death penalty debate. Stanford Law Review, 58, 791-845. [ Links ]
[8] Drago, F., Galbiati, R., & Vertova, P. (2009). The deterrent effects of prison: Evidence from a natural experiment. Journal of Political Economy, 117, 257-280. [ Links ]
[9] Durlauf, S. (1996). A theory of persistent income inequality. Journal of Economic Growth, 1, 75-93. [ Links ]
[10] Durlauf, S. (2001). The memberships theory of poverty: The role of group affiliations in Determining socioeconomic outcomes. Mimeo, University of Wisconsin Madison, Department of Economics. [ Links ]
[11] Ehrlich, I. (1975). The deterrent effect of capital punishment: A question of life and death. American Economic Review, 65(3), 397-417. [ Links ]
[12] Ehrlich, I. (1973). Participation in illegitimate activities: A theoretical and empirical investigation. The Journal of Political Economy, 81(3), 521- 265. [ Links ]
[13] Eide, E. (1997). Economics of criminal behavior: Survey and bibliography (Working Paper in Law and Economics, 5). University of Oslo. [ Links ]
[14] Fajnzylber, P., Lederman, D., & Loayza, N. (2001). Crimen y victimización: una perspectiva económica. En Fajnzylber, P., Lederman, D., & Loayza, N. (eds.), Crimen y violencia en América Latina, México D. F. México: Banco Mundial y Alfaomega Grupo Editor. [ Links ]
[15] Fajnzylber, P., Lederman, D., & Loayza, N. (2002). Inequality and violent crime. Journal of Law and Economics, 45(1) 1-40. [ Links ]
[16] Fender, J. (1999). A general equilibrium modelo of crime and punishment. Journal of Economic Behavior and Organization, 39(4), 437-453. [ Links ]
[17] Freeman, R. (1996). Why do so many young american men commit crimes and what might we do about it? (Working Paper, 5451). National Bureau of Economic Research. [ Links ]
[18] Galor, O. (1996). Convergence? Inferences from theoretical models. The Economic Journal, 106(437), 1056-1069. [ Links ]
[19] Galor, O., & Zeira, J. (1993). Income distribution and macroeconomics. The Review of Economic Studies, 60(1), 35-52. [ Links ]
[20] Gilby, T. (1975). Theological texts: St. Thomas Aquinas's summa theologica (vol. 38). Oxford: Oxford University Press. [ Links ]
[21] Kelly, M. (2000). Inequality and crime. The Review of Economics and Statistics, 82(4), 530-539. [ Links ]
[22] Lochner, L., & Moretti, E. (2001). The effect of education on crime: Evidence from prison inmates, arrests, and Self-Reports (Working Paper, 8605). National Bureau of Economic Research. [ Links ]
[23] Lochner, L. (2010). Education, work and crime: A human capital approach (Working Paper, 10478). National Bureau of Economic Research, 2004. [ Links ]
[24] Lochner, L. (2010). Education policy and crime (Working Paper, 15894). National Bureau of Economic Research. [ Links ]
[25] Machin, S., & Meghir, C. (2004). Crime and economic incentives J. Human Resources Fall 2004, XXXIX(4), 958-979. [ Links ]
[26] Mehlum, H., Moene, K., & Torvik, R. (2003). Predator or prey? Parasitic enterprises in economic development. European Economic Review, 47, 79-98. [ Links ]
[27] Mehlum, H., Moene, K., & Torvik, R. (2006). Parasites. In S. Bowles, S. Durlauf & K. Hoff (Eds.), Poverty traps (pp. 79-94). New York, NY: Russell Sage Foundation. [ Links ]
[28] Merton, R. (1938). Social structure and anomie. American Sociological Review, 3, 672-682. [ Links ]
[29] Owens, E. (2009). More time, less crime? Estimating the incapacitative effect of sentence enhancements. Journal of Law and Economics, 52(3), 551-579. [ Links ]
[30] Polterovich, V. (2008). Institutional trap. In S. N. Durlauf & L. E. Blume (Eds.), The new Palgrave dictionary of economics. New York: Palgrave Macmillan. [ Links ]
[31] Sánchez, E. (2012). Imitation and evolutionary stability of poverty traps. Journal of Bioeconomics, 14(1), 1-20. [ Links ]
[32] Soares, R. (2004). Development, crime and punishment: Accounting for the international differences in crime rates. Journal of Development Economics, 73, 155-184. [ Links ]
[33] Soares, R., & Naritomi, J. (2010). Understanding high crime rates in Latin America: The role of social and policy factors. In R. Di Tella, S. Edwards & E. Schargrodsky (Eds.), The economics of crime: Lessons for & from Latin America (pp. 19-55). National Bureau of Economic Research. Chicago: The University of Chicago Press. [ Links ]
[34] Shaw, C., & McKay, H. (1942). Juvenile delinquency and urban areas. Chicago: University of Chicago Press. [ Links ]
[35] Tauchen, H., Witte, A. D. and Griesinger, H. (1994). Criminal Deterrence: Revisiting the Issue with a Birth Cohort, Review of Economics and Statistics, 76(3), 399-412. [ Links ]
[36] Witte, A., & Tauchen, H. (1994). Work and crime: An exploration using panel data (Working Paper, 4794). National Bureau of Economic Research. [ Links ]













