Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.33 no.63 Bogotá July/Dec. 2014
https://doi.org/10.15446/cuad.econ.v33n63.45336
http://dx.doi.org/10.15446/cuad.econ.v33n63.45336
Non cooperative Stackelberg network formation
Formación de redes de Stackelberg no cooperativas
Formation de réseaux de Stackelberg non coopératifs
Formação de redes de Stackelberg não cooperativas
Juan M.C. Larrosaa
a Professor, Departamento de Economía, Universidad Nacional del Sur (UNS) Researcher, Instituto de Investigaciones Económicas y Sociales del Sur (IIESS) Contact Address: San Juan y 12 de octubre, Planta Baja, Oficina 5, Bahía Blanca, Email: jlarrosa@criba.edu.ar.
Abstract
Non-cooperative network formation games in industrial organizations analyze how firms create links. We assume that links portray cost-reducing information and that access to this information is not reciprocal. We study the consequences in terms of profits if one firm can move first in establishing a link. A classic model of exogenous Stackelberg leadership is developed and first-mover advantage is observed.
Keywords: Non-cooperative games; network formation strategies; Stackelberg equilibrium, sequential decision.
JEL: C72, D43, L13, D85.
Resumen
Los juegos de formación de red en organización industrial analizan cómo se crean enlaces entre empresas. El modelo supone que los enlaces conllevan información que reduce costos de producción y el acceso a dicha información no es recíproco. Se estudia las consecuencias en los beneficios si una firma puede mover primero al establecer los enlaces. Un modelo clásico de liderazgo exógeno de Stackelberg es desarrollado y las ventajas de primer movedor son observadas.
Palabras clave: juego no cooperativo; estrategias de formación de red; equilibrio de Stackelberg, decisión secuencial.
JEL: C72, D43, L13, D85.
Résumé
Les jeux de création de réseaux en organisation industrielle analysent comment se créent des liens entre entreprises. Le modèle implique que les liens sont porteurs d'une information qui réduit les coûts de production et l'accès à cette information n'est pas réciproque. On étudie les conséquences dans les avantages si un groupe peut prendre l'initiative lors de l'établissement du lien. On développe un modèle classique de leadership exogène de Stackelberg et on observe les avantages de prendre les devants.
Mots-clés: Jeu non coopératif, stratégies de formation de réseau, équilibre de Stackelberg, décision séquentielle.
JEL: C72, D43, L13, D85.
Resumo
Os jogos de formação de rede em organização industrial analisam como são criados vínculos entre empresas. O modelo supõe que os vínculos contêm informação que reduz os custos de produção e o acesso à mencionada informação não é recíproco. São estudadas as consequências nos benefícios se uma firma puder se movimentar primeiro estabelecendo os vínculos. É desenvolvido um modelo clássico de liderança exógena de Stackelberg e são observadas as vantagens de ser o primeiro a se mexer.
Palavras-chave: Jogo não cooperativo, estratégias de formação de rede, equilíbrio de Stackelberg, decisão sequencial.
JEL: C72, D43, L13, D85.
Este artículo fue recibido el 11 de octubre de 2013, ajustado el 3 de febrero de 2014 y su publicación aprobada el 11 de marzo de 2014.
INTRODUCTION
Sequential decisions arise in many fields of the literature relating to industrial organization. One key model is the Stackelberg oligopoly. In this model, agents (firms) act sequentially. One example is when an agent extracts information from a set of potential competitors. It could gather information on better practices and, therefore, reduce production costs. Once the cost structure of the firm that moves first (leader) is determined, competitors (followers) decide how much to produce accordingly. Another example is when a provider offers interconnection services to a network of customers. The firm must anticipate customers' service demand (nodes in the network) for investing in network capacity. Once installed, customers determine how much demand there is for what proportion of the service. The provider behaves as a classic Stackelberg leader, while the group of firms follows, taking the constraints imposed by the leader as a given (Hoesel, 2008; Korilis, Lazar & Orda, 1997).
This contribution focuses on network formation in an oligopoly where onefirm creates links in the first place (leader) and, after observing these connections,the other firms (followers) decide their structure of connection as well.In many circumstances, cooperation seems to facilitate the sharing of non-trivial information among firms. For example, firms can build alliances for the development or acquisition of cost-reducing technologies. This situation has been modeled by Goyal and Joshi (2003). Their model studies models of the emergence of networks of collaboration among firms that compete in terms of quantities (Cournot) and prices (Bertrand). They model linking benefits as a bidirectional externality that helps cooperating firms to reduce production costs. This is the usual modeling option in the literature for mutual consent agreements where technical information and collaboration are shared. On the other hand, connections can also be modeled as a one-way externality shedding light on new features of this network formation game. For instance, Billand and Bravard (2004) use Goyal and Joshi's basic structure but allow only for a one-way externality flow. This way of modeling the externality flow is meaningful in the case of firms that access other firms' cost-reducing public or private information without requiring reciprocity. A question arises as to the efficiency and stability of the structure of connections for exploiting these externalities. Different optimal topologies emerge when initial investments inconnection infrastructure are compared. The main point of this work is therefore: Which network topology emerges as optimal? In the previous case, optimal connection structures were: 1) for the case of the lowest cost investment infrastructure, the complete (in Cournot competition) and the star (in Bertrand competition) networks; and, 2) for the case of a higher cost investment infrastructure, the empty network is also the optimal structure of connections whether we consider markets of quantity or price competition. Intermediate topologies also emerge in the case of the Cournot market (see Table 1).
Our contribution adds the influence of sequential decisions in the formation of the structure of connections and simultaneous competition under the one-way externality case. Suppose a market with n firms and that, exogenously given, one firm can move first by establishing links with other firms in the market and the n - 1 follower firms observe this and then choose their own connection structure. In the following stage, they will compete in terms of quantities or prices. We investigate what topology emerges from this setting in equilibrium.
It must be noted that another branch of academic literature criticizes the exogeneity in the selection of any firm as leader firm, and considers all-equal firms a priori. These contributions model leader firm selection as a previous stage of the game where firms can choose whether they were going to move first or second. Examples of endogenous models of Stackelberg competition are Amir and Grilo (1999) and Damme and Hurkens (1999).
The main outcomes of this contribution are as follows. First, in the Stackelberg equilibrium in a market with a single leader firm and the rest of the firms behaving as followers (single-leader-rest-followers market hereafter) with (simultaneous) quantity competition, the leader firm can obtain, in the worst case, similar benefits as any (average) follower firm depending on the number of links and the cost of investment in network infrastructure. Second, the Stackelberg equilibrium in a single- leader-rest-followers market with (simultaneous) price competition, only the leader firm obtains benefits. More specifically, depending on the value of the initial fixed investment cost, optimal topologies vary. If this cost is low enough, the optimum topology is the complete network (where the leader firm connects to every follower firm and each follower firm connects to each other follower firm and to the leader firm as well) in a market with quantity competition. In markets with price competition, the optimum topology for this level of investment is the leaderfirm-sponsored star network, i.e. a star topology of connections with the leader firm acting as the hub. If this cost is high enough, for both types of competition, the optimum topology is the empty network. Notwithstanding, for intermediate costs, quantity competition allows for optimum architectures that are neither the empty network nor the complete network, but an intermediate structure of connections between firms. These results are relatively similar to those found by Billand and Bravard (2004). However, we found that the leader firm usually performs at leastas well as any follower firm and has a wider range of possible optimal outcomes. Sequential decision making allows the first mover to obtain higher profits.
The work is organized as follows. Section 2 describes the model and provides definitions. Section 3 presents the results in the quantity competition market and price competition market. Section 4 ends the contribution with the conclusions.
FRAMEWORK AND MODEL
We follow Billand and Bravard's (2004) modeling structure. In this framework, links represent the (positive) externality benefit of information accessing (technical, technological, legal, marketing, management practices, and the like). This information allows firms who initiate and maintain the link to reduce production costs by, for instance, adopting more efficient management practices. Thus, we assume that information improves the production function by (linearly) reducing costs. When the externality flow is asymmetric (technically, by using directed graphs), firms that form links have access to linked firm information and link formation cannot be refused. This modeling approach assumes situations such as:
1) Accessing to firms' public information by
a) Surfing competitors' web sites for acknowledging their products, pricing policies, market prestige and the like, for benchmarking management policy.2) Accessing to firms' private information byb) Analyzing balance sheets of firms operating in the stock exchange to determine their economic and financial performance,
c) Consulting the Patent Register for competitors' new products,
d) Reading business magazines that report competitors' best practices.
a) Accessing other firms' private information through illegal means; for example, industrial espionage, among others.
We define concepts to be applied later on. Let 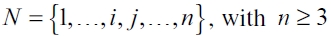 , be the set of ex ante identical firms. For any
, be the set of ex ante identical firms. For any 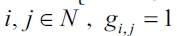 means that a firm i has formed a direct link with firm j, gi, j = 0 in any other case. Thus, we denote
means that a firm i has formed a direct link with firm j, gi, j = 0 in any other case. Thus, we denote 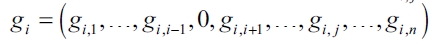 to firm i's link vector.
to firm i's link vector.
A network 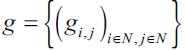 is a formal description of the directed links that exist among firms. Let G be the set of directed networks without self-loops (a firm cannot form a link with itself).
is a formal description of the directed links that exist among firms. Let G be the set of directed networks without self-loops (a firm cannot form a link with itself).
We assume that a link gi, j= 1 allows firm i to access to j's information but not vice versa. We focus on one-way resource flows. Let 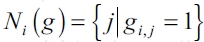 be the set of firms j such that i obtains externalities from j. Let ni (g) be the cardinal of Ni(g). We frequently refer to all other firms distinct from i as i's opponents and will be noted as -i. We note
be the set of firms j such that i obtains externalities from j. Let ni (g) be the cardinal of Ni(g). We frequently refer to all other firms distinct from i as i's opponents and will be noted as -i. We note 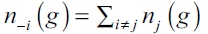 as the number of links in the network g excluding those links generated by firm i. n-i(g) can be interpreted as the number of externalities that benefit all other firms except firm i.
as the number of links in the network g excluding those links generated by firm i. n-i(g) can be interpreted as the number of externalities that benefit all other firms except firm i.
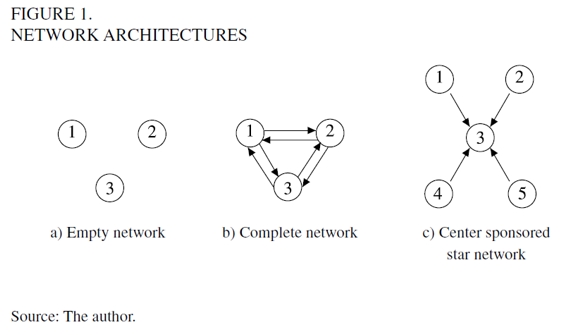
We define the main network topologies that will be used extensively through out our work. A network g is complete if for every pair of firms i and j, there exists a link from i to j. A complete network is denoted as gc. A network g is a center sponsored star if and only if there is a firm i such that i has formed one link with every firm j, and every j ≠ i has formed no link at all (Figure 1). Center sponsored star network is denoted as gs. A network g is empty if there is no firm that has formed any link. This network is denoted as ge.
Linking and Cost Reduction
We assume that establishing a link requires a fixed investment cost given by δ > 0 , and that firms are initially symmetric with identical cost functions. We consider that establishing a link is a way of reducing production costs, and, more specifically, that firm's marginal and average variable cost of a generic firm i ∈N has the same functional form:
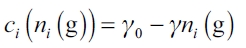 | [1] |
where 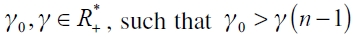 . A network g induces an average variable cost vector given by the following function:
. A network g induces an average variable cost vector given by the following function: 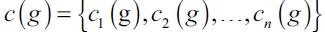 .
.
Equilibrium Networks
A network g ∈ G is said to be an equilibrium if, leaving the set of links formed by other firms as constant, any firm that has a connection to any other firm in g ∈ G has an incentive to keep that link. Moreover, any firm that is not connected to another firm in g ∈ G has no incentive to form a link to any other firm. Let g' be a network where i is the only firm that has the same links in g.
Let 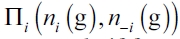 , be the net benefits of firm i ∈N . A network g is an equilibrium network, if for every i, we have that:
, be the net benefits of firm i ∈N . A network g is an equilibrium network, if for every i, we have that:
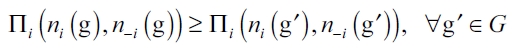 | [2] |
STACKELBERG NETWORK GAME
Competition in link formation in a Stackelberg game is represented by a threestage game. In the first stage, only the leader firm moves by choosing who to connect with. In the second stage, follower firms observe the leader firm's choice and make their own decisions in terms of connection. Finally, in the third stage, firms simultaneously compete in quantities or prices (Figure 2). As the leader firm moves first, it will envisage follower firms' behavior and maximize benefits accordingly by using backward-induction.
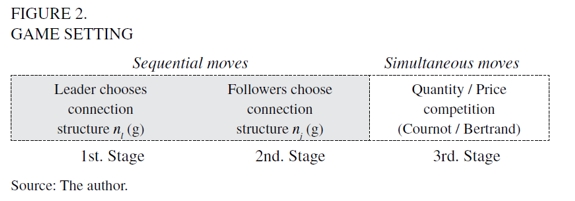
Single-leader-rest-followers is a market where two types of firms exist: the leader firm i with i ≠ j that for convenience we denote as i [1] and there are (n - 1) firms labeled with the subindex j such that j ≠ i and j∈ [2,....,n] that we will refer to as the set of follower firms. As mentioned above, two kinds of market competition will be modeled: quantity and price competition. The next section begins with quantity competition definitions and modeling.
Sequential Connection Structure with Simultaneous Quantity Competition
Let qi be the quantity produced by firm i and p the market price. We model a market with homogeneous products and quantity competition. We assume a linear inverse demand function:
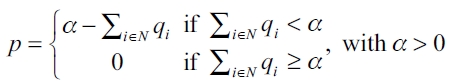 | [3] |
We also assume that the nonnegative production condition (NPC hereafter) 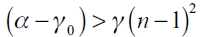 is verified. Given these definitions we postulate the following Lemma:
is verified. Given these definitions we postulate the following Lemma:
Lemma 1. Given any network g ∈ G assume (1), (3), and NPC. In a singleleader- rest-followers market with quantity competition, the leader firm's equilibrium quantity 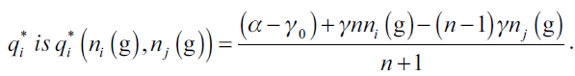 If all the above is verified, the representative follower firm's equilibrium quantity
If all the above is verified, the representative follower firm's equilibrium quantity 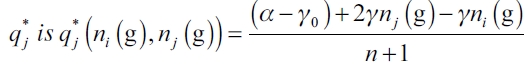 .
.
Proof: See Appendix.
Both reaction functions are increasing in the number of own links and decreasing in the creation of links made by the other firms. The isolation output is always positive as we assume that 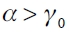 .
.
The benefit function in quantity competition at equilibrium is defined by:
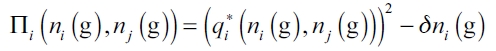 | [4] |
Following this, we postulate:
Proposition 1. Assume (1), (3), and NPC. Also assume a Stackelberg setting with single-leader-rest-followers market with quantity competition. Then, in an equilibrium network g* the leader firm i makes 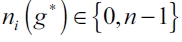 connections. More precisely:
connections. More precisely:
1) if 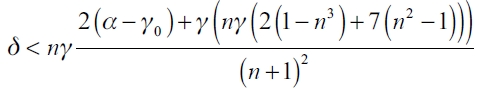 then the complete network gc is the only equilibrium network for the leader firm;
then the complete network gc is the only equilibrium network for the leader firm;
2) if 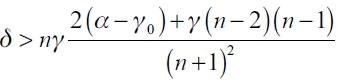 , then the empty network ge is the only equilibrium network the leader firm;
, then the empty network ge is the only equilibrium network the leader firm;
3) if 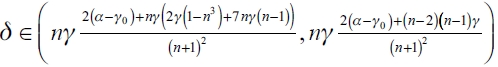 then in an equilibrium network g*, the leader firm i connects so that
then in an equilibrium network g*, the leader firm i connects so that 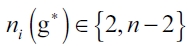 .
.
Proof: See Appendix.
For the case of a follower firm, which works with the analogous benefit function 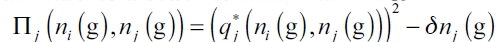 , the following proposition applies:
, the following proposition applies:
Proposition 2. Assume (1), (3), and NPC. Also assume a Stackelberg setting with single-leader-rest-followers market with quantity competition. Then, in an equilibrium network g* each of all follower firms j makes 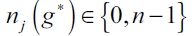 connections. More precisely:
connections. More precisely:
if 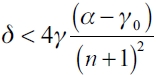 , then the complete network gc is the only equilibrium network for each follower firm;
, then the complete network gc is the only equilibrium network for each follower firm;
if 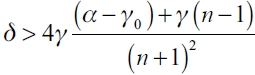 , then the empty network ge is the only equilibrium network for each follower firm;
, then the empty network ge is the only equilibrium network for each follower firm;
if 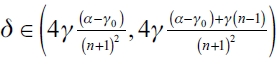 , then in an equilibrium network g* there are x firms
, then in an equilibrium network g* there are x firms 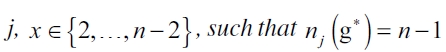 and n - x firms j such that
and n - x firms j such that 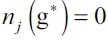 .
.
Proof: See Appendix.1
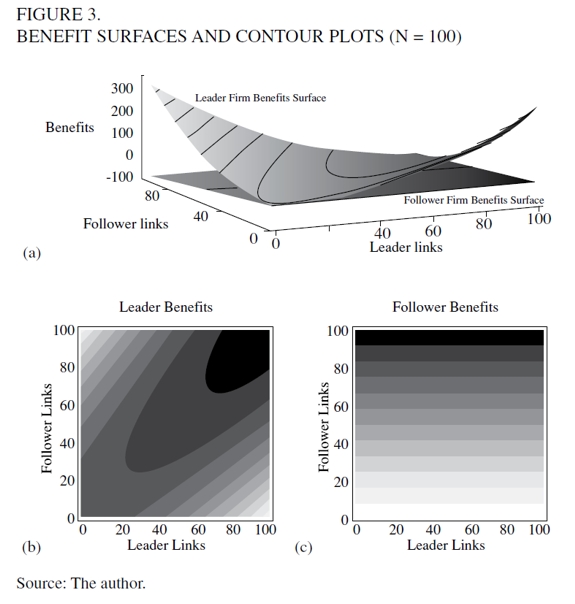
Example 1. We reproduce Example 1 from Billard and Bravard (2004, p. 598) so we define α = 200 , γ0 = 50 , γ = 0.2 , n = 100 and δ=1. Figure 3.a represents benefit surface for a leader and follower firm given these initial values and increasing link quantities for both, from 0 to 100. The leader firm shows exponential benefits when its number of links does not coincide with those of the followers as shown in Figure 3.a. In this example, the leader firm obtains, at least, the same benefits as any follower. If both agree on the number of links to be established, both will obtain the same amount of benefits. Disagreement in the numbers of established links reports higher benefits to leader firm.
However, an interesting aspect arises. We can present bi-dimensional information of Figure 3.a by plotting the functional form contours given the values in Example 1. This is done in Figures 3.b and 3.c where Figure 3.a's contour plot is presented. The axes represent the number of formed links by leader (horizontal) and follower (vertical) firms and the lighter gray scale indicates higher benefits surface, whereas the darker gray scale represents a lower benefits surface. The model assumes that connection infrastructure investment cost is exogenous. So, as the leader firm moves first, it will choose the number of connections that would maximize its benefits. Given the data in Example 1, this is observed in ni (g) = 99 (Figure 3.b). In the second stage of the game, follower firms will observe this choice and will choose their optimal connections' strategy. This is observed in Figure 3.c in the lighter color choice, that is nj (g) = 0. In this way, these connections' strategies sustain a leader firm sponsored star network.
Another interesting point emerges when we sort threshold cost values for optimum connections infrastructure investment for both players. So, let 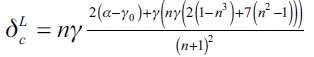 be the value of δ to which the leader firm (L) decides to establish links to all other firms (gc) if the current investment cost is lower, and let
be the value of δ to which the leader firm (L) decides to establish links to all other firms (gc) if the current investment cost is lower, and let 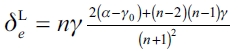 be the threshold value for determining whether the leader firm decides to adopt the empty network ge. Also, let
be the threshold value for determining whether the leader firm decides to adopt the empty network ge. Also, let 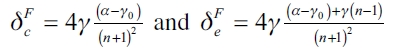 be the analogous δ threshold values for the follower firm (F). Next postulate:
be the analogous δ threshold values for the follower firm (F). Next postulate:
Corollary 1. Given the above definitions, the d threshold values in a quantity competition Stackelberg market are sorted, form highest to lowest, in the following way: 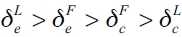 .
.
Proof: Trivial.
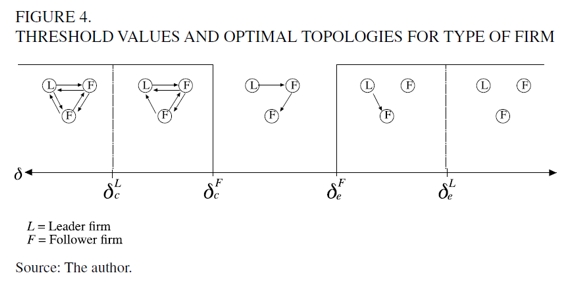
The interval of sorted δ threshold values shows that the leader firm critical values are significantly separated. The same range of critical values for follower firm strategy choice is narrower. Figure 4 represents a network with two follower firms and one leader firm over the range of δ threshold values. From left to right, we begin from the lowest δ value where the best response for the leader and the follower firms coincides, which means that gc (complete network) becomes optimal. However, just as the threshold value surpasses 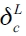 , the leader firm has no incentive to play gc and stops connecting to all follower firms. However, on the interval
, the leader firm has no incentive to play gc and stops connecting to all follower firms. However, on the interval 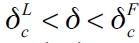 ,follower firms play the complete network as best response. Only on the interval
,follower firms play the complete network as best response. Only on the interval 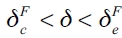 neither the leader nor the follower firms have incentives to play full connections, so connections exist but they are neither complete nor empty. Once
neither the leader nor the follower firms have incentives to play full connections, so connections exist but they are neither complete nor empty. Once 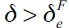 , follower firms will find it optimum to stay disconnected, while the leaderfirm still finds it best to remain connected but not making full connections. Finally, when
, follower firms will find it optimum to stay disconnected, while the leaderfirm still finds it best to remain connected but not making full connections. Finally, when 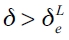 , the empty network (ge) topology is the best decision for both.
, the empty network (ge) topology is the best decision for both.
 >
>
The leader firm requires a much higher investment cost for choosing isolation as the optimal response and, for (1), isolation won't reduce production costs. Simply put, more links imply higher profits through cost reductions. So, it is more likely that the leader firm will play any strategy of connections compared to an average follower firm. Even in the worst case, when investment cost is highest, the leader firm generates as much profit as any follower firm (both play empty network.) The model as presented predicts that it is possible that diverse configurations of leaderfirm- sponsored star networks could emerge as the current optimal response, i.e., the leader firm will most probably establish links with the followers.
Sequential Connection Structure with Simultaneous Price Competition
New definitions are required. Let D(p) = a - p be the market demand function. For price competition, the case demand faced by firms is:
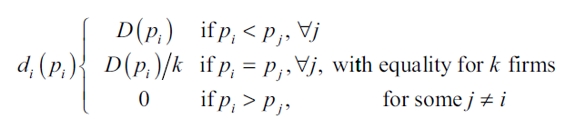 | [5] |
In price competition, the total net benefit function for firm i is given by:
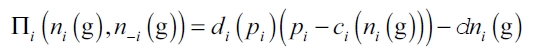 | [6] |
The game setting structure remains similar in the first two sequential decisions stages. However, in the third stage, competition focuses on prices (Figure 2). Following, we analyze what the optimum price is and what topology sustains it.
The leader firm would definitely expect follower firms to play Bertrand price in the second stage, so the leader firm should anticipate this move and play accordingly.
We assume that the demand faced by firm i if it fixes price pi is given by (5). Firm i's total net benefit function is determined by (6). The network equilibrium in a market with price competition competing à la Stackelberg is given by the following lemma:
Lemma 2. Assume a single-leader-rest-followers Stackelberg market. Assume also that (1), (5), (6) and the NPC are verified. In a price competition market, in equilibrium, there is only one firm establishing connections with all other firms and that firm is the leader firm.
Proof: See Appendix. In other words, in the first stage, the leader firm sets a price based on other firms' connections strategy profiles. As cost function decreases the number of links, prices quickly tend to the fixed cost. Then, the leader firm anticipates that follower firms will play Bertrand equilibrium price so it cuts the price by the minimum feasible amount of price reduction and follower firms will be out of the connection market in the second stage.
Once it is proven that by moving first, the leader firm obtains an advantage, all that has to be determined are the optimal market topologies. For that to be accomplished, we postulate the following proposition:
Proposition 3. Assume that equations (1), (5), (6) and the NCP verify. Assume that there is price competition in a Stackelberg market. Then the only firm which establishes links is the leader firm and for that firm it is verified that:
if 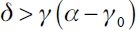 , the empty network, ge, is the only equilibrium network;
, the empty network, ge, is the only equilibrium network;
if 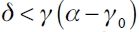 , the leader-firm sponsored star network, gs, is the only equilibrium network.
, the leader-firm sponsored star network, gs, is the only equilibrium network.
Proof: See Appendix II.
Paradoxically, there are few examples of Stackelberg price competition models in the economic literature. A good exception is Dastidar (2004) who finds that in a sequential price competition in duopoly, the leader firm gets a higher market share at a lower price and the follower firm gets a smaller market share but a higher price. In equilibrium, both earn equal profits. Neither the leader nor the follower firms have any advantage under this setting. In our case, in contrast, the leader firm gets it all. As pointed out in Goyal and Joshi (2003), in price competition markets, competition is so tight that the probability of connections among firms becomes really small.
CONCLUSIONS
This contribution extends previous literature on network formation in oligopolies. This case is another example of first mover advantage (Gal-Or, 1985) where firms look for resource allocation in economic intelligence investment. Early access to competitors' information might be associated with higher benefits. Depending on the cost structure of the intelligence sector, moving first (or investing higher) gives early movers better chances of obtaining higher benefits. Investing more in economic intelligence could imply copying competitors' best practices that will translate into the adoption of lower cost production techniques.
The leader firm enjoys a wider range of positive benefits when there is quantitycompetition. Follower firms could also enjoy nonnegative benefits but critical investment cost values in intelligence infrastructure are narrower. In the case of price competition, results are analogous to former contributions. Again, equilibrium architectures are sensitive to the way information is produced or accessed.
One path of future research relates to the exogenous parameters and other assumptions used in this first approach. We have assumed that role selection is exogenous. The leader firm is arbitrarily selected among a priori symmetric firms. No process of endogenous role selection is analyzed and this could enrich the analysis. We also assume that information has no decay or depreciation. A dynamical hierarchical analysis of wiring and rewiring links with changing value of information could also be considered a promising field of analysis.
APPENDIX
Proof of Lemma 1: This is a Stackelberg model with quantity competition. In the threestage leader-follower game, the leader firm chooses, first, its connection structure that determines quantities to be produced and, after observing the leader firm's connection structure, the follower firms establish, in a second stage, their own connection structure. In the third stage, firms compete in quantities. The game is solved by backward induction.
An (inverse) demand function is assumed 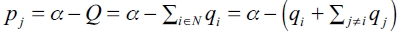 (where i refers to the leader firm and j, to the rest of the firms) that is twice differentiable, continuous and concave and a cost function that is twice differentiable, continuous and convex. In the first stage, the leader firm i chooses a quantity
(where i refers to the leader firm and j, to the rest of the firms) that is twice differentiable, continuous and concave and a cost function that is twice differentiable, continuous and convex. In the first stage, the leader firm i chooses a quantity 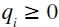 . In the second stage, given qi, firms j choose their optimal quantity qj. By deriving First Order Condition (FOC) (and Second Order Condition, SOC) to check whether it is a maximum) for the follower firm profit function
. In the second stage, given qi, firms j choose their optimal quantity qj. By deriving First Order Condition (FOC) (and Second Order Condition, SOC) to check whether it is a maximum) for the follower firm profit function 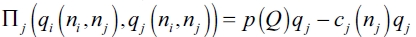 is derived the reaction function of the follower firm to any leader firm strategy.
is derived the reaction function of the follower firm to any leader firm strategy.
Then, the same FOC and SOC is derived for the leader firm but the reaction function of thefollowers is introduced into the optimum. In this way, the reaction function of the leader firm is obtained:
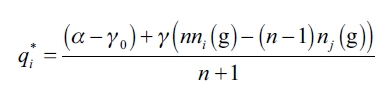 | [A.1] |
And then the follower reaction function is updated:
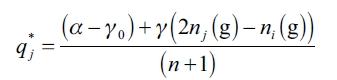 | [A.2] |
Outcomes (A.1) and (A.2) represents a subgame perfect equilibrium.
Proof of Proposition 1: Demonstration is in three parts. First, we show that in an equilibrium network g*, for the leader firm i, we have that 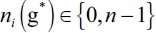 .
.
1) Let g* be an equilibrium network where at least the leader firm i is such that 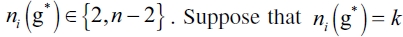 . We show that if i has no incentive to sever a link, then it has an incentive in forming a link (and inversely). We know that in an equilibrium network, a firm never has an incentive for severing a link. So we have that:
. We show that if i has no incentive to sever a link, then it has an incentive in forming a link (and inversely). We know that in an equilibrium network, a firm never has an incentive for severing a link. So we have that: 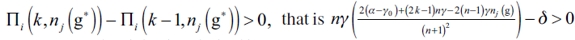 , and then
, and then 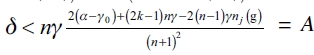 . In the same manner, in an equilibrium network, a firm never has incentive to form new links. That is to say that,
. In the same manner, in an equilibrium network, a firm never has incentive to form new links. That is to say that, 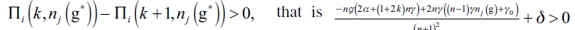 and then
and then 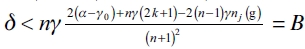 . This way, we must have that
. This way, we must have that 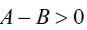 . That never verifies given
. That never verifies given 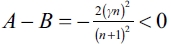 . Thus, if a leader firm i has formed k links such that
. Thus, if a leader firm i has formed k links such that 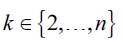 then it is never in equilibrium. In equilibrium, a leader firm forms none or n - 1 links with its followers.
then it is never in equilibrium. In equilibrium, a leader firm forms none or n - 1 links with its followers.
2) This is a two-part demonstration. In the first part, we are going to show that in equilibrium and once a firm has formed a complete network, it has no incentives in severing links. In 2.a we will show that if 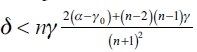 then gc is an equilibrium network and in 2.b we are going to show that there's no other network that could be an equilibrium network.
then gc is an equilibrium network and in 2.b we are going to show that there's no other network that could be an equilibrium network.
a) A leader firm has no incentives in severing link under complete network gc configuration. Then we have to prove that:in fact, we arrive at
which verifies that
. If this inequality verifies for k = n -1 , then it verifies for all k. So we have that
. This result will be necessary next.
b) Following, we show that a network g ≠ gc is not an equilibrium network. In (1), we proved that in equilibrium a leader firm forms links with all or none of the follower firms. To confirm this outcome, we are going to prove whether there is a chance that a leader firm could establish connections with every firm except one or maybe with a cluster of firms and this would be an equilibrium outcome. We establish that a contradiction by supposing that there exists an equilibrium network g* such that the leader firm establish no contacts. As it is an equilibrium network it should be check that: 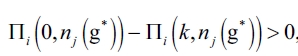 , or what is the same
, or what is the same 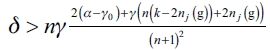 . Then, there is a configuration nj(g*) such that a leader firm i has no incentives for forming any links with the follower firms whatever their connection structure. So, we could have that:
. Then, there is a configuration nj(g*) such that a leader firm i has no incentives for forming any links with the follower firms whatever their connection structure. So, we could have that: 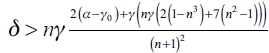 , that is a contradiction with (2.a).
, that is a contradiction with (2.a).
3) Finally, we show that network ge is an equilibrium network for the leader firm if 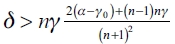 . We prove first that if ge is an equilibrium then, in the second part, there's no other equilibrium network.
. We prove first that if ge is an equilibrium then, in the second part, there's no other equilibrium network.
a) First, we establish that any firm has incentive to form links in ge. Then we have that: 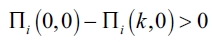 , from which we obtain that
, from which we obtain that 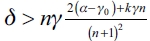 . If this result verifies for k = n - 1 then it is verified for all k. We obtain that
. If this result verifies for k = n - 1 then it is verified for all k. We obtain that 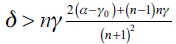 .
.
b) Now we demonstrate that there's no other equilibrium than the empty network ge when it emerges as an optimum topology. We have proved in the first part that a network g where there is a leader firm i such that 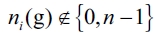 cannot be an equilibrium network. Then, we must prove that a network g, where there is at least one firm i such that
cannot be an equilibrium network. Then, we must prove that a network g, where there is at least one firm i such that 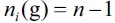 is not an equilibrium network. For establishing a contradiction, let suppose that an equilibrium network, g*, where there is at least one firm i such that
is not an equilibrium network. For establishing a contradiction, let suppose that an equilibrium network, g*, where there is at least one firm i such that 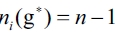 . We have that
. We have that 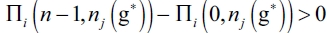 , which verifies that
, which verifies that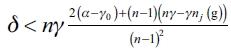 so in this particular case should also verify:
so in this particular case should also verify: 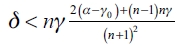 . Contradiction.
. Contradiction.
Proof of Proposition 2: This proof is analogous to what is proven by Proposition 1. Again, we divide it into three parts. First, we show that in an equilibrium network g*, for the follower firm j, we have that 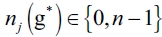 .
.
1) Let g* be an equilibrium network where there is at least one firm j such that. We suppose that
. We will show that if j has no incentive to sever a link, then it is interested in forming a link (and conversely). We know that in an equilibrium network a firm never has incentives to sever a link. Then we have that:
, and this is always accomplished if
. Again, in an equilibrium network, a follower firm never has incentives to form new links. That is to say,
, which is right if the following inequality is verified:
. This way, we must have that
. But this is not verified given that
. Then, a firm j that has formed k links such that
is never in equilibrium. In equilibrium, a follower firm initiates zero or n - 1 links with all other market firms.
2) We are going to show again, in two parts, that under certain cases the complete network is an equilibrium network and if this topology is an equilibrium network then there's no other equilibrium architecture.
a) A follower firm has no incentives in severing link in a complete network configuration, gc. We must prove that: 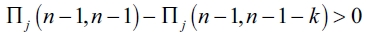 . That is verified always that
. That is verified always that 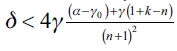 . If this inequality is verified for a follower firm, then k = n - 1 so we obtain
. If this inequality is verified for a follower firm, then k = n - 1 so we obtain 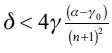 . This result will be necessary later.
. This result will be necessary later.
b) Now, we show that a network g≠gc cannot be an equilibrium network. In (1) it has been proved that a follower firm in equilibrium establishes links with all the follower firms or it does not establish any links at all. To confirm this result we are going to prove that if there's a chance that a follower firm could initiate a link with all but one or a group of the rest of follower firms or the leader firm less than the total number of firms. We establish a contradiction by supposing that there's an equilibrium network g* such that a follower firm does not establish connections. Given that it is an equilibrium network, it should be verified that: 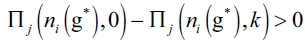 , that is,
, that is, 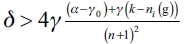 . Then, there's a configuration nj (g*) such that a follower firm i has no incentives to form any links with any other firm no matters the number of the links. So, we could have that
. Then, there's a configuration nj (g*) such that a follower firm i has no incentives to form any links with any other firm no matters the number of the links. So, we could have that 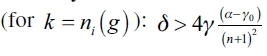 , which is a contradiction to (2.a).
, which is a contradiction to (2.a).
3) Finally, we show that the empty network ge is an equilibrium network for a follower firm if 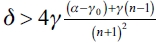 . First, we prove that ge is an equilibrium network and if that happens, then there's no other configuration that could be an equilibrium.
. First, we prove that ge is an equilibrium network and if that happens, then there's no other configuration that could be an equilibrium.
a) First, we establish that any firm has an incentive to form links in ge. We have that: 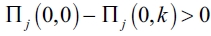 , where we obtain that
, where we obtain that 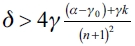 . If this result is verified for k = n - 1 then it is verified for all k. We then get
. If this result is verified for k = n - 1 then it is verified for all k. We then get 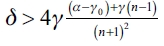 The demonstration follows.
The demonstration follows.
b) Now we have to proof that there's no other equilibrium different from the empty network ge when it is the optimal topology. We have proved in the first part that in a network g where there exists a firm j such that 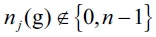 cannot be an equilibrium network. Then, we must prove that in a network g, where there exists at least one firm j such that
cannot be an equilibrium network. Then, we must prove that in a network g, where there exists at least one firm j such that 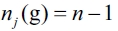 is not an equilibrium network. For establishing a contradiction, assume an equilibrium network, g*, where there is at least one firm j such that
is not an equilibrium network. For establishing a contradiction, assume an equilibrium network, g*, where there is at least one firm j such that 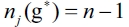 . We have that
. We have that 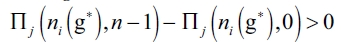 , which verifies that
, which verifies that 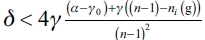 . Particularly, it is verified also for:
. Particularly, it is verified also for: 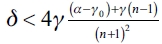 . Contradiction.
. Contradiction.
Proof of Lemma 2.
A. Backward induction first stage
We begin by presenting the following lemma:
Lemma AII.1. (Billand & Bravard, 2004, p. 601) In equilibrium, there is at least one follower firm that forms links
Proof of Lemma AII.1: We establish a contradiction by assuming that there exists an equilibrium network where two firms j1 and j2 have formed links such that 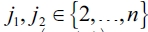 . Let us suppose that
. Let us suppose that 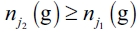 verifies. Given now that
verifies. Given now that 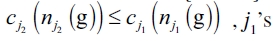 brute benefit is null given that in equilibrium
brute benefit is null given that in equilibrium 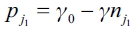 . Because of that, we obtain that the main component of the net benefit is δnj1:
. Because of that, we obtain that the main component of the net benefit is δnj1:
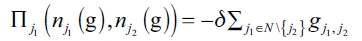
Given that firm j2 has a variable cost 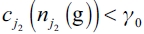 , firm j1 should not produce anything if it has not formed any link. Therefore, we have
, firm j1 should not produce anything if it has not formed any link. Therefore, we have
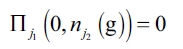
It follows that
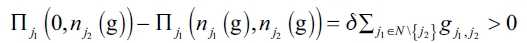
given that we have assumed that 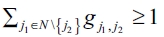 , . This is a contradiction. Specifically for our own setting, in equilibrium we have that in the second stage of the Stackelberg game only one firm will establish links, while the rest of the firms will not establish any links at all.
, . This is a contradiction. Specifically for our own setting, in equilibrium we have that in the second stage of the Stackelberg game only one firm will establish links, while the rest of the firms will not establish any links at all.
Let ε be the lowest feasible monetary denomination, which we suppose that converges to zero. Then, we postulate the price this firm would set in the market.
Lemma AII.2. (Billand & Bravard, 2004, p. 601) Suppose there is one and only one firm in the market (say firm l) that forms links. Then the Bertrand equilibrium price is given by 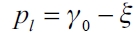 .
.
For our case, we suppose that l is such that 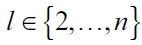 , i.e., it is part of the set of follower firms that the leader firm must anticipate. Given that follower firm l will face a demand function such that:
, i.e., it is part of the set of follower firms that the leader firm must anticipate. Given that follower firm l will face a demand function such that:
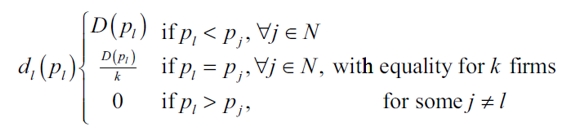 |
which means that if the follower firm sets a lower price than any other firm j, it will supply all the demand alone. If it sets an equal price to any other firm j, they will equally share the demand and if it sets a higher price than j's then it will not supply anything. Thus, if firm l is the only one that has formed a link, then it has the lowest marginal cost and it sets the price in 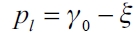 so as to displace the rest of the firms in the market. So, there will be n - 3 firms that will not establish any link while one of them, conventionally denoted as firm l will form links with all the others follower firms and the leader firm by setting a price a bit lower thank the fixed cost γ0 .
so as to displace the rest of the firms in the market. So, there will be n - 3 firms that will not establish any link while one of them, conventionally denoted as firm l will form links with all the others follower firms and the leader firm by setting a price a bit lower thank the fixed cost γ0 .
How does the leader firm react? Given that l has set a price 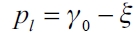 , i will play again and set an even lower price given that there would only be one firm establishing links. Using the same line of reasoning as Lemma AII.1 and AII.2, there would only be one firm forming links and that firm will set the lowest price. Facing the same demand function:
, i will play again and set an even lower price given that there would only be one firm establishing links. Using the same line of reasoning as Lemma AII.1 and AII.2, there would only be one firm forming links and that firm will set the lowest price. Facing the same demand function:
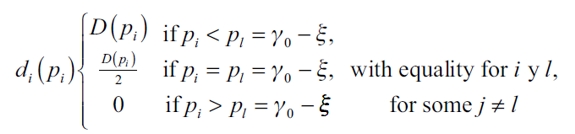 |
the leader firm has to decide whether it will match firm l's price or whether it will cut the price. If it matches pl given the model's demand rationing rule, they will share demand with l. If it cuts the price, they will earn nonnegative profits. The same would happen if the leader firm cut the price by another lowest feasible monetary unit, ξ, being the leader firm's new price set in 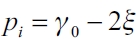 . Let see what decision brings more benefits to the leader firm:
. Let see what decision brings more benefits to the leader firm:
 |
Given that ξ→0, then we have that 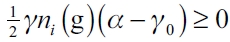 , which verifies for all feasible values of the game. So, the leader firm will set
, which verifies for all feasible values of the game. So, the leader firm will set 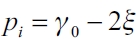 . Under some specific functional forms of D(pi), price elasticity could play a different role in this interpretation.
. Under some specific functional forms of D(pi), price elasticity could play a different role in this interpretation.
B. Backward Induction Second Stage
In the second stage, follower firms will watch the price set by the leader firm and they will set their own optimal price. But they will find that dj (pj) = 0 given that 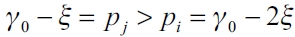 then for avoiding losses associated with
then for avoiding losses associated with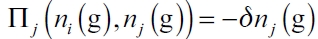 they will choose nj(g) = 0 .
they will choose nj(g) = 0 .
Proof of Proposition 3. The leader firm maximization problem will be determined by
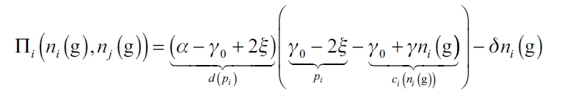 |
which is summarized in
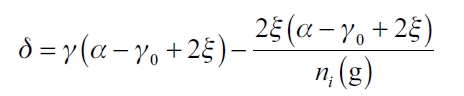 |
and given that ξ→0 , we have that
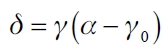 |
There are two distinguished cases:
If 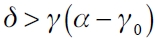 the benefit function
the benefit function 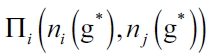 would be decreasing in ni (g* ), which implies that the leader firm will not have incentives to form links. The leader firm will remain isolated and optimal market topology will be the empty network.
would be decreasing in ni (g* ), which implies that the leader firm will not have incentives to form links. The leader firm will remain isolated and optimal market topology will be the empty network.
If 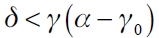 then the benefit function
then the benefit function 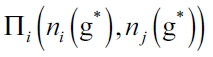 increases in ni (g*) which implies that the leader firm would have higher incentives to form links. The leader firm will connect to all of the follower firms and optimal market topology will be a leader-firm-sponsored star network.
increases in ni (g*) which implies that the leader firm would have higher incentives to form links. The leader firm will connect to all of the follower firms and optimal market topology will be a leader-firm-sponsored star network.
FOOTNOTES
1 Notice that condition 1 of Proposition 1 is nonnegative for a narrower range of parameter values.
REFERENCES
[1] Amir, R., & Grilo, I. (1999). Stackelberg versus Cournot equilibrium. Games and Economic Behavior, 26, 1-21. [ Links ]
[2] Billand, P., & Bravard, C. (2004). Non cooperative networks in oligopolies. International Journal of Industrial Organization, 22(5), 593-609. Doi http://dx.doi.org/10.1016/j.ijindorg.2004.01.004. [ Links ]
[3] Damme, E. van & Hurkens, S. (1999). Endogenous Stackelberg leadership. Games and Economic Behavior, 28, 105-129. Doi http://dx.doi.org/10.1006/game.1998.0687. [ Links ]
[4] Dastidar, K. G. (2004). On Stackelberg games in a homogeneous product market. European Economic Review, 48, 549-562. Doi http://dx.doi.org/10.1016/S0014-2921(03)00035-7. [ Links ]
[5] Gal-Or, E. (1985). First mover and second mover advantage. International Economic Review, 26, 649-653. [ Links ]
[6] Goyal, S., & Joshi, S. (2003). Networks of collaboration in oligopoly. Games and Economic Behavior, 43(1), 57-85. Doi http://dx.doi.org/10.1016/S0899-8256(02)00562-6. [ Links ]
[7] Hoesel, S. van (2008). An overview of Stackelberg pricing in networks. European Journal of Operational Research, 189(3), 1393-1402. Doi http://dx.doi.org/10.1016/j.ejor.2006.08.064. [ Links ]
[8] Korilis, Y. A., Lazar, A. A., & Orda, A. (1997). Achieving network optima using Stackelberg routing strategies. IEEE/ACM Transactions on Networking, 5(1), 161-173. Doi 10.1109/90.554730. [ Links ]













