Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.34 no.65 Bogotá July/Dec. 2015
https://doi.org/10.15446/cuad.econ.v34n65.43481
http://dx.doi.org/10.15446/cuad.econ.v34n65.43481
Social preferences are not enough: Accounting for anomalous behavior in a complex mixed-motive game.
Las preferencias sociales no alcanzan: dando cuenta de elecciones anómalas en un juego complejo de motivos mixtos.
Les préférences sociales ne suffisent pas : relation d'élections anomales dans un jeu complexe de motifs mixtes.
As preferências sociais não alcançam: Dando conta de eleições anómalas em um jogo complexo de motivos mistos.
Rodrigo Moro a
Esteban Freidin b
Fernando Tohmé c
a Investigador del Instituto de Investigaciones Económicas y Sociales del Sur, perteneciente al Centro Científico Tecnológico Bahía Blanca, Conicet. Bahía Blanca, Argentina. E-mail: rmoro@uns.edu.ar.
b Investigador del Instituto de Investigaciones Económicas y Sociales del Sur, perteneciente al Centro Científico Tecnológico Bahía Blanca, Conicet. Bahía Blanca, Argentina. E-mail: efreidin@criba.edu.ar.
c Investigador del Instituto de Investigaciones Económicas y Sociales del Sur, perteneciente al Centro Científico Tecnológico Bahía Blanca, Conicet. Bahía Blanca, Argentina. E-mail: ftohme@criba.edu.ar.
The current study was funded by Consejo Nacional de Investigaciones Científicas y Técnicas (PIP 112-201001-00187). We also want to thank three anonymous reviewers for helpful comments and suggestions on a previous version of this paper.
Sugerencia de citación: Moro, R., Freidin, E., & Tohmé, F. (2015). Social preferences are not enough: Accounting for anomalous behavior in a complex mixed-motive game. Cuadernos de Economía, 34(65), 261-278. doi:10.15446/cuad.econ.v34n65.43481.
Abstract
In some economic games, participants systematically display behavior that departs from the model of payoff maximization, and this is usually attributed to social preferences. In this paper we focus on a new interactive context, a mixed-motive game called "Alternative Traveler's Dilemma" (ATD). In this context, most participants choose strictly dominated strategies. Preliminary studies suggest the reason for such a tendency is that participants have social preferences, usually competitive in nature. The question is whether some cognitive factors should also be included in models that account for the tendency at stake. More specifically, we investigate whether participants neglect payoff maximization, that is, whether they fail to notice that, by pursuing some competitive goal, they are not maximizing their payoffs. We report the results of an experiment that supports this hypothesis. We conclude that in order to explain anomalous behavior in the ATD, and similar games, we need to study the cognitive factors that bound participants' strategies and understanding of the game.
Keywords: Mixed-motive games, anomalous behavior, social preferences, competition, cognitive factors, payoff-maximization.
JEL: C7, C91.
Resumen
En algunos juegos económicos el comportamiento de los participantes difiere de manera sistemática del modelo de maximización de pagos y esto es usualmente atribuido a preferencias sociales. En este artículo, nos enfocamos en un nuevo contexto interactivo, un juego de motivos mixtos llamado "dilema del viajero alternativo" (DVA). En este contexto, la mayoría de los participantes eligen estrategias estrictamente dominadas. Estudios preliminares sugieren que los participantes tendrían preferencias sociales, usualmente de naturaleza competitiva. La pregunta es si algún factor cognitivo debería ser también incluido en el modelo que explica la tendencia de elección en cuestión. Más específicamente, investigamos si los participantes son negligentes con respecto a la maximización de pagos; es decir, no se dan cuenta de que, al perseguir determinado fin competitivo, se están perdiendo de maximizar sus ganancias. Reportamos un experimento que soporta esta hipótesis. Concluimos que para explicar comportamiento anómalo en el DVA y juegos similares, se necesitan estudiar los factores cognitivos que limitan las estrategias y el entendimiento del juego por parte de los participantes.
Palabras clave: juegos de motivos mixtos, comportamiento anómalo, preferencias sociales, competición, factores cognitivos, maximización de pagos.
JEL: C7, C91.
Résumé
Dans certains jeux économiques, le comportement des participants diffère systématiquement du modèle de maximisation de paiements, ce qui est généralement attribué à des préférences sociales. Dans cet article, nous nous concentrons sur un nouveau contexte interactif, un jeu de motifs mixtes appelé «dilemme du voyageur alternatif(DVA). Dans ce contexte, la majorité des participants choisissent des stratégies strictement dominées. Des études préliminaires suggèrent que les participants auraient des préférences sociales, généralement de nature compétitive. La question est de savoir si un facteur cognitif devrait également être inclus dans le modèle qui explique la tendance du choix en question. Plus particulièrement, nous recherchons si les participants sont négligents en ce qui concerne la maximisation des paiements ; c'est-à-dire qu'ils ne se rendent pas compte de ce que, à rechercher une fin concurrentielle particulière, ils perdent celle de maximiser leurs gains. Nous présentons une expérience qui confirme cette hypothèse. Nous concluons que pour expliquer le comportement anomal dans le DVA et des jeux équivalents, il convient d'étudier les facteurs cognitifs qui limitent les stratégies et la compréhension du jeu par les participants.
Mots-clés : jeux de motifs mixtes, comportement anomal, préférences sociales, compétition, facteurs cognitifs, maximisation de paiements.
JEL : C7, C91.
Resumo
Em alguns jogos econômicos, o comportamento dos participantes difere, de maneira sistemática, do modelo de maximização de pagamentos e isto é usualmente atribuído a preferências sociais. Neste artigo, nos focamos em um novo contexto interativo, um jogo de motivos mistos chamado "dilema do viajante alternativo" (DVA). Neste contexto, a maioria dos participantes escolhem estratégias estritamente dominadas. Estudos preliminares sugerem que os participantes teriam preferências sociais, usualmente de natureza competitiva. A pergunta é se algum fator cognitivo deveria ser também incluído no modelo que explica a tendência dessa escolha. Mais especificamente, pesquisamos se os participantes são negligentes com relação à maximização de pagamentos; quer dizer, não percebem que, perseguindo determinado fim competitivo, estão deixando de maximizar os seus ganhos. Reportamos um experimento que sustenta esta hipótese. Concluímos que, para explicar o comportamento anómalo no DVA e jogos similares, é preciso estudar os fatores cognitivos que limitam as estratégias e o entendimento do jogo por parte dos participantes.
Palavras-chave: Jogos de motivos mistos, comportamento anómalo, preferências sociais, competição, fatores cognitivos, maximização de pagamentos.
JEL: C7, C91.
Este artículo fue recibido el 16 de mayo 2014, ajustado el 11 de julio de 2014 y su publicación aprobada el 8 de agosto de 2014.
INTRODUCTION
In many interactive contexts, participants tend to behave in ways that are inconsistent with the standard model of selfish payoff maximization (Camerer, 2003; Colman, 2003). Researchers in the area of Behavioral Game Theory have used different strategies to try to account for these anomalous tendencies. Some authors have appealed to models that postulate limited levels of reasoning in games, such as the one-shot Beauty-Contest Game (Nagel, 1998). In addition, learning models have been frequently applied to explain decisions in games with several rounds (Camerer, Ho & Chong, 2002), whereas experimental economists have also relied on insights from cognitive psychology that feature framing effects, heuristics, memory availability, etc. in diverse decision contexts (a succinct review of all these strategies can be found in Camerer, 2006). Last, and of special interest for the present study, social preferences have become trendy in explaining participants' behavior in several games, such as the Public Goods Game, the Prisoner's Dilemma, the Trust game, or the Ultimatum game (e.g., Eckel & Grossman, 1996; Fehr & Schmidt, 1999; Palacio & Parra, 2014; but also see Levitt & List, 2007 for a criticism). For example, consider the Ultimatum Game (UG). The UG is a game where two players have to divide an endowment given by the experimenter (e.g., $10). The first-mover has to make an offer (e.g., $7 dollars for himself and $3 dollars for the other person). The second-mover either accepts the offer, in which case each earns the amount stipulated in the offer, or he or she rejects the offer, in which case each player earns nothing. If the amount offered by the first-mover is positive (even the minimal unity), rejecting the offer is a dominated strategy since it pays less than accepting it. However, second-movers tend to reject low offers (less than 20% of the endowment), and this has been attributed to a second-movers' negative reciprocity (Fehr & Fishbacher, 2002). There is no attempt in the literature to attribute behavior in the UG to a misunderstanding of the rules, since the game is fairly straightforward. The question is whether the same type of explanation (i.e., exclusively based on social preferences) holds in more complex contexts. The problem is that in a more complex context, social preferences may interact with cognitive factors that influence the understanding of the situation (Devetag & Warglien, 2008). Particularly, we investigate whether an explanation only based on social preferences holds in a new context, a mixed-motive game that we called "Alternative Traveler's Dilemma" (ATD, hereafter; we describe the game in Section Two). In this context, the majority of participants tend to choose strictly dominated strategies. A preliminary study suggests that participants choosing dominated strategies have social preferences, usually competitive in nature. The question is whether the understanding of the situation should also be included in the explanation of the anomalous tendency. More specifically, we investigate whether participants choosing dominated strategies neglect payoff maximization, that is, whether they fail to notice that, by pursuing a competitive goal, they are not earning as much money as possible (hereafter referred to as the neglect hypothesis). We ran an experiment and found support for this possibility. Thus, we argue that in order to explain anomalous behavior in the ATD and similar games, cognitive factors should also be taken into account.
Our paper is organized as follows. In the Section Two, we present the ATD and briefly mention the evidence pointing towards competitive motives in this game. In Section Three we report the experiment in which we test the neglect hypothesis. In Section Four, we discuss the results and propose possible theoretical links to other results in the literature. In Section Five, we present our conclusions.
THE ALTERNATIVE TRAVELER'S DILEMMA (ATD)1
The context of decision at stake is the ATD that consists in the following game:
You and another person face the following situation:
1) You have to choose a single number between 180 and 300 (any extreme or intermediate number can be chosen).
2) The other participant has to do the same, but no communication is allowed between you two, so neither of you knows what number the other person chooses.
3) In the case you and the other person choose the same number, each of you receives exactly that amount.
4) In the case you and the other person choose different numbers, payments are delivered as follows:
a) The player who chooses the LOWER number receives that amount in $ PLUS $5.
b) The player who chooses the HIGHER number receives that amount in $ MINUS $5.What number do you choose?
Notice that, for example, playing 300 gives you a minimum of $295, while playing 289 may give you a maximum of $294. Thus, the strategy 300 strictly dominates 289. In greater detail, this game has no equilibrium in pure strategies, but all the strategies in the range 180-289 are strictly dominated by at least one strategy in the range 290-300. Thus, if a participant wants to maximize her profit, she should not play a strategy lower than 290. To see this point more clearly, suppose that one incorrectly thinks that 300-300 is an equilibrium: this is not true because if the other player chooses 300, one can maximize his/her own profit by choosing 299; and the best response to 299 from the other player is to play 298, and so on. However, there is a breaking point at 290. If one believes the other player chooses 290, one is better off by choosing 300 (since one obtains $295), rather than choosing 289 (where one obtains $294).
A nice feature of the ATD, in contrast with other mixed-motive games, is that it lacks the typical paradoxical character of this type of game. In general, mixed-motive games (such as the Prisoner's Dilemma, Public Good games, the original Traveler's Dilemma) have an equilibrium in pure strategies that are Pareto-dominated, creating a conflict between individual gain and social benefits. The ATD does not have any equilibrium in pure strategies, so it does not have such a feature. There is also an additional difference from the original TD. In the original TD, the recommendation from Game Theory is that both players choose the minimal value (i.e., 180 in the current setting), and it has been argued that this goes against our intuition of rational decision-making (Basu, 1994). This criticism is supported by experiments with university students (Rubinstein, 2007), and with experts in Game Theory (Becker, Carter & Naeve, 2005), in which most participants tend to choose high values. For the ATD, in contrast, the recommendation from Game Theory is just to play a number in the dominant range, which will be a high value.
The ATD also bears a strong resemblance to Arad and Rubinstein's (2012) 11-20 money request game, designed to study k-level reasoning. In this game, two players choose a value in the range 11-20. Each player receives the amount he or she requests and also receives an additional $20 if he or she asks for exactly one unit less than the other player. Thus, both games pay money as a function of what each player claims, and there is a prize for undercutting the other player's choice. But they also differ in a very important aspect: ATD has dominated strategies, while the 11-20 game lacks them. Since the 11-20 game has been designed to test the presence of k-level reasoning, this feature is crucial for the characterization of the 0-level of non-strategic choices. While in the 11-20 game this could be easily captured by any salient feature of the game (it is natural to assume that it is the highest value that can be chosen), in the ATD it is no longer obvious: rather it will require the ability of L0-type players to eliminate dominated strategies, which, as we will see, is the very point of our study. Nevertheless, once in the 300-290 range, since no action there dominates any other in the range, the situation becomes clearly more like the 11-20 game. Thus, we will compare our results within this range with the results by Arad and Rubinstein (see our Discussion Section below).
Going back to our game, in a preliminary study (Freidin, Moro, Auday & Tohmé, 2011); we found that an important proportion of participants (between 52 and 65%) chose dominated strategies in the ATD, that is, strategies in the range 180-289. The key question is, of course, how to explain this tendency. An important clarification should be made before we continue. We are interested in explaining underlying motivations behind subjects' intuitive and heterogeneous choices and thus we focus on initial play (see Brañas-Garza, 2011 for a similar point in the context of an experimental study on the original TD).
A suggestion about motivations behind responses in the ATD came to us from our preliminary study where we asked participants (N = 48) to list all the thoughts that came to mind while making the decision. Almost all participants mentioned the goal or goals they were pursuing with their choices. However, we found an important difference: those who played dominant strategies tended to mention the goal of maximizing profit, whereas those who played dominated strategies tended to mention other goals, most of which were competitive in nature (e.g., winning the bonus, avoiding the penalty, or defeating the other person). Thus, by trying to satisfy a competitive goal, participants may have lowered their chosen responses to the point of reaching the zone of strictly dominated strategies. The key question is, then, whether those participants were aware that they were failing to earn as much money as possible.
EXPERIMENT
General Purpose and Main Strategy
As previously suggested, one may attempt to account for the tendency to choose dominated strategies in the ATD by following two different strategies. On the one hand, one could explain the tendency at stake by appealing only to social preferences. That is, participants who choose dominated strategies simply prefer satisfying an alternative goal (e.g., defeating the other person) rather than maximizing their own profit (social preference hypothesis). On the other hand, one may attempt to include a cognitive factor in the explanation. More specifically, we propose that many participants neglect payoff maximization, that is, they fail to realize that, by pursuing an alternative goal, they are not maximizing their payoff (neglect hypothesis). Additionally, we postulate that many participants prefer to maximize their profits rather than to satisfy other goals. Thus, following the neglect hypothesis, we predict that if participants somehow become aware of their failure to maximize their selfish profit, they would tend to switch to dominant strategies.
We designed our experiment to test the neglect hypothesis. Our treatment condition involved an exercise whose solution exposed the fact that sometimes participants cannot maximize profit and satisfy a competitive goal at the same time in the ATD. In other words, our treatment condition was intended to minimize the possibility that participants did not pursue payoff maximization without being aware of it. Thus, if participants choose dominated strategies partially because they neglect payoff maximization, noticing the distinction between goals should elicit a change towards profit maximization, that is, they should choose strategies significantly higher than participants unaware of such a distinction. In contrast, if participants either do not neglect payoff maximization, or even if they do, they still prefer an alternative goal (e.g., competitive in nature), the distinction between goals should have no effect on their response to the ATD.
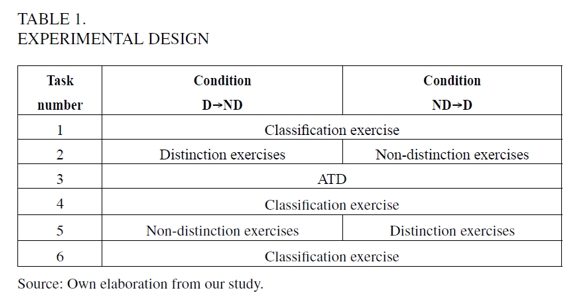
Materials and Design
The booklet contained several tasks (the complete design can be seen in Table 1). Each task was presented in a different page together with a reminder of the ATD rules (all material was presented in Spanish and payoffs were presented by using Argentinean currency). The first task was a classification exercise. Classification exercises were the same as the ATD, except that the number chosen by the other person was known (the numbers were randomly picked from the 240-260 range because that was the modal response in preliminary studies; Freidin et al., 2011). For example, participants were asked:
If you participate in a situation with the rules mentioned above and you know that the other person is going to choose the number 240, what value would you choose?
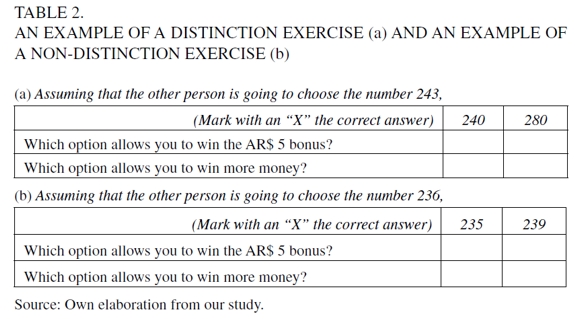
Classification exercises allowed us to classify participants into profit-maximizers (those who chose 300), and non-maximizers (those who chose any number lower than 300). The detection of profit-maximizers from the start was crucial since we expected their responses to remain unaffected by our treatment. In other words, the initial classification problem allowed us to focus on our group of interest, that is, the one composed only of people who choose strictly dominated strategies. The second task contained the treatment condition: half of the participants received three exercises that distinguished between the goals of maximization and competition (distinction exercises, see panel A of Table 2), and the other half received three structurally equivalent exercises, the solutions of which did not show the potential incompatibility between goals (non-distinction exercises, see panel B of Table 2). The idea was that distinction exercises made it salient that certain options, which allow you to win the prize, do not maximize your monetary payoff. In the third task, participants played the ATD. Next (task four), there was another classification exercise but with a number different from task one. The prediction from the neglect hypothesis is, again, that distinction exercises should move participants' responses in these classification exercises towards maximization (in comparison with non-distinction exercises). In other words, distinction exercises should elicit responses to classification exercises significantly higher than the ones elicited by non-distinction exercises. In the fifth task, the group that had solved distinction exercises in the second task was presented with non-distinction exercises and vice versa; the group that had solved non-distinction exercises in the second task was presented with distinction exercises. Finally, the sixth and last task was a classification exercise (again, featuring a value different from the previous classification exercises). The prediction from the neglect hypothesis is that distinction exercises, whenever presented, would increase the average response to both the ATD and classification exercises.
It is worth noting that distinction and non-distinction exercises also played another role in the procedure: they allowed the detection of individuals who misunderstood the payoff rules of the ATD. Each exercise involved two questions, and each participant responded to three distinction and three non-distinction exercises in the whole booklet (i.e., twelve questions in total). We established a criterion to distinguish those who seemingly understood the payoff rules of the ATD from those who did not: to be classified as understanding, a participant had to respond correctly to at least four (out of six) distinction, and four (out of six) non-distinction questions (i.e., a majority of correct responses in both types of questions). Booklets from participants who did not meet this criterion were discarded.2
Procedure
The experiment was run in four independent sessions and a total of 331 participants were involved. Participants were undergraduate students in Accounting (two sessions), Law, and Agricultural Engineering, taking courses during the first semester of 2010 at the Universidad Nacional del Sur, Bahía Blanca, Argentina. Participants were recruited in the classroom where the experimental session was run. We ran three sessions with real monetary payoffs (N = 231) and the fourth (Accounting) with hypothetical payoffs (N = 100). As we mentioned before, in each session, participants were randomly assigned to one of two condition orders: Distinction exercises → Non-Distinction exercises (hereafter D→ND; N = 167) and Non-Distinction exercises → Distinction exercises (hereafter ND→D; N = 164).
As the sequence of tasks was crucial in the present design (see Table 1), participants were not allowed to modify responses in previous pages of the booklet. There was no time restriction (each session took approximately 20-25 min). Students were told that: 1) after all participants of their group turned in the completed questionnaires, we would select one of them at random; 2) we would check the answers to questions on pages two and five (i.e., the distinction and non-distinction exercises), and, if at least one answer was wrong, we would discard that questionnaire and select another one until finding one with all correct responses (the intention of this step was to motivate participants to pay close attention to these questions and respond to them correctly); 3) we mentioned that the author of the chosen questionnaire would throw a six-sided dice which would determine the exercise number from which to infer his or her corresponding payoff (that payoff was immediately obvious for classification exercises -i.e., tasks one, four, and six- which already provided the other participants' responses to the ATD; but in the event that task three was drawn (the ATD), we would compare the person's response against the response from a randomly picked questionnaire from the group. We pointed out that we would not reveal the name of the person who filled in the second questionnaire; and last, 4) we announced that we would pay the chosen participant according to the rules of the game before ostentatiously showing the money.3 After explaining the procedure, we handed in the booklets. Once every participant had returned his or her booklet to the experimenter, we did the ballot and paid the selected participant as promised. In the first session (Accounting) the selected student received AR$ 245, and in the second and third sessions (Agricultural Engineering and Law, respectively) the selected students received AR$ 295 each.
Dependent Measures and Statistical Analyses
Responses to the ATD and ATD-like exercises do not usually show a normal distribution; hence we analyzed data with nonparametric statistics. We used Mann-Whitney U tests to make comparisons between both the hypothetical- and real-payoff sessions, and between conditions D→ND and ND→D. When comparing case frequencies in any response category (e.g., profit maximization response) between sessions or conditions, we used Fisher's exact test. For within-subject comparisons we used Wilcoxon Matched Pairs test. In the case of tasks one, four, and six (i.e., classification exercises), the difference between the participant's response and the number given in the exercise (i.e., the other participant's response) was used as dependent variable. The α value was set at 0.05.
Results
First, it was important to assess whether running sessions with or without real monetary payoffs had any detectable effect on participants' responses. From the 100 participants in the session with hypothetical payoffs, 92 (92%) passed the criterion of understanding the payoff rules of the ATD; while from the 231 participants in sessions with real payoffs, 202 (87%) passed that criterion. Thus, the real versus hypothetical incentive apparently had no effect on the amount of errors in distinction and non-distinction exercises from where game understanding was inferred (Fisher's exact test, two-tailed P = 0.26). Relative to the number of maximizers in exercise one (the first classification exercise; see Table 1), there were 36 (36%) in the hypothetical-payoff session, and 97 (42%) in real-payoff sessions (Fisher's exact test, two-tailed P = 0.33). This last result means that the majority of participants gave strictly dominated responses to an ATD-like exercise, as it was also found in our preliminary study (Freidin et al., 2011).
Maximizers in exercise one, and those participants who did not pass the understanding criterion were both discarded for subsequent analyses, unless otherwise stated. Therefore, 56 and 105 participants were left out in the hypothetical-payoff and real-payoff sessions, respectively. Mann-Whitney U tests comparing median responses in tasks one, three, four, and six (exercises two and five were the distinction and non-distinction exercises) showed no reliable difference between the hypothetical-payoff session and the real-payoff session (task one: Z = 0.74, P = 0.46; task three: Z = 1.29, P = 0.20; task four: Z = 0.46, P = 0.64; task six: Z = 1.41, P = 0.16). Based on this evidence, we pooled participants from the hypothetical-payoff session together with participants from real-payoff sessions to assess the predicted effects of the distinction and non-distinction exercises on ATD responses (N = 161; condition D→ND, n = 76; condition ND→D, n = 85).
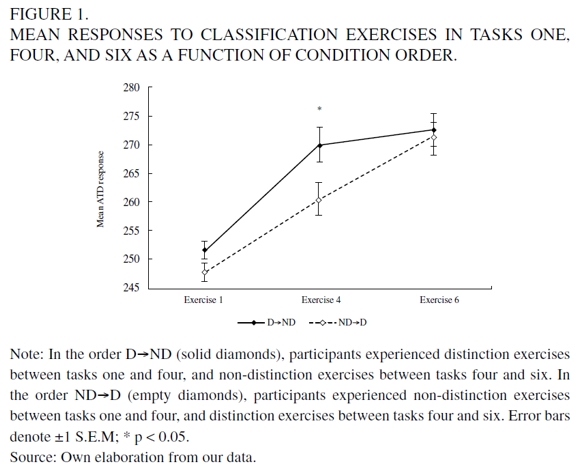
Second, it was crucial to show that participants in both conditions did not differ in their responses before applying the independent variable (i.e., in task one). Indeed, that was exactly what we found: Mann-Whitney U test, Z = 0.86, P = 0.39 (see Figure 1).
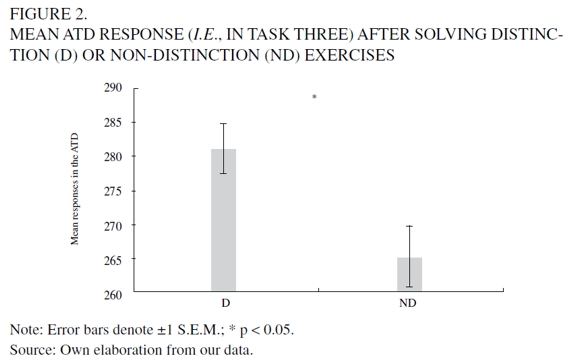
The main prediction was, then, that responses to the ATD (task three in the booklet) should be higher after distinction exercises than after non-distinction exercises. Indeed, median responses to the ATD were higher after distinction exercises than after non-distinction exercises (Mann-Whitney U test, Z = 2.34, P = 0.02; see Figure 2). Moreover, the percentage of dominant responses in the ATD (i.e., responses > 289) was significantly higher after distinction exercises (68%, 52 out of 76) than after non-distinction exercises (54%, 46 out of 85): Fisher's exact test, P < 0.05. We obtained similar results when we analyzed only the responses to the ATD of participants who gave 100% correct answers to distinctions and non-distinction questions (Mann-Whitney U test, Z = 2.58, P < 0.01; percent of dominant responses, after distinction exercises, 71%, 45 out of 63; after non-distinction exercises, 53%, 39 out of 74; Fisher's exact test, P < 0.05).
In task four (the second classification exercise; see Table 1), responses after distinction exercises were significantly higher than responses after non-distinction exercises (Mann-Whitney U test, Z = 2.02, P = 0.04; see Figure 1), which was also predicted by the neglect hypothesis.4
We also expected an increment in responses from classification tasks four to six in the condition ND → D because in between those tasks participants were presented with distinction exercises. As predicted, a significant increase from task four to six was found in condition ND→D but not in condition D→ND (Wilcoxon Matched Pairs tests, Z = 2.59, P < 0.01; Z = 0.76, P = 0.44, respectively). Additionally, conditions did not significantly differ in their median responses to task six as can be seen in Figure 2 (Mann-Whitney U test, Z = 0.04, P = 0.96).
These results, taken together, clearly support the neglect hypothesis: Noticing the distinction between goals made participants move their responses towards maximization in both the ATD and the classification exercises.
The reader may wonder about the treatment effect (if any) in those participants who maximized in exercise one. As expected, there was no significant effect, as these participants tended to keep maximizing in classification exercises and most gave dominant responses in the ATD. More precisely, from the 133 participants who gave maximizing responses in exercise one, 96% and 94% choose strategies within the dominant range of the ATD in conditions D→ND and ND→D, respectively.
Figure 3 shows the distribution of responses to the ATD of all participants who responded correctly to 100% of the distinction and non-distinction questions, including those who maximized in exercise one.
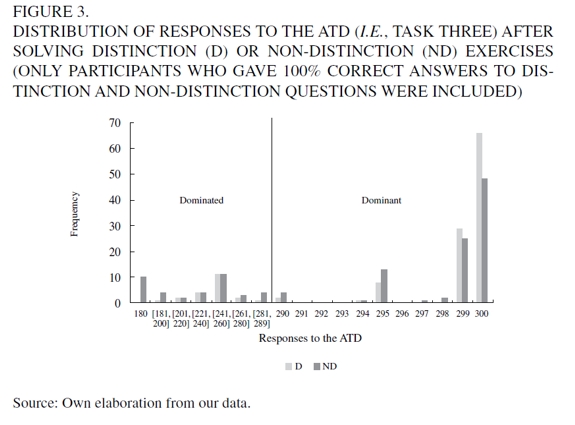
DISCUSSION
In this study, we found that participants exposed to the fact that profit maximization and competition could be incompatible goals in the ATD tended to switch towards profit maximization more frequently than those not exposed to that potential incompatibility of goals. This result provides support for the neglect hypothesis: some participants whose initial response was strictly dominated neglected pursuing profit maximization: either they thought that such a goal and a competitive goal could be simultaneously satisfied, or they were completely unaware of the profit maximization goal. Once participants were explicitly confronted with the possible incompatibility of these two goals, they tended to change their responses in the ATD from strictly dominated to dominant. This treatment effect presumably happened as a result of participants becoming aware of the mentioned incompatibility, and their latter recognition that profit maximization had a higher utility for them. Thus, motivational factors, such as social preferences, cannot completely account for behavior in the ATD: the understanding of the situation cannot be excluded from a complete account of the decisional tendency at stake.
The reader may object that it is possible to explain the present treatment effect by appealing again to competitive social preferences: results could be interpreted as if participants did not care about payoff maximization but rather wanted to maximize the payoff difference between their own payment and the payment of the other player. Then, the distinction exercises could have shown them a way to do so. That may be true, but the point we want to establish still holds. Even if the distinction exercises showed participants an alternative and more powerful way to satisfy a competitive preference, there is still a cognitive aspect involved. According to this reformulated competitive account, the distinction exercises would have affected participants' responses, not by affecting their motivation, but by affecting their awareness of strategies that better suited their goals.
We now turn to the relationship between our findings and the literature of k-level reasoning, especially the results reported in Arad and Rubinstein (2012). In order to do this, we need to restrict our attention to choices in the 290-300 range, as choices of dominated strategies cannot be explained by models of k-level reasoning. Our results are somewhat different to those from Arad and Rubinstein. They found evidence of four levels of iterative reasoning (L0-L3), whereas the distribution of responses in the ATD (figure 3) provided clear evidence of only two levels (L0, L1, namely responding 300 and 299, respectively).4 We think that a possible explanation for a difference in depth of reasoning between games could be related to the size of the prize parameter, which in the 11-20 game is much higher than in the ATD (it is not only four times higher but it is also higher relative to the range of values: a prize of $20 in a 11-20 range vs. a prize of $5 in a 180-300 range). Indeed, the size of the prize parameter greatly affects choices in the original TD (Basu, Becchetti & Stanca, 2011; Capra, Goeree, Gomez & Holt, 1999), as well as in the 11-20 game (Alaoui & Penta, 2013) in the expected direction: the greater the incentive, the more levels of reasoning and the lower the choice.
We want to finish our paper by suggesting a link between our results and some theoretical developments in the social-cognitive literature. An important contribution from psychological studies of decision-making has been to recognize that people may not have well-defined preferences. Instead, preferences are frequently constructed in situ and are highly contingent on situational factors (see Bettman, Luce & Payne, 1998; Slovic, 1995 and for surveys on the construction of preferences). Additionally, in many contexts, preferences are influenced by the goals participants pursue. The crucial point is that a goal, as any memory construct, fluctuates in accessibility across time and contexts according to classical knowledge activation processes. "Accessibility" meaning "... the ease (or effort) with which particular mental contents come to mind" (Kahneman, 2003, p. 699). In other words, activation of a given memory in turn activates/inhibits other memories based on their associative links, which may render a particular goal more or less accessible depending on situational factors (see Fishbach & Ferguson, 2007). Thus, a person may follow a goal simply because it is more accessible in memory, being unaware of other goals whose satisfaction may involve a higher utility. Going back to the ATD, we know that gains and losses are psychologically salient features similar to the perceptual salience of movement and change (people pay attention to such features and events even involuntarily; Bettman et al., 1998; Kahneman & Tversky, 1979). In this sense, we think that the bonus/discount rule in the ATD may have greatly captured people's attention. Such aspect of the game may have led some participants in our experiment to the pursuit of competitive goals, namely seeking to win-the-bonus/avoid-the-discount. However, it is likely that many of those participants also valued the goal of profit maximization. Thus, the explicit confrontation of goals in our experiment may have raised the accessibility and pursuit of the latter goal. Of course, it is clear that more evidence is needed to justify this link, but we think this is a promising avenue for future research.
CONCLUSION
In many interactive contexts, people behave in diverse anomalous ways because they have social preferences. However, an explanation exclusively based on social preferences may not be adequate to account for behavior in more complex contexts, where cognitive factors may also play an important role. Our study can be seen as empirical proof of such a possibility. More research is needed, however, to establish the details of the interaction between motivational and cognitive factors in this and other games.
FOOTNOTES
1 The reason behind the name "Traveler's Dilemma" (TD) is that Basu (1994), the proponent of the original TD, illustrates the game with the story of two travelers who, returning from a remote island, find that the airline has damaged the identical antiques that each had purchased. Thus, an airline manager designs the TD to decide how to compensate the travelers. In the original (i.e., Basu's) version, payments are made as a function of the lowest value chosen, while in our alternative version, payments are made as a function of the value each player chooses.
2 The justification for this determination is that participants who do not understand payoff rules are probably just playing a different game, so their responses will not be informative for finding out how participants behave in our game of interest, i.e., the ATD.
3 It is worth mentioning that the money involved (a range of AR$ 180-300) was a sizable amount of money for an undergraduate student in Argentina at the time of the study. To give the reader an idea, a lunch combo in the university cafeteria cost around AR$ 15 at that time.
4 Notice that, a priori, playing against someone would be different than imaging oneself playing against someone, especially when competitive motivations could be involved: in the imaginative case, one would know that it is not actually competing against anyone. However, as it turns out, many participants behaved as if they were actually competing against a real person, even in the imaginative case. That is, they sacrificed profit in order to win the prize and/or beat the other player. Nevertheless, it would be interesting to empirically test the difference between hypothetical and actual competition.
5 We do not think that choices of strategy (295) correspond to the sixth level of reasoning, but it could rather just be a salient point within the range.
REFERENCES
[1] Alaoui, L., & Penta, A. (2013). Level k-reasoning and Incentives. Deposit de la Recercade Catalunya, Universitat Pompeu Fabra, Barcelona. Retrieved from http://hdl.handle.net/2072/214104. [ Links ]
[2]. Arad, A., & Rubinstein, A. (2012). The 11-20 money request game: A level-k reasoning study. American Economic Review, 102(7), 3561-3573. [ Links ]
[3] Basu, K. (1994). The traveler's dilemma: Paradoxes of rationality in game theory. The American Economic Review, 84(2), 391-395. [ Links ]
[4] Basu, K., Becchetti, L., & Stanca, L. (2011). Experiments with the traveler's dilemma: Welfare, strategic choice and implicit collusion. Social Choice and Welfare, 37(4), 575-595. [ Links ]
[5] Becker, T., Carter, M., & Naeve, J. (2005) Experts playing the traveler's dilemma (Working Paper 252). Institute for Economics, Hohenheim University. Retrieved from http://ideas.repec.org/p/hoh/hohdip/252.html. [ Links ]
[6] Bettman, J. R., Luce, M. F., & Payne, J. W. (1998). Constructive consumer choice processes. The Journal of Consumer Research, 25(3), 187-217. [ Links ]
[7] Brañas-Garza, P., Espinosa, M., & Rey-Biel, P. (2011). Traveler's types. Journal of Economic Behavior and Organization, 78, 25-36. [ Links ]
[8] Camerer, C. (2003). Behavioral game theory: Experiments on strategic interaction. Princeton: Princeton University Press. [ Links ]
[9] Camerer, C. (2006). Behavioral game theory: Predicting human behavior in strategic situations. In C. Camerer, G. Loewenstein & M. Rabin (eds.), Advances in behavioral economics (pp. 374-392). Princeton: Princenton University Press. [ Links ]
[10] Camerer, C., Ho, T., & Chong, K. (2002). Sophisticated EWA learning and strategic teaching in repeated games. Journal of Economic Theory, 104, 137-188. [ Links ]
[11] Capra, C. M., Goeree, J., Gomez, R., & Holt, C. (1999). Anomalous behavior in a traveler's dilemma? American Economic Review, 89(3), 678-690. [ Links ]
[12] Colman, A. M. (2003). Cooperation, psychological game theory, and limitations of rationality in social interaction. Behavioral and Brain Sciences, 26, 139-198. [ Links ]
[13] Devetag, G., & Warglien, M. (2008). Playing the wrong game: An experimental analysis of relational complexity and strategic misrepresentation. Games and Economic Behavior, 62, 364-382. [ Links ]
[14] Eckel, C., & Grossman, P. (1996). Altruism in anonymous dictator games. Games and Economic Behavior, 16(2), 181-191. [ Links ]
[15] Fehr, E., & Fischbacher, U. (2002). Why social preference matters: The impact on non-selfish motives on competition, cooperation and incentives. The Economic Journal, 112, C1-C33. [ Links ]
[16] Fehr, E., & Schmidt, K. (1999). A theory of fairness, competition, and cooperation. Quarterly Journal of Economics, 114(3), 817-868. [ Links ]
[17] Fishbach, A., & Ferguson, M. J. (2007). The goal construct in social psychology. In A. W. Kruglanski & E. T. Higgins (eds.), Social Psychology: Handbook of Basic Principles (pp. 490-515). New York: The Guilford Press. [ Links ]
[18] Freidin, E., Moro, R., Auday, M., & Tohmé, F. (2011). Elecciones aparentemente irracionales en el dilema del viajero alternativo. In M. C. Richaud & V. Lemos (eds.), Psicología y otras ciencias del comportamiento: compendio de investigaciones actuales (vol. 1, pp. 289-300). Libertador San Martín: CIIPME. [ Links ]
[19] Kahneman, D. (2003). A perspective on judgment and choice: Mapping bounded rationality. American Psychologist, 58, 697-720. [ Links ]
[20] Kahneman, D., & Tversky, A. (1979). Prospect theory. Econometrica, 47, 263-292. [ Links ]
[21] Levitt, S., & List, J. (2007). What do laboratory experiments measuring social preferences reveal about the real world? The Journal of Economic Perspectives, 21(2), 153-174. [ Links ]
[22] Nagel, R. (1998). A Review of beauty contest games. In D. Budescu, I. Erev & R. Zwick (eds.), Games and human behavior: Essays in honor of Amnon Rapoport (pp. 105-142). Hillsdale, N. J.: Lawrence Erlbaum. [ Links ]
[23] Palacio, L. A., & Parra, D. F. (2014). El dilema de la contribución voluntaria a bienes públicos: una revisión de trabajos experimentales. Cuadernos de Economía, 33(62), 123-144. [ Links ]
[24] Rubinstein, A. (2007). Instinctive and cognitive reasoning: A study of response times. The Economic Journal, 117, 1243-1259. [ Links ]
[25] Slovic, P. (1995). The construction of preference. American Psychologist, 50(5), 364-371. [ Links ]













