Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.34 no.65 Bogotá July/Dec. 2015
https://doi.org/10.15446/cuad.econ.v34n65.48702
http://dx.doi.org/10.15446/cuad.econ.v34n65.48702
Predicción de la volatilidad en el mercado del petróleo mexicano ante la presencia de efectos asimétricos
Volatility forecasting for Mexican crude oil market in the presence of asymmetric effects
Prédiction de la volatilité dans le marché du pétrole mexicain devant la présence d'effets asymétriques
Predição da volatilidade no mercado do petróleo mexicano diante da presença de efeitos assimétricos
Raúl De Jesús Gutiérreza
Reyna Vergara González b
Miguel A. Díaz Carreñoc
a Universidad Autónoma del Estado de México. Correo electrónico: rdjesusg@uaemex.mx
b Universidad Autónoma del Estado de México. Correo electrónico: rvergarag@uamex.mx
b Universidad Autónoma del Estado de México. Correo electrónico: madiaz@colpos.mx
Sugerencia de citación: De Jesús Gutiérrez, R., Vergara González, R., & Díaz Carreño, M. (2015). Predicción de la volatilidad en el mercado del petróleo mexicano ante la presencia de efectos asimétricos. Cuadernos de Economía, 34(65), 299-326. doi:10.15446/cuad.econ.v34n65.48702
Resumen
Esta investigación evalúa el poder predictivo de una familia de modelos GARCH usados en la predicción de la volatilidad de los rendimientos de la Mezcla Mexicana de Exportación durante el periodo del 2 de enero de 1989 al 30 de diciembre de 2011. Los resultados empíricos evidencian un alto grado de persistencia y la presencia de efectos asimétricos en la volatilidad. Aunque la prueba de predicción sesgada muestra que el modelo IGARCH proporciona el mejor ajuste para recoger la persistencia infinita de los choques en la volatilidad, estos hallazgos no son sustentados por las robustas funciones de pérdidas y la prueba estadística de Diebold-Mariano, debido a que los modelos GARCH y EGARCH proporcionan mejores predicciones de la volatilidad fuera de muestra para los horizontes de 1 y 5 días.
Palabras clave: petróleo crudo, volatilidad, modelos GARCH, pruebas de predicción óptima.
JEL: Q40, C32, C52, E30.
Abstract
This article assesses the predictive ability of a GARCH-class model family, which can be used to forecast the volatility for Export Mexican Blend crude oil returns over the January 2, 1989 to December 30, 2011 period. The empirical results show a high degree of persistence and the presence of asymmetric effects in the volatility. Although forecast bias test results show that the IGARCH model yields the best fit to capture the infinite persistence of the shocks on the volatility. These findings are not supported by the robust loss functions and Diebold-Mariano test since the GARCH and EGARCH models provide the best accurate out of sample volatility forecasts of the crude oil returns for the 1 and 5 day horizons.
Keywords: Crude oil, volatility, GARCH-class models, optimal forecasting tests.
JEL: Q40, C32, C52, E30.
Résumé
Cette recherche évalue le pouvoir prédictif d'une famille de modèles GARCH utilisés dans la prédiction de la volatilité des rendements du Mélange Mexicain d'Exportations pour la période du 2 janvier 1989 au 30 décembre 2011. Les résultats empiriques montrent un fort degré de persistance et la présence d'effets asymétriques dans la volatilité. Bien que le test de prédiction biaisée montre que le modèle IGARCH fournit le meilleur ajustement pour saisir la persistance infinie des chocs dans la volatilité, ces constatations ne sont pas confirmées par les fortes fonctions de pertes et le test statistique de Diebold-Mariano, étant donné que les modèles GARCH et EGARCH fournissent de meilleures prédictions de la volatilité hors échantillon pour les périodes de 1 à 5 jours.
Mots-clés : pétrole brut, volatilité, modèles GARCH, tests de prédiction optima.
JEL: Q40, C32, C52, E30.
Resumo
Esta pesquisa avalia o poder preditivo de uma família de modelos GARCH utilizados na predição da volatilidade dos rendimentos da Mistura Mexicana de Exportação durante o período de 2 de janeiro de 1989 até 30 de dezembro de 2011. Os resultados empíricos mostram um alto grau de persistência e a presença de efeitos assimétricos na volatilidade. Embora o teste de predição tendenciosa mostre que o modelo IGARCH proporciona o melhor ajuste para recolher a persistência infinita dos choques na volatilidade, estes achados não são sustentados pelas robustas funções de perdas e o teste estatístico de Diebold-Mariano, devido a que os modelos GARCH e EGARCH proporcionam melhores predições da volatilidade fora de amostra para os horizontes de 1 e 5 dias.
Palavras-chave: Ãleo, volatilidade, modelos GARCH, testes de predição ótima.
JEL: Q40, C32, C52, E30.
Este artículo fue recibido el 12 de febrero de 2014, ajustado el 25 de junio de 2014 y su publicación aprobada el 8 de agosto de 2014.
INTRODUCCIÓN
El petróleo como principal fuente de energía natural no renovable juega un papel clave en el crecimiento de la economía global (Lee, Ni y Ratti, 1995; Ferderer, 1996; Huntington, 1998) y estabilidad de los mercados financieros, en particular en los mercados de derivados sobre activos subyacentes energéticos (Narayan y Narayan, 2010; Reboredo, 2012). Durante los periodos de la crisis subprime y la euro-crisis de deuda soberana, los precios de contado del petróleo alcanzaron exorbitantes récords nunca antes observados, seguidos de fuertes rebotes a la baja tanto en el corto como en el mediano plazo1, relacionados con la caída en la demanda por la recesión, que inició en 2008. Estos vaivenes en los precios del petróleo generan diferentes niveles de asimetría en la dinámica de los rendimientos, choques positivos y negativos que tienen diferentes efectos en la predicción de la volatilidad y, por consecuencia, efectos negativos directamente en la confianza de los consumidores industriales, productores y gobiernos, cuya principal fuente de ingreso proviene del combustible fósil, como en el caso de México.
Debido a las consecuencias económicas y financieras indeseables previamente mencionadas, la tarea de modelar y predecir la volatilidad de los cambios en los precios del petróleo ha sido uno de los tópicos y retos de mayor interés, en particular, durante periodos de extrema volatilidad de la materia prima, observados desde la liberalización del sector energético en la segunda mitad de los años ochenta y hasta la actualidad, como lo evidencian la crisis financiera global de 2007-2009 y la crisis de deuda soberana de la eurozona en 2010-2011. De esta manera, la precisión en la modelación y predicción del nivel de la volatilidad en los mercados internacionales del petróleo es un componente crucial en la generación de información clave, que puede ser aprovechada para entender mejor el funcionamiento y estructura de los mercados de energía globales. Así mismo, para la toma de decisiones financieras, particularmente en las áreas relacionadas con la valuación de productos derivados energéticos, la planeación financiera gubernamental, el desarrollo de medidas de riesgo eficientes en la estimación de pérdidas potenciales, así como en la innovación de estrategias de coberturas óptimas para administrar y minimizar los efectos negativos de los choques en los precios del petróleo.
Aunque la investigación empírica sobre la volatilidad condicional se encuentra documentada ampliamente en los mercados accionarios y cambiarios, en años recientes, numerosas investigaciones también han seguido la línea de modelado y predicción de la volatilidad dinámica en los mercados de contado y futuros sobre el petróleo crudo. Sin embargo, es importante resaltar que el grueso de la literatura relacionada, en términos relativos, ha centrado su atención en los principales marcadores (benchmarks) del petróleo de tipo WTI, Brent y Dubái, considerados por su alta calidad los crudos más reconocidos y negociados a nivel mundial2. Empero, al responder a los cambios en el incremento desmedido de la demanda de energía global, la disminución significativa en el volumen de la oferta de petróleo crudo en las áreas de extracción de América del Norte (WTI), Europa (Brent) y Asia (Dubái)3, así como regulaciones ambientales laxas, los países importadores de petróleo han mirado hacia otros mercados de energía en busca de suministros abundantes, confiables y baratos, pero de baja calidad y alto contenido de azufre. Este fenómeno, en cambio, ha generado una dramática caída en el volumen relativo de comercialización y una mayor vulnerabilidad en los tres principales marcadores internacionales de referencia. De acuerdo con el estudio de Montepeque (2005), aproximadamente el 50% de la producción mundial está constituida hoy en día por tipos de petróleo de baja calidad y menor grado de densidad.
Por tal motivo, este trabajo de investigación tiene como objetivo evaluar el poder predictivo de una familia de modelos GARCH usados para la modelación y predicción de la volatilidad en el mercado del petróleo de baja calidad y alto contenido de azufre, así como su utilidad para la identificación de las principales características de la heterocedasticidad condicional, persistencia y la presencia de asimetría en la volatilidad de las innovaciones de la Mezcla Mexicana de Exportación durante el periodo del 2 de enero de 1989 al 30 de diciembre de 2011.
La contribución del presente trabajo pretende reducir la brecha en la literatura de esta importante área de investigación, proporcionando evidencia empírica del poder predictivo de la volatilidad empleando los modelos GARCH, IGARCH, EGARCH y GARCH-GJR. La evaluación del poder predictivo de los cuatro modelos de volatilidad se analiza de dos maneras para los horizontes de predicción de 1, 5 y 20 días. En primer lugar, se aplica la prueba de predicción sesgada basada en la estimación de mínimos cuadrados ordinarios para medir el sesgo o discrepancia entre la volatilidad estimada y la volatilidad actual. Cabe mencionar que esta investigación extiende los trabajos de Agnolucci (2009) y Hou y Suardi (2012), quienes utilizan el coeficiente de determinación para evaluar la capacidad predictiva de los modelos de volatilidad, introduciendo la prueba estadística de Wald, que establece dos restricciones lineales sobre los coeficientes estimados de regresión. En segundo lugar, la significancia estadística de la predicción óptima entre dos modelos de volatilidad comparados es probada a través de la prueba estadística de Diebold-Mariano bajo tres funciones de pérdidas.
El trabajo está estructurado de la siguiente forma. En la primera sección se discute brevemente la literatura empírica previa. En la segunda, se introducen los datos y algunas características estadísticas. La tercera discute los modelos de volatilidad estimados y las medidas de evaluación de predicción sesgada y óptima. La sección cuarta proporciona la evidencia empírica del estudio. Finalmente, la quinta sección presenta las principales conclusiones y una breve discusión de los hallazgos empíricos.
Investigación empírica previa
En la primera década del siglo XXI, la literatura empírica se ha centrado en estudiar el alcance de los modelos GARCH para la estimación y predicción de la volatilidad condicional de los rendimientos de los precios del petróleo en los mercados de contado y futuros en un contexto internacional. Por ejemplo, ajustando un modelo semiparamétrico a los rendimientos del Brent, Morana (2001) demostró que las propiedades de predicción de los modelos GARCH, en horizontes de corto plazo, pueden ser apropiadamente utilizadas en el pronóstico de los precios futuros del petróleo. Más tarde, Fong y See (2002) analizaron, con base en un modelo generalizado de cambios de estado, el comportamiento temporal de la volatilidad en los rendimientos diarios de los futuros del marcador WTI. Los resultados empíricos demostraron que el modelo permite capturar las características complejas de la volatilidad condicional fuera de la muestra en periodos de corto plazo. Otro interesante trabajo pionero que se puede citar en la literatura es el de Sadorsky (2006), en donde se utilizan una variedad de modelos estadísticos univariados y multivariados para estimar la volatilidad condicional en el mercado de futuros durante el periodo 1988-2003. Con respecto a la comparación de los modelos de volatilidad, los hallazgos empíricos son mixtos fuera de la muestra, aunque el modelo TGARCH presenta el mejor desempeño para estimar la volatilidad dinámica de los futuros sobre gas natural y combustible para calefacción. Por su parte, la especificación GARCH estándar es más eficiente para explicar las características peculiares de la volatilidad de los futuros sobre el WTI y gasolina a pesar de la complejidad de los modelos de cambio de régimen, VAR y GARCH bivariado. En Narayan y Narayan (2007) se analiza la dinámica de la volatilidad en el mercado del petróleo adoptando un modelo GARCH exponencial. Para la muestra completa que comprende el periodo 1991-2006, la evidencia empírica demuestra que los choques en el petróleo tienen efectos permanentes y asimétricos sobre la volatilidad, que son inconsistentes en varios periodos submuestrales. El análisis de Cheong (2009), basado en diversas alternativas GARCH que capturan adecuadamente las características de la volatilidad en los principales marcadores del petróleo, proporciona evidencia empírica de persistencia más intensa y efectos simétricos en la volatilidad del WTI que en la del Brent, aunque con resultados mixtos en cuanto a la predicción óptima de la volatilidad.
Así mismo, Kang, Kang y Yoon (2009) indagan el poder predictivo de una familia de modelos GARCH para identificar las características de la volatilidad, en particular, su persistencia para los tipos de petróleo WTI, Brent y Dubái. De acuerdo con el análisis fuera de la muestra, los modelos CGARCH y FIGARCH proporcionan el mejor desempeño para capturar el grado de persistencia en la volatilidad que los modelos GARCH estándar e integrado. En consecuencia, Wei, Wang y Huang (2010) extienden el estudio empírico de Kang et al. (2009), estimando varios modelos GARCH para explicar la importancia del análisis de la volatilidad dinámica en los mercados de energía fósil, y demuestran que no existe un modelo que predomine notablemente a los demás en la predicción exacta de la volatilidad. Aunque cabe resaltar que los modelos GARCH no-lineales parecen ser más eficientes para predecir la volatilidad de largo plazo que los lineales4 .
El trabajo de Mohammadi y Su (2010) estudia el desempeño de cuatro modelos de volatilidad, GARCH, EGARCH, APARCH y FIGARCH, para modelar y predecir la media y volatilidad condicional en once mercados internacionales de países exportadores e importadores de crudo. Las pruebas de validación confirman, en la mayoría de los casos, que los modelos EGARCH y APARCH proporcionan resultados más robustos sobre la predicción óptima de la volatilidad. En un trabajo más reciente que ilustra la capacidad de los modelos GARCH para predecir la volatilidad condicional, Hou y Suardi (2012) proponen un modelo GARCH no-paramétrico que no requiere del conocimiento de la distribución de innovaciones; sus resultados empíricos, basados en el uso de robustas funciones de pérdidas para los precios diarios del petróleo WTI y Brent, evidencian un notable progreso en la capacidad predictiva de la volatilidad con respecto a una extensa clase de modelos GARCH.
Con relación a literatura más reciente de los mercados de futuros sobre petróleo, Agnolucci (2009) efectúa un análisis comparativo del poder predictivo de los modelos GARCH y modelos de volatilidad implícita para los futuros sobre el WTI, encontrando severas inconsistencias en el desempeño de los modelos derivado de las diferentes funciones de pérdidas y pruebas estadísticas, particularmente en los modelos de volatilidad que se obtienen al invertir la fórmula de forma cerrada de Black-Scholes. Marzo y Zagaglia (2010) estiman tres modelos GARCH (estándar, exponencial y GJR) basados en diferentes distribuciones de innovaciones para predecir la volatilidad de los futuros sobre petróleo negociado en la Bolsa Mercantil de Nueva York. Las pruebas de capacidad predictiva sugieren que el modelo GARCH estándar basado en la distribución de errores generalizada tiene el mejor desempeño para horizontes de 1 y 3 días, aunque para horizontes de 5 días no hay modelo superior o inferior.
Para el caso de México, el estudio de Dávila, Núñez y Ruíz (2006) busca predecir, a partir de un modelo GARCH estándar, la volatilidad del precio de la Mezcla Mexicana de Exportación. Los autores comprueban la no existencia de efectos asimétricos en la volatilidad del precio del petróleo y confirman la convergencia de la varianza condicional estimada a su varianza no condicional. Villalba y Flores (2013) utilizan un modelo similar para pronosticar la varianza y el rendimiento de diversas variables financieras, entre ellas, la de la Mezcla Mexicana de Exportación. Sus resultados muestran una alta persistencia de los choques en la volatilidad y la convergencia de la varianza hacia un valor estable, lo que confirma la capacidad predictiva de este tipo de modelos, tanto dentro como fuera de la muestra. A diferencia de los trabajos anteriores, en Coronado, Gatica y Ramírez (2012) se analiza el comportamiento de los precios del petróleo tipo Maya
5 y se cuestiona el uso de los modelos GARCH. Mediante dos tipos de pruebas no paramétricas (The Hinich Portmanteau y reversibility tests) muestran la existencia de una estructura no lineal en el comportamiento del precio del petróleo, que no puede ser capturada por modelos tipo GARCH. Finalmente, estimando modelos GARCH univariados y multivariados, Wang y Wu (2012) proporcionan evidencia empírica, dentro de la muestra, de que la volatilidad en los rendimientos del crudo WTI y sus productos refinados exhiben alta persistencia y efectos asimétricos. En tanto que el análisis fuera de la muestra confirma un mejor desempeño de los modelos GARCH multivariados para la predicción de la volatilidad de los combustibles fósiles y refinados.
DESCRIPCIÓN Y ANÁLISIS DE LOS DATOS
Para el análisis de la volatilidad se utilizan los precios diarios de la Mezcla Mexicana de Exportación. Los precios del petróleo se expresan en dólares estadounidenses y cubren el periodo del 2 de enero de 1989 al 30 de diciembre de 2011, para un total de 5968 observaciones. La serie de los datos es dividida en dos submuestras: el periodo 1989-2007 se usa para el análisis de la volatilidad dentro de la muestra, mientras que el periodo 2008-2011 se reserva para la evaluación del poder predictivo de los modelos de volatilidad. El periodo seleccionado proporciona evidencia más consistente de la predicción óptima de la volatilidad porque los modelos se evalúan en dos periodos en los que las fluctuaciones extremas en el precio del petróleo fueron notables, como consecuencia de los efectos negativos de la crisis financiera global y la crisis de deuda soberana europea. La serie de precios se obtuvo de la base de datos de Datastream.
En la Gráfica 1 se muestra la evolución que la Mezcla Mexicana de Exportación ha seguido en el periodo 1989-2011. Al igual que los mercados internacionales de energía, la naturaleza de los choques positivos y negativos en el precio del petróleo nacional también se ha afectado por diversos eventos exógenos que presentan aspectos económicos, geopolíticos, incluso de carácter especulativo. Por ejemplo, el estallido del conflicto en el Golfo Pérsico entre Kuwait e Irak en agosto de 1990 no solo ocasionó incertidumbre en los niveles de producción por la prohibición del consumo de petróleo de la zona conflictiva, sino también un incremento significativo en los precios de referencia del crudo. En consecuencia, el precio de la Mezcla Mexicana de Exportación alcanzó un precio de $32,70 dólares por barril cuando su cotización promedio se ubicaba por debajo de los $15 dólares en 1989, antes del conflicto. Sin embargo, esta tendencia alcista se vio interrumpida por la liberalización de Kuwait y algunas políticas de uso racional de consumo de energía empleadas por los países industrializados en 1991, lo que generó que los precios regresaran casi a su nivel promedio y mantuvieran una tendencia relativamente estable durante el periodo 1991-1997.
Otros eventos que afectaron el comportamiento del crudo nacional fueron la tensión en Medio Oriente y la crisis asiática de 1997-1998. La desaceleración económica en Filipinas, Indonesia, Malasia y Tailandia, así como el exceso de oferta del hidrocarburo, originaron la peor caída en el precio de la Mezcla Mexicana de Exportación, al promediar $7,69 dólares por barril durante el mes de diciembre de 1998, un precio nunca antes registrado en la historia desde 1989. A partir de 1999, la cotización de la Mezcla Mexicana de Exportación inició un ascenso de precios hasta alcanzar el promedio de $20,21 dólares por barril, como resultado de la reducción de 4,2 millones de barriles diarios entre 2000-2001 en la producción de los principales países miembros de la Organización de Países Exportadores de Petróleo (OPEP). A esto siguió un descenso, cuando se negoció a un precio de $17 dólares por barril después del estallido de la burbuja financiera del Ãndice NASDAQ en marzo de 2000 y el atentado del 11 de septiembre de 2001 contra las Torres Gemelas del World Trade Center.
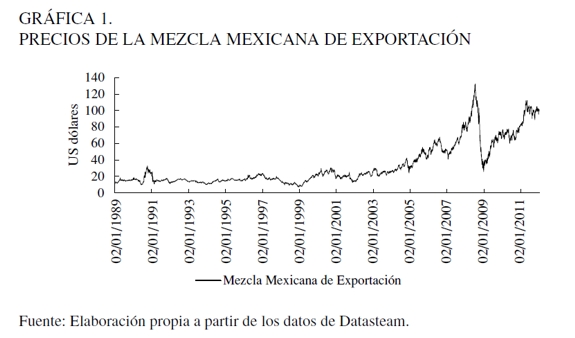
Desde el inicio del conflicto entre Estados Unidos e Irak en 2003, la Mezcla Mexicana de Exportación jamás volvió a alcanzar los niveles de 1998, y logró una cotización máxima de $42 dólares por barril en octubre de 2004. También es bien sabido que el sólido y constante crecimiento económico global y el cambio en la estructura de consumo de petróleo por parte de las economías emergentes de China y la India, en combinación con la ininterrumpida depreciación del dólar estadounidense en relación con euro durante el periodo 2003-2008 fueron factores fundamentales que modificaron la dinámica del mercado en el entorno internacional. A principios de 2007, aprovechando esta coyuntura, el barril de petróleo doméstico inicio cotizando en $52,22 dólares, y continuó su ascenso hasta alcanzar el precio histórico de $132,38 dólares en julio de 2008. A medida que se agudizó la crisis financiera global, este crecimiento exponencial de largo plazo sufrió un desplome espectacular a fines de 2008, precisamente cuando la economía mundial entró en una profunda recesión por la restricción del crédito. En consecuencia, la tendencia de la Mezcla Mexicana de Exportación se corrigió drásticamente en el corto plazo: en cuestión de meses se ubicó en $25,86 dólares, después de haber alcanzado el valor de tres dígitos, lo que creó severos trastornos en la economía mexicana, como la depreciación del peso mexicano en un 39,48%, lo que más tarde se reflejó en una contracción de 6,5% del PIB. Una vez absorbido el efecto negativo de la gran recesión de 2008-2009, otra tendencia alcista de largo plazo se observó en el periodo 2010-2011. Los principales factores que influyeron en este comportamiento se pueden resumir en la recuperación económica de Estados Unidos, la estabilización de la producción de la OPEP en 30,1 millones de barriles diarios, pero sobre todo por los disturbios en Libia y la inestabilidad política en Egipto. En este periodo, el barril de petróleo nacional se incrementó de $71,87 a $98,15 dólares en promedio y registró un precio máximo de $112 dólares aproximadamente.
Los niveles de los precios del petróleo se transforman a una serie estacionaria, calculando los rendimientos sobre una base continua de la siguiente forma: rt= 100ln (Pt/Pt-1), donde Pt y Ptâ1 son las cotizaciones actual y del día anterior. Las estadísticas básicas de los rendimientos de la Mezcla Mexicana de Exportación se resumen en el Cuadro 1. El rendimiento promedio es relativamente bajo (0,036%) y positivo, un hecho naturalmente obvio cuando se analizan datos de frecuencia alta, pero la desviación estándar es considerablemente más alta con valor de 2,69%, indicando que el mercado del petróleo parece ser bastante volátil y riesgoso. Los rendimientos máximo (23,68%) y mínimo (-53,72%) se observaron durante el conflicto entre Kuwait e Irak en 1990 y durante la liberalización de Kuwait a principios de 1991. Los rendimientos muestran sesgo negativo consistente con los principales marcadores de referencia y exceso de curtosis, lo que significa que presentan propiedades de colas más anchas y largas que la distribución normal, en particular la cola izquierda. Así mismo, el supuesto de normalidad es ampliamente rechazado por el alto valor del estadístico Jarque-Bera y su valor-p igual a cero.
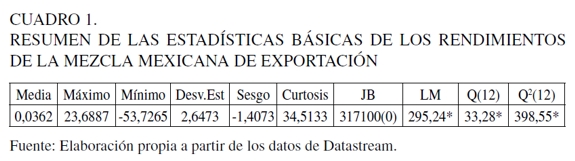
La Gráfica 2 describe la dinámica de los rendimientos de la Mezcla Mexicana de Exportación a través del tiempo. Existen fuertes vestigios de volatilidad en aglomeraciones que muestran la presencia de heterocedasticidad condicional y evidencia de persistencia observados en los rendimientos del petróleo, así como probablemente cambios estructurales debido a movimientos inesperados o extremos que ocurren más frecuentemente. También se realizó la prueba de efectos ARCH para analizar las características distribucionales de los rendimientos. El valor significativo del estadístico de la prueba del Multiplicador de Lagrange rechaza rotundamente la ausencia de heterocedasticidad condicional para cualquier nivel de significancia convencional. De esta manera, las características de los rendimientos de la Mezcla Mexicana de Exportación reportados en el Cuadro 1 y observados en la Gráfica 2 son pruebas contundentes para modelar y predecir su volatilidad a través de la familia de modelos GARCH.
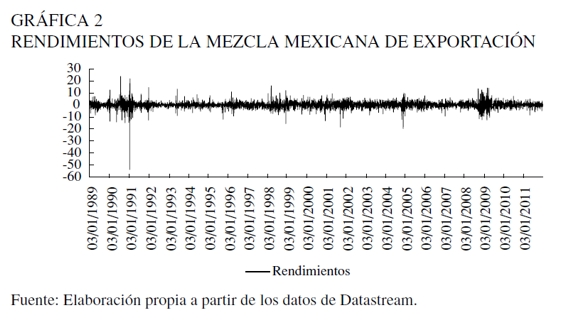
En este análisis también se evalúa la hipótesis nula del proceso de ruido blanco para los rendimientos de los niveles y cuadrados a través de la prueba estadística de Ljung-Box. La alta significancia de los estadísticos, Q(12) y Q2(12), muestra claramente la presencia de autocorrelación serial en los rendimientos de los precios del petróleo, y rechaza así la hipótesis nula de proceso de ruido blanco en las series, particularmente en los rendimientos cuadrados para cualquier nivel de significancia. En consecuencia, los resultados muestran fuerte evidencia de un alto grado de persistencia en el proceso de la volatilidad condicional del mercado del petróleo.
MODELOS DE VOLATILIDAD CONDICIONAL
En esta sección se discute una familia de modelos GARCH univariados para modelar y predecir la volatilidad condicional bajo innovaciones normales de los rendimientos del petróleo.
Modelo GARCH estándar
Una extensión al modelo ARCH de Engle (1982) es el modelo GARCH (1,1) estándar propuesto en la literatura por Bollerslev (1986). En este contexto, la modelación de la media y volatilidad condicional se lleva a cabo a través de la especificación de un modelo ARMA (1,1).
El modelo GARCH (1, 1) estándar está definido por las siguientes ecuaciones:
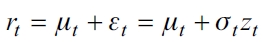 | [1] |
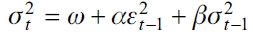 | [2] |
donde μt representa la media condicional; t indica las innovaciones en la ecuación de la media; 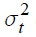 es la varianza condicional que depende de la última innovación de los residuales cuadrados
es la varianza condicional que depende de la última innovación de los residuales cuadrados 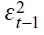 , comúnmente conocido como el efecto ARCH o persistencia de corto plazo, y la varianza condicional previa
, comúnmente conocido como el efecto ARCH o persistencia de corto plazo, y la varianza condicional previa 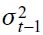 ; zt es un proceso de ruido blanco que sigue una distribución normal con media 0 y varianza 1; ω es un término determinístico que indica la convergencia de la volatilidad condicional a un valor positivo. Para evitar estimaciones negativas en la varianza condicional y la existencia del proceso GARCH, los parámetros ω, α y β deben ser estrictamente positivos y α + β < 1, puesto que la suma de los términos ARCH y GARCH cuantifica el grado de persistencia en la volatilidad en el largo plazo, una condición suficiente para asegurar un proceso estrictamente estacionario y ergódico.
; zt es un proceso de ruido blanco que sigue una distribución normal con media 0 y varianza 1; ω es un término determinístico que indica la convergencia de la volatilidad condicional a un valor positivo. Para evitar estimaciones negativas en la varianza condicional y la existencia del proceso GARCH, los parámetros ω, α y β deben ser estrictamente positivos y α + β < 1, puesto que la suma de los términos ARCH y GARCH cuantifica el grado de persistencia en la volatilidad en el largo plazo, una condición suficiente para asegurar un proceso estrictamente estacionario y ergódico.
Modelo GARCH integrado
El modelo generalizado integrado de heterocedasticidad condicional autorregresiva (IGARCH) de Engle y Bollerslev (1986) es otra alternativa que permite capturar la persistencia infinita de choques en la varianza condicional con solo restringir el parámetro ω=0, y satisfacer la condición α + β = 1.
La especificación del modelo IGARCH (1,1) está definida como
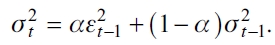 | [3] |
En este caso, la carencia de varianza finita se atribuye principalmente a que en el largo plazo la persistencia (α + β) implica una raíz unitaria en el proceso ARMA (1,1) de las innovaciones, esto es, el impacto del choque en la volatilidad nunca desaparece a diferencia del modelo GARCH (1,1).
Modelo GARCH exponencial
La literatura sobre econometría financiera ha sustentado ampliamente que la volatilidad condicional responde de manera asimétrica a innovaciones de la misma magnitud, pero con diferente signo. La presencia de diferentes niveles de asimetría en los rendimientos financieros ha dado la pauta para introducir otra clase de modelos de volatilidad que permitan capturar los efectos de apalancamiento o asimétricos. Para resolver este problema, en Nelson (1991) se desarrolló el modelo GARCH exponencial (EGARCH).
La especificación de la varianza condicional se puede expresar de la siguiente forma:
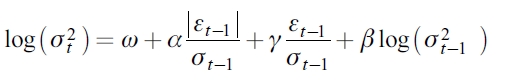 | [4] |
A diferencia del modelo GARCH (1,1) estándar, no hay necesidad de restringir ninguno de los parámetros estimados por el modelo para confirmar la varianza condicional positiva. El parámetro γ captura el comportamiento asimétrico de los choques negativos y positivos en la volatilidad condicional, cuyo efecto de apalancamiento es exponencial más que cuadrático. Para γ < 0, una de las implicaciones económicas es que las innovaciones negativas (noticias malas) tendrán un mayor impacto sobre la volatilidad condicional futura que las innovaciones positivas (noticias buenas) de la misma magnitud. Por último, las condiciones de proceso estacionario y ergódico se alcanzan por el modelo EGARCH (1,1) cuando 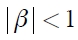 .
.
Modelo GARCH-GJR
Otra especificación reconocida en la literatura empírica que describe la reacción asimétrica de la volatilidad condicional asociada al signo de la innovación es el modelo GARCH-GJR desarrollado por Glosten, Jagannathan y Runkle (1993). El impacto significativo de las innovaciones negativas en la volatilidad condicional se captura con solo introducir una variable dummy o binaria en el modelo GARCH (1,1) estándar.
La varianza condicional a través del modelo GARCH-GJR (1,1) se define como
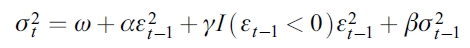 | [5] |
donde la variable dummy está representada por la función indicadora de Heaviside I(•), que se activa con valor igual a 1 si ε t-1 < 0 y cero en cualquier otro caso, lo que indica que las noticias catastróficas tienen un impacto de α + γ sobre el coeficiente de 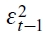 , mientras que el impacto de las noticias optimistas depende únicamente del parámetro α. En consecuencia, el efecto de apalancamiento se observa si γ > 0, a diferencia del modelo EGARCH (1,1), en el cual es negativo. De manera similar al modelo GARCH (1,1) estándar, todos los parámetros estimados en la especificación de la varianza condicional deben ser estrictamente mayores o iguales a cero para garantizar la varianza condicional positiva.
, mientras que el impacto de las noticias optimistas depende únicamente del parámetro α. En consecuencia, el efecto de apalancamiento se observa si γ > 0, a diferencia del modelo EGARCH (1,1), en el cual es negativo. De manera similar al modelo GARCH (1,1) estándar, todos los parámetros estimados en la especificación de la varianza condicional deben ser estrictamente mayores o iguales a cero para garantizar la varianza condicional positiva.
En este contexto, la correlación muestral entre los rendimientos simples y cuadrados es una prueba sencilla que permite detectar la presencia de volatilidad asi métrica como respuesta a choques de diferente magnitud en los rendimientos negativos y positivos. La evidencia de efectos asimétricos en los residuales estandarizados es alcanzada cuando el valor del coeficiente de correlación es negativo. Otra alternativa para el diagnóstico de la asimetría en la volatilidad se propone en Engle y Ng (1993). Esta prueba consiste en la estimación de tres regresiones simples basada en los residuales estandarizados cuadrados derivados de la estimación del modelo GARCH (1,1). En la literatura empírica, estas tres pruebas son conocidas como la prueba sesgada de signo, la cual detecta si la volatilidad reacciona de manera asimétrica a innovaciones positivas y negativas de la misma magnitud. La prueba sesgada de magnitud negativa determina si choques de diferente tamaño en las innovaciones negativas tienen diferente impacto en la volatilidad, mientras que la prueba sesgada de magnitud positiva se concentra en los diferentes efectos que tienen los choques positivos, tanto pequeños como grandes, en la volatilidad. Para estimar estas regresiones, es necesario definir una variable dummy 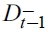 que toma el valor de 1 si νt-1 < 0 y cero en cualquier otro caso
que toma el valor de 1 si νt-1 < 0 y cero en cualquier otro caso 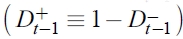 .
.
El conjunto de pruebas está conducido por la estimación de las siguientes regresiones simples:
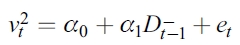 | [6] |
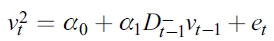 | [7] |
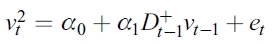 | [8] |
El valor significativo del parámetro estimado α1 a través de la prueba t-estándar es suficiente para señalar que existe evidencia de efectos asimétricos en los residuales estandarizados cuadrados 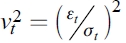 y, por ende, en la volatilidad condicional futura.
y, por ende, en la volatilidad condicional futura.
Sin embargo, la literatura ha demostrado que este diagnóstico proporciona mejores resultados cuando el conjunto de regresiones se estima en forma conjunta. De esta manera, la prueba conjunta para los tres efectos, con base en las regresiones anteriores, se puede expresar como:
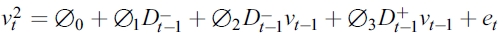 | [9] |
En este caso, la hipótesis nula de que no existen efectos de asimetría determinada por 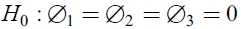 se contrasta con el estadístico de prueba del Multiplicador de Lagrange (LM, por sus siglas en inglés), igual a nR2 de la ecuación (9), que sigue una distribución χ2 con tres grados de libertad.
se contrasta con el estadístico de prueba del Multiplicador de Lagrange (LM, por sus siglas en inglés), igual a nR2 de la ecuación (9), que sigue una distribución χ2 con tres grados de libertad.
Evaluación predictiva de la volatilidad fuera de la muestra
Al evaluar el poder predictivo de la volatilidad, varias pruebas estadísticas se han desarrollado en la literatura; entre ellas se incluyen a las pruebas de predicción sesgada o volatilidad insesgada, óptima y beneficio económico. Una aproximación estadística fácil de implementar, que mide y prueba la existencia de sesgo en la predicción de la volatilidad univariada, es la regresión por mínimos cuadrados ordinarios, que utiliza la varianza estimada como variable explicativa de la varianza actual, que se aproxima por la serie de los rendimientos cuadrados (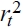 ) de los precios del petróleo, dado que no existen datos observables para dicha variable. Esta variable proxy se sustenta ampliamente en la literatura al ser un estimador insesgado de la varianza actual, aunque algo ruidosa, como consecuencia del exceso de curtosis observado en los datos reales (Sadorsky, 2006; Kang et al., 2009).
) de los precios del petróleo, dado que no existen datos observables para dicha variable. Esta variable proxy se sustenta ampliamente en la literatura al ser un estimador insesgado de la varianza actual, aunque algo ruidosa, como consecuencia del exceso de curtosis observado en los datos reales (Sadorsky, 2006; Kang et al., 2009).
La evaluación de la predicción de la volatilidad fuera de la muestra está determinada por la siguiente regresión:
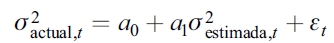 | [10] |
Aquí los parámetros a0 y a1 miden el grado de sesgo en la predicción de la volatilidad. La significancia de los parámetros estimados y la validación de la hipótesis nula conjunta de que a0=0 y a1=1, a través del estadístico de Wald para restricciones lineales que se distribuye asintóticamente como una distribución χ2 con dos grados de libertad, indican que la predicción de la volatilidad es insesgada. La hipótesis nula es rechazada cuando el valor de la probabilidad es pequeño con respecto a cualquier nivel de significancia.
A pesar de la amplia aplicación y los avances en la medida de predicción sesgada, su alcance es reducido para comparar el poder predictivo entre dos modelos de volatilidad, por lo que se sugiere su uso en forma conjunta con otras medidas y pruebas de predicción óptima.
Las funciones de pérdidas son los criterios más comunes para medir la discrepancia entre la varianza actual y la varianza estimada, aunque existe una familia de funciones de pérdidas para la selección y comparación del modelo de predicción. En este análisis se utilizan las medidas del error cuadrado medio (MSE), error absoluto medio (MAE) y cuasi-verosimilitud (QLIKE). Al igual que la función de pérdidas MSE, el QLIKE ha demostrado robustez en la evaluación del poder predictivo de los modelos de volatilidad ante la presencia de ruido en el estimador insesgado de la proxy de la volatilidad o varianza condicional desconocida (Patton, 2011). Otra de las razones de la preferencia de la medida QLIKE se atribuye a que solo depende del error de predicción multiplicativo, 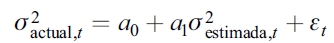 , lo que implica que los errores de predicción sean independientes e idénticamente distribuidos bajo la hipótesis nula de que no existe error de especificación en el modelo de predicción, a diferencia de la medida SME, que contiene altos niveles de dependencia serial, incluso bajo la hipótesis nula por el simple hecho de depender del error de predicción aditivo,
, lo que implica que los errores de predicción sean independientes e idénticamente distribuidos bajo la hipótesis nula de que no existe error de especificación en el modelo de predicción, a diferencia de la medida SME, que contiene altos niveles de dependencia serial, incluso bajo la hipótesis nula por el simple hecho de depender del error de predicción aditivo, 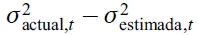 . Así mismo, cabe resaltar que la medida QLIKE penaliza las predicciones de la volatilidad cercanas a cero (Brownlees, Engle y Kelly, 2011).
. Así mismo, cabe resaltar que la medida QLIKE penaliza las predicciones de la volatilidad cercanas a cero (Brownlees, Engle y Kelly, 2011).
Los estadísticos asociados con el poder predictivo de los modelos de volatilidad condicional se definen de la siguiente manera:
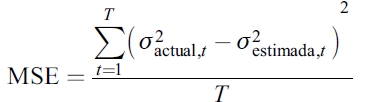 | [11] |
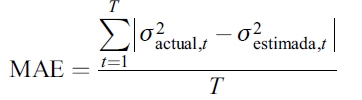 | [12] |
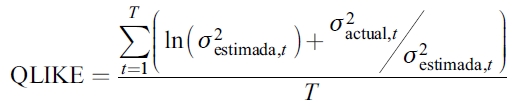 | [13] |
donde T es el número de predicciones fuera de la muestra, 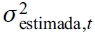 representa la varianza estimada de cada modelo en el tiempo t, mientras que
representa la varianza estimada de cada modelo en el tiempo t, mientras que 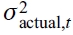 significa la varianza actual o no observable.
significa la varianza actual o no observable.
El objetivo de la funciones de pérdidas en la evaluación del desempeño de los modelos de volatilidad es simplemente minimizar el error de predicción. La capacidad de predicción óptima se alcanza cuando el valor del estadístico tiende a cero; sin embargo, sus resultados no se derivan necesariamente de pruebas estadísticas robustas, debido a que no existe certeza de que cualquier reducción en los errores de predicción sea estadísticamente significativa.
Para reducir las limitaciones de la prueba de predicción sesgada y las funciones de pérdidas asociadas a la clasificación del poder predictivo, se han sugerido diversas pruebas estadísticas en la literatura, pero la prueba de comparación predictiva entre dos modelos de volatilidad más utilizada es la prueba estadística de Diebold-Mariano6. Si definimos dos conjuntos de errores de predicción, e1,t y e2,t asociada a una función de pérdidas específica h(•) para t=1,....,n y si su diferencia se puede expresar como dt=h (e1,t)-h(e2,t) entonces, bajo la hipótesis nula de predicción óptima idéntica o media cero (E[dt]=0), la especificación del estadístico estandarizado de la prueba de Diebold-Mariano (1995) puede expresarse como:
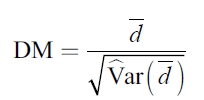 | [14] |
donde 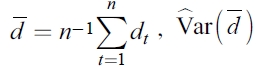 es un estimador consistente de la varianza asintótica de
es un estimador consistente de la varianza asintótica de 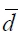 derivada de la suma ponderada de las autocovarianzas muestrales y
derivada de la suma ponderada de las autocovarianzas muestrales y 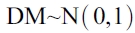 bajo la hipótesis nula, que se rechaza cuando el valor del estadístico es negativo y estadísticamente significativo.
bajo la hipótesis nula, que se rechaza cuando el valor del estadístico es negativo y estadísticamente significativo.
EVIDENCIA EMPÍRICA
En esta sección se reportan las estimaciones de los parámetros de las especificaciones de la media y varianza de los modelos GARCH, IGARCH, EGARCH y GARCH-GJR, las pruebas de diagnóstico sobre los residuales estandarizados y el análisis de la evaluación de los modelos de volatilidad fuera de la muestra. Para capturar la correlación serial y heterocedasticidad observada en los residuales estandarizados simples y cuadrados, es importante mencionar que, al principio del análisis de estimación, la especificación de la media condicional fue modelada con un proceso AR(1). Sin embargo, los resultados negativos y carencia de significancia en el término autorregresivo no apoyan empíricamente la especificación de los modelos AR(1)-GARCH, AR(1)-EGARCH y AR(1)-GARCH-GJR. Por ello, en el modelado de la volatilidad de los rendimientos de la Mezcla Mexicana de Exportación se implementaron especificaciones simples GARCH, EGARCH y GARCH-GJR. Además, Sadorsky (2006) ha demostrado que las especificaciones simples en las ecuaciones de la media condicional y varianza condicional son suficientes para la modelación y predicción de la volatilidad en los mercados de energía fósil.
Resultados estimados dentro de la muestra
Los parámetros de los modelos GARCH se estiman dentro de la muestra para los rendimientos diarios de la Mezcla Mexicana de Exportación para el periodo del 3 de enero de 1989 al 31 de diciembre 2007, utilizando el método de cuasi-máxima verosimilitud que proporciona errores estándar más robustos y asumiendo que las innovaciones siguen una distribución normal. Los resultados de los parámetros de cuasi-máxima verosimilitud de los cuatro modelos GARCH y sus errores estándar se muestran en el Cuadro 2. Al analizar los parámetros estimados de la especificación de la media se puede observar que todos los estimadores son estadísticamente significativos para los diferentes niveles de significancia, excepto para el modelo GARCH-GJR (1,1).
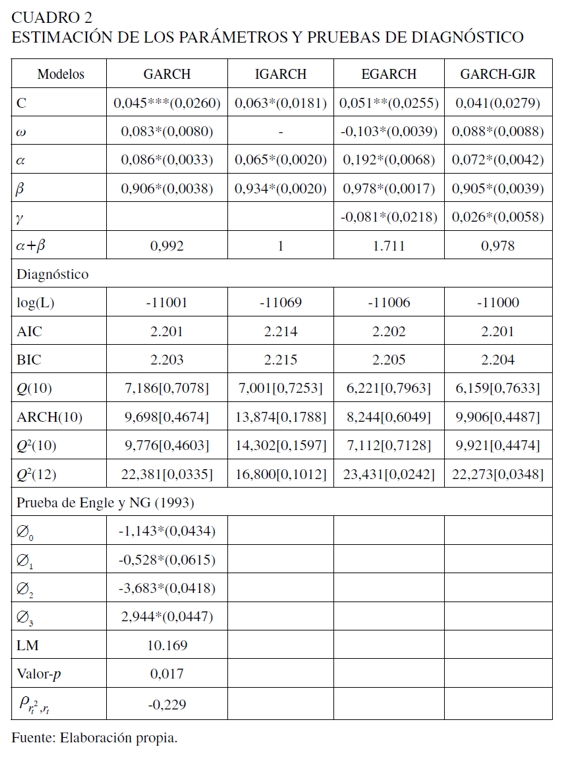
En cuanto a los parámetros de la ecuación de la varianza condicional, los modelos GARCH (1,1), IGARCH (1,1), EGARCH (1,1) y GARCH-GJR (1,1) capturan exitosamente los patrones dinámicos de la volatilidad condicional, ampliamente documentados en la literatura económica-financiera, dado que los estimadores son estadísticamente significativos en los niveles convencionales. En particular, los estimadores de los términos GARCH tienen valores positivos y caen en el rango 0,905-0,978, mientras que los coeficientes de los términos ARCH varían entre 0,065 y 0,192. Además, los valores del coeficiente de persistencia α + β se encuentran en el rango de 0,978-1,171, muy cerca de 1, lo que indica la presencia del componente de memoria larga en el proceso de la volatilidad. Este hecho favorece al modelo IGARCH (1,1) e implica que los choques en los rendimientos del petróleo tienen efectos permanentes y un alto grado de persistencia en la volatilidad, que desaparecen más lentamente a través del tiempo en proporción directa a una tasa hiperbólica que a una tasa de decaimiento exponencial. Por otra parte, pese a que el coeficiente de persistencia del modelo EGARCH (1,1) excede a 1, el proceso de la volatilidad continúa siendo estacionario y ergódico porque el valor absoluto del término GARCH se mantiene por debajo de 1; una condición necesaria y suficiente sustentada por Nelson (1991).
De acuerdo con los efectos asimétricos, los parámetros estimados asociados con la volatilidad asimétrica son significativamente diferentes de cero para cualquier nivel de significancia en ambos modelos asimétricos, aunque relativamente pequeños en términos absolutos, particularmente en el modelo GARCH-GJR (1,1). Obviamente, este hallazgo muestra que los efectos de apalancamiento están presentes en el mercado del petróleo de la Mezcla Mexicana de Exportación porque los choques negativos o noticias malas suelen tener mayor impacto en la volatilidad que los choques positivos o noticias buenas de la misma magnitud. Desde un punto de vista económico, este fenómeno puede ser explicado a través de la Gráfica 3, que presenta la predicción de la volatilidad condicional fuera de la muestra a través de los cuatro modelos GARCH, que es consistente con el comportamiento de la volatilidad actual.
Al analizar el periodo 2008-2009 de la Gráfica 3, se puede observar claramente cómo tanto choques negativos y positivos como la depreciación del dólar estadounidense, particularmente contra el euro7, y la recesión económica de los Estados Unidos se transmitieron inmediatamente a los mercados energéticos en forma más que proporcional. Por ejemplo, en la medida que el tipo de cambio nominal se devaluó, el petróleo presentó un comportamiento dinámico inverso al registrar altos precios nunca antes experimentados a lo largo de la historia, en parte generado por la burbuja especulativa en el mercado de materias primas, que finalmente ocasionó incertidumbre y una creciente volatilidad. En contraste, la agravación de la crisis financiera global, como consecuencia de la restricción del crédito, conllevó a los precios del petróleo a descender drásticamente en forma exponencial, y redujo la volatilidad en el mercado de la Mezcla Mexicana de Exportación. Este fenómeno de volatilidad asimétrica volvió a ocurrir, aunque con menor magnitud, en el periodo 2010-2011 debido al conflicto en Libia y a la crisis política en Medio Oriente, además de la incertidumbre de la crisis soberana de Grecia y el temor de una nueva recesión en Estados Unidos, como se puede observar en la Gráfica 3.
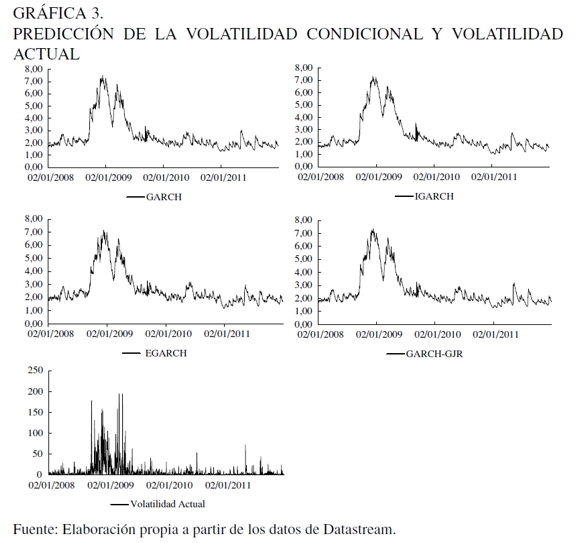
Así mismo, la presencia de asimetría en la estructura de la volatilidad está sustentada por la prueba estadística conjunta de Engle y Ng (1993). Los resultados reportados en el Cuadro 2 muestran que los parámetros estimados de la ecuación (9) son significativos estadísticamente. La significancia de φ1 indica la presencia de signo sesgado en el mercado de la Mezcla Mexicana de Exportación. Este resultado muestra que la volatilidad reacciona de manera asimétrica ante innovaciones negativas y positivas de la misma magnitud. Por otra parte, la existencia de magnitud sesgada alcanzada a través de la significancia de los parámetros φ2 y φ3 muestra que choques negativos (positivos) y grandes en las innovaciones de los rendimientos del petróleo tienen diferentes efectos en la volatilidad futura, a diferencia de choques pequeños en las innovaciones. Estos resultados también se sustentan por el valor negativo de la correlación muestral (-0,229) entre los rendimientos de los niveles y cuadrados aunado a la probabilidad pequeña (0,017) de la prueba del Multiplicador de Lagrange, que rechaza la hipótesis nula de que no existen efectos asimétricos en el mercado del petróleo mexicano, y que sugiere el uso de modelos GARCH asimétricos en la modelación del impacto de las innovaciones negativas y positivas sobre la volatilidad en el mercado del petróleo mexicano.
Regresando al análisis de las pruebas de diagnóstico, se analizan seis indicadores: el valor de la función de verosimilitud logarítmica Log(L); los criterios de información de Akaike y Schwarz (AIC y BIC); las pruebas estadísticas sobre los residuales estandarizados simples y cuadrados (Q(10) y Q2(10)) y la prueba de efectos ARCH, con el fin de evaluar los modelos de volatilidad con mejor desempeño dentro de la muestra. Considerando, en términos absolutos, los valores más pequeños de los indicadores Log(L), AIC y BIC reportados en el Cuadro 2. Los modelos GARCH (1,1) estándar y GARCH-GJR (1,1) presentan resultados superiores para capturar las características de la heterocedasticidad condicional, la volatilidad en aglomeraciones, la persistencia de los choques e incluso los efectos de apalancamiento, seguido por el modelo EGARCH (1,1). De acuerdo con la significancia de los valores del estadístico de la prueba de Ljung-Box con 10 rezagos, la evidencia muestra que la especificación de la ecuación de la media condicional es apropiada para explicar la dinámica de los rendimientos de los precios del petróleo, en particular, los modelos EGARCH (1,1) y GARCH-GJR (1,1), aceptando la hipótesis nula de inexistencia de correlación serial en los residuales estandarizados simples. Por su parte, la significancia de la prueba ARCH (10) también confirma la ausencia de evidencia estadística de efectos ARCH en los residuales estandarizados, mientras que la notable significancia de las pruebas de Ljung-Box con 10 rezagos sobre los residuales estandarizados cuadrados indica el buen ajuste de los cuatro modelos de volatilidad para explicar la heterocedasticidad observada en el mercado del petróleo mexicano, demostrando que no hay evidencia estadística de error de especificación en los modelos GARCH univariados. Sin embargo, los valores-p menores al nivel de significancia convencional del 5% de la prueba de Ljung-Box con 12 rezagos, indican que las especificaciones de la ecuación de la varianza podrían ser inapropiadas para modelar la volatilidad condicional de los rendimientos de la Mezcla Mexicana de Exportación. Aunque el modelo IGARCH (1,1) aún puede capturar apropiadamente la dinámica de la volatilidad a diferencia de los otros modelos.
Resultados de la predicción sesgada y óptima de los modelos de volatilidad
En esta sección, el análisis fuera de la muestra de la capacidad predictiva de los cuatro modelos GARCH está basado en la comparación de los errores de predicción para diferentes horizontes de operación. Para llevar a cabo la evaluación, se removieron las últimas observaciones que cubre el periodo 2008-2011; es decir, 1039 (1 día), 209 (5 días) y 52 (20 días). En el proceso del periodo de estimación para cada modelo de volatilidad se utiliza una ventana móvil, se agrega la observación más reciente y se elimina la observación más distante de la muestra de la siguiente manera: los parámetros estimados de la muestra r2,...,r4929 y la varianza condicional estimada 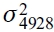 se utilizan para estimar
se utilizan para estimar 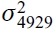 , que se compara con el valor de
, que se compara con el valor de 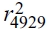 para determinar el error de predicción; para la comparación entre
para determinar el error de predicción; para la comparación entre 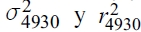 se utilizan los parámetros estimados de la muestra de r3,...,r4930 y la varianza estimada del periodo anterior. Este procedimiento se repite hasta obtener la predicción de la varianza condicional del 30 de diciembre de 2011 para cada horizonte de predicción. De esta manera, el tamaño de la muestra se mantiene fijo durante la reestimación de los modelos de volatilidad y las predicciones fuera de la muestra no se traslapan.
se utilizan los parámetros estimados de la muestra de r3,...,r4930 y la varianza estimada del periodo anterior. Este procedimiento se repite hasta obtener la predicción de la varianza condicional del 30 de diciembre de 2011 para cada horizonte de predicción. De esta manera, el tamaño de la muestra se mantiene fijo durante la reestimación de los modelos de volatilidad y las predicciones fuera de la muestra no se traslapan.
Los resultados del criterio informacional de las predicciones de la volatilidad que corresponden a la estimación de los parámetros, el coeficiente 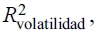 . La prueba estadística de Wald para restricciones lineales y su valor-p se reportan en el Cuadro 3. Analizando los valores de los estimadores se observa que el parámetro a1 es estadísticamente significativo a cualquier nivel y para 1, 5 y 20 días de operación. En contraste, el parámetro a0 no es estadísticamente significativo en los niveles convencionales, excepto para los modelos GARCH (1,1), EGARCH (1,1) y GARCH-GJR (1,1) para 1 y 5 días, además sus errores estándar tienden a incrementarse considerablemente con el horizonte del tiempo, excepto para el horizonte de 1 día.
. La prueba estadística de Wald para restricciones lineales y su valor-p se reportan en el Cuadro 3. Analizando los valores de los estimadores se observa que el parámetro a1 es estadísticamente significativo a cualquier nivel y para 1, 5 y 20 días de operación. En contraste, el parámetro a0 no es estadísticamente significativo en los niveles convencionales, excepto para los modelos GARCH (1,1), EGARCH (1,1) y GARCH-GJR (1,1) para 1 y 5 días, además sus errores estándar tienden a incrementarse considerablemente con el horizonte del tiempo, excepto para el horizonte de 1 día.
De acuerdo con la literatura sobre predicción de la volatilidad de los rendimientos del petróleo, la mayoría de los estudios evalúan el desempeño de los modelos GARCH, considerando solo el valor del coeficiente de determinación, 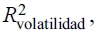 , aunque la variación en los coeficientes de determinación es mínima y no se encuentra diferencia significativa entre los modelos estimados para los diferentes periodos de predicción. La evidencia empírica muestra que el modelo GARCH (1,1) estándar presenta el poder predictivo más alto para capturar el comportamiento actual de la volatilidad condicional de los rendimientos de los precios de la Mezcla Mexicana de Exportación, seguido por el modelo GARCH-GJR (1,1) para los horizontes de 1 y 20 días y el modelo EGARCH (1,1) para 5 días de operación. En consecuencia, los resultados señalan que el modelo IGARCH (1,1) presenta el peor ajuste entre los modelos comparados para los tres horizontes de predicción. La proporción de variación total en la volatilidad capturada por el modelo GARCH (1,1) estándar es aproximadamente de 38,1%, 56,0% y 36,1% contra 33,3%, 39,0% y 35,2% del modelo GARCH integrado a pesar de que el valor de los parámetros estimados están muy cercanos a 0 y 1. Estos resultados se encuentran en línea con los hallazgos de Agnolucci (2009), que confirma el poder predictivo del modelo GARCH (1,1) para predecir la volatilidad en los mercados de futuros sobre petróleo WTI, aunque con valores
, aunque la variación en los coeficientes de determinación es mínima y no se encuentra diferencia significativa entre los modelos estimados para los diferentes periodos de predicción. La evidencia empírica muestra que el modelo GARCH (1,1) estándar presenta el poder predictivo más alto para capturar el comportamiento actual de la volatilidad condicional de los rendimientos de los precios de la Mezcla Mexicana de Exportación, seguido por el modelo GARCH-GJR (1,1) para los horizontes de 1 y 20 días y el modelo EGARCH (1,1) para 5 días de operación. En consecuencia, los resultados señalan que el modelo IGARCH (1,1) presenta el peor ajuste entre los modelos comparados para los tres horizontes de predicción. La proporción de variación total en la volatilidad capturada por el modelo GARCH (1,1) estándar es aproximadamente de 38,1%, 56,0% y 36,1% contra 33,3%, 39,0% y 35,2% del modelo GARCH integrado a pesar de que el valor de los parámetros estimados están muy cercanos a 0 y 1. Estos resultados se encuentran en línea con los hallazgos de Agnolucci (2009), que confirma el poder predictivo del modelo GARCH (1,1) para predecir la volatilidad en los mercados de futuros sobre petróleo WTI, aunque con valores 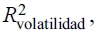 , muy pequeños en magnitud entre 2,2% y 2,7% y parámetros estimados casi iguales a 0 para a0 y por debajo de 1 para a1. En contraste, Hou y Suardi (2012) muestra que el modelo EGARCH (1,1) proporciona predicciones de la volatilidad superiores al modelo GARCH (1,1), pero con valores pequeños de a1 y coeficientes de determinación muy por debajo del 1%. La razón principal de los grandes valores en
, muy pequeños en magnitud entre 2,2% y 2,7% y parámetros estimados casi iguales a 0 para a0 y por debajo de 1 para a1. En contraste, Hou y Suardi (2012) muestra que el modelo EGARCH (1,1) proporciona predicciones de la volatilidad superiores al modelo GARCH (1,1), pero con valores pequeños de a1 y coeficientes de determinación muy por debajo del 1%. La razón principal de los grandes valores en 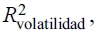 , y parámetros a1 por encima de 1 se atribuye al hecho de que la volatilidad condicional estimada tiende a exhibir un alto grado de persistencia, y probablemente cambios estructurales observados en los rendimientos de los precios de la Mezcla Mexicana de Exportación, como resultado del impacto de la crisis financiera global de 2008-2009 y la crisis de deuda soberana de la Eurozona en 2010-20118.
, y parámetros a1 por encima de 1 se atribuye al hecho de que la volatilidad condicional estimada tiende a exhibir un alto grado de persistencia, y probablemente cambios estructurales observados en los rendimientos de los precios de la Mezcla Mexicana de Exportación, como resultado del impacto de la crisis financiera global de 2008-2009 y la crisis de deuda soberana de la Eurozona en 2010-20118.
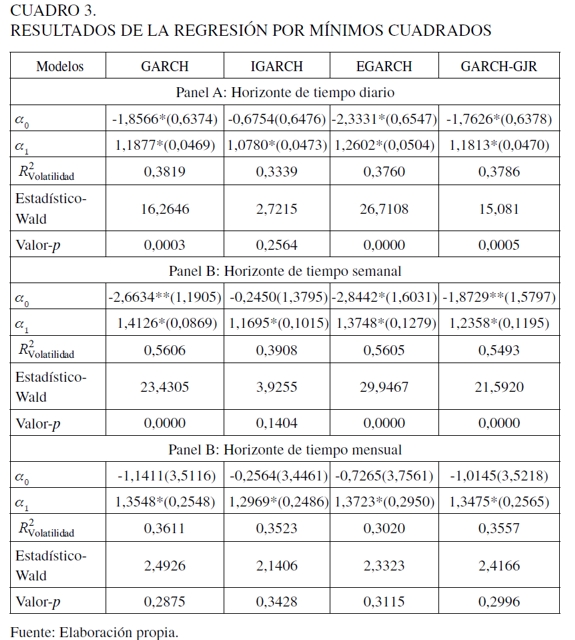
Aunque los resultados son aparentemente consistentes con la literatura empírica; sin embargo, la prueba estadística de Wald que establece dos restricciones lineales sobre los coeficientes estimados de regresión, muestra que el uso del coeficiente de determinación como medida para evaluar el poder predictivo de la volatilidad puede conducir a la selección de modelos de predicción insesgados, pero que carecen de predicción óptima. De acuerdo a los altos valores de las probabilidades de la prueba estadística de Wald reportados en el Cuadro 3, las predicciones de la volatilidad a través del modelo IGARCH (1,1) suelen capturar apropiadamente el movimiento en las fluctuaciones de los precios de la Mezcla Mexicana de Exportación, debido a su potencial para recoger la persistencia infinita de los choques en la varianza condicional que tardan más tiempo en desaparecer, a diferencia de lo que ocurre con los modelos GARCH estándar, EGARCH y GARCH-GJR, aunque no a la misma velocidad del nivel de la varianza actual. No obstante, cabe resaltar que para el horizonte de predicción de 20 días, los cuatro modelos predictivos muestran el mejor ajuste para explicar la dinámica de la volatilidad condicional. Este hallazgo puede ser atribuido, en gran parte, al hecho de que la proxy de la varianza actual es menos ruidosa, puesto que la evidencia empírica ha demostrado que el uso de datos de frecuencia baja reduce el grado del exceso de curtosis.
Para una mejor evaluación del poder predictivo entre dos modelos de volatilidad, analizamos los resultados de las funciones de pérdidas y la prueba estadística de Diebold-Mariano reportados en el Cuadro 4. Los resultados de los estadísticos MSE y QLIKE indican que los rendimientos de la Mezcla Mexicana de Exportación prefieren el modelo GARCH (1,1) estándar como benchmark para los horizontes de predicción de 1 y 5 días, mientras que el modelo EGARCH (1,1) proporciona los valores más pequeños de la medida MAE y superior capacidad para predecir la volatilidad fuera de la muestra que los otros modelos. Considerando el horizonte de predicción de 20 días, el modelo GARCH (1,1) estándar muestra, de nueva cuenta, la capacidad predictiva más alta para explicar las características estadísticas de la volatilidad condicional bajo las funciones de pérdidas SME y MAE. En tanto que el modelo IGARCH (1,1) proporciona el mejor ajuste bajo la medida QLIKE.
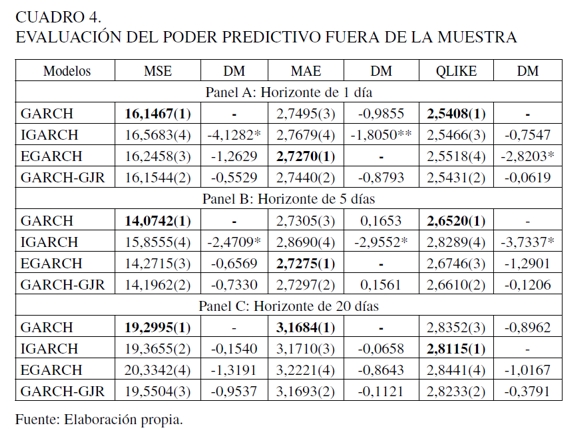
Los valores estimados del estadístico de DM evalúan el poder predictivo del modelo de volatilidad benchmark asociado con los diferentes modelos de volatilidad comparados, usando los diferenciales de las funciones de pérdidas MSE, MAE y QLIKE para los horizontes de predicción de 1, 5 y 20 días. Para el horizonte de 1 día, los valores negativos del estadístico de DM y su significancia rechazan la hipótesis nula de que los errores de predicción del modelo GARCH (1,1) estándar son similares a los de los modelos IGARCH (1,1) y EGARCH (1,1) bajo las medidas MSE y QLIKE, respectivamente. Los resultados basados en la medida MAE indican que el poder predictivo del modelo EGARCH es superior al del modelo IGARCH (1,1). Para el horizonte de predicción de 5 días, la significancia del estadístico de DM señala que el modelo GARCH (1,1) estándar, basado en las medidas SME y QLIKE y el modelo EGARCH (1,1) bajo la medida MAE, superan los modelos IGARCH (1,1) en cuanto al poder predictivo de la volatilidad condicional fuera de la muestra. Finalmente, para el horizonte de predicción de 20 días, la carencia de significancia en los estadísticos de DM revela que no existe diferencia en el poder de predicción de la volatilidad condicional entre los modelos benchmark y los modelos comparados bajo cualquier función de pérdidas; resultados que son sustentados por la prueba de predicción sesgada a través de la prueba estadística de Wald. Los resultados empíricos del presente trabajo revelan la eficiencia del modelo GARCH (1,1) estándar para desvanecer rápidamente en forma exponencial los choques en la volatilidad de los rendimientos en los precios de la Mezcla Mexicana de Exportación. Aunque es importante señalar la presencia de efectos de apalancamiento en las innovaciones de los rendimientos del petróleo mexicano originado por el impacto de las noticias asimétricas, como lo confirma el modelo EGARCH (1,1), particularmente en los horizontes de predicción de 1 y 5 días.
CONCLUSIONES
Este trabajo de investigación ha tratado de identificar un buen modelo para predecir la volatilidad, así como el comportamiento de las características empíricas de la volatilidad, particularmente la heterocedasticidad condicional, los efectos de asimetría y la persistencia en los rendimientos de los precios de la Mezcla Mexicana de Exportación durante el periodo del 2 de enero de 1989 al 30 de diciembre de 2011. Mediante la estimación de cuatro modelos GARCH, y usando dos pruebas estadísticas asociadas a tres funciones de pérdidas para la evaluación del poder predictivo de la volatilidad fuera de la muestra. El periodo de estudio parece muy interesante, dado que el mercado internacional del petróleo ha presentado momentos relativamente estables e inestables. En el análisis empírico dentro de la muestra, la evidencia indica que la estructura de la volatilidad condicional en el mercado del petróleo de baja calidad y alto contenido de azufre se caracteriza por exhibir frecuencias tanto bajas como altas de aglomeraciones en la volatilidad, efectos permanentes en el grado de persistencia sobre la volatilidad, y que presenta efectos de apalancamiento, fomentado por el impacto de las noticias asimétricas en los choques de los precios del petróleo, y sustentada por la prueba estadística conjunta de Engle y Ng (1993).
En términos del poder predictivo fuera de la muestra, los resultados muestran evidencia empírica mixta, de acuerdo con la aplicación de las dos pruebas estadísticas. La prueba de predicción sesgada confirma que el modelo IGARCH (1,1) proporciona el mejor desempeño, aunque no desde un punto de vista óptimo, para recoger la dinámica de la volatilidad de las innovaciones en los rendimientos de la Mezcla Mexicana de Exportación en comparación con los otros modelos de volatilidad, a pesar de que el modelo GARCH (1,1) estándar reporta coeficientes de determinación más altos y consistentes con los hallazgos de Agnolucci (2009). Entre tanto, los resultados de la evaluación de la predicción fuera de la muestra basados en el estadístico de Diebold-Mariano documentan mejor poder predictivo de los modelos GARCH (1,1) estándar y EGARCH (1,1) sobre los modelos IGARCH (1,1) y GARCH-GJR (1,1) para los horizontes de predicción de 1 y 5 días, pero manteniendo el mismo poder predictivo entre el modelo benchmark y los modelos de volatilidad comparados para el horizonte de 20 días.
En consecuencia, la información relevante del mercado energético obtenida de los hallazgos empíricos tiene implicaciones económicas-financieras para la toma de decisiones en materia de política monetaria, política energética, estrategias de cobertura, valuación de productos derivados energéticos, regulación, administración de riesgos e incluso en el pronóstico de precios futuros. Por ello, los gobiernos, consumidores industriales, autoridades reguladoras, inversionistas y analistas financieros no solo deben considerar la velocidad en la forma en que se desvanecen los choques en la varianza condicional, sino también los efectos de apalancamiento en la volatilidad originados por el impacto de las noticias optimistas y pesimistas en el momento de la selección de un modelo predictivo de volatilidad para los rendimientos del petróleo.
NOTAS AL PIE
1Durante el periodo de julio a diciembre de 2008, el precio del crudo fluctuó en una banda de alrededor de $145 a $30 dólares por barril para el West Texas Intermediate estadounidense (WTI), de $143 a $34 dólares para el Brent del Mar del Norte y de $132 a $26 dólares para la Mezcla Mexicana de Exportación.
2 Los tipos de petróleo WTI, Brent y Dubái, por sus propiedades químicas y físicas en cuanto al bajo porcentaje de azufre y alto grado de densidad, se utilizan como referencia para la formación de precios de otros tipos de petróleo de menor calidad y pesados que no cotizan en un mercado líquido, por lo que se negocian a un menor precio debido a sus altos costos de refinación.
3 Para más detalles acerca de los problemas de la oferta mundial de petróleo crudo generada por los principales marcadores del mercado, véase, por ejemplo, Montepeque (2005) y Fattouh (2007).
4 Los modelos lineales incluyen al GARCH estándar, IGARCH y RiskMetrics, mientras que los modelos no-lineales están formados por el EGARCH, GARCH-GJR, APARCH, FIGARCH, FIAPARCH y HYGARCH.
5 La Mezcla Mexicana de Exportación está compuesta por tres tipos de crudo: Olmeca, Maya e Istmo. El Maya es el crudo de densidad pesada que proporciona los mayores ingresos al país, equivalente al 83% del volumen total exportado en 2006 (Dávila et al., 2006).
6 Para más detalles técnicos de la prueba estadística, véase Diebold y Mariano (1995).
7 De acuerdo con De Jesús y Ortiz (2013), esta divisa extranjera ha experimentado un descenso significativo en su valor con respecto a las principales monedas duras y algunas monedas exóticas del mundo durante el periodo 2000-2010, por ejemplo, 30,81%, 19,70%, 23,47%, 40,73%, 20,29% y 7,86% contra el dólar canadiense, yen, euro, franco suizo, yuan chino y real brasileño, respectivamente.
8 En este marco, cabe mencionar que Liu y Shi (2013) obtuvieron coeficientes de determinación por arriba del 80%, pero para los precios intradía del mercado de energía eléctrica.
REFERENCIAS
[1] Agnolucci, P. (2009). Volatility in crude oil futures: A comparison of the predictive ability of GARCH and implied volatility models. Energy Economics, 31(2), 316-321. [ Links ]
[2] Bollerslev, T. (1986). Generalised autoregressive conditional heteroskedasticity. Journal of Econometrics, 31(3), 307-327. [ Links ]
[3] Brownlees, C., Engle, R. F. y Kelly, B. (2011). A practical guide to volatility forecasting through calm and storm. Journal of Risk, 14(2), 3-22. [ Links ]
[4] Cheong, C. W. (2009). Modeling and forecasting crude oil markets using ARCH-type models. Energy Policy, 36(6), 2346-2355. [ Links ]
[5] Coronado, S., Gatica, L. y Ramírez, M. (2012). Non-linear dependence in oil Price behavior. Journal of Mathematics and System Science, 2(2), 110-118. [ Links ] [ Links ]
[7] Diebold, F. X. y Mariano, R. S. (1995). Comparing predictive accuracy. Journal of Business and Economic Statistics, 13(3), 253-263. [ Links ]
[8] De Jesús, R. y Ortiz, E. (2013). El efecto de la volatilidad del peso mexicano en los rendimientos de la Bolsa Mexicana de Valores. Revista de Contaduría y Administración, 58(3), 89-119. [ Links ]
[9] Engle, R. F. (1982). Autoregresive conditional heteroskedasticity with estimates of the variance of the UK inflation. Econometrica, 50(4), 987-1008. [ Links ]
[10] Engle, R. F. y Ng, V. K. (1982). Measuring and testing the impact of news on volatility. Journal of Finance, 48(5), 1749-1778. [ Links ]
[11] Engle, R. F. y Bollerslev, T. (1986). Modelling the persistence of conditional variances. Econometric Reviews, 5(1), 1-50. [ Links ]
[12] Engle, R. F. y Ng V. K. (1993). Measuring and testing the impact of news on volatility. Journal of Finance, 48(5), 1749-1778. [ Links ]
[13] Fattouh, B. (2007). WTI benchmark temporarily breaks down: is it really a big deal? Middle East Economic Survey, 50(20), 1-8. [ Links ]
[14] Ferderer, J. P. (1996). Oil price volatility and the macroeconomic. Journal of Macroeconomics, 18(1), 1-26. [ Links ]
[15] Fong, W. M. y See, K. H. (2002). A Markov switching model of the conditional volatility of crude oil futures prices. Energy Economics, 24(1), 71-95. [ Links ]
[16] Glosten, L., Jaganathan, R. y Runkle, D. (1993). On the relation between the expected value and the volatility of the nominal excess returns on stocks. Journal of Finance, 48(5), 1779-1801. [ Links ]
[17] Hou, A. y Suardi, S. (2012). A nonparametric GARCH model of crude oil price return volatility. Energy Economics, 34(2), 616-626. [ Links ]
[18] Huntington, H. G. (1998). Crude oil prices and US economic performance: where does the asymmetry reside? Energy Journal, 19(4), 107-132. [ Links ]
[19] Kang, S. H., Kang, S. M. y Yoon, S. M. (2009). Forecasting volatility of crude oil markets. Energy Economics, 31(1), 119-125. [ Links ]
[20] Lee, K., Ni, S. y Ratti, R. A. (1995). Oil shocks and the macroeconomy: the role of Price variability. Energy Journal, 16(4), 39-56. [ Links ]
[21] Liu, H. y Shi, J. (2013). Appliying ARMA-GARCH approaches to forecasting short-term electricity prices. Energy Economics, 37(3), 152-166. [ Links ]
[22] Marzo, M. y Zagaglia, P. (2010). Volatility forecasting for crude oil futures. Applied Economics Letters, 17(16), 1587-1599. [ Links ]
[23] Meddahi, N. (2001). A theoretical comparison between integrated and realized volatilities. Manuscript, Université de Montréal. [ Links ]
[24] Mohammadi, H. y Su, L. (2010). International evidence on crude oil price dynamics: Application of ARIMA-GARCH models. Energy Economics, 32(5), 1001-1008. [ Links ]
[25] Montepeque, J. (2005). Sour crude pricing: a pressing global issue. Middle East Economic Survey, 48(14), 1-42. [ Links ]
[26] Morana, C. (2001). A semiparametric approach to short-term oil price forecasting. Energy Economics, 23(3), 325-338. [ Links ]
[27] Narayan, P. K. y Narayan, S. (2010). Modelling the impact of oil prices on Vietnam's stock prices. Applied Energy, 87(1), 356-361. [ Links ]
[28] Narayan, P. K. y Narayan, S. (2007). Modelling oil price volatility. Energy Policy, 35(12), 6549-6553. [ Links ]
[29] Nelson, D. (1991). Conditional heteroskedasticity in asset returns: A new approach. Econometrica, 59(2), 347-370. [ Links ]
[30] Patton, A. J. (2011). Volatility forecast comparison using imperfect volatility proxies. Journal of Econometrics, 160(1), 246-256. [ Links ]
[31] Reboredo, J. C. (2012). Modelling oil price and exchange rate co-movements. Journal of Policy Modeling, 34(3), 419-440. [ Links ]
[32] Sadorsky, P. (2006). Modeling and forecasting petroleum futures volatility. Energy Economics, 28(4), 467-488. [ Links ]
[33] Villalba, F. y Flores, M. (2013). Forecasting the variance and return of Mexican financial with symmetric GARCH models, Theoretical and Applied Economics, 20.3(580), 61-82. [ Links ]
[34] Wang, Y. y Wu, C. (2012). Forecasting energy volatility using GARCH models: Can multivariate models beat univariate models? Energy Economics, 34(6), 2167-2181. [ Links ]
[35] Wei, Y., Wang, Y. y Huang, D. (2010). Forecasting crude oil market volatility: Further evidence using GARCH-class models. Energy Economics, 32(6), 1477-1484. [ Links ]













