Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Cuadernos de Economía
Print version ISSN 0121-4772
Cuad. Econ. vol.34 no.65 Bogotá July/Dec. 2015
https://doi.org/10.15446/cuad.econ.v34n65.45936
http://dx.doi.org/10.15446/cuad.econ.v34n65.45936
Uso de variables de actividad económica en la estimación del PIB per cápita microterritorial
Using variables of economic activity in the estimation of microterritorial GDP per capita
Utilisation de variables d'activité économique dans l'évaluation du PIB per capita micro-territorial
Uso de variáveis de atividade econômica na estimação do PIB per capita micro-territorial
Alcides de Jesús Padilla Sierra a
a Universidad del Atlántico, Barranquilla, Colombia. Correo electrónico: alcidespadilla@mail.uniatlantico.edu.co.
Este artículo es el producto del proyecto de investigación "Crecimiento económico del distrito industrial y portuario de Barranquilla (1980-2006)", que se presentó como requisito de grado para optar al título de Magíster en Ciencias Económicas en la Universidad Nacional de Colombia, sede Bogotá.
Sugerencia de citación: Padilla Sierra, A. de J. (2015). Uso de variables de actividad económica en la estimación del PIB per cápita microterritorial. Cuadernos de Economía, 34(65), 349-376. doi: 10.15446/cuad.econ.v34n65.45936
Resumen
En este estudio se propone una metodología para calcular el producto interno bruto (PIB) per cápita de las principales ciudades de Colombia. Para este objetivo se utilizan algunas variables proxy de la actividad económica. Como resultado se señala que, a diferencia de estudios previos, el consumo de energía y el número de líneas telefónicas resultaron determinantes de la actividad económica urbana.
Palabras clave: medición del PIB per cápita, modelación econométrica, economía regional.
JEL: E01, C50, R10.
Abstract
This study proposes a methodology for the calculation of gross domestic product (GDP) per capita of major cities in Colombia. To do this, we used proxy variables of economic activity. As a result, it is noted that, unlike previous studies, the power consumption and the number of telephone lines proved to be determinants of urban economic activity.
Keywords: Measurement of GDP per capita, econometric modeling, regional economics.
JEL: E01, C50, R10.
Résumé
Dans cette étude une méthodologie est proposée pour calculer le produit intérieur brut (PIB) per capita des principales villes de Colombie. Pour cela nous utilisons plusieurs variables proxy de l'activité économique. Le résultat montre que, à la différence des études précédentes, la consommation d'énergie et le nombre de lignes téléphoniques sont des éléments déterminants de l'activité économique urbaine.
Mots-clés : mesure du PIB per capita, modélisation économétrique, économie régionale.
JEL : E01, C50, R10.
Resumo
Neste estudo, é proposta uma metodologia para calcular o produto interno bruto (PIB) per capita das principais cidades de Colômbia. Para este objetivo, são utilizadas algumas variáveis proxy da atividade econômica. Como resultado, afirma-se que, diferente de estudos prévios, o consumo de energia e o número de linhas telefônicas foram determinantes da atividade econômica urbana.
Palavras-chave: Medição do PIB per capita, modelação econométrica, economia regional.
Este artículo fue recibido el 29 de julio de 2013, ajustado el 25 de abril de 2014 y su publicación aprobada el 1o de julio de 2014.
INTRODUCCIÓN
La forma ortodoxa de medir el crecimiento económico de las naciones y provincias se funda en el cálculo del producto interno bruto per cápita (PIB per cápita). A su vez, la precisión de este cálculo determina en buena medida el nivel de bienestar de una unidad territorial. Sin embargo, a menudo solo se generan las estadísticas para el cálculo del PIB per cápita de las naciones y de los departamentos o provincias, pero no se estima el PIB per cápita de las ciudades. Para estimarlo, algunos países de Europa y América realizan sus cálculos por medio de algunas variables proxy. La labor de identificación de variables que den cuenta del PIB per cápita municipal constituye un ejercicio de monitoreo del desarrollo de la economía microterritorial. Este indicador entraría a formar parte del acervo informacional con el que debe contar cualquier administración pública local.
Dada la importancia del cálculo de esta variable microterritorial, se propone como objetivo una metodología de cálculo del PIB per cápita de las ciudades de Colombia. Este trabajo se desarrolla en tres dimensiones. Primera, se describe la teoría económica que sustenta esta investigación. Segunda, se calcula el PIB per cápita para las ciudades de Colombia, utilizando un par de variables de actividad económica sin precedentes empíricos en la estimación de este indicador y probando la capacidad predictiva de estas variables en la estimación. Tercera, se extrapolan de manera parcial algunas metodologías para calcular el PIB per cápita municipal.
REVISIÓN DE LA LITERATURA
Smith (1776) en el siglo xviii propuso la manera de medir el progreso de las naciones, estableciendo que debía hacerse por medio del PIB per cápita (en el lenguaje moderno):
El trabajo anual de cada nación es el fondo que le provee originalmente de todas las necesidades y comodidades de la vida que consumen anualmente y que siempre consiste en el producto inmediato de ese trabajo o en lo que se compra con ese producto a otras naciones. Así pues, como este producto o lo que se compra con él representa una proporción mayor o menor del número de personas que lo consumen, la nación estará mejor o peor abastecida de todas las necesidades y comodidades que es capaz de conseguir (Smith, 1776, p. 21).
El PIB per cápita hoy permite calcular el crecimiento de las naciones, y su cálculo se realiza mediante las llamadas cuentas nacionales1. En el pasado siglo, Kuznets (1901-1985) y en forma paralela Stone (1913-1991) y Meade (1907-1995) lideraron los procesos de armonización y sistematización de las cuentas nacionales en los Estados Unidos y la Gran Bretaña, respectivamente, con la coordinación institucional de las Naciones Unidas.
Estas primeras aproximaciones de cálculo del PIB contribuyeron en el desarrollo de los estudios macroeconómicos, gracias a que las variables determinantes para dichos cálculos se toman como base para las diferentes estimaciones. No obstante, han permitido calcular el PIB per cápita o el ingreso a otros niveles, es decir, regional, subregional, departamental y municipal, dada la carencia de información que desagregue las actividades económicas de las naciones.
De acuerdo con la teoría macroeconómica, existen tres formas de calcular el PIB, a saber: la del método del gasto, la del valor agregado y la del costo de los factores productivos. Todas son estimaciones del valor real del PIB2. Aunque estas metodologías indican la forma de calcular el PIB, es común encontrar en muchas naciones la inexistencia del cálculo del PIB microterritorial, esto es, municipio, provincia, etcétera. Al respecto, Jacobs (1985) y Glaeser, Kallal, Scheinkman y Shleifer (1992) consideran a las ciudades el epicentro del crecimiento económico, afirmando que su dinámica posibilita el desarrollo de las naciones.
Dada la importancia de las ciudades, se pueden encontrar diferentes trabajos que estiman el PIB per cápita de estas unidades microterritoriales y usan variables proxys para estimar el PIB per cápita o el ingreso per cápita. En Europa, Asia y los Estados Unidos, varios son los trabajos, entre los cuales se encuentran: Fellner (1923, 1924), Wilkins (1952), Cox (1968), Good (1994), Pammer (1997), Sutton y Costanza (2002), Chasco y López, (2004); Chasco Yrigoyen, Mella Márquez y López López (2005); Aparicio, Aznar y Aznar (2005) y Sutton, Elvidge y Ghosh (2007). Las estimaciones de Fellner (1923, 1924), Good (1994) y Pammer (1997) se orientan a calcular el ingreso nacional de algunos Estados europeos como el imperio Austro-Húngaro. Wilkins (1952) y Cox (1968), por su parte, estiman el ingreso per cápita de las ciudades británicas, Chasco y López (2004), Chasco et al. (2005) y Aparicio et al. (2005) calculan el ingreso per cápita de las ciudades españolas; Sutton y Costanza (2002) y Sutton et al. (2007) estiman el PIB de las ciudades de China, India, Turquía y los Estados Unidos. En América Latina los estudios del Instituto Brasileño de Geografía y Estadística (IBGE) (2004) y Cruz y Muñoz (2003) y los de Bonet y Meisel (1999), Núñez y Sánchez (2000) y Aguilera, Alvis y Arrieta (2000) para Colombia.
"Fellner, desarrolla la primera estimación del ingreso nacional en la víspera de la primera guerra mundial para el imperio Habsburg y sus dos más importantes subdivisiones, el imperio austríaco y el imperio húngaro" (Good, 1994, p. 870). Fellner estimó el ingreso nacional del reino de Hungría para los años 1899-1901 y 1911-1913. Estima el valor agregado de la agricultura, silvicultura y pesca, minería y la manufactura a pequeña escala, construcción, comercio, transporte y servicios (Eckstein, 2006, p. 154).
Wilkins (1952) utiliza el estatus social como medida de la situación económica de un área geográfica. Elaboró un índice de los niveles de ingresos para las mayores ciudades en el Reino Unido. Para cumplir con su objetivo realizó una serie de ecuaciones de estimación y utilizó una serie de variables proxy, de las cuales cuatro arrojaron la mayor correlación con respecto al porcentaje de hogares en los que el asalariado principal recibió un salario básico semanal de más de siete libras esterlinas; estas variables son: el inverso de la tasa de mortalidad infantil de la ciudad, el logaritmo del valor catastral de "otros bienes" per cápita, la tasa de ilegitimidad por cada mil nacidos vivos y el logaritmo del número de automóviles particulares per cápita.
Cox (1968) propone una metodología para estimar los ingresos y gastos de las ciudades británicas para el año 1961. En sus estimaciones utiliza la Encuesta de Presupuestos Familiares y el Censo del año 1961 publicada por el Gobierno. Encuentra dos relaciones entre las variables utilizadas. En la primera estimación, muestra una alta relación entre el número promedio de personas por hogar y los ingresos semanales de los hogares y demuestra que las mayores familias tienen más ingresos que las familias menores. En la segunda encuentra una relación inversa entre la clasificación socioeconómica de una ciudad (medida por el porcentaje de hombres ocupados y jubilados en la categoría profesional y de gestión) y el número medio de personas por hogar. Demuestra que los hogares en los que los hombres ocupados y jubilados están en la categoría profesional tienden a ser los de menor tamaño.
Good (1994), por su parte, obtuvo las estadísticas del ingreso a falta de estimaciones regionales del centro y del este de Europa para los años 1850-1910 y las usó para estimar el nivel de ingreso antes de 1914. Utilizó el producto nacional bruto per cápita (PNB per cápita) en función de varias variables proxy y realizó estimaciones de corte transversal y series de tiempo. En el desarrollo de su trabajo logró estimar diferentes modelos, combinando la variable dependiente PNB per cápita con las distintas variables independientes (proxy). Para el proceso de estimación, utilizó una moneda única, dada la diversidad de monedas existentes en la época en ese territorio, lo cual le permitió realizar comparaciones. Las variables regresoras del modelo son: tasa de mortalidad bruta, participación del trabajo del sector no agrícola en el total de fuerza laboral, cartas enviadas per cápita, tasa de incorporación escolar y depósitos reales de ahorro bancario. Todas las variables las presentó en logaritmo y trabajó su modelo con intercepto.
El mejor modelo estimado de acuerdo con el autor fue el PNB per cápita en función de la tasa de mortalidad bruta, participación del trabajo del sector no agrícola en el total de fuerza laboral y cartas enviadas per cápita. Se puede a su vez subrayar que los coeficientes resultaron con los signos esperados y estadísticamente significativos y la variable más importante fue la participación del trabajo en el sector no agrícola del total de fuerza laboral.
Pammer (1997) estima el PNB per cápita en función de algunas variables proxy en doce Estados europeos para el período 1850-1910, aunque su cálculo es una extrapolación del modelo de Good (1994). El autor, señala en su estudio, comprobará la robustez de la especificación del modelo presentado por Good (1994). La diferencia inicial del modelo de Good (1994) y Pammer (1997) es que este utiliza además como variable exógena el logaritmo de la participación de la agricultura en la fuerza de trabajo en la especificación de su modelo. Señala, a su vez, que mediante esta nueva variable proxy obtiene el 100% de la fuerza de trabajo. Además de utilizar una variable dummy que representa a Francia, Alemania, Italia y Noruega. "El diferencial entre los coeficientes de Good's... y los míos se debe al redondeo de los datos publicados por Good's, la diferencia es mínima y no perturba mi argumento" (Pammer, 1997, p. 448).
Sutton y Costanza (2002) calculan el PIB per cápita de las naciones del mundo utilizando como proxy la cantidad de luz eléctrica nocturna (LE) emitida por cada nación, medida por imágenes satelitales nocturnas. Además, miden el valor de los bienes no comercializables como los ecosistemas.
Chasco y López (2004) estiman la renta de los municipios de España utilizando un modelo espacial de ecuaciones aparentemente no relacionadas. El objetivo fundamental de estos autores es obtener una generalización de dichos modelos. Para ello utilizan una matriz de distancias espaciales3. Para predecir el ingreso municipal, los autores en primera instancia realizan sus estimaciones en el entorno provincial y luego extrapolan dichas estimaciones a un nivel geográfico más desagregado: las ciudades de la región. La técnica econométrica utilizada por Chasco y López (2004) es panel de datos, y en ella se tienen en cuenta los efectos de dependencia y heterogeneidad espacial.
En otro estudio, Chasco et al. (2005) realizan un ejercicio de predicción-extrapolación espacial partiendo de estadísticas oficiales existentes en escalas geográficas agregadas (provincias). Proceden a estimar el PIB per cápita en una escala desagregada (ciudades). Como variables explicativas incluyen el número de líneas telefónicas y los impuestos per cápita del total de actividades económicas empresariales y profesionales. Los resultados de la estimación caracterizada por la inclusión de un rezago espacial en el PIB per cápita condujeron a predicciones robustas.
Aparicio et al. (2005) plantean como objetivo estimar la renta disponible bruta de las comarcas y de las ciudades de la región de Aragón (España) con más de tres mil habitantes para el período 1999-2002. Utilizan dos metodologías. La primera consiste en cuantificar, por medio de producción, la renta municipal, para luego deducirle la renta bruta disponible; la segunda, obtener la renta bruta disponible mediante diferentes indicadores socioeconómicos. Las estimaciones obtenidas por estos autores con esta última metodología son consistentes con las del Instituto Nacional de Estadística de España.
Sutton et al. (2007) presentan un contraste de dos métodos para estimar el PIB subnacional de China, India, Turquía y los Estados Unidos en el año 2000. Utilizan la base de datos de la población mundial (Landscan) y la luz eléctrica nocturna de las ciudades de China, India, Turquía y los Estados Unidos tomada de Defense Meteorological Satellite Program's Operational Line Scan System (DMSP-OLS). Determinan las imágenes nocturnas como una medida aproximada de la actividad económica con dos metodologías de estimación del PIB. La primera emplea la suma de los valores de intensidad de luz y la segunda la extensión del área de las zonas iluminadas y una relación no lineal entre la población y la extensión del área.
El Instituto Brasileño de Geografía y Estadística (IBGE) (2004) calcula el PIB de algunas ciudades del Brasil para el período 1985-2001. Esta institución estima el PIB per cápita por medio del valor agregado de los sectores agropecuario, industrial, servicios, los impuestos y una variable dicotómica para el sector financiero. Cruz y Muñoz (2003) estiman el PIB per cápita combinando dos métodos: el del gasto y el de pago a los factores productivos. Su metodología consiste en seleccionar las variables que pueden dar cuenta del producto y que además se encuentren tanto en el ámbito estatal como en el municipal. Después de encontrar esas variables, proceden a estimar un modelo con las variables estatales para ver qué tanto se correlacionan con el PIB4. Utilizan diferentes formas funcionales y el método no paramétrico de predicción conocido como media de razones y razones de media5. Con esta metodología estiman el PIB del municipio de Puebla (México), y encuentran que las variables fiscales y las captaciones financieras son las que mejor explican el PIB estatal.
En Colombia, el Departamento Administrativo Nacional de Estadística (DANE) solo calcula el PIB del Distrito Capital de Bogotá y la alcaldía de Cali y mediante el Centro de Investigación en Economía y Finanzas (Cienfi) presenta el Sistema de Cuentas del Municipio anual y trimestral desde el año 1996. El resto de las ciudades de Colombia no calculan el PIB per cápita. En términos de estimaciones, Bonet y Meisel (1999) estiman el PIB per cápita utilizando como proxy los depósitos a la vista, las cuentas de ahorro y los depósitos a más de treinta días. Por su parte, Núñez y Sánchez (2000) estiman el PIB per cápita mediante los impuestos y Aguilera et al. (2000) determinan que el PIB per cápita de las ciudades es igual al PIB per cápita departamental menos las actividades económicas que no son propias de las zonas urbanas. Sin embargo, estas metodologías no están exentas de críticas.
A manera de crítica se puede inferir de las metodologías utilizadas por los autores mencionados lo siguiente: con respecto a las estimaciones realizadas por Bonet y Meisel (1999), estas solo se podrían realizar en las ciudades capitales o ciudades que tuvieran bancos. En el caso colombiano, existen municipios que no tienen bancos o por razones del conflicto interno se han tenido que trasladar a las ciudades capitales. Aplicar la metodología de Núñez y Sánchez (2000), por su parte, soslaya el problema de que en Colombia existen tres niveles de impuestos: el nacional, el departamental y el municipal, y dado que los municipios no tienen los mismos impuestos, sería difícil extrapolarlos. En cuanto a la metodología de Aguilera et al. (2000), utilizarla implicaría en gran parte organizar las cuentas municipales o desagregar las cuentas regionales para así contabilizar todas las actividades económicas.
Para la realización de esta metodología de cálculo del PIB per cápita para los municipios de Colombia se utilizaron las diferentes proxys propuestas por los distintos trabajos citados en párrafos anteriores y así observar el grado de correlación entre dichas variables y el PIB, pero los resultados no fueron los mejores. Este artículo propone realizar la predicción del PIB per cápita de algunas ciudades de Colombia por medio de la extrapolación de los parámetros estimados del PIB per cápita departamental. La idea principal es que no solo permitan estimar los valores en el ámbito agregado, que es donde ocurrirá el proceso de estimación de los modelos econométricos, sino también en el nivel desagregado microterritorial (municipal o distrital) al que se extrapolarán estos resultados y que es, en definitiva, el que se desea predecir. En otras palabras: el proceso consiste en realizar las estimaciones departamentales, es decir, de las unidades geográficas superiores, y luego extrapolar dichas estimaciones a un nivel geográfico más desagregado como los municipios de cada departamento. Para el proceso de selección de variables se necesita que las variables escogidas sean de carácter departamental, como en los municipios, para realizar la extrapolación.
DATOS
La información del PIB per cápita departamental proviene del DANE para los años 1996 y 2003. En el caso que se propone, el producto interno bruto departamental per cápita es una magnitud económica calculada mediante un sistema denominado cuentas regionales departamentales, y de acuerdo con la definición del DANE, se pueden extrapolar los estimadores obtenidos en el proceso de predicción del PIB per cápita departamental para calcular el PIB per cápita de los municipios de Colombia6. Las variables exógenas seleccionadas para el proceso de estimación con posterioridad a la realización de un análisis de componente principal son el consumo de energía y el número de líneas telefónicas per cápita. Con respecto a la variable consumo de energía, se obtuvo información del consumo anual total por departamentos y ciudades, apoyada en la nueva metodología de la Comisión de Regulación de Energía y Gas (CREG) y la información reportada por las empresas del sector eléctrico al Sistema Ãnico de Información (SUI)7.
El consumo final de energía se asocia al nivel y el crecimiento de la actividad económica (Stoft, 2002). Existen diversas investigaciones que prueban la importancia del consumo de energía eléctrica sobre el PIB, el progreso económico y el avance tecnológico de una sociedad. En este trabajo solo se enunciarán los que muestran la correlación entre el consumo de energía y el PIB. Se han realizado varios estudios de cobertura mundial que muestran la causalidad unidireccional y bidireccional entre estas dos variables. Dichos estudios se han llevado a cabo para algunos países desarrollados, entre los que destacan los de Kraft y Kraft (1978), que adelantaron un estudio para los Estados Unidos y encontraron causalidad unidireccional entre el ingreso (PIB) y el consumo de energía eléctrica. El estudio de Erol y Yu (1988) encuentra causalidad entre el PIB y el consumo de energía eléctrica para Japón y Alemania del Este. Hwang y Gum (1992), al igual que los autores mencionados, encuentran causalidad entre las dos variables para Taiwán. Soytas, Sari y ÖZdemir (2001) realizan un estudio para Turquía y encuentran causalidad por medio de un análisis de cointegración. Hrushikesh (2009) examina si el uso de la energía impulsaba el crecimiento económico, o viceversa, en el contexto de la India durante 1970-1971 y 2004-2005. El estudio emplea procedimientos econométricos de series de tiempo con el fin de comprender la relación dinámica de crecimiento de las diversas formas de energía. Realiza un análisis de descomposición de varianza y encuentra causalidad bidireccional entre el crecimiento del consumo de electricidad de la energía y el crecimiento económico.
En cuanto a las líneas telefónicas per cápita, se tomó la variable número de líneas de telefonía fija en servicio de las bases de datos de la Superintendencia de Servicios Públicos. Esta variable es una proxy de las telecomunicaciones. Existe evidencia sobre el efecto de los servicios de telecomunicaciones en el desarrollo y el crecimiento económico; muestra de ello son los estudios de Hardy (1980) y Narayana (2011). El primero estima como contribuye la telefonía en el desarrollo económico para sesenta países. La técnica de estimación es series de tiempo. Sus resultados muestran que la contribución del teléfono al desarrollo parece provenir de la ayuda del teléfono a la organización de la actividad económica. El otro investigador, por su parte, estima la contribución del crecimiento de los servicios de telecomunicaciones por los sectores público y privado y la distingue de los servicios de tecnología de información.
Se incluye, además, la distancia d como variable explicativa para tratar de capturar el efecto vecindario. Para capturar este efecto en las estimaciones, la distancia de cada departamento de Colombia se transforma siguiendo la metodología de Moreno y Vayá (2000). Específicamente, la distancia de cada departamento de Colombia se midió teniendo en cuenta las distancias entre las ciudades capitales. La información se toma del Ministerio de Transporte.
De acuerdo a [sic] la perspectiva geoestadística[,] se trata de un proceso espacial continuo, las observaciones se organizan por medio de la utilización de una distancia métrica, típicamente la distancia euclídea [sic], aunque no necesariamente. Asumiendo [sic] que la autocorrelación espacial es una función decreciente de la distancia, se compara la distancia que separa dos observaciones con una medida formal del valor de [d] similaridad entre ellas como, por ejemplo, la diferencia al cuadrado (Moreno y Vayá, 2000, pp. 47-48).
Para el caso de los departamentos y ciudades colombianos, la distancia a los centros de comercio es determinante para la producción de bienes y servicios. En forma específica se utiliza la distancia ponderada de cada departamento a las cuatro ciudades principales en términos comerciales, incluyendo la ciudad capital. En su orden, Bogotá como Distrito Capital y las ciudades capitales de los departamentos de Antioquia, Valle del Cauca y Atlántico con el resto de los departamentos de ciudades capitales de Colombia. El sentido de utilizar estas cuatro distancias de los organismos territoriales es el siguiente: cuanto más alejadas se encuentren las ciudades de estos centros de actividad económica comercial, el PIB per cápita tenderá a ser menor. Y además sirve, a su vez, para rezagar el PIB per cápita de cada uno de los departamentos8. En algunas investigaciones, la distancia se utiliza como un proxy para solucionar problemas de endogeneidad (Sánchez, López-Uribe y Fazio, 2010).
METODOLOGÍA
Lo primero que se realizó son las estadísticas descriptivas de cada una de las variables, para determinar la existencia de datos atípicos u outliers (Cuadro 1)9. Luego se estima por mínimos cuadrados ordinarios (MCO) para probar si las variables seleccionadas explican el PIB per cápita departamental. Los resultados muestran que algunas variables no son estadísticamente significativas (véase Anexo 1). Dados estos resultados, se hace un análisis de componente principal (ACP), como se expresa en anteriores párrafos (véase Anexo 2). Los resultados muestran que las componentes principales número de líneas telefónicas, impuestos y consumo de energía per cápita explican en conjunto el 94,70% y 90,33% para los años 1996 y 2003, respectivamente, de la variabilidad total del PIB per cápita. Las variables líneas telefónicas y consumo de energía, el 87,01% y el 80,9% para los años 1996 y 2003, respectivamente, de la variabilidad total del PIB10.
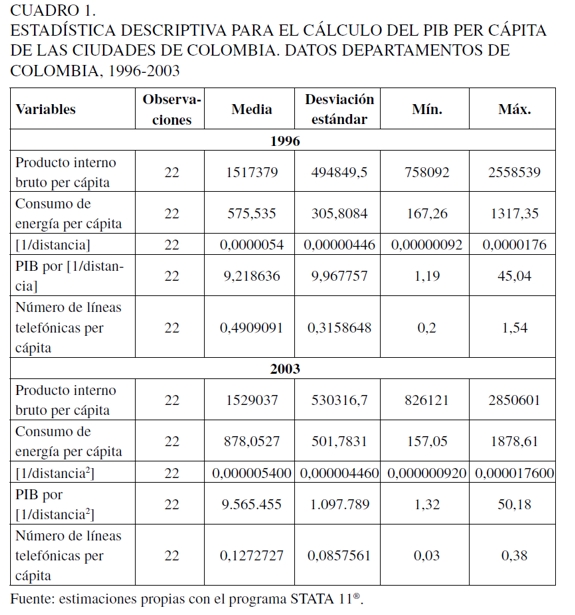
Después del proceso de selección de variables se ejecutaron tres métodos de estimación. El primero es un ejercicio de estimación ordinaria; al hablar de estimación ordinaria se trata de la utilización de los MCO. Un hecho muy importante para la estimación del PIB per cápita microterritorial es haber encontrado una variable de las actividades económicas que hasta ahora no se ha tenido en cuenta en la literatura, a saber: el consumo de energía per cápita. Con respecto a las estimaciones, los coeficientes obtenidos fueron estadísticamente significativos tanto en lo individual como en conjunto, superando a su vez las pruebas de violación de los supuestos clásicos como heterocedasticidad y normalidad de los residuos. Se estimaron dos modelos mediante MCO. Los modelos son los siguientes:
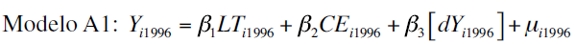 | [1] |
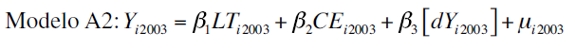 | [2] |
donde Y es el PIB per cápita, LT es el número de líneas telefónicas per cápita, CE es el consumo de energía per cápita, dY producto interno bruto per cápita de cada departamento multiplicado por la matriz de distancia y d es una matriz que contiene las distancias a los principales centros de actividad económica.
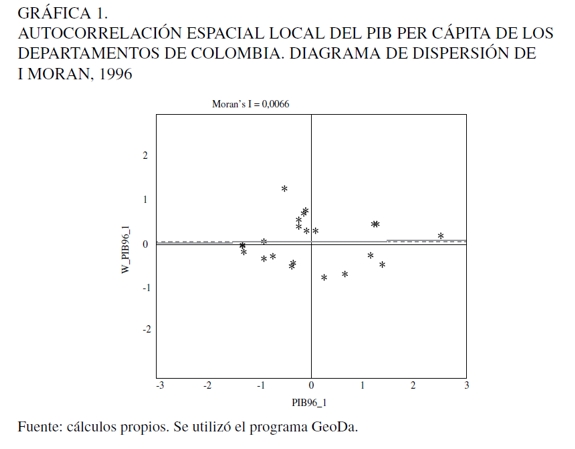
El segundo método es un ejercicio de predicción-extrapolación espacial; el supuesto básico es la existencia de problemas de autocorrelación espacial. El método de estimación es por máxima verosimilitud. Esta se realizó utilizando una variable exógena la cual se denomina PIB per cápita retardado, que no es más que la aplicación de la distancia entre departamentos al PIB per cápita. Para ello se utiliza una matriz de distancias espaciales que incluye la variable dependiente espacialmente retardada denominada W11. Antes de estimar por máxima verosimilitud se les aplicaron contrastes sobre los efectos espaciales de autocorrelación espacial. Cliff y Ord (1981) consideran la estimación por máxima verosimilitud la más aconsejable, la cual se ha perfilado a lo largo de los años de desarrollo de la econometría espacial como una de las alternativas dominantes. Las Gráficas 1 y 2 muestran el contraste aplicado denominado Scatterplot de Moran para los años 1996 y 2003, respectivamente, y en el Cuadro 2 se hace otra prueba de contraste conocida como el índice de Moran. Con el Scaterplot es posible inferir que entre los departamentos de Colombia tomados en este estudio -incluso Bogotá- existe un departamento atípico en el patrón global de asociación espacial. Este elemento atípico es propiamente Bogotá. Al respecto, de acuerdo con los significados de cada cuadrante, es un distrito rico rodeado de departamentos ricos. La Gráfica 1 indica la inexistencia de dependencia espacial de la variable PIB per cápita; sin embargo, se procedió a estimar los modelos utilizando la variable dependiente espacialmente retardada. Se hizo para saber si en los modelos la variable dependiente espacialmente retardada servía para predecir el PIB per cápita.
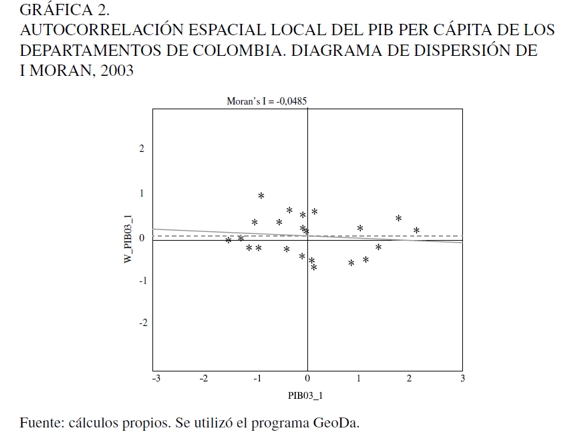
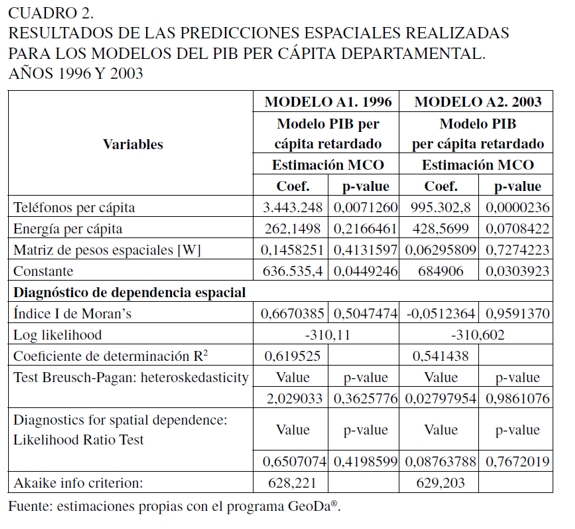
El Cuadro 2 muestra las estimaciones, las cuales corresponden al campo de la econometría espacial. Aunque no se encontraron problemas de autocorrelación espacial como lo expresan el índice I de Moran's y Scatter Plot de Moran's, se probó con los coeficientes obtenidos para conocer su capacidad de predicción. No obstante, los resultados arrojados en las estimaciones muestran que para el año 1996 las líneas telefónicas per cápita y la constante resultaron significativas estadísticamente y para el año 2003 todas las variables exógenas también, pero la matriz de pesos espaciales para corregir los problemas de autocorrelación no es estadísticamente significativa. Este resultado no es extraño, dado que el modelo no tiene problemas de autocorrelación espacial. Los modelos fueron los siguientes:
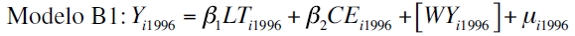 | [3] |
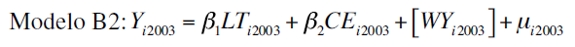 | [4] |
Y el tercero es la estimación por datos de panel que utiliza un panel equilibrado, el cual se realizó para contar con mayor información y ganar grados de libertad, entre otras razones.
La característica clave de los datos de panel que los diferencia de los datos fusionados de sección cruzada es el hecho de que se mantiene un registro de las mismas unidades de sección cruzada... durante un período de tiempo determinado. [Estos pueden ser dos, tres, cuatro, t períodos diferentes] (Wooldridge, 2006, p. 12).
Se estiman los parámetros por departamento y se utilizan para calcular el PIB per cápita microterritorial. El ejercicio de extrapolación se trabaja con dos períodos diferentes, el de 1996 y el 2003, y los departamentos son los mismos para los dos períodos. La justificación de estimar con datos en panel se puede resumir en los siguientes tres elementos.
1) El control de la heterogeneidad individual. Los datos de panel suponen que los individuos, las empresas, Estados o países son heterogéneos. Los estudios de series de tiempo y corte transversal no controlan esta heterogeneidad y corren el riesgo de obtener resultados sesgados. 2) Los datos de panel proporcionan datos más informativos, más variabilidad, menos colinealidad entre las variables, más grados de libertad y una mayor eficiencia. Los estudios de series están plagados de multicolinealidad. 3) Los datos de panel son más capaces de estudiar la dinámica de ajuste. Distribuciones transversales que parecen ocultar relativamente estable una multitud de cambios (Baltagi, 2005, pp. 18-19).
Se estimó por efectos fijos y aleatorios y se aplicó la prueba de Hausman (1978) para escoger el mejor método de estimación. La conclusión es que la estimación por efectos fijos es más conveniente que por efectos aleatorios. Dados los resultados de la predicción con datos en panel, donde se logró seleccionar la estimación por efectos fijos como la más adecuada, se utilizan los parámetros por la estimación en mención. La predicción estuvo en el orden del 50% del verdadero valor del PIB per cápita de los departamentos de Colombia; es decir, del PIB per cápita calculado por el DANE para ambos años. El resultado se obtuvo multiplicando cada coeficiente obtenido por los valores per cápita de cada variable. Los cálculos de la estimación por efectos aleatorios resultó más adecuada que la estimación por efectos fijos (véase Anexo 3).
RESULTADOS
En el Cuadro 3 se presentan las estimaciones de los modelos B. Se puede inferir que para el año 1996 las variables LT per cápita y CE per cápita fueron estadísticamente significativas al 5% y al 8%, respectivamente. Por su parte, las proxys de las distancias fueron significativas para las ciudades de Barranquilla y Medellín al 5%. Los resultados de la estimación implican que la distancia multiplicada por el PIB per cápita departamental tiene un efecto decreciente sobre el PIB per cápita municipal. A cuantos menos kilómetros de distancia se encuentren las ciudades periféricas de las ciudades capitales comerciales e industriales (Bogotá, Medellín y Barranquilla), mayor es el PIB per cápita municipal. Ahora, si se duplica dicha distancia, el PIB per cápita municipal tiende a disminuir. Por ejemplo, cada vez que se duplica la distancia a Barranquilla, la disminución del PIB per cápita es de [202,8557 - (1/2)*(15.360,12)(1)] = -$ 7.477,2043. Es pertinente aclarar que este es un valor relativo, dado que existen tres centros importantes de actividad económica y cada uno tiene un efecto marginal sobre cada departamento o ciudad. Los signos de cada estimador son los esperados.
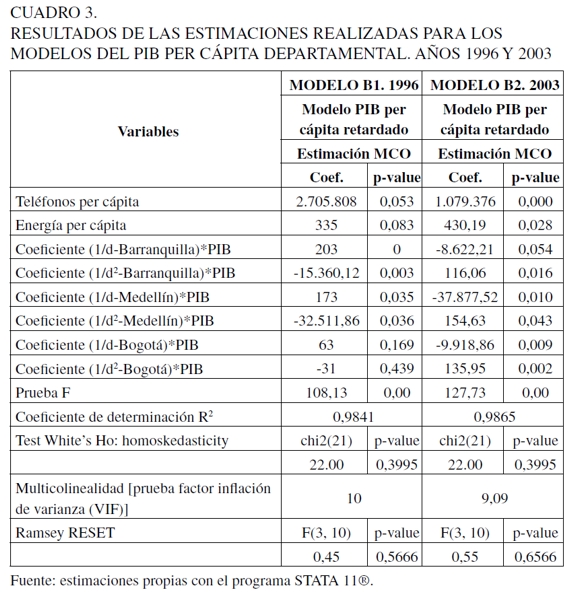
Para el 2003, Modelo B2, todas las variables al igual que las variables de distancia resultaron ser significativas al 1%, 5% y 10%. Los resultados fueron más robustos para el 2003 que para 1996. Se realizó la prueba de heterocedasticidad de White, la de especificación de Ramsey-Reset y la de factor de inflación de varianza para detectar multicolinealidad y no se violó ninguno de los supuestos clásicos del modelo.
Predicción del PIB per cápita de los departamentos de Colombia
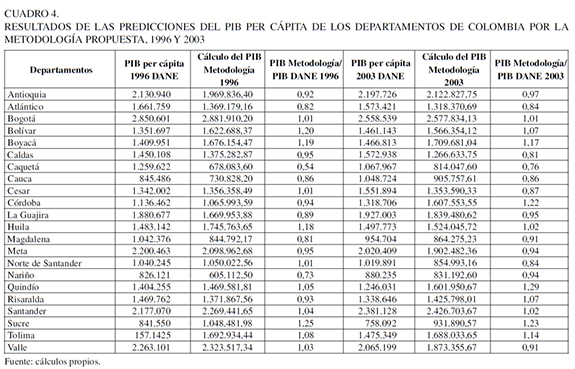
Se procede a obtener las predicciones del PIB per cápita de todos los departamentos de Colombia y para las ciudades capitales. El Cuadro 4 muestra las distintas estimaciones realizadas. Estas estimaciones logran predecir el PIB per cápita departamental y casi todas generan valores muy cercanos al verdadero valor observado. En efecto, los departamentos más importantes de Colombia como el Distrito Capital, Atlántico, Valle del Cauca y Antioquia generan las mejores predicciones.
Cálculo del PIB per cápita de los municipios de Colombia
Una vez estimados los modelos departamentales del PIB per cápita para los años 1996 y 2003 se supone que los estimadores obtenidos son similares a las de las ciudades. Para obtener el PIB per cápita de las ciudades de Colombia se multiplica el parámetro obtenido por medio de la estimación del PIB departamental por el valor per cápita del consumo de energía por municipio (CEM) y el número de líneas telefónicas por municipio (LTM) y los resultados se suman. De igual forma, se le adicionan los valores de la matriz de distancia utilizada. Las ecuaciones para el cálculo del PIB de las ciudades se expresan a continuación:
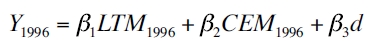 | [3] |
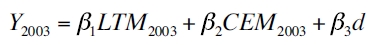 | [4] |
Y = producto interno bruto per cápita de los municipios de Colombia.
LTMi = número de líneas telefónicas por municipio per cápita de los años 1996 y 2003.
CEMi = consumo de energía por municipio en kw per cápita de los años 1996 y 2003.
d = distancia de cada ciudad a los centros de comercio.
β1, β2, β3 = parámetros estimados para los departamentos de Colombia, extrapolados para las ciudades capitales.
Los modelos expresados son una reespecificación de los modelos departamentales; lo que se desea es calcular el PIB per cápita de los municipios de Colombia. Con respecto a las ecuaciones, inicialmente se había presentado el componente [1-λW]-1. De acuerdo con Anselin (2002), es un multiplicador espacial global que une la variable endógena con todas las regresoras, pero en este modelo no se presenta autocorrelación espacial, por lo cual no se utilizó para la predicción.
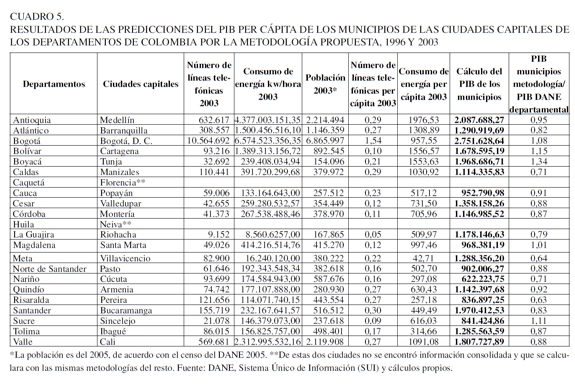
En el Cuadro 5 se presentan los resultados de la estimación del PIB per cápita de las ciudades de Colombia para el año 2003. Como se expresó, es una extrapolación. Aquí se utilizan los coeficientes generados por las estimaciones realizadas por MCO (modelo departamental) y se multiplican por los valores de cada municipio. Los resultados del cálculo muestran las ciudades capitales como Medellín, cuyo PIB per cápita es $ 2.087.688,27, el cual representa un 95% del PIB per cápita del departamento de Antioquia calculado por el DANE. Con la metodología empleada, el PIB calculado de Bogotá, D. C., es el 100% del PIB per cápita calculado por el DANE. Este hecho se concibe como un buen argumento para validar esta metodología. El PIB per cápita de Cali es de $ 1.807.727,89 y representa el 88% del PIB del departamento calculado por el DANE.
En estos cálculos de igual forma se demuestra la importancia de cada ciudad capital. En estos municipios se concentra la producción de cada departamento. Normalmente en Colombia las industrias se concentran en las urbes; este es un fenómeno económico de localización de las empresas, las cuales buscan la mayor población.
CONCLUSIONES
Calcular el PIB per cápita de los municipios es de suma importancia para las políticas económicas locales y para la nación en su conjunto. Este esfuerzo por estimar el PIB per cápita de las ciudades de Colombia permitió encontrar múltiples diferencias con las investigaciones de carácter local y con los estudios del resto del mundo. Una de esas diferencias con los estudios realizados en Colombia como los de Bonet y Meisel (1999) y Núñez y Sánchez (2000) se enmarca en que las variables fiscales y financieras no resultaron significativas. Y en realidad, al intentar realizar las predicciones ignorando los niveles de significancia estadística, no generaron los mejores resultados. Además, estas metodologías no se aplicarían a todos los municipios de Colombia, pues una utiliza las cuentas financieras porque en Colombia existen municipios que no tienen bancos o los productores y comerciantes realizan sus transacciones en las ciudades capitales; y en la que utiliza los impuestos no es buena la estimación, porque los municipios de Colombia tienen una estructura tributaria diferente de los departamentos, y aunque se realizó la estimación, estas variables no resultaron significativas. Esta investigación es el primer trabajo que utiliza el consumo de energía y el número de líneas telefónicas y logra estimar el PIB de los municipios.
Con referencia a los estudios de Chasco y López (2004) y Chasco et al. (2005), dado que se intentó extrapolar las metodologías desarrolladas por estos autores para el caso de los municipios de Colombia, se encontró una variable de actividad económica distinta de los estudios referenciados, la cual es el consumo de energía per cápita. Otra de las diferencias es que se adoptó una fórmula para estimar el PIB per cápita de los departamentos de Colombia sin utilizar la matriz de pesos espaciales. Los resultados fueron positivos porque se logró estimar el PIB per cápita, para el caso el de los departamentos de Colombia, y se extrapoló de igual forma para calcular el PIB per cápita de las ciudades de Colombia.
Desde el punto de vista de las estimaciones realizadas por MCO y Data Panel, se encontró que la mejor predicción del PIB per cápita departamental la arrojó la estimación por MCO. Y mediante esta se puede establecer que la estimación del PIB per cápita de los departamentos de Colombia y el Distrito Capital de Bogotá es muy cercana. Para el caso específico de la capital, es del 100% del PIB per cápita calculado por el DANE. De igual forma se logró calcular el PIB de las ciudades principales de Colombia. Además, a pesar de haberse escogido como la mejor metodología la estimación por MCO, se encontró que cuando se estimaron con datos de panel las variables seleccionadas, aunque resultaron significativas, la predicción no era la más cercana al verdadero valor del PIB per cápita departamental.
Todos los resultados encontrados hasta ahora pueden ayudar a desarrollar trabajos microterritoriales y solo constituye esta investigación una pequeña parte de lo que se puede lograr si se exploran muchas más variables y otras metodologías. Hoy sabemos que cuanto más consumo de energía eléctrica tenga una nación puede significar mayor subdesarrollo y qué decir sobre la telefonía fija, la cual ha sido en parte desplazada por la telefonía celular, aunque las empresas -que constituyen el elemento de mayor importancia del crecimiento de una economía- no dejan de usar este servicio y en efecto pueden aumentarlo a medida que crecen. Estas nuevas proxys podrán servir de base para otras investigaciones.
ANEXO 1
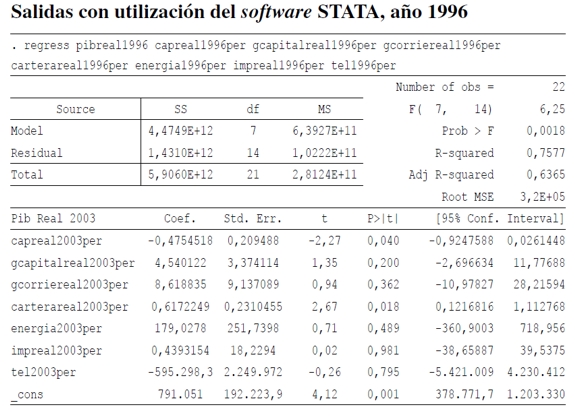
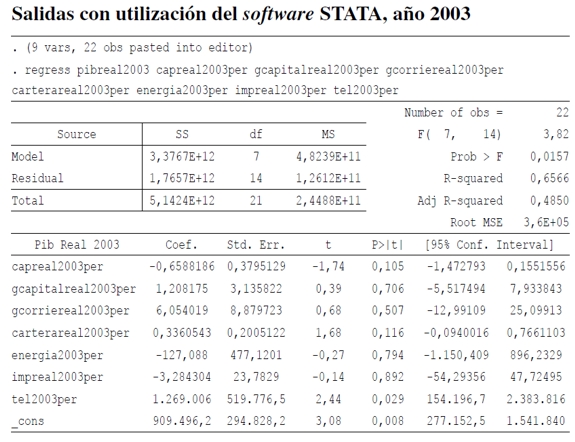
Donde:
pibreal = producto interno bruto real per cápita de los departamentos de Colombia, 1996 y 2003.
capreal = captaciones de los bancos reales per cápita de los departamentos de Colombia, 1996 y 2003.
gcorriereal = gastos corrientes reales de los departamentos de Colombia, 1996 y 2003.
carterareal = cartera de los bancos reales de los departamentos de Colombia, 1996 y 2003.
energía = consumo de energía per cápita de los departamentos de Colombia, 1996 y 2003.
impreal = impuestos reales per cápita de los departamentos de Colombia, 1996 y 2003.
tel = número de líneas telefónicas per cápita de los departamentos de Colombia, 1996 y 2003.
ANEXO 2
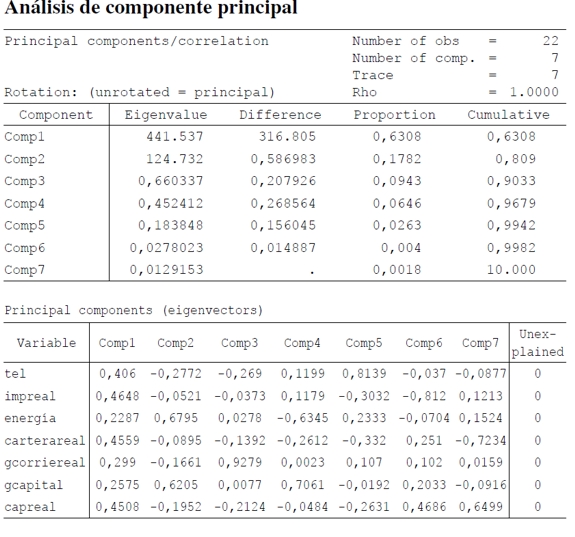
ANEXO 3
Estimación Data Panel
Modelo I. Estimación por efectos aleatorios
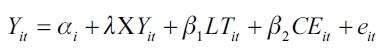 | [5] |
Donde:
Siendo Yit = producto interno bruto per cápita de cada departamento y de los años 1996 y 2003.
LTit = líneas telefónicas por habitante de cada departamento y de los años 1996 y 2003.
CEit = consumo de energía en kw por habitante de cada departamento y de los años 1996 y 2003.
XYit = producto interno bruto per cápita de cada departamento y de los años 1996 y 2003 con retardo.
α i = α + ui . = rs una variable aleatoria con un valor medio a y una desviación aleatoria ui de este valor medio.
λ, β1, β2 parámetros que hay que estimar.
eit = perturbaciones aleatorias con las consabidas buenas propiedades.
Sustituyendo α i = α + ui en (5) se obtiene:
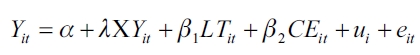 | [6] |
Al realizar las estimaciones, las dos variables exógenas del modelo no son significativas al 5%, aunque es mejor estimar por efectos aleatorios que con datos agrupados. Lo anterior se puede corroborar con los resultados de la prueba de Multiplicador de Lagrange de Breusch-Pagan.
El p-value indica que se rechaza la hipótesis nula; por tanto, los efectos aleatorios ui son relevantes y es preferible usar la estimación de efectos aleatorios en vez de datos agrupados.
Estimación por efectos fijos
Una vez estimado por efectos aleatorios se procede a estimar por efectos fijos. Este modelo no supone que las diferencias entre los departamentos de Colombia sean aleatorias, sino constantes o fijas, y por ello se estimará cada intercepto. Existen factores inobservables que influyen en la variable dependiente, en este caso el PIB per cápita.
Modelo II. Estimación por efectos fijos
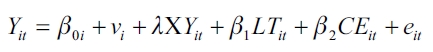 | [7] |
Donde:
Siendo Yit = producto interno bruto per cápita de cada departamento y de los años 1996 y 2003.
LTit = líneas telefónicas por habitante de cada departamento y de los años 1996 y 2003.
CEit = consumo de energía en kw por habitante de cada departamento y de los años 1996 y 2003.
XYit = producto interno bruto per cápita de cada departamento y de los años 1996 y 2003 con retardo.
vi = es un vector de variables dicotómicas para cada estado.
λ, β0i, β1, β2= parámetros que se han de estimar.
eit = perturbaciones aleatorias con las consabidas buenas propiedades.
Al igual que en la estimación por efectos aleatorios, en la estimación por efectos fijos las dos variables independientes del modelo no son significativas. Desde el punto de vista de la teoría económica, las variables no presentan los signos correspondientes.
Cuando se testea si se estima por efectos fijos o agrupados por medio de la prueba F, se puede inferir que es preferible estimar por efectos fijos que con datos agrupados, dado que el p-value indica que se rechaza la hipótesis nula.
Ahora se procede a determinar si es mejor estimar por efectos fijos o por efectos aleatorios. Para ello se utilizó el test de Hausman.
La prueba de Hausman (1978) sirve para determinar si se estima por efectos fijos o aleatorios. La hipótesis nula de la prueba de Hausman establece que los estimadores de efectos aleatorios y de efectos fijos no difieren sustancialmente. Por tanto, en este estudio se encontró que los estimadores sí diferían, y por consiguiente se rechazó la hipótesis nula. La conclusión es que la estimación por efectos fijos es más conveniente que por efectos aleatorios.
Salidas modelo


NOTAS AL PIE
1 Que tienen sus comienzos con William Petty (1623-1687).
2 El método del gasto es una estimación del PIB que utiliza variables de demanda agregada, a saber: consumo, inversión, gasto público y exportaciones netas (exportaciones menos importaciones). A su vez, el método del valor agregado es la suma de todos los valores añadidos en cada fase de la producción, teniendo en cuenta que el PIB es la suma de todos los bienes finales. Por su parte, el costo de los factores productivos es lo que un empresario paga por el uso de los elementos que intervienen en la producción: el capital y el trabajo. Por dicho uso se pagan salarios e intereses, respectivamente.
3 Se trata de una matriz que representa las distancias entre las regiones vecinas. Con ella se tienen en cuenta las relaciones de vecindad espacial contemporáneas y no contemporáneas.
4 Las variables seleccionadas fueron gastos totales, captación bancaria y número de afiliados al seguro social.
5 La media de razones se calcula como la media de una serie de datos de las variables explicativas estatales y municipales. Luego se calculan las razones correspondientes. Las razones de media, por su parte, se calculan obteniendo la media de una serie de datos de las variables explicativas estatales y municipales, para luego calcular el cociente de las medias.
6 El DANE establece que se trata de una operación estadística derivada sobre la totalidad de la actividad económica departamental, de la división político-administrativa del país. Asimismo, utiliza los resultados de las cuentas nacionales y, aplicando indicadores económicos para una parte del sistema y con información directa para otra parte de la actividad productiva del país, distribuye el valor agregado por departamento y por rama industrial, con apoyo en una metodología descendente para el cálculo de los respectivos agregados regionales en total coherencia con los nacionales. La recopilación de la información se realiza en los establecimientos industriales porque de acuerdo con tal entidad, es aquí en donde se realiza toda la producción de los bienes y servicios y se evidencian las relaciones insumo-producto para el correspondiente análisis de la producción.
7 La información reportada por la CREG como unidad de medida está dada en gigavatios-hora, facturada para la mayoría de los años y estandarizada en kilovatios-hora para efectos de la estimación que aquí se propone.
8 El término rezago se utiliza para determinar el grado de correspondencia del PIB per cápita con los centros de actividad comercial.
9 En el Cuadro 1 solo se describen las variables significativas seleccionadas en esta investigación para estimar el PIB per cápita de los municipios de Colombia. En el Anexo 1 se describen todas las variables utilizadas para probar si resultaban significativas según la literatura referenciada e incluye las estimaciones realizadas por MCO.
10 Aunque la variable impuesto junto con el consumo de energía y el número de líneas telefónicas explican más del 90% del comportamiento de la varianza del PIB per cápita, no se tuvo en cuenta en el proceso de estimación final por la siguiente razón: en Colombia los departamentos y municipios tienen dos estructuras de impuestos diferentes, lo cual no permitiría extrapolar los resultados del nivel agregado al microterritorial.
11 La idea principal es que los organismos territoriales más alejados de estos departamentos, incluso el Distrito Capital, tendrán un grado de crecimiento del PIB per cápita menor. En términos específicos se utilizaron ponderaciones de las distancias que tienen en cuenta el grado de interrelación entre los departamentos, es decir, el intercambio comercial entre sí.
REFERENCIAS
[1] Aguilera, M., Alvis, J. L., & Arrieta, J. (2000). Perfil socioeconómico de Barranquilla, Cartagena y Santa Marta, 1990-2000 (Documentos de Trabajo sobre Economía Regional 003320). Banco de la República. [ Links ]
[2] Anselin, L. (2002). Under the Hood: Issues in the specification and interpretation of spatial regression models. Agricultural Economics, 17, 247-267. [ Links ]
[3] Aparicio, M. T., Aznar, A., & Aznar, P. (2005). Estimación de la renta de las comarcas y municipios aragoneses. Serie 1999-2002. Zaragoza, España: Instituto Aragonés de Estadística (IAEST). [ Links ]
[4] Baltagi, B. H. (2005). Econometric analysis of panel data (3rd ed.). Nueva York: John Wiley & Sons Inc. [ Links ]
[5] Bonet, J., & Meisel, A. (1999). La convergencia regional en Colombia: una visión de largo plazo, 1926-1995 (Documentos de Trabajo sobre Economía Regional, pp. 69-106). Banco de la República, sucursal Cartagena. [ Links ]
[6] Chasco, M. del C., & López, F. (2004). Modelos de regresión espacio-temporales en la estimación de la renta municipal: el caso de la región de Murcia. Estudios de Economía Aplicada, 22(3), 1-24. [ Links ]
[7] Chasco, M. del C., Mella, J. M., & López, A. (2005). Crecimiento económico y convergencia urbana en España. Madrid: Instituto de Estudios Fiscales-Universidad Autónoma de Madrid. [ Links ]
[8] Cliff, A., & Ord, J. K. (1981). Spatial process, models and applications. Londres: Pion. [ Links ]
[9] Cox, W. E. Jr. (1968). The estimation of incomes and expenditures in british towns. Journal of the Royal Statistical Society, 17(3), 252-259. [ Links ]
[10] Cruz, J. J., & Muñoz, M. R. (2003). Metodología para medir el producto interno bruto del municipio de Puebla. Tesis de grado. Puebla: Universidad de las Américas. [ Links ]
[11] Eckstein, A. (2006). National income and capital formation in Hungary, 1900-1950. Review of Income and Wealth, 5(1), 152-223. [ Links ]
[12] Erol, U., & Yu, E. S. H. (1988). On the causal relationship between energy and income for industrialized countries. The Journal of Energy and Development, 13(1), 113-122. [ Links ]
[13] Fellner, F. (1923, 1924). Die Verteilung des Volksvermogen und Volkseinkommen der Länder des Ungarischen Heiigen Krone zwischen dem heutigem Ungarn und den Successions-Staaten. Metron, 3, 226-305. [ Links ]
[14] Glaeser, E. L., Kallal, H. D., Scheinkman, J. A., & Shleifer, A. (1992). Growth in cities. The Journal of Political Economy, 100(6), 1126-1152. [ Links ]
[15] Good, D. F. (1994). The economic lag of central and Eastern Europe: Income estimates for the Habsburg Successor States, 1870-1910. The Journal of Economic History, 54(4), 869-891. [ Links ]
[16] Hardy, A. P. (1980). The role of the telephone in economic development. Telecommunications policy. Elsevier, 4(4), 278. [ Links ]
[17] Hausman, J. A. (1978). Specification test in econometrics. Econométrica, 46, 1251-1271. [ Links ]
[18] Hrushikesh, M. (2009). Examining the linkage between energy consumption and economic growth in India. The Journal of Developing Areas, 43(1), 249-280. [ Links ]
[19] Hwang, D. B. K., & Gum, B. (1992). The causal relationship between energy and GNP: The case of Taiwan. The Journal of Energy and Development, 16(2), 219-226. [ Links ]
[20] Jacobs, J. (1985). Cities and the wealth of nations: Principles of economic life. Annals of the Association of American Geographers, 75(2) 277-279. [ Links ]
[21] Kraft, J., & Kraft, A. (1978). Note and comments: On the relationship between energy and GNP. The Journal of Energy and Development, 3, 401-403. [ Links ]
[22] Ministério do Planejamento, Orçamento e Gestão, & Instituto Brasileiro de Geografia e Estatística (IBGE) (2004). Diretoria de pesquisas. Coordenação de contas nacionais. Produto interno bruto dos municipios. Série Relatórios Metodológicos, 29, 1-49. [ Links ]
[23] Moreno, R., & Vayá, E. (2000). Técnicas econométricas para el tratamiento de datos espaciales. La econometría espacial. Barcelona: Universitat de Barcelona. [ Links ]
[24] Narayana, M. R. (2011). Telecommunications services and economic growth: Evidence from India. Journal Telecommunications Policy Archive, 35(2), 115-127. [ Links ]
[25] Núñez, J., & Sánchez, F. (2000). Geography and economic development: A Municipal Approach (Research Department Publications 3107). Inter-American Development Bank, Research Department. [ Links ]
[26] Pammer, M. (1997). Proxy data and income estimates: The economic lag of Central and Eastern Europe. The Journal of Economic History, 57(2), 448-455. [ Links ]
[27] Sánchez, F., López-Uribe, M., & Fazio, A. (2010). Land conflicts, property rights, and the rise of the export economy in Colombia, 1850-1925. The Journal of Economic History, 70, 378-399. [ Links ]
[28] Smith, A. (1776/1992). Investigación sobre la naturaleza y causas de la riqueza de las naciones. México: Fondo de Cultura Económica. [ Links ]
[29] Soytas, U., Sari, R., & ÖZdemir, O. (2001). Energy consumption and GDP relation in Turkey: A cointegration and vector error correction analysis. Global Business and Technology Association, 1, 838-844. [ Links ]
[30] Stoft, S. (2002). Power system economics. Designing markets for electricity (pp. 1-499). United States of America: IEEE Press/Wiley Interscience Press. [ Links ]
[31] Sutton, P. C., & Costanza, R. (2002). Global estimates of market and non-market values derived from nighttime satellite imagery, land cover, and ecosystem service valuation. Elsevier. Ecological Economics, 41, 509-527. [ Links ]
[32] Sutton, P. C., Elvidge, Ch. D., & Ghosh, T. (2007). Estimation of gross domestic product at sub-national scales using nighttime satellite imagery. International Journal of Ecological Economics & Statistics (IJEES), 8(S07), 5-21. [ Links ]
[33] Wilkins, L. T. (1952). Estimating the social class of towns. Journal of the Royal Statistical Society, 1(1), 27-33. [ Links ]
[34] Wooldridge, J. M. (2006). Introducción a la econometría. Un enfoque moderno. Madrid: Thomson Editores. [ Links ]













