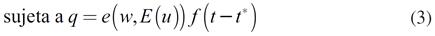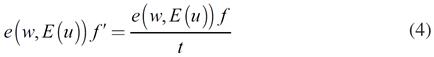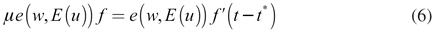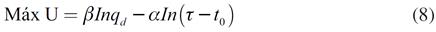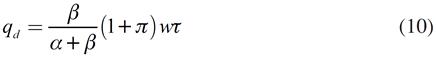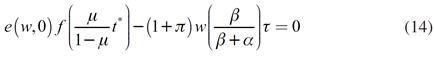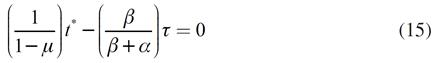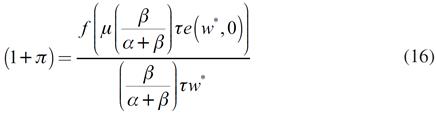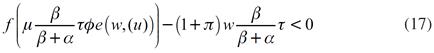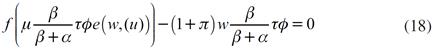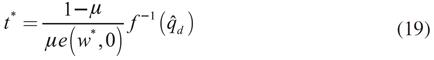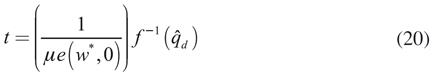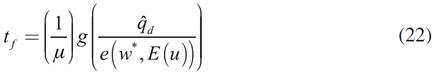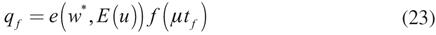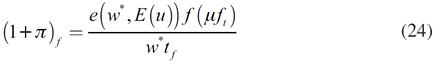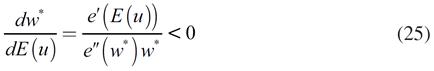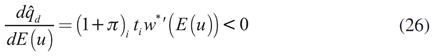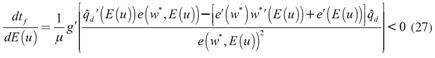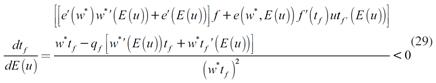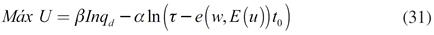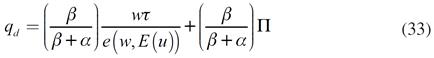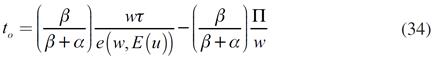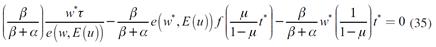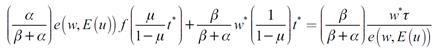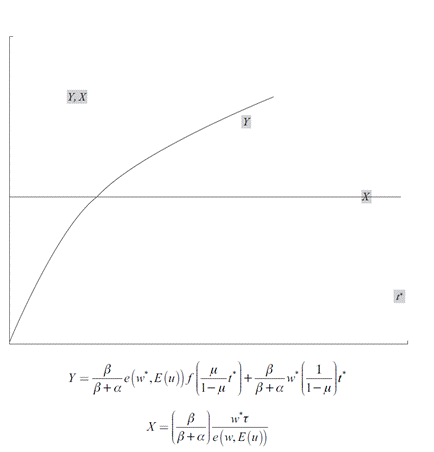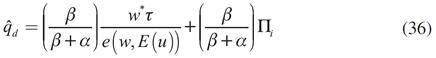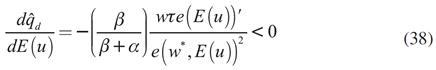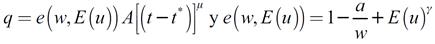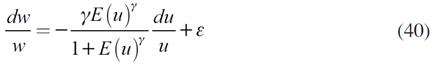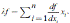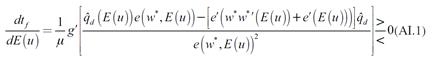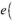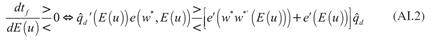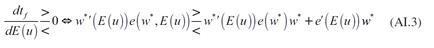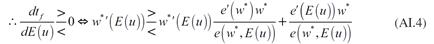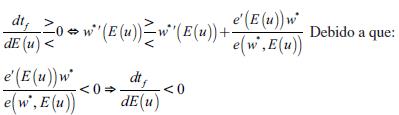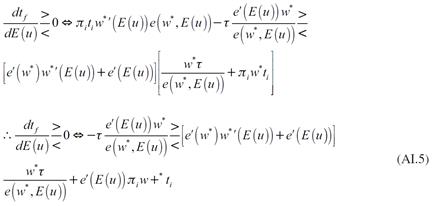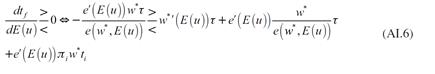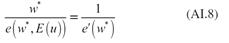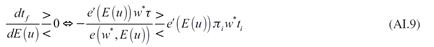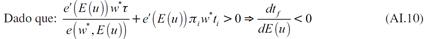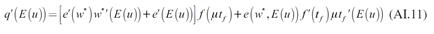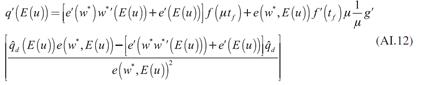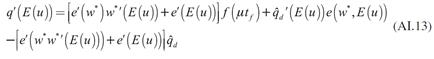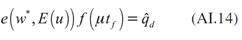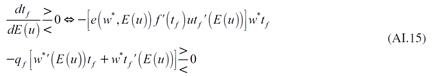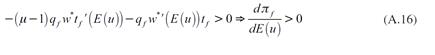INTRODUCCIÓN
La curva de salarios es la evidencia estadística que muestra que existe una relación inversa entre el logaritmo del salario individual (lnw) respecto al logaritmo de la tasa de desempleo regional (lnu). Esta curva usualmente se expresa a través de la siguiente ecuación:
La ecuación (1) es la curva de salarios; en ella X son variables de control donde se especifican características del sector y trabajadores estudiados, ε es el error de estimación. En la evidencia estadística internacional hay un consenso de que 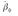 es negativa, pero hay un debate sobre el monto de esta.
es negativa, pero hay un debate sobre el monto de esta.
En la literatura especializada, la teoría de salarios de eficiencia suele emplearse para ofrecer una explicación teórica de la curva de salarios. De acuerdo con esta teoría, los trabajadores se esfuerzan cuando el desempleo es alto debido a que temen quedar desempleados, lo cual permite que las empresas reduzcan los salarios. Por otra parte, esta misma teoría suele emplearse para explicar el desempleo involuntario; de acuerdo con ella, el desempleo surge debido a que las empresas pagan altos salarios con el fin de motivar a los trabajadores a esforzarse. Así, por una parte, el desempleo alto reduce los salarios y, por otra, los salarios altos generan desempleo. Por lo tanto, hay una contradicción entre la forma en que se explica la curva de salarios y el desempleo involuntario.
En este artículo se propone un modelo de salarios de eficiencia en un marco analítico de equilibrio restringido por demanda. Se asume que los agentes esperan que el desempleo aumente, por ello, ante el miedo de perder su trabajo, incrementan su esfuerzo, lo cual permite a las empresas reducir el salario. A medida que la tasa de desempleo se mueva en el mismo sentido que su expectativa, la curva de salarios se verificará. Esto sucede porque el menor salario reduce el poder de compra de los trabajadores y, con ello, la demanda efectiva, de modo que las menores ventas motivan a las empresas a reducir su producción y contratar menos trabajo. Por lo que, tanto la explicación de la curva de salarios, como la del desempleo involuntario, son compatibles.
El artículo lo integran este apartado y cinco más. En el segundo se realiza una breve revisión de la literatura sobre la curva de salarios; en el tercero se expone un modelo de salarios de eficiencia con oferta de trabajo inelástica en un escenario de equilibrio restringido por demanda. En el cuarto apartado se prescinde del supuesto de oferta de trabajo inelástica, y se presenta el modelo cuando la oferta de trabajo es elástica. En el quinto apartado se exponen ejemplos numéricos de los dos modelos y se muestra que la pendiente de la curva de salarios, en general, es coherente con la evidencia estadística que postula que esta es cercana a -0,1. En el apartado final se ofrecen las conclusiones del artículo.
REVISIÓN DE LA LITERATURA
Card (1994), así como Blanchflower y Oswald (1994; 2005) muestran cómo, para una gran cantidad de países y en diferentes momentos en el tiempo, la elasticidad del salario individual con respecto a la tasa de desempleo regional es cercana a -0,1; en consecuencia, consideran que esta regularidad es una “ley empírica”.
En contraste con los autores mencionados en el párrafo anterior, Nijkamp y Poot (2005) argumentan que no puede considerarse que la pendiente de la curva de salarios cercana al -0,1 como una “ley empírica”, porque el tamaño de la elasticidad depende de las especificaciones de la estimación. A fin de sostener su argumento, analizan una muestra de 208 elasticidades derivadas de la literatura existente sobre este tema; por medio de técnicas de metaanálisis, muestran que la curva de salarios es un fenómeno empírico robusto, sin embargo, la elasticidad de -0,1 tiene sesgos de publicación. Una vez corregidos estos concluyen que esta es cercana a -0,07.
Longhi (2012) argumenta que la explicación que ofrecen los modelos de salario de eficiencia sobre la curva de salarios se sustenta en la idea según la cual la tasa de desempleo mide la dificultad que enfrentan los trabajadores de encontrar un nuevo puesto laboral. Sin embargo, señala que la tasa de desempleo no es el mejor indicador para medir esta dificultad. Por ello, con base en los modelos de búsqueda de trabajo, propone nuevas formas para medirla, y encuentra que la pendiente de la curva de salarios varía con cada forma que se proponga para medir la dificultad de encontrar empleo.
Para la economía colombiana, Sánchez y Nuñez (1998) encuentran que en el periodo 1984-1996, la elasticidad del salario respecto a la tasa de desempleo regional es de -0,13. Arango, Obando y Pasada (2010), al utilizar la tasa de desempleo correspondiente al grupo de estudio, en vez de la tasa de desempleo regional, hallan que la elasticidad se encuentra entre -0,086 y -0,09. Los resultados presentados en ambos trabajos son congruentes con los postulados por Blanchflower y Oswald (2005). En contraste, Ramos, Duque y Surinach (2010), con base en microdatos para la economía colombiana en el periodo 2002-2006, encuentran que la elasticidad salario individual-tasa de desempleo local es de -0,7, lo cual es acorde con lo que encuentran Nijikamp y Poot (2005).
Fingleton y Palombi (2013), con la finalidad de analizar si es posible considerar la curva de salarios como una ley empírica, comparan el poder explicativo de esta con el de la nueva geografía económica (NEG) y la economía urbana (EU). Para esto utiliza datos de Gran Bretaña durante el periodo 1998-2010 y, por medio de un modelo anidado artificial, encuentran que las tres teorías aportan elementos importantes para la predicción de los salarios. Sin embargo, ni la hipótesis de densidad, propia de la EU, ni la de mercados potenciales, postulada por la NGE, dominan a la curva de salarios, es decir, el logaritmo de la tasa de desempleo no pierde su poder predictivo cuando se incorporan las hipótesis de la EU y la NGE. Por lo tanto, la curva de salarios aporta elementos importantes que permiten predecir el comportamiento de los salarios. Estos autores encuentran que, si se incorporan a la curva de salarios los elementos explicativos de la EU y la NGE, la pendiente de la curva es cercana a -0,1. Como se ilustra en los párrafos anteriores, en la literatura empírica hay un consenso sobre la existencia de una relación inversa entre el logaritmo del salario y el logaritmo de la tasa de desempleo regional. No obstante, existe un debate sobre el monto de esta elasticidad.
La curva de salarios se puede explicar mediante modelos de contratos implícitos, negociación salarial y de salarios de eficiencia. En los modelos de contratación laboral se pueden asumir dos regiones para mostrar que las empresas y los trabajadores llegan a acuerdos implícitos, lo cuales provocan que la región con mayores salarios tenga los niveles de empleo más altos (Blanchflower y Oswald, 1994).
En los modelos de negociación salarial los trabajadores (sindicalizados) negocian con las empresas la parte del ingreso que les corresponde. A medida que el desempleo aumenta, la fuerza de los sindicatos se reduce y, con ello, el salario. Al respecto Blien, Dauth, Schank y Schnabel (2013) estudian la curva de salarios para Alemania Occidental en el periodo 1998-2006, a partir de diferentes regímenes de negociación salarial y muestran que esta únicamente se verifica para industrias donde hay negociación salarial colectiva a nivel de la empresa.
Los modelos de salarios de eficiencia suelen ser los más utilizados a fin de explicar la curva de salarios. En ellos se argumenta que los trabajadores suelen esforzarse si su salario es alto, o si existe un alto desempleo, de manera que la probabilidad de encontrar trabajo rápidamente sea baja. Así, en regiones donde el desempleo es alto, los trabajadores se esforzaran por miedo a perder su trabajo y permanecer en el desempleo un largo periodo. Por lo tanto, las empresas pueden pagar salarios bajos sin disminuir el esfuerzo de los trabajadores (Arango et al., 2010).
Por otra parte, la teoría de salarios de eficiencia ofrece una explicación de por qué surge el desempleo involuntario. Solow (1979), así como Shapiro y Stiglitz (1984), argumentan que en economías con información imperfecta y asimétrica, las empresas se ven obligadas a pagar altos salarios para motivar a los trabajadores a esforzarse, de manera que los altos salarios son la causa del desempleo involuntario.
Existe una contradicción entre la forma en que la teoría de salarios de eficiencia explica la curva de salarios, y la manera en que explica el desempleo involuntario. Esto debido a que en la primera explicación se argumenta que el alto desempleo provoca bajos salarios, en contraste, en la segunda se afirma que el desempleo involuntario se origina por altos salarios. Esta contradicción la ignoran los modelos que explican la curva de salarios al asumir el desempleo involuntario como exógeno, o al solo analizar cómo afecta la tasa de desempleo al salario real, pero no cómo el salario real determina al desempleo.
Ejemplos de lo descrito en el párrafo anterior se pueden encontrar en Campbell y Orszag (1998), quienes argumentan que la curva de salarios se explica por la elasticidad tasa de renuncia con respecto a la tasa de desempleo. Así, a medida que crezca el desempleo, disminuirá la probabilidad de encontrar trabajos mejor remunerados, por lo que los trabajadores permanecerán en sus puestos de trabajo pese a que se les page un salario bajo. Sin embargo, estos autores no analizan cómo afecta una disminución del salario al desempleo. Por otra parte, Campbell (2008) muestra cómo cuando se considera al desempleo y al salario, tanto local, como nacional, como elementos de la función esfuerzo, entonces un shock exógeno de la demanda de bienes genera una curva de salarios. No obstante, a que tanto el desempleo como los salarios son endógenos, la demanda de bienes está completamente desvinculada de los niveles de empleo y salarios. Blanchflower y Oswald (1994; 2005) proponen un modelo de dos sectores, en los que se ofertan salarios de eficiencia y los trabajadores deciden entre esforzarse o no. Los autores muestran a partir de shocks exógenos en la demanda de trabajo que la curva de salarios se verifica.
En este artículo se proponen dos modelos de salarios de eficiencia para explicar la curva de salarios, pero a diferencia de Campbell y Orszag (1998), de Campbell (2008), y de Blanchflower y Oswald (1994; 2005), se estudia de manera explícita, tanto el vínculo tasa de desempleo-salario real, como la relación salario real-tasa de desempleo. Esto con la finalidad de hacer compatible la explicación de la curva de salarios con el análisis del desempleo involuntario. En el primer modelo se asume que la oferta de trabajo es inelástica respecto al salario real. Este supuesto se sustenta en suponer que todos los ingresos de los consumidores provienen de la venta de su trabajo, incluso los derechos de propiedad de las empresas, es decir, se asume que solo los trabajadores son dueños de las empresas. Debido a lo poco plausible del supuesto, en el segundo modelo se prescinde de este y, por tanto, se formula una oferta de trabajo elástica. En ambos modelos las explicaciones sobre el desempleo, la curva de salarios y el vínculo entre ambas son las mismas.
La explicación del desempleo involuntario presentada en este artículo se basa en los trabajos de Noriega (1994; 2001) y Velázquez (2013). En estos documentos se presenta un modelo microfundamentado de equilibrio general restringido por la demanda efectiva, al ser esta última la que determina el nivel de empleo.
En los modelos aquí propuestos una reducción del salario real implica una menor demanda efectiva, por lo cual existe una relación directa entre salarios y empleo. Por otra parte, se recurre a una función esfuerzo, cuyos argumentos son el salario real y la expectativa de la tasa de desempleo, con el propósito de modelar la curva de salarios. Con base en estas dos premisas se muestra que si los agentes esperan que el desempleo aumente, entonces los trabajadores incrementaran su esfuerzo para conservar su trabajo, lo cual provoca que las empresas reduzcan el salario real. El menor salario real disminuirá la demanda efectiva e inducirá a las empresas a disminuir su producción y, con ello, contratar menos trabajo. La explicación del desempleo garantiza que la tasa de desempleo se mueva en el mismo sentido, aunque no necesariamente en el mismo monto que su expectativa. Esto asegura que la relación inversa entre la tasa de desempleo esperada y los salarios reales se verifique también para la relación tasa de desempleo-salarios, es decir, se confirma la curva de salarios.
MODELO CON OFERTA DE TRABAJO INELÁSTICA
Se asume una sociedad compuesta por un gran número de productores y consumidores. La función de utilidad de un consumidor es una transformación monótona de todos los demás, por lo que es posible trabajar con un consumidor representativo. De manera análoga, todos los productores tienen la misma función de producción, por lo cual se parte de un productor representativo. Solo hay un producto y un factor de la producción: el trabajo.
Productor representativo
La racionalidad del productor representativo se formaliza a través del siguiente ejercicio de maximización:
En las expresiones (2) y (3),ϖ es la tasa de ganancia, q es la oferta de producto, w es el salario real, t es la demanda de trabajo, e ( w, E (u)) es la función esfuerzo, u es la tasa de desempleo, E (u) es la tasa de desempleo esperada, y t* son los costos de organización; f es homogénea de grado donde µ ∈( 0, 1); e′( w)> 0,ε″( w ) < 0, e′( E ( u ))> 0, e ″ ( E( u ) , w) = 0 y e( w, 0)> 0. El supra índice coma (´) indica la primera derivada, entre paréntesis se muestra la variable con respecto a la cual se derivó. Las expectativas son racionales, por lo que u − E (u ) = ϕ. Donde ϕ es una caminata aleatoria de media cero y varianza constante.
La formalización del axioma de racionalidad del productor está integrada por tres elementos: 1. El productor maximiza su tasa de ganancia, es decir, el cociente del valor de su ingreso entre el valor de sus costos1; 2. Existen costos de organización positivos2, los cuales se definen como trabajo que se requiere para organizar la producción, de manera que es esto un prerrequisito para producir. Por lo tanto, el trabajo destinado a la organización no está asociado a producto positivo, es decir, únicamente después de que el trabajo ha cubierto la organización (t> t*) está asociado a producto positivo. Los costos de organización son un resultado del mercado, en consecuencia, para la empresa competitiva son un dato. No son una rigidez debido a que se modifican en función del mercado3. Y 3. Hay información incompleta y asimétrica, lo que implica que los productores no tienen certeza sobre qué trabajadores se esfuerzan y quienes holgazanean. Por su parte, de manera análoga a lo postulado por Shapiro y Stiglitz (1984), los trabajadores se esforzarán si se les remunera con salarios altos o si la expectativa sobre el desempleo es alta. Por lo tanto, las empresas ofertan un salario real que les garantice que los trabajadores se esfuercen.
Al resolver el ejercicio de maximización, se obtienen las condiciones de primer orden:
Además de la ecuación (3) -la cual muestra que la empresa produce en la frontera tecnológica de sus posibilidades-, las ecuaciones (4) y (5) son las condiciones de primer orden de la maximización, cuando se deriva con respecto a la demanda de trabajo y al salario real, respectivamente.
La ecuación (4) muestra que el productor maximiza cuando iguala la productividad marginal del trabajo e(w,E(u)) f’al producto medio 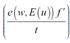 . Este resultado contrasta con la idea según la cual el productor maximiza cuando iguala la productividad marginal del trabajo al salario real4.
. Este resultado contrasta con la idea según la cual el productor maximiza cuando iguala la productividad marginal del trabajo al salario real4.
La expresión (5) es la ecuación de Solow y muestra que el productor maximiza su ganancia cuando iguala la elasticidad salario con respecto al esfuerzo a la unidad. Al salario que satisface esta condición se le conoce como salario de eficiencia (w*). El salario de eficiencia se determina independientemente da las fuerzas de oferta y demanda de trabajo. A fin de encontrar la demanda de trabajo se utiliza el teorema de Euler para funciones homogéneas5. Debido a que la función de producción (ecuación (3)) es homogénea de grado se obtiene:
Sustituyendo la ecuación (6) en (4), se arriba a:
La ecuación (7) es la demanda de trabajo, la cual se obtiene siempre que se maximice la tasa de ganancia en vez de la masa, incluso si hay más de un insumo (Noriega, 2001; 2006; Vargas, 2015; Velázquez, 2015). De esta demanda se resaltan dos características: 1. Es independiente del salario real, es decir, es inelástica. Esto implica que los productores no basan sus decisiones de cuánto trabajo demandar en el salario real, lo cual se debe a que no se verifica la igualdad salario real productividad marginal del trabajo. Y 2. Depende únicamente de los costos de organización. Para profundizar en este resultado es necesario precisar que los costos de organización se resuelven en el mercado, es decir, en el equilibrio general. Adelantando resultados, se mostrará que los costos de organización dependen del tamaño de mercado, por lo que, entre más grande sea la demanda efectiva, mayor serán estos. Así, los costos de organización vinculan la demanda de trabajo a la demanda efectiva.
Al sustituir la ecuación (7) en la función de producción se obtiene la oferta de producto, es decir, 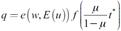 . Esta ecuación muestra que la oferta de producto depende de los costos de organización y de la función de esfuerzo.
. Esta ecuación muestra que la oferta de producto depende de los costos de organización y de la función de esfuerzo.
Consumidor
La conducta racional del consumidor representativo se formaliza a partir del siguiente ejercicio de maximización:
En las ecuaciones (8) y (9), U es la función de utilidad, 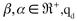 es la demanda de producto, τ es el tiempo máximo biológicamente disponible para trabajar, to es la oferta de trabajo. Por lo tanto, ( τ−t0 ) es el ocio. Por simplicidad se asume una oferta de trabajo inelástica, para ello se supone que todos los ingresos son producto del trabajo, incluso la ganancia. En el lado derecho de la ecuación (9) se observa que solo los trabajadores reciben salarios y ganancia.
es la demanda de producto, τ es el tiempo máximo biológicamente disponible para trabajar, to es la oferta de trabajo. Por lo tanto, ( τ−t0 ) es el ocio. Por simplicidad se asume una oferta de trabajo inelástica, para ello se supone que todos los ingresos son producto del trabajo, incluso la ganancia. En el lado derecho de la ecuación (9) se observa que solo los trabajadores reciben salarios y ganancia.
Del ejercicio de maximización resulta:
La ecuación (10) es la demanda de producto, esta depende de la tasa de ganancia y del salario real. Si bien esta demanda es un resultado estándar, difiere de la presentada por Campbell (2008), en la cual se asume una demanda de producto independiente del salario real. La (11) es la oferta de trabajo la cual es inelástica al salario real.
EQUILIBRIO GENERAL DE PLENO EMPLEO
El equilibrio general de pleno empleo se resolverá al asumir que los agentes esperan que no haya desempleo, por lo que e(w,0). Las funciones de demanda excedente de producto y trabajo determinan el nivel de empleo y producto, la ecuación (5), el salario real.
La ecuación (12) es la demanda excedente de producto, la (13) es la de trabajo. Al sustituir en estas los planes de compra y venta de producto y trabajo, se obtiene:
Las ecuaciones (14) y (15) son los mercados de producto y trabajo, respectivamente. Es importante resaltar que en el mercado de trabajo no aparece el salario real. La razón de esto es que los planes de compra y venta de trabajo no dependen del salario real, es decir, tanto las empresas, como las personas, demandan y ofertan trabajo independientemente del salario real. Por tanto, este mercado no aporta elementos para determinar al salario. Este resultado contrasta fuertemente con los postulados habituales de la teoría neoclásica, pero es estándar en los modelos que proponen la maximización de la tasa de ganancia y oferta de trabajo inelástica6 (Noriega, 1994; 2001; 2006; Vargas, 2015; Velázquez, 2013; 2015).
Al no determinarse el salario real en el mercado de trabajo, este lo fija el productor con base en la condición de Solow (ecuación 5). Es importante resaltar que aun si el mercado de trabajo ofreciera elementos para determinar el salario, sería fijado independiente de la oferta y demanda de trabajo, pues el productor lo determina por medio de la condición de Solow.
La ecuación (15) permite determinar los costos de organización compatibles con el pleno empleo; de esta ecuación resulta 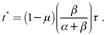 . Al sustituir esta expresión y el salario de eficiencia en el mercado de producto, se obtiene:
. Al sustituir esta expresión y el salario de eficiencia en el mercado de producto, se obtiene:
La ecuación (16) muestra la tasa de ganancia que determina el equilibrio en el mercado de bienes, la cual equivale al producto medio de pleno empleo. Una vez determinados los costos de organización de pleno empleo, el salario de eficiencia y la tasa de ganancia de pleno empleo, es posible conocer los niveles de producción y empleo de equilibrio.
El equilibrio general de pleno empleo es una posibilidad del modelo. Sin embargo, debido a que el mercado de trabajo no determinó el salario real, no existe un mecanismo de mercado que lo garantice. En la próxima sección se analiza la posibilidad de un equilibrio restringido por demanda.
Equilibrio restringido por demanda
Usualmente, se entiende por equilibrio restringido por demanda aquella situación en la cual el nivel de producción está determinado por la demanda efectiva, y esta no es lo suficientemente grande para garantizar el pleno empleo. En la literatura, una de las formas en las que surge el equilibrio restringido por demanda es porque los precios se mueven tan lentamente que permiten transacciones fuera del equilibrio (Argandoña, Gámez, y Mochón, 1996). A diferencia de esta literatura, pero de manera análoga a Noriega (1994; 2001) y Velázquez (2013; 2015), el equilibrio restringido por demanda surge debido a que los agentes no reconocen al salario real como la variable que guía sus planes de compra y venta de trabajo (véase la ecuación (15)). Por ello, no existe un mecanismo de mercado que permita a la insatisfacción de los trabajadores modificar las asignaciones del mercado7.
A fin de analizar el equilibrio restringido por demanda se asumirá la existencia de desempleo involuntario, aunque se eliminará esta hipótesis para analizar la curva de salarios. Bajo la hipótesis de desempleo, la ecuación (15) es una desigualdad estricta, tal que existe un ФЄ(0,1) que garantiza que: 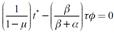 . Por lo cual, los costos de organización de desempleo involuntario son
. Por lo cual, los costos de organización de desempleo involuntario son 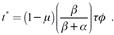 . Al sustituir estos en el mercado de bienes (ecuación (14)) se obtiene:
. Al sustituir estos en el mercado de bienes (ecuación (14)) se obtiene:
La expresión (17) simplemente indica el desequilibrio en el mercado de bienes debido al desequilibrio en el mercado de trabajo, es decir, muestra que los planes de demanda son mayores a los planes de oferta de producto, debido a la presencia de desempleo involuntario. Siempre que se utilice la demanda efectiva en vez de la demanda planeada, la ecuación (17) será una igualdad. La demanda efectiva 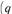
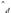
 es el plan de demanda que puede financiarse por medio de la oferta de trabajo que los consumidores lograron que se empleara y remunerara por las empresas, es decir:
es el plan de demanda que puede financiarse por medio de la oferta de trabajo que los consumidores lograron que se empleara y remunerara por las empresas, es decir: 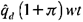 , donde
, donde 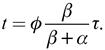 . Bajo esta idea, la ecuación (17) se puede reescribir como:
. Bajo esta idea, la ecuación (17) se puede reescribir como:
La ecuación (18) muestra que, en desempleo involuntario, el nivel de producción se ajusta a la demanda efectiva vigente. Hasta aquí se ha mostrado que existen costos de organización compatibles, tanto con el pleno empleo, como con el desempleo involuntario, pero no se ha estudiado cómo se determinan estos. Los costos de organización se determinan en el mercado de producto; para ver esto basta con sustituir los costos de organización de desempleo involuntario 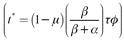 en (18) y resolver para ellos, así se obtiene:
en (18) y resolver para ellos, así se obtiene:
La expresión (19) muestra que los costos de organización tienen una relación directa con la demanda efectiva, es decir, entre más grande es esta, mayor es la organización que se requiere para la producción. Al sustituir la ecuación (19) en (7) se obtiene:
La ecuación (20) es análoga a la función ocupación8 de Keynes, al igual que esta muestra que la demanda de trabajo depende de forma positiva de la demanda efectiva, tal que si esta última aumenta o se reduce, entonces la demanda de trabajo también lo hará. La razón de esto es que las empresas demandan trabajo para ajustar su producción a la demanda efectiva vigente.
Adviértase que siempre que la demanda efectiva sea igual a la demanda planeada, entonces todo el trabajo que ofrecen los consumidores será contratado y remunerado por las empresas, es decir, se estará en pleno empleo. Sin embargo, no hay ningún mecanismo de mercado por el cual se garantice que la demanda efectiva sea lo suficientemente grande como para asegurar el pleno empleo.
Desempleo involuntario
En al apartado anterior se analizó cómo el equilibrio restringido por demanda es una situación posible, pero no se explicó cómo podría surgir este. En este apartado se analiza el surgimiento del desempleo involuntario. Para esto se parte de una economía en pleno empleo a fin de analizar cómo surge el desempleo involuntario y cómo se vincula este con la curva de salarios. Es importante aclarar que los trabajadores son remunerados de acuerdo con el salario de eficiencia. Por lo tanto, a partir de este apartado, siempre que se hable del salario se estará haciendo referencia al de eficiencia.
De forma análoga a Noriega (2001), se asumirá que el periodo de estudio puede dividirse entre inicial y final. Al inicio del periodo la demanda efectiva está determinada por el nivel de empleo y la tasa de ganancia de las empresas vigente al inicio del periodo, los cuales se consideran conocidos y fijos. Por su parte, el nivel de empleo al final del periodo está determinado por la demanda efectiva vigente. Al final del periodo, la producción y la tasa de ganancia están determinadas por el nivel de empleo final. Esta idea se formaliza en las siguientes ecuaciones:
En las ecuaciones (21), (22), (23) y (24) el subíndice i hace referencia a que la variable está al inicio del periodo, el subíndice f a que está al final. Adviértase que la ecuación (22) es análoga a (20), por lo que 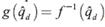 , donde
, donde 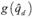 es una función homogénea de grado
es una función homogénea de grado 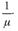 .
.
Se asumirá que al inicio del periodo de estudio los agentes esperan que la tasa de desempleo aumente. Esta expectativa provoca que los trabajadores incrementen su esfuerzo, debido a que no quieren quedar desempleados si los descubren holgazaneando. El incremento en el esfuerzo de los trabajadores permite que las empresas paguen un menor salario, esto es debido a que la reducción del esfuerzo motivada por un menor salario se compensa por el mayor esfuerzo, en razón a que se incrementó la probabilidad de ser despedido. Esta idea se observa a partir de diferenciar la ecuación (5) con respecto al salario y a la tasa esperada de desempleo, tal que:
La reducción en el salario disminuye el poder de compra de los trabajadores y, con ello, la demanda. Así, a partir de (21) se obtiene:
La inecuación (26) muestra que la expectativa de una mayor tasa de desempleo provoca que se reduzca demanda efectiva. Esto se debe a que la expectativa de un mayor desempleo permite a los empresarios pagar menores salarios y, por tanto, disminuyen los ingresos de los trabajadores y con ello su demanda.
La forma en que la expectativa de una mayor tasa de desempleo modifica la demanda de trabajo se observa al diferenciar (22) con respecto al nivel de empleo final, y a la tasa de desempleo esperada. De esta diferencial se obtiene:
La expresión (27) muestra dos fuerzas que interactúan y determinan la demanda de trabajo. La primera de ellas es el cambio en el esfuerzo de los trabajadores, es decir, la variación en su productividad debida al incremento en la expectativa de desempleo y a la reducción del salario; la segunda es la caída en la demanda efectiva ocasionada por la reducción en el salario. El signo negativo de la derivada muestra que la segunda fuerza determina el signo de la derivada, es decir, la demanda de trabajo se reduce debido a que disminuye la demanda de producto. Se resaltan dos características de esta expresión: 1. La caída en la demanda efectiva disminuye la demanda de trabajo. Esto se debe a que las empresas ajustan su producción a la demanda efectiva vigente, por lo que una reducción en esta última motiva a las empresas a contratar menos trabajo para ajustar su producción a la baja; 2. El esfuerzo de los trabajadores puede aumentar, reducirse o no cambiar ante un incremento en la tasa de desempleo. La razón de esto es que la mayor expectativa de desempleo, inicialmente, motiva a los trabajadores a esforzarse para no quedar desempleados, no obstante, el mayor esfuerzo de los trabajadores permite a las empresas pagar menores salarios, lo cual reduce el esfuerzo de los trabajadores.
Como ya se mencionó, la reducción en el nivel de empleo se debe a que las empresas redujeron su producción para que esta coincida con la menor demanda efectiva vigente. Esta idea se respalda a partir de diferenciar la ecuación (23), de donde se obtiene:
La expresión (28) simplemente muestra que la reducción en la producción es proporcional a la disminución en la demanda efectiva. La reducción en la producción, empleo y salarios modifica la tasa de ganancia. A partir de la ecuación (24) se obtiene:
La inecuación (29) muestra que la mayor expectativa de desempleo provoca que la tasa de ganancia aumente, pese a la caída en la producción. Esto se debe a que los rendimientos decrecientes a escala permiten que los costos laborales se reduzcan en un mayor monto que las ventas.
Curva de salarios
En la ecuación (1) es la curva de salarios -como ya se mencionó-; en la literatura empírica hay un consenso de que β <0 y un debate sobre el monto de esta. Por una parte, autores como Blanchflower y Oswald (2005), y Card (1994), consideran que β ≈-0,1, por otra, Nijkamp y Poo (2005) argumentan que β ≈-0,07.
Con el fin de estimar la pendiente de la curva de salarios se obtiene la diferencial de la ecuación (1), al considerar como variables el salario y la tasa de desempleo, tal que:
Una primera aproximación de la curva de salarios se obtiene a partir de considerar a u −E(u ) = ϕ. Siendo ϕ el error en las expectativas. De esta definición resulta que: E (u ) = u− φ. Al diferenciar esta ecuación y considerar que la tasa de desempleo se movió en la misma dirección que su expectativa, pero no necesariamente en el mismo monto se obtiene: dE (u ) = du − d φ. Al sustituir esta idea en la ecuación (25) se tiene:
En la ecuación [30] es una primera aproximación a la curva de salarios, en ella 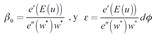 . Obsérvese que ß0 <0, por lo cual la pendiente de la curva de salarios también sería negativa, lo cual es congruente con el consenso encontrado en la literatura empírica. Sin embargo, no es posible aún decir nada sobre el monto de la pendiente de la curva de salarios. Para hacer un análisis más preciso de esta se utiliza una función esfuerzo paramétricamente definida en la penúltima sección.
. Obsérvese que ß0 <0, por lo cual la pendiente de la curva de salarios también sería negativa, lo cual es congruente con el consenso encontrado en la literatura empírica. Sin embargo, no es posible aún decir nada sobre el monto de la pendiente de la curva de salarios. Para hacer un análisis más preciso de esta se utiliza una función esfuerzo paramétricamente definida en la penúltima sección.
MODELO CON OFERTA DE TRABAJO ELÁSTICA
El modelo propuesto en el apartado anterior se construyó bajo la hipótesis de oferta de trabajo inelástica. Sin embargo, esto implica que todos los ingresos son producto del trabajo, incluso la ganancia. Este supuesto resulta difícil de sustentar en la realidad. Por esta razón, en este apartado se prescinde de este supuesto y se asume un consumidor con ingresos no salariales, y donde el mayor esfuerzo le significa desutilidad. Se muestra que los resultados obtenidos en el modelo anterior se verifican en este. Por tanto, la hipótesis de oferta de trabajo inelástica solo facilita el análisis.
Consumidor y productor representativo
El consumidor representativo se modela a partir del siguiente ejercicio de maximización:
La diferencia entre las ecuaciones (8) y (9), con respecto a (31) y (32), es que en el segundo par existen ingresos no salariales y el esfuerzo puesto en el trabajo implica desutilidad para el consumidor. Al resolver el ejercicio de maximización se obtiene:
Las ecuaciones (33) y (34) son respectivamente la demanda de producto y la oferta de trabajo. La primera depende positivamente, tanto del salario, como de la ganancia, y negativamente de la función esfuerzo. La segunda es una función positiva del salario, y negativa de la función esfuerzo y de la ganancia. Por lo tanto, la oferta de trabajo no es inelástica con respecto al salario.
La conducta racional del productor representativo se sigue representando por las ecuaciones (2) y (3). Por lo cual, los planes de compra y venta del productor y la condición bajo la cual se determina el salario, que se obtuvieron en el modelo anterior, siguen siendo válidos en este modelo.
Equilibrio general de pleno empleo
De manera análoga al modelo anterior, en este se resolverá el equilibrio general de pleno empleo asumiendo que los agentes esperan que no haya desempleo. El salario real se determina por la ecuación de Solow (ecuación 5). Por lo tanto, su determinación no depende ni de la oferta, ni de la demanda de trabajo. Sin embargo, los planes de venta de trabajo sí dependen del salario real. Una vez conocido el salario real, es posible determinar los costos de organización compatibles con el pleno empleo. Adviértase que los costos de organización no son un precio, por lo que ellos no se ajustan para garantizar el equilibrio. Esta función le correspondería al salario real, sin embargo, este se determina independientemente de las fuerzas de oferta y demanda de trabajo. Así, en este apartado únicamente se mostrará que existen costos de organización compatibles con un salario que, pese a que es determinado independientemente de las fuerzas del mercado, garantiza el pleno empleo.
Por la ley de Walras sabemos que si n-1 mercados están en equilibrio, el enésimo también lo estará. Por lo que solo se requiere encontrar los costos de organización que sean compatibles con el equilibrio de un mercado. Sustituyendo los planes de compra y venta de los consumidores y productores en el mercado de bienes se tiene:
La ecuación (35) es el mercado de bienes, éste se puede replantear como:
Para mostrar que existe una t* compatible con el equilibrio se grafica la parte izquierda y derecha de la ecuación, tal que:
Adviértase que Y ′(t * )> 0 para todo t* ∈ ℜ+ y que limt* →∞ y =∞. Por lo tanto, existe una t* compatible con el equilibrio en el mercado de bienes. Así, de manera análoga al modelo anterior, el equilibrio es una situación posible, aunque no hay nada que lo garantice sistemáticamente.
Equilibrio restringido por demanda, desempleo involuntario y curva de salarios
De manera análoga al modelo previo, el equilibrio restringido por demanda es aquella situación en la cual la demanda efectiva es menor a la demanda planeada, debido a la presencia de desempleo involuntario, y las empresas ajustan su producción a la demanda efectiva vigente. El análisis del desempleo involuntario se realiza en equilibrio restringido por demanda.
En este apartado se analiza el surgimiento del desempleo a partir de que los agentes esperan que la tasa de desempleo aumente. De manera análoga al modelo anterior se inicia en una situación de pleno empleo y se asume que el periodo de estudio puede dividirse entre inicial y final. Al inicio del periodo la demanda efectiva está determinada por el nivel de empleo y la ganancia de las empresas vigentes al inicio del periodo, los cuales se consideran conocidos y fijos. Por su parte, el nivel de empleo al final del periodo está determinado por la demanda efectiva vigente. Al final del periodo, la producción y la ganancia de las empresas están determinadas por el nivel de empleo final. En consecuencia, las ecuaciones (22) y (23) siguen siendo válidas. Sin embargo, la ecuación de demanda efectiva y masa de ganancia ahora son:
La ecuación (36) es la demanda efectiva al inicio del periodo, esta a diferencia de la ecuación (21), depende, tanto del salario real, como de la función esfuerzo. La ecuación (37) es la ganancia de las empresas al final del periodo. En el modelo anterior se empleó la tasa de ganancia (ecuación 24) en lugar de la masa, con el fin de facilitar el cálculo de la demanda efectiva, sin embargo, es posible usar en ambos modelos la masa de ganancia.
Como lo muestra la ecuación (24), una mayor tasa esperada de desempleo motiva a los trabajadores a esforzarse más y, por tanto, permite que las empresas reduzcan el salario. El menor salario real disminuye la demanda efectiva, como lo muestra la siguiente expresión:
De manera análoga al modelo anterior, la demanda de trabajo cambia ante la expectativa de una mayor tasa de desempleo por dos razones: 1. La caída en la demanda efectiva motiva a las empresas a ajustar su producción a la baja y, por tanto, las empresas requieren contratar menos trabajo; y 2. El cambio en el esfuerzo realizado por los trabajadores. Siendo la primera causa la que determina la reducción en la demanda de trabajo. Por ello, la ecuación (27) sigue siendo válida en este modelo.
Las empresas reducen su producción en el mismo monto en que disminuyó la demanda efectiva, por lo que la expresión (28) también se verifica en este modelo.
Finalmente, la curva de salarios se obtiene siguiendo la misma lógica que en el modelo anterior. En consecuencia, la ecuación (30) también arroja luz sobre el signo de la pendiente de la curva de salarios en este modelo. La única diferencia entre la curva de salarios del modelo previo y la de este modelo es que la tasa de desempleo sería distinta debido a que en este modelo la oferta de trabajo tiende a reducirse ante disminuciones en el salario real.
EJEMPLOS NUMÉRICOS
Con la finalidad de hacer más clara la exposición de los modelos presentados, se realizan ejemplos numéricos de estos. Para ello se define paramétricamente las funciones de producción y esfuerzo, de modo que para ambos modelos las funciones son:
Siempre que 0 < µ<1 la función de producción tendrá rendimientos decrecientes.En la función esfuerzo 0 < γ<1. De esta función se resaltan cuatro características:
1. e ( w, 0)> 0, ε( w)′> 0, e( w) ″ < 0, e( E (u))′> 0, e ( E(u ))″ < 0,ε ( w, E (u))= 0. Es decir, la función esfuerzo satisface todos los requisitos que usualmente se le pide.
2. El salario de eficiencia que resulta de la función de esfuerzo y de la ecuación (5) es:
3. 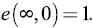 Es decir, cuando el salario tiende a infinito y la tasa de desempleo esperada es cero, el esfuerzo es uno. Lo anterior implica que si los trabajadores se comportaran como si el salario fuera infinito y no le tuvieran miedo al desempleo, entonces su esfuerzo sería del 100 %.
Es decir, cuando el salario tiende a infinito y la tasa de desempleo esperada es cero, el esfuerzo es uno. Lo anterior implica que si los trabajadores se comportaran como si el salario fuera infinito y no le tuvieran miedo al desempleo, entonces su esfuerzo sería del 100 %.
4. 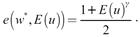 Por lo que, si 0 ≤ E (u)<1, entonces 0 <e ( w*, E (u))< 1. Sin embargo, lim
Por lo que, si 0 ≤ E (u)<1, entonces 0 <e ( w*, E (u))< 1. Sin embargo, lim Es decir, tanto en pleno empleo, como en desempleo involuntario, los trabajadores se esfuerzan menos del 100 %. No obstante, a medida que el desempleo aumenta los trabajadores se esfuerzan más.
Es decir, tanto en pleno empleo, como en desempleo involuntario, los trabajadores se esfuerzan menos del 100 %. No obstante, a medida que el desempleo aumenta los trabajadores se esfuerzan más.
La conducta optimizadora del consumidor en el primer modelo se formaliza con las ecuaciones (8) y (9), para el segundo con las ecuaciones (31) y (32). Los ejemplos numéricos se exponen a continuación.
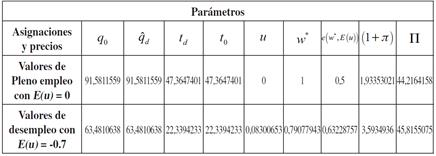
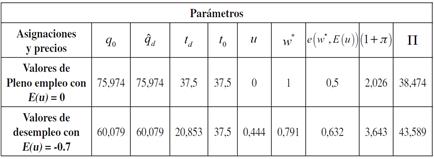
Tabla 1 Ejemplo numérico del primer modelo (oferta de trabajo inelástica)
Fuente: elaboración propia.
En las tablas 1 y 2 se muestran los resultados numéricos del primer y segundo modelo, respectivamente. En ambos ejercicios se utilizaron los mismos parámetros para facilitar el análisis. De los resultados se destacan los siguientes aspectos:
1. Pese a que los parámetros son los mismos en ambos modelos, los niveles de producción y empleo del segundo modelo son mayores, tanto en pleno empleo, como en desempleo involuntario. El análisis de esta observación se realizará primero en pleno empleo y después en desempleo: (a) en pleno empleo la intensidad con la que trabajan los consumidores es menor que la unidad, es decir: e ( w * , 0) 1. En el segundo modelo, al contemplarse que el trabajador decide, tanto cuánto trabajo ofrecer, como la intensidad de este, se obtiene que entre menor sea la intensidad mayor será la oferta de trabajo. En consecuencia, en pleno empleo los niveles de producción y empleo serán mayores en el segundo modelo que en el primero. Y (b) en desempleo involuntario, los montos en la producción y empleo son mayores en el segundo modelo; sin embargo, la reducción en la producción también fue mayor en el segundo modelo. Por tanto, más que las magnitudes, lo importante de los ejemplos numéricos es la dirección en que cambian los precios y las asignaciones.
2. El salario y el esfuerzo son los mismos en ambos modelos, tanto en pleno empleo, como en desempleo involuntario. La razón de esto es que estas dos variables dependen únicamente de los parámetros de la función esfuerzo y del desempleo esperado, los cuales son los mismos en ambos modelos.
3. En ambos modelos un incremento en la tasa de desempleo esperada motiva a los trabajadores a esforzarse más por miedo a perder su trabajo, lo cual permite que las empresas reduzcan el salario; el menor salario disminuye la demanda efectiva y con ella la venta de las empresas, en consecuencia, las empresas ajustan a la baja, tanto su producción, como su demanda de trabajo. La tasa de ganancia y la masa aumentan debido a la caída en los salarios (costos laborales), y el aumento en el esfuerzo de los trabajadores (mayor productividad).
Curva de salarios
La ecuación (39) es el salario que garantiza la máxima ganancia a las empresas, el cual no depende de la cantidad de trabajo que la empresa demande. Al diferenciar esta ecuación con respecto al salario y a la expectativa de la tasa de desempleo, y asumiendo que dE(u ) = du − d φ y E (u )≈ u se obtiene:
La ecuación (40) es la curva de salarios, en ella se observa que la pendiente es negativa y estrictamente menor que la unidad, lo cual concuerda con la evidencia estadística. Obsérvese que la elasticidad tasa de desempleo con respecto al salario depende únicamente de dos componentes: la tasa de desempleo esperada y de la elasticidad de esta con respecto al esfuerzo (γ). Para realizar un análisis más detenido del valor de la pendiente de la curva de salarios se realiza un ejercicio numérico.
En la Tabla 3 se estiman los distintos valores de la elasticidad salario con respecto a la tasa de desempleo, para diferentes valores de E(u) y γ. Por ejemplo, en la primera columna no iluminada, aparecen los valores de β para distintos valores de E(u) cuando γ = 0,1. De estas estimaciones existen cinco elementos a resaltar: 1. En general, las estimaciones realizadas sobre la pendiente de la curva de salarios es congruente con la evidencia estadística; de hecho, el promedio de las estimaciones realizadas es de -0,1, lo cual concuerda con lo encontrado por Blanchflower y Oswald (2005), y por Card (1994). 2. Las estimaciones de β realizadas con bajos valores de E(u) y/o γ son más cercanos a los encontrados por Nijkamp y Poot (2005). Por ejemplo, en promedio el valor de β para una tasa de desempleo esperada del 3 % es de -0,06. 3. Las estimaciones de β realizadas con altos valores de E(u) y γ no son congruentes con la evidencia estadística. Por ejemplo, el promedio de la estimación de β para una tasa de desempleo esperada del 30 % con γ que va de 0,5 a 0,9 es de -0,21, lo cual es poco más del doble de lo estimado por Blanchflower y Oswald (2005), y el triple de lo propuesto por Nijkamp y Poot (2005). 4. La tasa de desempleo promedio en los países miembros de la OCDE se cercana al 7 %. La β estimada promedio para E(u) = 0,7 es de -0,09, lo cual es bastante cercano al -0,1. 5) La economía colombiana tiene una tasa de desempleo cercana al 10 %, si calculamos el valor promedio de β para E(u) = 0,1 se obtiene que Este es de -0,1, lo cual es congruente con lo encontrado por Sánchez y Nuñez (1998). y Arango et al. (2010).
Tabla 3 Estimación de la elasticidad salario con respecto a la tasa de desempleo
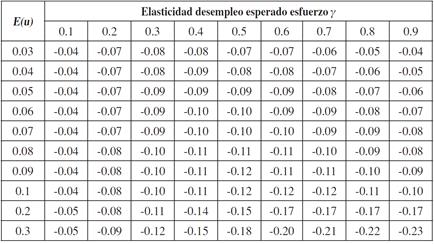
Fuente: elaboración propia con base en la ecuación (40).
CONCLUSIONES
Existe una contradicción entre la forma en que la teoría de salarios de eficiencia explica la curva de salarios y su explicación del desempleo involuntario. La explicación de la curva de salarios implica la relación negativa entre la tasa de desempleo y los salarios reales; en contraste, su explicación del desempleo se basa en una relación positiva entre salarios y la tasa de desempleo.
En este artículo se propuso un modelo de salarios de eficiencia en escenarios de equilibrios restringidos por demanda, con el fin de ofrecer una explicación congruente entre la curva de salarios y la relación salarios-desempleo. La explicación de la curva de salarios se sustenta en que un aumento en la expectativa de desempleo motiva a los trabajadores a esforzarse más por miedo a perder su trabajo, en consecuencia, las empresas reducirán el salario, sin que la productividad caiga y, con ella, sus ganancias. En la medida en que la tasa de desempleo se mueva en la misma dirección que la tasa de desempleo esperada, la curva de salarios se verificará. La explicación del desempleo se basa en las consecuencias que tiene la reducción del salario sobre el empleo. El menor salario merma el poder de compra de los trabajadores disminuyendo la demanda efectiva, lo cual obliga a las empresas a reducir su producción hasta que esta coincida con la demanda efectiva vigente, para lo cual las empresas contratan un menor monto de trabajo. Adviértase que la relación inversa entre los salarios y la tasa de desempleo garantiza que la tasa de desempleo se mueva en el mismo sentido que las expectativas sobre esta, aunque no necesariamente en la misma magnitud. Por lo cual la relación inversa entre salarios y empleo no solo es congruente con la curva de salarios, sino que es necesaria para que esta se verifique.
Además, se mostró que las explicaciones sobre la relación salarios-empleo y la curva de salarios no se modifican si la oferta de trabajo es inelástica o es elástica. La razón de esto es que el salario se fija con base en la ecuación de Solow, por lo que la oferta de trabajo no aporta elementos para su determinación y, por tanto, no influye en el comportamiento de la economía.
Finalmente, en el ejemplo numérico se encontró que los modelos propuestos, en general, son congruentes con la evidencia estadística según la cual la pendiente de la curva de salarios es cercana a -0,1.