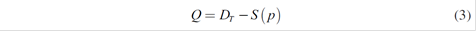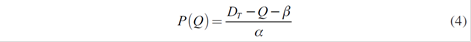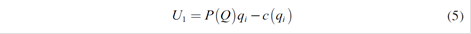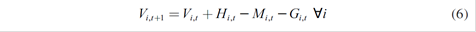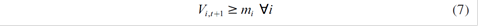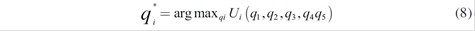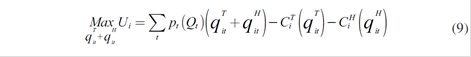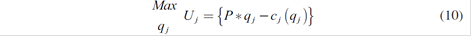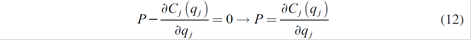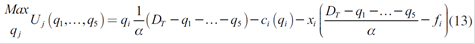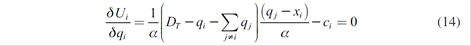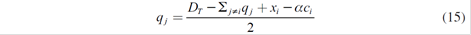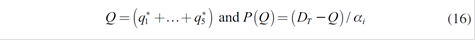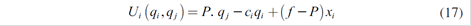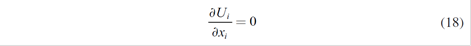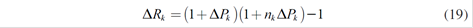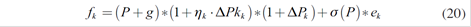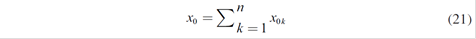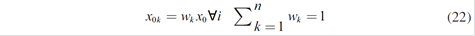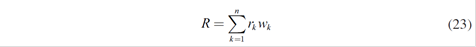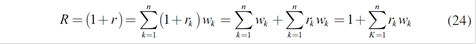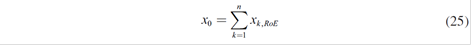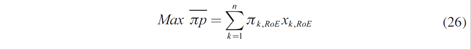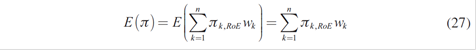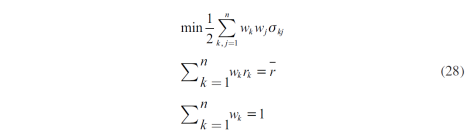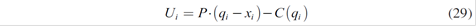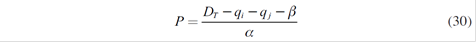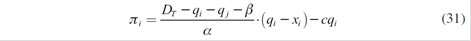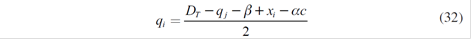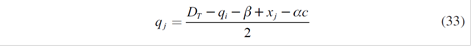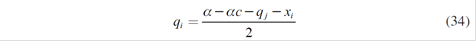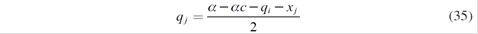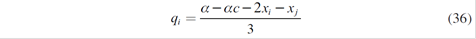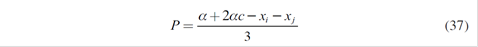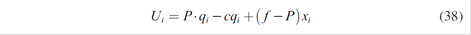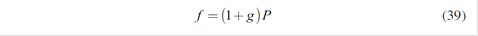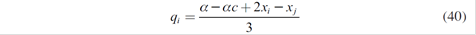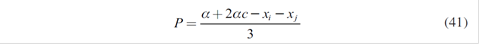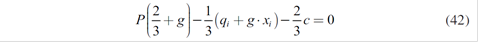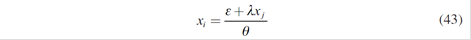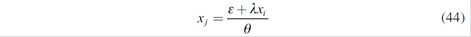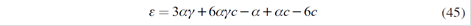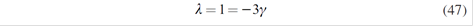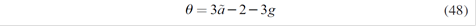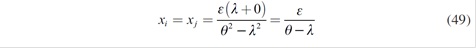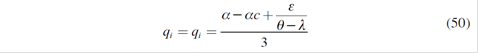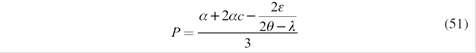INTRODUCTION
A forward contract is an over-the-counter derivative of an agreement to buy or sell an asset at a certain point in time in the future for a certain price. This type of contract is commonly used in electricity markets to mitigate spot price volatility caused by fuel price variations, weather conditions, and sensitive demand. According to Liski and Montero (2006), Green and Coq (2010), and Aichele (2014), the introduction of a forward market allows bidders to obtain additional collusive profits different from those obtained from a pure spot market, unless different measures to strengthen the competition or improve the position of the demand are used. This differs from the seminal work of Allaz and Vila (1993), in which forward contracting forces the firms to compete in both spot and forward markets, creating a kind of “prisoner dilemma” in which they voluntarily choose to hire forward, and find themselves in a more adverse situation. This result depends on full observability of the contracts as shown by Hughes and Kao (1997).
The objective of this paper is to determine whether the introduction of seasonal forwards facilitates taking advantage of both variability in the hydrology offer, as well as the elasticity of the demand, in turn, benefiting both the producers and the consumers of the Colombian electricity market; or if it serves only to enhance benefits for generators. The operation of the current spot price and non-seasonal forward markets is replicated using a Cournot competition model; and then the portfolio theory is applied to distribute the resulting amount of forwards according to hydrological seasonality between the different demands for several expected returns with minimal risk. It is consistently shown that when profitability increases, preference for forward buying over spot buying is more evident.
Forward contracts have been the focus of different studies in several markets. Allaz and Vila (1993) suggested a strategic reason to make forward transactions, even without considering uncertainty, due to the fact that firms have Stackelberg type incentives (leaders and followers gather) in order to anticipate production through long-term contracts. Holmberg (2011) analyzes different strategic behaviors and interactions that take place between the spot and forward markets. Through a two-stage game with a perfect equilibrium in sub-games, it can be seen under which conditions an increase in the forward market is a credible compromise in regard to aggressive biddings in the spot market. It also shows when prices in the spot market can be softened, which is facilitated by imperfections in the electricity market: volatile offer, non-storable feature, high capital intensity, and convexity in the costs function, among others (Anderson & Hu, 2008; Bushnell, 2007; Harvey & Hogan, 2001; Liski & Montero, 2006; Siddiqui, 2003). In fact, observable differences in the practice between forward and spot prices would mainly account for how the expectations of the agents are constructed and transferred to the forward prices when applying a premium that works as compensation for the risk of the spot market, among agents with different risk aversions (Redl & Bunn, 2011; Redl, Haas, Huber & Böhm, 2009).
Siddiqui (2003) generalizes Allaz-Vila’s model to an arbitrary number of firms and levels of response to the prices from the demand, showing how the transactions through forward markets and elasticity of the prices interact. Other works focus on the characteristics of electricity markets, such as the expectations on the production costs (Green, 2006); the relation among transaction costs, arbitrage, and risk aversion (Christensen, Jensen & Molgaard, 2007); or the differences between risk aversion and market power (Benth, Cartea & Kiesel, 2008); the differences be-tween the increase of price above the marginal cost and number of transaction periods (Breitmoser, 2012); and the influence of the demand elasticity (Anderson & Hu, 2008). In Colombia for example, according to Carrasquilla, Rendón & Pantoja (2012) efficient coverage of forwards depends on risk aversion, the volatility of the expected volume, the long-term risk premium, and the expected correlation between volume and contract price with due date. Taking into consideration that the risk of rain -which affects the hydroelectric offer- is not fully correlated with the prices, the risk volume cannot be hedged with them. Therefore, a buyer in the electricity market faces price risks, and in addition to this, the required volume when the contract time takes place is not exactly known. Liski and Montero (2006) obtain collusive results in the generation market by widening the discount factors range that is allowed if the competition is through prices or through quantities.
This status quo can be altered to benefit consumers through the introduction of variations in forward prices; for example, taking advantage of the seasonality in the offer. This depends on the elasticity of the demands for longer periods; a situation that occurs in some markets, especially in the European market. Additionally, profit sharing depends on the fulfilling of expectations, in terms of the seasonality defined in the contracts, as shown by Anderson and Hu (2008). By replicating the Allaz-Vila structure, these authors show that contracts lead to a maximization of social welfare if the consumer’s demand is elastic to the price, even when assuming that the price of forward contracts contains an additional component associated with risk.
Borovkova and Geman (2006) find seasonal components in the forward curves of most commodities. For seasonal commodities, the shape of the forward curve is largely determined by the anticipation of seasonal demand and/or supply. The Colombian electricity sector is hydro dominated, which means that prices are driven by seasonal supply according to rainfalls.
Even though there are some studies related to forward electricity markets, as shown by the literature review provided above, there are few studies regarding this topic for the Colombian electricity market. In this sense, this paper aims to contribute to the discussion of new schemes for forward contracting, taking into account particularities inherent to the Colombian power system.
METHODOLOGY
This section presents a strategic behavior model of the Colombian electricity market, taking into account leading agents that will act strategically among themselves through a Cournot competition. Based on this, a general model for price determination, considering the hydraulic resources of agents, is proposed. The risk premium of the Colombian electricity market is also analyzed, while forward prices based on spot prices, and spread and elasticity of demand are proposed. Finally, once contract prices and quantities are determined, a method to distribute electricity among different demands of forward contracts based on the portfolio theory is proposed.
Proposal of Strategic Behavior Modeling in the Colombian Electricity Generation Market
In the Colombian electricity generation market, two agent groups can be identified: five generator leaders - those with higher participation in the total generation: EPM (25%), EMGESA (22%), ISAGEN (15%), Electricaribe (10%), Chivor (7%); and followers (the remaining). The interaction between these two groups can be simulated as a Cournot competition; that is, leaders compete for quantities while followers act competitively and meet the residual demand. Leaders can supply quantities (both in the spot and forward markets), but in a situation where they must compete twice: first in the forward and then in the spot market. In the formal representation of the competition, this is solved through a backward induction, starting with the agent´s choice of spot quantities in the last stage, while taking as given the forward choice in the first stage.
Spot Market
Let (p) be the supply function of the followers. Such a function is stepped since in this market agents submit a discrete bid of prices and quantities. This function can be adjusted to a polynomial expression of first order (García & Arbeláez, 2002), as shown in equation (1).
With α, β > 0
D
r
is the residual demand resulting from subtracting from the total demand D
T
the one attended by the followers S (p), which must be equal to the added supply of the five leaders  :
:
Therefore,
Replacing (3) in equation (1):
Where β = 0 without loss of generality.
Now, the leaders will act strategically among themselves through the Cournot competition, which has replicated the functioning of an electricity market such as that in Colombia (Allaz & Vila, 1993; García & Arbeláez, 2002; Liski & Montero, 2006).
The utility function of each leader, if they only play in the spot market is:
This function is maximized for each period t, with two technical constraints: the balance of the dams in t+1 given by their initial volume of water (Vi,t ), plus the water flows received ( Hi,t ), minus the losses caused by spills and evaporations ( Mi,t ), and minus the volume used in generation (Gi,t ) (equation (6)); and the minimal operation of the dams1 (equation (7)).
The price P (.) can be obtained through successive approximations; in fact, few iterations are required to get this kind of equilibrium, achieving a lower market price when there is higher production2; consequently, a production agreement must be achieved (equilibrium Nash - Cournot). In order to obtain this competitive equilibrium, the optimal productions fulfill:
q *i, q*j are the production levels that maximize corresponding utility functions of the market leaders i,j, taking into account their rival’s production (also called reaction or response functions).
General Model of Spot Price Determination
The Colombian electricity market is made up of two main markets: a spot market and a long-term market based on non-standardized contracts. An independent system operator (ISO) solves the ideal dispatch in the spot market. Rather than minimizing the hourly costs of generation, the objective function of the ISO is set to an economic dispatch (twenty-four-hour optimization problem), where genera-tors submit bids and side payments are introduced. The bids specify an electricity supply price for the next twenty-four hours, startup costs, and maximum generating capacity for each hour of the next day. Once the optimization problem of the ideal dispatch is solved for the twenty-four hours, the equilibrium price is calculated as the price bid of the marginal plant that is not saturated. The hourly spot price is defined as the equilibrium price plus one uplift (De Castro, Oren, Riascos & Bernal, 2014).
The model proposed in this work, identifies price taker agents and leader agents (strategic), between thermal and hydraulic resources. In the selection of the leaders, some elements such as generation and regulation capacity are considered. These hydraulic resources allow leader agents to exert speculation when entering future periods by adjusting generation rates of the dams, where they would have a higher strategic value. For example, in hours or seasons of high demand, more benefits could be obtained, and there would be other flexibilities such as an easier adjustment to the fluctuations of offer and demand.
A strategic agent i that has thermal and hydraulic plants, producing thermal and hydraulic energy given by q itT and qitH, respectively, faces the following optimization problem:
pt being the marginal price and CiT and CiH the thermal and hydraulic costs (this last one corresponds to the opportunity water cost). Equation (9) is subject to the constraints of hydrological balance, residual demand, minimum and maximum volumes of the dams, etc., the agent is allowed to define how much energy to produce q itT , qitH each period t. Market price depends on the quantities that are offered by all five strategic agents, Qt = q1t +…+q5t .
When participating in the Cournot competition, each player chooses the production level that maximizes their benefits, assuming that the rest of the players maintain the production level from the former period. This process is updated each time period within a repetitive process. The idea is to find Nash equilibrium in which no agent would be willing to modify the intertemporal use of the hydroelectricity resources, since doing so would diminish the margin of operative benefit.
Agents without the Possibility of Coupling Resources through Time
For price taker agents, those that are fully thermal or have hydraulic resources without quantity regulation, the optimization problem is not linked. In the case of a thermal plant, it would be:
With
The expression for price equals marginal cost determines the optimal value of ( q∗j ) for any value of p. Subsequently, it is checked if this value respects the technical limitations of generation that have been defined; otherwise, it is necessary to correct this quantity and place it in its respective limit. Finally, utility for the generators is calculated, evaluating the corresponding variables in the target function. This analysis can be carried out at two levels: plant and technology, which reduce the number of problems to be solved.
Competitive Equilibrium in the Spot Market
The problem of the strategic agent i is given by:
ci ( qi )= ci qi + Fi ; where ci denotes the marginal cost and Fi the fixed costs that are not relevant for this analysis. Also, it is assumed that the generator has defined ex-ante long term non-standardized contracts xi at a fixed price fi .
When differentiating with respect to qi:
Hence
As a consequence, there are five equations associated with five strategic generators. Solving these equations simultaneously, Nash - Cournot equilibrium with a parallel market of long-term contracts is reached:
Forward Choice Quantities
Now generator i determines the amounts xi to be distributed in the long-term market contracts in the first stage of this Cournot competition:
Where f will be the proposed forward price which depends on the spot price P. a premium or spread g, the hydrology and the demand elasticity of each served consumer ηk (defined in section 2.3).
The first order condition for the xi yields:
Getting xi ∀i =1,…5 it is possible to obtain the specific spot quantities qi*, and therefore the equilibrium spot price P*.
The Risk Premium in the Colombian Electricity Market
The risk premium of a forward market is defined as the difference between its price and the forecasted spot price, which has a positive value in most of the cases found in the literature, representing an additional income for the generators. The particular characteristics of electricity created products that have been negotiated with different maturity and delivery periods, complicate the evaluation of the risk premium since there is not a standard pattern for comparison. Redl and Bunn (2011) analyze the stock market of the European energy (EEX) for the English market (APX). Relative differences were found: an average of 7%, between for-ward prices and spot prices, taking as reference the price of the last day of negotiation from the previous month to the expiration of the contract; with significant differences month by month. When analyzing the seasonal relative differences, a seasonal pattern in the risk premium is found: higher in January and lower in the intermediate seasons of April and September. Borovkova and Geman (2006) calculate the risk premium of several energy contracts in the International Petroleum Exchange, absorbed today by the ICE (IPE). Between April 2001 and December 2002, there were negotiated forward contracts which would expire in winter and had a positive premium, while those that would expire in summer were negotiated with a discount (negative premium), the highest in January (15%), February (approximately 11%), and December (7%). In more developed electricity markets the transaction volume of forward contracts is significantly higher than the physical demand. For example, Of gem (2009) reported quotients close to 7% and 8% between volume and real physical delivery for the German and Nordic markets, and more than 90% of power delivered in the English market came from forward contracts.
Unlike DeBenedictis Miller, Moore, Olson, and Woo (2011) who determine the risk premium in the Mid-Columbia North American market, characterized by its high hydrology through a crossed coverage model (cross-hedging), by modeling the spot price based on the price of natural gas, these papers acquired information from markets with a diversified energetic basket, but without remarkable weight in the hydraulic resource, as it happens in Colombia. This model showed that the premium differs a little from the others mentioned, with an average of 5.4% and a maximum value higher than 20% in March.
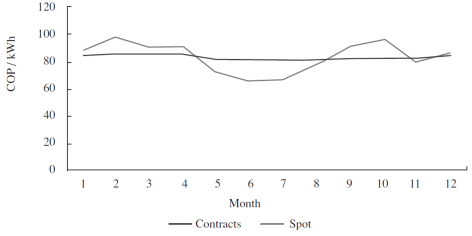
The derivatives market for the electricity in Colombia is recent and has little liquidity. Hence, a sufficient number of monthly contracts that help obtain a reliable risk premium has not been negotiated. A first approach was taken with the average price of the future contracts of monthly electricity (ELM) negotiated in Derivex, with a maximum premium value of 84% and a minimum of -38% (discount); the second approach used information that was available from the average prices of bilateral contracts. However, a risk premium, always positive, with a minimum value of 64% and a maximum value of 157% was found. These values are far from the ones found in the United States and Europe; however, they should be compared with regions analogous to Colombia, affected by the Niño and Niña phenomena. Another aspect to be considered is the lack of detail regarding the months of the contracts and their expiration dates. Another measurement alternative uses information of the stock market prices and contracts of the NEON database, and gathers the averages of monthly prices per type of contract in order to calculate the difference between the spot prices and contracts equivalent to the premium (see Figure 1).
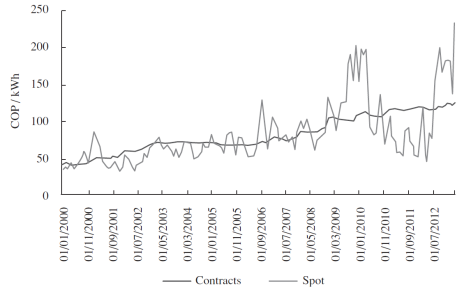
Source: Authors (data taken from NEON, 2013).
Figure 1 Evolution of the Monthly Average Prices: Spot and Contracts, in Colombia.
The expected differential of contract and spot prices constitutes another calculation alternative of spread which allows moving from spot price (P) to forward price (f) for each month of the year (Figure 2 and Table 1). The expression to calculate the forward price is given by f = (1 + g)P where g is the premium/spread between f and P. The weighted average of monthly forward contracts are illustrated in Figure 2 and Table 1 for the Colombian market.
Source: Authors (data taken from NEON, 2013).
Figure 2 Difference between Long Term Contracts and Spot Price (Gathered by Months).
Forward Prices Based on Spot Price, Spread and Elasticity of Demand
The forward price has conventionally been related to spot price and spread (Allaz & Vila, 1993). The spot price can be obtained through the non-cooperative game theory model, already presented above, and the spread is derived from the methodology previously illustrated. However, it is important to consider the sensitivity of the consumers’ demand to variation of the prices; i.e., elasticity. This variation considers the observed behavior which can be discriminated through the different branches of the activities that are present in the different voltage levels.
In order to establish the effect of the change in prices, reaction of the demand should be considered. This relationship is the most well-known form of the Ramsey pricing rule (Braeutigam, 1989). Let 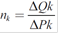 be price elasticity for the economic sector k, thus a change in price for this sector (Δ P
k
), would bring about a change in the demand with which the variation in the profitability derived from the change in price would be obtained:
be price elasticity for the economic sector k, thus a change in price for this sector (Δ P
k
), would bring about a change in the demand with which the variation in the profitability derived from the change in price would be obtained:
In order to consider the former issues, the following expression is proposed to obtain the forwards:
Where f k is the modified series of forward prices, P the spot price, g the premium or spread, η k the elasticity of sector k, and ΔP k the expected change in relation to the price in this sector, or the variance of the spot price and e k is a random variable, normally distributed - white noise - with an expected value of zero and constant variance. In the formation of the forward price diverse variables participate, which are not directly observable (i.e. the agents’ strategies in relation to marketing or promotion of the product, or the actions in business administration, etc.), some of those “hidden” actions should be absorbed in e k .
Note that electricity forward pricing depends on the strategic behavior of the agents and many non-observable variables, so expression (21) includes a random variable that accounts for these non-observable heterogeneities.
Investment Portfolio Theory: Average Variance Analysis
Once the Cournot competition has provided contract prices and quantities, leader firms face a new decision problem: how to distribute the electricity among the different demands of forward contracts - which can be clustered depending on economic activity or voltage level. In both cases, the forward contract will be defined according to a gap/spread that considers hydrology and elasticity per type of demand.
With this decision, a higher expected profitability is pursued, which is also related to a higher risk and a tradeoff between both of them, in turn, creating the necessity for some criteria that allow for the choice of an optimal combination profitability-risk; for example, the ones provided by the classic portfolio theory (Markowitz, 1952).
A portfolio formed by n alternatives and a budget x 0 equivalent to the quantity of estimated forward x 1 * is wanted to distribute to the different k served demands (sectors) by the generator i, so that:
Each x 0k can be expressed as a fraction of the total quantity available x 0 ; that is:
If r k is the return that is obtained from x 0k , the income received at the end of the period associated with this sector is r k x 0k , so the profitability or total return of the portfolio is given by:
In the same way:
So the rate of return on the portfolio is the sum of the rates of returns of the different sectors weighted by their participation in the portfolio.
It should be considered that the generator intends to distribute quantities produced in forward for each sector k, which at the same time, can be regular x k ≠1,R (current) and seasonal (if the elasticity of the sector is considered) x k ≠ 1,E , so that:
The aim of the generator will be to maximize the expected profitability or minimize the risk associated with this profitability. Let πk , RoE be the expected profit of each demand if the generator offers regular or seasonal contracts. In this case, the return on the expected portfolio that is required to maximize will be:
Therefore, the expected value of the portfolio return rate will be:
It should be considered that, as a general rule, the aim is to reduce the variance of a portfolio or diversify through the inclusion of additional options; that is, with more sectors or distributions of Xo, and ideally, uncorrelated.
The Markowitz Model is used to formulate the problem that allows the minimization of the variance of a portfolio. It is assumed that n options are available; such options exhibit expected return rates r 1 ,…,r n and co-variances σ k,j ∀ k,j = 1,…, n . To find the assignation, the expected value of its return rate E(r) is fixed in any fixed value that is wanted, then the feasible Portfolio of minimal variance for this rate is found.
The problem can be formulated as follows:
Additionally, it is maintained that w k ≥ 0, given that it is about the delivery of physical electricity sales, not about financial assets, and the factor ½ in front of the equation to be minimized is convenient for the final equations to be simpler. When solving this problem, the investment percentages were found in every option that exists in the Portfolio for each expected profitability.
TESTS AND RESULTS
Obtaining Spot Price and Quantities of the Five Leader Agents
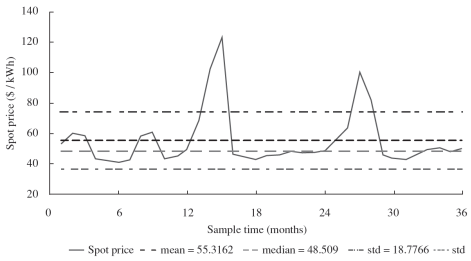
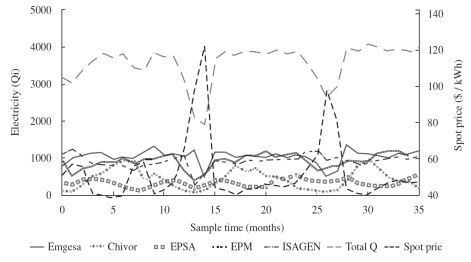
From the strategic behavior of the leader agents and taking into account the effects of the influential variables in the electricity price such as planned demand, levels of the dams, among others, the Cournot competition is used to establish price and quantities for the leaders, up to the year 2016 (Figures 3 and 4).
Parameters of the Cournot competition include the forecasted energy demand and historical hydrology data provided by UPME, as well as an estimate of the levelized costs of electricity in Colombia (see equation (18)). The picks in spot prices shown in Figure 3 are a consequence of hydrologic seasonality. Note that such picks coincide with an important reduction in electricity generated as can be seen in Figure 4.
Generation of Forward Contracts
Using the data spot price obtained from the Cournot competition as input, monthly gap or spread (Table 1), and the elasticity of diverse economic sectors reported in Barrientos, Velilla, Tobón-Orozco, Villada and López-Lezama (2018); the least inelastic and statistically significant sectors were selected for different Voltage Levels (VL)3 (except for AB in VL = 2); that is, the sectors in which short term elasticity presented a critical value of normal distribution around 1.96 or higher to be considered significant to 5% or less (Table 2). These sectors were: Food and Beverages (FB) in VL 1 and 2; Rubber and Plastic (RP) in all VL; Chemical Products (CP) only in VL 2; and Commerce (C) in VL 1 and 3.
Table 2 Price Elasticity of Demand for Several Branches of Economic Activities and Voltage Levels in Colombia.
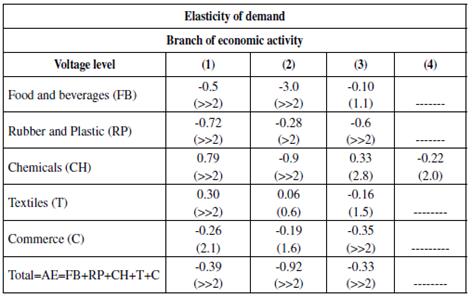
Own calculation
Value t in parenthesis
Source: Barrientos et al. (2018).
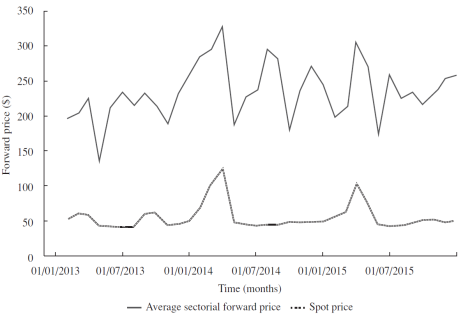
With the above data and using the equation 21, the average sectorial forward prices for these sectors were generated with addition of the spot price that was obtained from the Cournot competition (see Figure 5). As empirical evidence suggests, every electricity market in the world is volatile; of course spot markets are more volatile than forward markets. However, if we consider the average monthly forward price of all sectors along with the observed spot price, the volatility of the forward price could be as high as that of the spot price (see Figure 5). Moreover, if we want to produce forward seasonal prices which include the elasticity of demand, we have to burden the cost of eventually having more volatility. Note that, on average, forward prices turned out to be higher than spot prices.
Portfolio Evaluation
Once the spot price and the series of prices to be considered in the forward contracts for the sectors in the determined voltage levels were obtained, a standard portfolio was evaluated in order to distribute the quantities in each option (seasonal forward and spot). For this evaluation it is assumed that the portfolio is carried out in a determined period, at the beginning of which the financial good is agreed upon, and is fulfilled at the end. In addition to this, more historical data is collected each time and in turn, the portfolio is reconstructed again. That is to say, the new information that is produced in the market is integrated into the historical data. Following Green and Le Coq (2010), even though the theory does not state anything about the duration of the period, there is a tacit assumption that constant averages, variances and co-variances of the returns are adequate.
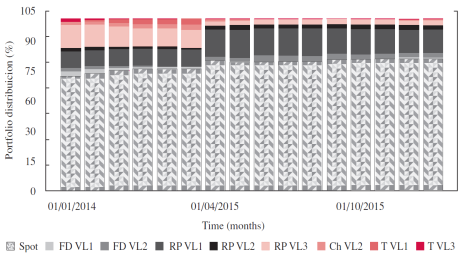
At an international level, profitabilities that oscillate between 5% and 10% are pursued, depending on diverse factors such as degree/level of competition of the electricity sector, existing regulation, level of indebtedness, and country risk, among others. Figure 6 depicts the results obtained by the portfolio from January 2014 for an expected profitability higher or equal to 5%.
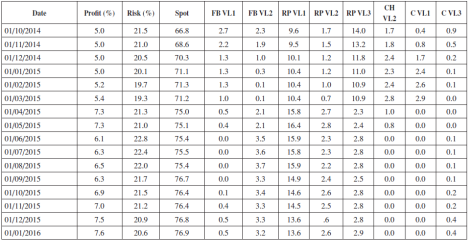
These results indicate a remarkable preference to sell more electricity quantities in the spot market than in the other sectors related to the forward markets in voltage levels 1, 2, and 3. This trend becomes more evident throughout time; that is, the distribution is focused on the spot, increasing the profitability during the last periods: from 5 to 7.5%, and reducing the risk from 21.6 to 20.6 (see Table 3).
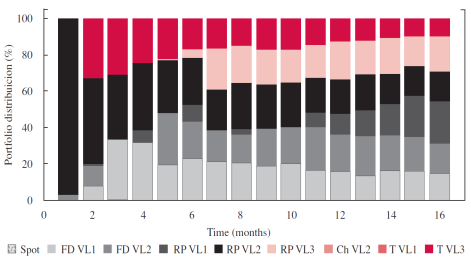
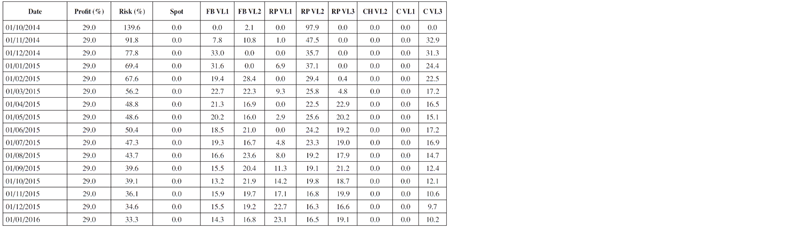
When profitability increases, preference for forwards over spots is more evident. However, for the case that was analyzed, the highest profitability that can be obtained is 29%, taking into consideration that higher values will keep the optimization problem from converging. Figure 7 displays the portfolio distribution for a profitability of 29%, which is focused mainly on the RP sector because of the low demand elasticity price; and in a less degree in the FB sector that exhibits higher elasticity.
It is important to highlight that for this case, the risk is very high at the beginning (approximately 140%), but throughout time it drastically decreases in a gradual manner (Table 4).
CONCLUSIONS AND DISCUSSION
The analytical game-based model proposed in this paper replicates the functioning of the Colombian electricity market, in which leader agents behave strategically. In this scenario, application of seasonal forwards keeps such structure and gives priority to contracts in sectors with inelastic demand in order to maximize the utility of the generators. However, some percentage of contacts is also assigned to the only sector with statistically significant elastic demand (FB in VL2). This shows the potential to take advantage of hydrological seasonality, offering forward contracts at lower prices, stimulating an increase in demand and benefiting both consumers and producers. If the demands of different economic sectors begin to react positively to seasonal forwards in an electricity market with a high percentage of hydropower, like the Colombian market, there might be dynamic results, allowing for the development of the electricity sector and increasing the competitiveness of consumers.
The interaction in the Cournot type market proposed in this paper allows the establishment of an equilibrium decision of the leader’s in an electricity market, in the sense that their benefits are maximized and there are no incentives to divert. This equilibrium depends on hydrology and possibility to couple resources throughout time, economic situation, elasticity of the demand, and costs structures. The combination of the game theory with the classical theory of the portfolio replicates the observed functioning of the Colombian market, and sufficiently captures the consequences of offering contracts different from the status quo of the market; that is, taking into consideration hydrological seasonality and elasticity of the demand, allowing for the deepening of the understanding of the electricity generation markets. Results show that in the long term, it will be more profitable for the generators to sell seasonal forwards rather than spots, as long as the profitability expectations are higher, given the response of the demand in forward contracts toward changes in prices.
There are some issues to be explored such as the effects of establishing seasonal forward contracts on the planning of the economic sectors’ consumptions. This is important given that the consumers benefit from the higher hydroelectricity situations as well as the particularities of these contracts and their duration. Finally, the interaction that is proposed can be generalized through a dynamic game in which the agents alternate repeatedly between selling forward contracts and competing in prices with the spot market directly, but with several time periods between each round of forward transactions (instead of being a one-period forward).