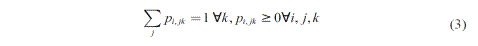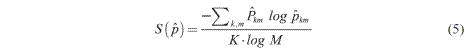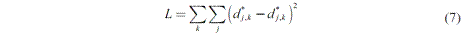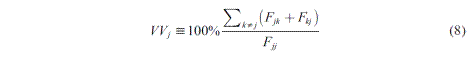Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
INTRODUCCIÓN
Cuando se comparan los resultados de la votación popular entre dos elecciones consecutivas se obtiene una imagen bastante incompleta de la dinámica electoral que subyace porque los resultados de votación agregados solo muestran las ganancias y pérdidas netas de los partidos políticos. El grado en que los votantes cambian sus preferencias desde una elección a otra puede ser capturado a través de encuestas electorales o aplicando técnicas econométricas a partir de datos electorales agregados, sin embargo, estos cambios pueden ser difíciles de identificar. El propósito de este trabajo es utilizar nuevas técnicas econométricas para estimar y analizar la migración de votantes y la ubicación política de las coaliciones o partidos políticos. Se utilizan los datos de cuatro elecciones de diputados recientes en Chile, para responder a una serie de preguntas acerca de la dinámica electoral.
De conocer los patrones de migración de votantes, tanto las coaliciones políticas como el público interesado podrían apreciar la composición de las ganancias (o pérdidas) netas observadas en una elección respecto de otra. En otras palabras, sería posible conocer, entre otras preguntas, cómo se desagrega el flujo de votantes que cambian de coalición y los que dejan de votar, qué coaliciones atraen nuevos votantes, qué coaliciones presentan mayor fidelidad electoral, entre qué coaliciones existe mayor distancia, es decir, entre cuáles el flujo de votantes es menor. Además, la estimación de la migración de votantes y distancia entre partidos puede también dar señales a historiadores y cientistas políticos sobre los patrones de conducta de los votantes o la dinámica electoral en el tiempo (Ferreira y Dionísio, 2012).
El uso de datos agregados para sacar conclusiones sobre el comportamiento individual cuando no se dispone de datos se define como un problema de inferencia ecológica (Schuessler, 1999). Cuando los patrones de migración de votantes no son medidos directamente (por ejemplo, a través de encuestas de salida) o cuando las mediciones existentes son de mala calidad, la migración de votantes necesita ser inferida a partir de datos electorales agregados usando métodos estadísticos apropiados. En tal contexto, una alternativa es utilizar estimadores convencionales basados en ecuaciones logit o probit, sin embargo, estos presentan problemas como la necesidad de elegir un partido de referencia y establecer supuestos específicos sobre la distribución. Otro método es el programa estadístico para inferencia ecológica propuesto por King (2004) que, lamentablemente, no trabaja bien los problemas de probabilidades de transición de votantes (Park, 2004). Una tercera alternativa, menos masificada, es utilizar métodos de programación cuadrática (McCarthy y Ryan, 1977), pero tienden a subestimar los elementos fuera de la diagonal principal de la matriz de probabilidades de transición (Upson, 1978).
El método analítico propuesto en este trabajo es conocido como máxima entropía generalizada (GME, por su sigla en inglés). Comparado con otros estimadores, GME ofrece un número considerable de propiedades estadísticas deseables (Mittelhammer, Scott y Marsh, 2013). El principio de máxima entropía (ME) constituye el punto de partida para la estimación por GME y se basa en la búsqueda de probabilidades que maximizan una función de entropía sujeta a condiciones de momento, restricciones de probabilidad acumulada y restricciones de adición sobre la variable aleatoria. El método se caracteriza por su robustez y por su capacidad de ajustarse a modelos sobre parametrizados como los relacionados con problemas de inferencia ecológica.
A pesar de sus virtudes y usos en otras aplicaciones en ciencias sociales y economía (Bernardini, 2010; Fernández, Lemelin y Rubiera, 2014; Ferreira, Dionísio y Pires, 2010; Rubiera, Fernández y Aponte, 2012), el método de GME ha sido poco utilizado para analizar patrones de migración en votantes. Uno de los primeros trabajos que usó máxima entropía lo hizo para estimar probabilidades de transición de votantes en el contexto de las elecciones de Reino Unido (Johnston y Hay, 1983). En ese trabajo se utilizaron datos de encuestas nacionales y resultados electorales para restringir el problema de estimación, pero no mejoraron las fronteras del error. Más recientemente, se ha estimado la migración de votantes en Canadá utilizando GME para las elecciones de la asamblea legislativa en British Columbia, en los períodos 1996, 2001 y 2005, y para las elecciones federales 2000, 2004 y 2006 (Antweiler, 2007). Este último trabajo demostró la creciente volatilidad de votantes, cuándo y dónde se produce la erosión en el apoyo de los ciudadanos a los partidos, cómo se distribuyen las ganancias o pérdidas entre partidos, el grado de fidelidad de los electores y la importancia de la transición entre votantes y no votantes. En otra aplicación reciente se han estimado las probabilidades de transición de votantes y la ubicación de partidos en un espacio político bidimensional para las elecciones parlamentarias del estado de Baviera en los períodos 1998, 2003 y 2008 (Odendahl, 2012). Allí se determinó que los patrones de transición difieren en los períodos electorales y utilizando la matriz de transiciones, calculó la distancia ideológica entre partidos políticos.
Los resultados de este estudio muestran que es posible estimar la migración de votantes a partir de datos electorales agregados en Chile, especialmente si se trabaja con un nivel que haga comparable los clústeres geográficos, como la escala municipal. Además, usando las transiciones estimadas, es factible calcular la distancia ideológica e inferir una ubicación de las coaliciones que refleje el comportamiento actual de los votantes. En otras palabras, la ubicación de las coaliciones puede ser estimada a partir de datos electorales agregados. Los resultados de este estudio podrían ayudar a los políticos a pensar sobre la asignación de sus gastos en campaña y dirigirlos con mayor eficiencia, en particular, cuando se busca revertir un resultado electoral insatisfactorio en una elección previa.
La estructura del trabajo consta de cuatro apartados. En el primero se aborda el sistema de elecciones parlamentarias en Chile y la evolución reciente de las elecciones de diputados. En el segundo se presentan los aspectos teóricos del método de GME y se plantea el modelo empírico a estimar. En la tercera parte de la investigación se presentan y analizan los resultados principales. En el cuarto y último apartado se exponen las conclusiones más relevantes del trabajo.
SISTEMA Y CONTEXTO ELECTORAL
Sistema electoral chileno: elecciones parlamentarias
Antes de la reforma electoral del año 2015, las elecciones parlamentarias se basaban en un sistema directo conocido como “sistema binominal”, dado que en cada distrito o circunscripción senatorial se elegían dos representantes al parlamento y los candidatos se presentaban en listas con dos integrantes. La Cámara de Diputados se componía de 120 miembros elegidos por un período de cuatro años en sesenta distritos de dos miembros cada uno, mientras que el Senado estaba compuesto por 38 miembros electos para un término de 8 años en 19 circunscripciones de 2 miembros.
El mecanismo del sistema binominal operaba en función de las votaciones obtenidas en los distritos y circunscripciones, independiente de los resultados de las agrupaciones a escala nacional. Para determinar los candidatos elegidos se realizaba la suma total de votos por cada lista o nómina. Así, las listas que obtenían las dos más altas mayorías elegían a un candidato de cada una, siendo electos aquellos que obtuvieran la mayor votación en cada lista. Sin embargo, el sistema binominal también establecía que en el caso que la lista que obtuviera mayores votos doblara la votación de la segunda lista, entonces la primera lista elegiría a sus dos integrantes. Inicialmente, se trataba de un sistema de representación proporcional, pero se limitaba a las dos primeras listas en votación lo que limitaba la representatividad de pactos menos fuertes e independientes y en ocasiones eran elegidos candidatos débiles arrastrados por el candidato fuerte de la lista. Probablemente, la principal crítica al sistema radicaba en que concedía una ventaja indebida a la colación electoral situada en la segunda posición (desde 1989, la derecha), al otorgarle la misma representación que a la primera lista en la mayoría de las divisiones (Carey, 2006).
Después de 25 años del sistema binominal se sustituyó el sistema electoral por uno de carácter proporcional inclusivo, estableciendo que a partir de 2017 la Cámara de Diputados estará compuesta por 155 miembros elegidos de manera directa y por una duración de 4 años, en 28 distritos de entre 3 y 8 miembros cada uno, mientras que el Senado estará integrado por 50 miembros electos de manera directa para un período de 8 años en 15 circunscripciones (una por región) de 2 a 5 miembros cada una. Del mismo modo que en el sistema binominal, las elecciones al Senado se seguirán celebrando cada 4 años, las regiones de número impar escogerán a sus senadores a partir de 2017, mientras que las regiones de número par y la Región Metropolitana celebrarán las elecciones senatoriales en el siguiente período. En cuanto al mecanismo de elección, para asegurar la proporcionalidad se usará el coeficiente D’Hondt que consiste en dividir los votos de cada lista por uno, dos, tres y así sucesivamente según la cantidad de escaños a elegir y luego ordenar los valores resultantes para determinar la cifra repartidora y el número de escaños por lista.
Elecciones de diputados en Chile
Participación electoral
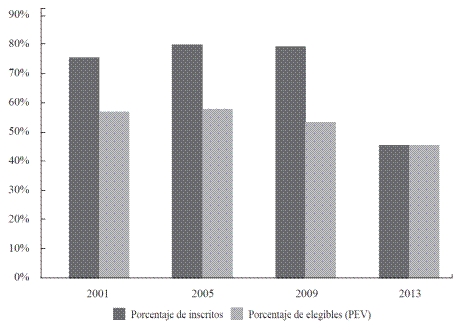
Desde el retorno a la democracia en 1990, la participación electoral en Chile ha venido en caída. A medida que la población se acostumbró a tener elecciones, el interés en estas mismas. Por ejemplo, en las elecciones de 1993, el 75,8% de la población en edad de votar (PEV) emitió votos válidos, cifra considerablemente menor a la participación ciudadana en los plebiscitos de 1989 y 1988, donde el 84,6% y el 89,1% emitió votos válidos. En lo sucesivo, la tasa de participación electoral experimentó una caída sostenida, bajando al 65,3% en 1996 y al 59,6% en 1997, para luego, a partir de las elecciones parlamentarias de 2001, quedarse bajo la barrera del 60%. En la Gráfica 1 se muestra la evolución reciente de la participación en elecciones de diputados a partir del año 2001.
Fuente: elaboración propia con datos del Servel.
Gráfica 1 Tasas de participación. Elecciones de diputados 2001-2013.
Como se aprecia en la gráfica, el porcentaje de votantes inscritos experimentó un leve aumento del 4,2% en las elecciones de diputados de 2005, al igual que la tasa de participación sobre la PEV, que aumentó un 0,8% en el mismo período. Las elecciones de diputados de 2009 mostraron una caída de la participación ciudadana del 4,3% de votantes y del 0,4% en el porcentaje de inscritos.
La entrada en vigencia de la Ley 20.568 sobre inscripción automática y voto voluntario trajo consecuencias importantes en términos de la edad del electorado, composición socioeconómica y participación electoral en las elecciones de 2013. En términos de la edad del electorado, la entrada en vigencia de la nueva ley disminuyó el sesgo etario ya que la distribución de quienes votaron en 2013 fue considerablemente más pareja por rangos de edad que los que estaban inscritos anteriormente. La participación electoral en 2013 fue más alta entre las personas mayores de 45 años (poco más del 60%) que entre los menores de 45 años (entre el 30% y el 50% dependiendo de la edad). Entre tanto, la sobrerrepresentación de los mayores de 45 años en el padrón cayó de 2,6 a 1,6 veces tras la entrada en vigencia de la ley. La composición socioeconómica, medida por nivel educacional, también experimentó cambios importantes lo que se vio reflejado en una mayor participación de los grupos medios a costa de los grupos más bajos. El grupo de mayor nivel educacional, en tanto, continúa con una participación electoral mayor que la que tenía en el sistema electoral anterior. Como se observa en la Gráfica 1, la participación de los votantes se redujo un 34% durante 2013, aunque el 100% de la población en edad de votar estaba inscrita. Esto significa que poco más de 6,2 millones de ciudadanos emitieron votos válidos. El número más bajo desde las elecciones de diputados de 2005.
Resultados electorales
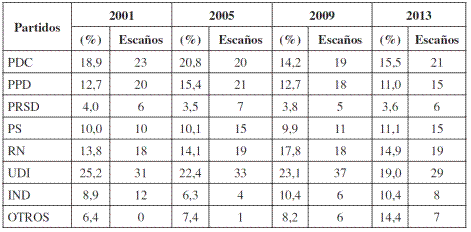
La Tabla 1 muestra los resultados nacionales de las elecciones de diputados desde 2001 hasta 2013 por partidos políticos. En los últimos cuatro períodos electorales la Unión Demócrata Independiente (UDI) ha sido el partido más votado, promediando un 22,4% de los sufragios. Sin embargo, exceptuando las elecciones de 2009, el porcentaje de votos obtenidos sobre el total nacional ha ido cayendo considerablemente para posicionarse en torno al 19% en 2013, esto es un 6,2% menor a la cifra obtenida en 2001. El Partido Demócrata Cristiano (PDC) es el segundo de mayor votación y promedia un 17,4% desde 2001, con un máximo del 20,8% de sufragios en las elecciones de 2005. Más atrás aparecen Renovación Nacional (RN) promediando el 15,2%, el Partido por la Democracia (PPD) con el 13%, el Partido Socialista (PS) con un 10,3%, otros partidos (OTROS1) con el 9,1%, los candidatos independientes (IND) con el 9% y el Partido Radical Social Demócrata (PRSD) con un 3,7%, promedio de la votación.
Tabla 1 Resultados elecciones de diputados 2001-2013.
Fuente: elaboración propia con datos del Servel.
Al mirar el número de escaños asignado a cada partido, llama poderosamente la atención el caso de la UDI que, a pesar de experimentar una caída en el porcentaje de votación, consiguió aumentar el número de escaños en 2005 y 2009, y apenas reducirlo en 2013, respecto de las elecciones de diputados en 2001. Una situación similar, pero en menor medida se observa en el PS que aumentó un 50% el número de escaños al comparar las elecciones de 2013 con las de 2001. La Ley de Inscripción Automática y Voto Voluntario tuvo un efecto notorio homogeneizando la votación entre los partidos políticos, pero no fue tan efectiva en cuanto al número de escaños asignados.
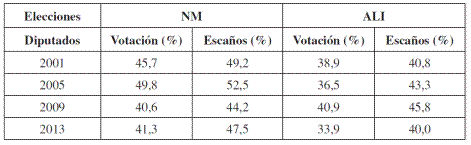
En las coaliciones, la Nueva Mayoría2 (NM, comúnmente conformada por el PDC, PS, PPD y PRSD) ha sido la más votada promediando un 44,3% de la votación nacional y un 48,3% del total de escaños de la Cámara de Diputados. La Alianza3 (ALI, comúnmente conformada por RN y UDI), por su parte, promedia cuotas del 37,5% de la votación y el 42,5% del total de escaños. Claramente, estos resultados revelan que ambas coaliciones han sido sobrerrepresentadas en la Cámara de Diputados. La Tabla 2 muestra los porcentajes de votación y escaños de ambas coaliciones políticas en el periodo 2001-2013.
Tabla 2 Porcentajes de votación y escaños coaliciones políticas 2001-2013.
Fuente: elaboración propia con base en datos del Servel.
Como se aprecia, ha existido una volatilidad considerable en los resultados electorales de ambas coaliciones. En las elecciones de 2005, la NM aumentó en un 4,1% su cuota de votación, correspondiente a poco más de 477.000 sufragios, mientras que la Alianza, en el mismo período, redujo su votación en un 2,4%, cerca de 202.000 sufragios. Las elecciones de 2009 mostraron mayor volatilidad sobre todo de parte de la NM que redujo su votación en un 9,2% (aproximadamente 601.000 sufragios) con relación a 2005. La Alianza, por su parte, obtuvo un aumento del 4,4% sobre el total nacional, correspondiente a 295.000 sufragios. Finalmente, en las elecciones de 2013 la caída más abrupta la experimentó la Alianza perdiendo un 7% de votación o 596.000 sufragios válidamente emitidos.
Al analizar la volatilidad de los resultados electorales en las coaliciones, inmediatamente aparecen las siguientes preguntas: ¿Cuál fue el origen/destino de los votos que obtuvo/perdió la NM y la Alianza en las últimas cuatro elecciones de diputados?; ¿Qué porcentaje de la votación obtenida en la elección inmediatamente anterior fue retenida por los partidos o coaliciones?; ¿Qué fracción de los votantes de la NM y de la Alianza decidió votar por independientes u otros partidos políticos? En otras palabras, ¿Cómo cambiaron las preferencias políticas de los votantes desde una elección a otra?; ¿Cómo es el grupo de no votantes? A continuación, se describirá el método usado para la estimación de la migración de votantes, para analizar los resultados posteriormente.
ENTROPÍA Y ESTIMACIÓN POR MÁXIMA ENTROPÍA GENERALIZADA (GME)
Entropía
La teoría de la información define entropía como una medida de incertidumbre o la cantidad de información esperada en determinada fuente. Esto refleja lo que se espera aprender desde una observación (en promedio), y depende de cómo se mida la cantidad de información. En otras palabras, entropía es una medida de la incertidumbre de una variable aleatoria o una medida de uniformidad (Golan, 2008).
Máxima entropía generalizada (GME)
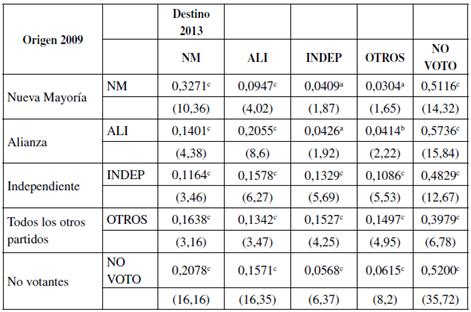
Frente a la pregunta fundamental de inferencia a partir de datos limitados e insuficientes, Jaynes propuso el principio de máxima entropía (ME), el cual es visto como una generalización del principio de razón insuficiente de Laplace. El formalismo de ME estuvo basado en la medida de entropía desarrollada por Shannon en 1948 (Jaynes, 1957). El principio de ME se basa en la búsqueda de las probabilidades p que maximizan una función H(p)4 sujeto a todas las restricciones existentes (condiciones de momento, restricciones de probabilidad acumulada, restricciones de adición) sobre la variable aleatoria.
A pesar de las potencialidades de la aproximación ME, el método de máxima entropía generalizada (GME) incrementó sustancialmente el número posible de extensiones y aplicaciones en economía, particularmente cuando existen problemas en modelos lineales mal planteados (Golan, Judge y Miller, 1996).
Al aplicar el método GME al comportamiento electoral definimos la cantidad de votos obtenida por la coalición k en la elección t en el distrito i como sigue:
Donde p jk es la probabilidad de que un ciudadano que votó por la coalición j en t 1 vote ahora por la coalición k. Al asumir que el error i ,t se puede escribir utilizando límites simétricos V ik1 y V ik 2 tendremos que la información contenida en los resultados electorales proviene de las transiciones p jk y de los errores ik .
Con esto, la función de entropía de Shannon queda expresada como
La que debe ser maximizada según las restricciones
El criterio de valorización de los puntos de soporteV
ik1
y V
ik2
puede suponer un vector simétrico o asimétrico, dependiendo del problema en consideración. Para el término de error, comúnmente se utiliza un vector de soporte simétrico centrado en 0. Golan et al. (1996) recomiendan usar la “regla de las tres sigmas” de Pukelsheim (1994) para definir los límites del vector de errores como V
ik1
=−3σ y V
ik2
= 3σ, donde σ es la desviación estándar de ε. Como σ es desconocido, puede ser reemplazado por un estimador. Se consideran dos posibilidades: 1) obtener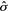 
desde la regresión por MCO, y 2) usar como proxy la desviación estándar muestral de v
i
k
,t
(Campbell y Hill, 2005). Tras someter a pruebas las dos posibilidades, los autores encontraron mejores resultados usando la segunda alternativa.
Las probabilidades de transición P jk resultantes se distribuyen asintóticamente normal, permitiendo el uso de pruebas paramétricas convencionales de significancia estadística5.
Medidas de diagnóstico en GME
Existe un estadígrafo de “bondad del ajuste” para GME llamado medida de entropía normalizada,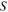 
(
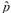), que cuantifica el contenido relativo de información presente en una muestra respecto al máximo nivel de incertidumbre (Golan, 2008). Esta medida normalizada para el modelo GME viene dada por:
Donde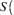 
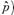0,1. Cuando este valor se aproxima a 0 refleja la ausencia de incertidumbre y cuando se aproxima a 1 refleja la completa incertidumbre. En el primer caso, los puntos de soporte y los datos reflejan información diferente sobre los parámetros y la solución no es uniforme, mientras que, en el segundo, significa que la solución es cercana a la distribución uniforme y que los datos concuerdan con los puntos de soporte definidos (Fraser, 2000). A partir de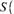 
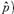se define un índice de reducción de incertidumbre (o índice de información de parámetros) debido a la información I (
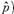= 1-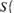 
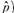. Este índice puede ser utilizado para evaluar la contribución marginal de las variables explicativas a la reducción de la incertidumbre si se comparan los valores antes y después de la inclusión de la variable. Si S(K) = S (K-1), entonces es factible concluir que la variable no es relevante ya que no conduce a una reducción de incertidumbre.
Medidas de distancia ideológica
Una vez estimadas las matrices de Markov, el siguiente paso es trasladar las probabilidades de transición a una medida de distancia ideológica entre cada par de coaliciones. Una forma sencilla y eficaz para medir la distancia ideológica entre dos coaliciones es el logaritmo del odds ratio. El odds ratio es una medida estadística comúnmente utilizada en la investigación biomédica como una medida de asociación entre un evento y la vulnerabilidad a este, intuitivamente similar al coeficiente de correlación. Existen aplicaciones del odds ratio en el contexto de transiciones de votantes para determinar la distancia ideológica entre pares de partidos políticos (Fisher y M, 2003; Heath et al., 1991; Odendahl, 2012). Como la matriz de distancias es mayor a 2 X 2, ya que hay j coaliciones, existirán varios odds ratios locales para cada par de coaliciones. Cuanto menor sea la transición entre un par de coaliciones y, por tanto, mayor sea la distancia entre ambas, mayor será el odds ratio. En otras palabras, la fidelidad de los votantes a la coalición de su preferencia es alta entre dos períodos electorales.
Esto implica que el odds ratio es simétrico y puede ser utilizado como una medida de flujo bidireccional de la migración de votantes. Una medida más fácil de interpretar es el logaritmo del odds ratio, donde un valor de 0 implicará probabilidades iguales de permanencia o migración entre los partidos. Formalmente, el logaritmo del odds ratio viene dado por:
Donde D j,k es el logaritmo del odds ratio que representa la distancia entre la coalición j y la coalición k, y P ( | ) es la probabilidad de votar por la coalición j (k) en el período t condicional a haber votado por la coalición j o k en el período anterior.
El numerador de la expresión (6) representa la capacidad de la coalición j para mantener votantes (fidelidad), el período t respecto del período t-1 y, el denominador, la capacidad para atraer nuevos votantes en el mismo período. Un valor mayor de D j,k implica que la fidelidad de los votantes es alta, traduciéndose en una mayor distancia ideológica entre las coaliciones políticas y menores tasas de migración.
Siguiendo lo realizado por Odendahl (2012), las medidas de distancia entre cada par de coaliciones se utilizaron para determinar las posiciones de las coaliciones en un espacio político bidireccional6. Este método toma el punto medio de la matriz de distancias como el origen y a partir de ello encuentra la mejor coordenada posible para las coaliciones. Las coordenadas óptimas se encuentran minimizando la siguiente función:
Donde d * j,k es la distancia observada entre las coaliciones j y k y d j , k es la distancia entre las ubicaciones estimadas de las coaliciones j y k.
RESULTADOS
Datos
El sistema de elección parlamentaria de Chile establece 60 distritos electorales (conformados como conjuntos de comunas) y 19 circunscripciones senatoriales (conformados como conjuntos de distritos de una misma región). Los partidos más grandes en Chile son Unión Demócrata Independiente (UDI) de derecha, Renovación Nacional (RN) de centro derecha, Partido Demócrata Cristiano (PDC) de centro, Partido por la Democracia (PPD) de centro izquierda y Partido Socialista de Chile (PS) de centro izquierda. Partidos de votación menor, pero de larga trayectoria son el Partido Comunista de Chile (PCCh) y el Partido Radical Socialdemócrata (PRSD). Los demás partidos no obtienen votaciones significativas y tienen una escasa representatividad.
Para estimar la matriz de probabilidades de transición de Markov se utilizó el software SAS 9.4 (procedimiento entropía) y se tomaron los datos agregados del servicio electoral SERVEL, de las elecciones de diputados en 2001, 2005, 2009 y 2013 de todas las comunas de Chile (346). Aunque la comuna de Alto Bío-Bío fue creada en 2003, al igual que Alto Hospicio y Hualpén fueron creadas en 2004, es posible separar sus resultados electorales para las elecciones de diputados del año 2001, pues funcionaban como circunscripciones electorales de las cuales es posible recuperar votaciones por coalición con el fin de homologarlas con los años siguientes. Los partidos fueron agrupados en las siguientes coaliciones: Nueva Mayoría7 (NM, formada por PDC, PPD, PS y PRSD), Alianza8 (ALI, formada por UDI y RN), OTROS (que incluye al PCCh y otros partidos de menor votación) e Independientes (INDEP). Para tratar los cambios netos de población (flujos de entrada y salida de votantes) y las tasas de participación electoral, se incluyó al grupo de no votantes (NO VOTO) definidos como la suma de abstención, votos nulos y blancos. La abstención en cada comuna se calculó como la diferencia entre los votantes elegibles (población de 18 años y más) y el total de votos (incluyendo nulos y blancos) para lograr una medida más acertada de la participación ciudadana y normalizar las elecciones de 2001, 2005, 2009 a la Ley de Inscripción Automática y Voto Voluntario9 que comenzó a regir en enero de 2012 y tendría su estreno en las elecciones municipales del mismo año.
Resultados de estimación
Los resultados se componen de cuatro partes. Primero, se muestran las matrices de transición estimadas utilizando máxima entropía (no generalizada) como punto de partida para el análisis. Segundo, se muestran las matrices de transición estimadas y migración de votantes de los periodos 2001-2005, 2005-2009 y 2009-2013. Tercero, con los resultados obtenidos, se presenta la matriz de distancia entre coaliciones. Finalmente, usando la matriz de distancias, se determinó la ubicación de las coaliciones en un espacio político bidimensional.
Método de máxima entropía (no generalizada)
En una primera aproximación, la Tabla 3 muestra el cálculo hecho a partir del uso del principio de máxima entropía (o problema inverso puro) para las probabilidades de transición. Cada valor de la tabla indica la probabilidad de que un elector haya votado por una coalición que llamaremos “de origen” en la elección pasada (en las filas de la tabla) vote por una coalición “de destino” en la elección siguiente (columnas de la tabla). La diagonal principal de la matriz de transición revela la capacidad de las coaliciones de mantener su apoyo previo. Los partidos pertenecientes a NM retienen aproximadamente el 29% de votantes de 2001, mientras que ALI logra retener alrededor del 23%. INDEP y OTROS lograron tasas de mantención de votantes débiles con un 15% y 17%, respectivamente. La pérdida del 71% de votos de NM se puede desagregar en el 23% que fueron hacia ALI, un 3% que fueron a INDEP, un 4% a OTROS y un 40% que NO VOTO. En tanto, la pérdida de apoyo de ALI del 77% fue captada mayoritariamente por NM con un 29%, seguida de OTROS con el 6% e INDEP con el 5%; finalmente, el grupo de NO VOTO recibió un 38%. Estos resultados son bastante cuestionables, especialmente por el alto número de personas que habría migrado entre votar y no votar en un sistema en el que, una vez inscrito, el ciudadano estaba obligado a votar en todas las elecciones posteriores a su inscripción.
Tabla 3 Matriz de transiciones. Elecciones de diputados 2001/2005.
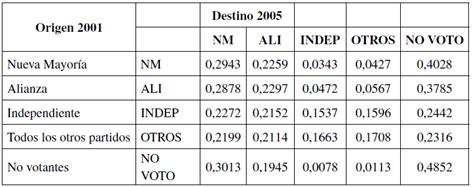
Medida de entropía normalizada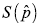 
= 0,6479
Índice de reducción de incertidumbre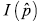 
= 0,3521
Nota: las probabilidades de transición se muestran desde las elecciones de 2001 (filas) a las elecciones de 2005 (columnas).
Fuente: elaboración propia con SAS 9.4.
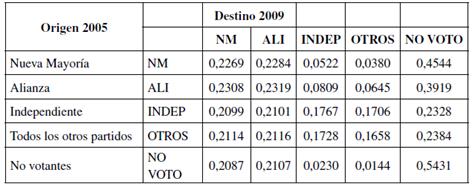
Algo similar ocurre con los resultados electorales de 2005 y 2009 en las tablas 4 y 5, aunque la coalición de centro izquierda pierde casi un 7% de fidelidad de sus votantes.
Tabla 4 Matriz de transiciones. Elecciones de diputados 2005/2009.
Medida de entropía normalizada 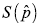= 0,6513
Índice de reducción de incertidumbre 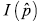= 0,3487
Nota: las probabilidades de transición se muestran desde las elecciones de 2005 (filas) a las elecciones de 2009 (columnas).
Fuente: elaboración propia con SAS 9.4.
Tabla 5 Matriz de transiciones. Elecciones de diputados 2009/2013.
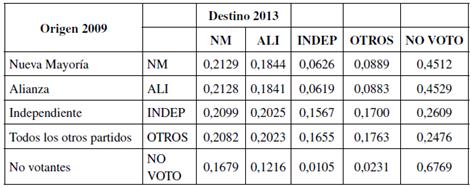
Medida de entropía normalizada 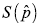= 0,6362
Índice de reducción de incertidumbre 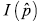= 0,3638
Nota: las probabilidades de transición se muestran desde las elecciones de 2009 (filas) a las elecciones de 2013 (columnas).
Fuente: elaboración propia con SAS 9.4.
En general, en todas las elecciones analizadas, la capacidad de retener votantes de las coaliciones principales apenas supera el 20%, mientras que la migración entre votantes y no votantes solo se reduce cuando el sistema de registro electoral pasó a ser automático y de voto voluntario, cuestión abiertamente contraintuitiva. Por ello, presentamos a continuación la estimación realizada con el método de máxima entropía generalizada, cuyos resultados no presentan este cuestionamiento.
Método de máxima entropía generalizada
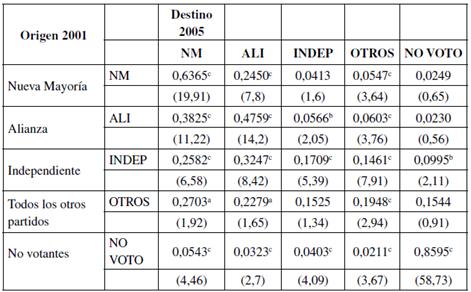
La Tabla 6 muestra los resultados de estimación para el primer período electoral 2001-2005. Las probabilidades de transición se indican desde una coalición (origen) en la elección pasada, filas de la tabla, hacia una coalición (destino) en la elección actual. Los superíndices a, b y c señalan los niveles de significancia y los valores t se muestran en paréntesis bajo cada estimador. Tal como en el apartado anterior, la diagonal principal de la matriz de transición revela la capacidad de las coaliciones de mantener su apoyo previo. Los partidos pertenecientes a NM retienen aproximadamente el 64% de votantes de 2001, mientras que ALI logra retener alrededor del 48%. INDEP y OTROS lograron tasas de mantención de votantes débiles con 17% y 19%, respectivamente. La pérdida del 36% de NM se puede desagregar en un 68% hacia ALI, el 12% de ganancias de INDEP (no significativas), un 15% de OTROS y un 5% de NO VOTO (no significativas). La fuerte pérdida de apoyo de ALI del 52% fue captada mayoritariamente por NM con un 74%, seguida de OTROS con el 12% e INDEP con el 11%; el grupo de NO VOTO no resultó estadísticamente significativo. El apoyo a INDEP y OTROS indica un fuerte grado de fragmentación. El grupo NO VOTO presentó la probabilidad de transición más alta, el 86%, lo que advierte que una proporción menor de quienes no votaron en 2001, decidieron participar en 2005.
Tabla 6 Matriz de transiciones. Elecciones de diputados 2001/2005.
Medida de entropía normalizada 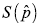= 0,5497
Índice de reducción de incertidumbre 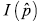= 0,4503
Nota: las probabilidades de transición se muestran desde las elecciones de 2001 (filas) a las elecciones de 2005 (columnas). Valores T en paréntesis. Significancia estadística para el 90%, 95% y 99% está indicado con los superíndices a, b y c, respectivamente.
Fuente: elaboración propia con SAS 9.4.
A partir de la matriz de transición se estimó la migración de votantes. El flujo se obtuvo multiplicando las probabilidades con el número de votos correspondiente a cada coalición y comparando las entradas y salidas se determinó la ganancia neta (o pérdida) correspondiente. La Tabla 7 muestra los flujos migratorios (expresados en miles de votos) para las elecciones 2001-2005. NM obtuvo la ganancia neta más grande en 2005, captando 384.000 votos adicionales (1.411.000 menos 1.027.000) de los cuales la mayoría provinieron de ALI (227.000) y de NO VOTO (178.000). ALI presentó una pérdida neta de 147.000 sufragios y el grupo NO VOTO, una variación negativa de 435.000 votos, destinado principalmente a NM.
Tabla 7 Migración de votos estimada. Elecciones de diputados 2001/2005.
Nota: estimaciones en miles de votos. VV j es la medida de volatilidad de votos específica del partido, definida en el texto. La ganancia neta podría diferir del valor real dado el error de estimación.
Fuente: elaboración propia.
Los resultados de la Tabla 7 sugieren una medida de volatilidad de votos específica para las coaliciones, definida como el valor absoluto de todos los flujos de entrada y salida relativos a los elementos de la diagonal principal de la matriz. La medida de volatilidad VV j para el partido j viene dada por:
Donde F jk ≥ 0 denota el flujo de votantes desde el partido j al partido k (Antweiler, 2007).
La Tabla 7 indica que el apoyo de ALI es más volátil que el de NM, y que INDEP y OTROS presentan volatilidades superiores a 1.000% respecto a las elecciones de 2001. La volatilidad de los votos de ALI es consistente con su pérdida de representatividad en 2005 a manos de NM, y la variabilidad de INDEP y OTROS se explica por la alta fragmentación de sus votos.
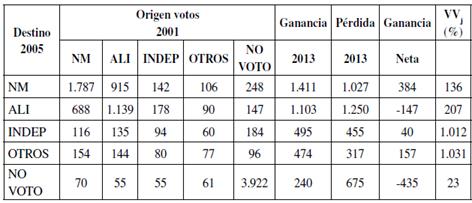
Los resultados de la siguiente elección, período 2005-2009, son presentados en las tablas 8 y 9. Inmediatamente, destaca la pérdida de capacidad de NM para captar los votos obtenidos en la elección pasada (51%) y el leve repunte de ALI (51%), INDEP (25%) y OTROS (24%). Un 51% de la pérdida de votantes de NM fue capitalizado por ALI, el 18% por INDEP, el 16% por OTROS y el 15% por NO VOTO. Dentro de ALI, que logró aumentar la fidelidad de su electorado, se repitió el patrón de la elección anterior y la pérdida de votantes fue captada por NM (43%). INDEP y OTROS presentaron una elevada fragmentación y NO VOTO fueron el grupo de mayor fidelidad.
Tabla 8 Matriz de transiciones. Elecciones de diputados 2005/2009.
Medida de entropía normalizada 
= 0,5762
Índice de reducción de incertidumbre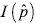 
= 0,4238
Nota: las probabilidades de transición se muestran desde las elecciones de 2005 (filas) a las elecciones de 2009 (columnas). Valores T en paréntesis. Significancia estadística para el 90%, 95% y 99% está indicado con los superíndices a, b y c, respectivamente.
Fuente: elaboración propia con SAS 9.4.
Tabla 9 Migración de votos estimada. Elecciones de diputados 2005/2009.
Nota: estimaciones en miles de votos. VV j es la medida de volatilidad de votos específica del partido, definida en el texto. La ganancia neta podría diferir del valor real dado el error de estimación.
Fuente: elaboración propia.
La estimación del flujo migratorio advierte que NM perdió más votos que los que ganó desde ALI, INDEP y OTROS. La pérdida neta asciende a 671.000 votos (936.000 menos 1.608.000). Por comparación, ALI obtuvo 318.000 votos desde NM y 181.000 desde el grupo de NO VOTO, pero cedió importantes votos a INDEP (452.000), que capitalizaron la ganancia neta más alta (540.000 votos).
Las volatilidades se aprecian similares al periodo electoral anterior. El cambio más llamativo se ve en OTROS, cuya medida de volatilidad retrocedió en un 273%, el grupo de NO VOTO sigue siendo el más estable, apenas el 26% de volatilidad, NM tuvo un aumento del 15% y ALI se mantuvo sin cambios en la medición.
Las elecciones de 2013 (período electoral 2009-2013) fueron particularmente interesantes por el estreno, en elecciones presidenciales y parlamentarias, de la llamada Ley de Inscripción Automática y Voto Voluntario que reguló la inscripción en registros electorales. Los resultados de estimación se muestran en la Tabla 10.
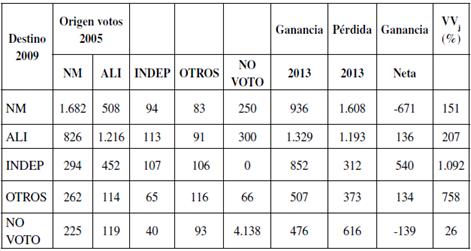
Tabla 10 Matriz de transiciones. Elecciones de diputados 2009/2013.
Medida de entropía normalizada 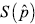= 0,6095
Índice de reducción de incertidumbre = 0,3905
Nota: las probabilidades de transición se muestran desde las elecciones de 2009 (filas) a las elecciones de 2013 (columnas). Valores T en paréntesis. Significancia estadística para el 90%, 95% y 99% está indicado con los superíndices a, b y, c respectivamente.
Fuente: elaboración propia con SAS 9.4.
Las entradas de la diagonal principal señalan una fuerte caída en la capacidad de las coaliciones de mantener su apoyo. NM retuvo apenas el 33% de los votos de 2009, un 18% menor al periodo 2005-2009 y un 31% menor a 2001-2005. Situación similar ocurrió en ALI, donde poco más de un quinto de los votantes mantuvo su preferencia, reduciendo en un 30% y 27% su apoyo respecto de los dos períodos previos. INDEP y OTROS presentaron caídas menores en el apoyo respecto a 2009, aunque persiste la fragmentación de votantes. Los efectos de la ley de inscripción automática y voto voluntario se dejan ver con fuerza en el grupo NO VOTO, hacia donde migraron porcentajes significativos desde los demás partidos políticos. Por ejemplo, de quienes votaron por NM y ALI en 2009, el 51% y el 57%, respectivamente, decidieron no votar en las elecciones 2013. En INDEP y OTROS el panorama no fue más alentador, el 48% de los primeros optó por no votar y el 40% de los segundos tomó la misma decisión. Dentro de quienes no votaron en 2009, el 48% optó por participar en las elecciones de 2013, porcentaje muy superior a las cifras de los períodos anteriores, lo que revela una leve inclinación a votar dentro de quienes pertenecían a este grupo.
Los resultados de la Tabla 11 demuestran que el flujo migratorio en el período 2009-2013 perjudicó ampliamente a ALI con pérdidas netas de 833.000 votos y en menor escala a NM con 97.000 votos. Como era de esperar, gran parte de la migración fue hacia NO VOTO que obtuvo una ganancia neta de 740.000 votos. Los efectos de la nueva ley también se pueden apreciar en la medida de volatilidad que creció para los cinco grupos, destacando las altísimas tasas en NM (4.433%) y ALI (3.216%).
Tabla 11 Migración de votos estimada. Elecciones de diputados 2009/2013.
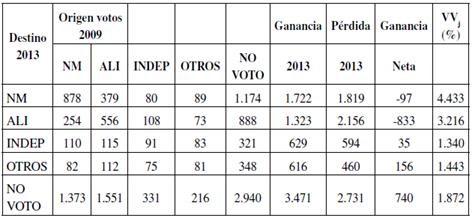
Nota: estimaciones en miles de votos. VVj es la medida de volatilidad de votos específica del partido, definida en el texto. La ganancia neta podría diferir del valor real dado el error de estimación.
Fuente: elaboración propia.
Evidentemente, los patrones de transición difieren a través de los períodos considerados, ya que persisten, en general, movimientos muy diferentes. Sin embargo, como se verá en las siguientes secciones, los patrones de distancia y ubicación de las coaliciones son consistentes con la transición de votos en los períodos.
Distancia entre coaliciones políticas
Para determinar la distancia entre las coaliciones, se utilizaron las matrices de transición de cada período y se calculó el logaritmo del odds ratio (ecuación (6)) para cada par de coaliciones. Las tablas 12, 13 y 14 muestran las distancias, en los tres períodos, en una matriz simétrica.
Tabla 12 Matriz de distancias 2001/2005.
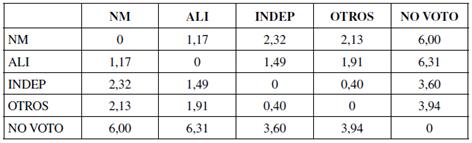
Nota: la tabla muestra el logaritmo del odds ratio entre cada par de partidos.
Fuente: elaboración propia.
Tabla 13 Matriz de distancias 2005/2009.
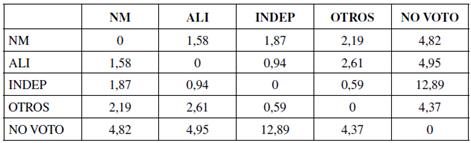
Nota: la tabla muestra el logaritmo del odds ratio entre cada par de partidos.
Fuente: elaboración propia.
Tabla 14 Matriz de distancias 2009/2013.
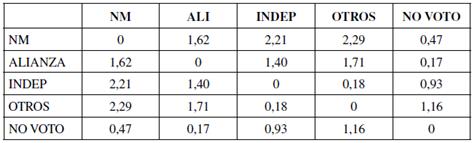
Nota: la tabla muestra el logaritmo del odds ratio entre cada par de partidos.
Fuente: elaboración propia.
En el período 2001-2005, la baja transición de votantes entre las coaliciones y el grupo NO VOTO condujo a las mayores distancias de la matriz. En el otro extremo, la distancia más baja se dio entre INDEP y OTROS explicada principalmente por la fragmentación de votos. NM y ALI se encuentran más cercanos entre sí que de las demás coaliciones. Se aprecia mayor cercanía de ALI hacia INDEP y OTROS que de NM.
El período 2005-2009 (Tabla 13) presentó patrones muy similares a los del período anterior. Nuevamente, la distancia menor se dio entre INDEP y OTROS y las mayores distancias entre todas las coaliciones y NO VOTO. Sin embargo, NM y ALI parecen haberse acercado a NO VOTO, debido a probabilidades de transición más altas, que de todas formas no resultaron estadísticamente significativas (véase Tabla 8).
Finalmente, las elecciones de 2013 mostraron la misma tónica entre coaliciones que los dos períodos anteriores. El gran punto a destacar es la abrupta caída de la distancia entre cada coalición y el grupo NO VOTO, confirmando el aumento del flujo migratorio desde y hacia este último grupo. Esto deja en evidencia una menor voluntad de votar por parte de la población.
Ubicación de las coaliciones políticas
Partiendo de las matrices de distancia, se usó escalamiento multidimensional para inferir la mejor posición de las coaliciones en un espacio bidimensional. Los resultados se presentan en las gráficas 2, 3 y 4. Mientras NM y OTROS se han movido más cerca del centro, ALI e INDEP han alternado posiciones. En los dos prime-ros períodos electorales se aprecia mayor cercanía entre las coaliciones; NM y ALI permanecen poco distantes y ambas se ubicaron más próximas al centro en las elecciones de 2009. En el último período, ALI retoma su posición de 2005 (hacia la izquierda) y se visualiza una mayor dispersión del espacio común. El grupo NO VOTO se mantiene en una ubicación muy lejana en relación con las coaliciones, pero se aprecia un leve movimiento desde la extrema derecha hacia el centro durante el año 2013.
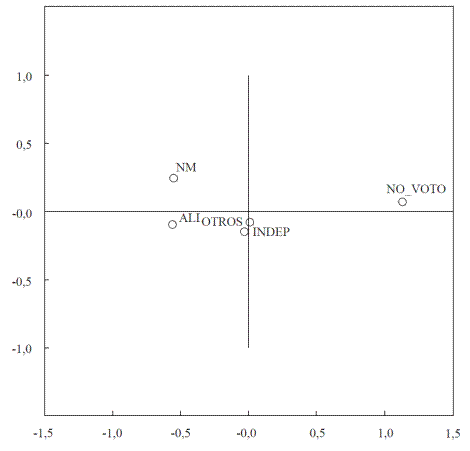
Fuente: elaboración propia con SPSS 19.
Gráfica 2 Ubicación de los partidos políticos, basada en transición de votos 2001-2005.
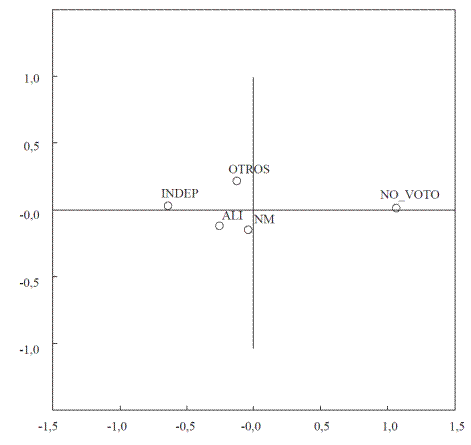
Fuente: Elaboración propia con SPSS 19.
Gráfica 3 Ubicación de los partidos políticos, basada en transición de votos 2005-2009.
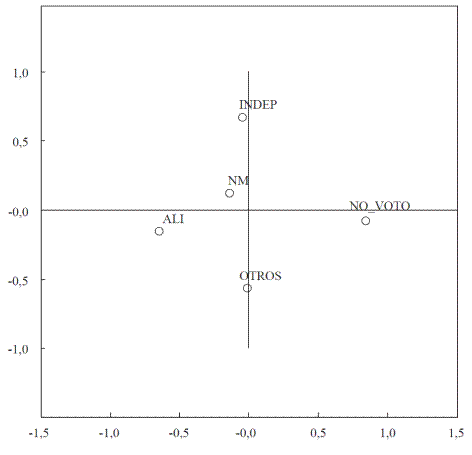
Fuente: Elaboración propia con SPSS 19.
Gráfica 4 Ubicación de los partidos políticos, basada en transición de votos 2009-2013.
Los resultados muestran que es posible estimar posiciones de coaliciones políticas desde datos electorales agregados. Las estimaciones son bastante consistentes a través de tres períodos electorales diferentes, sin mostrar movimientos significativos, y permiten apreciar cómo ha evolucionado la relación entre las coaliciones y entre estas y el grupo de no votantes.
COMENTARIOS FINALES
Este trabajo ha definido y aplicado GME para la estimación de la migración de votantes desde datos electorales agregados, y ha determinado la ubicación de coaliciones políticas en un espacio bidimensional en cuatro recientes elecciones de diputados en Chile. Los resultados obtenidos pueden ser de interés de cientistas políticos, historiadores, economistas o público en general. Dada la relativa simpleza y robustez del método, el análisis de migración de votantes y la ubicación de coaliciones podría ser incorporado en reportes electorales en Chile.
El análisis realizado en este trabajo contribuye a responder preguntas importantes sobre la dinámica electoral en Chile. La migración de votantes permite identificar algunas características importantes y hechos estilizados sobre el comportamiento de los votantes. Claramente, los resultados obtenidos son muchos más complejos que las ganancias o pérdidas netas obtenidas y esto último revela la importancia de las probabilidades de transición entre votantes y no votantes.
En concreto, la estimación del flujo migratorio de votantes permite identificar cuándo ocurre la erosión o pérdida de apoyo a los partidos y hacia dónde se dirigen aquellos votantes. Los resultados muestran con claridad que la capacidad de retener votantes desde una elección a otra ha ido cayendo en la Nueva Mayoría y en la Alianza y que el grupo más fiel es el de no votantes. Hasta antes de las elecciones de 2013, la mayoría del flujo migratorio ocurría entre la Nueva Mayoría y la Alianza, en una especie de intercambio de votantes, y desde los independientes y otros partidos hacia estos. Las coaliciones recibían pocos votos desde el grupo de no votantes, pero también las pérdidas eran pequeñas y estadísticamente no significativas, presumiblemente por la obligatoriedad de votar en votantes inscritos. Con el estreno de la Ley de Inscripción Automática y Voto Voluntario en las elecciones parlamentarias de 2013, la fidelidad de los votantes tuvo una considerable caída. Según las estimaciones, la Nueva Mayoría logró retener un 32,7% y la Alianza un 20,6% del apoyo obtenido en la elección anterior. La mayoría de flujo migratorio de votos se dirigió hacia los no votantes, que evidentemente fue el grupo de mayor crecimiento. Además de tener un impacto importante en la volatilidad del apoyo a las coaliciones, la nueva ley de votación tuvo un efecto leve aumentando la distancia entre los partidos y reduciéndola entre estos y los no votantes. Este último punto se pudo apreciar en el escalamiento multidimensional (ubicación de los partidos) realizado a partir de la matriz de distancias.
Para finalizar, la estimación del flujo migratorio de votantes puede ayudar a las coaliciones y partidos políticos a identificar hacia dónde se fueron sus votantes y cómo intentar atraerlos de nuevo. Esto puede ser muy importante, ya que gran parte del gasto electoral está dirigido a cautivar votantes de coaliciones adversarias más que hacia los no votantes, entonces, conocer la migración de votantes puede ayudar a las coaliciones a reasignar los gastos de campaña y posiblemente obtener mejores resultados electorales.
