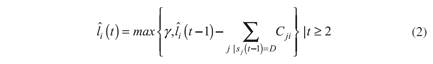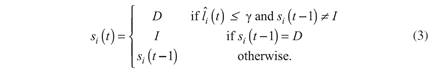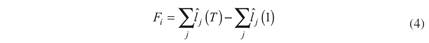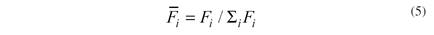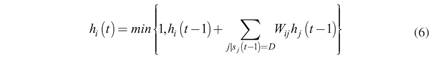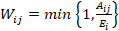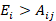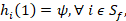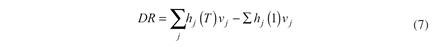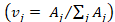INTRODUCTION
One lesson from the global financial crisis is that the soundness of each financial institution does not ensure the stability of the financial system, per se. Likewise, it has been suggested that a financial institution’s liquidity is not ensured by the liquidity position of each single institution, but that their interconnections may determine whether they are able to fulfil their short-term liquidity needs. In this sense, as Allen and Gale (2000) noted, interconnections between financial institutions determine the possibility and extent of financial contagion.
Financial institutions’ interconnections comprise direct and indirect linkages (Allen & Babus, 2009). Direct linkages are related to mutual exposures acquired in financial markets (e.g. interbank lending, securities, and foreign exchange settlements), whereas indirect linkages correspond to holding similar portfolios (as in fire-sales) or sharing the same mass of depositors (as in deposit runs). We focus on direct-linkage contagion.
Despite differing in their specific features and assumptions, most direct-linkage contagion simulation models focus on how defaults on mutual exposures may erode financial institutions’ solvency by affecting their capital buffer. From a net-work perspective, the literature related to direct-linkage contagion is composed by endogenous recovery models and exogenous recovery models.
The endogenous recovery models, as their name indicates, determine banks’ recovery rates that have been exposed to an insolvent counterparty in an endogenous way (Elsinger, Lehar, & Summer, 2006). Based on the Eisenberg and Noe (2001) model, this strand of the literature represents financial institutions as nodes connected to each other by their interbank obligations to replicate the shock transmission mechanism and assess the impacts that shocks imposed on an entity may cause to the entire financial system. Related research using a similar framework was proposed by Furfine (2003), who found that bilateral interbank exposures in the U.S. are neither large enough nor distributed in a way that cause a great risk of contagion by capital exhaustion. Very few cases of knock-on effects arise from a financial institution failing. Similarly, Upper (2011) pointed out that direct contagion based on actual interbank exposures is likely to be rare and can only happen if interbank exposures are large relative to a lender’s capital.
Several extensions have been developed using the Eisenberg and Noe (EN) model. From a theoretical point of view, Cifuentes, Ferrucci, and Shin (2005), used a similar framework to EN, and found that small shocks can trigger contagious failures via balance sheet interlinkages and asset prices. Rogers and Veraart (2013) proposed another theoretical extension considering the costs of default along with an incomplete refund of payments induced by a defaulting bank since this is precisely what can generate other collapses that may possibly end in financial contagion. From an empirical point of view, the EN model has also been considered. Elsinger, et al. (2006) included uncertainty and assessed the risk on system level using macroeconomic risk factors. Glasserman and Young (2015) modified the EN model from a clearing model to a valuation model and estimated the amplification of defaults and losses that may result from original shocks. Capponi, Chen, and Yao (2015) included the bankruptcy costs and additionally proposed a method that allows comparisons to be established between financial networks. Capponi and Chen (2015) adjusted the algorithm of the baseline network model (EN) to examine the dynamic component of systemic risk, while Capponi and Larsson (2015) analyse financial institutions’ reactions to changes in asset prices using the same framework.
The exogenous recovery models are mainly composed by default cascades models and the DebtRank method. Within default cascades models, the theoretical works of Nier, Yang, Yorulmazer, and Alentorn, (2007) and Gai and Kapadia (2010) investigate how financial systems’ structure and capitalization affect systemic risk using artificial networks. They found that contagion decreases with capitalization but increases with concentration or with the size of interbank liabilities. In terms of connectivity, they found that the relationship with contagion is non-monotonic: when connectivity is low (high), an increase in the number of links increases (decreases) the likelihood of knock-on defaults. Battiston, Gatti, Gallegati, Greenwald, and Stiglitz (2012) find that systemic risk will be reduced as long as the network density increases; while for Roukny, Bersini, Pirotte, Caldarelli, and Battiston (2013), the network topology only (but substantially) matters when financial markets are under stress (e.g. illiquid).
A recent development on direct-linkage contagion simulation models is DebtRank (Battiston, Puliga, Kaushik, Tasca, & Caldarelli, 2012a). Inspired by feedback centrality, DebtRank recursively measures the impact of the default of a selected financial institution on the capital buffer of financial institutions across the entire financial network. DebtRank serves to determine the size of the contagion caused by the initial default of a financial institution; it also provides an assessment of the systemic importance of each financial institution based on the severity of its impact on the system. However, unlike previous direct-linkage contagion models based on default cascade dynamics, the impact from default is not limited to those cases in which the capital buffer is exhausted: partial impact on solvency is quantified and accumulated recursively. There are some implementations of DebtRank on actual data (e.g. Battiston, Caldarelli, D’Errico, & Gurciullo, 2016; Poledna, Molina-Borboa, Martínez-Jaramillo, van der Leij, & Thurner, 2015; Tabak, Souza, & Guerra, 2013).
Most research on direct-linkage contagion focuses on the subsequent failure of other financial institutions through the exhaustion of capital buffers (a solvency issue). Nevertheless, liquidity is also a key factor. Furfine (2003) concludes that the liquidity effect, in the form of the unwillingness to lend money due to the inability to borrow, may be greater than the solvency effect in the U.S. interbank markets. Müller (2006) concludes that direct linkages affect solvency and liquidity substantially in the Swiss interbank market, and that both sufficient capital and liquidity buffers are necessary to mitigate spillovers. Cepeda and Ortega (2015) find that liquidity contagion in the Colombian large-value payment system is mitigated when considering the stock of high-quality assets available as a potential source of liquidity.
We implement a modified version of DebtRank in order to recursively measure the impact of the default of a selected financial institution on the short-term liquidity position of financial institutions across the entire interbank network. We construct the financial network based on actual interbank (i.e. non-collateralized) data from the Colombian financial market. We use the local version of the Liquidity Cover-age Ratio (LCR)1, the Liquidity Risk Indicator (IRL for its acronym in Spanish), as the initial short-term liquidity position of financial institutions. Our modified version of DebtRank allows for determining the size of short-term liquidity contagion caused by the default of a designated financial institution and for assessing the systemic importance of each of these institutions based on the severity of its impact over the short-term liquidity of the system.
Consistent with most related literature (e.g. Furfine, 2003; Roukny et al., 2013; Upper, 2011) we find that -ceteris paribus- in the Colombian interbank market the effects of contagion are not themselves a threat to the stability of the system. Unless a major -but unlikely- drop in the short-term liquidity position of all participants precedes contagion, we find that the effects of contagion are rather small. It is most likely that the small size of Colombian interbank market exposures, with respect to the short-term liquidity position of financial institutions (about 1.5% of IRL), along with the subsidiary contribution of interbank loans to liquidity exchanges between financial institutions (about 9.68%), explain why contagion effects alone are trivial.
Our results support a salient feature of the past financial crisis reported by Upper (2011): the vast majority of banking crises were followed by shocks that hit several banks simultaneously rather than domino effects from idiosyncratic failures. Our methodological proposal provides a quantitative assessment of financial institutions’ systemic importance based on their potential contagion effect on the short-term liquidity position of the remaining financial institutions across the Colombian interbank network. Moreover, based on the potential effect on the system’s liquidity, our results may provide a quantitative assessment of the liquidity that should be obtained from other available sources in case of a default by a financial institution such as collateralized borrowing (e.g. from other financial institutions or the central bank), selling financial assets, or increasing deposits. However, as our results are limited to the local interbank market, conclusions are to be weighted according to their contribution to the money market and to the size of the financial system.
METHODOLOGY
There is a rather recent interest in using network analysis in finance and economics, which places great emphasis on systemic risk and financial stability. Using this approach, financial institutions are nodes that participate in a system (e.g. large-value payment, securities settlement) or market (e.g. interbank, derivatives), that have exposures or payments as their links. In a formal setting, financial institutions as well as their connections are represented in a network of mutual claims or flows, with elements arranged in a squared and potentially non-symmetric matrix (i.e. non-reciprocal) that has elements in the main diagonal equal to zero due to self-connections’ absence or lack of economic interest.
Several methods or measurements belonging to the realm of network analysis have been used to assess the extent to which a default or failure-to-pay by a financial institution may affect others in a network environment. A natural choice is to use centrality measures as proxies for financial institutions’ systemic importance, and to use these measures to estimate their contagion potential in the network being analysed.
FROM CENTRALITY TO DEBTRANK
The simplest measures of centrality, namely degree centrality and strength centrality, corresponding to the number of links and their weight, are not particularly useful for quantifying contagion dynamics. They are local (non-global) measures of centrality (i.e. non-adjacent nodes are not considered), thus they do not allow to estimate impacts on a network-wide level. Path dependent centrality measures, namely closeness centrality and betweenness centrality, may take into account non-adjacent nodes by calculating how far nodes are in terms of the number of links that compose the shortest paths between them, and the fraction of those shortest paths that run through each node, respectively. However, measuring centrality based on the shortest path between financial institutions may be difficult to interpret in a financial contagion context (see Soramäki & Cook, 2013).
Feedback centrality refers to all those measures in which the centrality of a node depends recursively on the centrality of the neighbours (Battiston, Puliga, Kaushik, Tasca, & Caldarelli, 2012b). The simplest measure of feedback centrality is eigenvector centrality (Bonacich, 1972), whereby the centrality of a node is proportional to the sum of the centrality of its adjacent nodes. Thus, the eigenvector centrality of a financial institution is the weighted sum of all other financial institutions’ centrality at all possible order adjacencies (see Newman, 2010). Eigen-vector centrality’s analytical value to measure contagion dynamics is illustrated by Soramäki and Cook (2013), who depict eigenvector centrality as the proportion of time spent visiting each node during an infinite random walk through the network. Other popular feedback centrality measures based on eigenvector centrality are PageRank (Brin & Page, 1998), which is the algorithm behind Google’s search engine; hub centrality and authority centrality (Kleinberg, 1998); and SinkRank (Soramäki & Cook, 2013).
All feedback centrality measures share a common drawback when applied to contagion dynamics: in the presence of a cycle (i.e. a loop) in the network there is an infinite number of reverberations of a node’s impact on the others and back to itself, which impedes simple and measurable economic interpretations (Battiston et al., 2012a). That is, despite them being useful by providing relative measures (i.e. scores) of the importance of each node, feedback centrality measures fall short when a monetary value of contagion size is required.
DebtRank (Battiston et al., 2012a) is a centrality measure inspired by feedback centrality that overcomes this drawback by not allowing an infinite number of reverberations through the network. By excluding walks in which one or more links are repeated, it has a measurable economic interpretation (see Appendix 1). As defined by Poledna et al. (2015), it is a quantity that measures the fraction of the total economic value in the financial network that is potentially affected by the distress of an individual node or a set of nodes. Moreover, DebtRank also accounts for the fact that when a default does not propagate in the form of a subsequent default, there is still a contagion effect in the form of a reduction in the robustness (i.e. solvency) of those directly affected and potentially in the robustness of the entire network. These two features allow DebtRank to provide a simple and economically meaningful measurement of the size of the contagion dynamics following the default of a designated financial institution and a forthright measurement of its systemic importance.
Our methodological approach to determine the size of contagion caused by the default of a financial institution in an interbank exposures network is closely related to DebtRank. However, our approach does not rely on how the exposure among financial institutions may affect their capital buffer (i.e. a solvency issue) in case of a default by a designated financial institution but on how it may affect their short-term liquidity. Hence, in our case, we measure the depletion of short-term liquidity when financial institutions face failure-to-pay by a participant of the interbank claims network. A straightforward by-product is assessing the systemic importance of financial institutions in the local interbank market.
THE INPUTS
Two main inputs are used in our approach: a proxy for the short-term liquidity of financial institutions participating in the interbank market and the actual network of interbank financial claims.
The first input, a proxy for the estimated short-term liquidity position of the i-financial institution (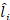 ), is our individual measurement of financial robustness -instead of a proxy for solvency. We use the coverage provided by financial institution i’s high-quality liquid assets to meet the estimated net liquidity requirements for a 7-day horizon (IRL) as reported by local financial institutions to the Colombian Financial Superintendency. Hence,
), is our individual measurement of financial robustness -instead of a proxy for solvency. We use the coverage provided by financial institution i’s high-quality liquid assets to meet the estimated net liquidity requirements for a 7-day horizon (IRL) as reported by local financial institutions to the Colombian Financial Superintendency. Hence, 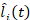 denotes the estimated short-term liquidity position of financial institution iat time t.
denotes the estimated short-term liquidity position of financial institution iat time t.
The calculation of the high-quality liquid assets and the estimated net liquid requirements for regulatory purposes in the Colombian case is intricate and has several non-linear features (see Annex 1 - Circular Externa 017 de 2014 of the Colombian Financial Superintendency). Nevertheless, for analytical purposes, we use the reported value of the expected short-term liquidity position (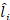 ) as a proxy of the short-term liquidity position of each financial institution, and we affect it in a linear manner: for example, not collecting $1 in interbank loans due to counterparty’s default will decrease the short-term liquidity position by $1. This simplification not only allows a generalized version of the algorithm to be designed, but it also makes changes in liquidity tractable, while preserving the analytical substance of the model.
) as a proxy of the short-term liquidity position of each financial institution, and we affect it in a linear manner: for example, not collecting $1 in interbank loans due to counterparty’s default will decrease the short-term liquidity position by $1. This simplification not only allows a generalized version of the algorithm to be designed, but it also makes changes in liquidity tractable, while preserving the analytical substance of the model.
The second main input in our approach is a directed weighted network in which nodes represent financial institutions participating in the interbank market with links representing non-collateralized financial claims. Let C be the weighted matrix representing the network of interbank claims, with C ij containing the outstanding amount that financial institution i owes to j.
If financial institution i is unable to refund an interbank loan to j, then j faces an unexpected reduction of its robustness, 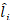 . It is an unexpected reduction because j could not anticipate i’s failure to pay when estimating its short-term liquidity position; that is, j had estimated its short-term liquidity position under the assumption that i would fulfil its commitment to refund. The unexpected reduction in short-term liquidity faced by i’s counterparties (i.e. the system) is Ci= Σj Cij. As bankruptcy procedures may be rather lengthy (see Battiston et al., 2012b; Tabak et al., 2013), we assume that in the short-run there are no recoveries of any losses. Likewise, as netting in interbank borrowing is not a common practice in the local market, we also assume that no netting of claims is available2.
. It is an unexpected reduction because j could not anticipate i’s failure to pay when estimating its short-term liquidity position; that is, j had estimated its short-term liquidity position under the assumption that i would fulfil its commitment to refund. The unexpected reduction in short-term liquidity faced by i’s counterparties (i.e. the system) is Ci= Σj Cij. As bankruptcy procedures may be rather lengthy (see Battiston et al., 2012b; Tabak et al., 2013), we assume that in the short-run there are no recoveries of any losses. Likewise, as netting in interbank borrowing is not a common practice in the local market, we also assume that no netting of claims is available2.
THE DYNAMICS
Whenever financial institution i fails to pay j the outstanding amount Cij at moment t, the liquidity position of j is unexpectedly affected: 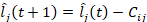 . The aftermath of the updated short-term liquidity position of j depends on the choice of a short-term liquidity threshold that allows j to be considered as imposing (or not) a significant risk for the system. Let γ be this short-term liquidity threshold, j fails to pay its counterparties as a consequence of the failure of i to refund the outstanding amount Cij whenever
. The aftermath of the updated short-term liquidity position of j depends on the choice of a short-term liquidity threshold that allows j to be considered as imposing (or not) a significant risk for the system. Let γ be this short-term liquidity threshold, j fails to pay its counterparties as a consequence of the failure of i to refund the outstanding amount Cij whenever 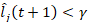 . In such case, j defaults (i.e. it is unable to pay), and the process continues recursively. On the other hand, if
. In such case, j defaults (i.e. it is unable to pay), and the process continues recursively. On the other hand, if 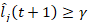 j is affected but it does not default: j is able to fulfil its commitments to refund its counterparties, but its short-term liquidity position and that of the entire system have decreased (i.e. the robustness of j means the system has weakened).
j is affected but it does not default: j is able to fulfil its commitments to refund its counterparties, but its short-term liquidity position and that of the entire system have decreased (i.e. the robustness of j means the system has weakened).
A natural choice for the short-term liquidity threshold is γ=0. A financial institution i with a short-term liquidity position below zero may be considered to be on the limit of failing to fulfil its immediate commitments to pay: liquidating the stock of high-quality liquid assets would not suffice to face estimated short-term net liquidity requirements. Technically speaking this does not mean that i is in default or that it is unable to pay; it may still be able to get new funds from financial institutions or the central bank in order to roll-over existing loans or to increase deposits. Nonetheless, 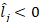 is a rather clear signal of substantial exposure to a potential liquidity risk, and it should force certain actions from the financial institution. Hence, for analytical purposes, we set γ=0 to determine the tipping point of the default cascade, which is the threshold that determines the transition from undistressed to distressed3.
is a rather clear signal of substantial exposure to a potential liquidity risk, and it should force certain actions from the financial institution. Hence, for analytical purposes, we set γ=0 to determine the tipping point of the default cascade, which is the threshold that determines the transition from undistressed to distressed3.
Formally, analogous to DebtRank, the dynamics are as follows: 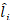 is the short-term liquidity position of financial institution i, which is a continuous variable with
is the short-term liquidity position of financial institution i, which is a continuous variable with 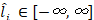 . si is a discrete variable with three possible states, undistressed (U), distressed (D), and inactive (I), corresponding to institutions able, currently unable (i.e. in default), and already unable (i.e. defaulted earlier or with
. si is a discrete variable with three possible states, undistressed (U), distressed (D), and inactive (I), corresponding to institutions able, currently unable (i.e. in default), and already unable (i.e. defaulted earlier or with 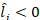 ) to refund their interbank loans, respectively (
) to refund their interbank loans, respectively (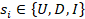 ). Let
). Let 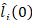 denote the actual value of
denote the actual value of 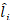 (i.e. the reported IRL), x be the set of financial institutions unable to pay (i.e. distressed or inactive) at t=1, and γ the selected short-term liquidity threshold that determines the ability to pay. The initial conditions (t=1) are4:
(i.e. the reported IRL), x be the set of financial institutions unable to pay (i.e. distressed or inactive) at t=1, and γ the selected short-term liquidity threshold that determines the ability to pay. The initial conditions (t=1) are4:
At a later stage (i.e. t ≥ 2), the dynamics of 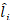 and Si are determined by the specification below (in (2) and (3)). As usual, the dynamics depend on the initial conditions, namely the initial allocation of robustness (
and Si are determined by the specification below (in (2) and (3)). As usual, the dynamics depend on the initial conditions, namely the initial allocation of robustness (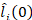 ), the structure of the interbank claims network (C
ij
), and the initial choice of financial institutions in distress (x). The key in the dynamics is that the sum in (2) (i.e. the liquidity impact) arises from those j financial institutions that entered in distress during the preceding period (i.e. those j that are neither undistressed nor inactive).
), the structure of the interbank claims network (C
ij
), and the initial choice of financial institutions in distress (x). The key in the dynamics is that the sum in (2) (i.e. the liquidity impact) arises from those j financial institutions that entered in distress during the preceding period (i.e. those j that are neither undistressed nor inactive).
and
The process continues recursively, and it is repeated for each financial institution that has commitments to refund. The process for each i-financial institution stops at time T when all financial institutions are either inactive or undistressed (i.e. no distressed institutions pending to impact the system). The measurement of the distress (in (4)) caused by the set x is the change in the overall short-term liquidity position of the system from t=1 to T. If x is a single financial institution, such change is denoted F
i
, and it gauges the impact of that i-financial institution in the system’s ability to pay as measured by the variation in the short-term liquidity position of its counterparties (i.e. the initial distress in x is not considered). In this case, the nominal value of F
i
and its contribution to all financial institutions’ impact (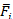 ) are, respectively,
) are, respectively,
As expected, F
i
and 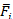 provide a straightforward assessment of the systemic importance of financial institution i in the interbank funds market. The higher the distress caused by a financial institution in the robustness of its counterparties (i.e. their short-term liquidity position), the greater its systemic importance in the interbank funds market.
provide a straightforward assessment of the systemic importance of financial institution i in the interbank funds market. The higher the distress caused by a financial institution in the robustness of its counterparties (i.e. their short-term liquidity position), the greater its systemic importance in the interbank funds market.
As pointed out by Tabak et al. (2013), it should be noted that adding the systemic importance of all financial institutions into a single figure (F= Σ i F i ) may not be considered a measurement of systemic risk or the financial system’s impact. As this is the sum of financial institutions’ individual potential stress, it should be considered a proxy for financial system’s stress. As usual, measuring systemic risk would require multiplying the size of the individual potential stress (F i ) by the probability of its occurrence over a determined time horizon (as in Poledna et al., 2015; and Tabak et al., 2013).
THE DATA
Interbank exposures in C are estimated by implementing Furfine’s algorithm (Furfine, 1999) using data from the Colombian large-value payment system (see León, Cely, & Cadena, 2016). Daily interbank exposures networks are available with daily frequency for the April 1, 2013 - December 30, 2014 period (i.e. 428 observations). During this period, 33 financial institutions participated in the market5. Despite many other types of financial institutions being authorized to borrow and lend in the interbank funds market (e.g. investment funds, broker-dealer firms), actual participants are credit institutions only. As usual in non-collateralized funds markets around the world, most loans have a low time-to-maturity at inception: 78.9% are overnight loans with an average maturity of about 2.6 calendar days.
Figure 1 exhibits a graph representing C for a randomly selected date. Nodes represent financial institutions, with their height (width) corresponding to financial institutions’ contribution to the total value of claims as a lender (borrower). The direction of the arrows represents the existence of an interbank claim (i.e. from the lender to the borrower), whereas their width represents its contribution to the total value of claims in the system. Interbank exposures in C allow us to follow the path of direct linkages considered by the algorithm.
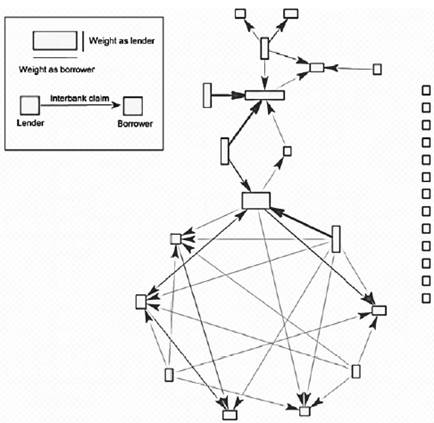
Nodes (in rectangles) correspond to participating financial institutions. The height (width) of each node corresponds to its contribution to the total claims of the market as a lender (borrower). The direction of the arrows represents the existence of an interbank claim (i.e. from the lender to the borrower), whereas their width represents its contribution to the total value of claims in the system. Non-connected nodes (in the right border of the graph) correspond to financial institutions without outstanding lent or borrowed amounts in the selected date. Source: León et al. (2016).
Figure 1 Interbank claims network for a randomly selected date
The proxy variable we use for the short-term liquidity position is the 7-day IRL calculated by the Colombian Financial Superintendency based on reports from financial institutions. This indicator, which measures financial institutions’ liquidity risk, is available on a weekly basis (each Friday) from January 4, 2013 to December 26, 2014 (i.e. 104 observations)6. As the proxy for the short-term liquidity position has the lowest frequency (i.e. weekly) and the least number of observations, this variable determines the period and the frequency of data used in the exercise. Thus, the sample period goes from April 5, 2013 to December 26, 2014, which corresponds to 90 weekly observations (n = 90).
In Colombia, the short-term liquidity position (7-day IRL) exceeds the interbank (i.e. non-collateralized) exposures by two orders of magnitude (see Table 1). The mean (and maximum) interbank exposure is about 1.5% the mean (and maximum) short-term liquidity position. This is expected because the size of the local inter-bank funds market is rather small. Most liquidity exchanges between financial institutions in the money market consists of collateralized lending in the form of sell/buy backs (i.e. simultáneas) and repos, with the interbank (i.e. non-collateralized) market contributing with about 9.68% of the total (see Banco de la República, 2015)7. Despite the size of the interbank exposures appearing to be negligible and incapable of resulting in sizeable liquidity contagion, examining how the short-term liquidity position is affected is relevant for analytical purposes.
Table 1 Descriptive Statistics for Interbank Exposures and Short-Term Liquidity Position Datasets
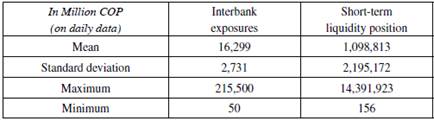
Measured in millions of Colombian pesos (COP) and based on daily data for the 90 days being analysed. The short-term liquidity position exceeds the interbank exposures by two orders of magnitude. Only data with values greater than zero were used to estimate the statistics.
Source: Authors’ calculations.
Other research works do not limit their analysis to non-collateralized borrowing as we do. For instance, it is unclear whether Battiston et al. (2012a) distinguish between collateralized or non-collateralized investments (i.e. funding) among financial institutions. However, in the case of collateralized funding (e.g. repos, sell/buy backs) the default would be followed by a rather swift process of liquidating and collecting the cash value of the pledged collateral, thus rendering direct contagion as an unlikely outcome. Consequently, despite collateralized borrowing could make contagion effects sizeable, they should have a negligible impact on our examination of direct contagion: the main impact arising from a default (i.e. principal risk) is minimized by pledged collateral8. The same argument applies for foreign exchange and securities transactions that are settled under exchange-for-value arrangements (e.g. delivery-versus-payment).
Accordingly, instead of including collateralized funding or exchange-for-value transactions to magnify and examine the dynamics of liquidity contagion under debatable assumptions, we consider short-term illiquidity scenarios. We choose to examine the dynamics of liquidity contagion following an ex-ante generalized reduction in the short-term liquidity position equivalent to a fraction of the observed short-term liquidity position (IRL). Let П be a fraction (П Є [0,0.99]), and Î Π is the short-term liquidity scenario after a drop of Π x Î, with Î Π =(1-Π ) Î. We expect that illiquidity scenarios, consisting in reducing the short-term liquidity position of financial institutions, will reveal how the dynamics of liquidity contagion may occur in a hypothetical stress setup9.
MAIN RESULTS
We choose to examine the dynamics of liquidity contagion following an ex-ante generalized reduction in the short-term liquidity position. 100 scenarios are selected, starting with a base scenario consisting of a null reduction (Î Π=0=1.00Î). This is a scenario consisting of a short-term liquidity reduction equivalent to 99% of observed IRL (Î Π=.99=0.01Î) with 1% increases (Π =0,0.01,0.02,…0.99). We expect the first scenario (Π = 0) to show slight contagion effects -if any. Regarding the other 99 scenarios, we expect results to be monotonically increasing in the size of the reduction in short-term liquidity: the higher Π (i.e. the size of ex-ante liquidity reduction), the higher the contagion effects.
First, we report the effect of contagion. For each day and scenario, we examine the average and maximum change in the short-term liquidity position of the system and the number of financial institutions defaulting as a result of contagion. Second, as we are concerned about financial institutions’ systemic importance, we report how designated individual financial institutions contribute to the contagion effect estimated for each day and illiquidity scenario.
CONTAGION EFFECTS
Figure 2 shows the average contagion effects. Each (blue) line in Figure 2 corresponds to one of the 90 n-day estimated average contagion effects initiated by all financial institutions with outstanding claims in the interbank market. That is, lines display the average percent drop in a financial system’s short-term liquidity (y-axis) as a function of the selected illiquidity scenario (Î Π=0,0.1,0.02,… 0.99). The bold (red) line is the average of the 90 lines.
As expected, the average contagion effect monotonically increases. In terms of the average contagion effect for the base case scenario (Î Π=0=1.00Î), effects are bound to a rather negligible reduction in short-term liquidity: between 0.00% and 0.11%. The greatest n-day average contagion effect in our sample is equivalent to a reduction of about 5.90% in short-term liquidity; however, this occurs in the worst-case scenario(Î Π=.99=0.01Î) It is straightforward that average contagion effects in short-term liquidity become relevant only after extreme illiquidity scenarios are considered (e.g. Î Π>.80)
Studying the average contagion may hinder identifying interesting effects in net-works that are characterized by an inhomogeneous connective structure. It is well-documented that most real-world networks are inhomogeneous and have particularly skewed distributions of their connections (i.e. degree) and their weights, allegedly following a power law distribution in the form of a scale-free network. Actual financial networks have also been characterized as particularly skewed, either following a power-law distribution of linkages (see Bech & Atalay, 2010; Boss, Elsinger, Summer, & Thurner, 2004; Inaoka, Ninomiya, Tanigushi, Shimizu, & Takayasu, 2004; Soramäki, Bech, Arnold, Glass, & Beyeler, 2007) or some other type of skewed distribution (see Craig & von Peter, 2014; Fricke & Lux, 2014; and Martínez-Jaramillo, Alexandrova-Kabadjova, Bravo-Benítez, & Solórzano-Margain, 2012). In the Colombian case, actual financial networks -including interbank networks- have been characterized as approximately following a power-law distribution of linkages and their weights (see Cepeda, 2008; León & Berndsen, 2014; and León, Machado, & Sarmiento, 2018).
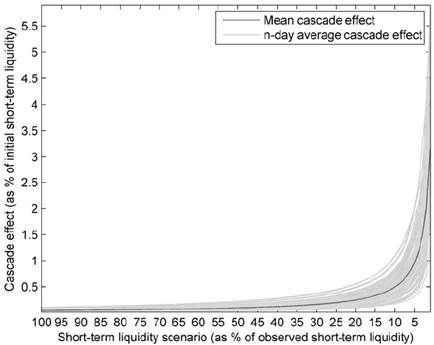
Each line corresponds to one of the 90 n-day estimated average contagion effects caused by all financial institutions with outstanding claims in the interbank market (y-axis) as a function of the selected scenario (Î Π=0,0.1,0.02,… 0.99). The bold line is the average of the 90 lines. Source: Authors’ calculations.
Figure 2 Average Contagion Effects
Consequently, by focusing on the average effect, we are implicitly relying on the existence of a typical financial institution. This is a misleading approach due to the well-documented heterogeneous distribution of linkages and their weights among institutions participating in financial networks. As it is advisable to study extreme cases in particularly heterogeneous systems -such as financial systems-, Figure 3 exhibits the maximum contagion effects.
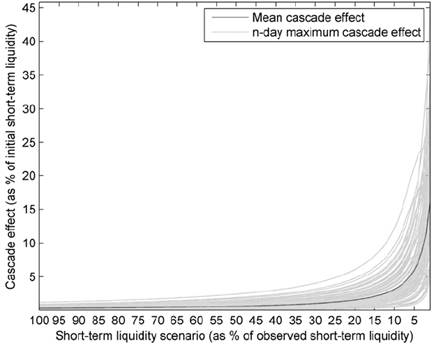
Each line corresponds to one of the 90 n-day estimated maximum contagion effects caused by all financial institutions with outstanding claims in the interbank market (y-axis) as a function of the selected scenario (Î Π=0,0.1,0.02,… 0.99). The bold line is the mean of the 90 lines. Source: Authors’ calculations.
Figure 3 Maximum Contagion Effects
Maximum contagion effect also increases monotonically. The maximum contagion effect for the base case scenario (Î Π=0=1.00Î) is bound to a reduction in short-term liquidity between 0.00% and 1.21%, which is -once more- rather negligible. The greatest n-day maximum contagion effect in our sample is equivalent to a short-term liquidity reduction of about 45.78%, but it occurs -again- only after a rather extreme and very unlikely illiquidity scenario (Î Π=.99=0.01Î)
Figure 4 compares the distribution of the average and maximum contagion effects for all financial institutions and all illiquidity scenarios. Similarly to the previous situation, the average contagion effect is negligible, below 6% of the initial short-term liquidity for any financial institution or illiquidity scenario. The distribution of the maximum contagion effects displays sizeable reductions in short-term liquidity, but they correspond to extreme illiquidity scenarios that appear to be implausible at best10.
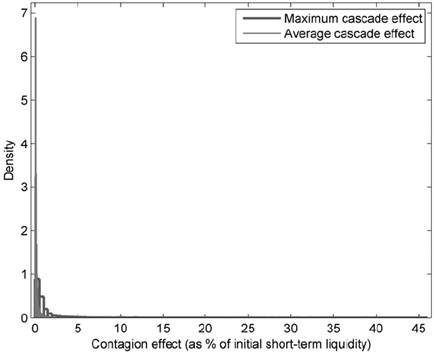
The average contagion effect is negligible, below 3% of the initial short-term liquidity for any financial institution or illiquidity scenario. The distribution of the maximum contagion effects displays sizeable reductions in short-term liquidity, but they correspond to extreme illiquidity scenarios that appear to be implausible at best. Source: Authors’ calculations.
Figure 4 Distribution of Average and Maximum Contagion Effects
The time-series dynamics of potential contagion effects may be illustrative for monitoring purposes by financial authorities. For instance, tracking the dynamics of the average and maximum contagion effect for the base scenario (Î Π=0=1.00Î) may help to identify changes in the potential outcomes of a default for the interbank market, and the potential liquidity needs that the system may face in such event. Correspondingly, Figure 5 presents the dynamics of the estimated average and maximum contagion effects throughout the sample in the absence ex-ante liquidity reductions. Consistent with previous results, in the base case scenario, the interbank market would face an average drop in short-term liquidity of between 0.00%-0.11%, whereas the maximum drop would be between 0.00%-1.21%. Once again, contagion in this type of base case scenario appears to be minor, but their time-series dynamics may be worth monitoring by financial authorities.
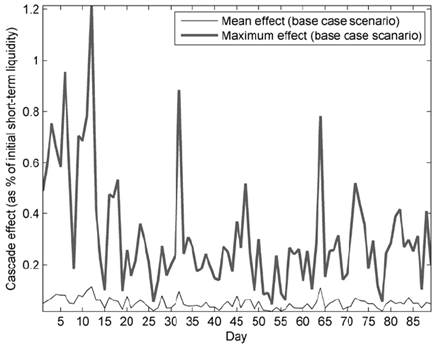
This figure displays the average and maximum contagion effect arising from the default of a financial institution for each day in the sample in the base case scenario (Î Π=0=1.00Î) Consistent with previous results, in this scenario, the interbank market would face an average drop in short-term liquidity of between 0.00%-0.11%. The maximum drop would be between 0.00%-1.21%. Source: Authors’ calculations.
Figure 5 Contagion Effects Throughout the Sample
Estimating the effects caused by each financial institution defaulting under each illiquidity scenario for each of the 90 days in the sample yields 138,900 observations (i.e. number of days (90) times the scenarios (100) times the number of financial institutions with outstanding borrowing in the interbank market in each day). 98.97% correspond to dynamics not leading to any default; that is, irrespective of the designated default or the illiquidity scenario, subsequent defaults caused by contagion are particularly rare. As exhibited in Figure 6, 1,197 (0.86%) observations correspond to one financial institution defaulting. Cascades consisting of two, three, four, five, and six defaulting institutions are rare as well, and they are observed on 172 (0.12%), 44 (0.03%), 17 (0.01%), 3 (0.00%), and 1 (0.00%) occasions, respectively. Consequently, as expected from the size of the Colombian interbank market, contagion effects are rather minor, and they tend to occur as the illiquidity scenario becomes tougher (e.g Î П>.80).
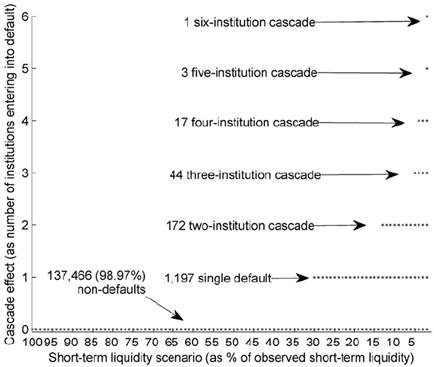
This figure displays the number of financial institutions that defaulted because of contagion dynamics (y-axis) for each one of the illiquidity scenarios (x-axis) for each of the 90 days in the sample. Each dot may represent more than one observation. Most of the observations (98.97%) correspond to no defaults. Source: Authors’ calculations.
Figure 6 Number of Financial Institutions Defaulting as a Result of Contagion
All in all, it is rather evident that contagion effects by themselves are not a threat to the stability of the system under analysis. Irrespective of the metric employed (i.e. the reduction in short-term liquidity or the number of institutions defaulting), results tend to display negligible or non-substantial contagion effects. Unless a major drop in the short-term liquidity of all participants precedes the contagion dynamics, we consistently find that the interbank network is rather robust to average events (i.e. the default of an average financial institution). Likewise, most maximum contagion events are far from substantial, whereas a major -but unlikely- drop precedes those that may be important for the short-term liquidity of all participants.
This result may be related to the size of the interbank market and its corresponding claims network. This lack of substantial contagion effects in the Colombian financial market is not limited to this study. Cepeda and Ortega (2015) also find that contagion in the Colombian large-value payment system is mitigated once high-quality assets are considered as potential sources of liquidity. Upper (2011) suggests that contagion due to exposures in the interbank loan market is an unlikely event in the sense that it happens in only a small fraction of the scenarios considered. In the same vein, Roukny et al. (2013) report that contagion effects in financial networks are not substantial if no additional sources of distress (e.g. deposit runs, fire-sales, credit runs) are considered. Battiston et al. (2015) suggest that as financial regulation recommends that financial institutions keep individual credit exposures to a manageable limit (e.g. with respect to equity or total credit exposure), it is very unlikely that a single initial financial institution’s default will trigger any other default. Therefore, our results regarding the limited impact of contagion effects on the local interbank market is an already documented trait of other financial markets.
SYSTEMIC IMPORTANCE OF FINANCIAL INSTITUTIONS
The previous section concluded that contagion effects are non-substantial. The number of financial institutions defaulting as a consequence of contagion dynamics is low, and it is a rather exceptional outcome that involves unlikely extreme illiquidity scenarios. Also, most reductions in short-term liquidity caused by contagion are non-substantial, and those that are non-negligible also involve implausible extreme illiquidity scenarios. However, examining how individual financial institutions contribute to the occurrence of defaults and the reduction in short-term liquidity may reveal important information about their systemic importance. Hence, the higher the contribution of financial institution i to defaults and short-term liquidity drops, the higher its systemic importance.
Figure 7 displays to what extent each financial institution (y-axis) contributes to the contagion-related total short-term liquidity reduction for all illiquidity scenarios. It is evident that the default of financial institution #26 contributes the most to reductions in the system’s short-term liquidity: about 14.2%. Accordingly, financial institution #26 may be easily deemed as the most systemically important for the interbank network under analysis in terms of its short-term liquidity effects. Financial institutions #24, 28, and 20 belong to a second tier of systemically important financial institutions and contribute about 8%-9% each, whereas those remaining contribute less than 7% each.
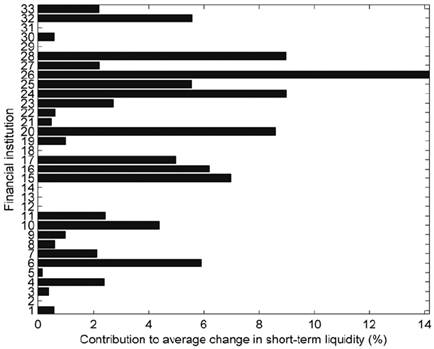
Financial institution #26’s default contributes the most to reductions in the system’s shortterm liquidity: about 14.2%. Source: Authors’ calculations.
Figure 7 Financial Institutions’ Individual Contribution to the System’s Short-Term Liquidity Reduction for All Illiquidity Scenarios
Regarding the contribution to the total number of defaults caused by contagion effects, Figure 8 shows that financial institution #24 is the most representative (21.2%), and, hence, it may be considered the most systemically important financial institution in the Colombian interbank market in terms of subsequent defaults. The second most representative financial institution is #11 (17.6%). Financial institutions #17 and 26 are part of the third tier of systemic importance, contributing about 11% and 10%, respectively. The remaining financial institutions contribute less than 6% each.
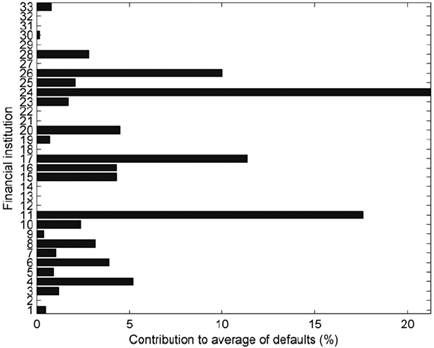
Financial institution #24’s default contributes 21.2% of the defaults. Source: Authors’ calculations.
Figure 8 Financial Institutions’ Individual Contribution to the System’s Total Defaults for All Illiquidity Scenarios
As expected when assessing financial institutions’ systemic importance, we find that the negative effects resulting from contagion are decidedly concentrated in just a few financial institutions: namely #26, 24, and 11. However, as most contagion effects portrayed here are conditional on the occurrence of major -but very unlikely- scenarios of generalized illiquidity, conclusions about the systemic importance of these financial institutions for the entire financial system may be unjustified. Furthermore, their systemic importance is bounded to the local inter-bank network, which, in the Colombian case, is not particularly representative of the whole financial system.
FINAL REMARKS
We used the DebtRank methodology (Battiston et al., 2012a) in order to examine how the default of a selected financial institution in the current Colombian inter-bank network impacts the short-term liquidity position of its counterparties and the system as a whole. Instead of focusing on the impact that default has on financial institutions’ capital buffer (i.e. their solvency), we focused on how an initial default eroded their ability to refund interbank loans (i.e. their short-term liquidity) and eventually forced them into default.
Consistent with the literature on direct-linkage financial contagion (Furfine, 2003; Roukny et al., 2013; Upper, 2011), contagion effects resulting from an initial default in the interbank market are non-substantial. Unless contagion dynamics are preceded by a major -but unlikely- drop in the short-term liquidity position of all participants, we consistently find that contagion effects on individual and system’s short-term liquidity are negligible. Our results are consistent with reported features of banking crises, which tend to be caused by shocks that hit several banks simultaneously rather than domino effects from idiosyncratic failures (see Upper, 2011). Likewise, our results concur with those reported by Roukny et al. (2013), who find that the network topology matters only when financial markets are under stress (e.g. illiquid).
The methodological contribution of our work is relevant. By modifying DebtRank to recursively measure contagion effects in the short-term liquidity position of financial institutions, we supplement financial authorities’ monitoring tools. In this sense, we capture the advantages of DebtRank to conveniently measure how contagion may affect financial institutions’ ability to refund interbank loans in the short-term.
Despite the lack of systemic impact of contagion effects in the base case scenario, our results are also valuable for financial authorities. The numerical outcomes provide an economically meaningful quantitative assessment of the systemic importance of financial institutions based on their potential effect on financial institutions’ short-term liquidity. Moreover, based on the potential effect on the system’s liquidity, our results provide a quantitative assessment of the liquidity that should be obtained from other available sources in case of a default by a financial institution, such as collateralized borrowing (e.g. from other financial institutions or the central bank), selling financial assets, or increasing deposits. Nevertheless, as most contagion effects here portrayed are conditional on the occurrence of major -but unlikely- scenarios of generalized illiquidity, conclusions about the systemic importance may be unjustified. Consequently, it is important to emphasize that systemic importance resulting from this exercise is bounded to the local interbank network, which may not be particularly representative of the whole financial system in the Colombian case.
Due to the aim and scope of our research, there are several issues that should be addressed in order to enhance the examination of financial contagion in the Colombian case. For instance, as in Müller (2006), it is advisable to simultaneously examine the impact of default contagion on solvency and liquidity. Estimating how financial institutions react to their counterparties’ defaults (see Martínez & Cepeda, 2015) and incorporating such reactions in the contagion dynamics may also enrich the analytical reach of the model; additionally, it may be interesting to consider financial authorities’ reactions. Moreover, as in Tabak et al. (2013) and Poledna et al. (2015), it is imperative to articulate this type of systemic importance assessment by estimating default probabilities to assess systemic risk of financial systems’ expected impact over a determined time horizon. Furthermore, as illustrated in the multi-layer financial exposures network model by Poledna et al. (2015), it is convenient to associate different sources of exposures among financial institutions (e.g. derivatives, security cross-holdings) in order to have a comprehensive measure of direct-linkage contagion; therefore, it is likely that the non-substantial contagion effects reported here may be due to underestimating systemic impact that results from focusing on the interbank market only. Finally, it is also convenient to couple direct- (e.g. mutual exposures) and indirect-linkage (e.g. fire-sales, deposit runs, credit runs) contagion models with the aim of attaining a comprehensive measure of financial contagion.